Определения и примеры
Одночлен — это произведение чисел, переменных и степеней. Например, выражения 5a, 3ab2 и −62aa2b3 являются одночленами.
Приведём ещё примеры одночленов:
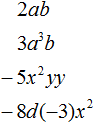
Одночленом также является любое отдельное число, любая переменная или любая степень. Например, число 9 является одночленом, переменная x является одночленом, степень 52 является одночленом.
Приведение одночлена к стандартному виду
Рассмотрим следующий одночлен:
![]()
Этот одночлен выглядит не очень аккуратно. Чтобы сделать его проще, нужно привести его к так называемому стандартному виду.
Приведение одночлена к стандартному виду заключается в перемножении однотипных сомножителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему.
Ещё один нюанс заключается в том, что в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.
Итак, приведём одночлен 3a25a3b2 к стандартному виду. В этом одночлене содержатся числа 3 и 5. Перемножим их, получим число 15. Записываем его:
15
Далее в одночлене 3a25a3b2 содержатся степени a2 и a3, которые имеют одинаковое основание a. Из тождественных преобразований со степенями известно, что при перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают. Тогда перемножение степеней a2 и a3 даст в результате a5. Записываем a5 рядом с числом 15
15a5
Далее в одночлене 3a25a3b2 содержится степень b2. Её не с чем перемножать, поэтому она остаётся без изменений. Записываем её как есть к новому одночлену:
15a5b2
Мы привели одночлен 3a25a3b2 к стандартному виду. В результате получили одночлен 15a5b2
3a25a3b2 = 15a5b2
Числовой сомножитель 15 называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.
Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице. Так, коэффициентом одночлена abc является 1, поскольку abc это произведение единицы и abc
abc = 1 × abc
А коэффициентом одночлена −abc будет −1, поскольку −abc это произведение минус единицы и abc
−abc = −1 × abc
Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.
Например, степенью одночлена 15a5b2 является 7. Это потому что переменная a имеет показатель 5, а переменная b имеет показатель 2. Отсюда 5 + 2 = 7. Показатель числового сомножителя 15 считать не нужно, поскольку нас интересуют только показатели переменных.
Ещё пример. Степенью одночлена 7ab2 является 3. Здесь переменная a имеет показатель 1, а переменная b имеет показатель 2. Отсюда 1 + 2 = 3.
Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю. Например, степень одночлена 11 равна нулю.
Не следует путать степень одночлена и степень числа. Степень числа это произведение из нескольких одинаковых множителей, тогда как степень одночлена это сумма показателей всех переменных входящих в этот одночлен. В одночлене 11 нет переменных, поэтому его степень равна нулю.
Пример 1. Привести одночлен 5xx3ya2 к стандартному виду
Перемножим числа 5 и 3, получим 15. Это будет коэффициент одночлена:
15
Далее в одночлене 5xx3ya2 содержатся переменные x и x. Перемножим их, получим x2.
15x2
Далее в одночлене 5xx3ya2 содержится переменная y, которую не с чем перемножать. Записываем её без изменений:
15x2y
Далее в одночлене 5xx3ya2 содержится степень a2, которую тоже не с чем перемножать. Её также оставляем без изменений:
15x2ya2
Получили одночлен 15x2ya2, который приведён к стандартному виду. Буквенные сомножители принято записывать в алфавитном порядке. Тогда одночлен 15x2ya2 примет вид 15a2x2y.
Поэтому, 5xx3ya2 = 15a2x2y.
Пример 2. Привести одночлен 2m3n × 0,4mn к стандартному виду
Перемножим числа, переменные и степени по отдельности.
2m3n × 0,4mn = 2 × 0,4 × m3 × m × n × n = 0,8m4n2
Числа, переменные и степени при перемножении разрешается заключать в скобки. Делается это для удобства. Так, в данном примере перемножение чисел 2 и 0,4 можно заключить в скобки. Также в скобки можно заключить перемножение m3 × m и n × n
2m3n × 0,4mn = (2 × 0,4) × (m3 × m) × (n × n) = 0,8m4n2
Но желательно выполнять все элементарные действия в уме. Так, решение можно записать значительно короче:
2m3n × 0,4mn = 0,8m4n2
Но чтобы в уме приводить одночлен к стандартному виду, тема умножения целых чисел и умножения степеней должна быть изучена на хорошем уровне.
Сложение и вычитание одночленов
Одночлены можно складывать и вычитать. Чтобы это было возможно, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути приведение подобных слагаемых, которое мы рассматривали при изучении буквенных выражений.
Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.
Пример 1. Сложить одночлены 6a2b и 2a2b
6a2b + 2a2b
Сложим коэффициенты 6 и 2, а буквенную часть 6a2b оставим без изменений
6a2b + 2a2b = 8a2b
Пример 2. Вычесть из одночлена 5a2b3 одночлен 2a2b3
5a2b3 − 2a2b3
Можно заменить вычитание сложением, и сложить коэффициенты одночленов, оставив буквенную часть без изменения:
5a2b3 − 2a2b3 = 5a2b3 + (−2a2b3) = 3a2b3
Либо сразу из коэффициента первого одночлена вычесть коэффициент второго одночлена, а буквенную часть оставить без изменения:
5a2b3 − 2a2b3 = 3a2b3
Умножение одночленов
Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.
Пример 1. Перемножить одночлены 5x и 8y
Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:
5x × 8y = (5 × 8) × (x × y) = 40xy
Пример 2. Перемножить одночлены 5x2y3 и 7x3y2c
Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:
5x2y3 × 7x3y2c = (5 × 7) × (x2x3) × (y3y2) × c = 35x5y5c
Пример 3. Перемножить одночлены −5a2bc и 2a2b4
−5a2bc × 2a2b4 = (−5 × 2) × (a2a2) × (bb4) × c = −10a4b5c
Пример 4. Перемножить одночлены x2y5 и (−6xy2)
x2y5 × (−6xy2) = −6 × (x2x) × (y5y2) = −6x3y7
Пример 5. Найти значение выражения ![]()
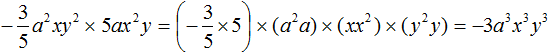
Деление одночленов
Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.
Например, разделим одночлен 8a2b2 на одночлен 4ab. Запишем это деление в виде дроби:
![]()
Первый одночлен 8a2b2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.
Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2. В исходном выражении ставим знак равенства и записываем этот коэффициент частного:
![]()
Теперь делим буквенную часть. В делимом содержится a2, в делителе — просто a. Делим a2 на a, получаем a, поскольку a2 : a = a2 − 1 = a. Записываем в частном a после 2
![]()
Далее в делимом содержится b2, в делителе — просто b. Делим b2 на b, получаем b, поскольку b2 : b = b2 − 1 = b. Записываем в частном b после a
![]()
Значит, при делении одночлена 8a2b2 на одночлен 4ab получается одночлен 2ab.
Сразу можно выполнить проверку. При умножении частного на делитель должно получаться делимое. В нашем случае, если 2ab умножить на 4ab, должно получиться 8a2b2
2ab × 4ab = (2 × 4) × (aa) × (bb) = 8a2b2
Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.
К примеру, одночлен 6xy2 нельзя разделить на одночлен 3xyz. В делителе 3xyz содержится переменная z, которая не содержится в делимом 6xy2.
Проще говоря, мы не сможем найти частное, которое при умножении на делитель 3xyz дало бы делимое 6xy2, поскольку такое умножение обязательно будет содержать переменную z, которой нет в 6xy2.
Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.
Например, при делении одночлена 4x2y2z на 2xy, получается 2xyz. Сначала разделили 4 на 2 получили 2, затем x2 разделили на x, получили x, затем y2 разделили на y, получили y. Затем приступили к делению переменной z на такую же переменную в делителе, но обнаружили, что такой переменной в делителе нет. Поэтому перенесли переменную z в частное без изменений:
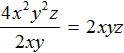
Для проверки умножим частное 2xyz на делитель 2xy. В результате должен получиться одночлен 4x2y2z
2xyz × 2xy = (2 × 2) × (xx) × (yy) × z = 4x2y2z
Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.
Так, в предыдущем примере нельзя было разделить одночлен 6xy2 на одночлен 3xyz. Но можно сократить эту дробь на одночлен 3xy. Напомним, что сокращение дроби это деление числителя и знаменателя на одно и то же число (в нашем случае на одночлен 3xy). В результате сокращения дробь становится проще, но её значение не меняется:
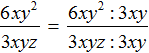
В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:
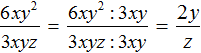
Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:
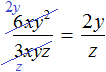
Пример 2. Разделить одночлен 12a2b3c3 на одночлен 4a2bc
![]()
Пример 3. Разделить одночлен x2y3z на одночлен xy2
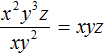
Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.
Например, разделить одночлен 2x на одночлен x2 нельзя, поскольку степень x, входящая в делимое, имеет показатель 1, тогда как степень x2, входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x2 даст в результате делимое 2x.
Конечно, мы можем выполнить деление x на x2, воспользовавшись свойством степени с целым показателем:
![]()
и такое частное при перемножении с делителем x2 будет давать в результате делимое 2x
![]()
Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное ![]() целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.
целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.
Возведение одночлена в степень
Одночлен можно возвести в степень. Для этого используют правило возведения степени в степень.
Пример 1. Возвести одночлен xy во вторую степень.
Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый сомножитель этого одночлена
(xy)2 = x2y2
Пример 2. Возвести одночлен −5a3b во вторую степень.
(−5a3b)2 = (−5)2 × (a3)2 × b2 = 25a6b2
Пример 3. Возвести одночлен −a2bc3 в пятую степень.
В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:
(−a2bc3)5 = (−1)5 × (a2)5 × b5 × (c3)5 = −1a10b5c15 = −a10b5c15
Когда коэффициент равен −1, то саму единицу не записывают. Записывают только минус и потом остальные сомножители одночлена. В приведенном примере сначала получился одночлен −1a10b5c15, затем он был заменён на тождественно равный ему одночлен −a10b5c15.
Пример 4. Представить одночлен 4x2 в виде одночлена, возведённого в квадрат.
В данном примере нужно найти произведение, которое во второй степени будет равно выражению 4x2. Очевидно, что это произведение 2x. Если это произведение возвести во вторую степень (в квадрат), то получится 4x2
(2x)2 = 22x2 = 4x2
Значит, 4x2 = (2x)2. Выражение (2x)2 это и есть одночлен, возведённый в квадрат.
Пример 5. Представить одночлен 121a6 в виде одночлена, возведённого в квадрат.
Попробуем найти произведение, которое во второй степени будет равно выражению 121a6.
Прежде всего заметим, что число 121 получается, если число 11 возвести в квадрат. То есть первый сомножитель будущего произведения мы нашли. А степень a6 получается в том случае, если возвести в квадрат степень a3. Значит вторым сомножителем будущего произведения будет a3.
Таким образом, если произведение 11a3 возвести во вторую степень, то получится 121a6
(11a3)2 = 112 × (a3)2 = 121a6
Значит, 121a6 = (11a3)2. Выражение (11a3)2 это и есть одночлен, возведённый в квадрат.
Разложение одночлена на множители
Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.
Пример 1. Разложить одночлен 3a3b2 на множители
Данный одночлен можно разложить на множители 3, a, a, a, b, b
3a3b2 = 3aaabb
Либо степень b2 можно не раскладывать на множители b и b
3a3b2 = 3aaab2
Либо степень b2 разложить на множители b и b, а степень a3 оставить без изменений
3a3b2 = 3a3bb
В каком виде представлять одночлен зависит от решаемой задачи. Главное, чтобы разложение было тождественно равно исходному одночлену.
Пример 2. Разложить одночлен 10a2b3c4 на множители.
Разложим коэффициент 10 на множители 2 и 5, степень a2 разложим на множители aa, степень b3 — на множители bbb, степень c4 — на множители cccc
10a2b3c4 = 2 × 5 × aabbbcccc
Задания для самостоятельного решения
Задание 1. Приведите одночлен −2aba к стандартному виду.
Задание 2. Приведите одночлен 0,5m × 2n к стандартному виду.
Решение:
0,5m × 2n = (0,5 × 2)(mn) = 1mn = mn
Задание 3. Приведите одночлен −8ab(−2,5)b2 к стандартному виду.
Решение:
−8ab(−2,5)b2 = −8 × (−2,5) × a × (b × b2) = 20ab3
Задание 4. Приведите одночлен 0,15pq × 4pq2 к стандартному виду.
Решение:
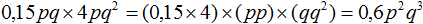
Задание 5. Приведите одночлен −2x3 × 0,5xy2 к стандартному виду.
Решение:
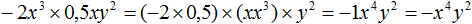
Задание 6. Приведите одночлен 2m3n × 0,4mn к стандартному виду.
Решение:

Задание 7. Приведите одночлен 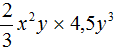 к стандартному виду.
к стандартному виду.
Решение:
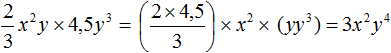
Задание 8. Приведите одночлен 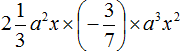 к стандартному виду.
к стандартному виду.
Решение:
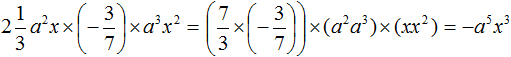
Задание 9. Перемножьте одночлены 2x и 2y
Задание 10. Перемножьте одночлены 6x, 5x и y
Решение:
6x × 5x × y = 30x2y
Задание 11. Перемножьте одночлены 2x2, 2x3 и y2
Решение:
2x2 × 2x3 × y2 = (2 × 2) × (x2x3) × y2 = 4x5y2
Задание 12. Перемножьте одночлены −8x и 5x3
Решение:
−8x × 5x3 = (−8 × 5)×(xx3) = −40x4
Задание 13. Перемножьте одночлены x2y5 и (−6xy2)
Решение:
x2y5 × (−6xy2) = −6 × (x2x) × (y5y2) = −6x3y7
Задание 14. Выполните умножение:
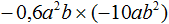
Решение:

Задание 15. Выполните умножение:
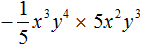
Решение:
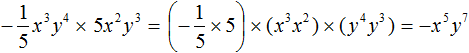
Задание 16. Возведите одночлен x2y2z2 в третью степень
Решение:
(x2y2z2)3 = (x2)3 × (y2)3 × (z2)3 = x6y6z6
Задание 17. Возведите одночлен xy2z3 в пятую степень.
Решение:
(xy2z3)5 = x5 × (y2)5 × (z3)5 = x5y10z15
Задание 18. Возведите одночлен 4x во вторую степень.
Решение:
(4x)2 = 42 × x2 = 16x2
Задание 19. Возведите одночлен 2y3 в третью степень.
Решение:
(2y3)3 = 23 × (y3)3 = 8y9
Задание 20. Возведите одночлен −0,6x3y2 в третью степень.
Решение:
(−0,6x3y2)3 = (−0,6)3 × (x3)3 × (y2)3= −0,216x9y6
Задание 21. Возведите одночлен −x2yz3 в пятую степень.
Решение:
(−x2yz3)5 = (−x2)5 × y5 × (z3)5= −x10y5z15
Задание 22. Возведите одночлен −x3y2z во вторую степень.
Решение:
(−x3y2z)2 = (−x3)2 × (y2)2 × z2 = x6y4z2
Задание 23. Представьте одночлен −27x6y9 в виде одночлена, возведённого в куб.
Решение:
−27x6y9 = (−3x2y3)3
Задание 24. Представьте одночлен −a3b6 в виде одночлена, возведённого в куб.
Задание 25. Выполните деление 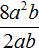
Решение:
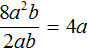
Задание 26. Выполните деление 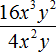
Решение:
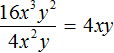
Задание 27. Выполните деление 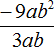
Решение:

Задание 28. Выполните деление 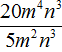
Решение:
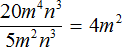
Задание 29. Выполните деление 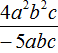
Решение:
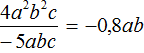
Задание 30. Выполните деление 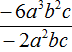
Решение:
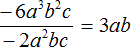
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Одночлены — это любое число, переменная, любая степень, а также произведение чисел, переменных и степеней, с которыми можно совершать разные математические действия. Примеры одночленов: 9, 52, x, 5a; 3ab2 ; −62aa2b3.
Приведение одночлена к стандартному виду
Приведение одночлена к стандартному виду заключается в умножении однотипных множителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему. Важно: в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.
Рассмотрим следующий одночлен: 3a25a3b2
— числа 3 и 5 перемножим и получим число 15,
— степени a2 и a3 имеют одинаковое основание a, поэтому мы можем записать результат a5,
— степень b2 остаётся без изменений.
Получили результат: 3a25a3b2 = 15a5b2
Для того, чтобы далее рассматривать одночлены и действия с ними, вспомним тему «Степень с натуральным показателем«
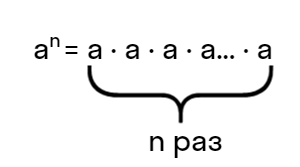
где: a — основание степени; n — показатель степени.
Коэффициент одночлена
- Числовой сомножитель (в примере 15) называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.
- Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице.
Например, для одночлена ab коэффициентом является 1, поскольку ab это произведение единицы и ab: abc = 1×ab. - Если перед одночленом стоит знак минуса, то коэффициент равен минус единице. Например, для одночлена —ab коэффициентом является -1, поскольку ab это произведение -1 и ab.
Степень одночлена
Степенью одночлена называют сумму показателей степеней всех переменных входящих в этот одночлен. Показатель числового множителя при этом не считается.
Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю.
Примеры:
- Степенью одночлена 15a5b2 является 7: переменная a имеет степень 5, а переменная b — 2. Отсюда 5 + 2 = 7. Показатель числового сомножителя 15 считать не нужно, поскольку нас интересуют только показатели переменных.
- Степенью одночлена 7ab2 является 3: переменная a имеет показатель 1, а переменная b — 2.
- Степень одночлена 11 равна нулю, так как это число.
Не следует путать степень одночлена и степень числа:
- Степень числа это произведение из нескольких одинаковых множителей.
- Степень одночлена это сумма показателей всех переменных входящих в этот одночлен.
Сложение и вычитание одночленов
Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.
Чтобы складывать и вычитать одночлены, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути представляет собой приведение подобных слагаемых.
Пример 1. Сложить одночлены 6a2b и 2a2b:
сложим коэффициенты 6 и 2, а буквенную часть 6a2b оставим без изменений.
Получим: 6a2b + 2a2b = 8a2b
Пример 2. Вычесть из одночлена 5a2b3 одночлен 2a2b3
Решение: 5a2b3 − 2a2b3 = 5a2b3 −2a2b3 = 3a2b3
Умножение одночленов
Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.
Пример 3. Перемножить одночлены 5x и 8y
Перемножим числовые и буквенные части по отдельности: 5x × 8y = (5 × 8) × (x × y) = 40xy
Пример 4. Перемножить одночлены 5x2y3 и 7x3y2c
Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:
5x2y3 × 7x3y2c = (5 × 7) × (x2x3) × (y3y2) × c = 35x5y5c
Пример 5. Перемножить одночлены −5a2bc и 2a2b4
−5a2bc × 2a2b4 = (−5 × 2) × (a2a2) × (bb4) × c = −10a4b5c
Деление одночленов
Для того, чтобы разделит один многочлен на другой, нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.
Пример 6. Разделить одночлен 8a2b2 на одночлен 4ab.
Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2.
Теперь делим буквенную часть:
— в делимом содержится a2, в делителе — просто a. Делим a2 на a, получаем a, поскольку a2 : a = a2 − 1 = a.
— в делимом содержится b2, в делителе — просто b. Делим b2 на b, получаем b, поскольку b2 : b = b2 − 1 = b. Значит, при делении одночлена 8a2b2 на одночлен 4ab получается одночлен 2ab.
Если переменная есть только в одном многочлене:
Если в делителе окажется переменная, которой нет в делимом, то деление невозможно.
Например, одночлен 6xy2 нельзя разделить на одночлен 3xyz, так как в делителе 3xyz содержится переменная z, которая не содержится в делимом 6xy2.
Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.
*сокращение дроби это деление числителя и знаменателя на одно и то же число.
Так, в примере нельзя разделить одночлен 6xy2 на одночлен 3xyz. Но можно сократить эту дробь на одночлен 3xy.
Если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.
Например, при делении одночлена 4x2y2z на 2xy, получается 2xyz.
Если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя, то деление одночлена на одночлен также невозможно.
Например, разделить одночлен 2x на одночлен x2 нельзя, поскольку степень x, входящая в делимое, имеет показатель 1, тогда как степень x2, входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x2 даст в результате делимое 2x.
Возведение одночлена в степень
При возведении степень одночлена каждый из множителей возводится в степень. Затем полученные результаты перемножаются: (a × b)n = an × bn
Пример 7. Возвести одночлен xy во вторую степень.
Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый множитель этого одночлена: (xy)2 = x2y2
Пример 8. Возвести одночлен −a2bc3 в пятую степень.
В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:
(−a2bc3)5 = (−1)5 × (a2)5 × b5 × (c3)5 = −1a10b5c15 = −a10b5c15
Когда коэффициент равен −1, то саму единицу не записывают. Записывают только минус и потом остальные множители одночлена.
Пример 9. Представить одночлен 121a6 в виде одночлена, возведённого в квадрат.
— число 121 получается, если число 11 возвести в квадрат — это первый множитель.
— степень a6 получается, если возвести в квадрат степень a3 — это второй множитель.
Таким образом, если произведение 11a3 возвести во вторую степень, то получится 121a6
(11a3)2 = 112 × (a3)2 = 121a6
Разложение одночлена на множители
Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.
Пример 10. Разложить одночлен 3a3b2 на множители
Данный одночлен можно разложить на множители:
3a3b2 = 3×a×a×a× b×b = 3×a×a×a×b2 = 3×a3×b×b
Понятие одночлена, примеры одночленов
и «не одночленов»
Рассмотри некоторые примеры:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
Найдем общие черты для приведенных выражений. Во всех трех случаях выражение является произведением чисел и переменных, возведенных в степень. На основании этого дадим определение одночлена: одночленом называют такое алгебраическое выражение, которое состоит из произведения степеней и чисел.
Теперь приведем примеры выражений, не являющихся одночленами:
4. ![]() ;
;
5. ![]() ;
;
6. ![]() ;
;
7. ![]() ;
;
Найдем отличие этих выражений от предыдущих. Оно состоит в том, что в примерах 4-7 есть операции сложения, вычитания или деления, тогда как в примерах 1-3, являющихся одночленами, этих операций нет.
Приведем еще несколько примеров:
8. ![]() ;
;
9. ![]() ;
;
Выражение под номером 8 является одночленом, так как это произведение степени на число, тогда как пример 9 не является одночленом.
Описание операции упрощения, определение понятий коэффициента и буквенной части одночлена
Теперь выясним действия над одночленами.
1.Упрощение. Рассмотрим пример №3 ![]() ;и пример №2
;и пример №2 ![]() /
/
Во втором примере мы видим только один коэффициент – ![]() , каждая переменная встречается только один раз, то есть переменная «а» представлена в единственном экземпляре, как «
, каждая переменная встречается только один раз, то есть переменная «а» представлена в единственном экземпляре, как «![]() », аналогично переменные «
», аналогично переменные «![]() » и «
» и «![]() » встречаются только один раз.
» встречаются только один раз.
В примере №3 наоборот, есть два различных коэффициента – ![]() и
и ![]() , переменную «
, переменную «![]() » мы видим дважды – как «
» мы видим дважды – как «![]() » и как «
» и как «![]() », аналогично переменная «
», аналогично переменная «![]() » встречается два раза. То есть, данное выражение следует упростить, таким образом, приходим к первому действию, выполняемому над одночленами – приведение одночлена к стандартному виду. Для этого приведем к стандартному виду выражение из примера 3, затем определим эту операцию и научимся приводить к стандартному виду любой одночлен.
» встречается два раза. То есть, данное выражение следует упростить, таким образом, приходим к первому действию, выполняемому над одночленами – приведение одночлена к стандартному виду. Для этого приведем к стандартному виду выражение из примера 3, затем определим эту операцию и научимся приводить к стандартному виду любой одночлен.
Итак, рассмотри пример:
![]()
Первым действием в операции приведения к стандартному виду всегда нужно перемножить все числовые множители:
![]() ;
;
Результат данного действия будет называться коэффициентом одночлена.
Далее необходимо перемножить степени. Перемножим степени переменной «х» согласно правилу умножения степеней с одинаковыми основаниями, в котором говорится, что при умножении показатели степени складываются:
![]() ;
;
теперь перемножим степени «у»:
![]() ;
;
Итак, приведем упрощенное выражение:
![]() ;
;
Дальше упростить данное выражение нельзя, такое выражение и называется стандартным видом исходного одночлена, где ![]() это коэффициент одночлена, а
это коэффициент одночлена, а ![]() – это буквенная часть.
– это буквенная часть.
Формулировка правила приведения одночлена к стандартному виду, решение примеров
Любой одночлен можно привести к стандартному виду. Сформулируем правило приведения к стандартному виду:
– перемножить все числовые множители;
– поставить полученный коэффициент на первое место;
– перемножить все степени, то есть получить буквенную часть;
То есть, любой одночлен характеризуется коэффициентом и буквенной частью. Забегая вперед, отметим, что одночлены, имеющие одинаковую буквенную часть, называются подобными.
Теперь нужно наработать технику приведения одночленов к стандартному виду. Рассмотри примеры из учебника:
Задание: привести одночлен к стандартному виду, назвать коэффициент и буквенную часть.
Для выполнения задания воспользуемся правилом приведения одночлена к стандартному виду и свойствами степеней.
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
Комментарии к первому примеру: Для начала определим, действительно ли данное выражение является одночленом, для этого проверим, есть ли в нем операции умножения чисел и степеней и нет ли в нем операций сложения, вычитания или деления. Можем сказать, что данное выражение является одночленом, так как вышеуказанное условие выполняется. Далее, согласно правилу приведения одночлена к стандартному виду, перемножим численные множители:
![]() – мы нашли коэффициент заданного одночлена;
– мы нашли коэффициент заданного одночлена;
Далее перемножим между собой соответствующие степени:
![]() ;
; ![]() ;
; ![]() ; то есть, получена буквенная часть выражения:
; то есть, получена буквенная часть выражения:![]() ;
;
запишем ответ: ![]() ;
;
Комментарии ко второму примеру: Следуя правилу выполняем:
1) перемножить числовые множители:
![]() ;
;
2) перемножить степени:
Переменные ![]() и
и ![]() представлены в единственном экземпляре, то есть их перемножить ни с чем нельзя, они переписываются без изменений, степень
представлены в единственном экземпляре, то есть их перемножить ни с чем нельзя, они переписываются без изменений, степень ![]() перемножается:
перемножается:
![]() ;
;
запишем ответ:
![]() ;
;
В данном примере коэффициент одночлена равен единице, а буквенная часть ![]() .
.
Комментарии к третьему примеру: аналогично предыдущим примерам выполняем действия:
1) перемножить численные множители:
![]() ;
;
2) перемножить степени:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
выпишем ответ: ![]() ;
;
В данном случае коэффициент одночлена равен «![]() », а буквенная часть
», а буквенная часть ![]() .
.
Описание операции вычисления конкретного численного значения одночлена, решение примеров
Теперь рассмотрим вторую стандартную операцию над одночленами. Поскольку одночлен это алгебраическое выражение, состоящее из буквенных переменных, которые могут принимать конкретные числовые значения, то мы имеем арифметическое числовое выражение, которое следует вычислить. То есть, следующая операция над многочленами состоит в вычислении их конкретного числового значения.
Рассмотрим пример. Задан одночлен:
![]()
данный одночлен уже приведен к стандартному виду, его коэффициент равен единице, а буквенная часть ![]()
Ранее мы говорили, что алгебраическое выражение не всегда можно вычислить, то есть переменные, которые в него входят, могут принимать не любое значение. В случае одночлена же входящие в него переменные могут быть любыми, это является особенностью одночлена.
Итак, в заданном примере требуется вычислить значение одночлена при ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Выполним действия:
![]() ;
;
Для вычисления мы воспользовались тем, что ![]() в любой четной степени равно единице.
в любой четной степени равно единице.
То есть, заданный одночлен при заданных значениях буквенных переменных будет принимать рассчитанное нами значение.
Рассмотрим еще один пример. Одночлен остается тот же самый, но значения буквенных переменных изменились:
![]() ;
;
![]() ;
;
выполним вычисление:
![]() .
.
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. Школьный помощник (Источник).
2. Google.com.ua (Источник).
3. Научная библиотека (Источник)
Рекомендованное домашнее задание
Задание 1: определить, является ли выражение одночленом:
а)![]() ; b)
; b)![]() ; c)
; c)![]() ; d)
; d)![]() ; e)
; e)![]()
Задание 2: привести одночлен к стандартному виду? Указать коэффициент и буквенную часть:
a)![]() ; b)
; b)![]() ; c)
; c)![]() ; d)
; d)![]() ; e)
; e)![]()
Задание 3: вычислить конкретное значение одночлена при заданных числовых значениях переменных:
a)![]()
b)![]()
c)![]()
Звучит страшно, но на деле все намного проще! Каждый семиклассник прошел через непонимание одночленов, потому что у него не было под рукой этой статьи!👇
Время чтения: 5 минут
Одночлен – что это?
Простыми словами одночлен – это произведение чисел, букв переменных и степеней.
Стандартный вид – это правильный и “красивый” вид одночлена. В стандартном виде одночлен выглядит так:
- Записывается числовой множитель
- Произведение одинаковых переменных записывается в виде степени
- Переменные записываются в алфавитном порядке
У каждого одночлена есть своя степень и коэффициент.
Коэффициент – число, записанное перед буквенной частью (если одночлен в стандартном виде).
Если перед буквенной частью отсутствует число, говорят, что коэффициент равен единице.
Степень одночлена – это сумма показателей степеней всех входящих в него переменных.
Пример
Давай разберем подробнее на примере📝
Тренажер
Предлагаю тебе самостоятельно попробовать решить несколько заданий по пройденной теме🥸
На этом все! Остались вопросы? Напиши о них в комментариях!👇
Обязательно подпишись на канал, чтобы не пропустить больше полезных статей!🧠
#математика #огэ #егэ #репетитор #алгебра #геометрия #одночлен #стандартныйвидодночлена #многочлен #7класс #школа #средняяшкола
Определение одночлена
Одночлен – это алгебраическое выражение, которое является произведением чисел, переменных и их степеней.
Одночленами также считают все числа, любые переменные и их степени.
Например:
Являются одночленами
Не являются одночленами
$ 5m^2 n $
$ left(frac{3}{4}right)^2 k $
$8^3$
$ -34m^7 pm^4 z$
abcde
$a^2 b+1$
$ 4(k+n)^2 $
$ 500-m^4+2m^2 $
$ 10p^2+k $
Стандартный вид одночлена – представление одночлена в виде произведения, в котором на первом месте стоит числовой множитель (коэффициент одночлена), а все остальные множители являются степенями различных переменных.
Степень одночлена – это сумма показателей всех переменных, в него входящих.
Например:
$x^2cdot23xy$ – одночлен нестандартного вида, с коэффициентом 23 и степенью 4 (x в кубе и y в первой степени);
$-frac{3}{15}a^3 b^2$ – одночлен стандартного вида, с коэффициентом $left(-frac{3}{15}right)$ и степенью 5 (a в кубе и b в квадрате);
9 – одночлен стандартного вида, с коэффициентом 9 и степенью 0;
a – одночлен стандартного вида, с коэффициентом 1 и степенью 1.
Число 0, а также одночлены, тождественно равные нулю (например, $0 cdot x^3, 0cdot mn$), называются нуль-одночленами. Считают, что нуль-одночлен степени не имеет. Одночлены с одинаковой буквенной частью (например, $2ab^3 c^2 и -frac{7}{5}ab^3 c^2$) называются подобными.
Приведение одночлена к стандартному виду
Любой одночлен можно преобразовать так, чтобы получился одночлен стандартного вида.
Алгоритм приведения одночлена к стандартному виду
- Определить коэффициент одночлена: перемножить все числовые множители и записать результат первым множителем.
- Используя свойства степеней, найти общую степень для каждой из переменных одночлена.
Если в одночлен в качестве множителей входят несколько переменных, их принято записывать по алфавиту. Но это не является обязательным.
Примеры
Пример 1. Преобразуйте выражение в одночлен стандартного вида, найдите его коэффициент и степень:
а) $ frac{1}{2}x^5y^4c cdot (-5xy^2 c^3) = frac{1}{2} cdot (-5) cdot c^{1+3} cdot x^{5+1} cdot y^{4+2} = -2,5c^4 x^6 y^6 $
коэффициент (-2,5), степень 4+6+6 = 16
б) $ -(3m^4)^2 cdot (-m^3 kp)^3 = -3^2 cdot (-1)^3 cdot k^3 cdot m^{8+9} cdot p^3 = 9k^3 m^17 p^3 $
коэффициент 9, степень 3+17+3 = 23
в) $ (-2)^3 xy cdot 1,5(x^4 y)^2 = -8 cdot 1,5 cdot x^{1+8} cdot y^{1+2} = -12x^9 y^3 $
г) $ (8m^3 )^2 n^3 cdot frac{1}{(4mn)^3} = frac{8^2 m^6 n^3}{4^3 m^3 n^3} = frac{(2^3)^2}{(2^2)^3} cdot frac{m^6}{m^3} cdot frac{n^3}{n^3} = m^3$
коэффициент 1, степень 3
Пример 2. Запишите одночлен в стандартном виде и найдите его числовое значение:
а) $ frac{1}{2} xycdot frac{1}{4}x^2 при x = 2, y = 3 $
$ frac{1}{2}xy cdot frac{1}{4}x^2 = frac{1}{2} cdot frac{1}{4} cdot x^{1+2}cdot y = frac{1}{8} x^3 y $
Подставляем: $ frac{1}{8}cdot2^3cdot3 = 3 $
б) $ (-2a^2 b^3) cdot left(frac{0,5}{ab}right)^2 при a = 73,b = 3 $
$ (-2a^2 b^3) cdot left(frac{0,5}{ab}right)^2 = -2 cdot frac{1}{2}^2 cdot frac{a^2}{a^2} cdot frac{b^3}{b^2} = -frac{1}{2}b $
Подставляем: $ -frac{1}{2}cdot3 = -1,5 $
Пример 3. Представьте выражение в виде квадрата одночлена:
а) $ 16x^4 y^2 z^6 = 4^2cdot(x^2 )^2cdot y^2cdot(z^3 )^2 = (4x^2 yz^3 )^2 $
б) $ frac{49}{64}x^{12} y^4 z^{16} = (frac{7}{8} x^6 y^2 z^8 )^2 $
Пример 4*. Известно, что $ 5a^2 b^3 = 7$. Найдите значение выражения $ -frac{4}{49} a^6 b^9 $
Выразим произведение переменных через число: $ a^2 b^3 = frac{7}{5} $
Преобразуем выражение:
$$ -frac{4}{49} a^6 b^9 = -frac{4}{49} left(underbrace{a^2 b^3}_{=7/5text{}}right)^3 = -frac{4}{7^2} cdot left(frac{7}{5}right)^3 = -frac{4}{5^3} cdot frac{7^3}{7^2} = -frac{28}{125} $$
Ответ: $ -frac{28}{125} $
