Математика 6 класс
ЗАДАЧИ НА НАХОЖДЕНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
1. Расстояние между двумя селами 24км. За первую неделю бригада заасфальтировала этого расстояния. Сколько километров осталось заасфальтировать?
2. На ветке сидело 12 птиц, их числа улетело. Сколько птиц осталось сидеть на ветке?
3. В классе 32 учащихся, всех учащихся каталось на лыжах. Сколько учащихся не каталось на лыжах?
4. Велосипедисты за два дня проехали 48км. В первый день они проехали всего пути. Сколько километров они проехали во второй день?
5. Папа, имея 3500 руб., потратил своих денег. Сколько денег у него осталось?
6. В тетради 24 страницы. Записи занимают числа всех страниц тетради. Сколько в тетради чистых страниц?
7. Автотуристы за три дня проехали 360 км. В первый день они проехали , а во второй день –
всего пути. Сколько километров проехали автотуристы в третий день?
8. В драмкружке занимается несколько мальчиков и 24 девочки. Число мальчиков составляет числа девочек. Сколько всего учащихся занимается в драмкружке?
9. Какова сумма денег, если 12 руб., составляют имеющейся суммы?
10. За первую неделю бригада заасфальтировала 15 км, что составило расстояния между двумя селами. Каково расстояние между селами?
11. Определите длину отрезка, которого имеют длину 15 см.
12. Сыну 10 лет. Его возраст составляет возраста отца. Сколько лет отцу?
13. Дочери 12 лет. Её возраст составляет возраста матери. Сколько лет матери?
14. За 1ч автобус проходит всего расстояния. За сколько часов он пройдет все расстояние?
15. Мальчик за 10мин прочитал всей книги. За какое время он может прочитать всю книгу?
16. В классе 18 мальчиков и 16 девочек. мальчиков и
девочек занимаются в литературном кружке. Сколько учащихся занимается в литературном кружке?
17. У машинистки 120 листов бумаги. Она использовала сначала всех листов, а потом
оставшихся. Сколько всего листов бумаги использовала машинистка?
18. Когда для компота нарезали всех яблок, то осталось еще 4 яблока. Сколько всего было яблок?
19. У мальчика было 240 руб. Он потратил этой суммы и
остатка. Сколько денег он потратил?
20. Было 1000 руб. На первую покупку потратили этой суммы, а на вторую –
остатка. Сколько рублей осталось?
21. Когда прочитали 35 страниц, то осталось прочитать книги. Сколько страниц в книге?
22. В первый день прочитали , а во второй –
числа всех страниц книги. После этого осталось прочитать 80 страниц. Сколько всего страниц в книге?
23. Туристы за три дня прошли 48 км. В первый день они прошли всего расстояния, а во второй день –
остатка. Сколько километров они прошли в третий день?
24. Половину книг школьной библиотеки составляют учебники, шестую часть всех учебников – учебники математики. Какую часть всех книг составляют учебники математики?
25. Мама израсходовала половину денег и остатка. У неё осталось 6000 руб. Сколько денег было первоначально?
26. На день рождения к Васе пришли 4 друга. Первый получил пирога, второй –
остатка, третий –
нового остатка. Оставшуюся часть пирога Вася разделил поровну с четвёртым другом. Кому досталась большая часть?
27. Уменьшите 90 руб. на этой суммы.
28. Увеличьте 80 рублей на этой суммы.
29. Сыну 8 лет, его возраст составляет возраста отца. Возраст отца составляет
возраста дедушки. Сколько лет дедушке?
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
||||||||||||||||
|
отв |
9 |
4 |
8 |
16 |
1000 |
9 |
81 |
33 |
16 |
24 |
25 |
35 |
30 |
6 |
||||||||||||||||
|
№ |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
25 |
26 |
27 |
28 |
|||||||||||||||
|
отв |
||||||||||||||||||||||||||||||
|
50 |
8 |
60 |
12 |
150 |
200 |
49 |
300 |
16 |
1/12 |
18000 |
81 |
Васе и 4 другу |
81 |
116 |
Время чтения: 15 минут
В задании 3 ты можешь встретить различные задачи на части. Давай разберемся, какие типы задач могут встречаться и как их решать!
В основном существует 2 типа задач: нахождение части от числа и нахождение числа по его части. Подробно разберем каждый из них.
Нахождение части от числа 🍕
Для нахождения части от числа необходимо целое умножить на дробь, соответствующую этой части.
Нахождение числа по его части🍎
Для нахождения числа по его части необходимо часть разделить на соответствующую дробь.
🚩Сохрани формулы, чтобы не потерять👇
Изменение числа 📊
Часто встречаются задачи, где исходное число уменьшают/увеличивают НА некоторое число, либо В несколько раз. Что нужно делать в этом случае?
Предлог НА означает операцию сложения или вычитания:
- Число 5 увеличили на 2: 5 + 2 = 7
- Число 9 уменьшили на 4: 9 – 4 = 5
Предлог В означает операцию умножения или деления:
- Число 4 увеличили В 3 раза: 4 * 3 = 12
- Число 15 уменьшили в 5 раз: 15 : 5 = 3
Решение задач с помощью уравнений👩🏫
Встречаются более сложные типы задач, для которых удобнее всего составить уравнение и решить его.
Алгоритм:
- За неизвестное (x), берут искомое число;
- Записывают уравнение по условию задачи;
- Находят значение х.
Задание 1 (см. картинку ниже): Если от задуманного числа отнять 220, то получится число, которое в пять раз меньше задуманного. Найдите задуманное число.
Решение:
- Обозначим задуманное число как x.
- “Если от задуманного числа отнять 220” – эту фразу можно записать в виде: x – 220.
- “Число, которое в пять раз меньше задуманного” – это значит, что задуманное число нужно разделить на 5: x/5.
- Получается следующее уравнение: x – 220 = x/5
Аналогичным образом решается Задание 2 (листай карусель ниже)
Разбор заданий из вариантов ВПР🥴
Давай посмотрим, каким типы задач могут встретиться тебе в Задании №3 и как их решать! Ниже представлено несколько примеров для ознакомления.
Больше различных заданий ты найдешь на сайте РЕШУ ВПР: https://math6-vpr.sdamgia.ru/?redir=1
На этом все! Остались вопросы? Напиши о них в комментариях!👇
Обязательно подпишись на канал, чтобы не пропустить больше полезных статей!🧠
#впр #огэ #егэ #математика #репетитор #6класс #алгебра #часть от числа #арифметика #средняяшкола
Математика
5 класс
Урок № 67
Нахождение части целого и целого по его части
Перечень рассматриваемых вопросов
– нахождение целого по его части;
– нахождение части целого;
– моделирование условий задачи с помощью рисунка.
Тезаурус
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Частное дробей – это дробь, которая при умножении на делитель даёт делимое.
Обязательная литература
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Мы уже рассмотрели, как выполняют умножение и деление дробей. Сегодня с помощью этих действий мы будем решать задачи.
Рассмотрим две задачи.

Теперь определим, какие условия в задачах одинаковы, а какие различаются.
Общее:
- в задачах одинаковые числовые данные;
- за целое принята длина всей ленты.
Разное:
- в первой задаче целое известно (длина ленты – 18 м);
- во второй задаче целое нужно найти.
Значит, в первой задаче нужно найти часть отрезанной ленты, то есть часть от целого; а во второй задаче нужно найти всю длину ленты, то есть целое по его части.
Подобные задачи решаются в соответствие с известными правилами.
- Чтобы найти часть от целого, надо целое (соответствующее ему число) умножить на дробь, соответствующую этой части.
- Чтобы найти целое по его части, надо часть (соответствующее этой части число) разделить на соответствующую дробь.
Если вы затрудняетесь определить тип задачи, обратите внимание на союз «что» и указательное местоимение «это». Они встречаются в задачах на нахождение целого по его части.

Решение.
Смоделируем условие задачи с помощью рисунка.

После этого мы увидим, что длина целой ленты известна, а длину части следует вычислить. Значит, мы будем находить часть от целого. Используем для этого соответствующее правило. Чтобы найти часть числа, нужно число умножить на дробь. Получим:

Решение.
Опять смоделируем условие задачи с помощью рисунка.

Таким образом, мы увидим, что длина целой ленты неизвестна, а длина части указана в условии. Значит, нам надо вычислить целое по его части. Для этого мы используем подходящее правило. Чтобы найти целое, нужно число, соответствующее части, разделить на дробь.
Получится:

Итак, сегодня на уроке мы научились:
-
- моделировать условие задачи с помощью рисунка;
- устанавливать соответствие между математическим выражением и его текстовым описанием;
- решать задачи на нахождение части целого и целого по его части.
Рассмотрим старинную индийскую задачу XII века.
Из множества лотосов были подарены: богу Шиве – треть всех цветов, богу Вишну – пятая часть, а Солнцу – шестая, четвёртую долю получила богиня Бхавани, а остальные шесть частей – уважаемый учитель. Сколько было всего лотосов?
Сегодня мы с вами научимся решать такие задачи с применением действий умножения и деления, изученных ранее.
Решение.
Смоделируем условие задачи с помощью рисунка.

Общее количество лотосов обозначим за единицу. Также укажем части (лотосы), которые распределялись между всеми, кто указан в задании.
Известно, что часть, доставшаяся учителю, равна шести лотосам. Значит, если мы будем знать, какая это доля от общего количества лотосов, то придём ко второму типу задачи – вычислению целого по его части.
Итак, найдём, какая часть от общего количества цветков досталась учителю.
Для этого вычислим сначала, сколько составляют все остальные части. Сложим все дроби, соответствующие частям, приведя их к общему знаменателю 60.


Ответ: 120 цветков.
Тренировочные задания
№ 1. Какие части изображены на рисунках?




Правильные ответы:

№ 2. Подставьте в текст нужные слова:
При решении задач на ___ сначала нужно определить ___ задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение ___ от целого;
- нахождение целого по его ___.
Варианты слов для подстановки в текст: части; тип; целого.
Правильный ответ: при решении задач на части сначала нужно определить тип задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение части от целого;
- нахождение целого по его части.
ПРАКТИКУМ: ЗАДАЧИ НА НАХОЖДЕНИЕ ЧАСТИ
ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
1.
В детской книге 24 страницы. За первый вечер Лиза прочитала ![]() страниц.
страниц.
Сколько страниц осталось прочитать?
2.
Сыну 12 лет. Его возраст составляет ![]() возраста отца.
возраста отца.
Сколько лет отцу?
3.
Велосипедисты за два дня проехали 48км. В первый день они
проехали ![]() всего пути. Сколько километров они проехали во
всего пути. Сколько километров они проехали во
второй день?
4.
У машинистки 120 листов бумаги. Она использовала сначала ![]() всех
всех
листов, а потом ![]() оставшихся. Сколько всего листов бумаги
оставшихся. Сколько всего листов бумаги
использовала машинистка?
5.
В классе 18 мальчиков и 16 девочек. ![]() мальчиков и
мальчиков и ![]() девочек
девочек
занимаются в литературном кружке. Сколько учащихся занимается в литературном
кружке?
6.
Туристы за три дня прошли 48 км. В первый день они прошли![]()
всего расстояния, а во второй день –![]() остатка. Сколько километров
остатка. Сколько километров
они прошли в третий день?
7.
В первый день Катя выучила ![]() от всех словарных слов, а во
от всех словарных слов, а во
второй день – 20 оставшихся слов. Сколько всего слов она выучила?
8. Пенсионер
страны Мажория приобрёл новый автомобиль за 10000 экю по системе треэйд-ин (при
покупке нового автомобиля принимается стоимость старого автомобиля). Стоимость
старого автомобиля составила ![]() стоимости нового,
стоимости нового, ![]() общей суммы
общей суммы
пенсионер добавил из своих сбережений,
1
еще внесла жена, а оставшуюся
сумму им подарил внук. Какую сумму внес внук? 5
Выпиши
ответы на задачи
|
Номер задачи |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
ответ |
|||||||||
|
буква |
в |
ё |
о |
р |
л |
о |
г |
у |
Выполни
действия; используя найденные ответы, заполни пропуски в тексте:
|
и |
|
ы |
|
|
ч |
|
к |
|
|
б |
|
а |
|
Учёный-востоковед,
писатель-фантаст Игорь Можейко знаком нам под псевдонимом
|
6 |
|
45 |
30 |
1000 |
8 |
|
|
42 |
9 |
|
ОТВЕТЫ
|
Номер задачи |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
ответ |
9 |
42 |
16 |
45 |
8 |
16 |
50 |
1000 |
|
буква |
в |
ё |
о |
р |
л |
о |
г |
у |
Выполни
действия; используя найденные ответы, заполни пропуски в тексте:
|
и |
|
ы |
|
|
ч |
|
к |
|
|
б |
|
а |
|
Учёный-востоковед,
писатель-фантаст Игорь Можейко знаком нам под псевдонимом
|
6 |
|
45 |
30 |
1000 |
8 |
|
|
42 |
9 |
|
|
к |
и |
р |
б |
у |
л |
ы |
ч |
ё |
в |
Задачи на дроби
- Выражение части в долях целого
- Нахождение дроби от числа
- Нахождение числа по его дроби
Выражение части в долях целого
Чтобы выразить часть в долях целого, нужно часть разделить на целое.
Задача. В классе 30 учащихся, отсутствуют четверо. Какая часть учащихся отсутствует?
Решение:
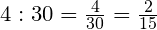
Ответ: В классе отсутствует 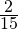 учащихся.
учащихся.
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей,  этой суммы истратили. Сколько денег истратили?
этой суммы истратили. Сколько денег истратили?
Решение: Чтобы найти  от 600 рублей, надо эту сумму разделить на 4 части, тем самым мы узнаем, сколько денег составляет одна четвёртая часть:
от 600 рублей, надо эту сумму разделить на 4 части, тем самым мы узнаем, сколько денег составляет одна четвёртая часть:
600 : 4 = 150 (р.).
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей,  этой суммы истратили. Сколько денег было истрачено?
этой суммы истратили. Сколько денег было истрачено?
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
1000 : 5 · 2 = 400 (р.).
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее  членов организации. В кооперативе 120 членов. При каком составе может состояться отчётное собрание?
членов организации. В кооперативе 120 членов. При каком составе может состояться отчётное собрание?
Решение:
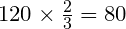
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение числа по его дроби
Для решения задач, в которых требуется найти целое по его части справедливо следующее правило:
Если часть искомого целого выражена дробью, то чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель.
Задача 1. Потратили 50 рублей, это составило  от первоначальной суммы. Найдите первоначальную сумму денег.
от первоначальной суммы. Найдите первоначальную сумму денег.
Решение: Из описания задачи мы видим, что 50 рублей в 6 раз меньше первоначальной суммы, т. е. первоначальная сумма в 6 раз больше, чем 50 рублей. Чтобы найти эту сумму, надо 50 умножить на 6:
50 · 6 = 300 (р.).
Ответ: Первоначальная сумма — 300 рублей.
Задача 2. Потратили 600 рублей, это составило  от первоначальной суммы денег. Найдите первоначальную сумму.
от первоначальной суммы денег. Найдите первоначальную сумму.
Решение: Будем считать, что искомое число состоит из трёх третьих долей. По условию две трети числа равны 600 рублей. Сначала найдём одну треть от первоначальной суммы, а затем сколько рублей составляют три третьих (первоначальная сумма):
600 : 2 · 3 = 900 (р.).
Ответ: Первоначальная сумма — 900 рублей.
Второй способ нахождения целого по его части:
Чтобы найти целое по величине выражающей его часть, можно разделить эту величину на дробь, выражающую данную часть.
Задача 3. Отрезок AB, равный 42 см, составляет 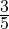 длины отрезка CD. Найти длину отрезка CD.
длины отрезка CD. Найти длину отрезка CD.
Решение:

Ответ: Длина отрезка CD 70 см.
Задача 4. В магазин привезли арбузы. До обеда магазин продал 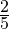 , после обеда —
, после обеда — 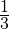 привезённых арбузов, и осталось продать 80 арбузов. Сколько всего арбузов привезли в магазин?
привезённых арбузов, и осталось продать 80 арбузов. Сколько всего арбузов привезли в магазин?
Решение: Сначала узнаем, какую часть от привезённых арбузов составляет число 80. Для этого примем за единицу общее количество привезённых арбузов и вычтем из неё то количество арбузов, которое получилось реализовать (продать):

Итак, мы узнали, что 80 арбузов составляет  от общего количества привезённых арбузов. Теперь узнаем сколько арбузов от общего количества составляет
от общего количества привезённых арбузов. Теперь узнаем сколько арбузов от общего количества составляет  , а затем сколько арбузов составляют
, а затем сколько арбузов составляют 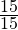 (количество привезённых арбузов):
(количество привезённых арбузов):
2) 80 : 4 · 15 = 300 (арбузов).
Ответ: Всего в магазин привезли 300 арбузов.
