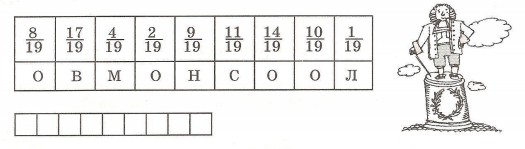
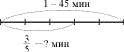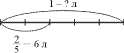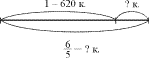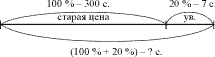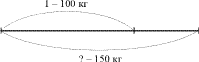Как найти часть от числа, выраженную дробь? Вычисли:
7
8
от 240 О;
5
6
от 90 Е;
9
7
от 56 Р;
17
12
от 84 С;
14% от 4000 Ж;
134% от 800 Д.
Расположив ответы примеров в порядке убывания и сопоставив им соответствующие буквы, ты узнаешь имя египетского фараона, в честь которого была построена самая первая пирамида.
reshalka.com
ГДЗ учебник по математике 4 класс Петерсон. 1 урок. Сравнение углов. Номер №10
Решение
Чтобы найти часть от числа, выраженную дробью от целого, нужно целое разделить на знаменатель этой дроби и умножить на числитель.
240 : 8 * 7 = 30 * 7 = 210 О;
90 : 6 * 5 = 15 * 5 = 75 Е;
56 : 7 * 9 = 8 * 9 = 72 Р;
84 : 12 * 17 = 7 * 17 = 119 С;
4000 : 100 * 14 = 40 * 14 = 560 Ж;
800 : 100 * 134 = 8 * 134 = 1072 Д.
1072(Д) > 560(Ж) > 210(О) > 119(С) > 75(Е) > 72(Р)
Ответ: ДЖОСЕР
Нахождение числа по его части. Урок по математике в 4-м классе по учебнику Л.Г. Петерсон
Грехова Ирина Сергеевна, учитель начальных классов
Цель урока.
Учить находить число по его части.
Формируемые УУД:
предметные: находить число по его части, решать текстовые задачи, примеры на порядок действия, сравнивать дроби;
метапредметные: определять и формулировать цель урока, понимать учебную задачу урока, отвечать на итоговые вопросы урока и оценивать свои достижения, работать в паре, ориентироваться в своей системе знаний, отличать новое от уже известного, контролировать свои действия в процессе выполнения задания и исправлять ошибки, делать выводы;
личностные: поддерживать интерес к математике; быть мотивированным к учебной деятельности, проводить самооценку на основе критерия успешности учебной деятельности.
Планируемые результаты :
уметь определять тему урока, цели урока
- развивать умение анализировать и обобщать
- оценивать свою работу
- читать информацию, заданную с помощью математической модели
- зная алгоритм , находить число по его части..
Оборудование: карточки с ключами, ножницы.
Ход урока
|
Этапы урока |
Деятельность учителя |
Деятельность ученика |
|
1. Организационный момент и мотивация к учебной деятельности |
Закрыли глаза. Сделали пару дыхательных упражнений. Настроились на урок. Взяли с собой улыбку и тепло вашей души. Открыли глазки. С чего начнем? А какая у меня будет роль? Какие качества вам понадобятся на уроке? |
Настрой ребят на урок. С повторения. Помощник и организатор Честность, активность, терпение и т. д. |
|
2. Актуализация знаний и фиксация затруднения в пробном действии. |
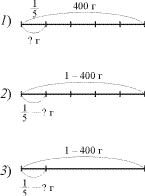
4. Сравните дроби: 1 и 1 ; 3 и 5 . 9 27 8 8 Сделайте вывод. Решите следующие задачи: 1. Сад занимает площадь 400 кв.м.Восьмая часть площади занята цветником. Сколько кв. м. занято цветником? 2. Сад занимает площадь 400 кв.м. Две восьмых этого сада занимают кустарники. Сколько кв. м. Занимают кустарники? Чем похожи эти задачи? Чем отличаются? Как найти 1/8 числа в первой задаче? Как найти 2/8 числа во второй задаче? Как вы думаете, какое сейчас будет предложено задание? Хорошо. Слушаем первую задачу. Цветник занимает 1/8 площади сада- это 400 кв. м. Найдите площадь всего сада? Чем отличается эта задача от предыдущих? Как найти число по его доле? Даю вторую задачу. Кустарники занимают 2/8 сада — это 400 кв. м. Чему равна площадь всего сада? Почему мнения ребят разделились? Что у вас возникло? Как к нему нужно относиться? Что будем делать? Чем похожи эти задачи? |
Если у дробей одинаковый знаменатель, то больше та дробь, числитель которой будет больше. Если у дробей одинаковый числитель, то больше та дробь, знаменатель которой будет меньше. Площадь сада равна 400 кв.м., Неизвестна часть числа. В первой задаче неизвестна 1/8, а во второй -2/8. Разделить число на 8. Чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель 8 и умножить на числитель дроби 2. Задание на пробное действие. В тех задачах необходимо было найти часть от числа. В этой- число надо найти, если известна его доля.. Нужно долю умножить на количество долей. Ответы ребят записываются на доске. Выслушиваются доказательства. Не знаем правила нахождения числа по его части, выраженной дробью.. Затруднение. Спокойно Разбираться и искать выход из нашего затруднения. Обе задачи на нахождение числа по его части. |
|
3. Выявление места и причины затруднения. |
Давайте разберемся. Что вы не смогли сделать. Почему? Что вызвало затруднение? задание вызвало затруднение? |
Не смогли решить задачу, так как не знаем правила нахождения числа по его части, выраженной дробью. |
|
4.Построение проекта выхода |
Сформулируйте цель сегодняшнего урока. А теперь попробуйте сформулировать тему нашего урока. Проверьте себя, открыв учебник. Составьте план выхода из затруднения. Работать предлагаю в группах. Какие знания возьмете с собой. |
Находить число по его части, выраженной дробь. Нахождение числа по его части. ( Все планы выслушиваются и записываются на доске. Лучший вариант, по мнению ребят, оставляют) Возьмем эталон нахождения числа по его доле. Возьмем схему прямоугольника и разобьем его на 8 частей. Проанализируем все это и сделаем вывод. Свой вывод сопоставим с выводом учебника. |
|
5.Этап реализации построенного проекта |
Сравните свой вывод с выводом в учебнике. Что вы можете сказать о результате вашей работы? |
Выслушиваются рассуждения ребят. Мы можем находить число, если известна одна доля из 8.Чтобы найти число , надо долю умножить на количество долей. У нас две таких доли из 8. Поэтому 400:2=200(кв. м.)-этим действием мы находим 1 долю числа. А теперь мы можем находить число.200*8=1600(кв. м.) Вывод: чтобы найти число, выраженную дробью, надо разделить эту часть на числитель и умножить на знаменатель дроби. Эталон 1-а-? m/n=с с:m*n=a Мы осуществили поставленную перед собой цель: нашли число по его части, выраженной дробью и составили эталон к этому правилу. |
|
6. Первичное закрепление во внешней речи. |
№ 1, с. 88 – с комментированием. а) х : 4 · 9; б) у : 7 · 12; № 2, с. 88 – (работа в парах) 8 : 4 · 15 = 30; 32 : 4 · 15 = 120. И т. д. (При проверке выясняют, на сколько уяснили правило нахождения числа по его части) |
|
|
7.Самостоятельная работа с проверкой по эталону |
№3, с. 89 – Кто допустил ошибки при выполнении задания? – В чем причина? – Что нам поможет исправить ошибки? (Эталон.) – Поднимите руки, у кого все верно. – Вы молодцы! |
(Учащиеся выполняют самостоятельную работу) |
|
8. Включение в систему знаний и повторение. |
2. Найти число по части. № 4, с. 89 – работа в парах. – Какое правило нужно помнить? Проверка по образцу. 3. Числовой луч. № 8, с. 89 – с комментированием. – Какие дроби являются равными? – Приведите примеры равных дробей. |
|
|
Нахождения числа по части9. Рефлексия учебной деятельности на уроке. |
Расскажите об открытии сегодня на уроке. Что узнали нового? Чему научились? Какое правило нужно запомнить? Расскажите. Приведите пример. Считаете ли вы, что хорошо усвоили данное правило. Оцените свою работу на лесенке успеха. |
Ответы ребят |
http://pedsovet.org/component/option,com_mtree/task,viewlink/link_id,140640/Itemid,118
Максимова Т. Н. Математике. 4 класс.-М.: ВАКО, 2014.-432с.
Обновлено: 19.05.2023
– Над какой темой мы работаем на протяжении нескольких уроков? (дроби)
– Что такое дробь? (дробь – это одна или несколько равных частей)
– Что обозначает черта дроби? (знак деления)
– Как называется делимое в записи дроби, делитель? (делимое – числитель, делитель – знаменатель)
– С какими новыми видами задач познакомились? (нахождение числа по части, нахождение части от числа)
– Как найти число по его части? (надо эту часть разделить на числитель и умножить на знаменатель)
– Как найти часть от числа? (чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель)
На доску вывешиваются опорные схемы.
– Перед вами на столе карточки с заданиями. Трое из вас будут выполнять эти задания на индивидуальных досках, а остальные на самих карточках. Итак, на досках работают …, …, …. На выполнение задания отводится 3 минуты. Возьмите карточки и начинайте работать.
(У детей на партах индивидуальное задание. Три ученика работают на индивидуальных досках.)
Дорисуйте схемы и решите задачи.
1. Вдоль улицы посадили 75деревьев. Из них 3/5 – липы. Сколько лип посадили?
_________________________ __________________________
2. В классе 20 мальчиков, что составляет 2/3 всех учеников класса. Сколько учеников в классе?
_________________________ __________________________
3. Кате нужно вырезать 10 снежинок. Она уже вырезала 3 снежинки. Какую часть работы она выполнила?
– А теперь проверим.
– Назовите задачи на нахождение числа по его части ( про учеников ), части от числа (про деревья).
– Давайте проверим решение первой задачи, второй задачи. (выставляются индивидуальные доски). Дети объясняют ход решения.
– Кто решил так же?
– Проверим решение третьей задачи. Объясни, почему ты решил так?
– А кто не смог решить задачу?
– Почему не все справились? (не изучали эту тему).
3. Постановка учебной проблемы.
– Задача про Катю тоже на нахождение части? (нет).
Какой будет тема урока? (решение задач нового вида).
– Прочитайте тему нашего урока. ( нахождение части, которую одно число составляет от другого)
– Чему должны научиться? (научиться решать такие задачи)
4. Построение проекта выхода из затруднения.
– А теперь эту задачу решим все вместе и запишем в тетрадь.
– С чего предлагаете начать? (со схемы).
– Начертим отрезок. Что он будет обозначать? (число всех снежинок)
– Значит, сколько клеточек удобно взять? (10) (дети чертят отрезок, учитель открывает на доске схему)
Гипермаркет знаний>>Математика>>Математика 4 класс>> Урок 2. Нахождение части, которую одно число составляет от другого


1. Сделай чертеж и реши задачу двумя способами:
а) Около дома стоит 8 машин. Из них 3 машины белые. Какую часть всех машин составляют белые машины?
б) От доски длиной 9 м отпилили 4 м. Какую часть доски отпилили?
2. Пролжительность урока 45 мин. На решение задачи ушло 7 мин. Какая часть урока ушла на решение задачи?
б) Испекли каравай, масса которого 3 кг. От него отрезали 375 г. Какую часть каравая отрезали?
3. Какую часть составляют:
а) 4 см от 5 см; б) 6 м2 от 10 м 2 ; в) 7 л от 25 л; г) 18 р. от 100 р.?
4. В неделе 5 рабочих дней. Какую часть недели составляют рабочие дни? Какую часть недели составляют выходные дни?
5. Человек спит примерно 8 часов в сутки. Какую часть суток он спит ? Какую часть суток он бодрствует?
6. В кинотеатре 2000 мест, причем 85% всех мест находится в партере, а остальные — на балконе. Сколько мест в этом кинотеатре находятся на балконе?
7. Реши уравнения:
а) (72 – х) : 6 + 25 = 34;
6) 28 : (20 • у – 76) = 7.
8. В х подарков разложили поровну 20 ирисок и 48 леденцов. Каких конфет в подарке больше — ирисок или леденцов, и на сколько? Составь выражение и найди его значение при х = 4. Придумай задачи про другие величины, которые решаются так же.
9. а) Что больше: ? Как сравнить дроби с одинаковыми знаменателями?
б) Что больше: 3 : 9 или 8 : 9? Как изменяется частное с увеличением делимого? Похожа ли эта задача на предыдущую? Почему?
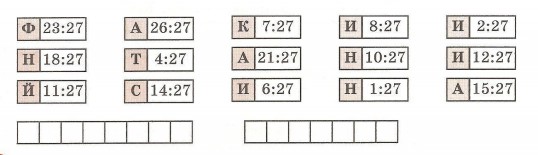
10. а) Расшифруй фамилию известного русского ученого XVIII века, расположив дроби в порядке возрастания. Чем знаменит этот ученый?
б) Расположи частные в порядке убывания, и ты узнаешь имя русского путешественника XV века, который первым из россиян побывал в Индии. В какой книге он описал свое путешествие?
11. а) 2 406 204 : (10 421 – 9 887) + 88 200 : 300;
б) (2 801 • 789 631) • (775 – 95 823 : 189) + 1 630 314 : 798.
12. Найди нарушенную закономерность:
а) 35, 32, 29, 27, 24, 21, 18;
6) 0, 12, 24, 36, 46, 58, 70.
Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 2. – М.: Издательство “Ювента”, 2005, – 64 с.: ил.
Помощь школьнику онлайн, Математика для 4 класса скачать, календарно-тематическое планирование
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Цели: сформировать способности находить часть, которую одно число составляет от другого;
развивать логическое мышление, речь учащихся.
Технология: проблемно-диалогическое обучение.
Самоопределение к деятельности.
– Сегодня на уроке мы продолжим решать задачи. Вам, как всегда на уроках математики, понадобится усердие, аккуратность, сообразительность. Желаю вам удачи!
Актуализация знаний и фиксация затруднения в деятельности.
– Над какой темой мы работаем на протяжении нескольких уроков? (дроби)
– Что такое дробь? (дробь – это одна или несколько равных частей)
– Что обозначает черта дроби? (знак деления)
– Как называется делимое в записи дроби, делитель? (делимое – числитель, делитель – знаменатель)
– С какими новыми видами задач познакомились? (нахождение числа по части, нахождение части от числа)
– Как найти число по его части? (надо эту часть разделить на числитель и умножить на знаменатель)
– Как найти часть от числа? (чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель)
На доску вывешиваются опорные схемы.
– Перед вами на столе карточки с заданиями. Трое из вас будут выполнять эти задания на индивидуальных досках, а остальные на самих карточках. Итак, на досках работают …, …, …. На выполнение задания отводится 3 минуты. Возьмите карточки и начинайте работать.
(У детей на партах индивидуальное задание. Три ученика работают на индивидуальных досках.)
Дорисуйте схемы и решите задачи.
1. Вдоль улицы посадили 75деревьев. Из них 3/5 – липы. Сколько лип посадили?
_________________________ __________________________
2. В классе 20 мальчиков, что составляет 2/3 всех учеников класса. Сколько учеников в классе?
_________________________ __________________________
3. Кате нужно вырезать 10 снежинок. Она уже вырезала 3 снежинки. Какую часть работы она выполнила?
– А теперь проверим.
– Назовите задачи на нахождение числа по его части ( про учеников ), части от числа (про деревья).
– Давайте проверим решение первой задачи, второй задачи. (выставляются индивидуальные доски). Дети объясняют ход решения.
– Кто решил так же?
– Проверим решение третьей задачи. Объясни, почему ты решил так?
– А кто не смог решить задачу?
– Почему не все справились? (не изучали эту тему).
3. Постановка учебной проблемы.
– Задача про Катю тоже на нахождение части? (нет).
Какой будет тема урока? (решение задач нового вида).
– Прочитайте тему нашего урока. ( нахождение части, которую одно число составляет от другого)
– Чему должны научиться? (научиться решать такие задачи)
4. Построение проекта выхода из затруднения .
– А теперь эту задачу решим все вместе и запишем в тетрадь.
– С чего предлагаете начать? (со схемы).
– Начертим отрезок. Что он будет обозначать? (число всех снежинок)
– Значит, сколько клеточек удобно взять? (10) (дети чертят отрезок, учитель открывает на доске схему)
– Отметим условие и вопрос задачи. (Делает сам учитель)
-Какую часть составляет І снежинка? ( І/10 )
-Какую часть составят 3 снежинки? ( 3/10)
– Каким действием мы найдем дробь, которую число 3 составляет от числа 10? (делением)
– Как это запишем? (3:10 = 3/10)
– Ответили на вопрос задачи. (да)
– Запишите ответ задачи.
– А теперь составим выражение, которое поможет решить любую задачу данного вида.
– Заменим числа буквами. (дети составляют выражение а : b )
На доске схема – опора
– Сформулируйте правило решения задач на нахождение части, которое одно число составляет от другого. (правило).
– Как мы можем себя проверить? (посмотреть определение в учебнике)
– Прочитайте правило по учебнику, проверьте себя. ( стр. 4 )
Физкультминутка.
– Прыгните столько раз, сколько 1/7 составляет от 21 (3)
– Присядьте столько раз, сколько 1/3 составляет от 12 (4)
– Наклонитесь вперед столько раз, сколько 1/9 составляет от 36 (4)
Первичное закрепление.
– Потренируемся в решении таких задач.
Выполнение заданий по учебнику
№ 2 (а,б) –ученики по одному выходят к доске и комментирует решение задачи.

Цель урока:уметь записывать и графически изображать доли величин достигнута.
Урок математики 4 класс
Учитель начальных классов
Цель: построить алгоритм решения задач на нахождения части числа.
– уметь записывать и графически изображать доли величин, сравнивать их, решать задачи на доли.
1. Познавательные УУД:
– развивать умение моделировать, выделять существенные признаки предмета (моделировать задачу, используя схемы);
– формировать умение строить доказательства, развить мышление и внимание;
– развивать умения анализировать и обобщать полученные знания;
2. Коммуникативные УУД:
– формировать умение работать в парах, группе;
– развивать умение высказывать свои мысли и доказывать свою точку зрения.
3. Регулятивные УУД:
– учить детей контролировать свою речь при выражении своей точки зрения по заданной тематике;
– формировать умения выполнять свои действия по образцу (правило);
-формирование умения адекватно оценивать свою работу, исправлять ошибки.
– учить осознавать смысл учения, важность изучаемого материала.
Оборудование: компьютер, программа PowerPoint(презентация), наглядный материал, листы с заданиями; эталон для проверки, учебник.
I. Организационный момент.
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
Мы в поход отправляемся смело,
В мир загадок и сложных задач.
Не беда, что идти далеко,
Не боимся, что путь будет труден.
Достижения крупные людям
Никогда не давались легко.
Каким бы вы хотели видеть наш урок? (интересным, увлекательным….)
Как вам нравиться работать больше всего? (парами, группами)
А почему ? (Вместе веселей; кто-то поможет, если непонятно; …)
II. Актуализация знаний.
Дайте определение этому понятию
Дробью называют одну или несколько равных долей целого
2). Расставь в порядке возрастания дроби
Выполни самооценку. Самооценка по алгоритму:
Что нужно было сделать в этом задании(задаче)? Какая была цель, что нужно было получить в результате?
Удалось получить результат? Найдено решение, ответ?
Выполнил полностью верно или с незначительной ошибкой(какой и в чём)?
Справился полностью самостоятельно или с чьей-то помощью(кто помогал, в чём)?
Какое умение отрабатывали при выполнении задания?
Каков был уровень задачи-задания?
Определи уровень успешности.
8. Определи отметку, которую ты себе поставишь.
Что еще мы знаем про дроби?
(Части величин, которые выражаются дробями со знаменателем 100, называются процентами)
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше, и наоборот
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше, и наоборот.
III. Создание проблемной ситуации.
Работа в группах. Сначала дети решают первую задачу.
Затем дети решают вторую задачу.
Задание было одно?
А как его выполнили? (По-разному.)
Почему так получилось? В чём затруднение? (Мы не знаем, как решаются такие задачи.)
Какую цель перед собой поставим? ( Научиться решать новые задачи.)
Подумайте, как называются эти задачи. Что неизвестно в задаче?
IV. Решение проблемной ситуации.
V. Закрепление материала.
Решите задачу. Масса творога составляет 8% от массы молока, идущего на его изготовление. Сколько творога получится из 300 кг молока?
300:100*8=24кг
Как найти часть числа?
Чтобы найти часть числа, выраженную дробью, можно это число разделить на знаменатель дроби и результат умножить на числитель.
Давайте посмотрим, согласна ли с нами Л.Г. Петерсон? Учебник стр.85
Запись в тетради краткого конспекта.
a:n.m
VII. Самостоятельная работа с самопроверкой.
Решение задачи №3 стр.85
Назовите ключевые слова нашего урока. Дроби, число, часть
VIII.Итог урока.
На уроке я научился…
Больше всего на уроке мне понравилось….
Самым трудным для меня было….
Чтобы найти часть числа….
Возьмите круг, разделите его на четыре равные части, оцените свою работу, закрасив нужное количество частей
4/4- я понял все, могу работать сам и объяснять другому
3/4- я все понял, могу работать сам, пользуясь правилом
2/4- я понял все, но у меня остались вопросы
IX.Домашнее задание
Стр.86 №4, №6 (на выбор) ; №10* (по желанию)
Я очень рада, что вы уйдете с урока с прекрасным настроением, хорошими отметками и отличными знаниями.
Математика. 4 класс. Учебник в 3 ч. Петерсон Л.Г. М.: 2016. – 96с.
Математика. 4 класс. Рабочая тетрадь в 3 ч. Петерсон Л.Г. М.: 2016. – 96с.
Читайте также:
- Климатические пояса и области земли конспект
- Метод площадей конспект урока
- Конспект по музыке плач ярославны
- Пользуясь учебником составьте и запишите план конспект сообщения на тему особенности строения
- Конспект урока анализ диктанта 9 класс
Тип урока: Рефлексия.
Тема: «Арифметические действия с дробями и смешанными
числами»
Автор: Калинина
Н.Ю. (МБОУ «СОШ №24», г. Ангарск)
Основные цели:
1) сформировать способность к исправлению
допущенных ошибок на основе рефлексии собственной деятельности,
2) повторить алгоритмы сложения, вычитания, умножения
и деления смешанных чисел,
повторить
и закрепить действия со смешанными числами.
Ход урока
1. Самоопределение к
учебной деятельности
Цель этапа: включить учащихся в учебную деятельность, определить содержательные
рамки урока: продолжаем работать над действиями со смешанными числами.
Организация
учебного процесса на этапе 1:
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте,
Все ль в порядке-
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Тут затеи и задачи,
Игры, шутки – все для вас!
Пожелаю всем удачи.
– Здравствуйте, ребята! Давайте вспомним, над какой большой темой мы
работаем? (Арифметика дробей.)
– Что изучает этот раздел математики? (Действия над дробями и
смешанными числами.)
– Что необходимо
сделать, чтобы ответить себе на вопрос: всё ли я понял, умею ли я выполнять
действия над дробями и смешанными числами? (Надо проверить свои знания.)
– Как можно проверить
свои знания? (Выполнить самостоятельно работу, проверить её и если ошибок не
будет, то можно сказать, что тему я понял, а если ошибки будут, то разобраться
в их причине, повторить все действия над дробями и смешанными числами и
исправить допущенные ошибки.)
– Вы очень хорошо
определили задачу сегодняшнего урока, начнём работать.
“Если
будешь дроби знать,
Точно смысл их понимать,
Станет лёгкой даже трудная задача”.
2. Актуализация знаний и фиксация затруднения
деятельности
Цель этапа:
1) актуализировать
знания обо всех изученных действиях над дробями и
смешанными числами;
2) актуализировать
мыслительные операции: сравнение, анализ, обобщение;
3) зафиксировать все
повторяемые понятия и алгоритмы в виде схем и таблиц;
4) зафиксировать
индивидуальное затруднение в деятельности, демонстрирующее на личностно
значимом уровне недостаточность имеющихся знаний;
5)выполнить
самостоятельную работу, зафиксировать задания, вызвавшие затруднения.
Организация
учебного процесса на этапе 2:
Фронтальная работа.
Учащиеся работают в
тетрадях.
1. Что интересного в произведениях? (Один множитель постоянный, а другой
– увеличивается.)
,
,
,
.
–
Найдите значения произведений. (;
;
;
.)
– Что вы
замечаете? Сделайте вывод. (С увеличением множителей произведение дробей увеличивается.)
2. Вычислите:
;
;
.
Один
из учащихся прописывает действие на доске.
–
Расставьте полученные результаты в порядке возрастания. ()
– Установите закономерность и продолжите ряд на три числа. (.)
– На какие группы можно
разбить данный ряд чисел?
–
Выделите целую часть из неправильных дробей. (1; 1; 1
.)
3. Из любой ли неправильной дроби можно выделить целую часть? Как?
(Учащиеся формулируют правило выделения целой части.)
– Любое ли смешанное
число можно представить в виде дроби? Что для этого нужно сделать? (Учащиеся
формулируют правило перевода смешанного числа в неправильную дробь.)
–
Представьте в виде дробей числа: 1; 2
; 3
; 3
. (
;
;
;
.)
–
Установите закономерность и запишите следующие три числа. (Числители дробей
увеличиваются на 5, а знаменатели – на 1. Дальше идут: ;
;
.)
–
Выделите из них целую часть. (3; 4; 4
.)
4. – Поставьте вместо звездочек нужное число. Какую закономерность вы
увидели?

,
каждая следующая дробь получается из первой умножением числителя и знаменателя
на 2, на 3, на 4).
–
Какое равенство, по вашему мнению, будет следующим? (3).
Учащимся предлагается
текст самостоятельной работы в одном варианте, который может быть написан на
доске или отпечатан каждому. На основную работу отводится 10 минут. Если учащиеся
основную работу выполняют раньше, они могут приступить к выполнению дополнительного
задания со звездочкой.
После выполнения работы
учащиеся сверяют решения с образцом, если ответ совпал, то в таблице против
соответствующего номера они ставят знак «+», если есть расхождения между ответами,
то фиксируют их знаком «?».
таблица фиксации
результатов.
|
№ задания |
Выполнено («+» или «?») |
Номер алгоритма, шаг |
Исправлено в процессе |
|
1 а) б) в) г) |
|||
|
2 а) б) в) |
|||
|
3 а) б) в) г) |
Раздаточный материал
самостоятельная
работа.
|
1. Выполните действия: а) 2. Найди произведение: а) 3. Выполните действия: а)
|
дополнительные
задания.
подробный образец
решения дополнительных заданий.
Задание № 1.
а) 5
1 =
б) 4
1) 3 – 2
=
3;
2) ;
3) ;
4) 1.
подробный образец решения дополнительных заданий.
подробный образец
выполнения самостоятельной работы.
|
1. а) б) в) г) 2. а) б) в) 3. а) б)
в) 7 г) 12 12
|
3. Выявление причин
затруднения и постановка цели деятельности
Цель этапа: указать место в задании, где допущена ошибка, определить правило, в
котором допущена ошибка, уточнить цель урока.
Организация
учебного процесса на этапе 3:
Учащиеся, не
допустившие ошибок, сравнивают свое решение с эталоном и далее выполняют
задания повышенной сложности или выступают консультантами.
Учащиеся, допустившие
ошибки, на основе алгоритма исправления ошибок анализируют решение, определяют
места ошибок, исследуют их происхождение, уточняют цель своей дальнейшей
деятельности по исправлению ошибок. (Определить причину ошибки и исправить её.)
4.
Построение проекта выхода из затруднения
Цель
этапа: уточнить способы действий, в которых
допущены ошибки; исправить ошибки на основе правильного применения правил.
Организация учебного процесса на этапе 4:
Ошибки
исправляются самостоятельно или с помощью эталона. Если ученик сам исправил, то
сверяет с эталоном.
ФИЗКУЛЬТМИНУТКА.
Вы,
наверное, устали?
Ну, тогда все дружно встали.
Ножками потопали, ручками похлопали.
Рисуй глазами треугольник.
Теперь его переверни.
И вновь глазами по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь веди горизонтально,
И в центре ты остановись.
Глазки крепко закрываем,
Дружно до пяти считаем.
Глаза открываем мы, наконец.
Зарядка окончилась. Ты молодец!
5. Включение в
систему знаний и повторение
Цель этапа: повторить сокращение дробей.
Организация
учебного процесса на этапе 5:
К математике способность проявляй,
Не ленись, а ежедневно развивай.
Умножай, дели, трудись, соображай,
С математикой дружить не забывай.
Знаете ли вы?
… что самая крупная змея на Земном шаре водится по берегам рек, озер и
болот Бразилии и Гаваны.
Название этой змеи зашифровано числами.
|
|
|
|
|
|
|
|
|
Сократите дроби, заменит каждую дробь буквой, прочтите название самой
крупной змеи на Земном шаре.
Вопросы:
1.
Объясните, как вы сократили дробь ? (разделили
числитель и знаменатель на 3 и получили )
2.
Какая дробь больше или
? (
)
3.
Что вы можете сказать про дробь ?
Узнать длину тела
(в метрах) анаконды поможет удивительный квадрат.
|
|
|
0 |
1 |
|
|
3 |
|
|
|
|
|
3 |
4 |
|
3 |
|
|
|
Выберите из каждой
строки и каждого столбца по одному числу. Сумма выбранных чисел и укажет вам (в
метрах) длину тела анаконды.
10 м – сколько это
дециметров? (100 дм) Километров? (1/100 км)
Задание.
- Напишите наименьшее число из первой строки таблицы.
- Напишите наибольшее число из второй строки таблицы.
- Из двух меньших чисел третьей строки таблицы напишите наибольшее
число. - Из двух больших чисел четвертой строки таблицы напишите наименьшее
число. - Найдите сумму четырех чисел. Что вы заметили?
- Найдите сумму чисел, записанных на главной диагонали таблицы. Что
вы заметили? - Найдите сумму чисел, записанных на побочной (второй) диагонали
таблицы. Что вы заметили? Как вы думаете, почему этот квадрат назвали
удивительным?
Анаконда большую
часть времени проводит в воде. Обитает она в бассейне реки Амазонки, её
называют водяным удавом, она очень хорошо плавает. Яд анаконды для человека
смертелен. В неволе долго жить анаконда не может. По неофициальным данным в
Амазонке существуют анаконды в 20 м и даже в 30 м. Таких анаконд никто не
видел.
Нью – Йорский
зоопарк в течение многих лет обещает 10 000 долларов тому, кто доставит
туда анаконду длиной свыше 10 м длины. Такая змея должна весить более 150
килограммов. Возможно по этой причине никто не занялся отловом такой анаконды.
Крупные змеи в
среднем живут от 80 до 100 лет. Какую часть 80 лет составляет от одного века?
№ 387(3)
Составь и реши
уравнения:
3)
Сумма двух чисел равна 12, одно из них в 3 раза
больше другого. Найти эти числа.
Пусть
одно число х, тогда другое 3х. Их сумма х+3х, что по
условию задачи равно 12.
х
+ 3х = 12;
1∙
х + 3х = 12;
4х
= 12;
х
= 12 : 4;
х
= ;
Ответ:
.
№ 386(7)
Реши
уравнение:
;
;
;
;
;
;
;
;
;
Ответ:
.
6. Рефлексия
деятельности на уроке
Цель этапа: зафиксировать, где были допущены ошибки, способ исправления допущенных
ошибок; зафиксировать содержание, которое повторили на уроке, оценить
собственную деятельность; записать домашнее задание.
Организация
учебного процесса на этапе 6:
– Какая была цель
нашего урока? (Проверить, усвоена ли тема «Арифметика дробей».)
– Те, кто допускал
ошибки при выполнении задания, какая перед вами стояла цель? (Найти ошибку,
понять её причину и исправить.)
– Кто из вас достиг
цели? (Учащиеся высказываются.)
– Дайте анализ собственной деятельности. (Учащиеся заполняют карточку для
этапа рефлексии. Можно предложить высказаться некоторым учащимся по плану,
который предложен в этой карточке.)
Домашнее задание:
задачи для самопроверки
№ № 655 (4, 6), 658, 660 (5), 663(2, 5, 8).
карточка для этапа
рефлексии.
|
Утверждения |
«+» или «-» |
|
1) У меня сегодня допускал ошибок. |
|
|
2) Я допустил работе |
|
|
3) Я исправил процессе работы |
|
|
4) Я не смог ошибки, но |
|
|
5) Я выполнил (перечислить |
|
|
6) В ошибки |
|
|
7) Мне необходимо |
Урок сегодня завершён,
Но каждый должен знать:
Познание, упорство, труд
К успеху в жизни приведут!
Мне было приятно
сегодня с вами работать. Спасибо за урок!
Дополнительно: Вы любите разгадывать
ребусы? Расшифруйте слова!
1 группа
2 группа
3 группа
4 группа
Ответы:
1. Смешанных
2. Чисел
3. Сложение
4. Вычитание
(Представитель каждой
группы записывает на доске расшифрованное слово).
Изрядно потрудились,
собрали вы слова.
Слова же следует теперь
соединить,
В какую фразу можно их
объединить?
(Сложение и вычитание
смешанных чисел).
Раздаточный материал
самостоятельная работа.
|
1. Выполните действия: а) 2. Найди произведение: а) 3. Выполните действия: а)
|
дополнительные
задания.
самостоятельная
работа.
|
1. Выполните действия: а) 2. Найди произведение: а) 3. Выполните действия: а)
|
дополнительные
задания.
Подробный образец
решения дополнительных заданий.
Задание № 1.
а) 5
1 =
б) 4
1) 3 – 2
=
3;
2) ;
3) ;
4) 1.
подробный образец решения дополнительных заданий.
Подробный образец
выполнения самостоятельной работы.
|
1. а) б) в) г) 2. а) б) в) 3. а) б)
в) 7 г) 12 12
|
Ф. И. __________________________________________________ 5 «Б» класс
таблица фиксации
результатов.
|
№ задания |
Выполнено («+» или «?») |
Номер алгоритма, шаг |
Исправлено в процессе |
|
1 а) б) в) г) |
|||
|
2 а) б) в) |
|||
|
3 а) б) в) г) |
_____________________________________________________________________________
Ф. И. __________________________________________________
5 «Б» класс
карточка для этапа
рефлексии.
|
Утверждения |
«+» или «-» |
|
1) У меня сегодня допускал ошибок. |
|
|
2) Я допустил работе |
|
|
3) Я исправил процессе работы |
|
|
4) Я не смог ошибки, но |
|
|
5) Я выполнил (перечислить |
|
|
6) В ошибки |
|
|
7) Мне необходимо |
Эталоны
|
А1: Ш. 1: привести дробные части к Ш. 2: выполнить отдельно сложение целых Ш. 3: если дробная часть суммы окажется Ш. 4: если дробная часть суммы окажется
|
|||
|
А2: Ш. 1: привести дробные части к Ш. 2: если дробная часть уменьшаемого Ш. 3: отдельно вычесть целые части и Ш. 4: если дробная часть разности
|
|||
А3: Алгоритм умножения дробей1) Произведение дробей записать в виде 2) Если возможно сократить, 3) Найти произведение чисел, стоящих в 4. Если получилась неправильная дробь,
|
|||
|
А4: Алгоритм умножения дроби на натуральное число 1. Записать дробь: в числители 2. Если возможно сократить, 3. Найти произведение чисел в 4. Если результат неправильная
|
|||
|
Чтобы преобразовать неправильную
|
|||
|
Чтобы записать смешанное число в 1) знаменатель умножить на целую часть; 2) к произведению прибавить числитель 3) полученную сумму записать в
|
Эталоны
|
А5: 1) Смешанные числа представить в виде 2) Перемножить, получившиеся дроби по 3) Если получилась неправильная дробь,
|
||
|
А6: 1) Умножить целую часть на натуральное 2) Умножить дробную часть на 3) Найти сумму результатов первого и
|
||
|
Правила нахождения неизвестного П. 1: Чтобы найти неизвестное П. 2: Чтобы найти неизвестное П. 3: Чтобы найти неизвестное П. 4: Чтобы найти неизвестный П. 5: Чтобы найти неизвестный делитель, П. 6: Чтобы найти неизвестное делимое,
|
||
|
Определение взаимно обратных чисел Числа взаимно обратные, если их a и b
|
||
|
А7: 1. Деление заменить умножением. 2. Делитель заменить числом, обратным. 3. Выполнить
|
||
|
Первый 1. Заменить деление умножением. 2. Натуральное число заменить дробью с 3. Выполнить умножение по известному
|
Эталоны
Второй алгоритм деление дроби на натуральное число1. В частном записать дробь. 2. Числитель оставить без изменения. 3. В знаменателе записать произведение 4. Сократить если возможно дробь. 5. Выделить целую часть, если дробь не
|
|
|
А8: 1. Перевести смешанные числа в 2. Выполнить деление по известному
|
|
|
Первый алгоритм деления смешанных 1. Перевести смешанное число в неправильную дробь. 2. Выполнить деление дроби на натуральное число.
|
|
|
Второй 1. Разделить целую часть на натуральное 2. Разделить дробную часть на 3. Найти сумму, получившихся
|
Задачи на дроби
|
Правило Чтобы найти часть от числа, выраженной b
|
1 – а
– b ?
|
Правило нахождения числа по его части, выраженной дробью. Чтобы найти a = b :
|
|||
1 –
а ?
– b
|
Правило нахождения дроби, которую одно число составляет от другого. Чтобы найти,
|
1 – а
? – b
|
|
Чтобы выразить в
процентах, надо результат умножить на 100%.
|
Алгоритм 1. Прочти задачу. 2. Составить схему к условию задачи. 3. Запишите формулу. 4. Поставить в формулу значения 5. Найдите значение неизвестной переменной. 6. Ответить на вопрос задачи.
|
|
|
Алгоритм 1 способ: 2 1. Построить схему; 1. 2. Найти часть от числа, выраженную дробью; 2. Найти, 3. Найти остаток от числа. 3.
|
Ольга ТАРАКАНОВА
Решение задач на дроби
Статья посвящена решению задач с дробями.
Примеры иллюстрируются задачами из учебника:
Петерсон Л.Г. “Математика”, 3 класс (1-3), часть
2,3, что соответствует 4 классу (1–4). Основное
внимание уделяется поиску решения задачи,
который проводится либо в виде диалога учителя с
учениками, либо в виде самостоятельного
рассуждения ученика. Большое внимание уделяется
грамотному оформлению решения задачи.
I. Этап мотивации изучения дробей
Первые задачи, которые рассматривает
учитель при введении темы, – это исторические
задачи, цель которых – заинтересовать учеников
изучением нового материала. Полезно рассмотреть
две или три задачи, а потом вернуться к ним, когда
материал о дробях будет уже как следует изучен.
Задача 1
В произведении знаменитого римского
поэта I в. до н.э. Горация так описана беседа
учителя с учеником в одной из римских школ этой
эпохи.
Учитель: Пусть скажет сын Альбина,
сколько останется, если от 5 унций отнять одну
унцию?
Ученик: Одна треть.
Учитель: Правильно. Ты
сумеешь беречь свое имущество.
Пользуясь схемой, докажи, что ученик
был прав. (Ч. 1, № 1, с. 64)*.
Поиск решения. Моделируем ситуацию
с помощью отрезков. Давайте одну унцию обозначим
отрезком. Тогда 5 унций – отрезок, состоящий из 5
данных отрезков. Отнимем одну унцию, сколько
унций останется? [4 унции.] А что ответил ученик на
вопрос: “Сколько останется, если от 5 унций
отнять одну?” [Одна треть.] Если одну треть
составляет 4 унции, сколько унций составляет все
имущество? [В 3 раза больше, чем 4 унции, – значит, 12
унций.]
Схема.
Решение. 1) 5 – 1 = 4 (унц.) – осталось.
2) 4 х 3 = 12 (унц.) – все имущество.
Ответ: 12 унций.
Задача 2
Задача из “Арифметики” известного
среднеазиатского математика IX в. Мухаммеда
ибн-Мусы ал-Хорезми. “Найди число, зная, что
если отнять от него одну треть и одну четверть, то
получится 10”. (Ч. 2, № 2, с. 64).
Поиск решения. Обозначим число
отрезком, длина которого делится на 3 и на 4, это
может быть 12, или 24, или 36 и т.д. Возьмем наименьшее
из них – 12, нарисуем 12 равных отрезков или мерок.
Найдем одну треть отрезка. [12 : 3 = 4 (ч.).] Найдем одну
четверть отрезка. [12 : 4 = 3 (ч.).] Сколько частей
вычли? [4 + 3 = 7 (ч.).] Сколько частей осталось? [12 – 7 = 5
(ч.).] 10 приходится на сколько частей? [На 5.] Сколько
приходится на одну часть? [10 : 5 = 2.] Число 2
приходится на одну часть, а сколько всего частей?
[12.] Как найти число? [2 х 12 = 24.]
Решение.
1) 12 : 3 = 4 (ч.) – треть числа.
2)12 : 4 = 3 (ч.) – четверть числа.
3) 3 + 4 = 7 (ч.) – вычли.
4)12 – 7 = 5 (ч.) – осталось.
5) 10 : 5 = 2 – приходится на одну часть.
6) 2 х 12 = 24 – число.
Ответ: Это число 24.
Задача 3
Задача из “Папируса Ахмеса”
(Египет, 1850 г. до н.э.).
“Приходит пастух с 70 быками. Его
спрашивают:
– Сколько приводишь ты своего
многочисленного стада?
Пастух отвечает:
– Я привожу две трети от трети скота.
Сочти!”
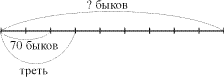
Используя схему, найди, сколько быков
было во всем стаде? (Ч. 2, № 3, с. 64)
Поиск решения.
Обозначим отрезком все стадо. Какой
должна быть длина отрезка, чтобы легко делилась
на части? [Длина должна быть кратна 9.] Обозначим
число быков отрезком, состоящим из 9 частей. Как
найти треть от 9? [9 разделить на 3, получится 3
части.] Покажем это на отрезке. Найдем две трети
от 3. Нужно 3 разделить на 3, получится 1 часть, и
взять две таких части. Сколько быков приходится
на 2 части? [70 быков.] Сколько быков приходится на
одну часть? [70 разделить на 2, получится 35 быков.]
Если 35 быков в одной части, сколько быков в 9
частях? [35 х 9 = 315.] Сколько быков в стаде? [315 быков.]
Схема.
Решение.
1) 9 : 3 = 3 (ч.) – треть стада.
2) 3 : 3 х 2 = 2 (ч.) – две трети от трети.
3) 70 : 2 = 35 (б.) – в I части.
4) 35 х 9 = 315 (б.) – в стаде.
Ответ: 315 быков.
Задача 4
Староиндийская задача (XI в.).
Есть кадамба цветок,
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда,
И на ней третья часть поместилась.
Разность их ты найди,
Ее трижды сложи
И тех пчел на кутай посади.
Только две не нашли
Себе места нигде,
Все летали то взад, то вперед и везде
Ароматом цветов наслаждались.
Назови теперь мне,
Подсчитавши в уме,
Сколько пчелок всего здесь собралось?
(Ч. 2, № 4, с. 64).
Поиск решения.
Обозначим число пчел отрезком. Сколько
мерок полезно взять в отрезке? [Число мерок
должно делиться на 5, на 3, т.е. на 15. Отрезок будет
состоять из 15 мерок.] Сколько мерок отрезка
составляет пятая часть? [15 разделим на 5,
получится 3 мерки.] Сколько мерок составляет
третья часть отрезка? [15 разделить на 3 получится 5
мерок.] Чему равна разность между третьей и пятой
частями? [Из 5 мерок вычтем 3 мерки, получится 2
мерки.] Три раза отложим по 2 мерки, сколько мерок
мы отложили? [2 умножим на 3, получится 6 мерок.]
Сколько мерок останется? [15 – 3 – 5 – 6 = 1, одна
мерка.] Сколько пчел приходится на одну мерку?
[Две.] Как найти все количество пчел? [2 умножить на
15, получится 30. Всего собралось 30 пчел.]
Схема.
Решение.
1) 15 : 5 = 3 (м.) – пятая часть.
2) 15 : 3 = 5 (м.) – третья часть.
3) 5 – 3 = 2 (м.) – разность.
4) 2 х 3 = 6 (м.) – кутай.
5) 15 – 3 – 5 – 6 = 1 (м.) – осталось.
6) 2 х 15 = 30 (пч.) – собралось.
Ответ: 30 пчел.
II. Этап решения задач на доли
Рассмотрим поиск решения, оформление
решения простых задач на доли. При составлении
схем к первым задачам полезно дроби писать над
выделенной частью (схема, 1). В дальнейшем
схема будет меняться. Изменения показаны на
схеме (3). Сначала меняется место записи дроби
и выделяется целая часть в виде единицы (схема, 2).
Сами части на отрезке сначала выделяются, затем
нет (схема, 3). Если ребенку трудно решить
задачу без деления отрезка на части, он может
продолжать их выделять.
Задача на нахождение части числа
Яблоко весит 400 г. Сколько весит часть
этого яблока. (Ч. 2, № 10, с. 68.).
Схема.
Рассуждение ученика. Обозначим
массу яблока отрезком, в котором 5 мерок. Чтобы
найти массу одной пятой части, нужно 400 разделить
на 5, получится 80. 80 граммов весит часть яблока.
Решение. 400 : 5 = 80 (г).
Ответ: 80 граммов.
Задача на нахождение числа по его
части
Сколько стоит книга, если часть ее цены составляет 30
рублей? (Ч. 2, № 2, с. 75).
Схема.
Рассуждения ученика. Известно, что часть цены книги
составляет 30 рублей. Чтобы найти цену книги, надо
30 умножить на 6, получится 180. 180 рублей цена книги.
Решение. 30 х 6 = 180 (р.).
Ответ: 180 рублей.
Составная задача с долями
Сделав 16 деталей, рабочий выполнил часть задания.
Сколько деталей ему осталось сделать? (Ч. 2, № 5, с.
75).
Схема.
Рассуждения ученика. Одна
четвертая часть задания составляет 16 деталей.
Чтобы найти объем всего задания, нужно 16 умножить
на 4, получится 64. 64 детали составляет все задание.
16 деталей сделано. Чтобы найти, сколько деталей
осталось сделать, нужно из 64 вычесть 16, получится
48. 48 деталей осталось сделать.
Решение.
По действиям с пояснениями:
1) 16 х 4 = 64 (д.) – все задание.
2) 64 – 16 = 48 (д.) – осталось сделать.
Или выражением:
16 х 4 – 16 = 48 (д.).
Ответ: 48 деталей.
Задачи на проценты
Задачи на проценты являются частным
случаем задач на доли.
Задача на нахождение части числа
Папа получил премию 8000 рублей. 1% премии
он потратил на покупку торта. Сколько стоил торт?
(Ч. 2, № 8, с. 73).
Схема.
Рассуждения ученика. 1% – это одна
сотая часть числа. Чтобы найти одну сотую часть
от числа 8000, надо 8000 разделить на 100, получится 80. 80
рублей потратил папа на торт.
Решение. 8000 : 100 = 80 (р.).
Ответ: 80 рублей.
Задача на нахождение числа по его
части
Сколько человек было в кинотеатре,
если 1% всех зрителей составляет 7 человек? (Ч.2, № 3,
с.75).
Схема.
Рассуждения ученика. Целое
составляет 100%, его нужно найти. 1% – это одна сотая
часть от целого. Одну сотую часть составляет 7
человек, значит, чтобы найти целое, нужно 7
умножить на 100, получится 700. 700 человек было в
кинотеатре.
Решение. 7 х 100 = 700 (чел.).
Ответ: 700 человек.
III. Этап решения задач на правильные
дроби
Задача на нахождение части числа
Урок длится 45 минут. части урока ученики писали
самостоятельную работу. Сколько времени она
длилась?
Схема.
Рассуждение ученика.
Найдем сначала часть от 45, для этого 45 разделим на
5, получится 9. Дальше найдем части, для этого 9
умножим на 3, получим 27. 27 минут ученики писали
самостоятельную работу.
Решение.
По действиям с пояснениями:
1) 45 : 5 = 9 (мин) – приходится на .
2) 9 х 3 = 27 (мин) – приходится на .
Или выражением: 45 : 5 х 3 = 27 (мин).
Ответ: 27 минут.
Задача на нахождение части числа,
выраженной в процентах
На строительство доставили 24 000
кирпичей. Бой составляет 3% всех кирпичей. Сколько
кирпичей разбилось по дороге? (Ч. 2, № 5, с. 85).
Схема.
Рассуждения ученика.
24 000 кирпича составляет 100%, 3% – это . Чтобы найти
части от числа 24 000,
нужно 24 разделить на 100 и умножить на 3, получится
720. 720 кирпичей разбилось.
Решение.
По действиям с пояснениями:
1) 24000 : 100 = 240 (к.) – приходится на 1%.
2) 240 х 3 = 720 (к.) – приходится на 3%.
Или выражением:
24000 : 100 х 3=720 (к.).
Ответ: 720 кирпичей.
Задача на нахождение числа по его
части
В аквариум налили 6 л воды, заполнив части его объема.
Сколько литров воды вмещает аквариум? (Ч.2, № 5, с.
90).
Схема.
Рассуждения ученика.
Известно, что части объема аквариума составляет 6 л,
следовательно, часть
составляет в 2 раза меньше, т.е. 6, деленное на 2.
Таким образом, часть
составляет 3 л. А объем аквариума в 5 раз больше,
т.е. 3, умноженное на 5. 15 л вмещает аквариум.
Решение.
По действиям с пояснениями:
1) 6 : 2 = 3 (л) – пятая часть.
2) 3 х 5 = 15 (л) – аквариум.
Или выражением:
6 : 2 х 5 = 15 (л).
Ответ: 15 литров.
Задача на нахождение числа по его
части, выраженной в процентах
Бурый медведь весит 320 кг, что
составляет 40% массы белого медведя. Какова масса
белого медведя? (Ч.2, № 5, с. 88).
Схема.
Рассуждения ученика.
Вариант 1. 320 кг составляют 40%. Чтобы
узнать, сколько килограммов приходится на 1%,
нужно 320 разделить на 40, получится 8. Чтобы узнать,
сколько килограммов приходится на 100%, нужно 8
умножить на 100, получится 800. 800 кг – масса белого
медведя.
Вариант 2. Чтобы найти число по его
части, выраженной дробью, надо разделить эту
часть на числитель и умножить на знаменатель. 40%
– это ,
значит, нужно 320 разделить на 40 и умножить на 100,
получится 800. 800 кг – масса белого медведя.
Решение.
По действиям с пояснениями:
1) 320 : 40 = 8 (кг) – приходится на 1%.
2) 8 х 100 = 800 (кг) – приходится на 100%.
Или выражением:
320 : 40 х 100 = 800 (кг).
Ответ: 800 кг.
Задача на нахождение части, которую
одно число составляет от другого
От доски длиной 9 м отпилили 4 м. Какую
часть доски отпилили? (Ч.3, № 1, с.4).
Схема.
Рассуждения ученика.
Чтобы выразить дробью часть, которую
одно число составляет от другого, надо первое
число разделить на второе. Аналогично, чтобы
выразить, какую часть отпилили от доски, нужно 4
разделить на 9, так как 4 – часть, которую
отпилили, а 9 – это целое.
Решение. 4 : 9 = (ч.).
Ответ: части.
IV. Этап решения задач на неправильные
дроби
Задачи на нахождение части числа
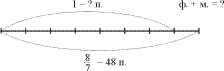
1. На стройке Дома дружбы Чебурашка
должен был за день положить 620 кирпичей, но ему
удалось положить части этого числа. На сколько Чебурашка
перевыполнил задание?
Схема.
Рассуждения ученика.
Вариант 1. 620 кирпичей приходится на
5 равных частей. Чтобы узнать, сколько кирпичей
приходится на 1 часть, нужно 620 разделить на 5,
получится 124. Чтобы узнать, сколько кирпичей
приходится на 6 таких частей, нужно 124 умножить на
6, получится 744. 744 кирпича приходится на . Чтобы
узнать, на сколько Чебурашка перевыполнил план,
нужно из 744 вычесть 620, получится 124. На 124 кирпича
Чебурашка перевыполнил задание.
Вариант 2. Чтобы найти от 620, нужно 620
разделить на 5 и умножить на 6, получится 744. Чтобы
найти, на сколько Чебурашка перевыполнил план,
нужно из 744 вычесть 620, получится 124. На 124 кирпича
Чебурашка перевыполнил задание.
Решение.
По действиям с пояснениями:
1) 620 : 5 = 124 (к.) – приходится на одну
часть.
2) 124 х 6= 744 (к.) – выполнил.
3) 744 – 620 = 124 (к.) – перевыполнил.
Или выражением:
620 : 5 х 6 – 620 = 124 (к.).
Ответ: на 124 кирпича.
2. Буратино решил купить для папы Карло
новый дом за 300 сольдо. Но пока он копил деньги,
цена дома увеличилась на 20%. Сколько теперь
должен заплатить Буратино за этот дом? Сколько
денег надо ему дополнительно заработать? (Ч.3, № 3,
с. 20).
Схема.
Рассуждения ученика.
Вариант 1. 300 сольдо приходится на
100%, значит, на 1% приходится 300, деленное на 100, т.е. 3.
Новая цена дома от старой составляет 120% – это 100 +
20. Чтобы узнать, сколько сольдо приходится на 120%,
нужно 3 умножить на 120, получится 360. 360 сольдо
стоит дом. Чтобы узнать, сколько дополнительно
заработать, нужно из 360 вычесть 300, получится 60. 60
сольдо нужно Буратино дополнительно заработать.
Вариант 2. Чтобы найти 20% от 300, нужно
300 разделить на 100 и умножить на 20, получится 60. 60
сольдо нужно дополнительно заработать Буратино.
Теперь дом будет стоить 300 плюс 60, т.е. 360 сольдо.
Решение.
Способ 1.
1) 300 : 100 = 3 (с.) – приходится на 1%.
2) 100 + 120 = 120 % – стоит дом от старой цены.
3) 3 х 120 = 360 (с.) – новая цена дома.
4) 360 – 300 = 60 (с.) – нужно заработать.
Способ 2.
1) 300 : 100 х 20 = 60 (с.) – надо заработать.
2) 300 + 60 = 360 (с.) – новая цена дома.
Ответ: 60 сольдо.
Задача на нахождение числа по его
части.
Почтальону Печкину пришло на почту в
марте 48 писем. Это составило части писем,
пришедших на почту в феврале. Сколько писем
пришло в феврале? Сколько писем пришло за эти 2
месяца? (Ч.3, №4, с. 20).
Схема.
Рассуждения ученика.
Вариант 1. 48 писем приходится на ,
т.е на 8 равных частей. Сначала узнаем, сколько
писем приходится на одну часть, для этого 48
разделим на 8, получится 6. Дальше найдем, сколько
писем приходится на 7 таких же частей. Для этого 6
умножим на 7, получится 42. Чтобы найти количество
писем за 2 месяца, нужно сложить 48 и 42, получится 90.
90 писем пришло за 2 месяца.
Вариант 2. Чтобы найти число по его
части, выраженной дробью, надо эту часть
разделить на числитель дроби и умножить на
знаменатель. Чтобы найти число, зная, что на
приходится 48, нужно 48 разделить на 8 и умножить на
7, получится 42. Чтобы найти, сколько писем пришло
за 2 месяца, надо сложить 48 и 42, получится 90. 90
писем пришло за 2 месяца.
Решение.
По действиям с пояснениями:
Способ 1.
1) 48 : 8 = 6 (п.) – приходится на 1 часть.
2) 6 х 7 = 42 (п.) – пришло в феврале.
3) 48 + 42 = 90 (п.) – пришло за 2 месяца.
Способ 2.
1) 48 : 8 х 7 = 42 (п.) – пришло в феврале.
2) 48 + 42 = 90 (п.) – пришло за 2 месяца.
Ответ: 42 письма и 90 писем.
Задача на нахождение части, которую
одно число составляет от другого
Мачеха, уходя с дочерьми на бал, велела
Золушке перебрать 100 кг крупы. Золушка, чтобы
угодить мачехе, перебрала 150 кг. Какую часть
своего задания выполнила Золушка? Вырази эту
часть в процентах. На сколько процентов Золушка
перевыполнила задание? (Ч. 3, № 7, с. 21).
Схема.
Рассуждения ученика.
Чтобы найти, какую часть задания
Золушка выполнила, нужно ту часть, которую она
выполнила, т.е. 150, разделить на само задание, т.е.
на 100, получится ,
или 150%. Так как все задание составля-ет 100%, то она
перевыполнила его на 150 – 100 = 50. На 50% Золушка
перевыполнила задание.
Решение.
1) 150 : 100 = (ч.) – выполнила.
2) =150%, 150 – 100 = 50%
– перевыполнила.
Ответ: части, 150%, 50%.
Надеемся, что рассмотренный материал
окажется полезным не только учителям, работающим
по авторской методике Л.Г. Петерсон, но и всем, кто
интересуется вопросами преподавания математики
в начальной школе.
* Здесь и далее по тексту ссылка на учебник
Петерсон Л.Г. “Математика”, 3 класс.