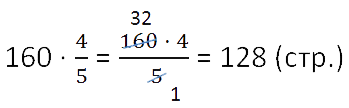Время чтения: 15 минут
В задании 3 ты можешь встретить различные задачи на части. Давай разберемся, какие типы задач могут встречаться и как их решать!
В основном существует 2 типа задач: нахождение части от числа и нахождение числа по его части. Подробно разберем каждый из них.
Нахождение части от числа 🍕
Для нахождения части от числа необходимо целое умножить на дробь, соответствующую этой части.
Нахождение числа по его части🍎
Для нахождения числа по его части необходимо часть разделить на соответствующую дробь.
🚩Сохрани формулы, чтобы не потерять👇
Изменение числа 📊
Часто встречаются задачи, где исходное число уменьшают/увеличивают НА некоторое число, либо В несколько раз. Что нужно делать в этом случае?
Предлог НА означает операцию сложения или вычитания:
- Число 5 увеличили на 2: 5 + 2 = 7
- Число 9 уменьшили на 4: 9 – 4 = 5
Предлог В означает операцию умножения или деления:
- Число 4 увеличили В 3 раза: 4 * 3 = 12
- Число 15 уменьшили в 5 раз: 15 : 5 = 3
Решение задач с помощью уравнений👩🏫
Встречаются более сложные типы задач, для которых удобнее всего составить уравнение и решить его.
Алгоритм:
- За неизвестное (x), берут искомое число;
- Записывают уравнение по условию задачи;
- Находят значение х.
Задание 1 (см. картинку ниже): Если от задуманного числа отнять 220, то получится число, которое в пять раз меньше задуманного. Найдите задуманное число.
Решение:
- Обозначим задуманное число как x.
- “Если от задуманного числа отнять 220” – эту фразу можно записать в виде: x – 220.
- “Число, которое в пять раз меньше задуманного” – это значит, что задуманное число нужно разделить на 5: x/5.
- Получается следующее уравнение: x – 220 = x/5
Аналогичным образом решается Задание 2 (листай карусель ниже)
Разбор заданий из вариантов ВПР🥴
Давай посмотрим, каким типы задач могут встретиться тебе в Задании №3 и как их решать! Ниже представлено несколько примеров для ознакомления.
Больше различных заданий ты найдешь на сайте РЕШУ ВПР: https://math6-vpr.sdamgia.ru/?redir=1
На этом все! Остались вопросы? Напиши о них в комментариях!👇
Обязательно подпишись на канал, чтобы не пропустить больше полезных статей!🧠
#впр #огэ #егэ #математика #репетитор #6класс #алгебра #часть от числа #арифметика #средняяшкола
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Нахождение дроби от числа
Поддержать сайт
Дроби используют в математике, чтобы кратко обозначить часть
рассматриваемой величины.
Но если есть часть, то обязательно есть и целое (то, отчего
была взята эта часть).
Зная целое, можно найти его часть, указанную соответствующей дробью.
Запомните!
Чтобы найти дробь (часть) от числа, нужно это число
умножить на данную дробь.
Пример. Рассмотрим задачу.
В книге 160 страниц. Юра прочитал
книги. Сколько страниц
прочитал Юра?
Прежде всего найдём в задаче целое. Это — вся книга и в ней всего
160 страниц.
Посмотрим на дробь (часть) от целого:
.
Знаменатель равен 5, значит, целое разделили
на 5 частей и мы можем найти сколько страниц составляет
часть.
- 160 : 5 = 32 (стр.) — составляет часть страниц.
- Числитель дроби равен 4, значит взято 4 части.
- 32 · 4 = 128 (стр.) — составляют книги.
Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.
Ответ: Юра прочитал 128 страниц.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Одна из простой, но интересной темы – это как найти дробь от целого (от числа).
Как найти часть от целого? У нас есть какое-то значение и нам нужно найти долю или дробь от этого значения.
К примеру, пицца весит 540 г. Сколько весит кусок пиццы, если ее разделили на 6 одинаковых кусков?
Пиццу разрезали на 6 одинаковых кусков, значит, один кусок – это 1/6 от всей пиццы.
Начертим схему: чертим отрезок, разделим его на 6 равных частей. Удобнее начертить отрезок длиной 6 или 12 см (см. статью здесь).
Если пиццу разрезали, то и весь вес надо разделить: 540:6=90 (г)
Если нужно узнать вес двух кусков, т.е. 2/6
то эти 90 взять 2 раза: 90х2= 180 (г)
В итоге, 540 : 6 х 2, или, зная правила работы с дробями — 540 х 2/6.
Видим, что для того, чтобы найти 2/6 от целой пиццы нужно просто умножить общий вес на значение этой части — 2/6.
Как-то странно. Не правда ли? И, тем не менее: чтобы найти часть, мы умножаем, а не делим. Потому что если вспомнить, что дробь, вернее, горизонтальная черта дроби — это деление. Итак:

Решение:
7/8 от 24 — 24:8х7=21
3/5 от 60 – 60:5х3=45
3/4 от 12 – 12:4х3=9
7/8 от 64 – 64:8х7=56
Похожие статьи
Задача. В пятом классе (25) учеников.
всех учащихся класса составляют мальчики.
Сколько мальчиков в классе?
| Вопросы к задаче | Ответы |
| 1. Какая величина принята за целое? |
1. За целое принято количество всех учеников класса |
| 2. Известна ли целая величина? | 2. Целое известно: (25) учеников |
| 3. Какую величину нужно найти? | 3. Количество мальчиков в классе, или часть от целого |
| 4. Как найти величину, которая приходится на 15? |
4. (25 : 5 = 5) учеников |
|
5. Как найти величину, которая приходится на 25 ? |
5. (5 · 2 = 10) мальчиков |
Ответ: в пятом классе (10) мальчиков.
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель
и результат умножить на числитель дроби, которая выражает эту часть.
Пример:
от (39) будет (39 : 3 · 2 = 13 · 2 = 26);
от (60) будет (60 : 4 · 3 = 15 · 3 = 45.)
Математика
5 класс
Урок № 67
Нахождение части целого и целого по его части
Перечень рассматриваемых вопросов
– нахождение целого по его части;
– нахождение части целого;
– моделирование условий задачи с помощью рисунка.
Тезаурус
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Частное дробей – это дробь, которая при умножении на делитель даёт делимое.
Обязательная литература
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Мы уже рассмотрели, как выполняют умножение и деление дробей. Сегодня с помощью этих действий мы будем решать задачи.
Рассмотрим две задачи.
Теперь определим, какие условия в задачах одинаковы, а какие различаются.
Общее:
- в задачах одинаковые числовые данные;
- за целое принята длина всей ленты.
Разное:
- в первой задаче целое известно (длина ленты – 18 м);
- во второй задаче целое нужно найти.
Значит, в первой задаче нужно найти часть отрезанной ленты, то есть часть от целого; а во второй задаче нужно найти всю длину ленты, то есть целое по его части.
Подобные задачи решаются в соответствие с известными правилами.
- Чтобы найти часть от целого, надо целое (соответствующее ему число) умножить на дробь, соответствующую этой части.
- Чтобы найти целое по его части, надо часть (соответствующее этой части число) разделить на соответствующую дробь.
Если вы затрудняетесь определить тип задачи, обратите внимание на союз «что» и указательное местоимение «это». Они встречаются в задачах на нахождение целого по его части.
Решение.
Смоделируем условие задачи с помощью рисунка.
После этого мы увидим, что длина целой ленты известна, а длину части следует вычислить. Значит, мы будем находить часть от целого. Используем для этого соответствующее правило. Чтобы найти часть числа, нужно число умножить на дробь. Получим:
Решение.
Опять смоделируем условие задачи с помощью рисунка.

Таким образом, мы увидим, что длина целой ленты неизвестна, а длина части указана в условии. Значит, нам надо вычислить целое по его части. Для этого мы используем подходящее правило. Чтобы найти целое, нужно число, соответствующее части, разделить на дробь.
Получится:
Итак, сегодня на уроке мы научились:
-
- моделировать условие задачи с помощью рисунка;
- устанавливать соответствие между математическим выражением и его текстовым описанием;
- решать задачи на нахождение части целого и целого по его части.
Рассмотрим старинную индийскую задачу XII века.
Из множества лотосов были подарены: богу Шиве – треть всех цветов, богу Вишну – пятая часть, а Солнцу – шестая, четвёртую долю получила богиня Бхавани, а остальные шесть частей – уважаемый учитель. Сколько было всего лотосов?
Сегодня мы с вами научимся решать такие задачи с применением действий умножения и деления, изученных ранее.
Решение.
Смоделируем условие задачи с помощью рисунка.
Общее количество лотосов обозначим за единицу. Также укажем части (лотосы), которые распределялись между всеми, кто указан в задании.
Известно, что часть, доставшаяся учителю, равна шести лотосам. Значит, если мы будем знать, какая это доля от общего количества лотосов, то придём ко второму типу задачи – вычислению целого по его части.
Итак, найдём, какая часть от общего количества цветков досталась учителю.
Для этого вычислим сначала, сколько составляют все остальные части. Сложим все дроби, соответствующие частям, приведя их к общему знаменателю 60.
Ответ: 120 цветков.
Тренировочные задания
№ 1. Какие части изображены на рисунках?
Правильные ответы:
№ 2. Подставьте в текст нужные слова:
При решении задач на ___ сначала нужно определить ___ задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение ___ от целого;
- нахождение целого по его ___.
Варианты слов для подстановки в текст: части; тип; целого.
Правильный ответ: при решении задач на части сначала нужно определить тип задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение части от целого;
- нахождение целого по его части.