Давно о геометрии не говорили, а о теореме ФАлеса (или ФалЕса?) вообще мало говорят. Хотя она весьма полезна. Начнем с формулировки, которая весьма не вразумительна, чем и объясняется не популярность данной теоремы.
Мутно, долго, не понятно. Мне больше нравится другая формулировка.
Тоже не понятно, но элегантно и коротко.
Задачи, которые решаются с помощью данной теоремы, довольно специфичны. Но есть одна задача на построение, которую можно встретить в реальной жизни. Это задача о делении отрезка в заданном отношении.
Суть вопроса: Дан отрезок. Его нужно поделить на два куска, чтобы их длины относились, как 2 : 5. Кусков может быть сколько угодно и отношение, может быть каким угодно. Алгебраически задача решается крайне легко: находим общее количество частей (2 + 5 = 7), делим длину отрезка на общее количество частей, находим длину каждого куска.
Но алгебраическое решение не всегда прокатывает. Например, мы не можем найти длину отрезка, или при делении получаются не целые числа. Тогда можно воспользоваться геометрическим способом.
Во-первых, проводим луч из конца отрезка. Любой, в любую сторону.
Дальше, на этом луче от точки А откладываем 7 (общее количество частей) равных отрезков.
Последнюю получившуюся точку – J соединяем с точкой В, а затем через каждую точку луча проводим прямую параллельную JB.
Таким образом, мы разделили отрезок АВ на 7 равных частей (по теореме Фалеса). Отсчитываем две части и ставим точку. Получаем: AK : KB = 2 : 5.
Вот таким простым образом, вы можете поделить свою комнату с соседом в любом отношении. Если вам кажется, что построение такого количества параллельных прямых дело сложное, то подумайте о перпендикулярах.
Урок 6. Правильные и неправильные части величин
Гипермаркет знаний>>Математика>>Математика 4 класс>> Урок 6. Правильные и неправильные части величин

Задача. Определи по рисунку, какую часть отрезка CD составляет АВ? Какую часть АВ составляет CD?
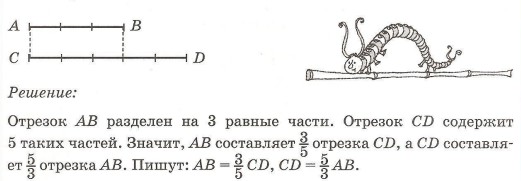
Правильные дроби величин называются их правильными частями, а неправильные дроби — неправильными частями. Например, отрезок АВ — это правильная часть отрезка CD, а отрезок CD — неправильная часть АВ.
Правильные части меньше целого, а неправильные части — больше или равны целому (они содержат столько же или больше долей, чем в целом). Отсюда и название — неправильные части. Для них не выполняются известные правила о взаимосвязи части и целого.
1. Определи по рисунку, какую часть отрезка KD составляет отрезок — ЕМ? Какую часть ЕМ составляет KD? Сделай записи и назови правильные и неправильные части.
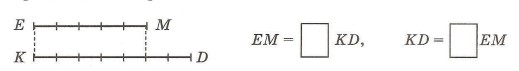
2. Какую часть отрезка CD составляет отрезок АВ? Какую часть АВ составляет CD? Сделай записи и назови правильные и неправильные части.
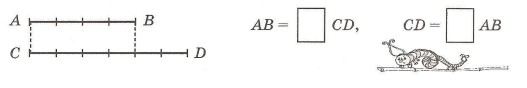
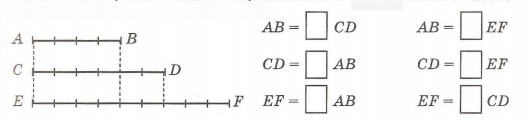
3. Какую часть каждый из отрезков АВ, CD и EF составляет от остальных отрезков? Назови правильные и неправильные части. Сделай записи.
4. Запиши с помошью фигурных скобок:
а) множество правильных дробей со знаменателем 5;
б) множество неправильных дробей с числителем 4.
5. Подчеркни одной чертой дроби, выражаюшие правильные части величин, а двумя чертами — неправильные части:
![]()
6. Составь задачу по схеме и придумай к ней две обратные задачи:
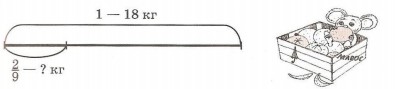
Как найти: а) часть числа; б) число по его части; в) часть, которую одно число составляет от другого?
7. “Блиц-турнир”.
а) Найди ![]() от числа m.
от числа m.
б) Найди 15% от числа n.
в) Найди число, ![]() которого составляют k.
которого составляют k.
г) Найди число, 36% которого составляют t.
д) Какую часть число х составляет от числа у?
8. На горе за селом катается 72 человека. На лыжах катается ![]() всех людей, а остальные — на санках. Сколько человек катается на лыжах и сколько на санках?
всех людей, а остальные — на санках. Сколько человек катается на лыжах и сколько на санках?
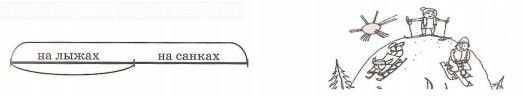
9. Василий прочитал 200 страниц, что составляет ![]() всей книги. Сколько страниц ему осталось прочитать?
всей книги. Сколько страниц ему осталось прочитать?

10. Из 100 кг винограда получают 25 кг изюма. Какую часть винограда составляет испарившаяся вода? Вырази эту часть в процентах.

11. Реши уравнения с комментированием и сделай проверку:
а) (180 : а – 54) : 6 = 6; б) 45 + (71 – b • 9) = 80.
12. Игра “Эстафета”. Выполни действия и определи, какая из полученных дробей меньше? Почему?
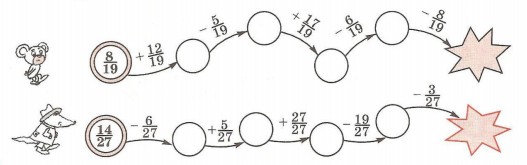
13. а) 83 685 + (20 216 – 537 999 : 1 507) • 80 – 502 • 968;
б) (2 908 • 537 – 1 243 074) : 6 – 7 840 • 400 : 490 + 953 313.
14*. Сколько отрезков ты видишь на чертеже? Назови их.
![]()
Найди пересечение отрезков АВ и CD, АС и BD, ВС и AD, АС и CD.
15*. Вставь пропущенные числа:
16*. Книга дороже карандаша в 3 раза, а альбом дороже карандаша в 5 раз. Книга дороже карандаша на 28 р. Сколько стоит альбом?
Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 2. – М.: Издательство “Ювента”, 2005, – 64 с.: ил.
Учебники по всему предметам скачать, разработка планов уроков для учителей, Математика для 4 класса онлайн
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Вычисление координат некоторой точки С, которая делит заданный отрезок АВ в определенном отношении, может быть выполнено по формулам:
хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ),
где (хА; уА) и (хВ; уВ) – координаты концов заданного отрезка АВ; число λ = АС/СВ – отношение, в котором отрезок АВ делится точкой С, имеющей координаты (хС; уС).
Если отрезок АВ делится точкой С пополам, то число λ = 1 и формулы для хС и уС примут вид:
хС = (хА + хВ)/2, уС = (уА + уВ)/2.
Нужно иметь ввиду, что в задачах λ – это отношение длин отрезков, а поэтому числа, входящие в данное отношение не есть длины самих отрезков в заданной единице измерения. Например, АС = 12 см, СВ = 16 см: λ = АС/СВ = 12 см / 16 см = 3/4.
1. Поиск координат середины некоторого отрезка, по заданным координатам его концов
Пример 1.
Точки А(-2; 3) и В(6; -9) – концы отрезка АВ. Найти точку С, являющиеся серединой отрезка АВ.
Решение.
В условии задачи задано, что хА = -2; хВ = 6; уА = 3 и уВ = -9. Требуется найти С(хС ; уС).
Применяя формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:
хС = (-2 + 6)/2 = 2, уС = (3 + (-9))/2 = -3.
Таким образом, точка С, являющаяся серединой отрезка АВ, имеет координаты (-2; 3) (рис. 1).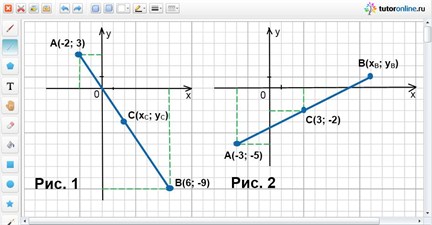
2. Вычисление координат конца некоторого отрезка, зная координаты его середины и другого конца
Пример 2.
Одним концом отрезка АВ является точка А, с координатами (-3; -5), а его серединой точка С(3; -2). Вычислите координаты второго конца отрезка – точки В.
Решение.
По условию задачи становится ясно, что хА = -3; уА = -5; хС = 3 и уС = -2.
Подставив эти значения в формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:
3 = (-3 + хВ)/2 и
-2 = (-5 + уВ)/2.
Решив первое уравнение относительно хВ и второе относительно уВ, найдем: хВ = 9 и уВ = 1, получается, что нужная точка В будет задаваться координатами (9; 1) (рис. 2).
3. Вычисление координат вершин некоторого треугольника по заданным координатам середин его сторон
Пример 3.
Серединами сторон треугольника АВС являются точки D(1; 3), E(-1; -2) и F(4; -1). Найти координаты вершин А, В и С данного треугольника.
Решение.
Пусть точка D и есть середина стороны АВ, точка Е – середина ВС и точка F – середина сторона АС (рис. 3). Необходимо найти точки А, В и С.
Обозначаем вершины треугольника через А(хА; уА), В(хВ; уВ) и С(хС; уС) и зная координаты точек D, Е и F, по формулам хС = (хА + хВ)/2, уС = (уА + уВ)/2 получим:
{1 = (хА + хВ)/2, 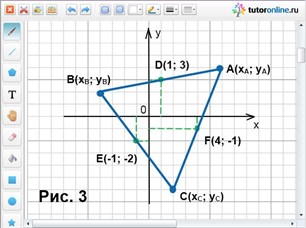
{-1 = (хВ + хС)/2,
{4 = (хА + хС)/2,
и
{3 = (уА + уВ)/2,
{-2 = (уВ + уС)/2,
{-1 = (уА + уС)/2.
Приведем уравнения к целому виду:
{хА + хВ = 2,
{хВ + хС = -2,
{хА + хС = 8,
и
{уА + уВ = 6,
{уВ + уС = -4,
{уА + уС = -2.
Решив системы, получим:
хА = 6; хВ = -4; хС = 2.
уА = 4; уВ = 2; уС = -6.
Точки А(6; 4), В(-4; 2) и С(2; -6) и есть необходимые вершины треугольника.
4. Вычисление координат точек, которые делят отрезок в определенном отношении, по заданным координатам концов этого отрезка
Пример 4.
Отрезок АВ поделен точкой С в отношении 3 : 5 (считая от точки А к точке В). Концы отрезка АВ – точки А(2; 3) и В(10; 11). Найти точку С.
Решение.
В условии задачи сказано, что хА = 2; хВ = 10; уА = 3; уВ = 11; λ = АС/СВ = 3/5. Найти С(хС; уС) (рис. 4).
по формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:
хС = (2 + 3/5 · 10) / (1 + 3/5) = 5 и уС = (3 + 3/5 · 11) / (1 + 3/5) = 6. Таким образом, имеем С(5; 6).
Выполним проверку: АС = 3√2, СВ = 5√2, λ = АС/СВ = 3√2/5√2 = 3/5.
Замечание. В условии задачи указано, что деление отрезка производится в заданном отношении от точки А к точке В. Если бы это не уточнялось, то задача имела бы два решения. Второе решение: деление отрезка от точки В к точке А.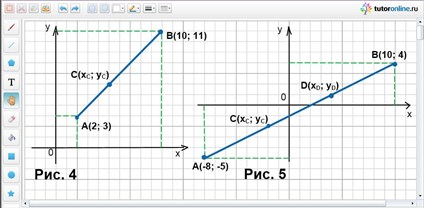
Пример 5.
Некоторый отрезок АВ разделен в отношении 2 : 3 : 5 (считая от точки А к точке В), его концы – есть точки с координатами А(-11; 1) и В(9; 11). Найти точки деления данного отрезка.
Решение.
Обозначим точки деления отрезка от А к В через С и D. В условии задачи дано, что
хА = -11; хВ = 9; уА = 1; уВ = 11. Найти С(хС; уС) и D(хD; уD), если АС : СD : DB = 2 : 3 : 5.
Точка С делит отрезок АВ в отношении λ = АС/СВ = 2/(3 + 5) = 2/8 = 1/4.
По формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:
хС = (-11 + ¼ · 9) / (1 + 1/4) = -7 и уС = (1 + ¼ · 11) / (1 + 1/4) = 3.
Таким образом, С(-7; 3).
Точка D – есть середина отрезка АВ. Применив формулы хD = (хА + хВ)/2, уD = (уА + уВ)/2, найдем:
хD = (-11 + 9)/2 = -1, уD = (1 + 11)/2 = 6. Значит, D имеет координаты (-1; 6).
5. Вычисление координат точек, которые делят отрезок, если заданы координаты концов этого отрезка и число частей, на которые этот отрезок разделен
Пример 6.
Концы отрезка – точки А(-8; -5) и В(10; 4). Найти точки С и D, которые делят этот отрезок на три равные части.
Решение.
Из условия задачи известно, что хА = -8; хВ = 10; уА = -5; уВ = 4 и n = 3. Найдем С(хС; уС) и D(хD; уD) (рис. 5).
Найдем точку С. Она делит отрезок АВ в отношении λ = 1/2. Деление производим от точки А к точке В. По формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) имеем:
хС = (-8 + ½ · 10) / (1 + 1/2) = -2 и уС = (-5 + ½ · 4) / (1 + 1/2) = -2. Таким образом, С(-2; -2).
Деление отрезка СВ выполняется в отношении 1 : 1, поэтому используем формулы
хD = (хА + хВ)/2, уD = (уА + уВ)/2:
хD = (-2 + 10)/2 = 4, уD = (-2 + 4)/2 = 1. Таким образом, D(4; 1).
Точки деления С(-2; -2) и D(4; 1).
Замечание: Точку D можно найти, производя деление отрезок АВ в отношении 2 : 1. В таком случае надо будет снова применить формулы хD = (хА + λхВ) / (1 + λ), уD = (уА + λуВ) / (1 + λ).
Пример 7.
Точки А(5; -6) и В(-5; 9) – концами отрезка. Найти точки, которые поделят данный отрезок на пять равных частей.
Решение.
Пусть последовательные точки деления от А к В будут С(хС; уС), D(хD; уD), Е(хE; уE) и F(хF; уF). В условия задачи сказано, что хА = 5; хВ = -5; уА = -6; уВ = 9 и n = 5.
Найдем по формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) точку С. Она делит отрезок АВ в отношении λ = 1/4:
хС = (5 + 1/4 · (-5)) / (1 + 1/4) = 3 и уС = (-6 + 1/4 · 9) / (1 + 1/4) = -3, получаем, что точка С имеет координаты (3; -3).
Деление отрезка АВ точкой D производится в отношении 2 : 3 (т.е. λ = 2/3), поэтому:
xD = (5 + 2/3 · (-5)) / (1 + 2/3) = 1 и уD = (-6 + 2/3 · 9) / (1 + 2/3) = 0, значит D(1; 0).
Найдем точку Е. Она делит отрезок АВ в отношении λ = 2/3:
XЕ = (5 + 3/2 · (-5)) / (1 + 3/2) = -1 и уЕ = (-6 + 3/2 · 9) / (1 + 3/2) = 3. Таким образом, Е(-1; 3).
Точка F делит отрезок АВ в отношении λ = 4/1, поэтому:
XF = (5 + 4 · (-5)) / (1 + 4) = -3 и уF = (-6 + 4 · 9) / (1 + 4) = 6, F(-3; 6).
Точки деления С(-2; -2); D(4; 1); Е(-1; 3) и F(-3; 6).
Остались вопросы? Не знаете, как решить задачу на деление отрезка?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
|
Вспомним общие термины: Отрезок – часть прямой, которая ограничена 2 точками. Отношение – результат деления одной величины на другую. Соответственно, можно понять, что отношением двух отрезков называется результат деления одного отрезка на другой. Благодаря отношению отрезков, во сколько раз один отрезок больше/меньше другого. Здесь нужно оговориться, что эти отрезки должны иметь длины в одних и тех же единицах измерения, например, сантиметрах. В ином случае, отношение найти не получится и оно не будет иметь смысла. Нужно будет перевести длины в одинаковые единицы измерения. Пример Отрезок AB = 5 см. Отрезок CD = 20 мм. Переведём миллиметры в сантиметры: 20 мм = 2 см. Теперь можно найти отношение: AB/CD = 5/2 = 2,5. Значит, отрезок AB больше отрезка CD в 2,5 раз. автор вопроса выбрал этот ответ лучшим
Galina7v7 7 лет назад Отношением двух отрезков в геометрии считается отношение их длин ,выраженных в той или иной метрической мере .То есть дан отрезок АВ = 5,7 см и отрезок ВС =10 см , то отношением отрезков АВ и ВС считается выражение : АВ : ВС = 5,7 см : 10 см = 0 ,57. В геометрии есть замечательная теорема Фалеса , позволяющая разделить любой отрезок в нужном отношении. Пусть дан отрезок АС .Требуется разделить его в отношении 2 : 3. Для решения откладываем отрезок АС.Из точки А проводим произвольно второй луч АД ,получили угол ДАС.На стороне угла ДА откладываем 5 = (2+3 ) равных отрезка,небольших ,но соразмерных с чертежом.АД1 = Д1Д2 = Д2Д3 =..Д4Д5.Точку Д5 соединяем с т.С.и проводим параллельные отрезки Д5С , Д4С4 ,…и так далее.Видим , что и исходный отрезок АС делится на 5 равных частей.Затем берем 2 части и остаётся 3 части , то есть отрезок разделили В ОТНОШЕНИИ 2: 3.
Само слово отношение определяет, как соотнести два предложенных отрезка. если вы слышите найти отношение, значит обязательно надо разделить одну величину на другую. Проще и красивее делить меньшую на большую -тогда всегда получается правильная дробь. Отношением длин двух отрезком тогда будет дробь у которой в числителе окажется длина одного отрезка, а в знаменателе – второго. При этом возможны два варианта ответа, которые можно рассмотреть на примере. Общий случай – длины не делятся без остатка. Например даны отрезки длиной 5 и 7 сантиметров. Их отношением будет дробь 5/7. Второй случай, частный. Длины отрезков делятся друг на друга. Пример 3 и 6. Тогда их отношением будет дробь 3/6 или 1/2 – происходит сокращение. natasha lykova 8 лет назад Отношением двух отрезков называется отношение тех чисел, которые выражают длины этих отрезков при условии, что отрезки измерены единицами одного наименования. В арифметике отношением одного числа к другому называется частное от деления первого числа на второе, поэтому можно сказать, что отношением одного отрезка к другому является частное от деления длины первого отрезка на длину второго, если длины отрезков выражены в единицах одного наименования. Если даны два отрезка АВ = 6 см и СD = 4 см, то отношение отрезка АВ к отрезку СD равно АВ/СД=6/4=1,5. В этом случае делимое (АВ) называется предыдущим членом отношения, делитель (СD) — последующим членом отношения, а частное (1,5) — отношением. Знаете ответ? |
Какую часть каждый из отрезков AB, CD и EF составляет от другого отрезка? Сделай записи и найди правильные и неправильные части.

AB = ☐ CD
CD = ☐ AB
EF = ☐ AB
AB = ☐ EF
CD = ☐ EF
EF = ☐ CD

reshalka.com
ГДЗ учебник по математике 4 класс Петерсон. Часть 2. 12 урок. Номер №7
Решение
Отрезок AB разделен на 5 равных частей;
отрезок CD разделен на 4 равные части;
а отрезок EF состоит из 8 частей.
Значит:
AB составляет
5
4
отрезка CD;
AB составляет
5
8
отрезка EF;
CD составляет
4
5
отрезка EF;
CD составляет
4
8
отрезка EF;
EF составляет
8
5
отрезка AB;
EF составляет
8
4
отрезка CD.
A
B
=
5
4
C
D
A
B
=
5
8
E
F
C
D
=
4
5
A
B
C
D
=
4
8
E
F
E
F
=
8
5
A
B
E
F
=
8
4
C
D
