ГДЗ и решебники
вип уровня
- ГДЗ
- 5 класс
- Математика
- Виленкин
- Задание 957
Условие
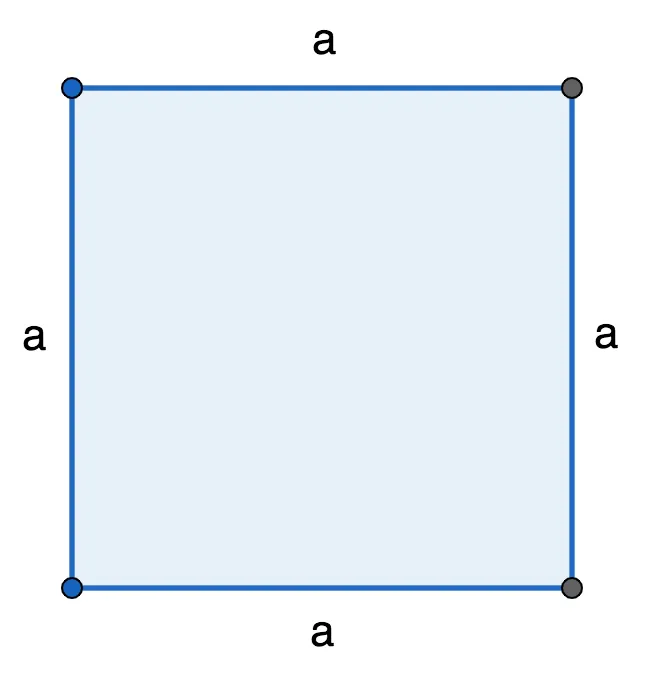
Какую часть периметра квадрата составляет длина одной стороны? длина трёх сторон?
Решение 1
Решение 2
Решение 3
Популярные решебники
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,912 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Помогите! Какую часть периметра квадрата составляет длина одной стороны? длина трёх сторон?
Найди верный ответ на вопрос ✅ «Помогите! Какую часть периметра квадрата составляет длина одной стороны? длина трёх сторон? …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Математика » Помогите! Какую часть периметра квадрата составляет длина одной стороны? длина трёх сторон?
Содержание
- Как найти периметр квадрата
- Основные определения
- Формула нахождения периметра квадрата
- Если известна длина стороны
- Если известна длина диагонали
- Решение задач
- 1. Найти периметр квадрата, диагональ которого равняется √4 см.
- 2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах
- 3. Периметр квадрата 48 см. Чему равна его сторона?
- 4. Периметр квадрата 20 см. Как найти его площадь?
- Нахождение периметра квадрата: формула и задачи
- Формула вычисления периметра
- По длине стороны
- По длине диагонали
- Примеры задач
- Как найти периметр фигуры
- Определение периметра
- Формула нахождения периметра
- Треугольник
- Квадрат и ромб
- Прямоугольник и параллелограмм
- Равнобедренная трапеция
- Решение задач
- Как найти периметр квадрата
- Что такое периметр квадрата
- Способы вычисления
- По длине стороны
- По длине диагонали
- По площади
- По радиусу описанной окружности
- По радиусу вписанной окружности
- Формула периметра квадрата
- Первый способ вычисления периметра квадрата
- Второй способ вычисления периметра квадрата
Как найти периметр квадрата
О чем эта статья:
2 класс, 3 класс
Основные определения
Квадратом принято называть правильный четырёхугольник, у которого равны все углы и стороны. Это частный случай прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов.
Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула нахождения периметра квадрата
Как находится периметр квадрата, всегда зависит от исходных данных. Рассмотрим две формулы, которые проходят 2 и 3 класс.
Если известна длина стороны
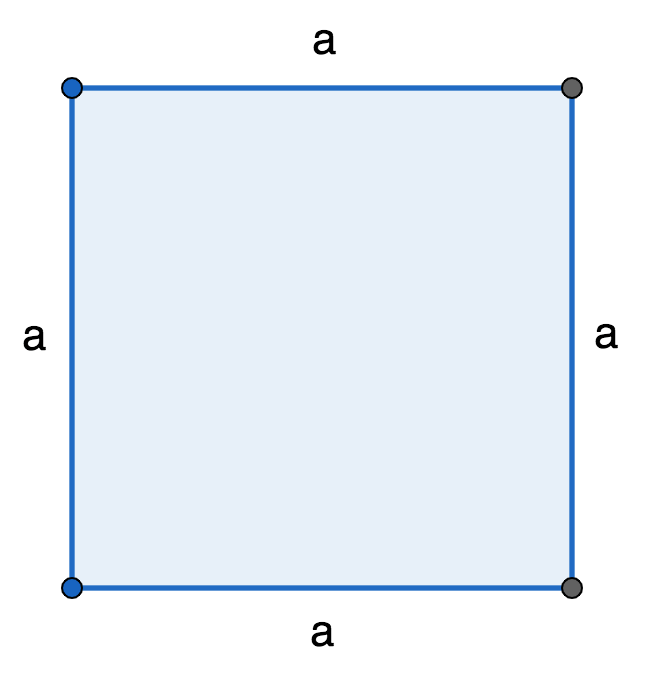
P = a + a + a + a, где a — сторона.
Так как все стороны фигуры равны, можно использовать формулу в таком виде: P = 4 * a
Если известна длина диагонали
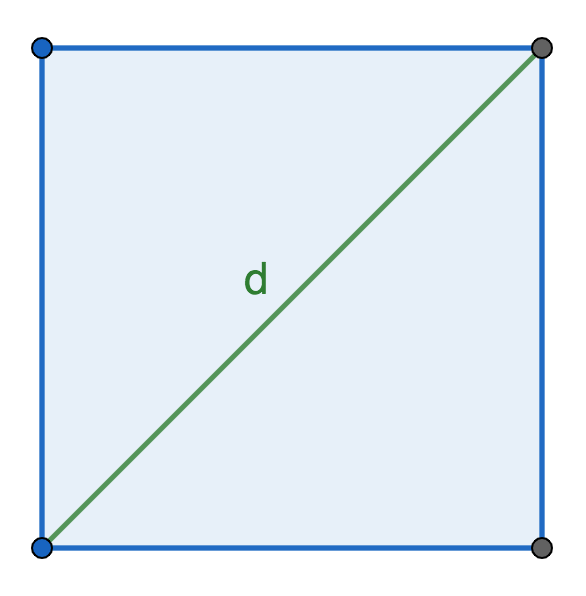
P = d * 2 * √2, где d — диагональ.
Диагональ — это отрезок, который соединяет противоположные стороны фигуры.
Математика, как и любой другой предмет не сразу дается легко. Сложности могут возникать из-за неумения быстро делать простые арифметические действия — именно поэтому полезно практиковаться в решении примеров, как можно чаще. Давайте сделаем это прямо сейчас!
Занимайся изучением математики онлайн! Курсы по математике для учеников с 1 по 11 классы!
Решение задач
1. Найти периметр квадрата, диагональ которого равняется √4 см.
- Воспользуемся формулой P = d * 2 * √2;
- P = √4 * 2 * √2;
2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах
- Воспользуемся формулой P = 4 * a;
- P = 4 * 97
3. Периметр квадрата 48 см. Чему равна его сторона?
- Воспользуемся формулой P = 4 * a;
- Значит a = P : 4;
- a = 48 : 4;
4. Периметр квадрата 20 см. Как найти его площадь?
- Воспользуемся формулой P = 4 * a;
- Тогда a = P : 4;
- a = 20 : 4 = 5 см;
- Воспользуемся формулой S = a * a;
- Значит S = 5 * 5;
Источник
Нахождение периметра квадрата: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.
Формула вычисления периметра
По длине стороны
Периметр (P) квадрата равняется сумме длин его сторон.
P = a + a + a + a
Так как все стороны квадрата равны, формулу можно представить в виде произведения:
P = 4 ⋅ a
По длине диагонали
Периметр (P) квадрата равен произведению длины его диагонали на число 2√ 2 :
P = d ⋅ 2√ 2
Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√ 2 .
Примеры задач
Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.
Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.
Задание 2
Найдите периметр квадрата, диагональ которого равняется √ 2 см.
Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √ 2 см ⋅ 2√ 2 = 4 см.
Решение 2:
Выразим длину стороны через диагональ:
a = d / √ 2 = √ 2 см / √ 2 = 1 см.
Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.
Источник
Как найти периметр фигуры
О чем эта статья:
Определение периметра
Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Формула нахождения периметра
Рассмотрим пять фигур.
Треугольник
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.
P = 3 * a, где a — длина стороны.
Квадрат и ромб
Периметр квадрата — это произведение длины стороны на четыре. Формула ромба выглядит идентично.
P = 4 * a, где a — длина стороны.
Прямоугольник и параллелограмм
Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно.
P = 2 * (a + b), где a — ширина, b — высота.
Записывайтесь на онлайн уроки по математике к лучшим преподавателям! Уроки для учеников с 1 по 11 классы!
Равнобедренная трапеция
Формула для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.
P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?
- Для использования формулы P = 2 * (a + b), нам нужно найти ширину;
- Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные переменные в формулу: (10 + 8) * 2 = 36 см;
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
- Используя формулу P = a + b + c вычислим сумму двух неизвестных сторон: 40 — 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны 17см.
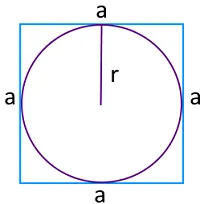
Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга.
- Периметр круга равен длине ограничивающей его окружности. Значит P = L = d * π;
- Сторона квадрата для круга является диаметром, поэтому P = 20 * 3,14;
Источник
Как найти периметр квадрата
Что такое периметр квадрата
Квадрат — это правильный четырехугольник, все его стороны и углы равны.
Про него также говорят, что это частный случай прямоугольника или ромба.
Периметр квадрата — это сумма длин всех его сторон или произведение одной его стороны на 4.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Способы вычисления
Для вычисления периметра квадрата применяется несколько видов несложных формул.
По длине стороны
Самый простой способ, если известна величина одной из его сторон. Сразу вспоминаем, что мы имеем дело с правильным четырехугольником, и подставляем значение в уравнение:
где (a) — это сторона фигуры.
По длине диагонали
Если известна только диагональ правильного прямоугольника, формула для нахождения суммы всех его ребер будет выглядеть так:
что следует из соотношения длин стороны и диагонали (d=asqrt2)
По площади
Зная площадь фигуры, найти ее периметр можно так:
По радиусу описанной окружности
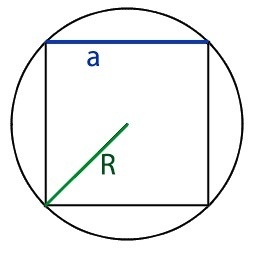
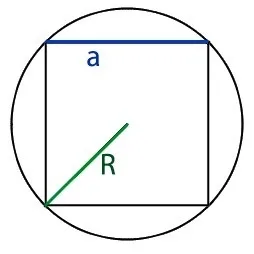
Радиус описанной вокруг квадрата окружности — это половина его диагонали. Формула для нахождения P в данном случае:
где R — радиус данной окружности.
По радиусу вписанной окружности
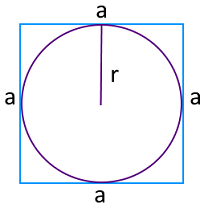
Радиус вписанной окружности — это половина величины ребра правильного прямоугольника. Таким образом, уравнение для нахождения P выглядит так:
где r — радиус вписанной окружности.
Найти P квадрата, если его ребро a равно 5 см.
Так как P = 4a, подставляем сюда известное значение, и получается (P = 4times5= 20 см.)
Узнать P правильного четырехугольника, если его диагональ d равна 6 см.
Используем формулу (P;=;2dsqrt2) и подставляем известное значение. Получается: (P = 2 * 6sqrt2 = 12sqrt2 см.)
Ответ: (12sqrt2 см.)
Площадь квадрата равна 16 см². Каков периметр?
Мы знаем, что (P;=;4sqrt S\) . Значит, подставляя значение в формулу (P;=;4sqrt S\) , мы имеем: (P;=;4sqrt 16 = 4times4 = 16) см.
Известно, что 1/2 диагонали правильного прямоугольника составляет (9sqrt2\ ) см. Вычислить P.
1/2 диагонали имеющейся фигуры — это как раз радиус описанной окружности. Подставляем значение в уравнение (P;=;4Rsqrt2\) . Получается: (P;=;4Rsqrt2 = 4times9sqrt2timessqrt2 = 72) см.
Дан квадрат и вписанная в него окружность. Половина стороны a фигуры равна 7 см, посчитать P.
Так как половина стороны данной фигуры — это радиус вписанной в нее окружности. Используем метод нахождения по радиусу вписанной окружности: (P;=;8r\) . Подставляем известное значение: (P;=;8r = 8times7 = 56 см.)
Источник
Формула периметра квадрата
Квадрат — правильный четырёхугольник, у которого все стороны и углы равны между собой. Может быть определён как прямоугольник, у которого две смежные стороны равны между собой, или как ромб, у которого все углы прямые. У квадрата есть две диагонали, соединяющие несмежные вершины.
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
Первый способ вычисления периметра квадрата
Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).
[ LARGE P = 4 cdot a ]
где:
P — периметр квадрата
a — длина стороны квадрата
Второй способ вычисления периметра квадрата
Периметр квадрата равен произведению длины его диагонали на два корня из двух.
где:
P — периметр квадрата
a — длина стороны квадрата
d — длина диагонали квадрата
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.
© 2021 Все калькуляторы online
Копирование материалов запрещено
Источник
Если длины даны в разных единицах, периметр квадрата найти невозможно. Поэтому, чтобы правильно решить эту проблему, все данные должны быть переведены в одну и ту же единицу измерения.
Формулы периметра и программы для расчета периметра
Квадрат также может быть прямоугольником, ромбом или прямоугольником, если у него одинаковые длины диагоналей, сторон и углов.
7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:
| AC ┴ BD | AO = BO = CO = DO = | d |
| 2 |
8. пересечение диагоналей называется центром квадрата, а также является центром антиклиники и периклиники.
ΔABC=ΔADC=ΔBAD=ΔBCDΔACB=∠ACD=∠BDC=∠BDA=∠CAD=∠DBC=∠DBA= 45°
10. Две диагонали делят квадрат на четыре равных треугольника, эти треугольники являются изоклетками и прямоугольниками.
Как посчитать периметр помещения
Периметр — это длина геометрической фигуры от внешней границы.
Периметр комнаты — это сумма сторон комнаты. Поэтому для вычисления периметра необходимо сложить все стороны.
Человек для расчета периметра помещения:.
A — длина помещения — B — ширина помещения, и
Для произвольных конфигураций помещений используются более сложные типы, а расчеты могут быть произведены быстрее и проще с помощью программного обеспечения для проектирования.
Проектные компании могут заказать расчет периметра помещения на основании технического или дизайнерского задания. Используйте современное программное обеспечение для 2D проектирования, чтобы выполнить расчеты для любой конфигурации в соответствии с проектом.
Онлайн-программа позволяет быстро выполнить это простое математическое упражнение. Просто введите исходные значения в соответствующие поля и нажмите на кнопку.
На этой странице вы найдете самый простой онлайн-калькулятор межевания. С помощью этого калькулятора вы можете рассчитать границы помещения в один клик, если вам известны длина и ширина.
Что необходимо знать о квадрате?
Прежде чем начать расчет, вам необходимо знать некоторую важную информацию о количестве
- все стороны квадрата равны;
- все углы квадрата прямые;
- площадь квадрата – это способ исчисления того, как много места занимает фигура в двухмерном пространстве;
- двухмерное пространство – это лист бумаги или экран компьютера, где нарисован квадрат;
- периметр не является индикатором наполненности фигуры, однако позволяет работать с его сторонами;
- периметр – это сумма всех сторон квадрата;
- подсчитывая периметр, мы оперируем одномерным пространством, что означает фиксацию результата в метрах, а не метрах квадратных (площадь).
Границы — это обычный геометрический термин в данной задаче. Чтобы понять, что такое граница, нужно спланировать любой многоугольник и вооружиться линейкой. В переводе с греческого этот термин означает «измерение».
Способы вычисления
Существуют различные простые виды вычисления периметра квадрата.
Самый простой способ — узнать цену одной из его сторон. Мы быстро вспомним, что имеем дело с правильным четырехугольником и заменим цену в уравнении.
Здесь Ǿ (a ) — это сторона фигуры.
По площади
Зная площадь фигуры, мы можем найти его границы таким образом.
Радиус окружности, описанной вокруг квадрата, равен половине его диагонали. Лицо, находящее P в данном случае, выглядит следующим образом
где R — радиус конкретного цикла.
По радиусу вписанной окружности
Радиус внутри клетки в два раза меньше, чем у обычного прямоугольного прыща. Таким образом, уравнение для нахождения P имеет вид
где r — радиус цикла регистрации.
Если диаметр прыща A равен 5 см, найдите площадь квадрата P.
Поскольку p = 4a, меняя известные значения местами, имеем (p = 4 раза5 = 20 см.
Если диагональ d равна 6 см, находим обычный четырехугольник p.
Используйте тип (p ; = ; 2d sqrt2 ) для замены известного значения. Доказательство: (p = 2 * 6 sqrt2 = 12 sqrt2 см).
Площадь квадрата равна 16 см². Каковы границы?
Мы видим, что (p ; = ; 4 sqrt s \\). Поэтому заменим ᢙ (p ; = ; 4 sqrt s sqrt s) на формулу.
Мы знаем, что половина диагонали нормального прямоугольника равна ዄ(9 sqrt2 sqrt s sqrt s sqrt s sqrt s ) см. Рассчитайте p.
1/2 диагонали существующей фигуры в точности равна радиусу круга. Подставьте это значение в уравнение (P ; = ; 4R sqrt2 \\). Доказательство: (P ; = ; 4R sqrt2 = 4 раза9 sqrt2 раза sqrt2 = 72 ) см.
Даются вырезанные квадрат и круг. Половина стороны a фигуры равна 7 см, вычислите P.
поскольку половина стороны этой фигуры равна радиусу вписанной в нее окружности. Используйте метод для нахождения радиуса конечного цикла: Ј(P ; = ; 8r \\). Замените известные значения на: ɑ (P ; = ; 8r = 8 7 = 56 см).
Таким образом, мы видим, что периметр 25-метрового прямоугольника соответствует длине 20,5 метра. В данном случае это размер экрана, используемый в данной конфигурации.
Формула периметра квадрата
Квадрат — это обычный четырехугольник, у которого все стороны и углы равны друг другу. Его можно определить как прямоугольник с двумя смежными сторонами, равными друг другу, или ромб со всеми правильными углами. Квадрат имеет две диагонали, соединяющие несмежные вершины.
Периметр геометрической фигуры — это общая длина границы плоской геометрической фигуры. Периметр равен длине.
Второй способ вычисления периметра квадрата
Периметр квадрата равен произведению длины диагонали и двух корней из 2.
Где P — периметр квадрата a — длина сторон квадрата d — длина диагонали квадрата
Если вам понравился этот материал и вы считаете его полезным, пожалуйста, поделитесь им со своими друзьями.
Биткоин, Bitcoin, часто Bitcoin (от ‘bit’ или ‘coin’) — одноранговая электронная платежная система (такая как torrent или e-mule), использующая одноименную виртуальную валюту.
Равное количество газа (V) при равных условиях (температура T и давление P) содержит одинаковое число молекул.
Четырехугольник — это многоугольник, состоящий из четырех точек (вершин) и четырех отрезков (сторон), которые соединены попарно.
Периметр квадрата равен сумме четырех длин его сторон или произведению четырех длин любой стороны квадрата (так как длина квадрата одинакова со всех сторон).
Местонахождение.
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц и справочных материалов для основных отраслей промышленности.
Самый простой способ производить расчеты в Интернете — использовать соответствующие онлайн-инструменты. Используйте поиск, чтобы найти нужный инструмент на нашем сайте.
calcsbox.com.
На этом сайте используется технология LaTeX. Поэтому, пожалуйста, подождите, пока страница полностью загрузится, прежде чем набирать текст, и формулы будут отображаться правильно.
Проектные компании могут заказать расчет периметра помещения на основании технического или дизайнерского задания. Используйте современное программное обеспечение для 2D проектирования, чтобы выполнить расчеты для любой конфигурации в соответствии с проектом.
Как найти периметр квадрата
После «черного квадрата» Казимира Малевича обычный четырехугольник стал самой загадочной фигурой в мире математики. У него есть свои теории и аргументы, но есть две формулы для нахождения периметра самого квадрата. Более подробно они описаны в данном документе.
Эта статья поддерживается методистами Skysmart. Если вы обнаружили ошибку, пожалуйста, сообщите о ней в веб-чате (в правом нижнем углу экрана).
Основные определения
Квадрат — это обычный четырехугольник с равными углами и сторонами. Поскольку это частный случай прямоугольника, вы можете заметить, что некоторые алгоритмы похожи.
Периметр — это сумма длин всех сторон многоугольника. Родовое название — заглавная латинская буква P. Полезно писать название формы в нижнем регистре под буквой ‘P’.
Если длины даны в разных единицах, периметр квадрата найти невозможно. Поэтому, чтобы правильно решить эту проблему, все данные должны быть переведены в одну и ту же единицу измерения.
Как измерить периметр:.
- миллиметр (мм);
- сантиметр (см);
- дециметр (дм);
- метр (м);
- километр (км) и другие единицы измерения длины.
Формула нахождения периметра квадрата
Метод нахождения периметра квадрата всегда зависит от исходных данных. Рассмотрим два типа, преподаваемых во 2 и 3 классах.
Если известна длина стороны
p = a + a + a + a + a + a + a, где a — одна сторона.
Все стороны фигуры равны, поэтому можно использовать типы в этой форме. p = 4 × a
Если известна длина диагонали
p = d x 2 x √2, где d — диагональ.
Диагональ — это отрезок, соединяющий противоположные стороны фигуры.
Математика, как и любой другой урок, не является простым и понятным. Трудности могут возникнуть из-за того, что простые числовые операции не могут быть выполнены быстро. Поэтому полезно практиковать примеры как можно чаще. Давайте сделаем это сейчас!
На этом сайте используется технология LaTeX. Поэтому, пожалуйста, подождите, пока страница полностью загрузится, прежде чем набирать текст, и формулы будут отображаться правильно.
Площадь и периметр
Площади и периметры очень важны для изучения плоскостности планет. Существуют специальные типы для вычисления площади и периметра.
Площадь и периметр — важные расчеты при изучении плоских фигур. Площадь — это мера поверхности фигуры, периметр — длина границы фигуры, а его значение — вычисление суммы всех сторон фигуры. При изучении многоугольников, которые являются частным случаем плоских фигур, достаточно сложить все стороны, чтобы найти периметр и вычислить площадь каждого особого типа многоугольника.
Формы областей и границ очень полезны в гражданском строительстве, при выращивании растений, а благодаря различным применениям этих понятий можно получить представление о размерах поверхности в повседневной жизни.
Что такое площадь?
Площади являются важным измерением геометрии. Для определенной геометрической формы площадь — это измерение поверхности этой формы. Для вычисления площади плоской фигуры используется специальный тип. При необходимости плоская геометрия делится на известные плоские геометрии и добавляются области. Ниже приведены основные уровни и типы для расчета площади каждого из них.
Периметр плоской фигуры равен сумме длин всех ее сторон. Поэтому для конкретной плоской фигуры существует один тип, но помните, что сумма сторон дает периметр.
Поскольку периметр всегда равен сумме всех сторон плоской фигуры, для некоторых плоских фигур можно использовать соответствующий тип. Рассмотрим базовый периметр плоской формы.
Определение квадрата
Квадрат — это плоская геометрическая фигура с четырьмя сторонами одинаковой длины, обычно называемая квадратом. Углы, образующие эти стороны квадрата, равны 90° (прямые углы). Также можно разделить квадрат по диагонали и соединить две диагонали противоположных вершин. Это означает, что вы можете провести линии, соединяющие углы (вершины) по диагонали.
Вычислить периметр квадрата несложно, и это можно сделать наизусть. Поскольку все стороны имеют одинаковую меру, периметр квадрата можно определить, только зная меру одной из его сторон. Наибольшее определение периметра — это измерение контура геометрической фигуры в двух измерениях.
Поэтому, исходя из этой концепции, периметр квадрата можно определить путем сложения каждой стороны квадрата. Уравнение выглядит следующим образом.
P = L + L + L + L + L + L + L + L или P = L x 4
Землевладелец разрешил участок площадью 25 метров на экранированной и огороженной территории. Он намерен посадить на этом небольшом пространстве листья и овощи. Однако он хочет использовать как можно меньше экрана в этой ручке. Какую плоскую геометрическую форму он будет использовать для ограждения этой области, используя минимально возможную сетку?
В данном случае это возможно только для четырехугольников.
Возможные размеры прямоугольника площадью 25 метров — 4 метра в ширину и 6,25 метра в длину, из которых можно взять периметр.
Таким образом, мы видим, что периметр 25-метрового прямоугольника соответствует длине 20,5 метра. В данном случае это размер экрана, используемый в данной конфигурации.
Далее давайте воспользуемся квадратной формой, чтобы вычислить периметр этого 25-метрового квадрата.
Единственное возможное измерение для площади в 25 метров из обычного квадрата — это 5 метров с каждой стороны.
Таким образом, используя угловые элементы, можно определить, что длина периметра забора составляет 20 метров. В этом случае владелец участка уменьшает количество используемого полотна при квадратной планировке забора.
Эта важная характеристика площади может быть упущена из виду при проектировании комнат и других помещений. Квадраты всегда меньше по площади, чем другие четырехугольники.
Радиус внутри клетки в два раза меньше, чем у обычного прямоугольного прыща. Таким образом, уравнение для нахождения P имеет вид
Квадрат. Формулы и свойства квадрата
Квадрат — это четырехугольник, у которого все четыре стороны и углы равны. Квадрат отличается только длиной одной стороны, но все четыре угла правильные, т.е. 90°.
Основные свойства квадрата
Квадрат также может быть прямоугольником, ромбом или прямоугольником, если у него одинаковые длины диагоналей, сторон и углов.
7. диагонали квадрата пересекаются под прямым углом и делятся пополам друг с другом.
| AC ┴ BD | AO = BO = CO = DO = | d |
| 2 |
8. пересечение диагоналей называется центром квадрата, а также является центром антиклиники и периклиники.
ΔABC=ΔADC=ΔBAD=ΔBCDΔACB=∠ACD=∠BDC=∠BDA=∠CAD=∠DBC=∠DBA= 45°
10. Две диагонали делят квадрат на четыре равных треугольника: равнобедренный треугольник и прямоугольник.
Круг, нарисованный вокруг квадрата, проходит через четыре вершины квадрата и находится в центре на пересечении диагоналей квадрата.
Радиус периметра квадрата всегда в два раза больше радиуса конечного цикла.
Радиус окружности квадрата равен половине радиуса диагонали.
Площадь круга, нарисованного вокруг квадрата, в π/2 раза больше площади квадрата.
Формулы определения радиуса окружности описанной вокруг квадрата
Периметр плоской фигуры равен сумме длин всех ее сторон. Поэтому для конкретной плоской фигуры существует один тип, но помните, что сумма сторон дает периметр.
Периметр и площадь квадрата
Он является суммой четырех его сторон. Как вы знаете, все стороны квадрата имеют одинаковый размер. Поэтому периметр квадрата можно найти, умножив длину периметра на четыре.
Например, перед вами квадрат с 10 см с каждой стороны.
Чтобы найти периметр и площадь, нужно понимать, что периметр — это расчетная длина контура фигуры, а площадь — размер всей ее поверхности.
Чтобы найти площадь квадрата, нужно воспользоваться простой формулой: s
S — площадь, а S — сторона квадрата.
Например, в вопросе говорится, что длина сторон квадрата равна 10 см.
Периметр и площадь прямоугольника
Стороны прямоугольника, имеющие одинаковую длину, называются противоположными сторонами. Это длина и ширина, обозначаемые латинскими буквами a и b. Тип для вычисления периметра прямоугольника следующий: a. Периметр прямоугольника вычисляется с помощью типа «периметр».
Используя этот тип, сначала найдите сумму ширины и длины, а затем умножьте на два.
Например, мы рассмотрим прямоугольник длиной 6 см и шириной 2 см.
Чтобы найти площадь прямоугольника, умножьте длину на ширину. Мужчина идет следом.
Например, условие заключается в том, что прямоугольник имеет длину 5 см и ширину 2 см. Замените буквы A и B заданными числами.
Периметр круга (длина окружности)
Каждый цикл имеет свой центр. Расстояние от центра любой окружности в круге называется радиусом круга. Часто учащиеся путают понятия «круг» и «площадь» и пытаются определить площадь круга. Это серьезная ошибка. Понятия «круг» и «площадь» необходимо разделить в сознании. У цикла нет площади и нет области. Есть только длина.
Чтобы найти окружность круга, нужно вычислить длину его окружности. Кто-то находит окружность круга:.
L — длина окружности
p — это p, математическая константа. Длина окружности равна причине длины ее диаметра. Древнее название числа Пи — число Лудольфо. Это число иррационально, и его десятичное представление никогда не заканчивается после точки.
p = 3.141 592 653 589 793 238 462 643 383 279 502
Для простоты расчетов обычно используется значение 3,14.
R — радиус окружности
D — диаметр круга
Поэтому, чтобы найти периметр круга, необходимо найти произведение радиуса и 2P. Если диаметр задан в задаче
Рассмотрите, например, цикл с радиусом 3 см. Найдите его периметр.