Онлайн калькулятор для вы нахождения числа по его процентам, может решать примеры, сохранять историю вычисления и копировать ссылку на расчет.
Правило: Чтобы найти число по его проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на 100.
Примеры вычисления исходного числа по известному проценту от числа:
Например: число 4 это 5% от неизвестного нам числа, чтобы найти это число нужно 4/5×100=80
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
Процент – это одна сотая доля числа, принимаемого за целое. Проценты используются для обозначения отношения части к целому, а также для сравнения величин.
1% = 1100 = 0,01
Онлайн калькулятор позволяет выполнить следующие операции:
Найти процент от числа
Чтобы найти процент p от числа, нужно умножить это число на дробь p100
Найдем 12% от числа 300:
300 · 12100 = 300 · 0,12 = 36
12% от числа 300 равняется 36.
Например, товар стоит 500 рублей и на него действует скидка 7%. Найдем абсолютное значение скидки:
500 · 7100 = 500 · 0,07 = 35
Таким образом, скидка равна 35 рублей.
Сколько процентов составляет одно число от другого числа
Чтобы вычислить процентное отношение чисел, нужно одно число разделить на другое и умножить на 100%.
Вычислим, сколько процентов составляет число 12 от числа 30:
1230 · 100 = 0,4 · 100 = 40%
Число 12 составляет 40% от числа 30.
Например, книга содержит 340 страниц. Вася прочитал 200 страниц. Вычислим, сколько процентов от всей книги прочитал Вася.
200340 · 100% = 0,59 · 100 = 59%
Таким образом, Вася прочитал 59% от всей книги.
Прибавить процент к числу
Чтобы прибавить к числу p процентов, нужно умножить это число на (1 + p100)
Прибавим 30% к числу 200:
200 · (1 + 30100) = 200 · 1,3 = 260
200 + 30% равняется 260.
Например, абонемент в бассейн стоит 1000 рублей. Со следующего месяца обещали поднять цену на 20%. Вычислим, сколько будет стоить абонемент.
1000 · (1 + 20100) = 1000 · 1,2 = 1200
Таким образом, абонемент будет стоить 1200 рублей.
Вычесть процент из числа
Чтобы отнять от числа p процентов, нужно умножить это число на (1 – p100)
Отнимем 30% от числа 200:
200 · (1 – 30100) = 200 · 0,7 = 140
200 – 30% равняется 140.
Например, велосипед стоит 30000 рублей. Магазин сделал на него скидку 5%. Вычислим, сколько будет стоить велосипед с учетом скидки.
30000 · (1 – 5100) = 30000 · 0,95 = 28500
Таким образом, велосипед будет стоить 28500 рублей.
На сколько процентов одно число больше другого
Чтобы вычислить, на сколько процентов одно число больше другого, нужно первое число разделить на второе, умножить результат на 100 и вычесть 100.
Вычислим, на сколько процентов число 20 больше числа 5:
205 · 100 – 100 = 4 · 100 – 100 = 400 – 100 = 300%
Число 20 больше числа 5 на 300%.
Например, зарплата начальника равна 50000 рублей, а сотрудника – 35000 рублей. Найдем, на сколько процентов зарплата начальника больше:
5000035000 · 100 – 100 = 1,43 * 100 – 100 = 143 – 100 = 43%
Таким образом, зарплата начальника на 43% выше зарплаты сотрудника.
На сколько процентов одно число меньше другого
Чтобы вычислить, на сколько процентов одно число меньше другого, нужно из 100 вычесть отношение первого числа ко второму, умноженное на 100.
Вычислим, на сколько процентов число 5 меньше числа 20:
100 – 520 · 100 = 100 – 0,25 · 100 = 100 – 25 = 75%
Число 5 меньше числа 20 на 75%.
Например, фрилансер Олег в январе выполнил заказы на 40000 рублей, а в феврале на 30000 рублей. Найдем, на сколько процентов Олег в феврале заработал меньше, чем в январе:
100 – 3000040000 · 100 = 100 – 0,75 * 100 = 100 – 75 = 25%
Таким образом, в феврале Олег заработал на 25% меньше, чем в январе.
Найти 100 процентов
Если число x это p процентов, то найти 100 процентов можно умножив число x на 100p
Найдем 100%, если 25% это 7:
7 · 10025 = 7 · 4 = 28
Если 25% равняется 7, то 100% равняется 28.
Например, Катя копирует фотографии с фотоаппарата на компьютер. За 5 минут скопировалось 20% фотографий. Найдем, сколько всего времени занимает процесс копирования:
5 · 10020 = 5 · 5 = 25
Получаем, что процесс копирования всех фотографий занимает 25 минут.
Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Что такое процент?
В повседневной жизни дроби 
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь 
Дробь
Процентом является одна сотая часть
Например, 
от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:
Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
1% = = 0,01
Два процента в дробном виде будут записаны как
2% =
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
Что означает запись 2% ? Запись 2% заменяет собой запись
Найти
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
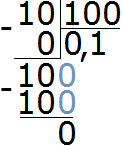
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
0,1 × 2 = 0,2
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:
0,2 см = 2 мм
Значит 2% от 10 см составляют 2 мм.
Пример 2. Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей на 100
300 : 100 = 3
Теперь полученный результат умножаем на 50
3 × 50 = 150 руб.
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
Например, те же 50% можно заменить на запись 
от 300 рублей, а решать такие задачи для нас пока проще
300 : 100 = 3
3 × 50 = 150
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.
Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
1200 : 100 = 12
12 × 32 = 384
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
300 × 0,5 = 150
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
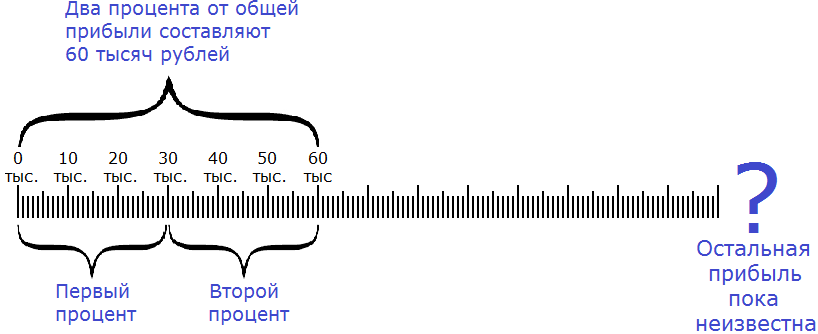
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
60 000 : 2 = 30 000
Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
35 : 7 = 5
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
5 × 100 = 500
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
500 : 100 = 5
5 × 7 = 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35 это 
от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
35 : 7 = 5
5 × 100 = 500
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Задания для самостоятельного решения
Задание 1. Найдите 20% от числа 200
200 : 100 = 2
2 × 20 = 40
Задание 2. Найдите 34% от числа 1050
1050 : 100 = 10,5
10,5 × 34 = 357
Задание 3. Найдите 25% от числа 80
80 : 100 = 0,80
0,8 × 25 = 20
Задание 4. Найдите 185% от числа 1,5
1,5 : 100 = 0,015
0,015 × 185 = 2,775
Задание 5. Найдите 150% от числа 1150
1150 : 100 = 11,50
11,50 × 150 = 1725
Задание 6. Представьте выражение 15% в виде обыкновенной дроби
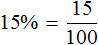
Задание 7. Представьте выражение 25% в виде обыкновенной дроби
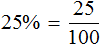
Задание 8. Представьте выражение 125% в виде обыкновенной дроби
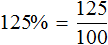
Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.
12 : 60 = 0,2
0,2 × 100 = 20
Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.
40 : 20 = 2
2 × 100 = 200
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Как найти число по его проценту?
Апр 10, 2021 | 4 класс |
Как найти число, если известен его процент?
Давайте разбираться.
Задание 1.
Надо найти число, если известно, что 23% — это 138.
Решение:
1). Сначала найдем чему равен 1%.
Нам известно, что 23% это 138, значит, чтобы найти 1%, надо — 138 : 23 = 6.
Т.е. 1% — это 6.
2). Теперь надо найти целое число.
Мы знаем, что в целом – 100%.
А, чтобы найти целое, надо 1% умножить на 100.
Т.е. 6 х 100 = 600.
Значит, 100% — это 600 и это – целое число.
Ответ: 600.
Задание 2.
Найти число, если 12% — это 48.
Решение:
1). Превратим 12 % в десятичную дробь.
Если 1% = 1/100, то 12% =12/100
2). 12/100 – это 48,
Найдем 1/100, для этого 48 разделим на 12 и умножим на 100, 48 : 12 х 100.
Заменим знак «:» дробной чертой, будет 48/12 х 100, или по правилу работы с дробями – 48 х 100/12.
Получается — 48 : 12 х 100 = 48/12 х 100 = 48х100/12 = 48 х 100/12.
Таким образом, видно, что часть мы умножаем на обратную дробь или делим на дробь.
Т.е. 48 х 100/12 = 4800/12 = 400
Ответ: 400.
При решении примеров надо выбирать удобный для вас вариант.
Похожие статьи
ОСНОВНЫЕ ТИПЫ РЕШЕНИЯ ЗАДАЧ НА ПРОЦЕНТЫ
I. НАХОЖДЕНИЕ ЧАСТИ ОТ ЦЕЛОГО
Чтобы найти часть (%) от целого, надо число умножить на часть (проценты, переведенные в десятичную дробь).
ПРИМЕР: В классе 32 ученика. Во время контрольной работы отсутствовало 12,5% учащихся. Найди, сколько учеников отсутствовало?
РЕШЕНИЕ 1: Целое в этой задаче – общее количество учащихся (32).
12,5% = 0,125
32 · 0,125 = 4
РЕШЕНИЕ 2: Пусть х учеников отсутствовали, что составляет 12,5%. Если 32 ученика –
общее количество учеников (100%), то
32 ученика – 100%
х учеников – 12,5%
х =
ОТВЕТ: В классе отсутствовало 4 ученика.
II. НАХОЖДЕНИЕ ЦЕЛОГО ПО ЕГО ЧАСТИ
Чтобы найти целое по его части (%-ам), надо число разделить на часть (проценты, переведенные в десятичную дробь).
ПРИМЕР: Коля истратил в парке аттракционов 120 крон, что составило75% всех его карманных денег. Сколько было карманных денег у Коли до прихода в парк аттракционов?
РЕШЕНИЕ 1: В этой задаче надо найти целое, если известна данная часть и значение
этой части.
75% = 0,75
120 : 0,75 = 160
РЕШЕНИЕ 2: Пусть х крон было у Коли, что составляет целое, т.е 100%. Если он потратил 120 крон, что составило 75%, то
120 крон– 75 %
х крон – 100 %
х =
ОТВЕТ:У Коли было 160 крон.
III. ВЫРАЖЕНИЕ В ПРОЦЕНТАХ ОТНОШЕНИЯ ДВУХ ЧИСЕЛ
ТИПОВОЙ ВОПРОС:
СКОЛЬКО % СОСТАВЛЯЕТ ОДНА ВЕЛИЧИНА ОТ ДРУГОЙ?
ПРИМЕР: Ширина прямоугольника 20м, а длина 32м. Сколько % составляет ширина от длины? (Длина является основой для сравнения)
РЕШЕНИЕ 1:РЕШЕНИЕ 2: В этой задаче длина прямоугольника 32м составляет 100%, тогда ширина 20м составляет х%. Составим и решим пропорцию:
20 метров – х %
32 метра – 100 %
х =
ОТВЕТ: Ширина составляет от длины 62,5%.
NB! Обратите внимание на то, как меняется решение в зависимости от изменения вопроса.
ПРИМЕР: Ширина прямоугольника 20м, а длина 32м. Сколько % составляет длина от ширины? (Ширина является основой для сравнения)
РЕШЕНИЕ 1:
РЕШЕНИЕ 2: В этой задаче ширина прямоугольника 20м составляет 100%, тогда длина 32м составляет х%. Составим и решим пропорцию:
20 метров – 100 %
32 метра – х %
х =
ОТВЕТ: Длина составляет от ширины 160%.
IV. ВЫРАЖЕНИЕ В ПРОЦЕНТАХ ИЗМЕНЕНИЯ ВЕЛИЧИНЫТИПОВОЙ ВОПРОС:
НА СКОЛЬКО % ИЗМЕНИЛАСЬ (УВЕЛИЧИЛАСЬ, УМЕНЬШИЛАСЬ) ПЕРВОНАЧАЛЬНАЯ ВЕЛИЧИНА?
Чтобы найти изменение величины в % надо:
1) найти на сколько изменилась величина (без %)
2) разделить полученную величину из п.1) на величину, являющуюся основой для сравнения
3) перевести результат в % (выполнив умножение на 100%)
ПРИМЕР: Цена платья снизилась с 1250 крон до 1000 крон. Найди на сколько процентов снизилась цена платья?
РЕШЕНИЕ 1:
1) 1250 –1000= 250 (кр) на столько изменилась цена
2) Основа для сравнения здесь 1250 крон (т.е. то, что было изначально)
3)
Решение задачи одним действием:
ОТВЕТ: Цена платья уменьшилась на 20%.
NB! Обратите внимание на то, как меняется решение в зависимости от изменения вопроса.
ПРИМЕР:
Цена платья повысилась с 1000 крон до 1250 крон. Найди на сколько процентов повысилась цена платья?
РЕШЕНИЕ 1:
1) 1250 –1000= 250 (кр) на столько изменилась цена
2) Основа для сравнения здесь 1000 крон (т.е. то, что было изначально)
3)
Решение задачи одним действием:
РЕШЕНИЕ 2:
1250 –1000= 250 (кр) на столько изменилась цена
В этой задаче первоначальная цена 1000 крон 100%, тогда изменение цены 250 крон составляет х%. Составим и решим пропорцию:
1000 крон – 100 %
250 крон – х %
х =
ОТВЕТ: Цена платья увеличилась на 25%.
V. ПОСЛЕДОВАТЕЛЬНОЕ ИЗМЕНЕНИЕ ВЕЛИЧИНЫ (ЧИСЛА)
ПРИМЕР: Число уменьшили на 15%, а затем увеличили на 20%. Найди на сколько процентов изменилось число?
Самая распространенная ошибка: число увеличилось на 5 %.
РЕШЕНИЕ 1:
1) Хотя исходное число не дано, для простоты решения можно принять его за 100 (т.е. одно целое или 1)
2) Если число уменьшилось на 15%, то полученное число составит 85%, или от 100 это было бы 85.
3) Теперь полученный результат надо увеличить на 20%, т.е
85 – 100%
а новое число х – 120% (т.к. увеличилось на 20%)
х =
4)Таким образом в результате изменений число 100 (первоначальное) изменилось и стало 102, а это означает, что первоначальное число увеличилось на 2%
РЕШЕНИЕ 2:
1) Пусть исходное число Х
2) Если число уменьшилось на 15%, то полученное число составит 85% от Х, т.е. 0,85Х.
3) Теперь полученное число надо увеличить на 20%, т.е
0,85Х – 100%
а новое число ? – 120% (т.к. увеличилось на 20%)
? =
4) Таким образом в результате изменений число Х (первоначальное), является основой для сравнения, а число 1,02Х(полученное), (см. IV тип решения задач), тогда
ОТВЕТ: Число увеличилось на 2%.
