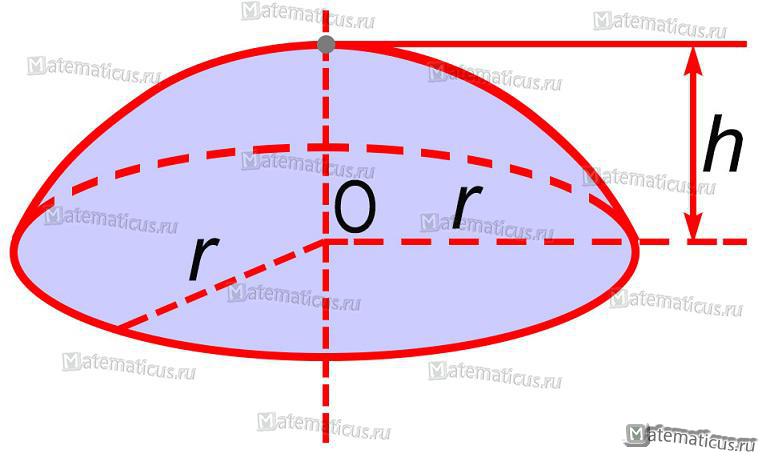
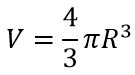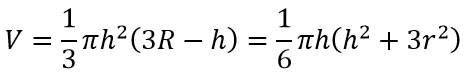Калькулятор вычисляет объем части полусферы, полученной путем сечения полусферы плоскостью, проходящей на заданном расстоянии от центра полусферы под заданным углом.
Угол может быть в пределах (0..180) градусов.Расстояние h не должно превышать диаметра полусферы. Формулы вычисления можно найти сразу под калькулятором.
Объем полусферы, рассеченной плоскостью под заданным углом
Расстояние между центром основания полусферы и режущей плоскостью вдоль основания полусферы.
Угол в градусах между основанием полусферы и плоскостью разреза.
Точность вычисления
Знаков после запятой: 5
Формулы объема сечения полусферы плоскостью
Начинаем с простых случаев
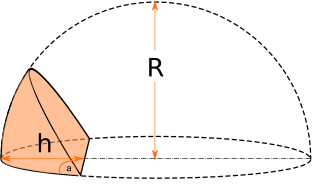
Разрез проходит строго по центру полусферы, h=R
Это самый простой случай, формула получается путем легкой модификации формулы объема полусферы:
Следующим образом:
, где a угол разреза в радианах.
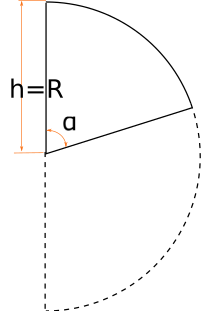
Полусфера разрезана под углом 90 градусов
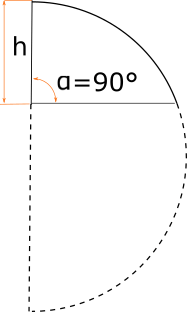
Если полусфера разрезана под прямым углом, мы попросту берем половину объема сечения сферы.
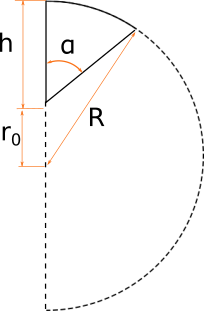
Полусфера разрезана ниже центра h > R
Если разрезать полусферу таким, образом, что центр полусферы окажется в части, для которой нужно вычислить объем мы получим самый сложный случай. Для такого случая мы вычисляем объем другой отрезанной части и вычитаем полученный объем из объема всей полусферы:
Vd вычисляется по формулам приведенным далее, с предварительным преобразованием угла
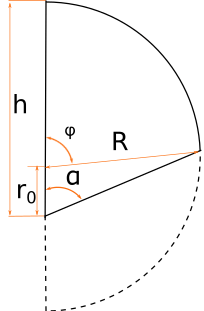
Сечение проходит выше центра полусферы h < R
Это наиболее общий случай, который решается интегрированием по объему.
Разместим полусферу на координатной плоскости таким образом, чтобы секущая плоскость была параллельна плоскости Z-O-Y, центр полусферы в начале координат. Секущая плоскость будет удаена от плоскости Z-O-Y на расстояние sin(α)*r0, где r0=R-h расстояние от пересечения основания полусферы и секущей плоскости до центра полусферы:
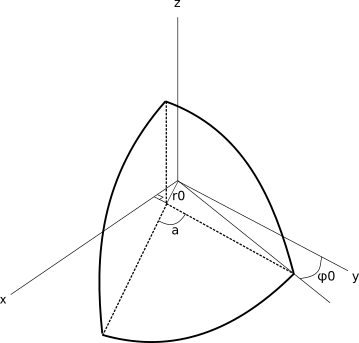
В линейной 3-мерной координатной системе секущая плоскость будет иметь уравнение .
В сферической системе координат (ISO): (1)
Далее будем решать интеграл в сферической системе координат:
(2)
Так как разрезанная полусфера расположена симметрично относительно плоскости X-O-Y мы будем интегрировать только половину возможного угла тета и домножим интеграл на 2.
Интервалы интегрирования
- Интервал угла φ постоянный:
Где a угол сечения к основанию полусферы в радианах
и согласно изображению (6) угол(3)
- Интервал радиусов
Верхняя граница упрается в радиус полусферы – R. Плоскость сечения ограничивает интервал снизу, согласно формуле (1) имеем:
(4)
- Интервалы угла θ
Так как мы интегрируем только верхнюю половину интервала θ то верхняя граница θ равна, а нижнюю можно выразить из формулы (1), принимая r=R. Таким образом:
(5)
Используя (3) мы можем сократить формулу так:
(6)
Формула объема
Для получения формулы объема сечения полусферы, решим интеграл (2) в интервалах (3),(4),(6):
-
Интегрируем по r
Результат:
-
Интегрируем по θ
Результат:
- Интегрируем по φ
Получаем окончательную формулу:
Где:
,
.
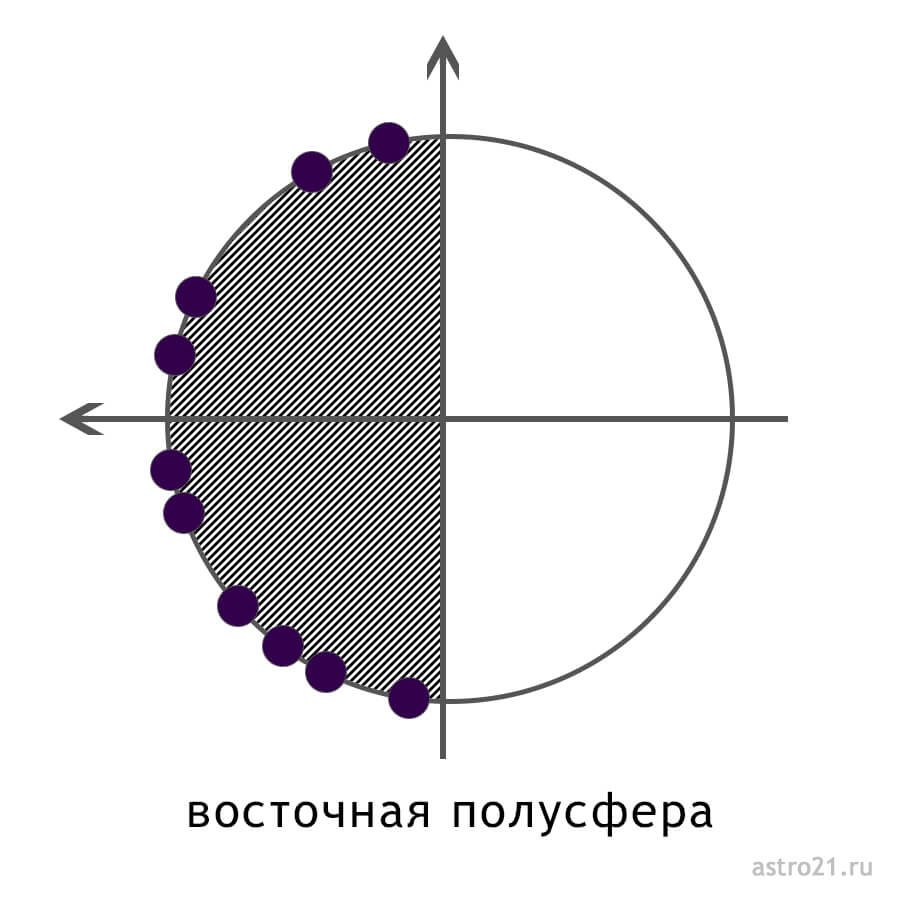
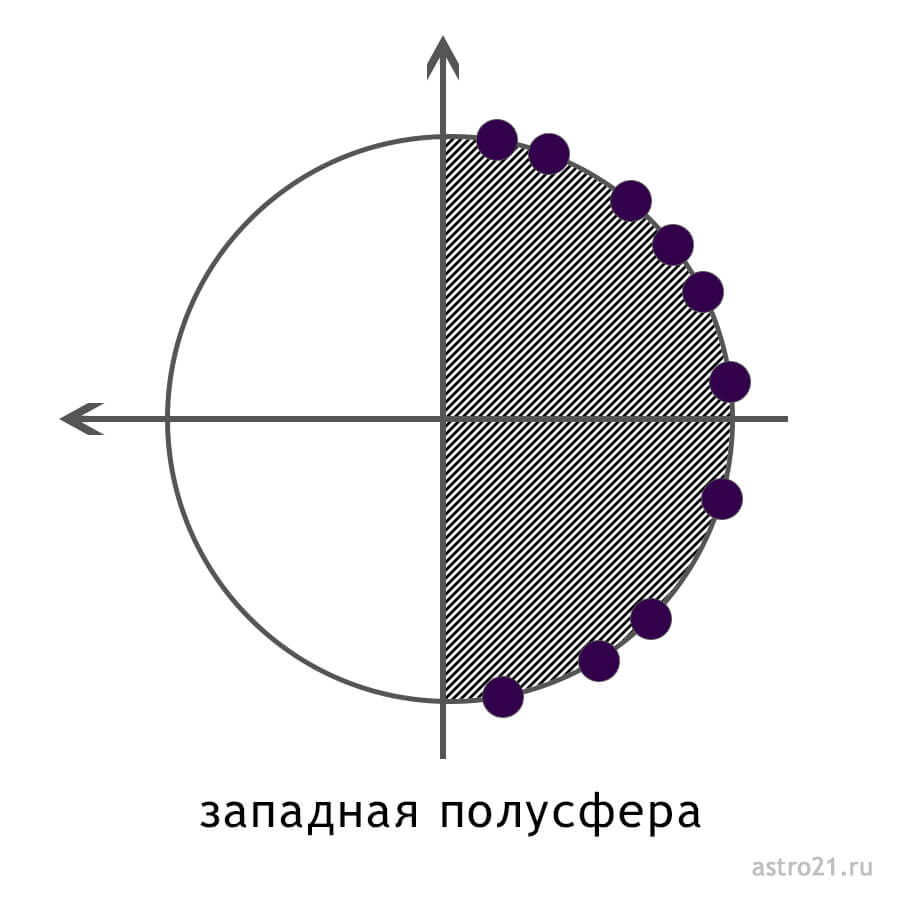
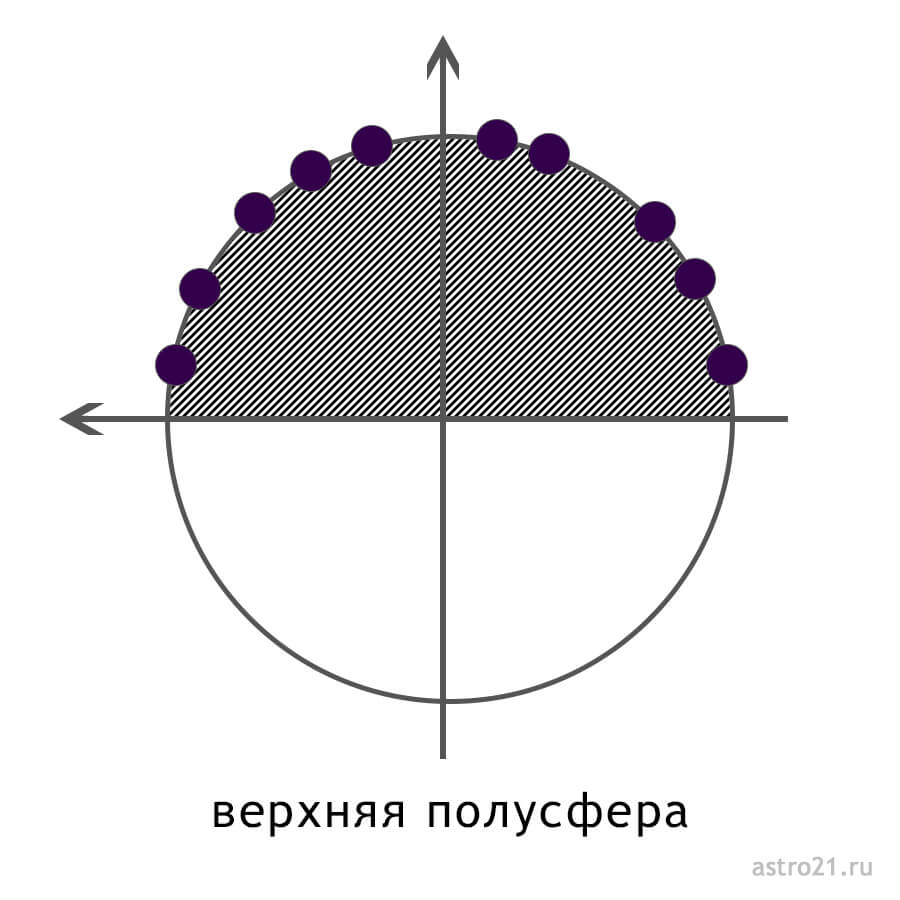
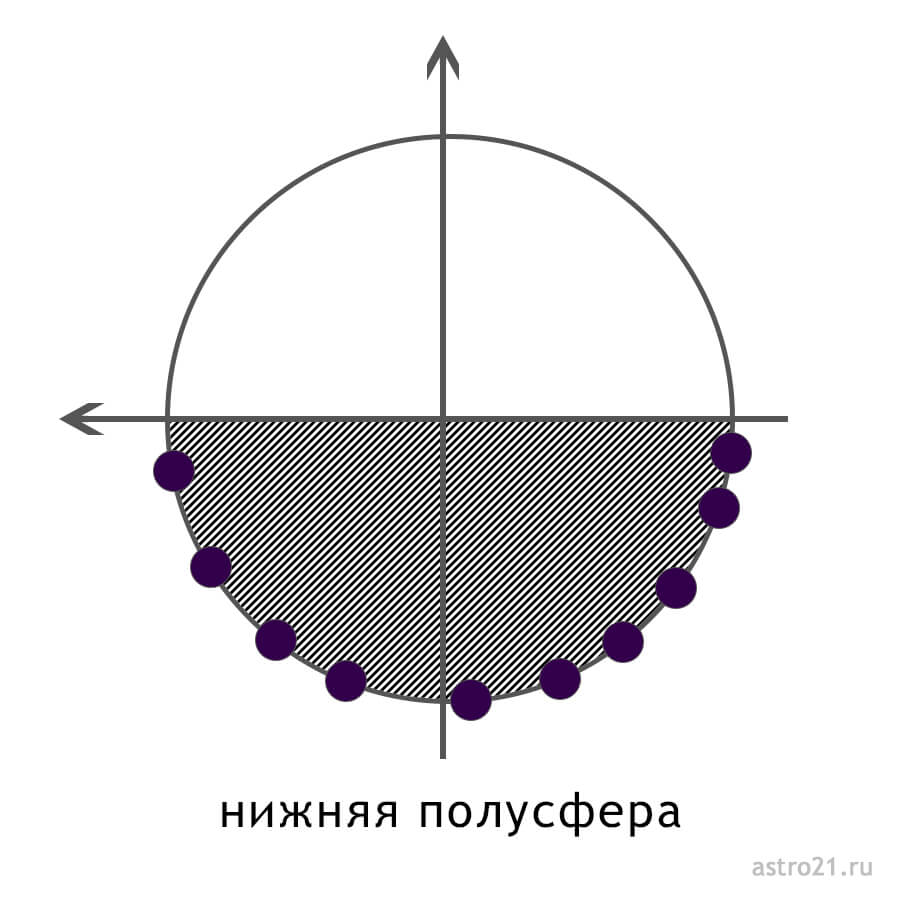
Карту можно поделить на полусферы — половинки карты. По оси Иц-Мц карта делится на восточную и западную полусферу, а по оси Асцендент-Десцендент — на верхнюю и нижнюю.
Нам нужно посчитать, в какой полусфере планет больше. Чем больше перевес, тем выраженнее эта полусфера.
Преобладающая полусфера — это интегральный показатель, так как тут берутся сразу все планеты и обобщается их положение.
Восточная полусфера
Восточная полусфера включает дома с 10 по 3. Это полусфера, где находится Асцендент, а Асцендент — это «я». Все дома этой полусферы связаны с нашим личным развитием и нашими личными интересами. Тут мы должны сами все «вывозить», но зато самостоятельны.
1 дом — это, собственно, «я», 2 — наши личные ресурсы, 3 — наше обучение и близкое окружение, 10 — наше личное развитие. А вот 11 дом — наше развитие в коллективе, этот дом самый спорный в восточной полусфере, так как он — про коллектив, а не про индивидуальность. Почему же он тут? 11 дом — это еще и дом нашей личной свободы и независимости. В плане общества, коллектива тут мы не уступаем и пытаемся понравиться, как в 7 доме, а находим единомышленников по душе. 12 дом — это наше подсознание, в нем вроде как зона альтруизма, почему же он относится к эгоистичной восточной полусфере? В 12 доме все-таки живут наши личные страхи, эмоции, переживания и «тараканы». Благодаря 12 дому мы вписываемся в коллективное бессознательное, но он покажет, как именно мы туда вписаны. Это теневая сторона нашего «я».
Выраженная восточная полусфера — это:
- индивидуалист, одиночка, «сами с усами»
- эгоизм (в том числе здоровый эгоизм)
- независимость
- может быть сложно с партнерством
- инициатор
- либо мир ждет от человека инициативы, отдает ему «руль»
Западная полусфера
Западная полусфера включает дома с 4 по 9. Это полусфера, где находится Десцендент, и это — зона «ты». Все дома этой зоны связаны с другими людьми, их интересами и нашим взаимодействием с ними. Тут мы зависим от других, местами вынуждены уступать, но зато можем положиться на них. 4 дом — это наша семья. 5 дом — наши дети. Но 5 дом — довольно эгоцентричен, почему он относится к западной полусфере? 5 дом все-таки отвечает за то, как мы выражаем себя для других, а не для себя (в отличие от 1 дома), тут важно произвести впечатление. 6 дом — это служение другим людям через работу, труд, заботу, 7 — просто другие люди и их интересы, 8 — ресурсы других людей и наши совместные с ними, 9 — идеи, с помощью которых люди влияют на нас и мы влияем на людей.
Выраженная западная полусфера — это:
- коллективист, командный игрок
- альтруизм (в том числе нездоровый альтруизм)
- зависимость от окружающих и их мнения, ведомый
- сложно одному
- нужны поддержка, одобрение, диалог, партнерство
- либо мир задвигает инициативы человека и заставляет его считаться с другими, сотрудничать
Верхняя полусфера (южная)
Верхняя полусфера включает дома с 7 по 12. Это полусфера, где находится Мц — точка, связанная с социальным развитием. Эта полусфера — видимая (небо над нами), поэтому тут должны быть видимые внешние результаты, это зона внешнего.
7 дом — это дом социальных отношений, 8 — социальных ресурсов, 9 — социального успеха и признания, 10 — социального развития и достижений, 11 — общения в социуме. А вот с 12 домом интересно: казалось бы, он отвечает за внутреннее, скрытое, но находится в верхней полусфере, почему? Дело в том, что он слабо связан с нашими личными делами. 12 дом все-таки связывает нас с людьми и глобально — с человечеством. Поэтому он отвечает за самопожертвование, сопереживание.
Выраженная верхняя полусфера — это:
- развитие вовне
- ориентация на внешний мир, нечто глобальное
- социальное развитие, развитие в обществе, в профессии
- важна оценка обществом
- либо мир заставляет человека развиваться социально, вписываться в систему, вытаскивает его «на поверхность»
Нижняя полусфера (северная)
Нижняя полусфера включает дома с 1 по 6. Это полусфера, где находится Иц — точка, связанная с семьей и близкими. Эта полусфера — невидима (невидимая для нас часть неба), поэтому она связана с нашими внутренними процессами и личными делами, это зона внутреннего.
1 дом — это наше «я» и личные дела, 2 — личные финансы, 3 — близкое окружение, 4 — семья и близкие, 5 — дети и то, что мы любим, 6 — работа и ежедневная рутина.
Выраженная нижняя полусфера — это:
- развитие внутрь
- важна внутренняя жизнь и личное развитие
- ориентация на нечто локальное
- важно ближнее окружение, близкие, семья
- важна внутренняя оценка или оценка близкими
- либо мир заставляет человека обустраивать в первую очередь свою личную жизнь, семью, прокачивать себя изнутри, а в плане соц. реализации может «задвигать»
О расчете преобладающей полусферы
У нас получается 2 пары полусфер: восточная и западная, верхняя и нижняя. Мы должны оценить количество планет в каждой паре по отдельности. Если количество планет в паре полусфер равное, то мы пропускаем трактовку этой пары полусфер в данной карте.
Имеет смысл учитывать личные планеты как более важные факторы, то есть оценивать не только количество планет в той или иной полусфере, но и качество. Например, если Луна и Солнце в одной полусфере, а другие планеты — в другой, то полусфера, где Луна и Солнце, все-таки будет важна. В общем, учитываем и количество, и качество планет. И опираемся только на явный перевес.
В карте выше есть явный перевес в верхнюю полусферу, а вот восточная-западная — в балансе, там планет поровну.
Как работают выраженные полусферы
Полусферы все-таки основаны на домах, а это значит, что они, как и дома, отражают по большей части событийность (но не только). Натура человека, которую мы видим через планеты в знаках и их аспекты, может противоречить акцентированным полусферам, но судьба все равно склоняет его к такому сценарию. Если психологический срез карты говорит об обратном, то нам нужно это учитывать.
Например, если в карте заполнен знак Весов, но при этом большинство планет в восточной полусфере, то партнерство и взаимодействие будет для натива очень важным, но жизнь будет склонять человека самого проявлять инициативу, возможно, через партнерство, деликатно и тактично.
Итого
- Восточная полусфера со стороны Асц — область личного развития и личных интересов.
- Западная полусфера со стороны Дсц — область партнерства и сотрудничества.
- Верхняя (южная) полусфера со стороны Мц — область социальной реализации и проявления вовне, в мире.
- Нижняя (северная) полусфера со стороны Иц — область развития внутрь, интересов личных и ближнего круга.
Задания
- Какие полусферы выделены у вас в карте? Как это проявляется?
- Посмотрите карты близких и знакомых, какие полусферы выделены у них и как это проявляется?
- Как думаете, как может проявиться выделенная западная полусфера, если при этом преобладает огонь?
- Как может проявиться выделенная верхняя полусфера, если при этом стеллиум в 12 доме?
- Как может проявиться выделенная нижняя полусфера, если при этом стеллиум в Козероге?
- Какие полусферы преобладают в карте ниже? Как вы можете это интерпретировать?
Следующий урок
Все уроки «Астрологии с нуля от Афы Суари»
Профессиональный астролог, изучает астрологию с 2001, консультирует с 2010 года. Преподаватель западной астрологии, ведет курсы и вебинары. Автор собственной методики ректификации и алгоритмов астрологического анализа по разным сферам. Руководитель проекта «Astrodox» (астрологический процессор для Android). Основатель проекта «Астрология 21 века».
2 (дно) = S
Полусфера, как форма обладающая приятным видом не имеющим углов и граней, часто используется в качестве малых архитектурных форм для оформления детских площадок, загородных участков, газонов и рекреационных зон. Цветные бетонные полусферы эстетично подходят под любой стиль оформления пространства, одновременно выполняя роль ограничителя проезда для транспорта. Полусфера яркого цвета, раскрашенная в виде арбуза, божий коровки, цветка, глобуса или любого другого предмета схожей формы, станет заметным и долговечным примером малых архитектурных форм.
Среди множества вариантов ограждений для тротуаров и парковочных зон, золотой серединой в соотношении цены, качества и долговечности являются бетонные полусферы. Бетонные полушары обладают всеми качествами которыми должны обладать дорожные ограждения. Это прочный долговечный материал устойчивый к ультрафиолету, воздействию химических реагентов и солей, не поддающийся коррозии и обладающий хорошим весом. Гладкая не травмоопасная форма полушара идеально подходит для применения в качестве ограждения для пешеходных зон, тротуаров, детских площадок, площадей перед станциями метрополитена и других мест скопления людей.
Особенностью бетонной полусферы как преграды для проезда автомобиля является ее прочность и долгое сохранение первоначального вида. Это несомненно делает выгодным установку бетонных полусфер перед другими вариантами ограждений из пластика или металла. Для фиксации полусферы из бетона на устанавливаемой поверхности используется арматурный штырь который вставляется в засверленное отверстие в тротуаре, асфальте, бетоне или плитке. То есть без разрушения поверхности дороги или тротуара и проведения сложных черновых работ. Таким образом полусфера аккуратно и прочно фиксируется, но в любой момент может быть демонтирована с помощью специальных средств. После снятия полусферы на месте установки остается малозаметное отверстие.
Во все эпохи и времена примером самой прочной архитектурной формы являлась пирамида, конус и полусфера/полушар. По сей день жители севера выстраивают свои жилища (иглу) в форме половины шара с заниженным входом у основания. Сферическая форма позволяет распределять возможные нагрузки по всей конструкции по принципу яичной скорлупы, и дает возможность разведения костра, без опасения задымления помещения.
Футуристичный вид зданий в виде полусферы используется в частном загородном строительстве, при строительстве городских зданий и сооружений, при возведении шатров и куполов с внутренней эко системой. Примером здания в виде полушара (сферической формы) в Москве является дом на Ленинградском проспекте.
В Санкт-Петербурге строение полушар вмещает в себя целый аквапарк. Конструкция выполнена по современной технологии повышенной прочности с симпатичной иллюминацией снаружи.
Совсем новый, но быстро обретающий популярность вид уличных и домашних светильников — светящаяся полусфера. Полушары правильной формы имеют внушительные размеры от 40 см в диаметре и излучают на выбор 14 цветов при четырех режимах свечения. Выбор цвета и режима свечения осуществляется при помощи пульта дистанционного управления.
Особенностью таких ламп является их обычный вид при дневном свете и совсем необычное свечение в темное время суток. Днем эти полусферы выглядят как бетонные или каменные, а ночью сияют мягким светом.
Рабочий диапазон полусферических ламп от -40 до +80 градусов C. Корпус полусферы влагонепроницаем, устойчив к физическим воздействиям и легко моется. По вопросу установки светящихся полусфер для улицы и помещения или как купить, обращайтесь по эл адресу: radair[собака]yandex.ru или по телефону в контактах сайта.
Самыми удобными креслами в мире считаются именно кресла в виде полусфер. Придуманное неизвестным изобретателем кресло полусфера Papasan обрело популярность еще в 50 годах двадцатого века.
К началу двадцать первого века появилось множество кресел и диванов в виде полушаров/полусфер не только из разных видов древесины, но из пластика, стеклопластика и даже металла. Кресло полусфера не редкий элемент дизайнерской мебели в современном доме. Ведь именно такая форма, по мнению владельцев, придает чувство особенной расслабленности и комфорта.
Во многих смыслах универсальный тренажер для развития координации, равновесия и не только. Все та же форма полусферы, но на это раз из резины, в народе более известный как полу-мяч. Изобретатель резиновой полусферы для фитнеса утверждает, что все упражнения совершаемые на неустойчивой поверхности, на такой как резиновая полусфера, заставляют работать большое количество мелких мышц, улучшает координацию и положительно влияет на работу вестибулярного аппарата.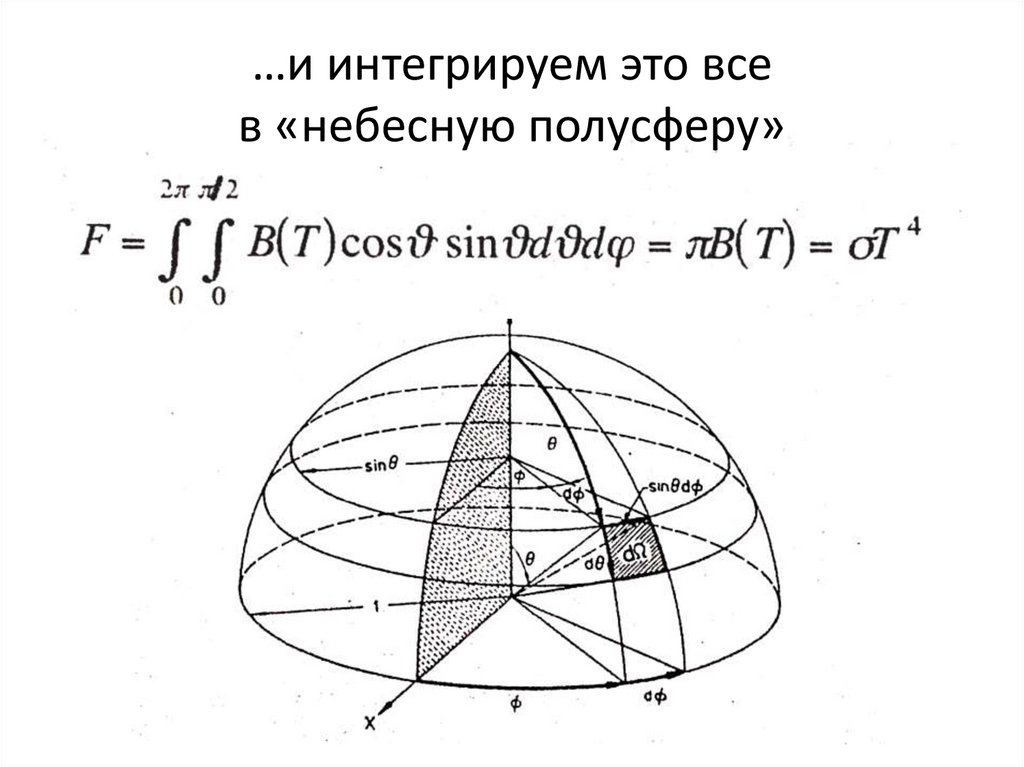
То есть воздействие мяча повышает тонус опорно-двигательного аппарата и улучшает осанку. Регулировать жесткость полушара можно при помощи воздуха, накачивая или спуская через специальный клапан, это в свою очередь регулирует сложность выполнения упражнений используя резиновую полусферу для фитнеса.
Если не все, то многие выросшие в СССР помнят этот атрибут каждой детской площадки во дворе. Пользующаяся огромной популярностью, на ровне с качелями, горка в виде металлической паутинки полусферической формы — прекрасное спортивное и развлекательное сооружение в одном флаконе. Детвора кружилась по ней как стая обезьян, играя в салки, перебиралась на руках с одного края на другой. Достаточно подобных детских паутинок сохранилось и по сей день, что в очередной раз является примером прочности конструкции с применением формы полушара, полусферы.
Еще одно воплощение в виде полусферической формы направленное на развитие и образование деток дошкольного и школьного возраста.
Шатер в виде полушара олицетворяющий небесный свод с захватывающей анимационной проекцией на астрономическую тему, легко устанавливается в спортивных или актовых залах учебных заведений.
Под куполом мобильных планетариев читаются интереснейшие лекции с сопровождением анимации при помощи проектора. Форма полусферы как нельзя лучше подходит для имитации небесного пространства.
Объем части полусферы, отрезанной под углом
УчебаМатематикаГеометрия
Объем несимметрично отрезанной части полусферы.
Калькулятор вычисляет объем части полусферы, полученной путем сечения полусферы плоскостью, проходящей на заданном расстоянии от центра полусферы под заданным углом.
1)Разрез полусферы под углом
Угол может быть в пределах (0..180) градусов.Расстояние h не должно превышать диаметра полусферы. Формулы вычисления можно найти сразу под калькулятором.
Объем полусферы, рассеченной плоскостью под заданным углом
Радиус
Высота
Расстояние между центром основания полусферы и режущей плоскостью вдоль основания полусферы.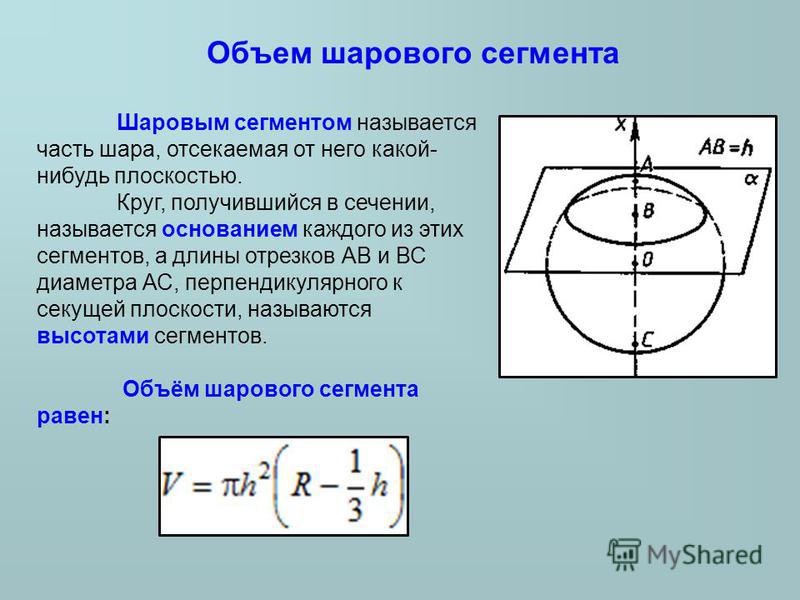
Угол в градусах между основанием полусферы и плоскостью разреза.
Точность вычисления
Знаков после запятой: 5
Объем
Начинаем с простых случаев
Разрез проходит строго по центру полусферы, h=R
2)Центральный разрез полусферы, боковая проекция.
Это самый простой случай, формула получается путем легкой модификации формулы объема полусферы:
Следующим образом:
, где a угол разреза в радианах.
Полусфера разрезана под углом 90 градусов
3)Прямой разрез полусферы. Боковая проекция.
Если полусфера разрезана под прямым углом, мы попросту берем половину объема сечения сферы.
Полусфера разрезана ниже центра h > R
4)Разрез ниже середины полусферы. Боковая проекция.
Если разрезать полусферу таким, образом, что центр полусферы окажется в части, для которой нужно вычислить объем мы получим самый сложный случай. Для такого случая мы вычисляем объем другой отрезанной части и вычитаем полученный объем из объема всей полусферы:
Vd вычисляется по формулам приведенным далее, с предварительным преобразованием угла
Сечение проходит выше центра полусферы h < R
5) Разрез полусферы под углом выше центра
Это наиболее общий случай, который решается интегрированием по объему.
Разместим полусферу на координатной плоскости таким образом, чтобы секущая плоскость была параллельна плоскости Z-O-Y, центр полусферы в начале координат. Секущая плоскость будет удаена от плоскости Z-O-Y на расстояние sin(α)*r0, где r0=R-h расстояние от пересечения основания полусферы и секущей плоскости до центра полусферы:
6)Расположение разрезанной полусферы в системе координат
В линейной 3-мерной координатной системе секущая плоскость будет иметь уравнение .
В сферической системе координат (ISO): (1)
Далее будем решать интеграл в сферической системе координат:
(2)
Так как разрезанная полусфера расположена симметрично относительно плоскости X-O-Y мы будем интегрировать только половину возможного угла тета и домножим интеграл на 2.
Интервалы интегрирования
- Интервал угла φ постоянный:
Где a угол сечения к основанию полусферы в радианах
и согласно изображению (6) угол (3) - Интервал радиусов
Верхняя граница упрается в радиус полусферы — R.Плоскость сечения ограничивает интервал снизу, согласно формуле (1) имеем:
(4) - Интервалы угла θ
Так как мы интегрируем только верхнюю половину интервала θ то верхняя граница θ равна , а нижнюю можно выразить из формулы (1), принимая r=R. Таким образом:
(5)
Используя (3) мы можем сократить формулу так:
(6)
Формула объема
Для получения формулы объема сечения полусферы, решим интеграл (2) в интервалах (3),(4),(6):
-
Интегрируем по r
Результат:
-
Интегрируем по θ
Результат:
- Интегрируем по φ
Получаем окончательную формулу:
Где:
,
.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Объем жидкости в наклоненном баке со сферическими торцами
- • Радиус шара, вычисляемый по объему
- • Объем геометрических фигур
- • Сфера
- • Куб
- • Раздел: Геометрия ( 96 калькуляторов )
#геометрия #полусфера Геометрия матан Матанализ Математика объем плоскость полусфера сечение сфера
PLANETCALC, Объем части полусферы, отрезанной под углом
Anton2020-11-03 14:19:36
Калькулятор полушария
Форма полушария
r = радиус
C = окружность основания
В = объем
A = площадь изогнутой поверхности
B = площадь базовой поверхности
К = общая площадь поверхности
π = пи = 3,1415926535898
√ = квадратный корень
Калькулятор Использование
Этот онлайн-калькулятор рассчитает различные свойства полушария по любой 1 известной переменной.
шар разрезать пополам, проведя плоскость через центр шара. Объем V и площадь A рассчитаны по существу для половины сферы. Видеть
Полушария в Mathworld.
Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на расчеты. Единицы используются для указания порядка результатов, таких как футы, футы 2 или фут 3 . Например, если вы начинаете с мм и знаете, что r в мм, ваши расчеты дадут A в мм 2 , V в мм
3 и C в мм.
Полушарие Формулы для радиуса r:
- Объем полушария:
- В = (2/3)πr 3
- Окружность основания полушария:
- С = 2πr
- Площадь криволинейной поверхности полусферы (1 сторона, только внешняя):
- А = 2πr 2
- Рассчитайте площадь основания полусферы (окружности):
- В = πr 2
- Суммарная площадь поверхности полушария:
- К = (2πr 2 ) + (πr 2 ) = 3πr 2
Расчет полушария:
Используйте следующие дополнительные формулы вместе с формулами выше.
- Зная радиус полушария, рассчитайте объем, площадь кривизны поверхности, длину окружности и общую площадь поверхности.
Дано r найти V, A, C, K- используйте формулы выше
- Зная объем полушария, рассчитайте радиус, площадь криволинейной поверхности, длину окружности и общую площадь поверхности.
По данному V найти r, A, C , K- r = кубический корень (3V / 2π)
- Зная площадь криволинейной поверхности полушария, рассчитайте радиус, объем, длину окружности и общую площадь поверхности.
Дано A найти r, V, C, K- г = √(А / 2π)
- Зная общую площадь поверхности полушария, рассчитайте радиус, объем, площадь криволинейной поверхности и длину окружности.
По данным K найти r, V, A, C- г = √(К / 3π)
- Зная длину окружности полушария, рассчитайте радиус, объем, площадь криволинейной поверхности и общую площадь поверхности.
По данному C найти r, V, A , K- г = С / 2π
Объем полушария – формула, определение, примеры
объем полушария – это пространство, занимаемое полушарием. Объект большего объема занимает больше места. Полушарие — это трехмерный объект, который составляет половину полной сферы, например чаши, наушники, иглу, купола в архитектуре и т. д. Следовательно, объем полусферы составляет половину объема сферы. Давайте научимся находить объем полушария с помощью нескольких решенных примеров и практических вопросов.
1. |
Каков объем полушария? |
| 2. | Формула объема полушария |
| 3. | Как найти объем полушария? |
| 4. | Часто задаваемые вопросы об объеме полушария |
Каков объем полушария?
Полушарие — это трехмерная фигура (3D-форма), которая составляет половину сферы. Когда сфера разрезается плоскостью, проходящей через ее центр, форма, которую мы получаем, называется полусферой. Полусфера имеет криволинейную поверхность и одно плоское круглое основание. Объем полушария — это количество единичных кубов, которые могут в него поместиться. Единицей объема являются кубические единицы, следовательно, объем полушария можно выразить как м 3 , см 3 , в 3 и так далее.
Давайте узнаем больше о формуле объема полушария.
Объем полушария Формула
Объем полушария составляет половину объема сферы, поэтому он выражается как
Объем полушария = 2πr 3 /3, где r — радиус полушария.
Давайте посмотрим, как выводится формула объема полушария. Поскольку полушарие является половиной сферы, мы можем разделить объем сферы на 2, чтобы получить объем ее полусферы. Теперь, учитывая, что радиус сферы равен r.
Объем сферы можно рассчитать по формуле Объем сферы = 4πr 3 /3. Итак, объем полушария = 1/2 от 4πr 3 /3 = 1/2 × 4πr 3 /3 = 2πr 3 /3
Как найти объем полушария?
Объем полушария рассчитывается по формуле Объем полушария = 2πr 3 /3. Итак, найдем объем полушария, радиус которого равен 7 единицам.
- Шаг 1: Обратите внимание на радиус полушария. Здесь радиус (r) = 7 единиц.
- Шаг 2: Подставьте значение радиуса в формулу Объем полушария = 2πr 3 /3 и представьте окончательный ответ в кубических единицах.
- Шаг 3: После подстановки значения r = 7 получаем, Объем полушария = 2πr 3 /3 = (2 × 3,14 × 7 3 )/3 = 718,01 кубических единиц.
☛ Статьи по теме
- Объем 3D-фигур
- Объем куба
- Объем цилиндра
- Объем прямоугольного параллелепипеда
- Объем сферы
- Объем прямоугольной призмы
Примеры объема полушария
-
Пример 1: Найдите объем полусферы с радиусом, равным 9 единицам. (Возьмем π = 3,14)
Решение:
Дано, что радиус (r) полушария = 9 единиц
Объем полушария = 2πr 3 /3Подставляя r вместо 9, получаем
Объем полушария = (2π × 9 3 )/3
Объем полушария = (2 × 3,14 × 9 3 )/3
Следовательно, объем полушария равен 1526,04 единицы 3 .
-
Пример 2: Радиус полусферы равен 3 дюймам. Каков объем полушария? (Возьмите пи = 3,14)
Решение:
Объем полусферы равен половине объема сферы.
Итак, объем полушария вычисляется по формуле Объем полушария = 2πr 3 /3
После подстановки значения r = 3 получаем,
Объем полушария = 2πr 3 /3 = = (2 × 3,14 × (3) 3 )/3 = 56,57 кубических дюймов.
Следовательно, объем полусферы равен 56,57 кубических дюймов.
-
Пример 3: Сфера радиусом 4 м разрезана на две равные половины. Найдите объем каждого образованного полушария.
Решение:
Радиус полученной таким образом полусферы равен
Радиус полусферы, r = 4 м
Мы знаем, что Объем полусферы = 2πr 3 )/3 = 133,9 м 3 .
Следовательно, объем каждой полусферы = 133,9 м 3
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по объему полушария
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об объеме полушария
Каков объем полушария?
Объем полусферы определяется как общее пространство, занимаемое трехмерной формой в трехмерной плоскости. Объем полушария выражается в кубических единицах: см 3 , м 3 , фут 3 и т. д.
Что такое полушарие?
Полусфера — это трехмерная фигура, которая является половиной сферы. Когда мы разрезаем шар на две половины, то форма, которую мы получаем, называется полушарием.
Как найти объем полушария?
Объем полушария можно рассчитать по формуле: Объем полушария = 2πr 3 /3; где «r» — радиус сферы.
Какова формула объема полушария?
Формула, используемая для расчета объема полушария, выражается следующим образом: Объем полушария = 2πr 3 /3, где r — радиус полушария.
Сфера, полусфера
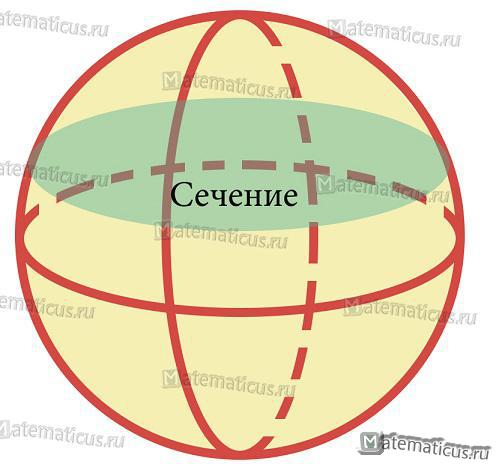
Сфера
Сфера (от греч. «сфайра» — «шар», «мяч») — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки в центре сферы.
Шар — это тело, ограниченное сферой.
Радиус сферы — отрезок, соединяющий центр и любую точку сферы.
Получить сферу можно вращением полуокружности вокруг ее диаметра.
Секущая плоскость делит сферу на два шаровых сегмента.
Любое сечение шара или сферы плоскостью есть круг или окружность.
R – радиус сферы или шара;
Формула объёма сферы:
Формула площади сферы (поверхности шара):
S=4 π R 2
Полусфера
Формула объёма полусферы:
Формула площади полусферы:
S= 2 π Rh = π (r 2 +h 2 )
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.8 / 5. Количество оценок: 5
Сегмент шара
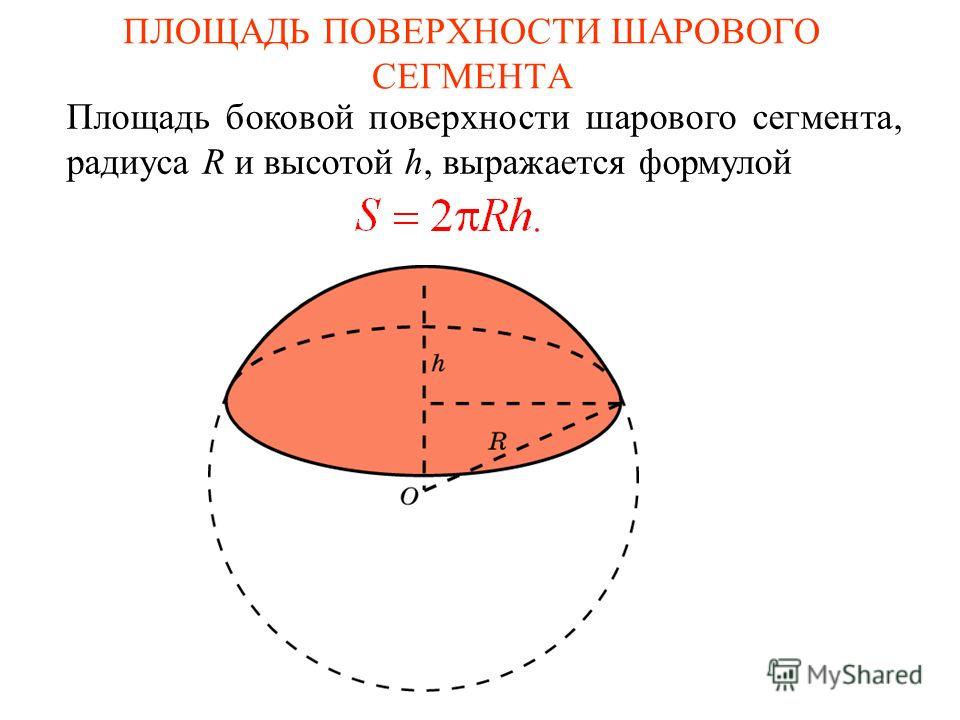
Вычисление площади поверхности и объема шарового сегмента или шарового слоя.

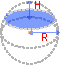
Шаровым сегментом называется часть шара, отсеченная от него плоскостью.
Формулы:
— площадь боковой поверхности
— площадь основания
— формула объема
Формулы площади поверхности геометрических фигур
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2
3. Параметрическое уравнение сферы с центром в точке ( x 0, y 0, z 0):
x = x 0 + R · sin θ · cos φ y = y 0 + R · sin θ · sin φ z = z 0 + R · cos θ
где θ ϵ [0, π ], φ ϵ [0,2 π ].
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда:
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя .
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс , у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента .
По той же причине всю сферу можно рассматривать как сферический пояс , у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
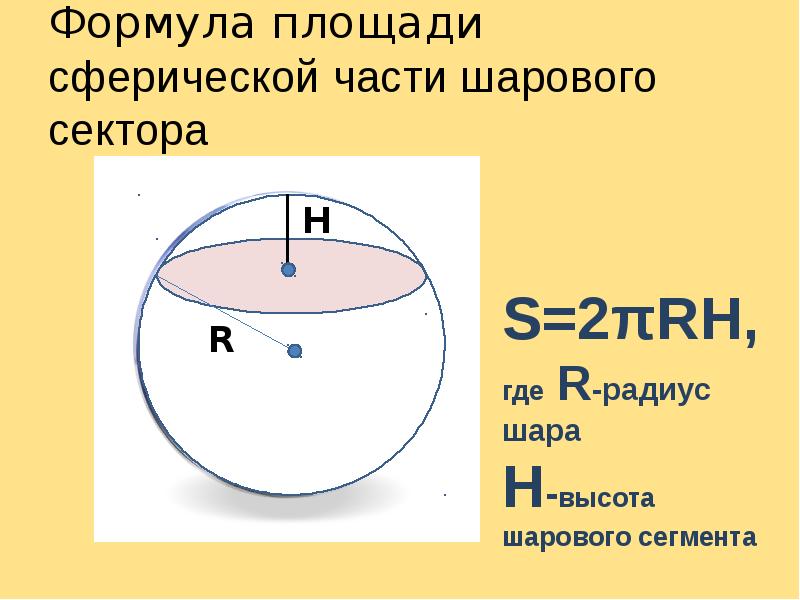
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Высотой шарового сектора называют высоту его сферического сегмента .
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы .
Трактовка значений
Это следует знать:
- Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра.
- Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
- Число «пи» – это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
- Радиус шара равен ½ его диаметру. Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
- Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
- Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.
- Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.
Введите радиус сферы:
Сфера – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние называется радиусом шара.
Площадь поверхности сферы формула:
S = 4 π R 2 , где R – радиус сферы, π – число пи
Через диаметр
Как известно, диаметр шара равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы:
S = 4 π (d/2) 2
Терминология и сферическая геометрия
Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).
Круги на сфере, проходящие параллельно экватору, называются линиями широты. Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.
[spoiler title=”источники:”]
http://planetcalc.ru/283/
http://exceltut.ru/formuly-ploshhadi-poverhnosti-geometricheskih-figur/
[/spoiler]
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.
- Определение сегмента шара
-
Формулы для нахождения площади сегмента шара
- Площадь основания
- Площадь сферической поверхности
- Площадь полной поверхности
- Пример задачи
Определение сегмента шара
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.
- R – радиус шара;
- r – радиус основания сегмента;
- h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.
Связь между радиусом основания сегмента, его высотой и радиусом шара:
Формулы для нахождения площади сегмента шара
Площадь основания
Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):
Sосн. = πr 2
Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.
Площадь сферической поверхности
Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.
Sсфер. пов. = 2πRh
Площадь полной поверхности
Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.
Sполн. = Sосн. + Sсфер. пов. = π (2Rh + r 2)
Пример задачи
Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.
Решение
Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.
Sосн. = 3,14 ⋅ (4,7 см) 2 = 69,3626 см 2
Sсфер. пов. = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см 2
Sполн. = Sосн. + Sсфер. пов. = 69,3626 см 2 + 90,432 см 2 = 159,7946 см 2





 Плоскость сечения ограничивает интервал снизу, согласно формуле (1) имеем:
Плоскость сечения ограничивает интервал снизу, согласно формуле (1) имеем: