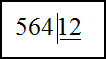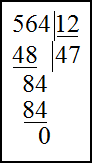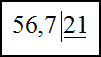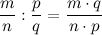Вся математика состоит из арифметических действий. Все прекрасно знают их: сложение, вычитание, умножение, деление. Где же здесь место частному?
Ответ прост. Результатом сложения будет сумма, вычитания – разность, умножения – произведение, а деления – наше частное. Говоря другими словами:
Частное – это результат, полученный в результате деления одного числа на другое.
Число, которое делят – называется делимое, а число, на которое делят – делитель. Деление в более понятном варианте – это вычисление, сколько в делимом содержится значений делителя.
Например, нам нужно узнать, сколько бутылок по 2 литра нам понадобится, чтобы разлить 10 литров воды по ним. Мы считаем, сколько раз в 10 литрах содержится 2 литра, то есть делим 10 на 2 и получаем число 5 (частное). Итого, нам понадобится 5 бутылок.
10:2=5
Или можно обозначить деление как многократное вычитание. Возьмем тот же самый пример. Будем вычитать из 10 число 2, пока не останется ноль, а потом посчитаем, сколько раз мы вычли двойку, получится 5.
10-2=8 (1)
8-2=6 (2)
6-2=4 (3)
4-2=2 (4)
2-2=0 (5)
Не каждый студент может себе позволить за семестр в ВУЗе отдать 100 000 ₽. Но круто, что есть гранты на учебу. Грант-на-вуз.рф – это возможность учиться на желанной специальности. По ссылке каждый получит бонус от 300 ₽ до 100 000 ₽ – грант-на-вуз.рф
Свойства частного
- Основное свойство гласит, что если мы умножим или разделим и делимое и делитель на одно и то же число (n), то значение частного не поменяется.
(a x n)/(b x n)=a/b
Проверяем: (10×3)/(5×3)=30/15=2, то же самое 10/5=2
(a/n)/(b/n)=a/n
Проверяем^ (20/2)/(10/2)=10/5=2, то же самое 20/10=2
- Если мы возьмем некое число и разделим его само на себя, то в результате частное будет равно единице.
a/a=1
- Если некое число разделить на единицу, то его частное будет равно этому же числу, то есть делимому.
a/1=a
- При умножении или делении делимого на некоторое число (n), частное увеличится или уменьшится на это же число соответственно.
(a x n)/b=c x n
(a/n)/b=c/n
Напоминаем про сервис грант-на-вуз.рф. Не упусти свой шанс изучать то, что тебе нравится. Ну или просто сэкономить на учебе. Ты точно получишь от 300 ₽ до 100 000 ₽, перейдя по ссылке грант-на-вуз.рф!
- При умножении или делении делителя на некоторое число (n), частное увеличится или уменьшится на это же число соответственно.
a/(b x n)=c x n
a/(b/n)=c/n
Спасибо, что прочитали статью. Не забывайте про подписку на канал, а также рекомендую почитать канал наших друзей:
https://zen.yandex.ru/fgbnuac — последние научные достижения и лучшие образовательные практики.
Хорошего дня и не болейте.
Определение частного чисел
Определение
Частное чисел – это результат деления одного числа на другое. Таким образом, частное чисел
$a$ и
$b$ будет число
$c$, которое равно
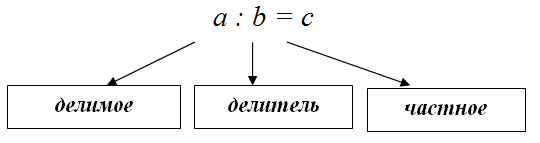
$c = a : b$ . При этом число
$a$ будет делимым, а число
$b$ – делителем.
Пример
Задание. Найти частное чисел:
1) $39 : 3$ ;
4) $124 : 4$
Ответ. $39 : 3 = 13$
$124 : 4 = 31$
Для нахождения частного больших чисел или
десятичных дробей используют способ
деления в столбик.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти частное чисел:
1) $564 : 12$ ;
2) $0,567 : 0,21$
Решение. Для нахождения частного в первом примере выполним деление в столбик.
Для этого запишем делимое и делитель следующим образом
Берем первую цифру слева, она не делится на 12, значит, берем две цифры: 56 и делим их на 12 с остатком.
Возьмем по $4 : 4 cdot 12 = 48$ . Записываем 48 под 56 и находим остаток:
$56 – 48 = 8$ . Восьмерку записываем под чертой и сносим к ней следующее
число из делимого, получим 84. Делим 84 на 12, получаем 7. остаток от деления 0 и цифр в делимом больше нет. Деление окончено.
Таким образом, $564 : 12 = 47$
Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число.
Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее
запишем полученные числа в столбик, как и в первом примере:
Берем в делимом первые две цифры слева и делим их на делимое с остатком. Получаем $56 : 21$ , можно взять по 2. Двойку записываем в частное.
И так как целая часть делимого закончилась, ставим в частном запятую. Умножаем $2 cdot 21 = 42$ , записываем 42 под 56 и вычитаем:
$56 – 42 = 14$ . Остаток 14 списываем к нему следующую
незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное,
и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.
Таким образом $0,567 : 0,21 = 2,7$
Ответ. $564 : 12 = 47$
$0,567 : 0,21 = 2,7$
Частное рациональных дробей находится по правилу
$$frac{m}{n}: frac{p}{q}=frac{m cdot q}{n cdot p}$$
Пример
Задание. Найти частное рациональных дробей:
1) $frac{2}{3}: frac{1}{3}$ ;
2) $1 frac{1}{14}: 1 frac{3}{7}$
Решение. 1) Воспользуемся правилом вычисления частного рациональных дробей:
$$frac{2}{3}: frac{1}{3}=frac{2 cdot 3}{3 cdot 1}=2$$
Для вычисления частного во втором примере, сначала запишем дроби в виде неправильных дробей. Для этого целую часть
умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:
$$1 frac{1}{14}: 1 frac{3}{7}=frac{1 cdot 14+1}{14}: frac{1 cdot 7+3}{7}=frac{15}{14}: frac{10}{7}=$$
$$=frac{15 cdot 7}{14 cdot 10}=frac{15}{2 cdot 10}=frac{15}{20}=frac{3}{4}$$
Ответ. $frac{2}{3}: frac{1}{3}=2$
$1 frac{1}{14}: 1 frac{3}{7}=frac{3}{4}$
Читать дальше: что такое иррациональное число.
Что такое частное чисел
Определение
Частное — это результат процесса деления. Делением называется такая операция, которая обратна умножению, то есть показывает, сколько одинаковых чисел способно содержаться в другом.
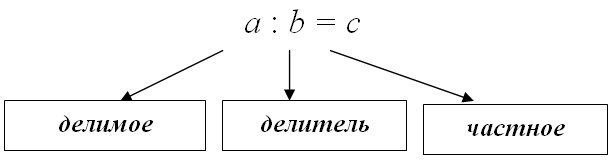
Буквенный вид этого действия выглядит следующим образом: a: b = c, где:
- a – это делимое (число, которое делят)
- b – это делитель (число, которым делят)
- с – это частное (результирующее число деления)
- : — арифметический знак, с помощью которого обозначается деление
Важно! Число 0 никогда не может быть делителем
Нахождение значения частного чисел
Пример:
12 : 3 = 4 (в числе 12 4 раза содержится по 3)
15 : 5 = 3 (в числе 15 5 раз содержится по 5)
Нужно знать, что правильность определения частного от деления числа всегда можно проверить путем перемножения его на делитель, либо делимое поделить на частное и получить делитель.
Например:
20 : 4 = 5
Перемножим частное двух чисел на делитель и получим делимое:
4 * 5 = 20
Разделим делимое на частное и получим делитель:
20 : 5 = 4
Таким образом, мы доказали правильность определения частного.
Что такое частное значение чисел с остатком?
Иногда при делении от делимого остается остаток, который меньше делителя, но более нуля. Приведем выражение частного чисел:
8 : 3 = 2 (ост. 2)
Это значит, что делимое 8 поделилось 2 раза по 3 и остался остаток 2, который меньше трех, но больше нуля.
Таким образом: 0 < ост. <делитель
Основные понятия о частном суммы и разности чисел
Что такое частное суммы чисел?
Определение
Частное от деления суммы чисел – это когда делимое либо делитель выступает в роли суммы двух слагаемых.
Общий вид: (a+b):(c+d), где сумма чисел (a+b) – делимое, а сумма (c+d) – делитель
Пример: (12+3):(3+2)=3
Важно, в подобных примерах последовательность решения определяется следующим образом: сначала решаются выражения в скобочках, потом выражения со знаками деления или умножения, после – вычитание или сложение.
Нет времени решать самому?
Наши эксперты помогут!
Поговорим о частном разности чисел
Аналогично, как и с частностью суммы, только в роли делимого или делителя выступает значение разности: (a-b):(c-d), где разность чисел (a-b) – делимое, а разность (c-d) – делитель
Пример нахождения разности чисел: (12-3):(5-2)=3, где
3 и 2 — это вычитаемое частное чисел
Также в математике находят сумму частного произведения чисел:
(12+3)*(1+2)=45
И произведение частного чисел:
(12*5):(5*2)=6
Основные правила при делении
- При делении одного числа на единицу – получаем в ответ делимое: 6 : 1 = 6
- При делении одного числа на само себя – получаем в ответ 1: 7 : 7 = 1
- Если произведение поделить на один из множителей, то получится другой множитель:
6*3=18, 18:6=3, 18:3=6.
При делении на десятки (10, 100…) у частной, запятой с левой стороны отделяется столько цифр, сколько нулей в делителе: 34:10=3,4, 34:100=0,34, 34:1000=0,034.
Частное чисел в математике: что это такое? В школе учат действие деление, где есть делимое, делитель и частное. Что означают эти названия? Давайте разбираться!
Частное чисел в математике: что это такое
Однажды клоун Бим решил выучить математическое действие деление и нашел для себя в интернете вот такое определение:
Определение. Говорят, что a делится на b, если существует натуральное число с, при умножении которого на b получается а: a=b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
Как мне это понять? — задумался Бим. — Но скоро представление, пойду ребят к нам приглашать.
Как найти частное чисел
Пришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
— Мне надо подарить вам шарики, какое математическое действие я буду применять?
— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.
Клоун хитро прищурился:
— А как называются члены деления?
— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!
— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!
Коля продолжил:
— У каждого из нас будет часть шариков, и результат от деления называется частным.
— Какое же здесь будет частное? — спрашивает Бим.
— Два! — не сговариваясь, хором ответили ребята.
— Правильно, каждому из вас достанется по два шарика, это и есть частное.
Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:
6 (делимое) : 3 (делитель) = 2 (частное).
Запишем цифрами:
6:3=2
| Делимое | Делитель | Частное |
| 6 | 3 | 2 |
В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.
Итак, частное — это число, которое получается в результате деления делимого на делитель.
Полное и неполное частное
А потом было замечательное представление.
В антракте дети пошли в буфет. На подносе лежало семь пирожных. Как же их разделить поровну на трёх ребят?
Друзья задумались и взяли по 2 пирожных, а последним, которое было в остатке, угостили клоуна Бима.
— Теперь я понял! — воскликнул Бим. — Если нельзя всё число пирожных поделить между ребятами без остатка, то такой результат от деления называется неполным частным. А то, что осталось после деления, так и называется остатком и записывается это вот так:
7:3=2(1)
| Делимое | Делитель | Неполное частное | Остаток |
| 7 | 3 | 2 | 1 |
Здесь 7 (делимое) по-прежнему стоит в начале выражения, 3 (делитель) — в середине, 2 (неполное частное) — справа. Но после неполного частного ещё пишем в скобках остаток (1).
- Полное частное — результат деления, когда делимое делится нацело на делитель (остаток равен 0, его и писать незачем).
- Неполное частное — это результат деления с остатком (когда делимое не делится нацело на делитель).
Как найти делитель
Когда дети ушли занимать свои места, буфетчица подошла к Биму и спросила:
— Я забыла, сколько было ребят. Помню только, что каждый из них съел по два пирожных, а всего им досталось 6 штук. Сколько же посетителей было у меня?
Тут в буфет заглянул дрессировщик Бом и быстренько решил эту задачку. Он разделил 6 (делимое) на 2 (частное) и получил 3 (делитель).
— Всего было трое ребят, — ответил Бом.
— Верно! — вспомнил Бим.
Для того чтобы найти делитель, надо делимое разделить на частное.
6:2=3
Здесь 6 – делимое, 2 – частное, а 3 – делитель.
Как найти делимое
— А сколько ты подарил всего шариков трём ребятам? — спросил Бом.
— Забыл, — ответил Бим. — Помню только, что детей было трое, и каждому досталось по два шарика.
Бом и говорит:
— Тогда надо 3 (делитель) умножить на 2 (частное), получится 6.
Для того чтобы найти делимое, надо делитель умножить на частное.
Запишем это цифрами:
3*2=6.
3 — наш делитель, 2 — частное, а 6 — делимое.
Проверка деления умножением
— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?
— Да, — ответил Бом.
Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.
Заключение
А клоун для себя сделал плакаты и теперь каждый день может сразу вспомнить, что:
Определение. Говорят, что а делится на b, если существует число с, при умножении которого на b получается а: a= b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
- Деление — действие, обратное умножению;
- умножение проверяет правильность математического действия — деления;
- для того чтобы найти делимое, надо делитель умножить на частное;
- для того чтобы найти делитель, надо делимое разделить на частное.
Итак, теперь мы знаем, что же такое частное в математике. Оказывается, оно бывает полным и неполным! Кроме того, нетрудно будет найти делитель, делимое и проверить деление умножением. И если учитель спросит в школе: «Частное чисел в математике: что это такое?» — сможем ответить сразу. И пусть любой пример или задача на эту тему будет вам по плечу!
Учим правила деления и умножения на 0 вместе с клоуном Бимом и Бомом.
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания. Комментарии приветствуются! По желанию подписывайтесь на нас в Яндекс.Дзен и в других социальных сетях!!!)))
Не знаю как вы, но я порой нет нет да и задаюсь вопросом, – что такое частное чисел? …вот в голове очень хорошо уложилось что такое сумма (произведение), разность (вычитание), произведение (умножение), а вот деление никак не ассоциируется со словом частное! Ведь подобное слово в нашей жизни в большинстве случаев применяется для определения какой-либо особенности, то есть скажем частного из общего, но никак не в качестве слова поделить что-то на что-то.
Ну да ладно, на вопрос о том, что такое частное можно сказать я уже ответил в своих рассуждениях! Сейчас осталось рассказать о частном из всех возможных простых математических операций, то есть о делении, однако уже в ключе математического мышления, с определением что такое частное и примерами деления для разных чисел.
Определение частного чисел (деление)
Частное чисел – это результат получаемый при определении количества содержания одного числа в другом. Проще говоря это обычное деление. При этом общепринятые оперируемые понятия для частного это делимое, делитель и само частное – результат.
Пример. Найти частное чисел:
1) 20:2=10;
2) 35:7=5.
Ответ: 20:2=10 и 35:7=5.
Это был самый простой пример. Все самое интересное впереди! Проблемы с делением начинаются тогда, когда числа становятся большими и выходят за рамки таблицы умножения. Здесь приходится делить большое число по определенному правилу. Такое деление еще называется деление в столбик.
Пример. Найти частное чисел:
1) 894:3=298
-894| 3__
6 |298
-29
27
– 24
24
0Ответ: 894:3=298
Как делить столбиком (о правилах деления столбиком)
1 -При подсчете столбиком необходимо записать делимое слева, а делитель в Т – образной повернутой скобке, смотрите выше. Далее определим сколько знаков будет в частном. Если первое число делимого позволяет поделить на него делитель, то условно принимаем, что с этого числа и начнется исчисление частного. Все остальные цифры делимого будут образовывать по одному знаку. То есть в нашем случае у частного – 8 есть возможность взять из него число 3, а значит она образует первый знак, а все остальные по 1 знаку, – всего 3! Если такой возможности нет, то постепенно слева направо добавляем по одной цифре, пока не сможем взять из набора этих цифр наш делитель. Все остальные знаки дадут как и в описании выше по одному знаку.
2 – Дальше смотрим сколько в нашем первом выделенном числе можно взять делителей. При этом надо брать их максимальное количество в делимом. То есть в 8 это 2 раза по 3, а итого 6. Далее из выделенного числа в нашем случае 8 вычитаем максимально возможное количество делителей, в нашем случае 6 и получаем – 2. Записываем в Т- образную повернутую скобку цифру 2.
3 – К получившемуся числу сносим цифру из цифр делимого выше. Это 9. Если получившееся число позволяет продолжить подбор по правилу выше, то проводим такой подбор. То есть в 29 цифра 3 содержится 9 раз, что равно числу 27. Записываем в Т- образную повернутую скобку цифру 9.
А оставшийся остаток 29-27 образует следующую цифру для оперирования с ней по этому же правилу. То есть 2 и сносим 4. Получается 24. Если вдруг получается так, что из оставшегося числа и снесенного сверху числа невозможно взять делитель ни разу, то в Т- образной повернутой скобке пишем 0 и сносим еще одну цифру, до тех пор пока не сможем взять из получившегося числа как минимум хотя бы 1 раз делитель.
4. Если в конце таких вычислений получается число которое невозможно поделить на делитель и сносить уже нечего, то это было деление с остатком. То есть оставшееся число или цифра, это остаток. Надо понимать, что остаток всегда должен быть меньше делителя. В этом вся соль остатка, он не позволяет взять из себя делитель даже одного раза!
Деление рациональных дробей
Для деления дробей используется следующее правило.
То есть если сказать без глубоких объяснений процессов происходящего, берем дробь, где в числителе произведение числителя делимого и знаменателя делителя, а в знаменателе этой дроби произведение знаменателя делимого и числителя делителя!
Что же, я думаю вы уже утомились воспринимать информацию и теперь вам лучше всего развеяться, поиграв с онлайн калькулятором на деление. А и тут сразу же в голове всплыло еще одно правило, на ноль делить нельзя, так как даже в самом маленьком числе нулей великое множество, то есть бесконечность, а наш курс все же для школьников начальных и средних классов, где о бесконечности знают лишь то, что можно бесконечно играть в компьютер и не более:) А как на деление с нолем отреагирует калькулятор, можете проверить сами.
Побалуемся с делением!?
|
Вводим циферки Цифра которую будем делить (делимое) |
|
На которую будем делить (делитель) |
|
|
* -Infinity (бесконечность)
