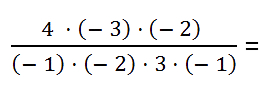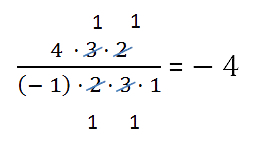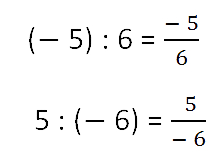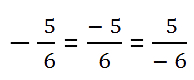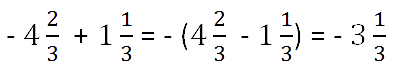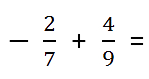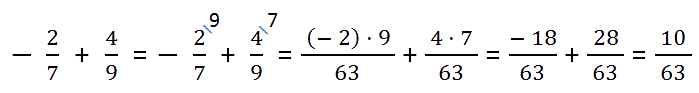Как найти частное чисел с одинаковыми знаками

Действия с рациональными числами

• Сложение
• Вычитание
• Умножение
• Деление

Сложение

При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.

Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.

При сложении двух рациональных чисел с разными знаками нужно взять их модули и из большего вычесть меньший. В результате ставится знак того числа, у которого модуль больше.

Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:

Из данных примеров следует, что в результате сложения двух чисел с разными знаками, может получится как положительное, так и отрицательное число.

Сумма двух противоположных чисел равна нулю.

Вычитание

Вычитание одного рационального числа из другого можно заменить сложением. При этом уменьшаемое берётся со своим знаком, а вычитаемое – с противоположным.

Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.

Умножение

При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.

Ниже представлена схема (правило знаков при умножении):

+	·	+	=	+
+	·	–	=	–
–	·	+	=	–
–	·	–	=	+

Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.

При умножении любого числа на  -1  получится число, противоположное данному.

Деление

При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.

При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):

+	:	+	=	+
+	:	–	=	–
–	:	+	=	–
–	:	–	=	+

Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.

При делении любого числа на  -1  получится число, противоположное данному.

Как выполнять деление отрицательных чисел легко понять, вспомнив, что
деление — это действие, обратное умножению.

Если «a» и «b» положительные числа, то
разделить число «a» на число «b», значит найти
такое число «с», которое при умножении на
«b» даёт число «a».

Данное определение деления действует для любых рациональных
чисел, если делители отличны от нуля.

Поэтому, например, разделить число «−15» на
число 5 — значит, найти такое число, которое при умножении
на число 5 даёт число «−15». Таким числом будет «−3», так как

(−3) · 5 = −15

значит

(−15) : 5 = −3

Примеры деления рациональных чисел.

1. 10 : 5 = 2, так как 12 · 5 = 10
2. (−4) : (−2) = 2, так как 2 · (−2) = −4
3. (−18) : 3 = −6, так как (−6) · 3 = −18
4. 12 : (−4) = −3, так как (−3) · (−4) = 12

Из примеров видно, что частное двух чисел с одинаковыми знаками — число
положительное (примеры 1, 2), а частное двух чисел с разными знаками—
число отрицательное (примеры 3, 4).

Правила деления отрицательных чисел

Чтобы найти модуль частного, нужно разделить модуль
делимого на модуль делителя.

Итак, чтобы разделить два числа с одинаковыми знаками, надо:

• модуль делимого разделить на модуль делителя;
• перед результатом поставить знак «+».

Примеры деления чисел с одинаковыми знаками:

• (−9) : (−3) = +3
• 6 : 3 = 2

Чтобы разделить два числа с разными знаками, надо:

• модуль делимого разделить на модуль делителя;
• перед результатом поставить знак «−».

Примеры деления чисел с разными знаками:

• (−5) : 2 = −2,5
• 28 : (−2) = −14

Для определения знака частного можно также пользоваться следующей таблицей.

Правило знаков при делении

+ : (+) = +	+ : (−) = −
− : (−) = +	− : (+) = −

При вычислении «длинных» выражений, в которых фигурируют только умножение и деление,
пользоваться правилом знаков очень удобно. Например, для вычисления дроби

Можно обратить внимание, что в числителе два знака «минус», которые при
умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус».
Поэтому в конце результат получится со знаком «минус».

Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и
раньше:

Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.

• а : 1 = a
• а : (−1) = −a
• а : a = 1

, где «а» — любое рациональное число.

Зависимости между результатами умножения и деления, известные для
положительных чисел, сохраняются и для всех
рациональных чисел (кроме числа нуль):

• если a · b = с;     a = с : b;     b = с : a;
• если a : b = с;     a = с · b;     b = a : c

Данные зависимости используются для нахождения неизвестного
множителя, делимого и делителя (при решении уравнений), а также для
проверки результатов умножения и деления.

Пример нахождения неизвестного.

Знак «минус» в дробях

Разделим число «−5» на
«6» и число «5» на «−6».

Напоминаем, что черта в записи обыкновенной дроби — это тот же знак
деления, поэтому можно записать частное каждого из этих действий в виде отрицательной дроби.

Таким образом знак «минус» в дроби может находиться:

• перед дробью;
• в числителе;
• в знаменателе.

Это часто используется при выполнении действий с дробями, облегчая вычисления.

Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего
модуля вычитаем меньший по
правилам сложения чисел с разными знаками.

Пример.

Используя описанное свойство переноса знака в дроби, можно действовать, не выясняя, модуль какого из данных дробных чисел больше.

---

Ваши комментарии

Оставить комментарий:

---

Математика

6 класс

Урок № 27

Частное целых чисел. Часть 1.

Перечень рассматриваемых вопросов:

1. Деление рациональных чисел.
2. Правила знаков при делении.

Глоссарий по теме

При делении отрицательного числа на отрицательное число, надо разделить модуль делимого на модуль делителя, частное будет положительным.

При делении чисел с разными знаками, надо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак «минус».

На ноль делить нельзя!

Частное от деления нуля на любое целое число, не равное нулю, всегда равно нулю.

Основная литература

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142с.

Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95с.

Теоретический материал для самостоятельного изучения

Арифметика – раздел математики, изучающий числа, их отношения и свойства. В арифметике рассматриваются различные вычислительные операции, такие как сложение, вычитание, умножение и деление. При этом деление издревле считалось очень сложной и громоздкой операцией.

Сегодня мы поговорим об этой вычислительной операции применительно к целым числам. При этом мы будем выполнять деление чисел как с одним знаком, так и с разными знаками.

Смысл деления заключается в том, что по данному произведению и одному из множителей находится второй множитель. Что касается знаков при делении, то соблюдается та же закономерность, что и при умножении.

Например,

(– 18 : 3) –это значит найти такое число x, что

(3 ·x) = – 18

Сначала определим знак числа x. При умножении на положительное число 3 получилось отрицательное число (– 18), значит, 3 иx должны иметь разные знаки, откуда следует, что x– числоотрицательное.

Теперь найдём модуль числа x.

|x| = 18 : 3 = 6

Значит,x = – 6.

Совместим все наши рассуждения и выполним действие:

(– 18 : 3) = – 6

Ещё один пример:

– 20 :(– 4)

Поступаем также: надо найти такое число x, которое при умножении на (– 4) даст (– 20).

– 4 · x = – 20

Определим знак числа x.

При умножении отрицательного числа на другое число получилось отрицательное число, значит, перемножаемые числа были разных знаков, значит,x– положительное число.

Теперь найдём модуль числа x.

|x| = 20 : 4 = 5

Совместим все наши рассуждения и выполним действие:

– 20 : (– 4) = 5

Теперь мы можем сформулировать правило деления целых чисел:

При делении чисел с разными знаками надо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак «минус».

При делении чисел с одинаковыми знаками надо разделить модуль делимого на модуль делителя, частное будет положительным.

Иначе сформулируем общее правило для нахождения частного чисел.

Частное чисела и b равно частному их модулей, взятому со знаком “+”, если эти числа одинаковых знаков, и со знаком “-“, если они разных знаков.

При этом стоит помнить, что деление противоположно умножению, поэтому его можно проверить, воспользовавшись свойством умножения, как и было показано в наших рассуждениях.

Например,

80 :(– 2) = – 40

Проверим умножением:

– 40· (– 2) = 80 (так как при умножении чисел с одним знаком результат будет положительным)

Часто, чтобы запомнить правила деления чисел с разными знаками, используют такое правило:

При делении двух чисел с одинаковыми знаками частное будет иметь знак «+».

При делении двух чисел с разными знаками частное будет иметь знак «минус».

Осталось рассказать о делении чисел на ноль.

Помните, что на ноль делить нельзя!

А частное от деления нуля на любое целое число, не равное нулю, всегда равно нулю.

Например,

0 : (– 4) = 0

0 : 14 = 0

Итак, сегодня мы познакомились с нахождением частного двух чисел как одного, так и разных знаков, узнали о том, что на ноль делить нельзя и о том, что частное от деления нуля на любое целое число, не равное нулю, всегда равно нулю.

Знак деления

Деление записывается с использованием различных знаков. Символы, которые можно использовать выглядят так:

«/» – это символ самый старый, его впервые использовал английский математик Уильям Отред в 1631 г.

«:»– этот символ предпочитал немецкий математик Лейбниц (1684 г.). Он до сих пор используется в русскоязычных учебниках математики.

«÷» – этот символ (обелюс) ввёл швейцарский математик Йоханн Ранв 1659г. Его часто называют «английским знаком деления».

Тренировочные задания

Какой знак имеет частное?

28 : (– 4)

Решение:

Для нахождения знака используем правило нахождения частного двух чисел с разными знаками. Частное чисел а и b равно частному их модулей со знаком “-“, если они разных знаков. Следовательно, частное будет со знаком минус. Далее выполним деление данных чисел по модулю, т.е. 28 : 4 = 7. Следовательно,

28 : (–4) = – 7

Решите уравнение.

5 · х = –65

Решение:

Деление обратно умножению, значит, чтобы найти х нужно:

(– 65) : 5 = x

Далее находим знак, используя правило нахождения частного двух чисел с разными знаками. Частное чисел а и b равно частному их модулей со знаком “-“, если они разных знаков. Следовательно, частное будет со знаком минус. Далее выполним деление данных чисел по модулю, результат равен 13, но с учетом знака получим:

x = –13.

Вы перешли к вопросу Как найти произведение и частное чисел с одинаковыми знаками?. Он относится к категории Математика,
для 5 – 9 классов. Здесь размещен ответ по заданным параметрам. Если этот
вариант ответа не полностью вас удовлетворяет, то с помощью автоматического
умного поиска можно найти другие вопросы по этой же теме, в категории
Математика. В случае если ответы на похожие вопросы не раскрывают в полном
объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части
сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете
ознакомиться с вариантами ответов пользователей.