Математика
6 класс
Урок № 42
Деление дробей
Перечень рассматриваемых вопросов:
- деление рациональных чисел, правила знаков при делении.
Тезаурус
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Частным двух дробей с одинаковыми знаками является положительная дробь, модуль которой равен частному модулей делимого и делителя.
Частное дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
На прошлом уроке мы изучали правила умножения дробей.
Сегодня рассмотрим правила деления.
Аналогично умножению, дроби с любыми знаками делят по тем же правилам, что и положительные дроби.
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Найдём частное от деления двух дробей.
Запишем равенство, которое можно получить на основании правила деления.
Доказательство
Чтобы разделить дробь на целое, не равное нулю число, можно её знаменатель умножить на это число.
Найдём частное
Знак «–» перед дробью, можно записывать и в знаменателе, и в числители дроби, то есть верны равенства:
Используя свойство взаимно обратных дробей, что их произведение равно 1, можем сформулировать следующее утверждение:
Чтобы одну дробь разделить на другую, отличную от нуля, можно делимое умножить на дробь, обратную делителю.
Найдём частное
Правила знаков, при делении дробей
Правило деления дробей с одинаковыми знаками
Частным двух дробей с одинаковыми знаками является положительная дробь, равная частному модулей делимого и делителя.
Выполним деление
Правило деления дробей с разными знаками
Частное от деления дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Выполним деление
Из правил деления дробей с любыми знаками следует, что их можно делить по тем же правилам, что и целые числа. То есть мы можем сначала определять знак результата, а потом выполнять действия с модулями.
Выполним деление
Дополнительный материал
Решение задачи
Решение
Найдём, сколько автомобиль проехал за второй час. Известно, что в 2 раза меньше, чем за первый, значит, путь за первый час разделим на 2.
Найдём общую часть пути за два часа.
Для этого сложим части пути за первый и за второй час.
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Какие действия изображены?
Варианты ответов:
деление дробей с одинаковыми знаками
деление дробей с разными знаками
деление дроби на целое число
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
Правильный ответ
№ 2. Вставьте в текст нужные слова.
Частное двух дробей есть дробь, … которой равен … числителя первой дроби и … второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Варианты слов для вставки:
числитель
произведению
частному
сумме
разности
знаменателя
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
Правильный ответ:
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
В данной публикации мы рассмотрим, каким образом можно обыкновенную (простую) дробь разделить на число или другую дробь, и как найти частное от деления смешанных дробей. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
-
Деление дроби
- На число
- На другую дробь
-
Деление смешанных дробей
- Примеры задач
Деление дроби
На число
Результатом деления обыкновенной дроби на число n является дробь, знаменатель которой равняется произведению знаменателя исходной дроби и этого числа n. Числитель при этом остается тем же.
Примечание: после выполнения деления не забываем проверить, можно ли сократить новую дробь.
На другую дробь
Чтобы разделить одну дробь на другую, переворачиваем дробь-делитель (меняем местами числитель и знаменатель) и умножаем ее на дробь-делимое, которое оставляем без изменений.
a/b
:
c/d
=
a/b
⋅
d/c
=
a ⋅ d/b ⋅ c
Деление смешанных дробей
Чтобы найти частное от деления смешанных дробей, для начала их нужно представить в виде неправильных дробей, и только после этого выполнить деление.
X
a/b
: Y
c/d
=
X ⋅ b + a/b
:
Y ⋅ d + c/d
=
X ⋅ b + a/b
⋅
d/Y ⋅ d + c
=
(X ⋅ b + a) ⋅ d/(Y ⋅ d + c) ⋅ b
Примеры задач
Задание 1
Разделите дробь
5/6
на число 5.
Решение
5/6
: 5 =
5/6⋅5
=
5/30
=
1/6
Задание 2
Разделите дробь
4/15
на
2/9
.
Решение
4/15
:
2/9
=
4/15
⋅
9/2
=
4⋅9/15⋅2
=
36/30
=
6/5
= 1
1/5
Задание 3
Найдите частное от деления дроби 6
1/4
на дробь 4
2/3
.
Решение
Т.к. даны смешанные дроби, сначала запишем их в виде неправильных, потом выполним требуемое действие.
6
1/4
: 4
2/3
=
6⋅4+1/4
:
4⋅3+2/3
=
25/4
:
14/3
=
25/4
⋅
3/14
=
25⋅3/4⋅14
=
75/56
=1
19/56
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:
Найдём частное двух обыкновенных дробей.
При необходимости дробь сокращают.
Пример:
.
В случае деления целого числа на обыкновенную дробь целое число можно умножить на дробь, обратную делителю, или сначала представить целое число в виде неправильной дроби, а затем выполнить деление обыкновенных дробей:
8:45=8⋅54=82⋅541=2⋅51=101=10;8:45=81:45=81⋅54=82⋅541=2⋅51=101=10.
Чтобы найти частное смешанных чисел, смешанные числа представляют в виде неправильных дробей и выполняют деление по правилу деления обыкновенных дробей:
325:15=3⋅5+25:15=175:15=175⋅51=17⋅5151⋅1=17⋅11⋅1=171=17;412:634=92:274=92⋅427=91⋅4221⋅273=1⋅21⋅3=23.
Содержание
- Деление и дроби
- Дробные выражения
- —>Сайт учителя математики А.В.Капитановой —>
- Умножение дроби на натуральное число
- Пример: Найти произведение дроби и натурального числа:
- Пример: Найти произведение двух смешанных чисел:
- Пример: Найти частное от деления дроби на натуральное число:
- Пример: Найти частное от деления дробей:
- Пример: Найти частное от деления смешанных чисел:
Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 
, т.е. 2 : 3 = .
Пример:
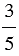= 3 : 5; 
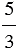= 5 : 3.
В результате деления двух натуральных чисел может получится натуральное число или дробное число.
Пример:
20 : 4 =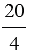 
= 5; 13 : 25 = 
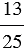; 45 : 4 = 
.
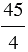Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем.
Пример:
а) 1 =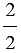 
= 
= . = 
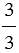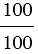= . т.к. 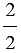= 2 : 2 = 1, 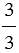= 3 : 3 = 1, . 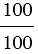= 100 : 100 = 1, .
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
б) 7 =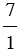 
= 
= 
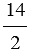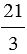= . т.к. 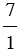= 7 : 1 = 7, 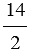= 14 : 2 = 7; 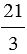= 21 : 3 = 7 .
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
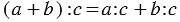
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
Частное от деления одного выражения на другое можно записать с помощью черты дроби. Например, выражение (3,5 — 1,1) : (7,3 + 2,7) можно записать в виде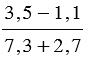 
. А выполнив действия в числителе и в знаменателе полученной дроби, найдем значение данного выражения: 
.
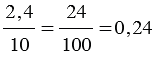Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
К дробным выражениям относятся:
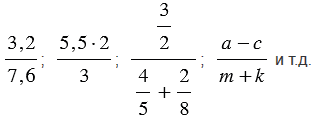
Числитель дробного выражения — выражение, стоящее над чертой.
Знаменатель дробного выражения — выражение, стоящее под чертой.
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
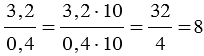, обычно запись упрощают, и пишут так: 
.
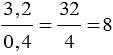То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
.
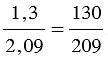Поделись с друзьями в социальных сетях:
Источник
—>Сайт учителя математики А.В.Капитановой —>
Умножение дроби на натуральное число
Пример: Найти произведение дроби и натурального числа:
Умножение обыкновенных дробей
- перемножить числители и знаменатели дробей;
- сократить полученную дробь.
| 3 | · | 2 | = | 3 · 2 | = | 6 |
| 7 | 5 | 7 · 5 | 35 |
Умножение смешанных чисел
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Пример: Найти произведение двух смешанных чисел:
| 2 | 1 | · | 1 | 2 | = | 2 · 2 + 1 | · | 1 · 3 + 2 | = | 5 | · | 5 | = | 5 · 5 | = | 25 | = | 6 · 4 + 1 | = 4 | 1 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 · 3 | 6 | 6 | 6 |
Пример: Найти произведение смешанного числа и целого числа:
| 4 | 1 | · | 6 | = | 4 · 3 + 1 | · | 6 | = | 13 · 6 | = | 26 |
| 3 | 3 | 3 |
Пример: Найти произведение смешанного числа и обыкновенной дроби:
| 2 | 1 | · | 3 | = | 2 · 7 + 1 | · | 3 | = | 15 | · | 3 | = | 15 · 3 | = | 5 · 9 | = | 9 | = | 7 + 2 | = 1 | 2 |
| 7 | 5 | 7 | 5 | 7 | 5 | 7 · 5 | 7 · 5 | 7 | 7 | 7 |
Деление дроби на натуральное число
Пример: Найти частное от деления дроби на натуральное число:
Определение: Чтобы получить дробь, обратную данной, следует поменять местами числитель и знаменатель.
Деление натурального числа на дробь
Пример: Найти частное от деления натурального числа на дробь:
| 2: | 4 | = | 2· | 5 | = | 2 · 5 | = | 2 · 5 | = | 5 | = | 2 · 2 + 1 | = 2 | 1 |
| 5 | 4 | 4 | 2 · 2 | 2 | 2 | 2 |
Деление обыкновенных дробей
Пример: Найти частное от деления дробей:
| 3 | : | 4 | = | 3 | · | 5 | = | 3 · 5 | = | 15 |
| 7 | 5 | 7 | 4 | 7 · 4 | 28 |
Деление смешанных чисел
- преобразовать смешанные дроби в неправильные;
- умножить первую дробь на дробь, обратную второй;
- сократить полученную дробь;
- если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Пример: Найти частное от деления смешанных чисел:
| 1 | 1 | : | 2 | 2 | = | 1 · 2 + 1 | : | 2 · 3 + 2 | = | 3 | : | 8 | = | 3 | · | 3 | = | 3 · 3 | = | 9 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 | 8 | 2 · 8 | 16 |
Пример: Найти частное от деления смешанного числа на дробь:
Источник
Определение частного чисел
Определение
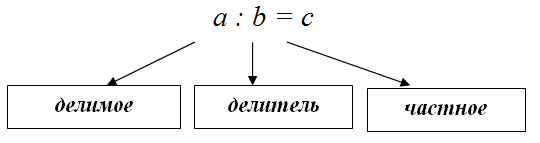
Частное чисел – это результат деления одного числа на другое. Таким образом, частное чисел
$a$ и
$b$ будет число
$c$, которое равно
$c = a : b$ . При этом число
$a$ будет делимым, а число
$b$ – делителем.
Пример
Задание. Найти частное чисел:
1) $39 : 3$ ;
4) $124 : 4$
Ответ. $39 : 3 = 13$
$124 : 4 = 31$
Для нахождения частного больших чисел или
десятичных дробей используют способ
деления в столбик.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти частное чисел:
1) $564 : 12$ ;
2) $0,567 : 0,21$
Решение. Для нахождения частного в первом примере выполним деление в столбик.
Для этого запишем делимое и делитель следующим образом
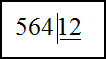
Берем первую цифру слева, она не делится на 12, значит, берем две цифры: 56 и делим их на 12 с остатком.
Возьмем по $4 : 4 cdot 12 = 48$ . Записываем 48 под 56 и находим остаток:
$56 – 48 = 8$ . Восьмерку записываем под чертой и сносим к ней следующее
число из делимого, получим 84. Делим 84 на 12, получаем 7. остаток от деления 0 и цифр в делимом больше нет. Деление окончено.
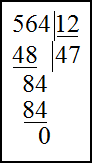
Таким образом, $564 : 12 = 47$
Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число.
Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее
запишем полученные числа в столбик, как и в первом примере:
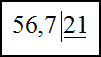
Берем в делимом первые две цифры слева и делим их на делимое с остатком. Получаем $56 : 21$ , можно взять по 2. Двойку записываем в частное.
И так как целая часть делимого закончилась, ставим в частном запятую. Умножаем $2 cdot 21 = 42$ , записываем 42 под 56 и вычитаем:
$56 – 42 = 14$ . Остаток 14 списываем к нему следующую
незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное,
и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.
Таким образом $0,567 : 0,21 = 2,7$
Ответ. $564 : 12 = 47$
$0,567 : 0,21 = 2,7$
Частное рациональных дробей находится по правилу
$$frac{m}{n}: frac{p}{q}=frac{m cdot q}{n cdot p}$$
Пример
Задание. Найти частное рациональных дробей:
1) $frac{2}{3}: frac{1}{3}$ ;
2) $1 frac{1}{14}: 1 frac{3}{7}$
Решение. 1) Воспользуемся правилом вычисления частного рациональных дробей:
$$frac{2}{3}: frac{1}{3}=frac{2 cdot 3}{3 cdot 1}=2$$
Для вычисления частного во втором примере, сначала запишем дроби в виде неправильных дробей. Для этого целую часть
умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:
$$1 frac{1}{14}: 1 frac{3}{7}=frac{1 cdot 14+1}{14}: frac{1 cdot 7+3}{7}=frac{15}{14}: frac{10}{7}=$$
$$=frac{15 cdot 7}{14 cdot 10}=frac{15}{2 cdot 10}=frac{15}{20}=frac{3}{4}$$
Ответ. $frac{2}{3}: frac{1}{3}=2$
$1 frac{1}{14}: 1 frac{3}{7}=frac{3}{4}$
Читать дальше: что такое иррациональное число.
