Следующее действие, которое можно выполнять с дробями это деление. Выполнять деление дробей достаточно просто главное знать несколько правил деления. Разберем правила деления и рассмотрим решение примеров на данную тему.
Деление дроби на дробь.
Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.
(bf frac{a}{b} div frac{c}{d} = frac{a}{b} times frac{d}{c}\)
Пример:
Выполните деление обыкновенных дробей .
Деление дроби на число.
Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.
(bf frac{a}{b} div n = frac{a}{b} div frac{n}{1} = frac{a}{b} times frac{1}{n}\)
Рассмотрим пример:
Выполните деления дроби на натуральное число (frac{4}{7} div 3).
Как мы уже знаем, что любое число можно представить в виде дроби (3 = frac{3}{1} ).
(frac{4}{7} div 3 = frac{4}{7} div frac{3}{1} = frac{4}{7} times frac{1}{3} = frac{4 times 1}{7 times 3} = frac{4}{21}\)
Деление числа на дробь.
Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.
Рассмотрим пример:
Выполните деление числа на дробь.
Деление смешанных дробей.
Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.
Пример:
Выполните деление смешанных дробей.
(2frac{3}{4} div 3frac{1}{6} = frac{11}{4} div color{red} {frac{19}{6}} = frac{11}{4} times color{red} {frac{6}{19}} = frac{11 times 6}{4 times 19} = frac{11 times color{red} {2} times 3}{2 times color{red} {2} times 19} = frac{33}{38}\)
Деление числа на число.
Чтобы поделить простые числа, нужно представить их в виде дроби и выполнить деление по правилам деления дроби на дробь.
Пример:
(2 div 5 = frac{2}{1} div color{red} {frac{5}{1}} = frac{2}{1} times color{red} {frac{1}{5}} = frac{2 times 1}{1 times 5} = frac{2}{5}\)
Примечание к теме деление дробей:
На нуль делить нельзя.
Вопросы по теме:
Как делить дроби? Как разделить дробь на дробь?
Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.
Как делить дроби с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.
Пример №1:
Выполните деление и назовите делитель, дробь, обратную делителю: а) (frac{5}{9} div frac{8}{13}) б) (2frac{4}{5} div 1frac{7}{8})
Решение:
а) (frac{5}{9} div frac{8}{13} = frac{5}{9} times frac{13}{8} = frac{65}{72}\\)
( frac{8}{13}) – делитель, ( frac{13}{8}) – обратная дробь делителя.
б) (2frac{4}{5} div 1frac{7}{8} = frac{14}{5} div frac{15}{8} = frac{14}{5} times frac{8}{15} = frac{14 times 8}{5 times 15} = frac{112}{75} = 1frac{37}{75}\\)
( frac{15}{8}) – делитель, ( frac{8}{15}) – обратная дробь делителя.
Пример №2:
Вычислите деление: а) (5 div 1frac{1}{4}) б) (9frac{2}{3} div 8)
Решение:
а) (5 div 1frac{1}{4} = frac{5}{1} div frac{5}{4} = frac{5}{1} times frac{4}{5} = frac{color{red} {5} times 4}{1 times color{red} {5}} = frac{4}{1} = 4 \\)
б) (9frac{2}{3} div 8 = frac{29}{3} div frac{8}{1} = frac{29}{3} times frac{1}{8} = frac{29 times 1}{3 times 8} = frac{29}{24} = 1frac{5}{24}\\)
Математика
6 класс
Урок № 42
Деление дробей
Перечень рассматриваемых вопросов:
- деление рациональных чисел, правила знаков при делении.
Тезаурус
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Частным двух дробей с одинаковыми знаками является положительная дробь, модуль которой равен частному модулей делимого и делителя.
Частное дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
На прошлом уроке мы изучали правила умножения дробей.
Сегодня рассмотрим правила деления.
Аналогично умножению, дроби с любыми знаками делят по тем же правилам, что и положительные дроби.
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Найдём частное от деления двух дробей.
Запишем равенство, которое можно получить на основании правила деления.
Доказательство
Чтобы разделить дробь на целое, не равное нулю число, можно её знаменатель умножить на это число.
Найдём частное
Знак «–» перед дробью, можно записывать и в знаменателе, и в числители дроби, то есть верны равенства:
Используя свойство взаимно обратных дробей, что их произведение равно 1, можем сформулировать следующее утверждение:
Чтобы одну дробь разделить на другую, отличную от нуля, можно делимое умножить на дробь, обратную делителю.
Найдём частное
Правила знаков, при делении дробей
Правило деления дробей с одинаковыми знаками
Частным двух дробей с одинаковыми знаками является положительная дробь, равная частному модулей делимого и делителя.
Выполним деление
Правило деления дробей с разными знаками
Частное от деления дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Выполним деление
Из правил деления дробей с любыми знаками следует, что их можно делить по тем же правилам, что и целые числа. То есть мы можем сначала определять знак результата, а потом выполнять действия с модулями.
Выполним деление
Дополнительный материал
Решение задачи
Решение
Найдём, сколько автомобиль проехал за второй час. Известно, что в 2 раза меньше, чем за первый, значит, путь за первый час разделим на 2.
Найдём общую часть пути за два часа.
Для этого сложим части пути за первый и за второй час.
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Какие действия изображены?
Варианты ответов:
деление дробей с одинаковыми знаками
деление дробей с разными знаками
деление дроби на целое число
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
Правильный ответ
№ 2. Вставьте в текст нужные слова.
Частное двух дробей есть дробь, … которой равен … числителя первой дроби и … второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Варианты слов для вставки:
числитель
произведению
частному
сумме
разности
знаменателя
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
Правильный ответ:
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Перед тем как перейти к делению дробей, вспомним теоретические основы. Итак, дробь — это форма записи числа:
где a — числитель, b — знаменатель.
Дробь называется правильной — если числитель меньше знаменателя (к примеру, 7/8), неправильной — если числитель больше знаменателя (например, 9/6).
Как разделить дробь на дробь?
Правило деления дробей заключается в следующем:
- Числитель первой дроби умножается на знаменатель второй, в результате получим числитель итоговой дроби;
- Знаменатель первой дроби умножаем на числитель второй, в результате получим знаменатель итоговой дроби.
В общем виде, деление дробей выглядит следующим образом:
Другими словами, деление обыкновенных дробей заключается в умножении первой дроби на обратную от второй.
Пример 1:
3 7
÷
5 7
Решение:
3 7
÷
5 7
=
3 7
×
7 5
=
3 ∙ 7 7 ∙ 5
=
21 35
=
3 5
Как делить дроби с разными знаменателями?
Деление дробей с разными знаменателями никак не отличается от деления дробей с одинаковыми знаменателем и выполняется по единому алгоритму.
Пример 2:
7 9
÷
2 3
Решение:
7 9
÷
2 3
=
7 9
×
3 2
=
7 ∙ 3 9 ∙ 2
=
21 18
=
7 6
=
1
1 6
Как разделить дробь на целое число?
Чтобы разделить дробь на натуральное число нужно это число привести к неправильному виду, а затем воспользоваться вышеописаным правилом.
Пример 3:
5 4
÷ 3
Решение:
5 4
÷ 3
=
5 4
×
1 3
=
5 ∙ 1 4 ∙ 3
=
5 12
Деление целого числа на дробь
Для деления целого числа на дробь, аналогично предыдущему пункту, переводим число в неправильную дробь и производим деление дробей по общему правилу.
Пример 4:
5 ÷
2 6
Решение:
5 1
÷
2 6
=
5 1
×
6 2
=
5 ∙ 6 1 ∙ 2
=
30 2
=
15 1
=
15
Как делить смешанные дроби?
Деление смешанных дробей сводится к переводу их к неправильному виду и дальнейшим действиям согласно вышеописанным алгоритмам. Перевод смешанного числа в неправильную дробь, в общем виде, выглядит следующим образом:
Пример 5:
3
2 5
÷
4 9
Решение:
3
2 5
÷
4 9
=
3 ∙ 5 + 2 5
÷
4 9
=
17 5
÷
4 9
=
17 5
×
9 4
=
17 ∙ 9 5 ∙ 4
=
153 20
=
7
13 20
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Калькулятор деления дробей
Оцените материал:
Загрузка…
Содержание
- Деление и дроби
- Дробные выражения
- —>Сайт учителя математики А.В.Капитановой —>
- Умножение дроби на натуральное число
- Пример: Найти произведение дроби и натурального числа:
- Пример: Найти произведение двух смешанных чисел:
- Пример: Найти частное от деления дроби на натуральное число:
- Пример: Найти частное от деления дробей:
- Пример: Найти частное от деления смешанных чисел:
Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 
, т.е. 2 : 3 = .
Пример:
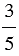= 3 : 5; 
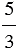= 5 : 3.
В результате деления двух натуральных чисел может получится натуральное число или дробное число.
Пример:
20 : 4 =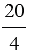 
= 5; 13 : 25 = 
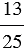; 45 : 4 = 
.
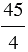Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем.
Пример:
а) 1 =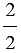 
= 
= . = 
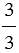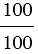= . т.к. 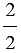= 2 : 2 = 1, 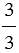= 3 : 3 = 1, . 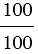= 100 : 100 = 1, .
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
б) 7 =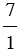 
= 
= 
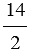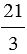= . т.к. 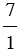= 7 : 1 = 7, 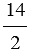= 14 : 2 = 7; 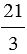= 21 : 3 = 7 .
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
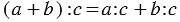
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
Частное от деления одного выражения на другое можно записать с помощью черты дроби. Например, выражение (3,5 — 1,1) : (7,3 + 2,7) можно записать в виде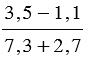 
. А выполнив действия в числителе и в знаменателе полученной дроби, найдем значение данного выражения: 
.
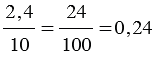Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
К дробным выражениям относятся:
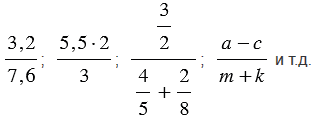
Числитель дробного выражения — выражение, стоящее над чертой.
Знаменатель дробного выражения — выражение, стоящее под чертой.
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
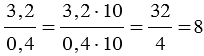, обычно запись упрощают, и пишут так: 
.
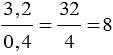То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
.
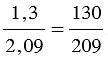Поделись с друзьями в социальных сетях:
Источник
—>Сайт учителя математики А.В.Капитановой —>
Умножение дроби на натуральное число
Пример: Найти произведение дроби и натурального числа:
Умножение обыкновенных дробей
- перемножить числители и знаменатели дробей;
- сократить полученную дробь.
| 3 | · | 2 | = | 3 · 2 | = | 6 |
| 7 | 5 | 7 · 5 | 35 |
Умножение смешанных чисел
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Пример: Найти произведение двух смешанных чисел:
| 2 | 1 | · | 1 | 2 | = | 2 · 2 + 1 | · | 1 · 3 + 2 | = | 5 | · | 5 | = | 5 · 5 | = | 25 | = | 6 · 4 + 1 | = 4 | 1 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 · 3 | 6 | 6 | 6 |
Пример: Найти произведение смешанного числа и целого числа:
| 4 | 1 | · | 6 | = | 4 · 3 + 1 | · | 6 | = | 13 · 6 | = | 26 |
| 3 | 3 | 3 |
Пример: Найти произведение смешанного числа и обыкновенной дроби:
| 2 | 1 | · | 3 | = | 2 · 7 + 1 | · | 3 | = | 15 | · | 3 | = | 15 · 3 | = | 5 · 9 | = | 9 | = | 7 + 2 | = 1 | 2 |
| 7 | 5 | 7 | 5 | 7 | 5 | 7 · 5 | 7 · 5 | 7 | 7 | 7 |
Деление дроби на натуральное число
Пример: Найти частное от деления дроби на натуральное число:
Определение: Чтобы получить дробь, обратную данной, следует поменять местами числитель и знаменатель.
Деление натурального числа на дробь
Пример: Найти частное от деления натурального числа на дробь:
| 2: | 4 | = | 2· | 5 | = | 2 · 5 | = | 2 · 5 | = | 5 | = | 2 · 2 + 1 | = 2 | 1 |
| 5 | 4 | 4 | 2 · 2 | 2 | 2 | 2 |
Деление обыкновенных дробей
Пример: Найти частное от деления дробей:
| 3 | : | 4 | = | 3 | · | 5 | = | 3 · 5 | = | 15 |
| 7 | 5 | 7 | 4 | 7 · 4 | 28 |
Деление смешанных чисел
- преобразовать смешанные дроби в неправильные;
- умножить первую дробь на дробь, обратную второй;
- сократить полученную дробь;
- если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Пример: Найти частное от деления смешанных чисел:
| 1 | 1 | : | 2 | 2 | = | 1 · 2 + 1 | : | 2 · 3 + 2 | = | 3 | : | 8 | = | 3 | · | 3 | = | 3 · 3 | = | 9 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 | 8 | 2 · 8 | 16 |
Пример: Найти частное от деления смешанного числа на дробь:
Источник
Деление дробей онлайн
Чтобы разделить дробь на дробь нужно умножить первую дробь на дробь обратную второй.
Правила деления дробей
Чтобы разделить дробь на дробь, нужно делимое умножить на дробь обратную делителю
Как делить обыкновенные дроби
Чтобы разделить обыкновенную дробь на обыкновенную дробь, нужно вторую дробь сделать обратной затем умножить на вторую дробь по правилам умножения дробей.
Разберём пример: разделим дробь 1/4 на 1/3. Для этого развернём вторую дробь 3/1. Получится выражение 1/4 × 3/1. Перемножим числители 1 × 3 = 3 и знаменатели 4 × 1 = 4 в итоге у нас получится дробь 3/4
Как разделить натуральное число на дробь
Чтобы разделить натуральное число на дробь, нужно сделать дробь обратной. Числитель обратной дроби умножить на натуральное число а знаменатель обратной дроби останется без изменения.
Как разделить смешанную дробь на целое число
Чтобы разделить смешанную дробь на целое число нужно смешанную дробь перевести в неправильную. Затем целое число представить в виде обратной дроби и умножить на неправильную дробь. После чего выполнить умножение обыкновенных дробей.
Разберём пример: разделим смешанную дробь 3 целые 3/4 на целое число 7.
Перед делением нужно смешанную дробь перевести в неправильную 3 целые 3/4 = 15/4. Представим целое число в виде обратной дроби7 это 1/7. Умножим дроби 15/4 и 1/7. Перемножим числители 15*1 = 15, перемножим знаменатели4*7 = 28
Как разделить смешанную дробь на смешанную дробь
Для деления смешанной дроби ра смешанную дробь нужно обе дроби представить в виде неправильных. Затем вторую дробь преобразовать в обратную. После чего перемножить обе дроби по правилам умножения обыкновенных дробей.
Разберём пример: разделим смешанную дробь 2 целые 3/5 на смешанную дробь 3 целые 1/2
Преобразуем обе дроби в неправильные
Развернём вторую дробь и изменим знак деления на умножение
Перемножим дроби по правилам умножения обыкновенных дробей
Похожие калькуляторы
