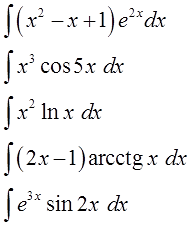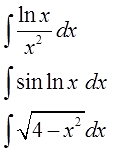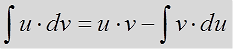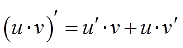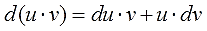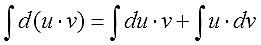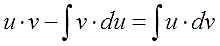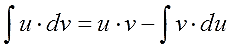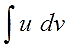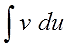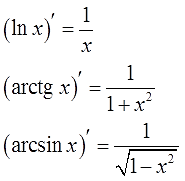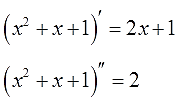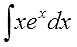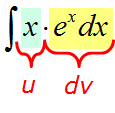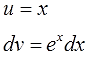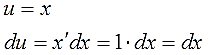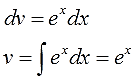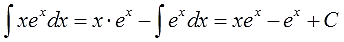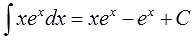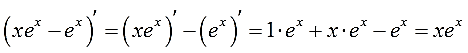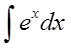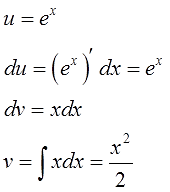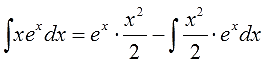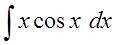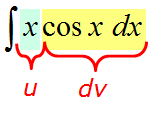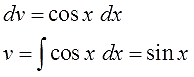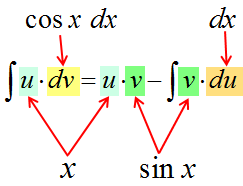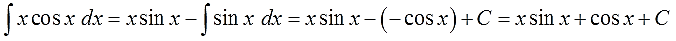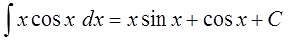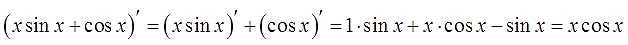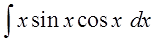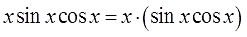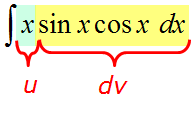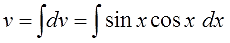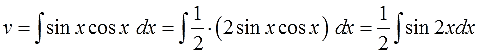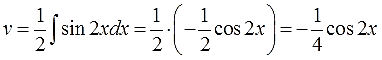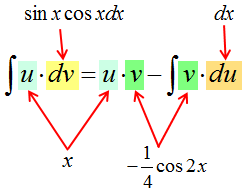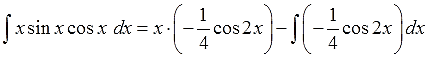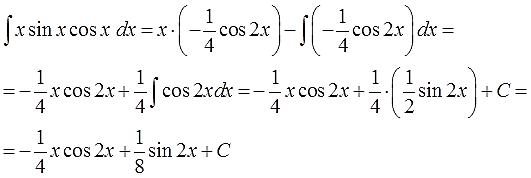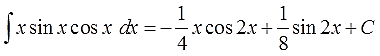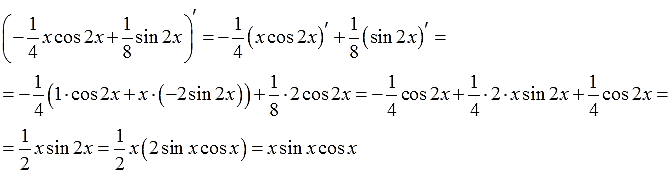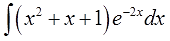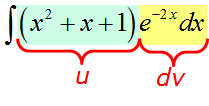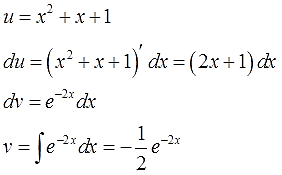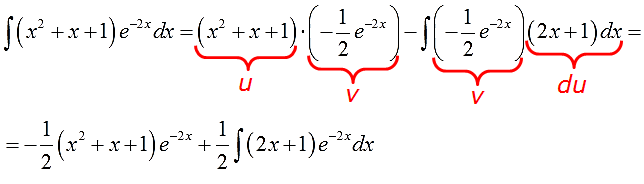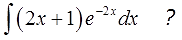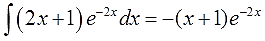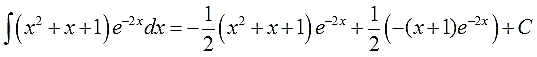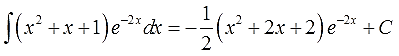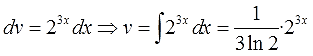Как найти частное интегралов - Сайт, где вы сможете решить свои вопросы

Метод интегрирования по частям.

Продолжаем осваивать базовые приёмы интегрирования. В предыдущих уроках мы рассмотрели три таких приёма – непосредственное интегрирование (то бишь, по таблице), метод подведения функции под знак дифференциала и метод замены переменной. Три ножки для стула. Сидеть уже можно, но… как-то неудобно.)

Сегодняшний наш урок будет началом изучения ещё одной обширной темы интегрального исчисления. Последней, четвёртой ножки для нашего стула.) А именно – метода интегрирования по частям. Великого и могучего. Фраза “интегрируем по частям” вселяет уверенность и так же обнадёживает студентов, как и фраза “решаем через дискриминант” у школьников. 🙂

В чём же заключается столь сильная мощь данного метода и почему именно он так популярен при вычислении львиной доли неопределённых интегралов? А дело вот в чём.

Ключевой момент №1

Как мы уже знаем, в отличие от производных, в матанализе не существует стандартных правил для интегралов от произведения, частного и сложной функции. Но в процессе интегрирования такие операции с функциями встречаются сплошь и рядом. И очень часто именно метод интегрирования по частям позволяет свести вычисление интеграла от навороченной функции к совсем простенькому выражению, проинтегрировать которое не составит труда. Если таблицу знать, конечно.

Ключевой момент №2

Нередко под интегралом могут стоять всякие нехорошие трансцендентные конструкции — логарифмы, арксинусы, арктангенсы и прочие ужасы. Таблица интегралов не катит: нету в ней ни логарифмов, ни арков. И замена не годится тоже.

И в таких случаях тоже надо уметь как-то выкручиваться, да…

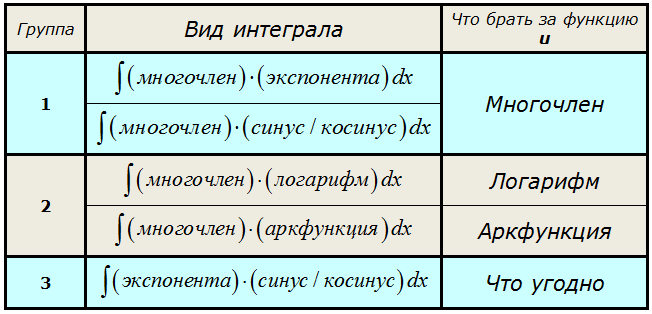
Какие же именно интегралы берутся по частям?

Вот типовые схемы подынтегральных функций:

Например, что-то в таком духе:

Что общего во всех таких интегралах? А общее то, что подынтегральная функция представляет собой произведение (а в ряде случаев и частное) “разнородных” функций. Многочлена и логарифма, синуса и экспоненты и так далее… Или же под интегралом тусуются всякие там арксинусы, арктангенсы и прочая жесть.

Под последним шестым пунктом стоит слово “прочие”. Это такие функции, которые не относятся к предыдущим пяти типам, но которые также вполне можно проинтегрировать по частям (а иногда и только по частям). Как правило, сочетая в себе и другие способы интегрирования — замену переменной, подведение под дифференциал и т.п. Это всякие сложные экзотические функции, а также некоторые дроби и функции с корнями.

Например:

И тому подобные примеры. Их разберём в соответствующем уроке.

Ну вот. Про таинственный метод упомянули, какие именно интегралы с его помощью вычисляются — тоже. Пора бы уже начать более близкое знакомство. Знакомимся? Поехали!

Формула интегрирования по частям — вывод и смысл.

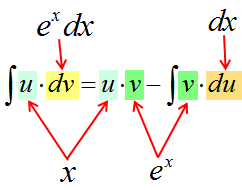
Итак, прошу любить и жаловать:

Это и есть формула интегрирования по частям собственной персоной.)

Откуда же она берётся и почему так называется? Она берётся из обычного правила дифференцирования произведения.

Все вы (надеюсь) его хорошо помните ещё со школы:

Или почти то же самое, только по-взрослому, через дифференциалы:

Все формулы в матанализе, если слева и справа стоят функции или их производные (или дифференциалы), можно почленно интегрировать. Вот и проинтегрируем левую и правую части нашего правила. Имеем полное право!

Подвешиваем на крючки левую и правую части и получаем:

Осталось сообразить, что значок интеграла всегда “съедает” значок дифференциала (согласно соответствующему свойству). Стало быть, слева останется просто произведение u∙v. А справа приведём первый интеграл к приличному виду и отправим его влево к u·v (со сменой знака, разумеется). Получим:

И, наконец, финальный бросок. Меняем местами левую и правую части и получаем:

Всё! Больше никаких научных хитростей.)

Собственно, формула производной произведения и формула интегрирования по частям — это две взаимно обратных формулы. 🙂 Так же, как и операции дифференцирования сложной функции и подведения функции под знак дифференциала. Вот и вся суть.

Запоминается формула на удивление легко и просто. Чаще всего, в виде секретного заклинания:

Интеграл у-дэ-вэ равен у на вэ минус интеграл вэ-дэ-у. 🙂

Итак, будем считать, что с происхождением формулы разобрались. Теперь разбираемся с названием – что ещё там за части какие-то. 🙂

Смотрим на формулу ещё разок:

В чём основная суть? Исходное подынтегральное выражение (то, что слева) разбивается на два кусочка. Или две части.) Причём только с помощью умножения! Именно поэтому в общей формуле я отдельно и выделяю знаки умножения.

Первая часть (первый множитель) — это некоторая функция u. Функция как функция. Выражаемая какой-то формулой.

Вторая часть (второй множитель) — это не функция, а дифференциал некоторой другой функции v. То есть, dv.

Что это за таинственные u и v? Об этом дальше подробненько будет. Никаких тайн.)

Что же происходит при применении формулы? С точки зрения математики ничего особенного не происходит:

1. Первый множитель — u — дифференцируется. Было u, а становится du.

2. Второй множитель – dv – наоборот, интегрируется. Было dv, а после интегрирования стало просто v.

Зато с точки зрения наших хотелок происходит оч-чень много полезного! Исходный интеграл:

который, по каким-то причинам, нам не очень нравится, заменяется на другой интеграл

вычисление которого должно оказаться проще исходного.

Вот и всё. Вот и вся ключевая идея применения формулы!

Что брать за u, а что за dv?

Вопрос хороший! Этот момент – стратегически самый важный при применении формулы. Давайте разбираться. В самых общих чертах.) Выпишем ещё раз формулу:

Как видно из формулы, нам надо интегрировать новое выражение v∙du. И оно должно оказаться проще старого подынтегрального выражения u∙dv. Вот такая ключевая идея — упростить исходное подынтегральное выражение!

Поскольку в новом подынтегральном выражении стоит дифференциал du, то за функцию u всегда принимается функция, упрощающаяся при дифференцировании.

И какие же функции упрощаются при дифференцировании? Как правило, это всякие ужасы типа логарифмов или “арков”. Почему же они упрощаются при дифференцировании? А потому, что их производные — гораздо более простые функции! Рациональные дроби или, в худшем случае, выражения с корнями (для арксинуса/арккосинуса). Вспоминаем нашу старую добрую таблицу производных:

И так далее. С дробью 1/х всяко проще работать в процессе интегрирования, чем с логарифмом, правда? И с арками та же история.

Точно так же упрощаются при дифференцировании и многочлены, степень которых после каждого дифференцирования понижается на единичку:

В общем, принцип выбора функции u предельно ясен — упрощение после дифференцирования. А что же со вторым множителем dv?

Поскольку множитель dv нам придётся интегрировать, то за dv всегда берётся конструкция, не усложняющаяся при интегрировании!

Например, это вполне может быть экспонента. Или же тригонометрическая функция — синус там или косинус… Или степенная функция или многочлен. Эти функции никак не усложняются при интегрировании! Почему? Вспоминаем теперь уже таблицу интегралов (первообразных): экспонента при интегрировании превращается сама в себя, синус/косинус — друг в друга (с точностью до знака), а любой многочлен степени n — также в многочлен, но степени n+1.

Запоминаем:

За функцию u всегда принимаем выражение, упрощающееся при дифференцировании.

За dv принимаем выражение, не усложняющееся при интегрировании.

Разумеется, сразу увидеть и сообразить в уме, что упростится/усложнится после дифференцирования/интегрирования, не всегда возможно. Всё от конкретного примера и от опыта зависит. Не всегда с первого раза получается. Бывает.)

Но для некоторых типовых схем я всё же приведу небольшую сводную табличку. Пользуйтесь на здоровье! 🙂

Что ж, думаю, хватит грузной теории, давайте перейдём к конкретным примерам — всё станет куда понятнее.) В этом уроке рассмотрим интегралы из группы №1.

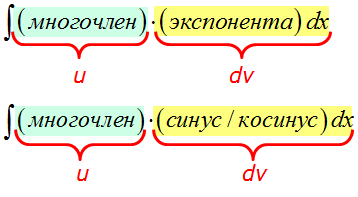
Произведение многочлена и показательной/тригонометрической функции.

Это интегралы из первой группы нашей сводной таблички.

Общий рецепт здесь следующий:

Если под интегралом стоит произведение многочлена и показательной/тригонометрической функции, то за функцию u всегда берётся МНОГОЧЛЕН.

А что берётся за dv? А за dv всегда берётся оставшаяся часть подынтегрального выражения вместе с dx! Что уж там осталось, то и берётся, так уж формула интегрирования по частям устроена: всё подынтегральное выражение надо по кусочкам распределить между u и dv.

Вот так:

Ну что, посмотрим на формулу интегрирования по частям в действии?)

Например, пусть надо найти вот такой интересный интеграл:

Пример 1

Казалось бы, всё просто. Под знаком интеграла стоит произведение знакомых табличных функций — икса и e^x. Вроде, всё хорошо. Но есть одна проблемка: общей стандартной формулы для интеграла от произведения не существует! По отдельности каждая функция интегрируется без проблем, а вот произведение — уже проблема, да…) Как быть?

Как-как… Надо разделить разные типы функций!

Вот и разбиваем наше подынтегральное выражение на кусочки! Наша задача представить конструкцию

xe^xdx

в виде произведения функции u и дифференциала другой функции dv.

Определяемся, что выбираем за u и за dv!

Работаем прямо по правилу для группы №1. В роли показательной функции у нас, очевидно, e^x. А множитель х служит как раз тем самым многочленом, который целесообразно брать в качестве функции u. Не так очевидно, что это многочлен, но это именно он.) Состоящий всего из одного члена — икса. Бывает.)

А вот к dv мы должны отнести то, что осталось — выражение e^xdx.

Так и пишем:

Да-да, именно так и выделяем, прямо в тетрадке!

Итак, выбор u и dv сделан. Вот он:

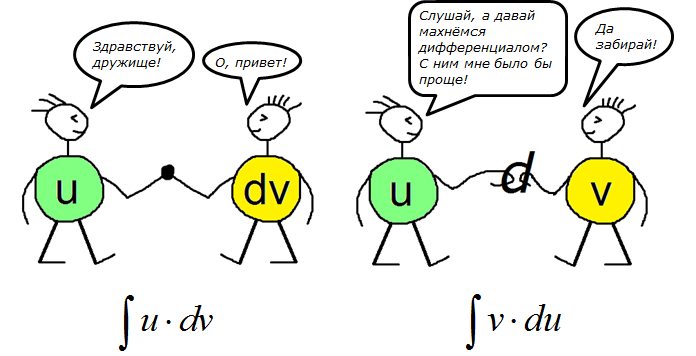
Теперь следующим шагом мы начинаем операцию, которую я условно называю “миграция дифференциала”: функцию u мы будем дифференцировать и превращать в du, а dv — наоборот интегрировать и превращать в v. Таким образом, под дифференциалом вместо функции v окажется функция u. Вспоминаем нашу картинку с пляшущими человечками.)

Поехали!

Дифференцируем функцию u, считаем du:

Интегрируем множитель dv и ищем функцию v:

Внимание! Не прибавляем константу С после отыскания функции v! Ведь в качестве функции v нам нужна только какая-то одна конкретная первообразная! А не всё бесконечное множество, да…) Самая простая такая первообразная — очевидно, с константой С, равной нулю (С=0). Именно поэтому я и пишу

v = e^x,

а не

v = e^x + C.

А теперь берём формулу интегрирования по частям

и аккуратно подставляем все исходные данные на свои места:

И считаем:

Вот и все дела.)

Ответ:

Как всегда, для пущей уверенности, дифференцируем результат:

Ура! Совпало! 🙂

Что у нас произошло после применения формулы интегрирования по частям? А произошло то, что мешающий нам множитель х исчез из примера, и исходный интеграл от нехорошего произведения

свёлся к табличному (!) интегралу от безобидной экспоненты

Берущемуся в уме. Если таблицу знать.) Здорово, правда?

Именно так и работает формула интегрирования по частям. Разделяет разнотипные функции и превращает ужасный на вид интеграл в белый и пушистый. Вот и вся суть метода интегрирования по частям.)

А что будет, если поступить наоборот – за u принять e^x, а за dv — xdx?

Не вопрос, давайте посмотрим:

Тогда, подставляя всё в формулу, получим:

Хм… И что нам с таким интегралом делать?! Даже ещё хуже стало, чем было…

Да! При таком выборе u и dv новый интеграл не упрощается, а, наоборот, усложняется! Экспоненте-то всё равно, что с ней делают — дифференцируют/интегрируют. У неё ко всем воздействиям врождённый иммунитет.) В отличие от многочлена, который при таком раскладе не понижает свою степень, а повышает. Что никак не делает пример проще, да…)

Собственно в этом-то и кроется причина выбора именно многочлена в качестве функции u для интегралов первой группы — понизить его степень.

А для общего развития запоминаем:

Если после применения формулы новый интеграл получился сложнее исходного, то, скорее всего, неудачно сделан выбор u и dv. Не падаем духом и пробуем другую комбинацию.

Эта рекомендация относится не только к этому уроку, на примеры из первой группы, а ко всему интегрированию по частям вообще.

Но самое надёжное — не бездумно расчленять подынтегральное выражение и комбинировать кусочки, задумчиво глядя на пример, а понимать общий смысл формулы и принцип выбора u и dv для конкретного типа интеграла. Уметь заранее просчитывать ситуацию и оценивать последствия того или иного выбора. Такой опыт только с практикой приходит. Прорешаете хотя бы 20-30 примеров — и проблема выбора u и dv отпадёт сама собой.)

Ну вот. Первый пример разобран по косточкам. Разумеется, так подробно расписывать следующие примеры я уже не буду. Это чисто для знакомства сделано. Чтобы общую идею уловить.)

А теперь можно записать и общий алгоритм вычисления неопределённых интегралов по частям.

Алгоритм вычисления неопределённых интегралов по частям.

1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.

2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.

3. Дифференцируем функцию u и считаем дифференциал du.

4. Интегрируем дифференциал dv и ищем саму функцию v.

5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.

6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.

Ну что, потренируемся в применении алгоритма?)

Пример 2

И опять под интегралом стоит произведение функций разной природы — икса и косинуса. Значит, разделяем разнородные функции и интегрируем по частям: у нас просто нет других вариантов!

Работаем строго по пунктам.

1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.

Очевидно, это интеграл из первой группы — типа “многочлен на синус/косинус”. Переходим к пункту 2.

2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.

Наше правило для первой группы гласит, что за функцию u следует принимать многочлен — то есть, просто множитель x.

Ну, а за dv, ясен перец, принимаем то что осталось, т.е. cos x dx.

Вот так:

Итак, выбор сделан. Переходим к пунктам 3 и 4. Тут всё просто, без фокусов:

3. Дифференцируем функцию u и считаем дифференциал du.

4. Интегрируем дифференциал dv и ищем саму функцию v.

5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.

Итак, все исходные данные для применения формулы подготовлены. Подставляем:

Вперёд!

Ответ:

Готово дело.)

Проверяем ответ дифференцированием:

Всё путём.)

Мы видим, что новый интеграл опять оказался табличным и берущимся в уме! От синуса. Халява! 🙂 Но далеко не всегда выпадает такое счастье. Иногда при поиске функции v надо дополнительно потрудиться. Поэтому теперь решим что-нибудь посложнее. Чтобы в ступор не впасть, в случае чего…

Пример 3

Чем-то похоже на предыдущий пример, правда? Только синус ещё затесался, в качестве третьего множителя. Поскольку перед нами снова произведение разнородных функций — икса и тригонометрии, то такой интеграл можно попробовать взять только по частям. Но под интегралом произведение трёх функций, а не двух, как обычно! Что делать?

Что-что… Не бояться, вот что! Ибо из трёх множителей всегда можно сделать два. Нас спасут… скобочки! Вот так:

А дальше опять по алгоритму. Поехали!

1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.

Всё ясно. Это первая группа, т.к. под интегралом произведение многочлена (икса) и тригонометрии (sinx∙cosx).

2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.

И здесь вопросов нет. Икс — это u. То, что осталось (т.е. sinx∙cosxdx) — это dv.

Итого имеем следующее:

3. Дифференцируем функцию u и считаем дифференциал du.

4. Интегрируем дифференциал dv и ищем саму функцию v.

А вот здесь начинается самое интересное.) Для поиска v нам надо проинтегрировать выражение sinx∙cosxdx.

Вот так:

Вот тут уже с ходу, в уме, этот интеграл не возьмёшь. В одно действие. Подумать надо.)

Варианта два. Можно внести косинус (или синус) под знак дифференциала и старым добрым способом, но в данном случае гораздо выгоднее искусственно выделить под интегралом синус двойного угла:

А проинтегрировать синус двойного угла уже никакого труда не составляет. В уме интегрируется. Как это делается, смотрим этот урок. Самое главное — не забываем про дополнительные коэффициенты и про знаки.

Всё. Функцию v мы нашли. Идём дальше по алгоритму.

5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.

И снова мы видим, что новый интеграл, от косинуса двойного угла, много проще старого интеграла от сборной солянки x∙sinx∙cosx. Интегрируем косинус двойного угла, “причёсываем” ответ и добиваем наш злой пример.

Пишу подробно, со всеми знаками и коэффициентами, поскольку именно в них народ и косячит на 99%:

Ответ:

Вот и все дела.) Кому не нравятся двойные углы, те могут перейти обратно к одинарным по соответствующим формулам, но в таком виде ответ выглядит гораздо компактнее.

Что, сомнения нахлынули? Не ленимся, дифференцируем:

Нет, всё честно.)

Всё бы ничего, но… могут случаться и такие сюрпризы, когда по частям приходится интегрировать несколько раз. Разберём ещё один пример.

Пример 4

Надеюсь, общий алгоритм интегрирования по частям уже запомнился? Можно не расписывать подробно в четвёртый раз?)

В этот раз на экспоненту умножается не одинокий икс, а вполне себе полноценный многочлен. Но схема выбора u и dv та же самая.

Действуем в соответствии с алгоритмом:

Отлично. Функции u и v, а также их дифференциалы du и dv найдены. Пора приступать к интегрированию по частям. Снова прямо по формуле вставляем все исходные данные, упрощаем что упрощается и получаем:

А вот и обещанный сюрприз! Что делать с новым интегралом

В таблице такого и близко нет, обычными преобразованиями с подынтегральной функцией тоже ничего не сделаешь… Но! Можно заметить, что под новым интегралом у нас опять произведение многочлена и экспоненты! Поэтому… снова интегрируем по частям (да-да!). Утешает то, что новый многочлен (2х+1) стал уже линейным (а не квадратичным, как был изначально)! Казалось бы, мелочь, но очень существенная: новый интеграл в целом проще старого! Как и должно быть.)

Если мы сейчас отдельно возьмём этот интеграл по частям и упростим до упора, то получим такой результат:

Что, у вас не так получилось? А за знаками следили? А за коэффициентами? Не забываем, что е^-2х — сложная функция! Со всеми вытекающими.)

Вот практически и всё. Возвращаемся к исходному примеру, вставляем результат промежуточного интегрирования по частям на своё место и константу не забываем.)

Получим:

В принципе, интеграл мы уже нашли. Если требуются дальнейшие упрощения и наведение марафета, то, раскрыв скобки и приведя подобные, окончательно получим:

Ответ:

Вот такой ответ. Проверочное обратное дифференцирование предлагаю провести самостоятельно.)

Чем поучителен этот пример? Как видите, здесь нам пришлось интегрировать по частям два раза! Почему? Всему виной является вторая степень нашего многочлена x²+x+1. Проблема в том, что после каждого применения формулы (т.е. взятии дифференциала du) степень многочлена понижается лишь на единичку. Как и при любом дифференцировании, да.

Например, если бы под интегралом стоял многочлен 10-й степени (да даже хотя бы простое произведение x¹⁰e^x), то последовательно интегрировать по частям пришлось бы (о, ужас!) десять раз! Это огорчает. Но зато при каждом новом интегрировании степень многочлена будет становиться всё ниже. Пускай на единичку, но — ниже. Это радует.)

Запоминаем:

Интегрировать по частям требуется столько раз, какова степень многочлена.

Между прочим, в качестве показательной функции совершенно не обязательно должна стоять именно экспонента (e^x, е^2х и тому подобные конструкции). Запросто может оказаться вообще не “е”, а что-то типа 2^3х и т. п. Не надо пугаться. Принцип интегрирования тот же самый. Отличие состоит лишь в том, что при вычислении функции v будут всплывать дополнительные коэффициенты с логарифмами, которые ни в коем случае нельзя терять.

Например:

И так далее…

Итак, с первой группой интегралов, берущихся по частям, поработали. Переходим ко второй группе — логарифмам, аркам и прочим питомцам нашего зоопарка элементарных функций. В следующей теме.)

Источник

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Помощь в написании работы

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x, как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х), с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

$[y{}'=frac{dy}{dx}]$

переписываем дифференциальное уравнение, получаем

$[xcdot frac{dy}{dx}=y.]$

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

$[frac{dy}{y}=frac{dx}{x}]$

Далее интегрируем полученное уравнение:

$[int frac{dy}{y}=int frac{dx}{x}]$

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

То есть,

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

y=Cx, где С=Const.

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

$[frac{dy}{dx}=-2y]$

$[frac{dy}{y}=-2dx]$

$[int frac{dy}{y}=-2int dx]$

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

$[left | y right |=e^{-2x+C*}]$

$[left | y right |=e^{C*}cdot e^{^{-2x}}]$

Если – это константа, то

$[e^{C*}>0]$

– тоже некоторая константа, заменим её буквой С:

$[y=Ce^{-2x}]$

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

$[y=Ce^{-2x},]$

где С=const.

Ответ

$[y=Ce^{-2x},]$

где С=const.

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

$[frac{dy}{dx}+left ( 2y+1 right )cot =0]$

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

$[frac{dy}{dx}=-left ( 2y+1 right )cot]$

$[frac{dy}{2y+1}=-cot x]$

После разделения переменных, интегрируем уравнение, как в примерах выше.

$[int frac{dy}{2y+1}=-int cot x]$

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

$[int frac{dy}{2y+1}=-int frac{cosxdx}{sinx}]$

$[frac{1}{2}int frac{d(2y+1)}{2y+1}=-intfrac{d(sin x)}{sin x}]$

$[frac{1}{2}ln left | 2y+1 right |=-lnleft | sin x right |+ln left | C* right |]$

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

$[ln left | 2y+1 right |^frac{1}{2}=ln left | sin x right |^{-1}+ln left | C* right |]$

$[ln sqrt{left | 2y+1 right |}=ln frac{1}{left | sin x right |}+ln left | C* right |]$

$[ln sqrt{left | 2y+1 right |}=ln left | frac{C*}{sin x} right |]$

$[sqrt{2y+1}=frac{C*}{sin x}]$

Приводим полученный общий интеграл к виду: F(x,y)=C:

$[sqrt{left | 2y+1 right |}=frac{C*}{sin x}]$

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Общий интеграл:

$[(2y+1)cdot sin ^{2}x=C,]$

где С=const.

Задание

Найти частное решение дифференциального уравнения

$[e^{y-x^{2}}dy-2xdx=0,]$

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

$[e^{y}cdot e^{-x^{2}}dy-2xdx=0]$

$[e^{y}cdot e^{-x^{2}}dy=2xdx]$

$[e^{y}dy=frac{2xdx}{e^{-x^{2}}}]$

$[e^{y}dy=2xe^{x^{2}}dx]$

$[int e^{y}dy=2intxe^{x^{2}}dx]$

$[int e^{y}dy=int e^{x^{2}}dleft ( x^{2} right )]$

$[e^{y}=e^{x^{2}}+C]$

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

$[ln e^{y}=ln left (e^{x^{2}}+C right )]$

$[y=ln left (e^{x^{2}}+C right )]$

Получаем общее решение:

$[y=ln left (e^{x^{2}}+C right ),]$

где С=const

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

$[ln 2=ln left ( e^{0}+C right )]$

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Частное решение:

$[y=ln left( e^{x^{2}}+Cright )]$

Задание

Решить дифференциальное уравнение

$[2left( xy+y right )y{}'+xleft ( y^{4}+1right )=0]$

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

$[2left( x+1 right )ycdot frac{dy}{dx}=-x(y^{4}+1)]$

$[frac{2ydy}{y^{4}+1}=-frac{xdx}{x+1}]$

$[2int frac{2ydy}{y^{4}+1}=-int frac{left ( x+1-1 right )dx}{x+1}]$

$[int frac{dleft ( y^{2} right )}{left ( y^{2} right )^{2}+1}=-int left ( 1-frac{1}{x+1} right )dx]$

$[arctan left ( y^{2} right )=x+ln left | x+1 right |+C]$

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Общий интеграл:

$[arctan left( y^{2} right )=x+ln left | x+1 right |+C где С=const.]$

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

$[xcdot frac{dy}{dx}=-yln y]$

$[frac{dy}{ydy}=-frac{dx}{x}]$

Интегрируем:

$[int frac{dy}{ydy}=-int frac{dx}{x}]$

$[int frac{dln left ( y right )}{ln y}=-int frac{dx}{x}]$

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

$[ln left | ln y right |=ln frac{1}{left | x right |}+ln left | C right | ln y=frac{C}{x}]$

Используя

$[ln a=bRightarrow a=e^{b}]$

можно выразить функцию в явном виде.

Общее решение:

$[y=e^{}frac{C}{x},]$

где С=const.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

$[yleft( 1 right )=e^{frac{C}{1}}=e^{C}=eRightarrow C=1]$

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Частное решение:

$[y=e^{}frac{C}{x}]$

Проверка

Необходимо проверить, выполняется ли начальное условие:

$[yleft ( 1 right )=e^{}frac{1}{1}=e^{1}=e.]$

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

$[yleft( 1 right )=e^{frac{1}{x}}]$

дифференциальному уравнению. Для этого находим производную:

$[y{}'=left ( e^{frac{1}{x}} right ){}'=-frac{e^{frac{1}{x}}}{x^{2}}]$

Подставим полученное частное решение

$[y=e^{frac{1}{x}}]$

и найденную производную в исходное уравнение

$[ylny+xy{}'=0: e^{frac{1}{x}}cdot ln e^{frac{1}{}x}+xcdot left ( -frac{e^{frac{1}{x}}}{x^{2}} right )=0]$

$[e^{frac{1}{x}}cdot frac{1}{x}-frac{e^{frac{1}{x}}}{x}=0]$

$[frac{e^{frac{1}{x}}}{x}-frac{e^{frac{1}{x}}}{x}=0]$

0=0

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

$[sqrt{3+y^{2}}dx+sqrt{1-x^{2}}ydy=0.]$

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

$[sqrt{1-x^{2}}ydy=-sqrt{3+y^{2}}dx]$

$[frac{ydy}{sqrt{3+y^{2}}}=-frac{dx}{sqrt{1-x^{2}}}]$

$[int frac{dleft ( 3+y^{2} right )}{2sqrt{3+y^{2}}}=-int frac{dx}{sqrt{1-x^{2}}}]$

$[sqrt{3+y^{2}}=-arcsinx+C]$

Ответ

Общий интеграл:

$[sqrt{3+y^{2}}=-arcsinx+C где С=const.]$

Задание

Найти частное решение ДУ.

$[2y{}'sin ycdot cos ycdot sin ^{2}x+cos x=0, yleft ( frac{pi }{2} right )=0.]$

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

$[2frac{dy}{dx}sin ycdot cos ycdot sin ^{2}x=-cos x]$

$[2sin ycdot cosydy=-frac{cosxdx}{sin ^{2}x}]$

$[sin 2ydy=-frac{cosxdx}{sin ^{2}x}]$

Интегрируем:

$[int sin 2ydy=-int frac{cosxdx}{sin ^{2}x}]$

$[frac{1}{2}int sin 2yd(2y)=-int frac{dleft ( sin x right )}{sin ^{2}x}]$

Общий интеграл:

$[-frac{1}{2}cos 2y=frac{1}{sin x}+C]$

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

$[yleft ( frac{pi }{2} right )=0.]$

Подставляем в общее решение

$[x=frac{pi }{2} и y=0]$

$[-frac{1}{2}cos 0=frac{1}{sin frac{pi }{2}}+C]$

$[-frac{1}{2}cdot 1=frac{1}{1}+C]$

$[-frac{1}{2}=1+CRightarrow C=-frac{3}{2}]$

Ответ

Частный интеграл:

$[-frac{1}{2}cos 2y=frac{1}{sin x}+C.]$

Задание

Решить дифференциальное уравнение

$[left( 1+e^{^{x}} right )ydy-e^{y}dx=0.]$

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

$[left ( 1+e^{^{x}} right )ydy=e^{y}dx]$

$[intye^{-y}dy=int frac{dx}{1+e^{x}}]$

Левую часть интегрируем по частям:

$[dnu =e^{-y}dyRightarrow nu =-e^{-y}]$

В интеграле правой части проведем замену:

$[t=1+e^{x}]$

$[e^{x}=t-1]$

$[dt=e^{x}dxRightarrowdx=frac{dt}{e^{x}}=frac{dt}{t-1}]$

Таким образом:

$[-ye^{-y}+int e^{-y}dy=int frac{dt}{tleft ( t-1 right )}]$

$[-ye^{-y}-e^{-y}=int left ( frac{1}{t-1} right -frac{1}{t})dt]$

(здесь дробь раскладывается методом неопределенных коэффициентов)

$[-e^{-y}left ( y+1 right )=ln left | t-1 right |-ln left | t right |+C*]$

Обратная замена:

$[t=1+e^{x}]$

$[-e^{-y}left ( y+1 right )-ln left | 1+e-1 right |+ln left | 1+e^{x} right |=C*]$

$[-e^{-y}left ( y+1 right )-x+ln left ( 1+e^{x} right )=C*]$

Ответ

Общий интеграл:

$[-e^{-y}left ( y+1 right )-x+ln left ( 1+e^{x} right )=C*,]$

где С=const.

Задание

Решить дифференциальное уравнение

$[y-xy{}'=3(1+x^{2}y{}').]$

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

$[y-xy{}'=3+3x^{2}y{}']$

$[3x^{2}y{}'+xy{}'=y-3]$

$[left( 3x^{2} +xright )frac{dy}{dx}=y-3]$

$[frac{dy}{y-3}=frac{dx}{3x^{2}+x}]$

$[int frac{dy}{y-3}=int frac{dx}{3x^{2}+x}]$

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

$[frac{A}{x}+frac{B}{3x+1}=frac{1}{xleft ( 3x+1 right )}]$

$[3A+B=0 && \]$

$[A=1&& \]$

$[ln left | y-3 right |=int left ( frac{1}{x} -frac{3}{3x+1}right )dx]$

$[ln left | y-3 right |=ln left | frac{Cx}{3x+1} right |]$

$[y-3=frac{Cx}{3x+1}]$

Ответ

Общее решение:

$[y-3=frac{Cx}{3x+1},]$

где С=const.

Источник

Частный интеграл

Предмет
Высшая математика

Разместил

🤓 idagcumi1987760

👍 Проверено Автор24

название частного решения обыкновенного дифференциального уравнения

Научные статьи на тему «Частный интеграл»

Формула Грина

Формула Грина связывает двойной интеграл по области D с криволинейным интегралом по замкнутому контуру…
Криволинейный интеграл по положительно ориентированному контуру L обозначается так:

[ointlimits_L…
Тогда криволинейный интеграл можно переписать:

[ointlimits_L{Pleft(x,yright)dx+Qleft(x,yright…
помощью формулы Грина можно найти формулу для определения площади плоской фигуры через криволинейный интеграл…
круга $S=pi r^2$, тогда:

[iintlimits_D{dxdy}=pi r^2.]

Подставим это значение вместо нашего интеграла

Статья от экспертов

Об устойчивости стационарных движений транспортных систем при существовании частного интеграла

Изучение многих механических объектов на транспорте можно моделировать тяжелыми твердыми телами. Для их описания удобнее использовать системы обыкновенных дифференциальных уравнений. Рассматривая исследуемые объекты покоящимися на платформе, в вагоне или иных движущихся транспортных средствах, изолированными от влияния диссипативных сил, можно считать систему консервативной. При изучении динамических свойств модельных систем можно опираться на свойства известных консервативных систем, предпочтительно автономных. В таких системах существуют первые интегралы уравнений движения. Среди консервативных систем наиболее популярна задача о вращении твердого тела вокруг неподвижной точки. В самом общем виде для нее известны первые интегралы: полной энергии, момента количества движения, ингеграл Пуассона. Для трех хорошо изученных случаев существования четвертого общего интеграла известны основные динамические свойства систем: записаны аналитические решения в форме эллиптических или гиперэллип…

Интегрирование методом Чебышева

методов численного интегрирования, который позволяет вычислить приближенное значение определенного интеграла…
Уравнения динамики океана представляют собой шесть нелинейных уравнений в частных производных, а именно…
Автор24 — интернет-биржа студенческих работ
Формулу Чебышева для нахождения интеграла в интервале от…
Автор24 — интернет-биржа студенческих работ
Результаты работы программы приведены ниже
Интеграл sín(…
x)^4=
Задайте интервалы интегрирования
0 2
Метод Гаусса:0.970118
Метод Чебышева:0.970082
Интеграл sqrt

Статья от экспертов

Особые точки одной кубической двумерной системы, имеющей частный интеграл в виде алгебраической кривой третьего порядка

Выяснен характер особых точек одной кубической двумерной системы как в конечной, так и в бесконечной частях плоскости, имеющей частный интеграл в виде алгебраической кривой третьего порядка.

Повышай знания с онлайн-тренажером от Автор24!

Напиши термин
Выбери определение из предложенных или загрузи свое
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек

Источник

Примеры решения дифференциальных уравнений с ответами

Алгоритм решения дифференциальных уравнений

Примеры решения дифференциальных уравнений

Частный интеграл

Научные статьи на тему «Частный интеграл»

Формула Грина

Об устойчивости стационарных движений транспортных систем при существовании частного интеграла

Интегрирование методом Чебышева

Особые точки одной кубической двумерной системы, имеющей частный интеграл в виде алгебраической кривой третьего порядка

Повышай знания с онлайн-тренажером от Автор24!

Вам также может понравиться

Как найти ток фазы в треугольнике

Как найти производную обратной функции пример

Как найти фильм про кошку

Добавить комментарий Отменить ответ