В данной публикации мы рассмотрим формулы, с помощью которых можно найти частное двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.
- Деление в алгебраической форме
- Деление в геометрической форме
Деление в алгебраической форме
Результатом деления (т.е. частное) двух комплексных чисел x = a1 + b1i и y = a2 + b2i также является комплексное число z:
![]()
Порядок действий следующий:
- Делимое и делитель умножаем на число, комплексно сопряженное делителю. Не забываем, что i2 = -1.

Примечание: Для (a + bi) комплексно сопряженным будет число (a – bi), т.е. действительная часть остается той же, а у мнимой знак меняется на противоположный. - В результате выполнения умножения в знаменателе получается обычное действительное число.
(a2 + b2i)(a2 – b2i) = a2 ⋅ a2 – a2 ⋅ b2i + b2i ⋅ a2 – b2i ⋅ b2i = a22 – b22 ⋅ i2 = a22 + b22. - Теперь выполним аналогичное действие в числителе:
(a1 + b1i)(a2 – b2i) = a1 ⋅ a2 – a1 ⋅ b2i + b1i ⋅ a2 – b1i ⋅ b2i = a1a2 – b1b2i2 – a1b2i + b1a2i = (a1a2 + b1b2) + (a2b1 – a1b2) ⋅ i. - Делим полученный числитель на знаменатель:

Пример 1:
Разделим комплексное число (3 – i) на (-5 + 2i).
Решение:
Руководствуемся планом действий, описанным выше, и получаем:
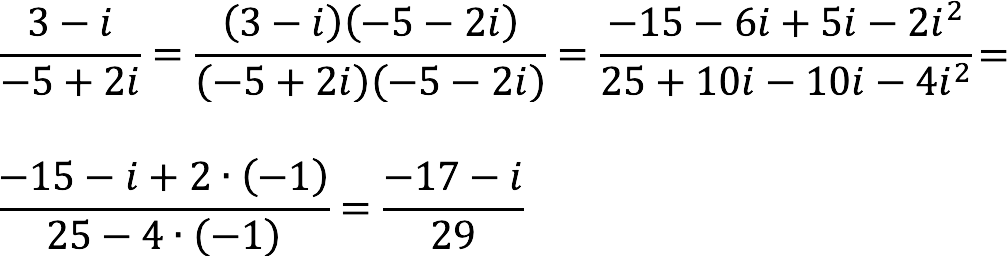
Деление в геометрической форме
Если комплексные числа заданы в тригонометрической форме, например, x = |x| ⋅ (cos φ1 + i ⋅ sin φ1) и y = |y| ⋅ (cos φ2 + i ⋅ sin φ2), то разделить их можно по формуле ниже:
![]()
Пример 2
Найдем частное комплексных чисел: x = 4 ⋅ (cos 60° + i ⋅ sin 60°) и y = 2 ⋅ (cos 25° + i ⋅ sin 25°).
Решение:
|x| : |y| = 4 : 2 = 2
φ1 – φ2 = 60° – 25° = 35°
x : y = 2 ⋅ (cos 35° + i ⋅ sin 35°)
Найти сумму, разность, произведение и частное комплексных чисел
Пусть даны два комплексных числа в алгебраической форме $z_1 = a + bi, z_2 = c + di$, тригонометрической форме $z_1 = r_1 (cos varphi_1 + isin varphi_1), z_2 = r_2(cos varphi_2 + isin varphi_2)$ и показательной форме $z_1 = r_1 e^{varphi_1 i} , z_2 = r_2 e^{varphi_2 i}$.
| Формула суммы и разности |
|
В алгебраической форме $$z_1 + z_2 = (a+bi) + (c+di) = (a + c) + (b + d)i, $$ $$z_1 – z_2 = (a+bi) – (c+di) = (a-c) + (b – d)i, $$в тригонометрической и показательной форме тоже можно выполнять сложение и вычитание, но удобнее это делать в алгебраической. |
| Формула произведения |
|
В алгебраической форме $$z_1 cdot z_2 = (a+bi) cdot (c+di) = (ac – bd) + i(ad + bc),$$ в тригонометрической форме $$z_1 cdot z_2 = r_1 r_2 (cos (varphi_1 + varphi_2) + isin (varphi_1 + varphi_2)),$$в показательной форме $$z_1 cdot z_2 = r_1 r_2 e^{(varphi_1+varphi_2)i}.$$ |
| Формула деления |
| В алгебраической форме $$frac{z_1}{z_2} =frac{z_1 overline{z_2}}{z_2 overline{z_2}} = frac{ac+bd}{c^2+d^2} + frac{bc-ad}{c^2+d^2}i, $$в тригонометрической форме $$frac{z_1}{z_2} = frac{r_1}{r_2} (cos(varphi_1 – varphi_2)+isin(varphi_1-varphi_2)),$$в показательной форме $$frac{z_1}{z_2} = frac{r_1}{r_2}e^{(varphi_1 – varphi_2)i}.$$ |
Введите первое комплексное число
Введите второе комплексное число
| Пример 1 |
| Найти сумму, разность, произведение, частное комплексных чисел $$z_1 = 1+2i, z_2 = -2+i.$$ |
| Решение |
|
Сначала находим сумму. Для этого раскрываем скобки и проводим вычисления с подобными $$z_1 + z_2 = (1+2i) + (-2+i) = 1+2i – 2 + i = (1-2) + (2i+i) = -1 + 3i.$$ Тоже самое делаем для того, чтобы найти разность. Раскрываем скобки и вычисляем $$z_1 – z_2 = (1+2i) – (-2+i) = 1+2i + 2 – i = 3 + i.$$ Теперь найдем произведение чисел. Раскрываем скобки попарно перемножая слагаемые в скобках. Но не забываем, что $i = sqrt{-1}$, а это значит, что $i^2 = -1$, получаем $$z_1 cdot z_2 = (1+2i)cdot (-2+i) = -2 + i – 4i + 2i^2 = $$ $$ = -2 – 3i – 2 = -4-3i.$$ Выполним деление комплексных чисел. Здесь необходимо числитель и знаменатель домножить на комплексно-сопряженное число к знаменателю, чтобы избавиться от дроби $$frac{z_1}{z_2} = frac{1+2i}{-2+i} = frac{(1+2i)(-2-i)}{(-2+i)(-2-i)} = $$ В числителе и знаменателе раскрываем скобки, то есть выполняем умножение комплексных чисел по соответствующей формуле. И не забываем про то, что $i^2 = -1$ $$ = frac{-2-i-4i-2i^2}{4+2i-2i-i^2} = frac{-2-5i+2}{4+1} = frac{-5i}{5} = -i.$$ |
| Ответ |
| $$z_1 + z_2 = -1+3i, z_1 – z_2 = 3+i, z_1 cdot z_2 = -4-3i, frac{z_1}{z_2} = -i$$ |
| Пример 2 |
| Найти произведение и частное комплексных чисел $z_1 = 2(cos frac{pi}{3} + isin frac{pi}{3})$ и $z_2 = 4(cos frac{pi}{6} + isin frac{pi}{6})$ |
| Решение |
|
Начнем с умножения двух чисел. Вычисляем произведение модулей и складываем аргументы синуса и косинуса $$z_1 cdot z_2 = 2(cos frac{pi}{3} + isin frac{pi}{3}) cdot 4(cos frac{pi}{6} + isin frac{pi}{6}) = $$ $$ = 8 (cos (frac{pi}{3} + frac{pi}{6}) + isin (frac{pi}{3}+frac{pi}{6})) = 8(cosfrac{pi}{2} + isin frac{pi}{2}).$$ Деление выполняется наоборот. Ищем частное модулей и разность аргументов $$frac{z_1}{z_2} = frac{2}{4} (cos (frac{pi}{3} – frac{pi}{6}) +isin (frac{pi}{3}-frac{pi}{6}) = frac{1}{2} (cos frac{pi}{6} + isin frac{pi}{6}).$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$z_1 cdot z_2 = 8(cosfrac{pi}{2} + isin frac{pi}{2}), frac{z_1}{z_2} = frac{1}{2} (cos frac{pi}{6} + isin frac{pi}{6})$$ |
| Пример 3 |
| Найти произведение и частное комплексных чисел $ z_1 = 6e^{frac{pi}{2}i} $ и $ z_2 = 2e^{frac{pi}{4}i} $ |
| Решение |
|
Для умножения двух комплексных чисел необходимо перемножить их аргументы и сложить показатели степеней $$z_1 cdot z_2 = 6e^{frac{pi}{2}i} cdot 2e^{frac{pi}{4}i} = 12e^{(frac{pi}{2}+frac{pi}{4})i} = 12e^{frac{3pi}{4}i}.$$ Для деления нужно найти частное аргументов двух комплексных чисел и вычислить разницу показателей степеней $$frac{z_1}{z_2} = frac{6e^{frac{pi}{2}i}} {2e^{frac{pi}{4}i}} = frac{6}{2} e^{(frac{pi}{2}-frac{pi}{4})i} = 3e^{frac{pi}{4}i}.$$ |
| Ответ |
| $$z_1 cdot z_2 = 12e^{frac{3pi}{4}i}, frac{z_1}{z_2} = 3e^{frac{pi}{4}i}$$ |
Содержание:
- Деление комплексных чисел в алгебраической форме
- Деление комплексных чисел в геометрической форме
Деление комплексных чисел в алгебраической форме
Определение
Частным двух комплексных чисел
$z_{1}=a_{1}+b_{1} i$ и
$z_{2}=a_{2}+b_{2} i$ называется число
$z$, которое задается соотношением:
$z=frac{z_{1}}{z_{2}}=frac{a_{1} a_{2}+b_{1} b_{2}}{a_{2}^{2}+b_{2}^{2}}+frac{a_{2} b_{1}-a_{1} b_{2}}{a_{2}^{2}+b_{2}^{2}} i$
На практике деление комплексных чисел проводят по следующей схеме:
- сначала делимое и делитель умножают на число,
комплексно сопряженное делителю, после чего делитель становится действительным числом; - в числителе умножают два комплексных числа;
- полученную дробь почленно делят.
Пример
Задание. Найти частное
$frac{-2+i}{1-i}$
Решение. Домножим и числитель, и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю
$1-i$, это будет
$1+i$, тогда имеем:
$frac{-2+i}{1-i}=frac{-2+i}{1-i} cdot frac{1+i}{1+i}=frac{(-2+i)(1+i)}{(1-i)(1+i)}$
Далее перемножаем комплексные числа как алгебраические двучлены, учитывая, что
$i^{2}=-1$:
$frac{-2+i}{1-i}=frac{(-2+i)(1+i)}{(1-i)(1+i)}=frac{-2-2 i+i-1}{1^{2}-i^{2}}=$
$=frac{-3-i}{1-(-1)}=frac{-3-i}{2}=-frac{3}{2}-frac{i}{2}$
Ответ. $frac{-2+i}{1-i}=-frac{3}{2}-frac{i}{2}$
Деление комплексных чисел в геометрической форме
Если надо поделить комплексные числа $z_{1}$ и
$z_{2}$ в геометрической форме:
$frac{z_{1}}{z_{2}}=frac{left|z_{1}right|left(cos phi_{1}+i sin phi_{1}right)}{left|z_{2}right|left(cos phi_{2}+i sin phi_{2}right)}$ , то искомое число
$z=frac{z_{1}}{z_{2}}=frac{left|z_{1}right|}{left|z_{2}right|}left[cos left(phi_{1}-phi_{2}right)+i sin left(phi_{1}-phi_{2}right)right]$
То есть модуль частного двух комплексных чисел равен частному модулей, а аргумент – разности аргументов делимого и делителя.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти частное
$frac{z_{1}}{z_{2}}$, если
$z_{1}=2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right)$, а
$z_{2}=cos frac{pi}{4}+i sin frac{pi}{4}$
Решение. Искомое частное
$frac{z_{1}}{z_{2}}=frac{2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right)}{cos frac{pi}{4}+i sin frac{pi}{4}}=$
$=frac{2}{1} cdotleft[cos left(frac{3 pi}{4}-frac{pi}{4}right)+i sin left(frac{3 pi}{4}-frac{pi}{4}right)right]=$
$=2 cdotleft[cos frac{pi}{2}+i sin frac{pi}{2}right]=2 cdot(0+i)=2 i$
Ответ. $frac{z_{1}}{z_{2}}=2 cdotleft(cos frac{pi}{2}+i sin frac{pi}{2}right)=2 i$
Читать дальше: возведение комплексного числа в степень.
Деление комплексных чисел
В данной публикации мы рассмотрим формулы, с помощью которых можно найти частное двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.
Деление в алгебраической форме
Результатом деления (т.е. частное) двух комплексных чисел и также является комплексное число z :

Порядок действий следующий:
-
Делимое и делитель умножаем на число, комплексно сопряженное делителю. Не забываем, что .

Примечание: Для комплексно сопряженным будет число , т.е. действительная часть остается той же, а у мнимой знак меняется на противоположный.
Пример 1:
Разделим комплексное число на .
Решение:
Руководствуемся планом действий, описанным выше, и получаем:
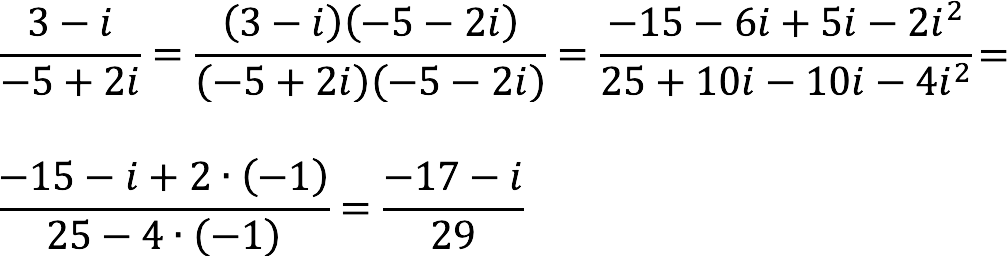
Деление в геометрической форме
Если комплексные числа заданы в тригонометрической форме, например, и , то разделить их можно по формуле ниже:

Пример 2
Найдем частное комплексных чисел: и .
Деление комплексных чисел
Деление комплексных чисел в алгебраической форме
Частным двух комплексных чисел $z_<1>=a_<1>+b_ <1>i$ и $z_<2>=a_<2>+b_ <2>i$ называется число $z$, которое задается соотношением:
На практике деление комплексных чисел проводят по следующей схеме:
- сначала делимое и делитель умножают на число, комплексно сопряженное делителю, после чего делитель становится действительным числом;
- в числителе умножают два комплексных числа;
- полученную дробь почленно делят.
Задание. Найти частное $frac<-2+i><1-i>$
Решение. Домножим и числитель, и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю $1-i$, это будет $1+i$, тогда имеем:
Далее перемножаем комплексные числа как алгебраические двучлены, учитывая, что $i^<2>=-1$:
Деление комплексных чисел в геометрической форме
Если надо поделить комплексные числа $z_<1>$ и $z_<2>$ в геометрической форме: $frac>>=frac<left|z_<1>right|left(cos phi_<1>+i sin phi_<1>right)><left|z_<2>right|left(cos phi_<2>+i sin phi_<2>right)>$ , то искомое число
То есть модуль частного двух комплексных чисел равен частному модулей, а аргумент – разности аргументов делимого и делителя.
Деление комплексных чисел
Деление комплексных чисел определяется как действие, обратное умножению.
Частным двух комплексных чисел z1 и z2≠0 называется комплексное число z , при умножении которого на z2 получается z1:
Для комплексных чисел, записанных в алгебраической форме:
На практике частное комплексных чисел находят умножением делимого и делителя на число, комплексно-сопряженное делителю.
С помощью формулы правило деления комплексных можно записать так:
Найти частное комплексных чисел:
1) Чтобы выполнить деление комплексных чисел, записанных в алгебраической форме, и делимое, и делитель умножаем на число, комплексно-сопряженное делителю (вариант: и числитель, и знаменатель умножаем на число, сопряженное знаменателю):
Умножение комплексных чисел выполняем как умножение многочленов.
i² заменяем на -1.
Деление комплексных чисел, представленных в тригонометрической форме, будет рассмотрено позже.
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_16_10.php
[/spoiler]
Частное комплексных чисел в тригонометрической и показательной формах
Для комплексных
чисел
и
частное
может быть записано в следующем виде
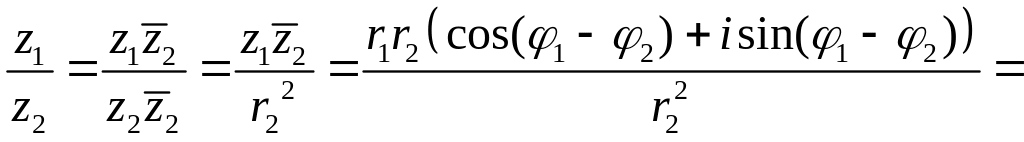
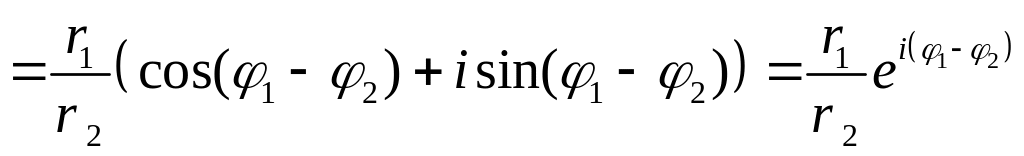
,
откуда следует, что модуль
частного двух комплексных чисел равен
отношению модулей делимого и делителя,
а главное значение
аргумента
частного с точностью до
равно разности
аргументов делимого и делителя.
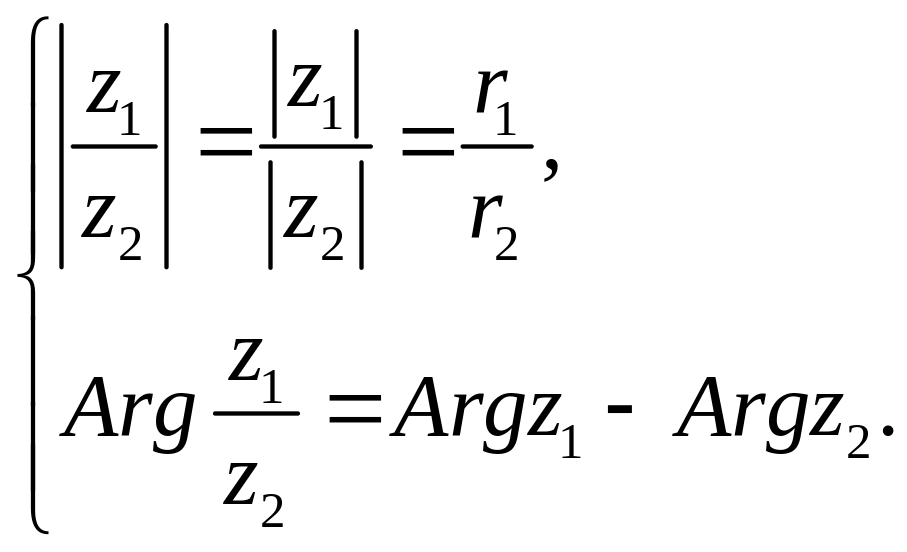
(9)
Пример 18.
Представить в показательной форме числа
а)
![]()
; б)
![]()
.
Решение. а)
![]()
.
Для этого числа
.
![]()
,
поэтому
![]()
.
б)
Найдем модуль
и аргумент числа
,
предварительно представив его в
алгебраической форме.
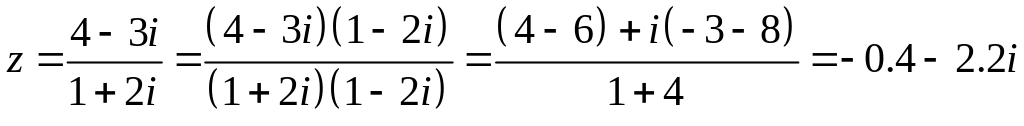
.
![]()
– алгебраическая форма данного числа и
![]()
,
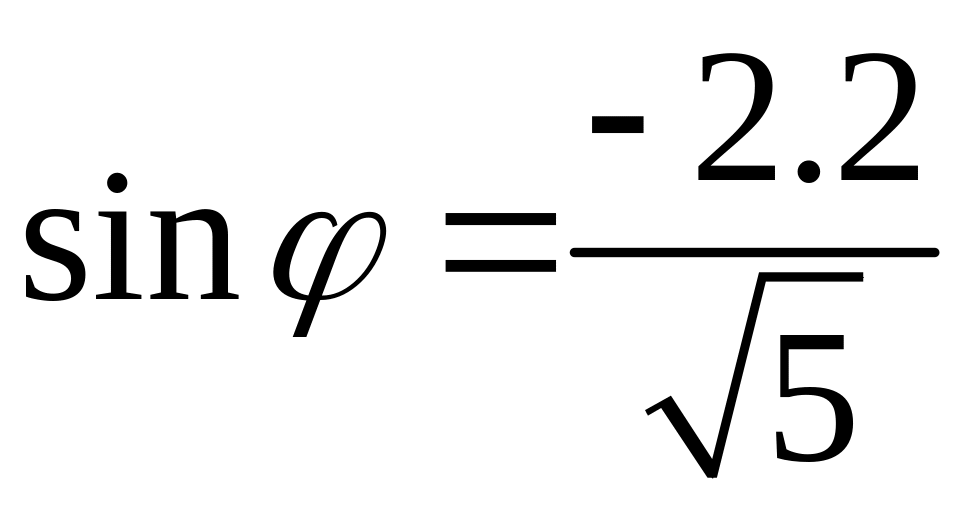
,
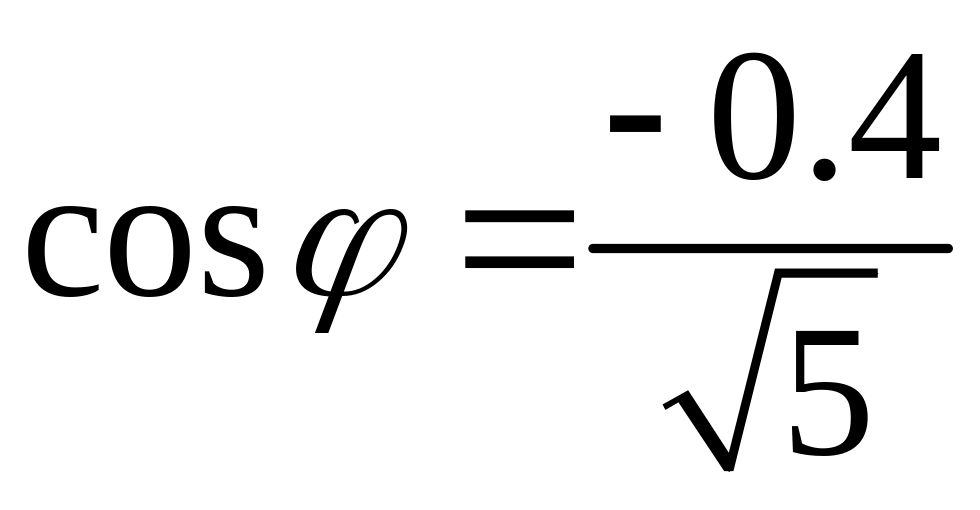
.
Так как действительная
и мнимая части числа
отрицательны, то главное значение
аргумента равно
![]()
,
т.е.
![]()
и
![]()
.
Замечание.
При сложении и вычитании комплексных
чисел, как правило, целесообразнее
использовать алгебраическую форму этих
чисел. При умножении, возведении в
степень и извлечении корня более
рациональным может оказаться
тригонометрическая или показательная
форма.
Извлечение корня целой положительной степени из комплексного числа
Извлечь корень
целой положительной степени
![]()
из числа
значит найти такое число
![]()
,
![]()
-ая
степень которого равна
.
Пусть
![]()
.
Тогда
![]()
и
![]()
,
откуда
![]()
,
![]()
и
![]()
![]()
,
откуда
![]()
,
(10)
т. е.
![]()
,
![]()
.
(10) – формула для
извлечения корня целой положительной
степени
из комплексного числа
.
Пример 19
Представить следующие выражения в
алгебраической форме: а)
![]()
;
б)
![]()
.
Решение.
а)
![]()
,
![]()
,
откуда
![]()
и
![]()
.
б)
![]()
При
![]()
![]()
и
при
![]()
![]()
.●
Пример 20.
Решить уравнение
![]()
и изобразить корни этого уравнения на
комплексной плоскости.
Решение.
![]()
![]()
![]()
Подставляя
последовательно
![]()
,
![]()
,
и
![]()
,
получим четыре
различных корня исходного уравнения:
![]()
,
![]()
,
![]()

и
![]()
(рис. 15).●
Рис. 15
ПОНЯТИЕ О ФУНКЦИИ
КОМПЛЕКСНОго
ПЕРЕМЕННОго.
Понятие функции
комплексного переменного вводится по
аналогии с понятием функции действительной
переменной.
Определение.
Величина
![]()
называется функцией
комплексного переменного
в области
![]()
,
если задан закон, по которому каждому
значению
![]()
,
ставится в соответствие одно или
несколько значений
.
Это соответствие
обозначается в виде
![]()
.
Определение.
Переменную
называют независимой
переменной
или аргументом,
а
– зависимой
переменной
или функцией.
Пусть
![]()
.
Тогда
из
имеем
![]()
и
![]()
.
Определение.
Если каждому значению
поставлено
в соответствие одно и только одно
значение
,
то функцию
называют однозначной,
а если несколько значений – то
многозначной.
Определение.
Множество значений
![]()
,
где
,
называется областью
значений функции
и обозначается это множество через
![]()
.
Геометрически
можно рассматривать
,
заданную на
,
как отображение области
плоскости
(рис. 16) в некоторую область
плоскости
![]()
.
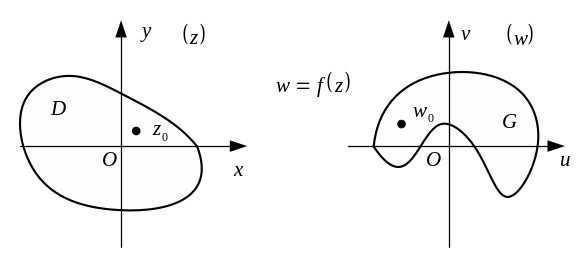
Рис.
16
Определение.
Если
![]()
,
то точка
![]()
называется образом
точки
при отображении
,
а точка
называется
прообразом
точки
.
З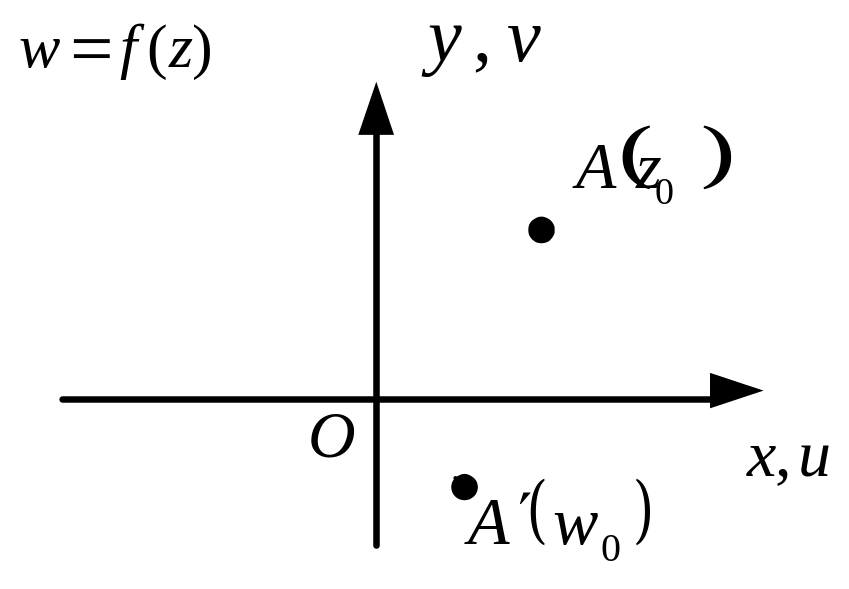
амечание.
Иногда удобно совмещать плоскости
и
.
Тогда функция
«перемещает» точку
![]()
в точку
![]()
(рис. 17).
Рис.
17
Например,
при отображении
![]()
образом точки
![]()
является точка

,
т. е
функция
«перемещает» точку
![]()
в точку
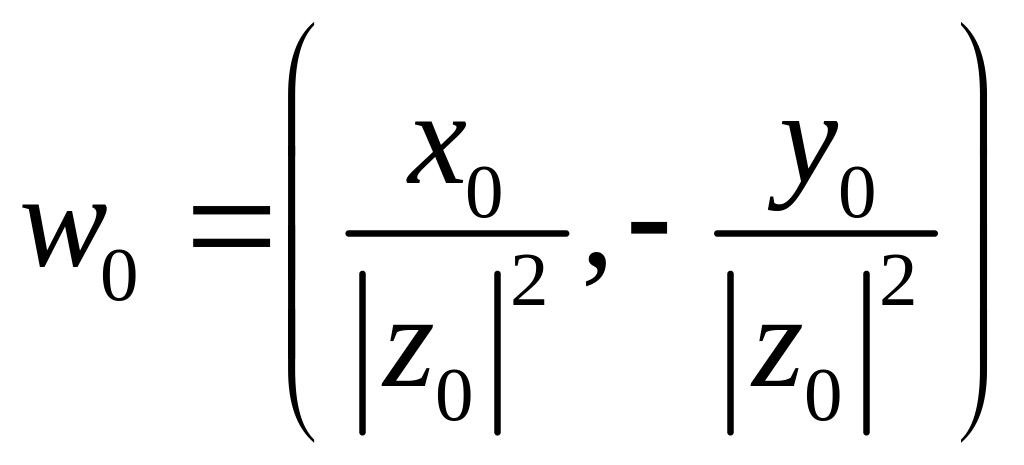
.
Очевидно,
![]()
.
Пример 21
Найти образ точки
![]()
,
если отображение задано формулой
![]()
.
Решение.
![]()
.●
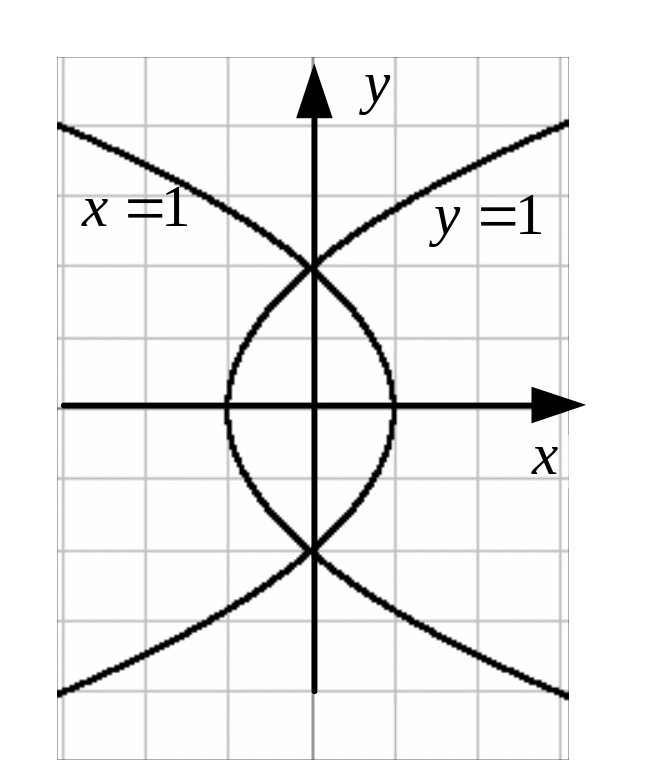
Пример 22.
Найти уравнения линий в плоскости
![]()
,
на которые с помощью функции
![]()
отображаются прямые
и
![]()
.
Решение.
![]()
,![]()
,
откуда
![]()
,![]()
. (11)
Подставляя
в уравнения (11), получим
![]()
,![]()
,
откуда
![]()
.
Это , уравнение
параболы, симметричной
относительно оси
![]()
.
Подставляя
в уравнения (11), получим
![]()
,
![]()
,
т.е. еще одну параболу
![]()
(рис. 18).●
Рис. 18
Пример 23.
Найти образ окружности
при отображении
.
Решение 1.
Так как
,
то
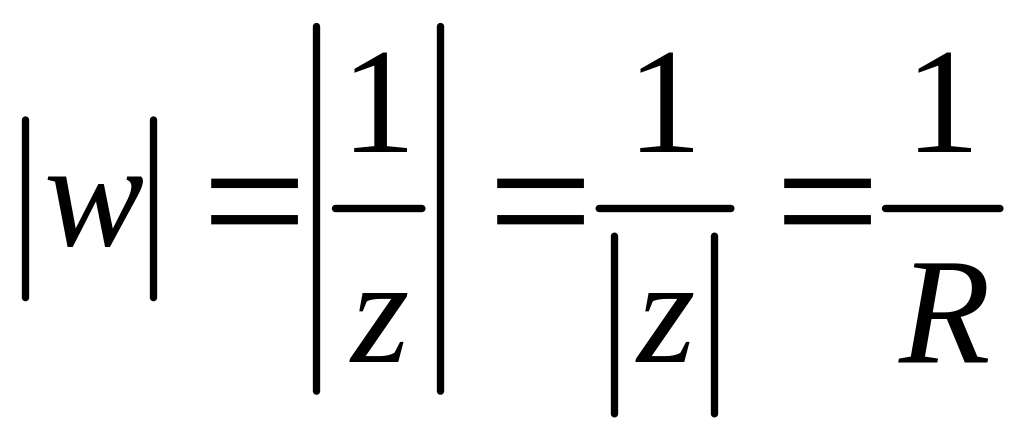
,
т. е. образом окружности
при указанном отображении является
окружность
![]()
.
Решение
2.
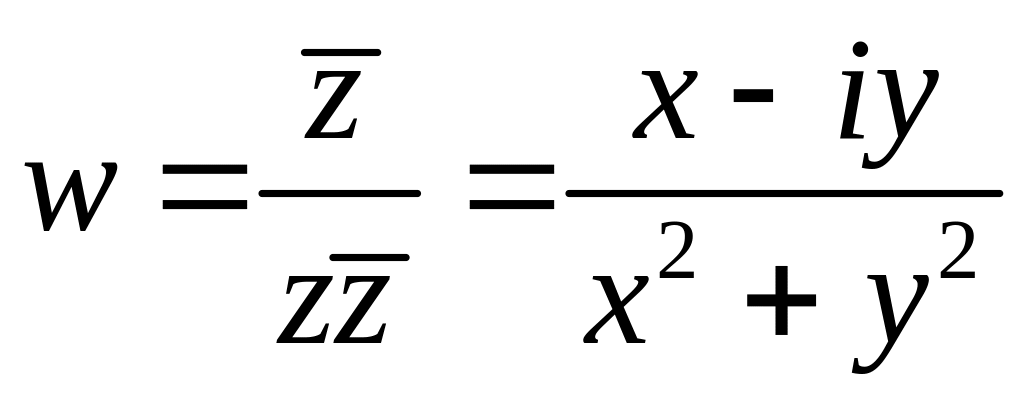
,
откуда
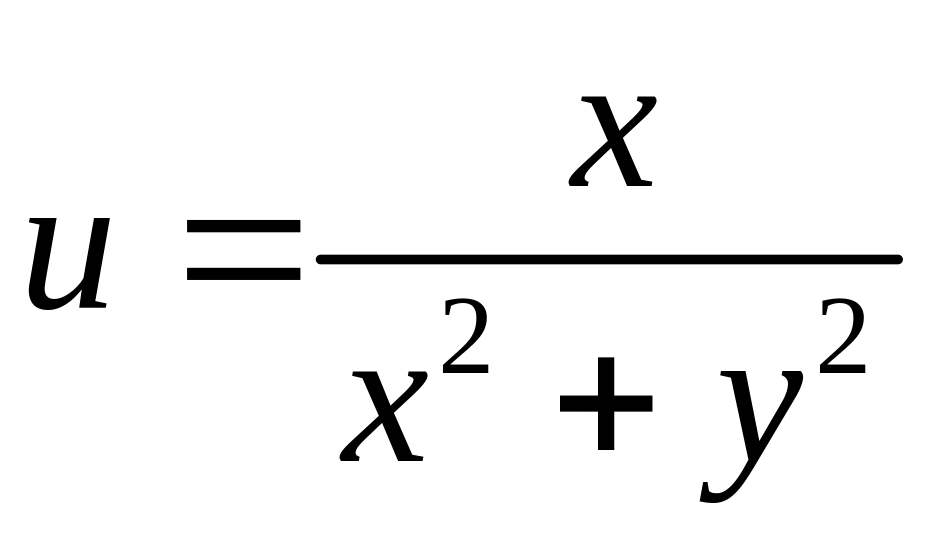
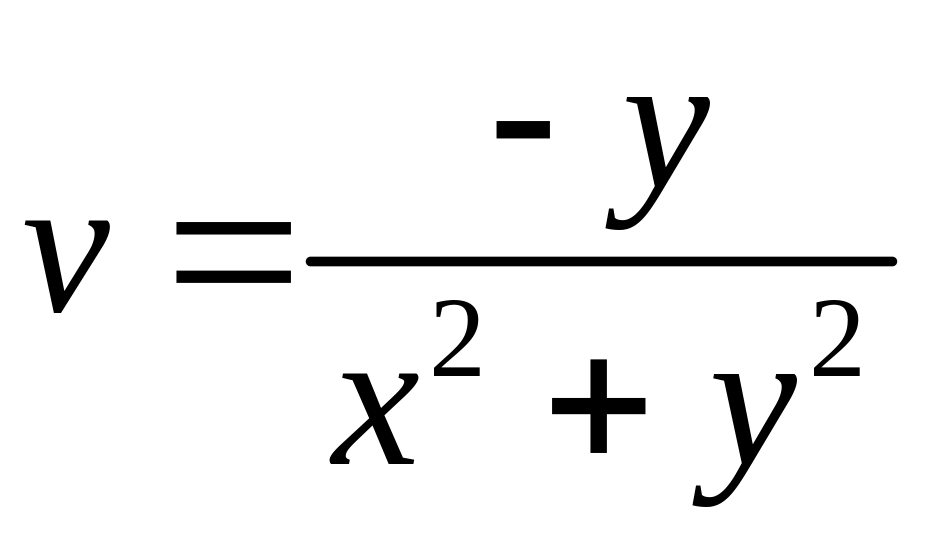
.
Так как
,
то
,
![]()
,
![]()
и
![]()
,
т.е. образом окружности
при отображении
является окружность
.●
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
