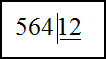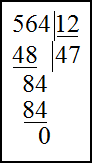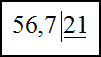Что такое частное чисел
Определение
Частное — это результат процесса деления. Делением называется такая операция, которая обратна умножению, то есть показывает, сколько одинаковых чисел способно содержаться в другом.
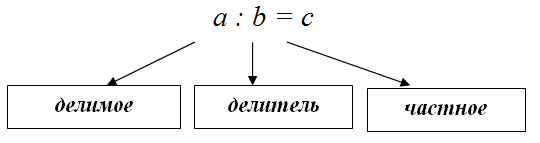
Буквенный вид этого действия выглядит следующим образом: a: b = c, где:
- a – это делимое (число, которое делят)
- b – это делитель (число, которым делят)
- с – это частное (результирующее число деления)
- : — арифметический знак, с помощью которого обозначается деление
Важно! Число 0 никогда не может быть делителем
Нахождение значения частного чисел
Пример:
12 : 3 = 4 (в числе 12 4 раза содержится по 3)
15 : 5 = 3 (в числе 15 5 раз содержится по 5)
Нужно знать, что правильность определения частного от деления числа всегда можно проверить путем перемножения его на делитель, либо делимое поделить на частное и получить делитель.
Например:
20 : 4 = 5
Перемножим частное двух чисел на делитель и получим делимое:
4 * 5 = 20
Разделим делимое на частное и получим делитель:
20 : 5 = 4
Таким образом, мы доказали правильность определения частного.
Что такое частное значение чисел с остатком?
Иногда при делении от делимого остается остаток, который меньше делителя, но более нуля. Приведем выражение частного чисел:
8 : 3 = 2 (ост. 2)
Это значит, что делимое 8 поделилось 2 раза по 3 и остался остаток 2, который меньше трех, но больше нуля.
Таким образом: 0 < ост. <делитель
Основные понятия о частном суммы и разности чисел
Что такое частное суммы чисел?
Определение
Частное от деления суммы чисел – это когда делимое либо делитель выступает в роли суммы двух слагаемых.
Общий вид: (a+b):(c+d), где сумма чисел (a+b) – делимое, а сумма (c+d) – делитель
Пример: (12+3):(3+2)=3
Важно, в подобных примерах последовательность решения определяется следующим образом: сначала решаются выражения в скобочках, потом выражения со знаками деления или умножения, после – вычитание или сложение.
Нет времени решать самому?
Наши эксперты помогут!
Поговорим о частном разности чисел
Аналогично, как и с частностью суммы, только в роли делимого или делителя выступает значение разности: (a-b):(c-d), где разность чисел (a-b) – делимое, а разность (c-d) – делитель
Пример нахождения разности чисел: (12-3):(5-2)=3, где
3 и 2 — это вычитаемое частное чисел
Также в математике находят сумму частного произведения чисел:
(12+3)*(1+2)=45
И произведение частного чисел:
(12*5):(5*2)=6
Основные правила при делении
- При делении одного числа на единицу – получаем в ответ делимое: 6 : 1 = 6
- При делении одного числа на само себя – получаем в ответ 1: 7 : 7 = 1
- Если произведение поделить на один из множителей, то получится другой множитель:
6*3=18, 18:6=3, 18:3=6.
При делении на десятки (10, 100…) у частной, запятой с левой стороны отделяется столько цифр, сколько нулей в делителе: 34:10=3,4, 34:100=0,34, 34:1000=0,034.
Частное чисел в математике: что это такое? В школе учат действие деление, где есть делимое, делитель и частное. Что означают эти названия? Давайте разбираться!
Содержание статьи:
Частное чисел в математике: что это такое
Однажды клоун Бим решил выучить математическое действие деление и нашел для себя в интернете вот такое определение:
Определение. Говорят, что a делится на b, если существует натуральное число с, при умножении которого на b получается а: a=b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
Как мне это понять? — задумался Бим. — Но скоро представление, пойду ребят к нам приглашать.
Как найти частное чисел
Пришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
— Мне надо подарить вам шарики, какое математическое действие я буду применять?
— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.
Клоун хитро прищурился:
— А как называются члены деления?
— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!
— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!
Коля продолжил:
— У каждого из нас будет часть шариков, и результат от деления называется частным.
— Какое же здесь будет частное? — спрашивает Бим.
— Два! — не сговариваясь, хором ответили ребята.
— Правильно, каждому из вас достанется по два шарика, это и есть частное.
Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:
6 (делимое) : 3 (делитель) = 2 (частное).
Запишем цифрами:
6:3=2
В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.
Итак, частное — это число, которое получается в результате деления делимого на делитель.
Полное и неполное частное
А потом было замечательное представление.
В антракте дети пошли в буфет. На подносе лежало семь пирожных. Как же их разделить поровну на трёх ребят?
Друзья задумались и взяли по 2 пирожных, а последним, которое было в остатке, угостили клоуна Бима.
— Теперь я понял! — воскликнул Бим. — Если нельзя всё число пирожных поделить между ребятами без остатка, то такой результат от деления называется неполным частным. А то, что осталось после деления, так и называется остатком и записывается это вот так:
7:3=2(1)
Здесь 7 (делимое) по-прежнему стоит в начале выражения, 3 (делитель) — в середине, 2 (неполное частное) — справа. Но после неполного частного ещё пишем в скобках остаток (1).
- Полное частное — результат деления, когда делимое делится нацело на делитель (остаток равен 0, его и писать незачем).
- Неполное частное — это результат деления с остатком (когда делимое не делится нацело на делитель).
Как найти делитель
Когда дети ушли занимать свои места, буфетчица подошла к Биму и спросила:
— Я забыла, сколько было ребят. Помню только, что каждый из них съел по два пирожных, а всего им досталось 6 штук. Сколько же посетителей было у меня?
Тут в буфет заглянул дрессировщик Бом и быстренько решил эту задачку. Он разделил 6 (делимое) на 2 (частное) и получил 3 (делитель).
— Всего было трое ребят, — ответил Бом.
— Верно! — вспомнил Бим.
Для того чтобы найти делитель, надо делимое разделить на частное.
6:2=3
Здесь 6 – делимое, 2 – частное, а 3 – делитель.
Как найти делимое
— А сколько ты подарил всего шариков трём ребятам? — спросил Бом.
— Забыл, — ответил Бим. — Помню только, что детей было трое, и каждому досталось по два шарика.
Бом и говорит:
— Тогда надо 3 (делитель) умножить на 2 (частное), получится 6.
Для того чтобы найти делимое, надо делитель умножить на частное.
Запишем это цифрами:
3*2=6.
3 — наш делитель, 2 — частное, а 6 — делимое.
Проверка деления умножением
— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?
— Да, — ответил Бом.
Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.
Заключение
А клоун для себя сделал плакаты и теперь каждый день может сразу вспомнить, что:
Определение. Говорят, что а делится на b, если существует число с, при умножении которого на b получается а: a= b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
- Деление — действие, обратное умножению;
- умножение проверяет правильность математического действия — деления;
- для того чтобы найти делимое, надо делитель умножить на частное;
- для того чтобы найти делитель, надо делимое разделить на частное.
Итак, теперь мы знаем, что же такое частное в математике. Оказывается, оно бывает полным и неполным! Кроме того, нетрудно будет найти делитель, делимое и проверить деление умножением. И если учитель спросит в школе: «Частное чисел в математике: что это такое?» — сможем ответить сразу. И пусть любой пример или задача на эту тему будет вам по плечу!
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Определение частного чисел
Определение
Частное чисел – это результат деления одного числа на другое. Таким образом, частное чисел
$a$ и
$b$ будет число
$c$, которое равно
$c = a : b$ . При этом число
$a$ будет делимым, а число
$b$ – делителем.
Пример
Задание. Найти частное чисел:
1) $39 : 3$ ;
4) $124 : 4$
Ответ. $39 : 3 = 13$
$124 : 4 = 31$
Для нахождения частного больших чисел или
десятичных дробей используют способ
деления в столбик.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти частное чисел:
1) $564 : 12$ ;
2) $0,567 : 0,21$
Решение. Для нахождения частного в первом примере выполним деление в столбик.
Для этого запишем делимое и делитель следующим образом
Берем первую цифру слева, она не делится на 12, значит, берем две цифры: 56 и делим их на 12 с остатком.
Возьмем по $4 : 4 cdot 12 = 48$ . Записываем 48 под 56 и находим остаток:
$56 – 48 = 8$ . Восьмерку записываем под чертой и сносим к ней следующее
число из делимого, получим 84. Делим 84 на 12, получаем 7. остаток от деления 0 и цифр в делимом больше нет. Деление окончено.
Таким образом, $564 : 12 = 47$
Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число.
Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее
запишем полученные числа в столбик, как и в первом примере:
Берем в делимом первые две цифры слева и делим их на делимое с остатком. Получаем $56 : 21$ , можно взять по 2. Двойку записываем в частное.
И так как целая часть делимого закончилась, ставим в частном запятую. Умножаем $2 cdot 21 = 42$ , записываем 42 под 56 и вычитаем:
$56 – 42 = 14$ . Остаток 14 списываем к нему следующую
незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное,
и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.
Таким образом $0,567 : 0,21 = 2,7$
Ответ. $564 : 12 = 47$
$0,567 : 0,21 = 2,7$
Частное рациональных дробей находится по правилу
$$frac{m}{n}: frac{p}{q}=frac{m cdot q}{n cdot p}$$
Пример
Задание. Найти частное рациональных дробей:
1) $frac{2}{3}: frac{1}{3}$ ;
2) $1 frac{1}{14}: 1 frac{3}{7}$
Решение. 1) Воспользуемся правилом вычисления частного рациональных дробей:
$$frac{2}{3}: frac{1}{3}=frac{2 cdot 3}{3 cdot 1}=2$$
Для вычисления частного во втором примере, сначала запишем дроби в виде неправильных дробей. Для этого целую часть
умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:
$$1 frac{1}{14}: 1 frac{3}{7}=frac{1 cdot 14+1}{14}: frac{1 cdot 7+3}{7}=frac{15}{14}: frac{10}{7}=$$
$$=frac{15 cdot 7}{14 cdot 10}=frac{15}{2 cdot 10}=frac{15}{20}=frac{3}{4}$$
Ответ. $frac{2}{3}: frac{1}{3}=2$
$1 frac{1}{14}: 1 frac{3}{7}=frac{3}{4}$
Читать дальше: что такое иррациональное число.
В этой статье мы рассмотрим правила и алгоритмы деления натуральных чисел. Сразу отметим, что здесь мы смотрим только на деление нацело, то есть без остатка. О делении натуральных чисел с остатком читайте в нашем отдельном материале.
Перед тем, как формулировать правило деления натуральных чисел, нужно понять связь деления с умножением. После того, как мы установим эту связь, последовательно рассмотрим самые простые случаи: деление натурального числа на себя и на единицу. Далее разберем деление с помощью таблицы умножения, деление методом последовательного вычитания, деление на числа, кратные числу 10, различные степени числа 10.
Для каждого случая приведем и подробно рассмотрим примеры. В конце статьи покажем, как проводить проверку результата деления.
Связь деления с умножением
Чтобы проследить связь между делением и умножением, вспомним, что деление представляется, как разбиение исходного делимого множества на несколько одинаковых множеств. Умножение связано с объединением нескольких одинаковых множеств в одно.
Деление – действие, обратное умножению. Что это значит? Приведем аналогию. Представим, что у нас есть b множеств, в каждом из которых – по с предметов. Общее количество предметов во всех множествах равно a. Умножение – это объединение всех множеств в одно. Математически оно запишется так:
b·c=a.
Обратный процесс разбиения полученного общего множества на b множеств по с предметов в каждом соответствует делению:
a÷b=c.
На основе сказанного можно перейти к следующему утверждению:
Если произведение натуральных чисел c и b равно a, то частное чисел a и b равно c. Перепишем в буквенном виде.
Если b·c=a, то a÷b=c
Пользуясь переместительным свойством умножения, можно записать:
c·b=a
Отсюда также следует, что a÷с=b.
На основании сказанного можно сформулировать общий вывод. Если произведение чисел c и b равно a, то соответственно частные a÷b и a÷c равны c и b.
Подытожим все изложенное выше и дадим определение деления натуральных чисел.
Деление – нахождение неизвестного множителя по известному произведению и другому известному множителю.
Это определение станет базой, на основе которой мы будем строить правила и методы деления натуральных чисел.
Деление методом последовательного вычитания
Только что мы говорили о делении в контексте умножения. На основе этого знания можно проводить операцию деления. Однако, существует еще один, достаточно простой и достойный внимания подход – деление методом последовательного вычитания. Этот способ понятен интуитивно, поэтому рассмотрим его на примере, не приводя теоретических выкладок.
Сколько будет 12 разделить на 4?
Иными словами данную задачу можно сформулировать так: имеется 12 предметов (например, апельсинов), и их нужно разделить на равные группы по 4 предмета (разложить в коробки по 4 штуки). Сколько будет таких групп или коробок по четыре апельсина в каждой?
Шаг за шагом будем отнимать от исходного количества по 4 апельсина и формировать группы по 4 до того момента, пока апельсины не закончатся. Количество шагов, которые нам придется сделать, и будет ответом на изначальный вопрос.
Из 12 апельсинов откладываем первую четверку в коробку. После этого в исходной куче апельсинов остается 12-4=8цитрусовых. Из этих восьми в другую коробку забираем еще 4. Теперь в исходной куче апельсинов осталось 8-4=4штуки. Из этих четырех штук как раз можно сформировать еще одну, отдельную третью коробку, после чего в исходной куче останется 4-4=0 апельсинов.
Итак, мы получили 3 коробки, по 4 предмета в каждой. Иными словами, мы разделили 12 на 4, и получили в результате 3.
Работая с числами, не нужно каждый раз проводить аналогию с предметами. Что мы делали с делимым и делителем? Последовательно вычитали делитель из делимого, пока не получили нуль в остатке.
При делении методом последовательного вычитания количество операций вычитания до получения нулевого остатка и есть частное от деления.
Для закрепления рассмотрим еще один, более сложный пример.
Вычислим результат деления числа 108 на 27 методом последовательного вычитания.
Первое действие: 108-27=81.
Второе действие: 81-27=54.
Третье действие: 54-27=27.
Четвертое действие: 27-27=0.
Более действий не требуется. Мы получили ответ:
108÷27=4
Отметим, что данный метод удобен только в случаях, когда необходимое количество последовательных вычитаний невелико. В остальных случаях целесообразно применять правила деления, которые мы рассмотрим ниже.
Деление равных натуральных чисел
Согласно свойствам натуральных чисел, сформулируем правило, как делить равные натуральные числа.
Частное от деления натурального числа на равное ему натуральное число равно единице!
aa=1.
Например:
1÷1=1; 141÷141=1; 2589÷2589=1; 100000000÷100000000=1.
Деление на единицу
Основываясь на свойствах натуральных чисел, можно также сформулировать правило деление натурального числа на единицу.
Частное от деления любого натурального числа на единицу равно самому делимому числу.
a1=a.
Например:
1÷1=1; 141÷1=141; 2589÷1=2589; 100000000÷1=100000000.
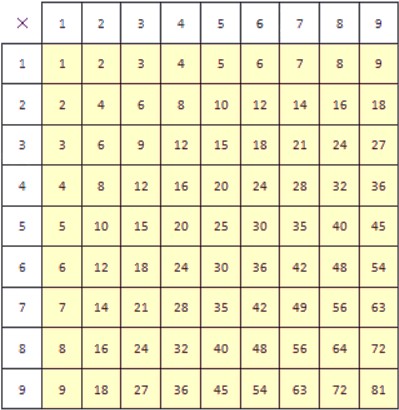
Деление с помощью таблицы умножения
Таблица умножения – удобный инструмент, который позволяет найти произведения однозначных натуральных чисел. Однако, ее можно использовать и для деления.
Таблица умножения позволяет находить не только результат произведения множителей, но и множитель по известному произведению и другому множителю. Как мы выяснили ранее, деление – это как раз и есть нахождение неизвестного множителя по известному произведению и еще одному множителю.
С помощью таблицы умножения можно проводить деление любого числа на желтом фоне на любое однозначное натуральное число. Покажем, как это делать. Есть два способа, применение которых мы будем рассматривать на примерах.
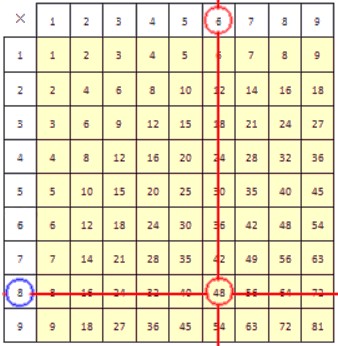
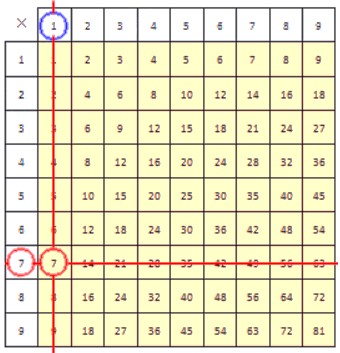
Разделим 48 на 6.
Способ первый.
В столбце, верхняя ячейка которого содержит делитель 6, находим делимое 48. Результат деления при этом находится в крайней левой ячейке строки, содержащей делимое. Он обведен синей окружностью.
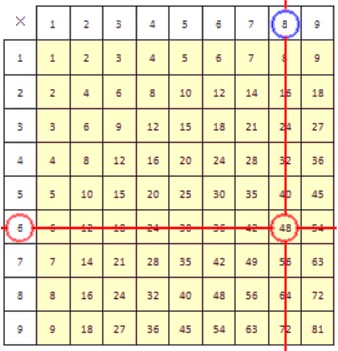
Способ второй.
Сначала в строке с делителем 6 находим делимое 48. Результат деления при этом находится в крайней верхней ячейке столбца, содержащем делимое. Он обведен синей окружностью.
Итак, мы разделили 48 на 6 и получили 8. Результат был найден по таблице умножения двумя способами. Оба способа абсолютно идентичны.
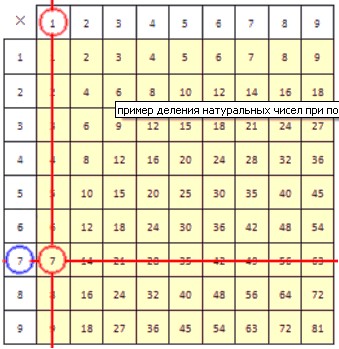
Для закрепления рассмотрим еще один пример. Разделим 7 на 1. Приведем рисунки, иллюстрирующие процесс деления.
В результате деления числа 7 на 1, как вы уже догадались, получается число 7. В делении с помощью таблицы умножения очень важно знать эту таблицу наизусть, так как не всегда можно иметь ее под рукой.
Настоятельно рекомендуем выучить таблицу умножения!
Деление на 10, 100, 1000 и т.д.
Сразу сформулируем правило деления на натуральных чисел на 10, 100, 1000 и т.д. Сразу будем считать, что деление без остатка возможно.
Результатом деления натурального числа на 10, 100, 1000 и т.д. является такое натуральное число, запись которого получается из записи делимого если справа от него отбросить 1, 2, 3 и т.д. нулей.
Отбрасывается столько нулей, сколько из есть в записи делителя!
Например, 30÷10=3. От числа 30 мы отбросили один нуль.
Частное 120000÷1000 равно 120 – от числа 120000 отбрасываем справа три нуля, именно столько их содержится в делителе.
Обоснование правила строится на правиле умножения натурального числа на 10, 100, 1000 и т.д. Приведем пример. Пусть нужно разделить 10200 на 100.
10200=102·100
10200÷100=102·100100=102.
Представление делимого в виде произведения
При делении натуральных чисел не стоит забывать о свойстве деления произведения двух чисел на натуральное число. Иногда делимое можно представить в виде произведения, один из множителей в котором делится на делитель.
Рассмотрим типичные случаи.
Разделим 30 на 3.
Делимое 30 можно представить в виде произведения30=3·10.
Имеем: 30÷3=3·10÷3
Воспользовавшись свойством деления произведения двух чисел, получаем:
3·10÷3=3÷3·10=1·10=10
30÷3=10
Приведем еще несколько аналогичных примеров.
Вычислим частное 7200÷72.
Представляем делимое в виде 7200=72·100. При этом, результат деления будет следующим:
7200÷72=72·100÷72=72÷72÷100=100
Вычислим частное: 1600000÷160.
1600000=160·10000
1600000÷160=160·10000÷160=160÷160·10000=10000
В более сложных примерах удобно пользоваться таблицей умножения. Проиллюстрируем это.
Разделим 5400 на 9.
Таблица умножения подсказывает нам, что 54 делится на 9, поэтому делимое целесообразно представить в виде произведения:
5400=54·100.
Теперь закончим деление:
5400÷9=54·100÷9=54÷9·100=6·100=600
Для закрепления данного материала рассмотрим еще один пример, уже без подробных словесных пояснений.
Посчитаем, сколько будет 120 разделить на 4.
120=12·10
120÷4=12·10÷4=12÷4·10=3·10=30
Деление натуральных чисел, оканчивающихся на нуль
При делении чисел, записи которых оканчиваются цифрой 0, полезно помнить свойство деления натурального числа на произведение двух чисел. При этом, делитель представляется в виде произведения двух множителей, после чего указанное свойство находит применение в совокупности с таблицей умножения.
Как всегда, поясним это на примерах.
Разделим 490 на 70.
Запишем 70 в виде:
70=7·10.
Используя свойство деления натурального числа на произведение, можно записать:
490÷70=490÷7·10=490÷10÷7.
Деление на 10 мы уже разобрали в предыдущем пункте.
490÷10÷7=49÷7=7
490÷70=7.
Для закрепления разберем еще один, более сложный пример.
Возьмем числа 54000 и 5400 и разделим их.
54000÷5400=?
Представим 5400 в виде 54·100 и запишем:
54000÷5400=54000÷54·100=54000÷100÷54=540÷54.
Теперь делимое 540 представляем в виде 54·10 и записываем:
540÷54=54·10÷54=54÷54·10=10
54000÷5400=10.
Подведем итог по изложенному в данном пункте.
Если в записях делимого и делителя справа присутствуют нули, то нужно избавиться от одинакового количества нулей как в делимом, так и в делителе. После этого выполнить деление получившихся чисел.
Например, деление чисел 64000 и 8000 сведется к делению чисел 64 и 8.
Метод подбора частного
Прежде чем рассматривать этот способ деления, введем некоторые условия.
Пусть числа a и b делятся друг на друга, причем произведение b·10 дает число, большее, чем a. В таком случае частное a÷b является однозначным натуральным числом. Иными словами, это число от 1 до 9. Это типичная ситуация, когда метод подбора частного удобен и применим. Последовательно умножая делитель на 1, 2, 3, .. , 9 и сравнивая результат с делимым, можно найти частное.
Рассмотрим пример.
Разделим 108 на 27.
Легко заметить, что 27·10=270; 270>108.
Начнем подбор частного.
27·1=2727·2=5427·3=8127·4=108
Бинго! Частное найдено методом подбора:
108÷27=4.
Отметим, что в случаях, когда b·10>a частное также удобно находить методом последовательного вычитания.
Представление делимого в виде суммы
Еще один способ, который может помочь найти частное – это представить делимое в виде суммы нескольких натуральных чисел, каждое из которых легко делится на делитель. После этого нам пригодится свойство деления суммы натуральных чисел на число. Вместе с примером рассмотрим алгоритм и ответим на вопрос: в виде каких слагаемых представлять делимое?
Пусть делимое равно 8551, а делитель равен 17.
- Вычислим, на сколько в записи делимого больше знаков, чем в записи делителя. В нашем случае делитель содержит два знака, а делимое – четыре. Значит в записи делимого на два знака больше. Запоминаем число 2.
- Справа в делителе дописываем два нуля. Почему два? В предыдущем пункте мы как раз и определили это число. Однако, если записанное в результате число окажется больше делителя, из числа, полученного в предыдущем пункте, нужно вычесть 1. В нашем примере, дописав нули к делителю, мы получили число 1700<8551. Таким образом, отнимать единицу из двойки, полученной в первом пункте, не нужно. В памяти так же оставляем число 2.
- К числу 1 справа приписываем нули в количестве, определенном числом из предыдущего пункта. Тем самым мы получаем рабочую единицу разряда, с которым будем оперировать далее. В нашем случае, к единице приписываются два нуля. Рабочий разряд – сотни.
- Проводим последовательное умножения делителя на 1, 2, 3 и т.д. единицы рабочего разряда до того момента, пока не получим число, большее, чем делимое. 17·100=1700; 17·200=3400; 17·300=5100; 17·400=6400; 17·500=8500; 17·600=10200Нас интересует предпоследний результат, так как следующий после него результат произведения больше делимого. Число 8500, которое получено на предпоследнем шаге при умножении, и является первым слагаемым. Запоминаем равенство, которое мы будем использовать далее: 8500=17·500.
- Вычисляем разность между делимым и найденным слагаемым. Если она не равна нулю, возвращаемся к первому пункту и начинаем поиск второго слагаемого, используя вместо делимого уже полученную разность. Повторяем пункты до тех пор, пока в результате не получим нуль. В нашем примере разность равна 8551-8500=51. 51≠0, поэтому, переходим к пункту 1.
Повторяем алгоритм:
- Сравниваем количество знаков в новом делимом 51 и делителе 17. В обоих записях по две цифры, разность количества знаков равно нулю. Запоминаем число 0.
- Так как мы запомнили число 0, в записи делителя не нужно дописывать дополнительных нулей.
- К единице также не будем добавлять нулей. Опять же, потому что в первом пункте мы запоминали число 0. Таким образом, нашим рабочим разрядом являются единицы
- Последовательно умножаем 17 на 1, 2, 3,.. и т.д. Получаем: 17·1=17; 17·2=34; 17·3=51.
- Очевидно, на третьем шаге мы получили число, равное делителю. Это и есть второе слагаемое. Так как 51-51=0, на этом этапе останавливаем поиск слагаемых – он завершен.
Теперь осталось найти частное. Делимое 8551 мы представили в виде суммы 8500+51. Запишем:
8500+51÷17=8500÷17+51÷17.
Результаты делений в скобках известны нам из проведенных ранее действий.
8500+51÷17=8500÷17+51÷17=500+3=503.
Результат деления: 8551÷17=503.
Рассмотрим еще несколько примеров, уже не комментируя каждое действие столь детально.
Найдем частное: 64÷2.
1. В записи делимого на один знак больше, чем в записи делителя. Запоминаем цифру 1.
2. Справа у делителя приписываем один нуль.
3. К числу 1 приписываем один нуль и получаем единицу рабочего разряда – 10. Рабочий разряд, таким образом – десятки.
4. Начинаем последовательное умножение делителя на единицы рабочего разряда. 2·10=20; 2·20=40; 2·30=60; 2·40=80; 80>64.
Первое найденное слагаемое – число 60.
Равенство 60÷2=30 ещё пригодится нам в будущем.
5. Ищем второе слагаемое. Для этого вычисляем разность 64-60=4. Число 4 делится на 2 без остатка, очевидно, это и есть второе слагаемое.
Теперь находим частное:
64÷2=60+4÷2=60÷2+4÷2=30+2=32.
Решим: 1178÷31=?
1. Видим, что в записи делимого на два знака больше, чем в делителе. Запоминаем число 2.
2. К делителю справа добавляем два нуля. Получаем число 3100.
3100>1178, поэтому запомненное число 2 из первого пункта нужно уменьшить на единицу.
2-1=1.
3. К единице справа добавляем один нуль и получаем рабочий разряд – десятки.
4. Умножаем 31 на 10, 20, 30, .. и т.д.
31·10=310; 31·20=620; 31·30=930; 31·40=1240
1240>1178, следовательно, первым слагаемым является число 930.
5. Вычисляем разность 1178-930=248. С числом 248 на месте делимого начинаем искать второе слагаемое.
1. В записи числа 248 на один знак больше, чем в числе 31. Запоминаем цифру 1.
2. К 31 прибавляем справа один нуль. Так как 310>248, уменьшаем полученную в предыдущем пункте единицу, и в итоге имеем число 0.
3. Так как мы запомнили число 0, то к единице не нужно приписывать дополнительных нулей, и разряд единиц – рабочий разряд.
4. Последовательно умножаем 31 на 1, 2, 3, .. и т.д., сравнивая результат c делимым.
31·1=31; 31·2=62; 31·3=93; 31·4=124; 31·5=155; 31·6=186; 31·7=217; 31·8=248
Таким образом, именно число 248 и является вторым слагаемым, которое делится на 31.
5. Разность 248-248 равна нулю. Заканчиваем поиск слагаемых, запоминаем соотношение 248÷31=8 и находим частное.
1178÷31=930+248÷31=930÷31+248÷31=30+8=38.
Постепенно увеличиваем сложность примеров.
Разделим 13984 на 32.
В данном случае описанный выше алгоритм нужно будет применить три раза. Не будем приводить все выкладки, просто укажем, в виде каких слагаемых будет представлен делитель. Вы можете проверить себя, и провести вычисления самостоятельно.
Первое слагаемое равно 12800.
12800÷32=400.
Второе слагаемое равно 960.
960÷32=30.
Третье слагаемое равно 224.
224÷32=7.
Результат:
13984÷32=12800+960+224÷32=12800÷32+960÷32+224÷32=400+30+7=437.
Казалось бы, мы рассмотрели практически все возможные способы деления натуральных чисел. На этом, тему можно считать закрытой. Однако, есть способ, который в ряде случаев позволяет провести деление быстрее и рациональнее.
Рассмотрим его напоследок.
Представление делимого в виде разности натуральных чисел
Иногда делимое проще и удобнее представлять в виде разности, а не суммы. Это может значительно ускорить и облегчить процесс деления. Как именно? Покажем на примере.
Разделим 594 на 6.
Если воспользоваться алгоритмом из предыдущего пункта, мы получим в результате:
594÷6=540+54÷6=540÷6+54÷6=90+9=99.
Однако, если число 594 представить в виде разности 600-6, все становится гораздо очевиднее. Оба числа 600 и 6) делятся на 6. По свойству деления разности натуральных чисел, мы получаем:
594÷6=600-6÷6=600÷6-6÷6=100-1=99
Результат тот же, но действия объективно легче и проще.
Решим еще один пример тем же методом. Отметим, что важно уметь правильно заметить, какую манипуляцию сделать с числами, чтобы провести деление легко. Скажем даже, что в этом присутствует некоторый элемент искусства.
483÷7=?
Вспоминаем таблицу умножение и понимаем: число 483 удобно представить в виде 483=490-7.
490÷7=707÷7=1
Проводим деление:
483÷7=(490-7)÷7=490÷7-7÷7=70-1=69.
Проверка результата деления
Проверка никогда не бывает лишней, особенно, если мы делили большие числа. Как проверять, правильно ли выполнено деление натуральных чисел? При помощи умножения!
Чтобы проверить правильно ли выполнено деление, нужно частное умножить на делитель. В результате должно получится делимое.
Если выходит иначе, можно сделать вывод о том, что где-то закралась ошибка.
Смысл этого действия очень прост. Например, у нас было a предметов, и эти a предметов мы разложили на b кучек. В каждой кучке оказалось по с предметов. Математически это выглядит так:
a÷b=c.
Теперь объединим обратно все b кучек по с предметов. В результате должно получится та же совокупность предметов a.
b·c=a.
Рассмотрим проведение проверки на двух примерах.
Число 475 разделили на 19. В результате получилось 25. Правильно ли выполнено деление?
Умножим частное 25 на делитель 19 и выясним, верно ли разделили числа.
25·19=475.
Число 475 равно делимому, значит, деление выполнено верно.
Разделите и проверьте результат:
1024÷32=?
Будем представлять делимое в виде суммы слагаемых и осуществлять деление.
1024÷32=960+64÷32=960÷32+64÷32=30+2=32.
Проверим результат:
32·32=1024.
Вывод: деление выполнено верно.
Проверка результата деления чисел делением
Рассмотренный выше способ проверки основан на умножении. Существует также проверка делением. Как ее проводить?
Чтобы проверить верно ли найдено частное, нужно делимое разделить на полученное частное. В результате должен получится делитель.
Если выходит иначе, можно сделать вывод о том, что где-то закралась ошибка.
Правило основано на той же связи между делимым, делителем и частным, что и правило из предыдущего пункта.
Рассмотрим примеры.
Верно ли равенство:
104÷13=8.
Разделим делимое на частное:
104÷8=80+24÷8=80÷8+24÷8=10+3=13.
В результате получился делитель, значит, деление выполнено верно.
Вычислим и проверим: 240÷15=?
Представляя делимое в виде суммы, получаем:
240÷15=150+90÷15=150÷15+90÷15=10+6=16.
Проверяем результат:
240÷16=?
240÷16=160+80÷16=160÷16+80÷16=10+5=15.
Деление выполнено верно.
Подобно тому, как вычитание является обратным действием для сложения, так и для умножения существует свое обратное арифметическое действие.
Рассмотрим задачу. В школьной столовой раздали 90 яблок по 3 яблока каждому ученику класса. Сколько учеников учатся в этом классе?
Если бы нам было известно количество учеников в классе и количество яблок, которое получил каждый из них, то общее число яблок мы узнали бы, умножив число учеников на число яблок, доставшееся каждому. То есть, количество учеников – это первый сомножитель, количество яблок – второй сомножитель, а сколько яблок раздали – это произведение.
Таким образом, в нашей задаче даны произведение и множитель (один из сомножителей), а неизвестный второй сомножитель необходимо отыскать. То есть, нам нужно найти число, умножив которое на 3, мы получим 90. Это число 30, потому что (textcolor{red} {30 cdot 3 = 90})
Деление – это арифметическое действие, которое состоит в нахождении одного из
сомножителей при помощи данного произведения и второго сомножителя.
Делимое – это число, которое мы делим на другое. Это то самое произведение,
которое нам дано.
Делитель – это число, на которое мы делим делимое. Это данный нам один из
множителей.
Частное – это результат действия деление, то есть, искомый нами второй
сомножитель.
На записи действие деление обозначается: двоеточием ( (textcolor{red} {:}) ), знаком обелюс ( (textcolor{red} {div}) ), горизонтальной чертой или косой чертой ( (textcolor{red} {/}) ).
Так, решение нашей задачи
можно записать следующими способами:
- (textcolor{red} {90:3=30})
- (textcolor{red} {90div 3=30})
- (textcolor{red} {90/3=30})
- (textcolor{red} {Large frac{90}{3} normalsize =30})
При записи от руки действие деление принято записывать в виде двоеточия, обелюс применяется в печатной литературе, косая черта, которая по-другому называется слеш, – при записи на компьютере, а горизонтальная черта используется при записи деления в виде обыкновенной дроби.
Итак, разделить число a на число b – это значит найти такое число c, которое при умножении его на число b дает в результате числа a.
То есть: (textcolor{red} {adiv b=c}) , если (textcolor{red} {bcdot c=a}) .
И еще одно пояснение для понимания: разделить число a на число b означает разделить число a на b одинаковых частей, каждая из которых равна c. Иными словами, мы одно число a делим на равные части. Количество этих частей равно числу b. А величина каждой из этих частей – это результат действия деления, и эта величина равна c.
Например, нам нужно разделить 15 роз между пятью девочками так, чтобы каждая получила одинаковое количество цветов. Чтобы узнать, какое количество роз получит каждая девочка, нужно общее количество (15) цветов разделить на количество девочек (5), то есть, на 5 одинаковых частей. Нетрудно понять, что каждая из девочек получит 3 розы, потому что (textcolor{red} {5cdot 3=15}) .
Компоненты действия
деление:
Деление с остатком и неполное частное
Но не всегда можно одно число разделить на другое. Вернее сказать, что не всегда можно сделать это полностью. Например, 37 нельзя разделить на 5, потому что нет такого натурального числа, умножив которое на 5, мы получили бы 37. В этом случае говорят, что 37 не делится нацело на 5.
К примеру, если мы захотим раздать все 37 яблок поровну между пятью детьми, то у нас это сделать не получится. Мы сможем раздать (использовать из всего количества яблок) только по 7 яблок каждому ( (textcolor{red} {7cdot 5=35}) ), и у нас останется 2 яблока ( (textcolor{red} {37-35=2}) ).
В таком случае действие деление также состоит из делимого (в нашем случае 37) и делителя (5). Полученное число 7 называется неполное частное, потому что не все делимое число мы смогли разделить на необходимое число частей. А разница между полным делимым (37) и использованными из него единицами (35), то есть число 2, называется остаток.
Итак, деление с остатком – это нахождение
такого наибольшего целого числа, умножив которое на делитель, мы получим число,
максимально близкое к делимому, но не превосходящее его. Это искомое число
называется неполное частное. Разница
между делимым и неполным частным называется остаток.
Остаток всегда меньше делителя!
Отсюда следует общий вид действия деления натуральных чисел для случаев деления без остатка и с остатком.
Разделить целое число a (делимое) на целое число b (делитель) означает найти такие числа c и d, при которых справедливы следующие соотношения:
(textcolor{red} {a=bcdot c+d}) ;
(textcolor{red} {d<b}) .
Если (textcolor{red} {d=0}) , тогда говорят, что a делится на b без остатка.
Компоненты действия
деление с остатком:
Задачи, которые решаются при помощи
действия деления
В курсе математики
средней школы наиболее часто используется деление при решении таких задач,
когда нужно:
- Узнать, во сколько раз одно число меньше и больше другого? Этот вопрос может звучать по-другому: сколько раз меньшее число содержится (помещается) в большем? Или: сколько раз поместится в большем числе меньшее?
Например: сколько пятиграммовых стиков сахара находится в килограммовой упаковке? (1000 г : 5 г = 200 шт.). - Число разделить на заданное количество равных частей.
Например: сколько получится грамм сахара в каждом пакете, если пересыпать килограмм сахара в 5 одинаковых пакетов поровну? (1000 г : 5 шт. = 200 г). - Уменьшить число в заданное количество раз.
Например: для приготовления блюда на 5 человек использовали 1 кг сахара, а сколько сахара потребуется для приготовления этого же блюда для одного человека? (1000 г : 5 чел. = 200 г).
Связь деления с умножением, сложением и
вычитанием
Когда мы выполняем находим
произведение двух чисел, эти числа нам известны, а от нас требуется найти
результат действия умножение. При делении (без остатка) нам известно
произведение двух чисел, а найти нужно такое число, которое при умножении на
известное данное число дает это самое произведение.
Следовательно, действие
деление является обратным действию умножения.
Справедливо также и
обратное, что действие умножение обратно действию деления. Таким образом:
Умножение и деление – это
взаимно обратные действия.
Связь деления с
умножением, а также со сложением и вычитанием прекрасно видна, если
рассмотреть, как с помощью этих действий можно выполнить действие деление.
Рассмотрим их на примере: 345 разделить на 69.
Деление двух чисел при помощи сложения
Чтобы узнать при помощи сложения, сколько раз число 69 содержится в 345, нужно складывать последовательно 69 до тех пор, пока не получим нужного нам числа:
(textcolor{red} {69+69=138}) ; (textcolor{red} {138+69=207}); (textcolor{red} {207+69=276}); (textcolor{red} {276+69=345}).
Число 69 было слагаемым всего 5 раз, значит, (textcolor{red} {345div 69=5}) .
Деление двух чисел при помощи вычитания
Аналогично предыдущему способу, мы можем узнать, сколько раз в числе 345 содержится число 69, вычитанием. Для этого мы будем последовательно вычитать из 345 число 69 до тех пор, пока не получим нуль, и считать количество действий:
(textcolor{red} {345-69=276}); (textcolor{red} {276-69=207}); (textcolor{red} {207-69=138});
(textcolor{red} {138-69=69}); (textcolor{red} {69-69=0}).
То есть, 69 от 345 можно отнять 5 раз, поэтому (textcolor{red} {349div 69=5}).
Деление двух чисел при помощи умножения
При помощи умножения узнать ответ на наш вопрос можно перебирая множитель числа 69 до тех пор, пока не получим заданное нам 345:
(textcolor{red} {69cdot 2=138}); (textcolor{red} {69cdot 3=207}); (textcolor{red} {69cdot 4=276}); (textcolor{red} {69cdot 5=345}).
Искомое частное равно полученному множителю числа 69, то есть, 5.
Но эти три способа очень
громоздки, особенно если частное представляет собой очень большое число. Их
нужно знать только для того, чтобы понимать суть действия деления, суть тех
задач, которые решаются посредством него.
Общий принцип деления в столбик
Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.
Решим пример (textcolor{red} {295383div 34}).
Прежде всего, нужно узнать количество цифр в частном и первое неполное делимое; как их находить, я подробно расписал в этой статье. В нашем случае первое неполное делимое равно 295 тысяч, а в частном будет 4 цифры.
Далее записываем известные
компоненты деления следующим образом:
и начинаем вычисление:
1. Берем первое неполное делимое
и пытаемся его разделить на делитель.
Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.
Записываем в частное первую найденную цифру
разряда тысяч, а под неполным делимым пишем результат произведения неполного
частного и делителя. И сразу же находим остаток от этого действия, т.е.
вычитаем из неполного частного результат этого произведения.
В результате умножения первой найденной цифры частного на делитель у нас получилось (textcolor{red} {8cdot 37=272}). Записываем его под 295 и находим разницу: (textcolor{red} {295-272=23}). Значит, 23 тысячи у нас остаются неразделенными.
В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.
2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.
Находим результат деления второго неполного делимого на делитель. 233 сотни разделить на 34 будет 6 сотен. Значит, в разряде сотен частного будет цифра 6. Умножаем ее на делитель 34, получаем 204 и еще 29 сотен неразделенных.
3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.
При делении второго неполного делимого 298 десятков на делитель 34 получается 8 десятков, и еще 26 десятков неразделенных (как и в предыдущих действиях, я умножил 8 на 34 и результат отнял от 298). Поэтому, в частном, в разряде десятков записываем цифру 8.
4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.
Разделив 263 единицы на 34, получаем 7 полных единиц и 25 неразделенных. Записав в частном последнюю цифру разряда единиц, получаем окончательный ответ действия (textcolor{red} {295383div 34=8687}) и 25 в остатке.
Рассмотрим еще один пример. (textcolor{red} {25326div 63}).
Первое неполное делимое будет 253 сотни, количество цифр в частном – 3.
Делим 253 сотни на 63, получается 4 полных сотни и неразделенная 1 сотня в остатке.
1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.
Но 12 не делится нацело на 63 части, то есть, нет ни одного целого десятка в каждой части. Значит, мы в частном в разряде десятков должны записать 0, поскольку все 12 десятков оказались неразделенными. А к этим 12 десяткам (т.е. 120 сотням) добавить (снести) 6 единиц делимого.
Итак, запомните, что
каждое неполное делимое образует в частном одну цифру соответствующего разряда
и что даже если неполное делимое меньше делителя, то в частном все равно нужно
записать нулевой результат этого действия.
126 единиц делим на 63, получается 2 единицы без остатка. Теперь мы можем записать окончательный ответ деления (textcolor{red} {25326div 63=402}).
Итак, в общем виде алгоритм деления в столбик выглядит так:
1. Находим первое неполное делимое и количество цифр в частном.
2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.
3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.
4. Ставим между ними знак минус и выполняем действие.
5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.
6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.
7. Если неполное делимое невозможно разделить на делитель, то в частном ставится 0 и к этому неполному делимому сносится следующая цифра.
Деление на числа, заканчивающиеся нулями
Как и в случае с
умножением, деление чисел облегчается, если делитель заканчивается одним или
несколькими нулями. Рассмотрим два возможных случая:
- частный – когда делитель является единицей с нулями
- общий – когда делитель любое число, оканчивающееся нулями.
Рассмотрим первый случай.
Деление на единицу с любым количеством
нулей
Единица с любым количеством нулей – это не что иное как единица соответствующего разряда. Например, 10 – это 1 единица разряда десятков, 1000 – это одна единица разряда тысяч, 10000000 – 1 единица разряда десятков миллионов и т.д.
Следовательно, разделить число, к примеру, на 10, 1000, 10000000 и т.д. – это значит определить, сколько в нем содержится десятков, тысяч, десятков миллионов. А как узнать, сколько в каком-либо числе содержится единиц любого разряда я уже рассказывал в уроке разряды и классы. Для завершения действия деления нужно лишь записать в остаток число, которое получается из отбрасываемых нами цифр.
Например:
(textcolor{red} {75427916div 10=7542791}) (остаток 6);
(textcolor{red} {75427916div 1000=75427}) (остаток 916);
(textcolor{red} {75427916div 10000000=7}) (остаток 5427916).
Запишите:
Чтобы разделить какое-нибудь число на единицу с любым количеством нулей, нужно отсчитать в делимом справа столько цифр, сколько нулей содержится в делителе; тогда все цифры, находящиеся слева от разделения, составят частное, а те, что справа – будут остатком.
Деление на число, оканчивающееся нулями
Рассмотрим на примере (textcolor{red} {284556div 2800}).
Делитель здесь не что иное как 28 сотен. Логично предположить, что эти 28 сотен могут хотя бы один раз содержаться только в сотнях делимого. Значит, нам нужно определить, сколько в делимом всего единиц разряда сотен, и разделить их на 28 единиц разряда сотен делимого. А отброшенные цифры десятков и простых единиц добавятся к остатку.
В числе 284556 всего 2845 сотен да еще 56 единиц. Разделим 2845 сотен на 28 сотен, получим частное 101 и 17 сотен неразделенными. Прибавив к неразделенным 17 сотням 56 единиц из делимого, получим 1756. В этом числе делитель 2800 не помещается ни один раз, значит, 1756 – это остаток: (textcolor{red} {284556div 2800=101}) (остаток 1756).
Запишите:
Чтобы разделить какое-нибудь число на число, заканчивающееся нулями, нужно отбросить мысленно нули в делителе, в делимом тоже отбросить мысленно такое же количество цифр, как и нулей в делителе. Получившееся число в делимом разделить на получившееся число в делителе, а к остатку прибавить (снести) те цифры делимого, которые отбросили ранее.
Проверка деления
Так как делимое – это
делитель, умноженный на частное и плюс остаток, что следует из определения
деления, то результат выполнения деления можно проверить умножением.
Например:
После того, как мы умножили частное 241 на делитель 33, а к полученному произведению прибавили остаток 9, мы получили число 7962, что равно делимому. Значит, можно с большой уверенностью сказать, что действие деление выполнено верно.
Если в результате
действия деления не получилось остатка, то деление можно проверить и делением.
Действительно, если делимое – это произведение делителя и частного, то разделив
делимое на частное (один из сомножителей), мы должны получить второй
сомножитель, то есть, делитель.
Например:
Свойства деления
Свойства деления я
представлю двумя группами:
- действия с
единицей и нулем; - распределительные
свойства деления.
Давайте рассмотрим каждую
группу подробнее.
Действия деления с единицей и нулем
При делении числа на единицу получается то же самое число.
Действительно, разделить
число на единицу означает узнать, сколько единиц содержится в данном числе. А
количество единиц в числе – это не что иное, как само это число.
И ли вот, например, если 10 яблок нужно раздать одному человеку (10 поделить на 1), то ему все эти 10 яблок и достанутся, правда?
При деление одинаковых чисел (числа на равное число) в результате будет 1 (единица).
В самом деле, если все единицы какого-то числа разделить на количество частей, равное количеству единиц этого числа, то в каждая часть получит по 1 единице.
Например, если 20 яблок раздать 20 школьникам, то каждому достанется по 1 яблоку.
При делении нуля на любое число, отличное от нуля, в результате будет нуль.
Разделить нуль на число
означает найти такое число, умножив которое на данный делитель, мы получим в
результате нуль. А такое число только одно – это нуль.
На нуль делить нельзя, то есть, нуль не может выступать в роли делителя.
При делении каких угодно
чисел делителем может быть любое число, кроме нуля.
Рассмотрим два случая:
когда нулём является только делитель, и когда делимое и делитель оба нули.
Пусть делимое равно какому угодно числу, отличному от нуля, например, 12. Разделить число 12 на нуль – это значит найти такое число, которое при умножении на 0 дало бы в результате число 12. Но как известно, если любое число умножить на 0, то и получим тоже нуль. Следовательно, такого числа, какое нам нужно, не существует.
Допустим, что делимое и делитель оба являются нулями. В этом случае нам нужно отыскать такое число, которое при умножении на 0 дало бы в результате 0. А поскольку какое бы мы ни взяли число, при умножении его на 0, получим тоже нуль, то частным может выступать любое число из бесконечного множества чисел, следовательно, какого-то определенного результата от такого деления быть не может.
Распределительные свойства деления
Чтобы найти частное от деления суммы на число, нужно поделить каждое слагаемое на это число, и найти сумму полученных частных.
(textcolor{red} {(a+b+c)div d=adiv d+bdiv d+cdiv d}).
При этом подразумевается, что все действия деления получаются без остатка.
Например, чтобы найти результат деления суммы (textcolor{red} {24+16+48}) на 8, то есть, определить, какое количество восьмерок находится в сумме этих чисел, мы узнаем, сколько раз восьмерка содержится отдельно в каждом из чисел, а потом складываем полученные результаты.
Так, в 24 находится 3 восьмерки, в 16 – две, в 48 – шесть, итого (textcolor{red} {3+2+6=11}). А если мы сперва найдем значение всей суммы (textcolor{red} {24+16+48=88}), и поделим ее на 8, то ответ будет также (textcolor{red} {88div 8=11}).
Чтобы найти частное от деления разности на число, нужно поделить на это число отдельно сперва уменьшаемое, а потом вычитаемое, после чего найти разность первого частного и второго.
(textcolor{red} {(a-b)div c=adiv c-bdiv c})
При этом также предполагается, что при делениях уменьшаемого и вычитаемого на число не получается остатков.
Например: [textcolor{red} {(36-24)div 6=36div 6-24div 6=6-4=2}] Число 36 состоит из 6 шестерок, а 24 – из 4 шестерок, а забрав у 6 шестерок 4 шестерки, получим 2 шестерки. Такой же итог будет и если мы сперва у 36 отнимем 24 единицы (останется 12), а потом найдем, сколько в этой разнице содержится шестерок: (textcolor{red} {12div 6=2}).
Чтобы найти частное от деления произведения на число, нужно поделить на него только один из сомножителей, а результат умножить на неизмененные остальные.
(textcolor{red} {(acdot bcdot c)div d=adiv dcdot bcdot c=bdiv dcdot acdot c=cdiv dcdot acdot b}).
В самом деле, разделить, к примеру, (textcolor{red} {20cdot 25cdot 35}) на 5 означает уменьшить произведение в 5 раз. А так как если уменьшить один из сомножителей в определенное количество раз, то и произведение уменьшится в это же количество раз, тогда нам достаточно разделить любое из чисел 20, 25 или 35 на 5, чтобы получить ответ:
(textcolor{red} {(20cdot 25cdot 35)div 5=20div 5cdot 25cdot 35=3500}).
Чтобы найти частное от деления числа на произведение, нужно это число поделить на первый сомножитель, результат деления поделить на второй сомножитель, полученное частное – на третий и так далее.
(textcolor{red} {adiv (bcdot ccdot dcdot e)=adiv bdiv cdiv e}).
При этом предполагается, что при всех этих делениях не получается остатков.
Допустим, нужно поделить 30 на произведение (textcolor{red} {2cdot 3}). Мы знаем, что деление – это разложение числа на равные части. Значит, разделив 30 единиц на 2, мы находим, что в каждой из 2 равных частей содержится по 15 единиц. После этого мы эти 15 единиц делим на 3 равные части, и узнаем, что каждая из них содержит по 5 единиц.
На рисунке наглядно видно, что в итоге после применения этого правила, число 30 получилось разделенным на 6 равных частей.
Изменение частного при изменении
делимого и делителя
При рассмотрении
изменений частного в результате изменений делимого и делителя предполагается,
что действие деление происходит без остатка. В противном случае изменения могут
быть не такими, о которых идет речь ниже.
При увеличении делимого в определенное количество раз, частное увеличится в это же количество раз, а при уменьшении – уменьшится.
Если мы в примере (textcolor{red} {24div 4=6}) делимое увеличим, к примеру, в 3 раза, то мы можем переписать это выражение в виде (textcolor{red} {(24+24+24)div 4}). Используя свойство деления суммы на число, мы увидим, что теперь нам нужно сложить три слагаемых, каждое из которых равно начальному выражению: (textcolor{red} {24div 4+24div 4+24div4}). Отсюда очевидно, что результат будет больше начального в 3 раза.
Если мы в этом же примере (textcolor{red} {24div 6}) уменьшим делимое в 3 раза, то есть, разделим его на три равные части, то очевидно, что результат деления одной части на 6 будет в 3 раза меньше, чем результат деления трех таких же частей. Посмотрите сами. Начальное выражение (textcolor{red} {24div 6}) можно записать в виде: (textcolor{red} {(8+8+8)div 6=8div 6+8div 6+8div 6}), а уменьшенное в 3 раза делимое даст нам только одно из трех таких слагаемых: (textcolor{red} {8div 6}).
При увеличении делителя в определенное количество раз, частное уменьшится в это же количество раз, а при уменьшении – увеличится.
Действительно, изменение
делителя означает, что делимое необходимо разделить на большее или меньшее
количество равных частей. Соответственно, если нужно разделить на большее число
частей, то каждая часть будет меньше, чем изначально, а если делить на меньшее
число частей, то каждая часть будет крупнее.
В случае одновременного изменения делимого и делителя, частное может вести себя по-разному, или же вообще оставаться без изменений. Если нужно узнать, станет оно больше или меньше, нужно сперва посмотреть, как частное изменится после изменения делимого, а потом – как изменится после изменения делителя.
При увеличении или уменьшении делимого и делителя в одинаковое количество раз, частное не меняется.
Попробуйте самостоятельно
доказать справедливость этого утверждения. Пишите в комментариях, получилось
это, или нет.