Частное чисел в математике: что это такое? В школе учат действие деление, где есть делимое, делитель и частное. Что означают эти названия? Давайте разбираться!
Содержание статьи:
Частное чисел в математике: что это такое
Однажды клоун Бим решил выучить математическое действие деление и нашел для себя в интернете вот такое определение:
Определение. Говорят, что a делится на b, если существует натуральное число с, при умножении которого на b получается а: a=b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
Как мне это понять? — задумался Бим. — Но скоро представление, пойду ребят к нам приглашать.
Как найти частное чисел
Пришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
— Мне надо подарить вам шарики, какое математическое действие я буду применять?
— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.
Клоун хитро прищурился:
— А как называются члены деления?
— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!
— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!
Коля продолжил:
— У каждого из нас будет часть шариков, и результат от деления называется частным.
— Какое же здесь будет частное? — спрашивает Бим.
— Два! — не сговариваясь, хором ответили ребята.
— Правильно, каждому из вас достанется по два шарика, это и есть частное.
Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:
6 (делимое) : 3 (делитель) = 2 (частное).
Запишем цифрами:
6:3=2
В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.
Итак, частное — это число, которое получается в результате деления делимого на делитель.
Полное и неполное частное
А потом было замечательное представление.
В антракте дети пошли в буфет. На подносе лежало семь пирожных. Как же их разделить поровну на трёх ребят?
Друзья задумались и взяли по 2 пирожных, а последним, которое было в остатке, угостили клоуна Бима.
— Теперь я понял! — воскликнул Бим. — Если нельзя всё число пирожных поделить между ребятами без остатка, то такой результат от деления называется неполным частным. А то, что осталось после деления, так и называется остатком и записывается это вот так:
7:3=2(1)
Здесь 7 (делимое) по-прежнему стоит в начале выражения, 3 (делитель) — в середине, 2 (неполное частное) — справа. Но после неполного частного ещё пишем в скобках остаток (1).
- Полное частное — результат деления, когда делимое делится нацело на делитель (остаток равен 0, его и писать незачем).
- Неполное частное — это результат деления с остатком (когда делимое не делится нацело на делитель).
Как найти делитель
Когда дети ушли занимать свои места, буфетчица подошла к Биму и спросила:
— Я забыла, сколько было ребят. Помню только, что каждый из них съел по два пирожных, а всего им досталось 6 штук. Сколько же посетителей было у меня?
Тут в буфет заглянул дрессировщик Бом и быстренько решил эту задачку. Он разделил 6 (делимое) на 2 (частное) и получил 3 (делитель).
— Всего было трое ребят, — ответил Бом.
— Верно! — вспомнил Бим.
Для того чтобы найти делитель, надо делимое разделить на частное.
6:2=3
Здесь 6 – делимое, 2 – частное, а 3 – делитель.
Как найти делимое
— А сколько ты подарил всего шариков трём ребятам? — спросил Бом.
— Забыл, — ответил Бим. — Помню только, что детей было трое, и каждому досталось по два шарика.
Бом и говорит:
— Тогда надо 3 (делитель) умножить на 2 (частное), получится 6.
Для того чтобы найти делимое, надо делитель умножить на частное.
Запишем это цифрами:
3*2=6.
3 — наш делитель, 2 — частное, а 6 — делимое.
Проверка деления умножением
— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?
— Да, — ответил Бом.
Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.
Заключение
А клоун для себя сделал плакаты и теперь каждый день может сразу вспомнить, что:
Определение. Говорят, что а делится на b, если существует число с, при умножении которого на b получается а: a= b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
- Деление — действие, обратное умножению;
- умножение проверяет правильность математического действия — деления;
- для того чтобы найти делимое, надо делитель умножить на частное;
- для того чтобы найти делитель, надо делимое разделить на частное.
Итак, теперь мы знаем, что же такое частное в математике. Оказывается, оно бывает полным и неполным! Кроме того, нетрудно будет найти делитель, делимое и проверить деление умножением. И если учитель спросит в школе: «Частное чисел в математике: что это такое?» — сможем ответить сразу. И пусть любой пример или задача на эту тему будет вам по плечу!
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Что такое частное чисел
Определение
Частное — это результат процесса деления. Делением называется такая операция, которая обратна умножению, то есть показывает, сколько одинаковых чисел способно содержаться в другом.
Буквенный вид этого действия выглядит следующим образом: a: b = c, где:
- a – это делимое (число, которое делят)
- b – это делитель (число, которым делят)
- с – это частное (результирующее число деления)
- : — арифметический знак, с помощью которого обозначается деление
Важно! Число 0 никогда не может быть делителем
Нахождение значения частного чисел
Пример:
12 : 3 = 4 (в числе 12 4 раза содержится по 3)
15 : 5 = 3 (в числе 15 5 раз содержится по 5)
Нужно знать, что правильность определения частного от деления числа всегда можно проверить путем перемножения его на делитель, либо делимое поделить на частное и получить делитель.
Например:
20 : 4 = 5
Перемножим частное двух чисел на делитель и получим делимое:
4 * 5 = 20
Разделим делимое на частное и получим делитель:
20 : 5 = 4
Таким образом, мы доказали правильность определения частного.
Что такое частное значение чисел с остатком?
Иногда при делении от делимого остается остаток, который меньше делителя, но более нуля. Приведем выражение частного чисел:
8 : 3 = 2 (ост. 2)
Это значит, что делимое 8 поделилось 2 раза по 3 и остался остаток 2, который меньше трех, но больше нуля.
Таким образом: 0 < ост. <делитель
Основные понятия о частном суммы и разности чисел
Что такое частное суммы чисел?
Определение
Частное от деления суммы чисел – это когда делимое либо делитель выступает в роли суммы двух слагаемых.
Общий вид: (a+b):(c+d), где сумма чисел (a+b) – делимое, а сумма (c+d) – делитель
Пример: (12+3):(3+2)=3
Важно, в подобных примерах последовательность решения определяется следующим образом: сначала решаются выражения в скобочках, потом выражения со знаками деления или умножения, после – вычитание или сложение.
Нет времени решать самому?
Наши эксперты помогут!
Поговорим о частном разности чисел
Аналогично, как и с частностью суммы, только в роли делимого или делителя выступает значение разности: (a-b):(c-d), где разность чисел (a-b) – делимое, а разность (c-d) – делитель
Пример нахождения разности чисел: (12-3):(5-2)=3, где
3 и 2 — это вычитаемое частное чисел
Также в математике находят сумму частного произведения чисел:
(12+3)*(1+2)=45
И произведение частного чисел:
(12*5):(5*2)=6
Основные правила при делении
- При делении одного числа на единицу – получаем в ответ делимое: 6 : 1 = 6
- При делении одного числа на само себя – получаем в ответ 1: 7 : 7 = 1
- Если произведение поделить на один из множителей, то получится другой множитель:
6*3=18, 18:6=3, 18:3=6.
При делении на десятки (10, 100…) у частной, запятой с левой стороны отделяется столько цифр, сколько нулей в делителе: 34:10=3,4, 34:100=0,34, 34:1000=0,034.
Определение частного чисел
Определение
Частное чисел – это результат деления одного числа на другое. Таким образом, частное чисел
$a$ и
$b$ будет число
$c$, которое равно
$c = a : b$ . При этом число
$a$ будет делимым, а число
$b$ – делителем.
Пример
Задание. Найти частное чисел:
1) $39 : 3$ ;
4) $124 : 4$
Ответ. $39 : 3 = 13$
$124 : 4 = 31$
Для нахождения частного больших чисел или
десятичных дробей используют способ
деления в столбик.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти частное чисел:
1) $564 : 12$ ;
2) $0,567 : 0,21$
Решение. Для нахождения частного в первом примере выполним деление в столбик.
Для этого запишем делимое и делитель следующим образом
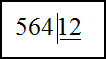
Берем первую цифру слева, она не делится на 12, значит, берем две цифры: 56 и делим их на 12 с остатком.
Возьмем по $4 : 4 cdot 12 = 48$ . Записываем 48 под 56 и находим остаток:
$56 – 48 = 8$ . Восьмерку записываем под чертой и сносим к ней следующее
число из делимого, получим 84. Делим 84 на 12, получаем 7. остаток от деления 0 и цифр в делимом больше нет. Деление окончено.
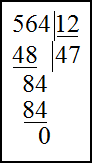
Таким образом, $564 : 12 = 47$
Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число.
Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее
запишем полученные числа в столбик, как и в первом примере:
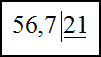
Берем в делимом первые две цифры слева и делим их на делимое с остатком. Получаем $56 : 21$ , можно взять по 2. Двойку записываем в частное.
И так как целая часть делимого закончилась, ставим в частном запятую. Умножаем $2 cdot 21 = 42$ , записываем 42 под 56 и вычитаем:
$56 – 42 = 14$ . Остаток 14 списываем к нему следующую
незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное,
и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.

Таким образом $0,567 : 0,21 = 2,7$
Ответ. $564 : 12 = 47$
$0,567 : 0,21 = 2,7$
Частное рациональных дробей находится по правилу
$$frac{m}{n}: frac{p}{q}=frac{m cdot q}{n cdot p}$$
Пример
Задание. Найти частное рациональных дробей:
1) $frac{2}{3}: frac{1}{3}$ ;
2) $1 frac{1}{14}: 1 frac{3}{7}$
Решение. 1) Воспользуемся правилом вычисления частного рациональных дробей:
$$frac{2}{3}: frac{1}{3}=frac{2 cdot 3}{3 cdot 1}=2$$
Для вычисления частного во втором примере, сначала запишем дроби в виде неправильных дробей. Для этого целую часть
умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:
$$1 frac{1}{14}: 1 frac{3}{7}=frac{1 cdot 14+1}{14}: frac{1 cdot 7+3}{7}=frac{15}{14}: frac{10}{7}=$$
$$=frac{15 cdot 7}{14 cdot 10}=frac{15}{2 cdot 10}=frac{15}{20}=frac{3}{4}$$
Ответ. $frac{2}{3}: frac{1}{3}=2$
$1 frac{1}{14}: 1 frac{3}{7}=frac{3}{4}$
Читать дальше: что такое иррациональное число.
Как находить частное от деления?
Георгий Амиян
Ученик
(160),
закрыт
5 лет назад
Я тут почитал но все равно не понял. Частное от деления это остаток, чтоли. Напишите как это делать и, что такое это частное от деления.
Булатова Римма
Искусственный Интеллект
(126427)
9 лет назад
Частное – это итог деления одного числа на другое. Произвести деление можно столбиком или на калькуляторе.
Частное может быть целым числом, если числа разделятся без остатка, или десятичной дробью конечной, бесконечной или периодической.
Частное чисел
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Частным числа называется результат деления какого-либо числа, называемого делимым, на какое-либо другое число, называемое делителем.
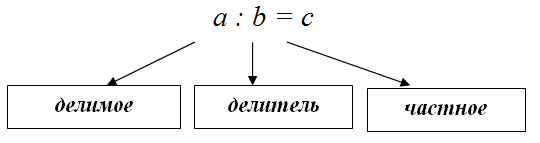
Рисунок 1. Частное, делимое и делитель. Автор24 — интернет-биржа студенческих работ
Частное, может быть целым числом, такие числа записываются без каких-либо знаков после запятой, а также без знаков дроби или дробным. Также различают деление с остатком, в котором поимо частного получается ещё некоторый остаток, который дальше на делитель уже не делится. Обычно при делении с остатком сам остаток записывают отдельно.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Для частного, полученного после деления без остатка, характерно следующее свойство: если частное домножить на делитель, получится делимое.
При выполнении деления двух чисел, не являющихся дробями, можно воспользоваться способом получения значения частного в столбик, ниже приведён пример осуществления такого деления:
Рисунок 2. Частное при делении целого на целое. Автор24 — интернет-биржа студенческих работ
В случае же если необходимо получить частное от деления дробей с запятой, иначе называемых десятичными, сначала можно домножить делитель и делимое на $10$ в $n$-ой степени чтобы избавиться от запятой в делителе, а затем выполнить деление в столбик как для целых или дробных десятичных чисел.
Пример 1
Чтобы найти частное от деления $0,1232$ на $0,25$ сначала можно оба числа умножить на $100$ и затем разделить в столбик $12,32$ на $25$. Получающееся частное равно частному от деления $0,1232$ на $0,25$.
Рисунок 3. Частное от деления. Автор24 — интернет-биржа студенческих работ
Если необходимо найти частное от деления обыкновенной дроби на другую обыкновенную дробь, нужно перевернуть дробь-делитель «вверх ногами» и домножить перевёрнутую дробь на дробь-делимое:
$frac{a}{b}: frac{c}{d}=frac{a}{b} cdot {d}{c}=frac{a cdot d} {b cdot c}$.
Если одна из дробей-участниц деления имеет целую часть, то сначала эту дробь необходимо перевести в неправильную.
Пример 2
Узнайте, какое частное получится от деления $3frac{1}{2}$ на $frac{5}{7}$.
Решение:
$3frac{1}{2}:frac{5}{7}= frac{7}{2} : frac{5}{7}=frac{7}{2} cdot frac{7}{5}=frac{7 cdot 7}{2 cdot 5}=frac{49}{10}=4frac{9}{10}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 17.04.2023




