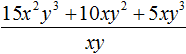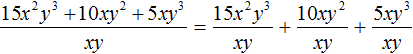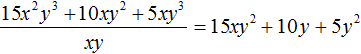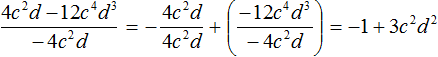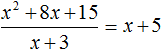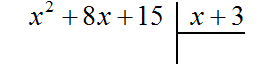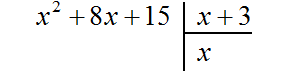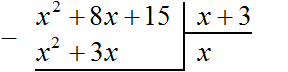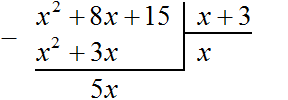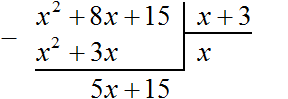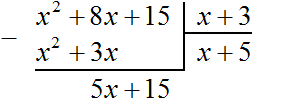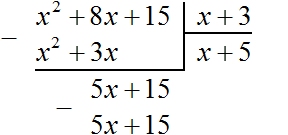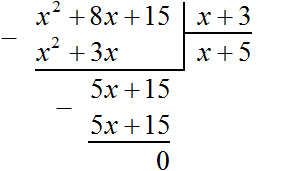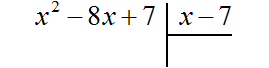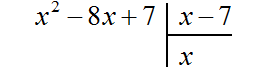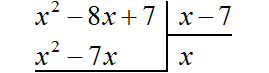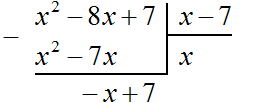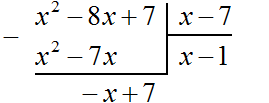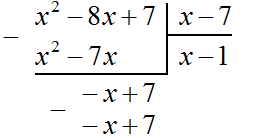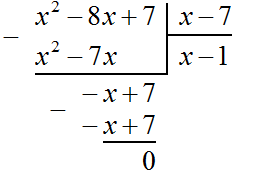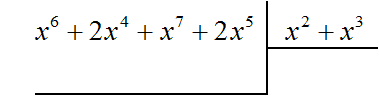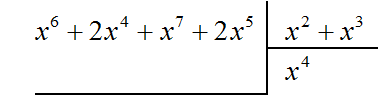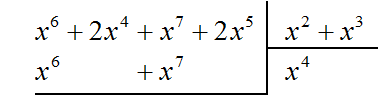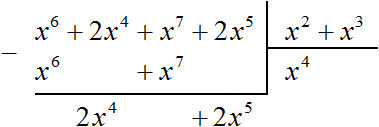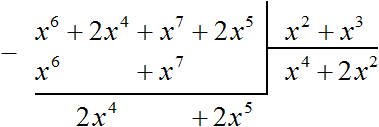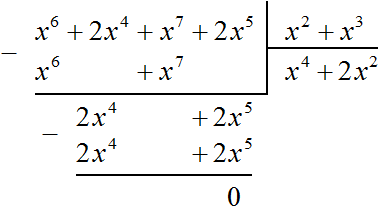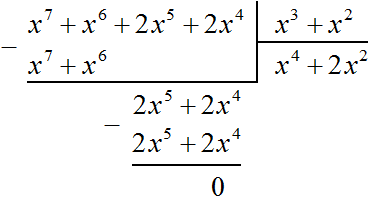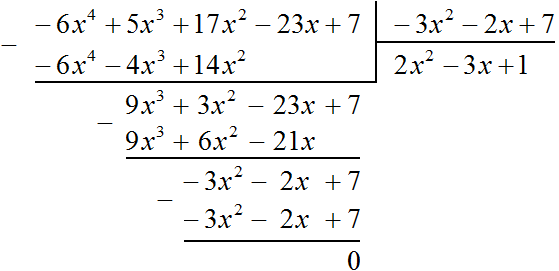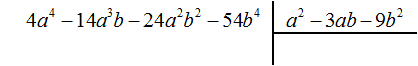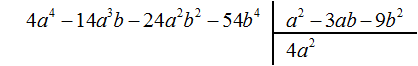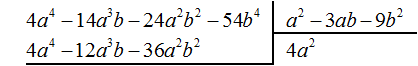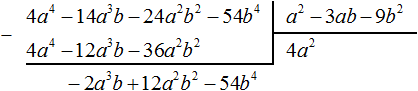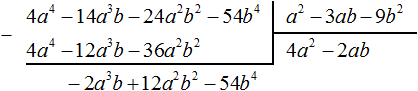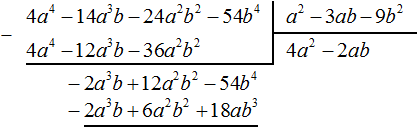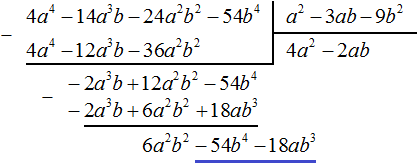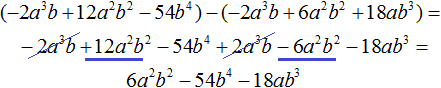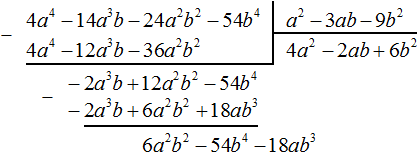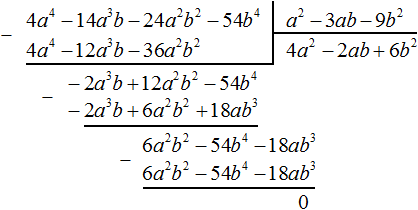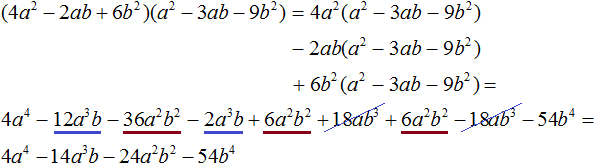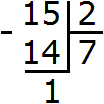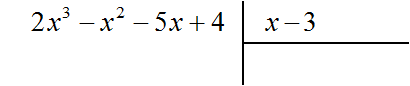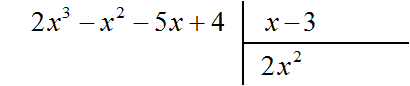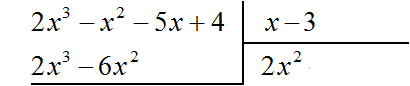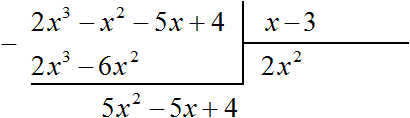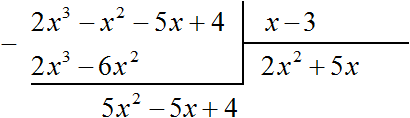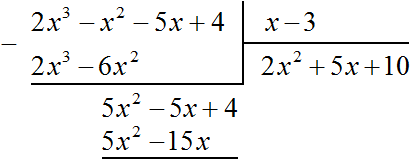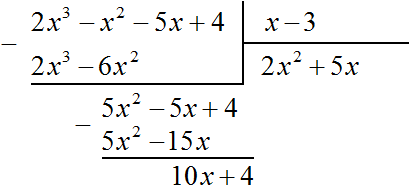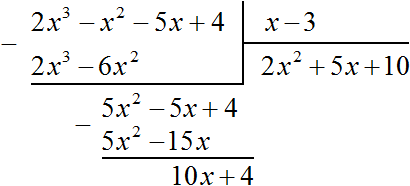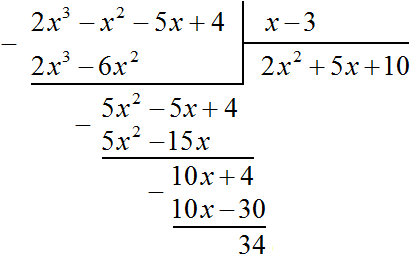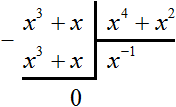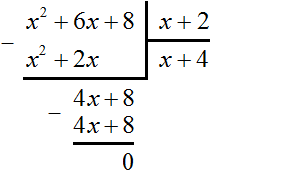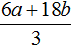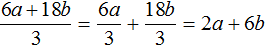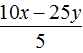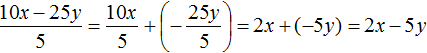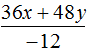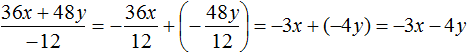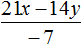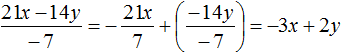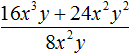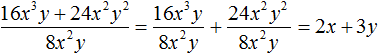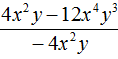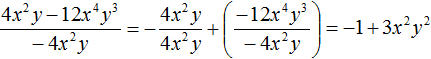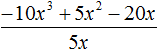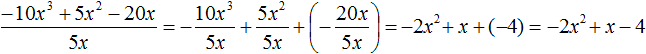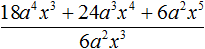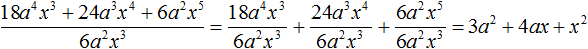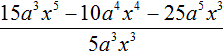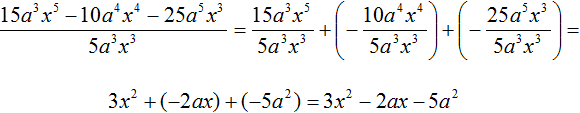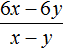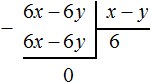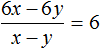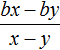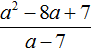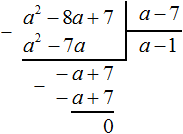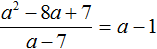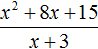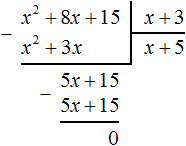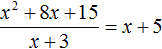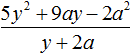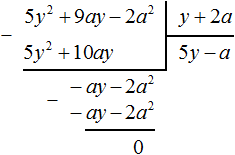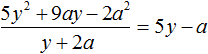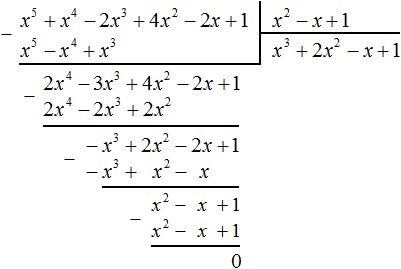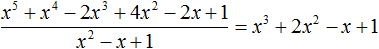Как найти частное от деления многочленов - Сайт, где вы сможете решить свои вопросы

Продолжаем изучать многочлены. В данном уроке мы научимся их делить.

Деление многочлена на одночлен

Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.

Например, разделим многочлен 15x²y³+ 10xy²+ 5xy³ на одночлен xy. Запишем это деление в виде дроби:

Теперь делим каждый член многочлена 15x²y³+ 10xy²+ 5xy³ на одночлен xy. Получающиеся частные будем складывать:

Получили привычное для нас деление одночленов. Выполним это деление:

Таким образом, при делении многочлена 15x²y³+ 10xy²+ 5xy³ на одночлен xy получается многочлен 15xy²+ 10y + 5y².

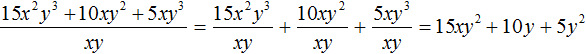
При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.

В нашем примере произведение полученного многочлена 15xy²+ 10y + 5y² и делителя xy должно быть равно многочлену 15x²y³+ 10xy²+ 5xy³, то есть исходному делимому. Проверим так ли это:

(15xy²+ 10y + 5y²)xy = 15x²y³+ 10xy²+ 5xy³

Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.

Например, чтобы сложить дроби , и нужно записать следующее выражение:

Если мы вычислим выражение , то получим дробь , значение которой равно 1,5.

При этом выражение мы можем вернуть в исходное состояние , и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5

Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена ax + bx + cx на многочлен x, образуется три дроби с общим знаменателем x

Вычисление каждой дроби даст в результате многочлен a + b + c

Пример 2. Разделить многочлен 8m³n + 24m²n² на одночлен 8m²n

Пример 3. Разделить многочлен 4c²d − 12c⁴d³ на одночлен −4c²d

Деление одночлена на многочлен

Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.

Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5.

Результатом этого деления должен быть многочлен, перемножение которого с многочленом 5x + 3y + 5 даёт одночлен 2xy. Но не существует многочлена, перемножение которого с многочленом 5x + 3y + 5 давало бы в результате одночлен 2xy, поскольку перемножение многочленов даёт в результате многочлен, а не одночлен.

Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.

Например, найдём значение выражения при x = 2.

Выражение представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования. Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:

Деление многочлена на многочлен

Если первый многочлен умножить на второй многочлен, получается третий многочлен. Например, если умножить многочлен x + 5 на многочлен x + 3, получается многочлен x²+ 8x + 15

(x + 5)(x + 3) = x² + 5x + 3x + 15 = x² + 8x + 15

(x + 5)(x + 3) = x² + 8x + 15

Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.

Тогда согласно этому правилу, деление полученного нами многочлена x²+ 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5.

Деление многочлена на многочлен выполняется уголком. Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.

Выполним уголком деление многочлена x²+ 8x + 15 на многочлен x + 3. Так мы поэтапно увидим, как получается многочлен x + 5.

В данном случае результат нам известен заранее. Это будет многочлен x + 5. Но чаще всего результат бывает неизвестным. Поэтому решение будем комментировать так, будто результат нам неизвестен.

Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.

Сейчас наша задача найти первый член нового многочлена. Как это сделать?

Когда мы изначально перемножали многочлены x + 5 и x + 3, мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:

Если мы обратно разделим первый член третьего многочлена на первый член второго многочлена, то получим первый член первого многочлена. А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.

Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.

Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.

Если первый член делимого (в нашем случае это x²) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:

Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3. На этом этапе нужно суметь умножить одночлен на многочлен. При умножении x на x + 3, получается x²+ 3x. Записываем этот многочлен под делимым x²+ 8x+ 15 так, чтобы подобные члены располагались друг под другом:

Теперь из делимого x²+ 8x + 15 вычитаем x²+ 3x. Подобные члены вычитаем из подобных им членов. Если из x² вычесть x², получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x

Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:

Теперь делим многочлен 5x + 15 на x + 3. Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5x) разделить на первый член делителя (это член x). Если 5x разделить на x, получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)

Теперь умножаем 5 на делитель x + 3. При умножении 5 на x + 3, получается 5x + 15. Записываем этот многочлен под делимым 5x + 15

Теперь из делимого 5x + 15 вычитаем 5x + 15. Если из 5x + 15 вычесть 5x + 15 получится 0.

На этом деление завершено.

После выполнения деления можно выполнить проверку, умножив частное на делитель. В нашем случае, если частное x + 5 умножить на делитель x + 3, должен получаться многочлен x²+ 8x + 15

(x + 5)(x + 3) = x² + 5x + 3x + 15 = x² + 8x + 15

Пример 2. Разделить многочлен x²− 8x + 7 на многочлен x − 7

Записываем уголком данное деление:

Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x. Записываем x под правым углом:

Умножаем x на x − 7, получаем x²− 7x. Записываем этот многочлен под делимым x²− 8x + 7 так, чтобы подобные члены располагались друг под другом:

Вычитаем из x²− 8x + 7 многочлен x²− 7x. При вычитании x² из x² получается 0. Ноль не записываем. А при вычитании −7x из −8x получается −x, поскольку −8x − (−7x) = −8x + 7x = −x. Записываем −x под членами −7x и −8x. Далее сносим следующий член 7

Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:

Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7. Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x) разделить на первый член делителя (это член x). Если −x разделить на x, получится −1. Записываем −1 под правым углом вместе со своим знаком:

Умножаем −1 на x − 7, получаем −x + 7. Записываем этот многочлен под делимым −x + 7

Теперь из −x + 7 вычитаем −x + 7. Если из −x + 7 вычесть −x + 7 получится 0

Деление завершено. Таким образом, частное от деления многочлена x²− 8x + 7 на многочлен x − 7 равно x − 1

Выполним проверку. Умножим частное x − 1 на делитель x − 7. У нас должен получиться многочлен x²− 8x + 7

(x − 1)(x − 7) = x² − x − 7x + 7 = x² − 8x + 7

Пример 3. Разделить многочлен x⁶+ 2x⁴+ x⁷+ 2x⁵ на многочлен x²+ x³

Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x⁴

Умножаем x⁴ на делитель x²+ x³ и полученный результат записываем под делимым. Если x⁴ умножить на x²+ x³ получится x⁶+ x⁷. Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:

Теперь из делимого вычитаем многочлен x⁶+ x⁷. Вычитание x⁶ из x⁶ даст в результате 0. Вычитание x⁷ из x⁷ тоже даст в результате 0. Оставшиеся члены 2x⁴ и 2x⁵ снесём:

Получилось новое делимое 2x⁴+ 2x⁵. Это же делимое можно было получить, выписав отдельно многочлен x⁶+ 2x⁴+ x⁷+ 2x⁵ и вычтя из него многочлен x⁶+ x⁷

Разделим многочлен 2x⁴+ 2x⁵ на делитель x²+ x³. Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x². Записываем этот член в частном:

Умножаем 2x² на делитель x²+ x³ и полученный результат записываем под делимым. Если 2x² умножить на x²+ x³ получится 2x⁴+ 2x⁵. Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:

Вычитание многочлена 2x⁴+ 2x⁵ из многочлена 2x⁴+ 2x⁵ дало в результате 0, поэтому деление успешно завершилось.

В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.

Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.

Решим предыдущий пример, упорядочив члены исходных многочленов в порядке убывания степеней. Если члены многочлена x⁶+ 2x⁴+ x⁷+ 2x⁵ упорядочить в порядке убывания степеней, то получим многочлен x⁷+ x⁶+ 2x⁵+ 2x⁴. А если члены многочлена x²+ x³ упорядочить в порядке убывания степеней, то получим многочлен x³+ x²

Тогда деление уголком многочлена x⁶+ 2x⁴+ x⁷+ 2x⁵ на многочлен x²+ x³ примет следующий вид:

Деление завершено. Таким образом, частное от деления многочлена x⁶+ 2x⁴+ x⁷+ 2x⁵ на многочлен x²+ x³ равно x⁴+ 2x²

Выполним проверку. Умножим частное x⁴+ 2x² на делитель x²+ x³. У нас должен получиться многочлен x⁶+ 2x⁴+ x⁷+ 2x⁵

(x⁴+ 2x²)(x²+ x³) = x⁴(x²+ x³) + 2x²(x²+ x³) = x⁶+ 2x⁴+ x⁷+ 2x⁵

При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.

Перепишем умножение (x⁴+ 2x²)(x²+ x³) упорядочив члены многочленов в порядке убывания степеней.

(x⁴+ 2x²)(x³+ x²) = x⁴(x³+ x²) + 2x²(x³+ x²) = x⁷+ x⁶+ 2x⁵+ 2x⁴

Пример 4. Разделить многочлен 17x²− 6x⁴+ 5x³− 23x + 7 на многочлен 7 − 3x²− 2x

Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:

Значит,

Пример 5. Разделить многочлен 4a⁴− 14a³b − 24a²b²− 54b⁴ на многочлен a²− 3ab − 9b²

Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a². Записываем 4a² в частном:

Умножим 4a² на делитель a²− 3ab − 9b² и полученный результат запишем под делимым:

Вычтем из делимого полученный многочлен 4a⁴− 12a³b − 36a²b²

Теперь делим −2a³b + 12a²b²− 54b⁴ на делитель a²− 3ab − 9b². Разделим первый член делимого на первый член делителя, получим −2ab. Записываем −2ab в частном:

Умножим −2ab на делитель a²− 3ab − 9b² и полученный результат запишем под делимым −2a³b + 12a²b²− 54b⁴

Вычтем из многочлена −2a³b + 12a²b²− 54b⁴ многочлен −2a³b + 12a²b²− 18ab³. При вычитании подобных членов обнаруживаем, что члены −54b⁴ и 18ab³ не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a³b из −2a³b и 6a²b² из 12a²b², а вычитание 18ab³ из −54b⁴ запишем в виде разности −54b⁴− (+18ab³) или −54b⁴− 18ab³

Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:

Вернёмся к нашей задаче. Разделим 6a²b²− 54b⁴− 18ab³ на делитель a²− 3ab − 9b². Делим первый член делимого на первый член делителя, получим 6b². Записываем 6b² в частном:

Умножим 6b² на делитель a²− 3ab − 9b² и полученный результат запишем под делимым 6a²b²− 54b⁴− 18ab³. Сразу вычтем этот полученный результат из делимого 6a²b²− 54b⁴− 18ab³

Деление завершено. Таким образом, частное от деления многочлена 4a⁴− 14a³b − 24a²b²− 54b⁴ на многочлен a²− 3ab − 9b² равно 4a²− 2ab + 6b².

Выполним проверку. Умножим частное 4a²− 2ab + 6b² на делитель a²− 3ab − 9b². У нас должен получиться многочлен 4a⁴− 14a³b − 24a²b²− 54b⁴

Деление многочлена на многочлен с остатком

Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.

Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:

То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:

Рациональное число читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.

Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:

Например, разделим многочлен 2x³− x²− 5x + 4 на многочлен x − 3

Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x². Записываем 2x² в частном:

Умножим 2x² на делитель x − 3 и полученный результат запишем под делимым:

Вычтем из делимого полученный многочлен 2x³− 6x²

Теперь делим 5x²− 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном:

Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x²− 5x + 4

Вычтем из многочлена 5x²− 5x + 4 многочлен 5x²− 15x

Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном:

Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4. Сразу вычтем этот полученный результат из делимого 10x + 4

Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4, является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34.

Поэтому при делении многочлена 2x³− 2x²− 5x + 4 на многочлен x − 3 получается 2x²+ 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:

Когда деление многочленов невозможно

Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.

Например, нельзя разделить многочлен x³+ x на многочлен x⁴ + x², поскольку делимое является многочленом третьей степени, а делитель — многочленом четвёртой степени.

Вопреки этому запрету можно попробовать разделить многочлен x³+ x на многочлен x⁴ + x², и даже получить частное x⁻¹, которое при перемножении с делителем будет давать делимое:

Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x⁻¹ многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x⁻¹ это дробь , которая не является произведением.

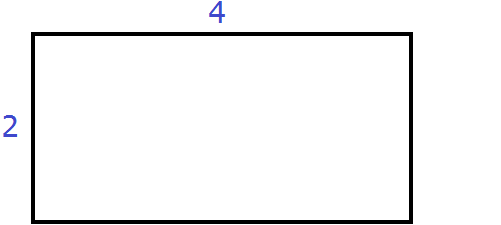
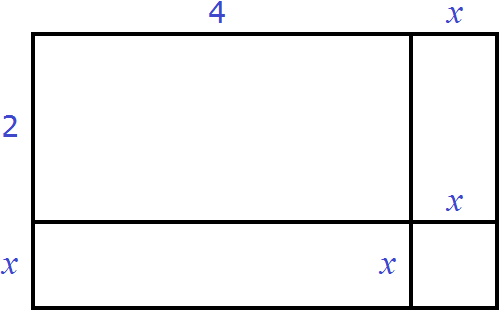
Пусть имеется прямоугольник со сторонами 4 и 2

Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.

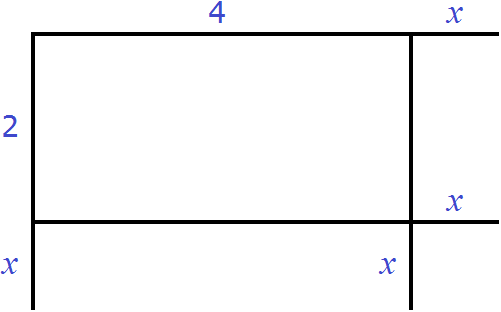
Увеличим длину и ширину этого прямоугольника на x

Достроим отсутствующие стороны:

Теперь прямоугольник имеет длину x + 4 и ширину x + 2. Площадь этого прямоугольника будет равна произведению (x + 4)(x + 2) и выражаться многочленом x²+ 6x + 8

(x + 4)(x + 2) = x²+ 4x + 2x + 8 = x²+ 6x + 8

При этом мы можем выполнить обратную операцию, а именно разделить площадь x²+ 6x + 8 на ширину x + 2 и получить длину x + 4.

Степень многочлена x²+ 6x + 8 равна сумме степеней многочленов-сомножителей x + 4 и x + 2, а значит ни одна из степеней многочленов-сомножителей не может превосходить степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным, степень делителя должна быть меньше степени делимого.

Задания для самостоятельного решения

Задание 1. Выполните деление:

Решение:

Задание 2. Выполните деление:

Решение:

Задание 3. Выполните деление:

Решение:

Задание 4. Выполните деление:

Решение:

Задание 5. Выполните деление:

Решение:

Задание 6. Выполните деление:

Решение:

Задание 7. Выполните деление:

Решение:

Задание 8. Выполните деление:

Решение:

Задание 9. Выполните деление:

Решение:

Задание 10. Выполните деление:

Решение:

Задание 11. Выполните деление:

Решение:

Задание 12. Выполните деление:

Решение:

Задание 13. Выполните деление:

Решение:

Задание 14. Выполните деление:

Решение:

Задание 15. Выполните деление:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Деление многочленов — операция деления с остатком в евклидовом кольце многочленов от одной переменной над некоторым полем. Наивный алгоритм, реализующий эту операцию, представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.

Для любых многочленов f(x) и g(x) , , существуют единственные многочлены q(x) и r(x) , такие что

$frac{f(x)}{g(x)}=q(x) + frac{r(x)}{g(x)}$

причем r(x) имеет более низкую степень, чем g(x) .

Целью алгоритмов деления многочленов является нахождение частного q(x) и остатка r(x) для заданных делимого f(x) и ненулевого делителя g(x) ^[1].

Постановка задачи[править | править код]

Задача о делении многочленов с остатком может быть сформулирована в следующих эквивалентных постановках^[2].

Частное и остаток[править | править код]

Многочлены ${displaystyle S(x)=s_{0}+s_{1}x+dots +s_{m}x^{m}}$ степени и ${displaystyle T(x)=t_{0}+t_{1}x+dots +t_{n}x^{n}}$ степени , заданы своими коэффициентами. Необходимо найти частное ${displaystyle Q(x)=q_{0}+q_{1}x+dots +q_{m-n}x^{m-n}}$ и остаток ${displaystyle R(x)=r_{0}+r_{1}x+dots +r_{n-1}x^{n-1}}$ , такие что^[2]

(1)

Определённые таким образом многочлены Q(x) и R(x) единственны — если допустить, что у уравнения (1) существует два решения ${displaystyle Q_{1}(x),R_{1}(x)}$ и ${displaystyle Q_{2}(x),R_{2}(x)}$ , то

${displaystyle T(x)left(Q_{1}(x)-Q_{2}(x)right)=R_{1}(x)-R_{2}(x),}$

из чего следует, что либо ${displaystyle Q_{1}(x)=Q_{2}(x)}$ , что также влечёт ${displaystyle R_{1}(x)=R_{2}(x)}$ , либо степень ${displaystyle R_{1}(x)-R_{2}(x)}$ не меньше степени T(x) , что невозможно по определению R(x) ^[3].

Матричная постановка[править | править код]

Данную задачу можно переписать в матричном виде, если считать, что даны ${displaystyle s_{0},s_{1},dots ,s_{m}}$ и ${displaystyle t_{0},t_{1},dots ,t_{n}}$ , а посчитать нужно ${displaystyle q_{0},q_{1},dots ,q_{m-n}}$ и ${displaystyle r_{0},r_{1},dots ,r_{n-1}}$ такие что^[2]

${displaystyle {begin{bmatrix}s_{m}\vdots \s_{n+1}\s_{n}\s_{n-1}\vdots \s_{0}end{bmatrix}}={begin{bmatrix}t_{n}&dots &0&0\vdots &ddots &vdots &vdots \dots &dots &t_{n}&0\dots &dots &t_{n-1}&t_{n}\dots &dots &t_{n-2}&t_{n-1}\vdots &ddots &vdots &vdots \0&dots &0&t_{0}end{bmatrix}}{begin{bmatrix}q_{m-n}\vdots \q_{1}\q_{0}end{bmatrix}}+{begin{bmatrix}0\vdots \0\0\r_{n-1}\vdots \r_{0}end{bmatrix}}_{textstyle .}}$

(2)

Обратная тёплицева матрица[править | править код]

В силу того, что , для решения задачи достаточно найти ${displaystyle q_{m-n},dots ,q_{0}}$ по первым уравнениям системы. Если рассматривать только эти уравнения, задача принимает вид

${displaystyle {begin{bmatrix}s_{m}\vdots \s_{n+1}\s_{n}end{bmatrix}}={begin{bmatrix}t_{n}&dots &0&0\vdots &ddots &vdots &vdots \dots &dots &t_{n}&0\dots &dots &t_{n-1}&t_{n}end{bmatrix}}{begin{bmatrix}q_{m-n}\vdots \q_{1}\q_{0}end{bmatrix}}_{textstyle .}}$

(3)

Матрица данной системы уравнений является нижнетреугольной и тёплицевой, составленной из старших коэффициентов и нулей, а решение системы эквивалентно нахождению обратной к ней^[2].

Обратный многочлен по модулю[править | править код]

Пусть ${displaystyle S^{R}(x)=x^{m}S(x^{-1})=s_{m}+s_{m-1}x+dots +s_{0}x^{m}}$ и ${displaystyle T^{R}(x)=x^{n}T(x^{-1})=t_{n}+t_{n-1}x+dots +t_{0}x^{n}}$ — многочлены, полученные из S(x) и T(x) разворотом последовательности коэффициентов. Систему уравнений (3) можно сформулировать как

${displaystyle S^{R}(x)equiv T^{R}(x)Q^{R}(x){pmod {x^{k}}},}$

где , а ${displaystyle {bmod {x}}^{m-n}}$ означает, что остатки от деления многочленов ${displaystyle S^{R}(x)}$ и ${displaystyle T^{R}(x)Q^{R}(x)}$ на $x^{k}$ равны. Деление многочлена P(x) на $x^{k}$ может быть представлено как ${displaystyle P(x)=x^{k}Q(x)+R(x)}$ , поэтому остаток R(x) равен многочлену, полученному из первых коэффициентов P(x) , то есть,

${displaystyle R(x)=p_{0}+p_{1}x+dots +p_{k-1}x^{k-1}.}$

Если многочлены ${displaystyle S^{R}(x)}$ и ${displaystyle T^{R}(x)}$ известны, то ${displaystyle Q^{R}(x)equiv S^{R}(x)T^{R}(x)^{-1}{pmod {x^{k}}}}$ , где ${displaystyle T^{R}(x)^{-1}}$ — обратный к ${displaystyle T^{R}(x)}$ многочлен в кольце остатков по модулю $x^{k}$ . Таким образом, поиск Q(x) может быть сведён к нахождению ${displaystyle V(x)=v_{0}+v_{1}x+dots +v_{k}x^{k}}$ , такого что

${displaystyle V^{R}(x)equiv T^{R}(x)^{-1}{pmod {x^{k}}}.}$

(4)

Данная постановка позволяет также находить обратную матрицу в системе (3):

Доказательство

Система (3) эквивалентна уравнению ${displaystyle S^{R}(x)equiv T^{R}(x)Q^{R}(x){pmod {x^{k}}}}$ . Соответственно, система

${displaystyle {begin{bmatrix}v_{m-n}&dots &0&0\vdots &ddots &vdots &vdots \v_{1}&dots &v_{m-n}&0\v_{0}&dots &v_{m-n-1}&v_{m-n}end{bmatrix}}{begin{bmatrix}s_{m}\vdots \s_{n+1}\s_{n}end{bmatrix}}={begin{bmatrix}q_{m-n}\vdots \q_{1}\q_{0}end{bmatrix}}}$

может быть представлена в виде ${displaystyle V^{R}(x)S^{R}(x)equiv Q^{R}(x){pmod {x^{k}}}}$ , что в случае (4) эквивалентно системе (3).■

В силу произвольности многочлена T(x) , определяющего элементы , данный факт позволяет находить обратную к произвольной тёплицевой нижнетреугольной матрице^[2].

Формальные степенные ряды[править | править код]

Уравнение ${displaystyle S^{R}(x)=T^{R}(x)Q^{R}(x)}$ можно рассматривать не только по модулю ${displaystyle x^{m-n}}$ , но и как равенство в кольце формальных степенных рядов. Пусть и t(x) — формальные степенные ряды, совпадающие с многочленами ${displaystyle S^{R}(x)}$ и ${displaystyle T^{R}(x)}$ . Если в таких терминах найти формальный ряд

${displaystyle q(x)={frac {s(x)}{t(x)}},}$

(5)

то его коэффициенты при младших степенях будут соответствовать искомому многочлену ${displaystyle Q^{R}(x)}$ . Такой подход также позволяет рассмотреть задачу (2) как систему с бесконечно продлённой тёплицевой матрицей и бесконечно продлённым столбцом , в которой исключён столбец остатков . Решение первых строк такой системы даст первые коэффициентов ряда q(x) , а именно ${displaystyle q_{m-n},q_{m-n-1},dots ,q_{m-n-h+1}}$ . В то же время, работа со степенными рядами в целом, при которой интерес представляют только первые коэффициентов ряда (например, из-за ограниченности доступной памяти), эквивалентна работе с многочленами, операции над которыми производятся в кольце остатков по модулю ${displaystyle x^{h}}$ ^[4]. В частности, поиск первых коэффициентов q(x) эквивалентен решению уравнения ${displaystyle s(x)equiv t(x)q(x){pmod {x^{h}}}}$ ^[2].

Методы решения[править | править код]

Деление столбиком[править | править код]

В ходе алгоритма, коэффициенты при старших степенях S(x) последовательно зануляются за счёт вычитания из него T(x) , умноженного на некоторую степень с коэффициентами, которые затем образуют частное Q(x) . Изначально, коэффициент ${displaystyle q_{m-n}}$ определяется равным ${textstyle {frac {s_{m}}{t_{n}}}}$ . Если разложить ${displaystyle Q(x)=q_{m-n}x^{m-n}+Q'(x)}$ , то

${displaystyle S(x)=T(x)(q_{m-n}x^{m-n}+Q'(x))+R(x).}$

С помощью замены ${displaystyle S'(x)=S(x)-q_{m-n}x^{m-n}T(x)}$ , данное уравнение приобретает вид

аналогичный уравнению (1). При этом -й коэффициент , по определению ${displaystyle q_{m-n}}$ , равен , поэтому степень будет меньше, чем степень S(x) . Процедура повторяется, пока степень не станет меньше степени T(x) , что будет означать, что очередной равен R(x) и для него ^[3].

Пример[править | править код]

Пусть ${displaystyle S(x)=x^{3}-12x^{2}-42}$ и . Для данных многочленов, деление столбиком S(x) на T(x) может быть записано как

${displaystyle {begin{array}{rr}-{begin{array}{llll}x^{3}&-12x^{2}&{color {gray}+0x}&-42\x^{3}&-3x^{2}&&\hline end{array}}&{begin{array}{|l}x-3\hline x^{2}-9x-27end{array}}\-{begin{array}{lll}-9x^{2}&&-42\-9x^{2}&+27x&\hline end{array}}&\-{begin{array}{ll}-27x&-42\-27x&+81\hline end{array}}&\-123end{array}}}$

Таким образом,

${displaystyle {frac {x^{3}-12x^{2}-42}{x-3}}=x^{2}-9x-27-{frac {123}{x-3}},}$

то есть, многочлен ${displaystyle Q(x)=x^{2}-9x-27}$ — частное деления, а — остаток.

Алгоритм Зивекинга — Кона[править | править код]

В 1972 году Мальте Зивекинг предложил алгоритм для поиска решения B(x) уравнения ${displaystyle A(x)cdot B(x)=C(x){pmod {x^{n+1}}}}$ при заданных A(x) и C(x) ^[5]. В 1974 году Кон Сянчжун^[en] показал, что при алгоритм представляет собой итерацию метода Ньютона для ${displaystyle f(V)=V^{-1}-A}$ ^[6]. При таком подходе, итерация принимает вид

${textstyle V_{k+1}=V_{k}-{frac {f(V_{k})}{f'(V_{k})}}=2V_{k}-AV_{k}^{2},}$

Где ${displaystyle f'(V_{k})=-V_{k}^{-2}}$ обозначает производную функции в точке $V_{k}$ . Для оценки точности алгоритма, можно оценить разность

${textstyle V_{k+1}-B=A(2V_{k}A^{-1}-V_{k}^{2}-A^{-2})=-A(V_{k}-B)^{2},}$

из чего следует, что если ${displaystyle V_{k}-B}$ делится на ${displaystyle x^{t}}$ (что равносильно тому, что первые коэффициентов $V_{k}$ определены корректно), то ${displaystyle V_{k+1}-B}$ будет делиться уже на ${displaystyle x^{2t}}$ . Таким образом, при начальном условии ${displaystyle V_{0}=b_{0}=a_{0}^{-1}}$ , каждая итерация удваивает число точно определённых коэффициентов B(x) . Поэтому для вычисления ${displaystyle A(x)^{-1}{pmod {x^{n+1}}}}$ достаточно итераций. Применение быстрого преобразования Фурье к умножению многочленов в формуле выше позволяет прийти к итоговому времени работы , что существенно улучшает оценку для обычного длинного умножения^[7].

Пример[править | править код]

Пусть ${displaystyle S(x)=x^{3}-12x^{2}-42}$ и . В силу (4), необходимо найти ${displaystyle Q^{R}(x)=(-42x^{3}-12x+1)(-3x+1)^{-1}{pmod {x^{3}}}}$ . Обратный многочлен ${displaystyle V(x)=(-3x+1)^{-1}{pmod {x^{3}}}}$ ищется следующим образом:

Начальное приближение определяется как ${textstyle V_{0}={frac {1}{T^{R}(0)}}=1}$ ;
Первое приближение определяется как ${displaystyle V_{1}=V_{0}(2-(-3x+1)V_{0})=3x+1}$ ;
Второе приближение определяется как ${displaystyle V_{2}=(3x+1)(2-(-3x+1)(3x+1))=(3x+1)(9x^{2}+1)=27x^{3}+9x^{2}+3x+1}$ .

В силу свойств метода Ньютона, первые $2^{2}=4$ коэффициента ${displaystyle V_{2}(x)}$ определены верно. Так как дальнейшие вычисления происходят по модулю $x^{3}$ , коэффициенты при более высоких степенях можно отбросить. Отсюда

${displaystyle Q^{R}(x)equiv (-12x+1)(9x^{2}+3x+1)equiv -108x^{3}-27x^{2}-9x+1equiv -27x^{2}-9x+1{pmod {x^{3}}},}$

в силу чего ${displaystyle Q(x)=x^{2}-9x-27}$ .

Анализ алгоритмов[править | править код]

Для оценки эффективности различных методов используется арифметическая схемная сложность^[en] — суммарное количество операций сложения, умножения, вычитания и деления над полем комплексных чисел, которые необходимо произвести в ходе работы алгоритма. Также оценивается количество параллельных шагов, требуемых для многопроцессорной реализации алгоритма, в предположении, что каждый процессор на любом шаге может выполнять не более одной операции^[7].

Каждая итерация алгоритма деления столбиком заключается в вычитании смещённого на некоторую величину T(x) из S(x) , что может быть выполнено за O(n) . Так как степень S(x) , изначально равная , уменьшается, пока она не станет меньше , общее время работы алгоритма можно оценить как , где k=m-n ^[2].

См. также[править | править код]

Теорема Безу
Правило Руффини
Базис Грёбнера
Наибольший общий делитель двух многочленов^[en]
Синтетическое деление^[en]

Примечания[править | править код]

↑
Сканави М. И. Элементарная математика. — 2-е изд., перераб. и доп. — М.: Наука, 1972. — С. 142—147. — 592 с.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ Bini, Pan, 1986, pp. 184—186
↑ ¹ ² Knuth, 1997, pp. 420—421
↑ Knuth, 1997, pp. 525—533
↑ Sieveking, 1972
↑ Kung, 1974
↑ ¹ ² Bini, Pan, 1986, pp. 186—188

Литература[править | править код]

Bini D., Pan V. [ ] // // [ Polynomial division and its computational complexity] (англ.) // Journal of Complexity — Elsevier BV, 1986. — . — P. . — ISSN 0885-064X; 1090-2708 — doi:10.1016/0885-064X(86)90001-4
Knuth D. [ ] // // [ The Art of Computer Programming] (англ.): Seminumerical Algorithms — 3 — Addison-Wesley, 1997. — . — P. . — 784 p. — ISBN 978-0-201-89684-8
Kung H. T. [ ] // // [ On computing reciprocals of power series] (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1974. — . — P. . — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01436917
Sieveking M. [ ] // // [ An algorithm for division of powerseries] (англ.) // Computing — Springer Science+Business Media, 1972. — . — P. . — ISSN 0010-485X; 1436-5057 — doi:10.1007/BF02242389
Schönhage A. [ ] // // [ Variations on Computing Reciprocals of Power Series] (англ.) // Algorithms Seminar, 2000-2001 / F. Chyzak — Institut National de Recherche en Informatique et en Automatique, 2001. — . — P. . — 197 p.

Источник

Калькулятор онлайн.
Деление многочлена на многочлен (двучлен) столбиком (уголком)

С помощью данной математической программы вы можете поделить многочлены столбиком.
Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение
с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.

Если вам нужно или упростить многочлен или умножить многочлены, то для этого у
нас есть отдельная программа Упрощение (умножение) многочлена

Что значит поделить многочлен на многочлен?

Правила ввода выражений многочленов >>

Пример подробного решения >>

Наши игры, головоломки, эмуляторы:

Немного теории.

Деление многочлена на многочлен (двучлен) столбиком (уголком)

В алгебре деление многочленов столбиком (уголком) — алгоритм деления многочлена f(x) на многочлен (двучлен) g(x),
степень которого меньше или равна степени многочлена f(x).

Алгоритм деления многочлена на многочлен представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.

Для любых многочленов ( f(x) ) и ( g(x) ), ( g(x) neq 0 ), существуют единственные полиномы
( q(x) ) и ( r(x) ), такие что
$$ frac{f(x)}{g(x)} = q(x)+frac{r(x)}{g(x)} $$
причем ( r(x) ) имеет более низкую степень, чем ( g(x) ).

Целью алгоритма деления многочленов в столбик (уголком) является нахождение частного ( q(x) ) и остатка ( r(x) )
для заданных делимого ( f(x) ) и ненулевого делителя ( g(x) )

Пример

Разделим один многочлен на другой многочлен (двучлен) столбиком (уголком):
$$ frac{x^3-12x^2-42}{x-3} $$

Частное и остаток от деления данных многочленов могут быть найдены в ходе выполнения следующих шагов:
1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой ( (x^3/x = x^2) )

( x^3 )

( -12x^2 )

( +0x )

( -42 )

( x )	( -3 )
( x^2 )

2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми
двумя элементами делимого ( (x^2 cdot (x-3) = x^3-3x^2) )

( x^3 )	( -12x^2 )	( +0x )	( -42 )
( x^3 )	( -3x^2 )

( x )	( -3 )
( x^2 )

3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой
( (x^3-12x^2+0x-42-(x^3-3x^2)=-9x^2+0x-42) )

( x^3 )	( -12x^2 )	( +0x )	( -42 )
( x^3 )	( -3x^2 )
	( -9x^2 )	( +0x )	( -42 )

( x )	( -3 )
( x^2 )

4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.

( x^3 )	( -12x^2 )	( +0x )	( -42 )
( x^3 )	( -3x^2 )
	( -9x^2 )	( +0x )	( -42 )
	( -9x^2 )	( +27x )
		( -27x )	( -42 )

( x )	( -3 )
( x^2 )	( -9x )

5. Повторяем шаг 4.

( x^3 )	( -12x^2 )	( +0x )	( -42 )
( x^3 )	( -3x^2 )
	( -9x^2 )	( +0x )	( -42 )
	( -9x^2 )	( +27x )
		( -27x )	( -42 )
		( -27x )	( +81 )
			( -123 )

( x )	( -3 )
( x^2 )	( -9x )	( -27 )

6. Конец алгоритма.
Таким образом, многочлен ( q(x)=x^2-9x-27 ) — частное деления многочленов, а ( r(x)=-123 ) — остаток от деления многочленов.

Результат деления многочленов можно записать в виде двух равенств:
( x^3-12x^2-42 = (x-3)(x^2-9x-27)-123 )
или
$$ frac{x^3-12x^2-42}{x-3} = x^2-9x-27 + frac{-123}{x-3} $$

Источник

Определение
3.3. Одночленом называют
выражение, представляющее собой
произведение чисел, переменных и степеней
с натуральным показателем.

Например, каждое
из выражений
,,является одночленом.

Говорят, что
одночлен имеет стандартный
вид, если
он содержит только один числовой
множитель, стоящий на первом месте, а
каждое произведение одинаковых переменных
в нем представлено степенью. Числовой
множитель одночлена, записного в
стандартном виде, называют коэффициентом
одночлена.
Степенью
одночлена
называют
сумму показателей степеней всех его
переменных.

Определение
3.4. Многочленом называют
сумму одночленов. Одночлены, из которых
составлен многочлен, называют членами
многочлена.

Подобные слагаемые
– одночлены в многочлене – называют
подобными
членами многочлена.

Определение
3.5. Многочленом стандартного вида
называют
многочлен, в котором все слагаемые
записаны в стандартном виде и приведены
подобные члены. Степенью
многочлена стандартного вида
называют наибольшую из степеней входящих
в него одночленов.

Например,
– многочлен стандартного вида четвертой
степени.

Действия над одночленами и многочленами

Сумму и разность
многочленов можно преобразовать в
многочлен стандартного вида. При сложении
двух многочленов записываются все их
члены и приводятся подобные члены. При
вычитании знаки всех членов вычитаемого
многочлена меняются на противоположные.

Например:

Члены многочлена
можно разбивать на группы и заключать
в скобки. Поскольку это тождественное
преобразование, обратное раскрытию
скобок, то устанавливается следующее
правило
заключения в скобки:
если перед
скобками ставится знак «плюс», то все
члены, заключаемые в скобки, записывают
с их знаками; если перед скобками ставится
знак «минус», то все члены, заключаемые
в скобки, записывают с противоположными
знаками.

Например,

Правило умножения
многочлена на многочлен:
чтобы умножить
многочлен на многочлен, достаточно
каждый член одного многочлена умножить
на каждый член другого многочлена и
полученные произведения сложить.

Например,

Итак, многочлены
можно складывать, вычитать и умножать.
При этом в результате снова получится
многочлен.

Определение
3.6. Многочленом от одной переменной
степениназывают
выражение вида

где
–
любые числа, которые называют коэффициентами
многочлена,
причем
,–
целое неотрицательное число.

Если
,
то коэффициентназываютстаршим
коэффициентом многочлена
,
одночлен–
его старшим
членом,
коэффициент
–
свободным
членом.

Если вместо
переменной
в многочленподставить действительное число,
то в результате получится действительное
число,
которое называютзначением
многочлена

при.

Определение
3.7. Число

называют
корнем
многочлена

,
если

.

Рассмотрим деление
многочлена
на многочлен,
гдеи– натуральные числа. Деление возможно,
если степень многочлена-делимогоне меньше степени многочлена-делителя,
то есть.

Разделить многочлен
на многочлен,,–
значит найти два таких многочлена
и,
чтобы

При этом многочлен

степениназываютмногочленом-частным,
–
остатком,
.

Замечание 3.2.
Если делитель

–
не нуль-многочлен, то деление
на,,
всегда выполнимо, а частное и остаток
определяются однозначно.

Замечание 3.3.
В случае, когда
при всех
,
то есть

говорят, что
многочлен
нацело делится(или
делится)
на многочлен
.

Деление многочленов
выполняется аналогично делению
многозначных чисел: сначала старший
член многочлена-делимого делят на
старший член многочлена-делителя, затем
частное от деления этих членов, которое
будет старшим членом многочлена-частного,
умножают на многочлен-делитель и
полученное произведение вычитают из
многочлена-делимого. В результате
получают многочлен – первый остаток,
который делят на многочлен-делитель
аналогичным образом и находят второй
член многочлена-частного. Этот процесс
продолжают до тех пор, пока получится
нулевой остаток или степень многочлена
остатка будет меньше степени
многочлена-делителя.

При делении
многочлена на двучлен можно воспользоваться
схемой Горнера.

Схема Горнера

Пусть требуется
разделить многочлен

на двучлен
.
Обозначим частное от деления как
многочлен

а остаток –
.
Значение,
коэффициенты многочленов,и остатокзапишем в следующей форме:

				…

В этой схеме каждый
из коэффициентов
,
,,
…,получается из предыдущего числа нижней
строки умножением на числои прибавлением к полученному результату
соответствующего числа верхней строки,
стоящего над искомым коэффициентом.
Если какая-либо степеньв многочлене отсутствует, то соответствующий
коэффициент равен нулю. Определив
коэффициенты по приведенной схеме,
записываем частное

и результат деления,
если
,

или
,

если
,

Теорема 3.1.
Для того чтобы несократимая дробь
(,)
была корнем многочлена
с целыми коэффициентами, необходимо,
чтобы числобыло делителем свободного члена,
а число– делителем старшего коэффициента.

Теорема 3.2.
(Теорема
Безу)
Остаток
от деления многочленана двучленравен значению многочленапри,
то есть.

При делении
многочлена
на двучленимеем равенство

Оно справедливо,
в частности, при
,
то есть.

Пример 3.2. Разделить
на.

Решение. Применим
схему Горнера:

Следовательно,

или
.

Пример 3.3. Разделить
на.

Решение. Применим
схему Горнера:

Следовательно,

или

Пример 3.4. Разделить
на.

Решение. Проведем
деление многочленов столбиком:

В итоге получаем

Пример 3.5. Разделить
на.

Решение. Проведем
деление многочленов столбиком:

Тогда получаем

Иногда бывает
полезным представление многочлена в
виде равного ему произведения двух или
нескольких многочленов. Такое тождественное
преобразование называют разложением
многочлена на множители.
Рассмотрим основные способы такого
разложения.

Вынесение
общего множителя за скобки.
Для того
чтобы разложить многочлен на множители
способом вынесения общего множителя
за скобки, необходимо:

1) найти общий
множитель. Для этого, если все коэффициенты
многочлена – целые числа, в качестве
коэффициента общего множителя
рассматривают наибольший по модулю
общий делитель всех коэффициентов
многочлена, а каждую переменную, входящую
во все члены многочлена, берут с наибольшем
показателем, который она имеет в данном
многочлене;

2) найти частное
от деления данного многочлена на общий
множитель;

3) записать
произведение общего множителя и
полученного частного.

Группировка
членов. При
разложении многочлена на множители
способом группировки его члены
разбиваются на две или более групп с
таким расчетом, чтобы каждую из них
можно было преобразовать в произведение,
и полученные произведения имели бы
общий множитель. После этого применяется
способ вынесения за скобки общего
множителя вновь преобразованных членов.

Применение
формул сокращенного умножения. В
тех случаях, когда многочлен, подлежащий
разложению
на множители,
имеет вид правой части какой-либо формулы
сокращенного умножения, его разложение
на множители достигается применением
соответствующей формулы, записанной в
другом порядке.

Пусть
,
тогда справедливы следующиеформулы
сокращенного умножения:





Для :
Если нечетное ():
Бином Ньютона: , где – число сочетаний изпо.

Введение новых
вспомогательных членов. Данный
способ заключается в том, что многочлен
заменяется другим многочленом,
тождественно равным ему, но содержащим
другое число членов, путем введения
двух противоположных членов или замены
какого-либо члена тождественно равной
ему суммой подобных одночленов. Замена
производится с таким расчетом, чтобы к
полученному многочлену можно было
применить способ группировки членов.

Пример 3.6. Разложить
на множители многочлен
.

Решение. Все
члены многочлена содержат общий множитель
.
Следовательно,.

Ответ:
.

Пример 3.7. Разложить
на множители многочлен
.

Решение. Группируем
отдельно члены, содержащие коэффициент
,
и члены, содержащие.
Вынося за скобки общие множители групп,
получаем:

Ответ:
.

Пример 3.8. Разложить
на множители многочлен
.

Решение. Используя
соответствующую формулу сокращенного
умножения, получаем:

Ответ:
.

Пример 3.9. Разложить
на множители многочлен
.

Решение. Используя
способ группировки и соответствующую
формулу сокращенного умножения, получаем:

Ответ:
.

Пример 3.10.
Разложить
на множители многочлен
.

Решение. Заменим
на,
сгруппируем члены, применим формулы
сокращенного умножения:

Ответ:
.

Пример 3.11.
Разложить
на множители многочлен

Решение. Так
как
,,,
то

Ответ:
.

Источник

Многочленом с одной переменной называется выражение вида

`P(x) = a_n x^n + a_(n-1) x^(n-1) +a_(n-2) x^(n-2) + … + a_2 x^2 + a_1 x + a_0 (a_n != 0)`. (8)

Числа `a_0`, `a_1`, `…`, `a_n` – это коэффициенты многочлена; `a_n` называют старшим коэффициентом, `a_0` – свободным членом.

Степенью многочлена называют наибольшую степень переменной, входящую в многочлен.

Например, степень многочлена `P = x^4 – x^3 – x^2 + 2x + 1` равна `4`; степень многочлена `25 + x^5 – 3x` равна `5`; степень многочлена `17` равна `0`, т. к. переменная в это выражение не входит; наконец, выражение `3x^2 + x +5+ 2/x` многочленом не является, поэтому о его степени говорить бессмысленно. Многочлен `P(x) = 0` называют нулевым многочленом. Степень нулевого многочлена не определена.

Два многочлена называются равными, если равны все их коэффициенты. Многочлен равен нулю, если все его коэффициенты равны нулю.

Число `a` называется корнем многочлена `F(x)`, если `F(alpha) = 0`.

Приведём основные сведения о многочленах.

Для любых двух многочленов `F(x)` и `G(x)` существует единственная пара многочленов `P(x)` (частное) и `Q(x)` (остаток) такая, что `F(x) = G(x) * P(x) + Q(x)`, причём степень остатка `Q(x)` меньше степени делителя `G(x)`, или `Q(x)` есть нулевой многочлен. Покажем, как на практике находят частное и остаток от деления многочленов.

Разделите с остатком многочлен `F(x) = 18x^5 + 27x^4 -37x^3 – 14x + 20`

на многочлен `G(x) = 2x^2 + 3x -5`.

Процедура деления многочленов очень похожа на деление целых чисел. Если степень делимого не меньше степени делителя, то делаем следующее: делим старший член многочлена `F(x)` на старший член многочлена `G(x)`, получившийся результат записываем в частное. Умножаем результат на весь делитель `G(x)` и вычитаем полученное из исходного многочлена `F(x)`. После этих действий член со старшей степенью `x` сокращается. Если в результате вычитания у оставшегося многочлена степень не меньше, чем степень делителя, то можно сделать ещё один шаг деления и т. д.

Деление закончится тогда, когда степень делимого будет меньше степени делителя. В случае, когда в делимом отсутствуют некоторые степени переменных, для удобства записи лучше оставить пустые места для соответствующих членов (хотя это не обязательно).

Вернёмся к нашему примеру. Первый член частного равен `(18x^5)/(2x^2) = 9x^3`. При умножении на делитель `2x^2 +3x-5` получаем `18x^5 + 27x^4 – 45x^3`. После вычитания из исходного многочлена от него остаётся `8x^3 -14x +20`. Степень многочлена, оставшегося после вычитания, равна `3`. Это больше степени делителя, поэтому можно сделать следующий шаг деления. Делим `8x^3` на `2x^2` и получаем `4x`, умножаем `4x` на `2x^2 +3x-5`, получаем `8x^3 +12x^2 -20`; вычитаем этот многочлен из `8x^3 -14x +20` и т. д.

Частное равно `9x^3 +4x -6`; остаток равен `24x-10`.

Таким образом, `18x^5 + 27x^4 – 37x^3 -14x + 20 = (2x^2 + 3x – 5)(9x^3 + 4x – 6) + (24x – 10)`.

1) Теорема Безу. Остаток от деления многочлена `F(x)` на многочлен `(x-alpha)` равен `F(alpha)`.

2) Число `alpha` является корнем многочлена `F(x)` тогда и только тогда, когда многочлен `F(x)` делится на многочлен `(x-alpha)`.

3) Если `alpha` и `beta` – различные корни многочлена `F(x)`, то он делится на многочлен `(x- alpha)(x- beta)`.

4) Многочлен степени `n` не может иметь более `n` корней.

1) Разделим с остатком многочлен `F(x)` на многочлен `(x-alpha)`. Тогда остаток либо равен нулю, либо является многочленом нулевой степени (т. к. степень остатка меньше степени делителя, а степень делителя равна `1`). Поэтому можно записать, что

`F(x) = (x-alpha) G(x) +C` (9)

Через `G(x)` здесь обозначено частное от деления, вид которого нас не интересует.

Равенство (9) верно при всех значениях `x`. Подставим в него `x=alpha`.

Тогда `F(alpha) = (alpha – alpha)G(alpha) + C`, или `F(alpha) = C`.

Подставим `C=F(alpha)` в (9) и получим

`F(x) = (x – alpha) G (x) + F(alpha)`. (10)

Первая часть доказана.

2) Из (10) следует, что `F(x)` делится на `(x – alpha)` тогда и только тогда, когда `F(alpha) = 0`, т. е. тогда и только тогда, когда `alpha` есть корень многочлена `F(x)`.

3) `alpha` – корень `F(x) => F(x)` делится на `(x- alpha) => F(x) = (x- alpha) G(x)`. Подставим в последнее равенство (которое верно для всех значений переменной `x`) `x= beta`. Тогда `F(beta) = (beta – alpha) G(beta)`.

`F(beta) = 0` (т. к. `beta` -корень `F(x)`), поэтому `(beta – alpha)G(beta) = 0 =>G(beta) = 0` (т. к. `beta != alpha`); отсюда `G(x)` делится на `(x- beta)`, т. е. `G(x) = H(x) * (x- beta)`. Подведём итог: `F(x) = (x- alpha) G(x) = (x -alpha)(x- beta) H(x)`, т. е. `F(x)` делится на `(x- alpha)(x- beta)`.

4) Теперь становится понятным, что многочлен степени `n` не может иметь больше, чем `n` корней.

Остатки от деления многочлена `F(x)` на многочлены `(x-3)` и `(x+5)` равны `2` и `(-9)` соответственно. Найдите остаток от деления многочлена `F(x)` на многочлен `x^2 + 2x -15`.

Заметим, что `x^2 + 2x -15 = (x-3)(x+5)`.

По теореме Безу `F(3) = 2`; `F(-5) =-9`.

Поделим `F(x)` с остатком на `x^2 + 2x -15`:

`F(x) = (x^2 + 2x – 15)G(x) + r(x)`.

Степень остатка не превосходит степени делителя, поэтому остаток – это либо многочлен первой степени, либо нулевой степени, либо равен нулю. В любом случае, остаток представим в виде `r(x) = ax +b` (если `a!= 0`, то получим многочлен первой степени; если `a=0`, `b!=0`, то будет многочлен нулевой степени; если `a=b=0`, то получим нулевой многочлен). Итак,

`F(x) = (x^2 + 2x-15)G(x) + ax+b`. (11)

Подставим в равенство (11) `x=3` и `x=-5`:

`F(3) = 0 * G(3) + 3a + b`; `F(-5)=0 * G(-5) -5a+b`, откуда $$ left{begin{array}{l}3a+b=2,\ -5a+b=-9.end{array}right.$$

Решая эту систему, нахоим, что `a=(11)/8`, `b=- (17)/8`.

Остаток равен `(11)/8 x – (17)/8`.

Докажите, что

$$ sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}=4$$. (12)

Пусть $$ sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}=x$$. Возведём обе части этого равенства в куб и преобразуем:

$$ 26-15sqrt{3}+3sqrt[3]{{left(26-15sqrt{3}right)}^{2}}sqrt[3]{26+15sqrt{3}}+3sqrt[3]{26-15sqrt{3}}sqrt[3]{{left(26+15sqrt{3}right)}^{2}}+26+15sqrt{3}={x}^{3}$$;

$$ 52+3sqrt[3]{26-15sqrt{3}}sqrt[3]{26+15sqrt{3}}left(sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}right)={x}^{3}$$;

$$ 52+3sqrt[3]{{26}^{2}-{left(15sqrt{3}right)}^{2}}left(sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}right)={x}^{3}$$;

$$ 52+3left(sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}right)={x}^{3}$$;

`52+3x=x^3`;

`x^3-3x-52=0`. (13)

Число `x=4` является корнем этого уравнения. Докажем, что других корней нет (и тем самым будет доказана справедливость равенства (12)). Поскольку `x=4` является корнем, многочлен `x^3 – 3x-52` делится на `x-4` без остатка. Выполняя деление, получаем:

$$ {x}^{3}-3x-52=0iff left(x-4right)left({x}^{2}+4x+13right)=0iff left[begin{array}{l}x-4=0,\ {x}^{2}+4x+13=0.end{array}right.$$

У квадратного трёхчлена `x^2 +4x+13` отрицательный дискриминант, поэтому уравнение (13) имеет ровно один корень `x=4`.

При каких `a` и `b` многочлен `F(x)=x^4 +ax^3 – 2x^2 +19x+b` делится на многочлен `x^2 -3x+2`?

1-й способ. Выполним деление с остатком:

Приравниваем коэффициенты остатка к нулю

$$ left{begin{array}{l}7a+28=0,\ b-6a-10=0,end{array}right.iff left{begin{array}{l}a=-4,\ b=-14.end{array}right.$$

2-й способ. `x^2 -3x+2=(x-1)(x-2)`.

Многочлен делится на `(x-1)(x-2)` тогда и только тогда, когда `x=1` и `x=2` являются корнями многочлена. То есть,

$$ begin{array}{c}Fleft(1right)=1+a-2+19+b=0, \ Fleft(2right)=16+8a-8+38+b=0,end{array}iff left{begin{array}{l}18+a+b=0,\ 46+8a+b=0,end{array}right.iff left{begin{array}{l}a=-4,\ b=-14.end{array}right.phantom{rule{0ex}{0ex}}$$

`a=-4`, `b=-14`.

Источник

Деление многочлена на одночлен

Деление одночлена на многочлен

Деление многочлена на многочлен

Деление многочлена на многочлен с остатком

Когда деление многочленов невозможно

Задания для самостоятельного решения

Постановка задачи[править | править код]

Частное и остаток[править | править код]

Матричная постановка[править | править код]

Обратная тёплицева матрица[править | править код]

Обратный многочлен по модулю[править | править код]

Формальные степенные ряды[править | править код]

Методы решения[править | править код]

Деление столбиком[править | править код]

Пример[править | править код]

Алгоритм Зивекинга — Кона[править | править код]

Пример[править | править код]

Анализ алгоритмов[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Немного теории.

Пример

Действия над одночленами и многочленами

Вам также может понравиться

Как найти красную карту тарков

Как динозаврик нашел друзей

Как найти человека при выключенном телефоне бесплатно

Добавить комментарий Отменить ответ