Математика
6 класс
Урок № 69
Приближение суммы, разности, произведения и частного двух чисел
Перечень рассматриваемых вопросов:
– десятичная дробь, приближённое значение, округление;
– значащая цифра десятичной дроби;
– приближение суммы, разности, произведения и частного двух чисел.
Тезаурус
Округление десятичной дроби – замена десятичной дроби приближённым значением с меньшим количеством значащих цифр.
Десятичная дробь – это дробь, записанная в десятичной форме.
Значащая цифра десятичной дроби – это первая слева направо отличная от нуля цифра, а также все следующие за ней цифры.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Зачастую необходимо быстро прикинуть результат, который получается при сложении, вычитании, умножении или делении двух десятичных дробей. Если дроби имеют много знаков после запятой, выполнить эти действия быстро довольно сложно. Для этого используют правила приближения суммы, разности, произведения и частного двух чисел.
Сумма (разность, произведение, частное) двух чисел считается приближённо равной сумме (разности, произведению, частному) их приближений.
Поясним на примере.
1,45 + 2,32
Округлим данные числа до десятых.
1,45 ≈ 1,5
2,32 ≈ 2,3
Сложим приближённые значения дробей.
1,5 + 2,3 = 3,8
Проверим с исходными числами.
1,45 + 2,32 = 3,77
Округлим сумму до десятых.
3,77 ≈ 3,8
Получили тот же результат.
Итак, чтобы вычислить приближённую сумму или разность двух чисел, надо округлить эти числа с одинаковой точностью, то есть до одного и того же разряда. Затем сложить или вычесть полученные приближения.
Рассмотрим пример.
23,184567 + 4,4486
Округлим эти числа с точностью до одной сотой.
23,184567 ≈ 23,18
4,4486 ≈ 4,45
Найдём сумму приближённых значений.
23,18 + 4,45 = 27,63
23,184567 + 4,4486 ≈ 27,63
Теперь рассмотрим умножение и деление.
Чтобы вычислить приближённое произведение или частное двух чисел, надо округлить эти числа с точностью до одной и той же значащей цифры, перемножить или разделить полученные приближения и результат округлить до той же значащей цифры.
Пусть даны числа.
246,76556 и 0,0078653
Найдём их произведение и частное.
Округлим числа до трёх значащих цифр.
246,76556 ≈ 247
0,0078653 ≈ 0,00787
Вычислим произведение их приближений.
247·0,00787 = 1,94389
Округлим результат также до трёх значащих цифр.
1,94389 ≈ 1,94
Получаем, что
246,76556 · 0,0078653 ≈ 1,94
Вычислим частное приближений этих чисел и тоже округлим его до трёх значащих цифр.
247 : 0,00787 = 31385,00635… ≈ 31400
Получаем, что
246,76556 : 0,0078653 ≈ 31400
Точность вычислений находится в противоречии с простотой вычислений. Чем большим количеством цифр мы пользуемся, тем точнее наш результат.
Пример
Вычислить 2,26372.
Для простоты вычислений округлим до одной значащей цифры.
2,2637 ≈ 2
Тогда 22 = 4.
Округлим до двух значащих цифр.
2,2637 ≈ 2,3
Тогда 2,32 = 5,29
Округлим до трёх значащих цифр.
2,2637 ≈ 2,26
2,262 = 5,1076
Если же посчитать не приближённый, а реальный результат, то получается
2,26372 = 5,12433769
Видим, что наиболее приближённый к реальному результат дало нам округление до трёх значащих цифр. А самый далёкий от реального результат дало округление до одной значащей цифры.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте
Вставьте вместо пропусков верные цифры.
Задание. Вычислите приближённое значение произведения, округлив множители до двух значащих цифр.
2,465·1,923 ≈ …
Решение
Округлим множители до двух значащих цифр.
2,465≈ 2,5
1,923≈1,9
Найдём произведение приближённых значений.
2,5·1,9=4,75
Округлим произведение также до двух значащих цифр.
4,75≈4,8
Ответ:2,465·1,923 ≈4,8.
Тип 2. Подстановка элементов в пропуски в тексте
Нахождение приближённого значения частного десятичных дробей
Задание. Вставьте вместо пропуска цифру, чтобы получилось верное равенство.
3,_781 : 0,00494 ≈ 3,6 : 0,0049
Решение. При нахождении приближённого значения частного, числа были округлены до двух значащих цифр. В делимом третья значимая цифра 7, значит, при округлении ко второй цифре прибавили единицу. Получилось 6, значит, исходная цифра – это 5.
Ответ: 3,5781 : 0,00494 ≈ 3,6 : 0,0049
Тип 3. Добавление подписей к изображениям
Нахождение приближённого значения произведения и частного десятичных дробей
Задание. Округлив числа a и b с точностью до двух значащих цифр, найдите и впишите результаты действий.
a = 191,452; b = 0,004868
a : b =
a · b =
Решение
Округлим числа до двух значащих цифр.
191,452 ≈ 190
0,004868 ≈ 0,0049
Найдём частное приближённых значений.
190 : 0,0049 = 38775,5
Округлим до двух значащих цифр.
38775,5… ≈ 39000
Найдём произведение приближённых значений.
190 · 0,0049 = 0,931
Округлим произведение также до двух значащих цифр.
0,931 ≈ 0,93
Ответ:
a : b = 39000
a · b = 0,93
Действия над приближенными значениями величин
Для
того чтобы правильно производить
действия над приближенными значениями
величин, надо уметь находить погрешности
этих действий.
В
таблице приведены формулы для оценки
границ погрешностей результатов
действий:
|
Действие |
Граница абсолютной погрешности |
Граница погрешности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Вычислить
сумму приближенных чисел 0.6, 0.42 и 0.286.
Найти границу погрешности результата.
Решение. Округлим
все данные, сохранив два десятичных
знака, и выполним сложение:
![]()
Граница
погрешности каждого слагаемого не
превосходит единицы последнего разряда;
тогда
![]()
Пример
3. Найти частное приближенных чисел
654.1 и 8.5 и границу погрешности результата.
Решение.
Округлим делимое, сохранив три значащие
цифры, т.е. до единиц:
![]()
.
Выполним деление и оставим в результате
две значащие цифры:
![]()
Чтобы
ответить на вопрос, с какой точностью
найдено частное, сначала вычислим
границу относительной погрешности
результата:
![]()
Границу
погрешности частного находим по формуле
![]()
,
т.е.
![]()
Итак, частное равно
![]()
При
возведении в квадрат и в куб в результате
сохраняют столько значащих цифр,
сколько их имеет подкоренное число.
Пример
4. Вычислить приближенное значение
числа
![]()
и найти относительную погрешность
вычисления.
Решение.
Сначала находим квадрат числа 4.13 и
оставляем в результате три значащие
цифры:
![]()
Относительную погрешность вычисления
находим по формуле
![]()
![]()
![]()
Итак,
![]()
с относительной точностью до 0.5%.
Замечание.
Для более точных вычислений в результатах
промежуточных действий рекомендуется
сохранять одну запасную цифру, т.е.
сохранять на один десятичный знак или
на одну значащую цифру больше, чем
рекомендует правило.
Пример
5. Вычислить приближенное значение
выражения
![]()
и найти границу погрешности результата.
Решение.
Находим значение квадрата числа 5.62 и
квадратного корня из числа 18.50; имеем
![]()
Теперь получаем
![]()
где сначала
выполнено деление, а затем умножение.
Найдем
границу относительной погрешности
результата:
![]()
Граница
погрешности результата есть
![]()
Итак,
![]()
Пример
6. Вычислить приближенное значение
выражения
![]()
и найти границу погрешности результата.
Решение.
Находим значение квадратного корня из
числа 6.24 и
![]()
;
имеем
![]()
;
![]()
.
Далее получим
![]()
где сначала
выполнено деление, а затем умножение.
Найдем
границу относительной погрешности
результата:
![]()
Граница
погрешности результата есть
![]()
Итак,
![]()
Задачи
-
Найдите
абсолютную погрешность приближенного
равенства

. -
Округлите
число до единиц и найдите абсолютную
и относительную погрешности округления:
а) 10.59; б) 0.892. -
Сколько
верных цифр имеет число: а)

б)

;
в)

-
Вычислите
приближенное значение выражения и
границу погрешности результата:
а)
![]()
б)
![]()
в)
![]()
-
Найти
относительную погрешность при вычислении
определителя
а)
![]()
,
б)
![]()
ПРАКТИЧЕСКОЕ
ЗАНЯТИЕ № 2
ПРИБЛИЖЕНИЕ
И АППРОКСИМАЦИЯ ФУНКЦИЙ
Постановка
задачи. Пусть
величина у
является функцией аргумента х.
Это означает, что любому значению х
из области определения поставлено в
соответствие значение у.
Вместе с тем на практике часто неизвестна
явная связь между у
и х,
т.е. невозможно записать эту связь в
виде некоторой зависимости
![]()
.
В некоторых случаях даже при известной
зависимости
она настолько громоздка (например,
содержит трудно вычисляемые выражения,
сложные интегралы и т.д.), что её
использование в практических расчетах
затруднительно.
Задача
о приближении (аппроксимации) функций
формулируется так: данную функцию
![]()
требуется приближенно заменить
(аппроксимировать) некоторой функцией
![]()
так, чтобы отклонение (в некотором
смысле)
от
в заданной области было наименьшим.
Функция
при этом называется аппроксимирующей.
Для
практики весьма важен случай аппроксимации
функции многочленом
![]()
(1)
При
этом коэффициенты
![]()
будут подбираться так, чтобы достичь
наименьшего отклонения многочлена от
данной функции.
Одним
из основных типов аппроксимации является
интерполирование. Оно состоит в следующем:
для данной функции
строим многочлен (1), принимающий в
заданных точках
![]()
те же значения
![]()
что и функция
,
т.е.
![]()
(2)
При
этом предполагается, что среди значений
![]()
нет одинаковых, т.е.
![]()
при
![]()
Точки
называются узлами интерполяции, а
многочлен
– интерполяционным многочленом.
Пусть
функция
![]()
определена таблицей
|
|
|
… |
|
|
|
|
|
|
… |
|
Задачей
интерполяции является построение
многочлена
![]()
,
значения которого в узлах интерполяции
{xi}
равны соответствующим значениям
заданной функции, т.е.
=yi
(i=0,1,…,n).
Интерполяционной
формулой Лагранжа называется формула,
представляющая многочлен
в виде
![]()
![]()
,
(3)
где
![]()
– многочлен степени n,
принимающий значение, равное единице
в узле
![]()
,
и равные нулю значения в остальных узлах
![]()
(![]()
),
(i,k=0,1,…,n).
Многочлен
называется интерполяционным многочленом
Лагранжа. Следует отметить, что степень
многочлена Лагранжа не превышает числа
n.
определяется по следующей формуле
![]()
.
(4)
Пример.
Для функции, заданной таблицей, построить
интерполяционный многочлен Лагранжа.
|
-1 |
0 |
1 |
|
|
|
3 |
2 |
5 |
Решение.
Многочлен Лагранжа для трех узлов
интерполирования запишется так:
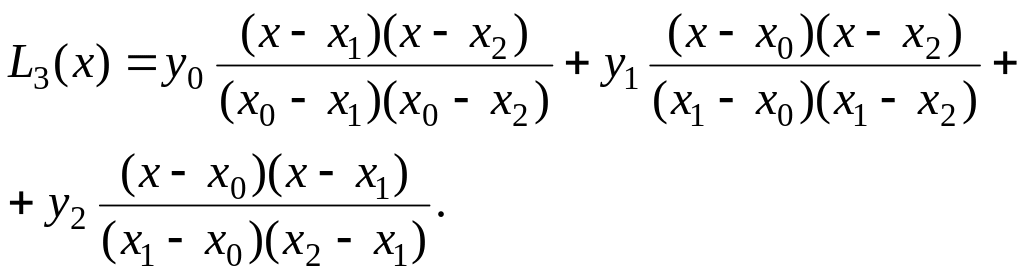
Применяя формулу
Лагранжа, получим

После
элементарных преобразований получаем
интерполяционный многочлен Лагранжа
второй степени
![]()
.
Задачи
Для
функции
,
заданной
таблицей,
построить интерполяционный многочлен
Лагранжа.
1.
|
0.0 |
0.5 |
1.0 |
1.5 |
2.0 |
|
|
1.5708 |
1.5738 |
1.5828 |
1.5981 |
1.62 |
2.
|
2.5 |
3.0 |
3.5 |
4.0 |
|
|
1.649 |
1.6858 |
1.7313 |
1.7868 |
3.
|
0.3 |
0.4 |
0.50 |
0.6 |
0.7 |
|
|
0.29131 |
0.37995 |
0.46212 |
0.53705 |
0.60437 |
4.
|
0.8 |
0.9 |
1.0 |
|
|
0.66404 |
0.7163 |
0.76159 |
5.
|
0.0 |
0.5 |
1.0 |
1.05 |
2.0 |
|
|
1.5708 |
1.5678 |
1.5589 |
1.5442 |
1.5238 |
ПРАКТИЧЕСКОЕ
ЗАНЯТИЕ №3
МЕТОД
НАИМЕНЬШИХ КВАДРАТОВ
Пусть,
изучая неизвестную функциональную
зависимость между y
и x,
в результате серии экспериментов
произвели ряд измерений этих величин
и получили таблицу значений
|
x0 |
x1 |
x2 |
… |
xn |
|
y0 |
y1 |
y2 |
… |
yn |
Задача
состоит в том, чтобы найти приближенную
зависимость
![]()
(1)
значения
которой при
![]()
мало отличаются от опытных данных
.
Приближенная функциональная зависимость
(1), полученная на основании экспериментальных
данных, называется эмпирической
формулой.
Задача
построения эмпирической формулы
отличается от задачи интерполирования.
График эмпирической зависимости, вообще
говоря, не проходит через заданные
точки
![]()
,
как в случае интерполяции. Это приводит
к тому, что экспериментальные данные
в некоторой степени сглаживаются, а
интерполяционная формула повторила бы
все ошибки, имеющиеся в экспериментальных
данных.
Построение
эмпирической формулы состоит из двух
этапов: подбор общего вида этой формулы
и определения наилучших значений
содержащихся в ней параметров.
В
методе наименьших квадратов в качестве
эмпирической функции выбран многочлен.
Согласно этому методу за меру отклонения
многочлена
![]()
(2)
от
данной функции
на множестве точек
![]()
,
![]()
,
…,![]()
принимают величину
![]()
,
(3)
равную
сумме квадратов отклонений многочлена
![]()
от функции
на заданной системе точек.
Очевидно,
что
![]()
есть функция коэффициентов
![]()
,
![]()
,
…,![]()
.
Эти коэффициенты надо подобрать так,
чтобы величина
была наименьшей. Полученный многочлен
называется аппроксимирующим для данной
функции, а процесс построения этого
многочлена – точечной квадратичной
аппроксимацией или точечным квадратичным
аппроксимированием функции.
Для
решения задачи точечного квадратичного
аппроксимирования воспользуемся общим
приемом дифференциального исчисления.
Найдем частные производные от величины
![]()
где![]()
по всем переменным
![]()
![]()
,
…,
![]()
.
Приравнивая эти частные производные к
нулю, получим для определения неизвестных
,
…,
![]()
систему m+1
уравнений с m+1
неизвестными:
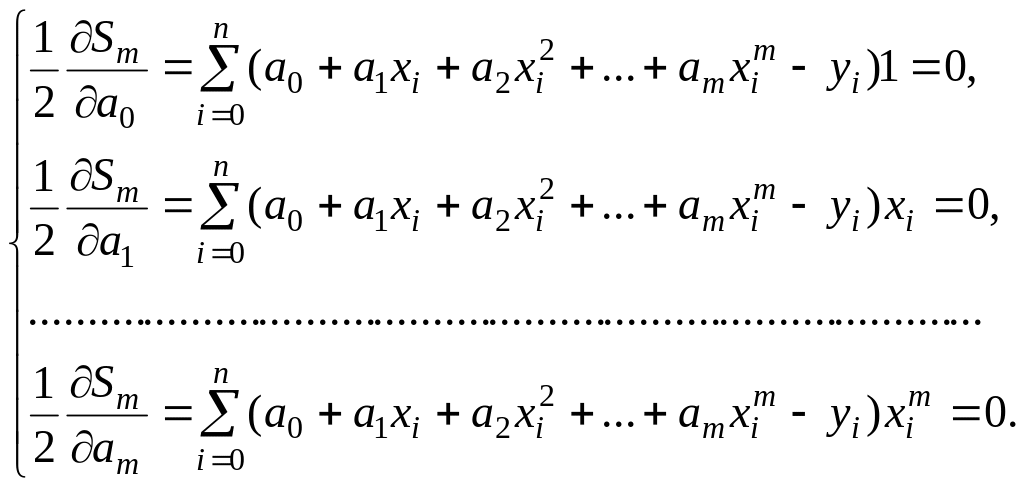
(4)
Введем обозначения:
![]()
,
![]()
![]()
,
![]()
Преобразуя систему
(11) и используя введенные обозначения,
будем иметь:
![]()
(5)
где
![]()
.
Можно
доказать, что если среди точек
,
,
…,
нет совпадающих и
![]()
,
то определитель системы (5) отличен от
нуля и, следовательно, эта система имеет
единственное решение
![]()
,
![]()
,
…,
![]()
.
Многочлен (2) с такими коэффициентами
будет обладать минимальным квадратичным
отклонением
![]()
.
Таким
образом, аппроксимирование функций
представляет собой более общий процесс,
чем интерполирование.
Для
составления системы (4) рекомендуется
схема способа наименьших квадратов,
приведенная в таблице 1, где принято
m=2.
Таблица 1
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
1 |
|
|
|
|
|||
|
1 |
|
|
|
|
|
||
|
1 |
|
|
|
|
|
||
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Пример.
Подобрать аппроксимирующий многочлен
второй степени
![]()
для данных
|
|
0.78 |
1.50 |
2.34 |
3.12 |
3.81 |
|
|
2.50 |
1.20 |
1.12 |
2.25 |
4.28 |
Решение.
Вычисления, которые нам нужно произвести,
расположим по схеме (для m=2,
n=4),
приведенной в таблице 1.
Для данного примера
получаем таблицу 2 (вычисления проводятся
с тремя десятичными знаками).
Таблица 2
|
|
|||||||
|
1 |
0.78 |
0.608 |
0.475 |
0.370 |
2.50 |
1.950 |
1.520 |
|
1 |
1.56 |
2.434 |
3.796 |
5.922 |
1.20 |
1.872 |
2.921 |
|
1 |
2.34 |
5.476 |
12.813 |
29.982 |
1.12 |
2.621 |
6.133 |
|
1 |
3.12 |
9.734 |
30.371 |
94.759 |
2.25 |
7.020 |
21.902 |
|
1 |
3.81 |
14.516 |
55.306 |
210.717 |
4.28 |
16.307 |
62.128 |
|
5 |
11.61 |
32.768 |
102.761 |
341.750 |
11.35 |
29.770 |
94.604 |
Отсюда
система для определения коэффициентов
![]()
,
,
![]()
:
![]()
(6)
Решив
систему (6), получим
![]()
,
![]()
,
![]()
.
Следовательно, искомый многочлен есть
![]()
(7)
Сравним
исходные значения для
с соответствующими значениями
![]()
,
полученными из приближенной формулы
(7). Соответствующие результаты приведены
в таблице 3.
Таблица
3
|
|
|
||
|
0.78 |
2.50 |
2.505 |
0.005 |
|
1.56 |
1.20 |
1.194 |
0.006 |
|
2.34 |
1.12 |
1,110 |
0.010 |
|
3.12 |
2.25 |
2.252 |
0.002 |
|
3.81 |
4.28 |
4.288 |
0.008 |
Задачи
Подобрать
аппроксимирующий многочлен второй
степени
для функций
1.
|
0.0 |
0.5 |
1.0 |
1.5 |
2.0 |
|
|
1.5708 |
1.5738 |
1.5828 |
1.5981 |
1.62 |
2.
|
2.5 |
3.0 |
3.5 |
4.0 |
|
|
1.649 |
1.6858 |
1.7313 |
1.7868 |
3.
|
0.3 |
0.4 |
0.50 |
0.6 |
0.7 |
|
|
0.29131 |
0.37995 |
0.46212 |
0.53705 |
0.60437 |
4.
|
0.8 |
0.9 |
1.0 |
|
|
0.66404 |
0.7163 |
0.76159 |
5.
|
0.0 |
0.5 |
1.0 |
1.05 |
2.0 |
|
|
1.5708 |
1.5678 |
1.5589 |
1.5442 |
1.5238 |
ПРАКТИЧЕСКОЕ
ЗАНЯТИЕ № 4
ЧИСЛЕННОЕ
ДИФФЕРЕНЦИРОВАНИЕ
1.
Аппроксимация производных.
Напомним, что производной функции
![]()
называется предел отношения приращения
функции
![]()
к приращению аргумента
![]()
при стремлении
к нулю:
![]()
(1)
Значение
шага
полагают равным некоторому конечному
числу и для вычисления значения
производной получают приближенное
равенство
![]()
(2)
Это
соотношение называется аппроксимацией
(приближением) производной с помощью
отношения конечных разностей (значения
,
в формуле (2) конечные в отличии от их
бесконечно малых значений в (1)).
Рассмотрим
аппроксимацию производной для функции
,
заданной в табличном виде:
![]()
при
![]()
.
Пусть шаг – разность между соседними
значениями аргумента – постоянный и
равен h.
Запишем выражения для производной
![]()
при
![]()
.
В зависимости от способа вычисления
конечных разностей получаем разные
формулы для вычисления производной в
одной и той же точке:
![]()
(3)
с
помощью левых разностей;
![]()
(4)
с помощью правых
разностей;
![]()
(5)
с помощью центральных
разностей.
Выражения для
второй производной
![]()
(6)
2.
Использование интерполяционных формул.
Предположим, что функция
![]()
,
заданная в виде таблицы с постоянным
шагом
![]()
![]()
,
может быть аппроксимирована
интерполяционным многочленом Ньютона:
![]()
.
(7)
Дифференцируя
этот многочлен по переменной
с учетом правила дифференцирования
сложной функции:
![]()
можно
получить формулы для вычисления
производных любого порядка:

Пример.
Вычислить в точке
![]()
первую и вторую производные функции,
заданной таблицей.
Здесь
![]()
Используя полученные выше формулы,
находим

|
|
|
|
|
|
||
|
0 0.1 0.2 0.3 0.4 0.5 |
1.2833 1.8107 2.3606 2.9577 3.5969 4.2833 |
0.5274 0.5599 0.5971 0.6392 0.6864 |
0.0325 0.0372 0.0421 0.0472 |
0.0047 0.0049 0.0051 |
0.0002 0.0002 |
0.0000 |
Запишем
интерполяционный многочлен Лагранжа
![]()
и его остаточный член
![]()
для случая трех узлов интерполяции (![]()
)
и найдем их производные:

Здесь
![]()
– значение производной третьего порядка
в некоторой внутренней точке
![]()
Запишем
выражение для производной
![]()
при
![]()
:

Аналогичные
соотношения можно получить и для
значений
![]()
при
![]()
![]()
(8)
Записывая
интерполяционный многочлен Лагранжа
и его остаточный член для случая четырех
узлов (![]()
),
получаем следующие аппроксимации
производных:

(9)
В
случае пяти узлов
![]()
получим

(10)
Выпишем
аппроксимации производных для узла с
произвольным номером
![]()
,
считая его центральным:

(11)
С
помощью интерполяционных многочленов
Лагранжа можно получить аппроксимации
для старших производных. Приведем
аппроксимации для вторых производных.
В
случае трех узлов интерполяции (
)
имеем
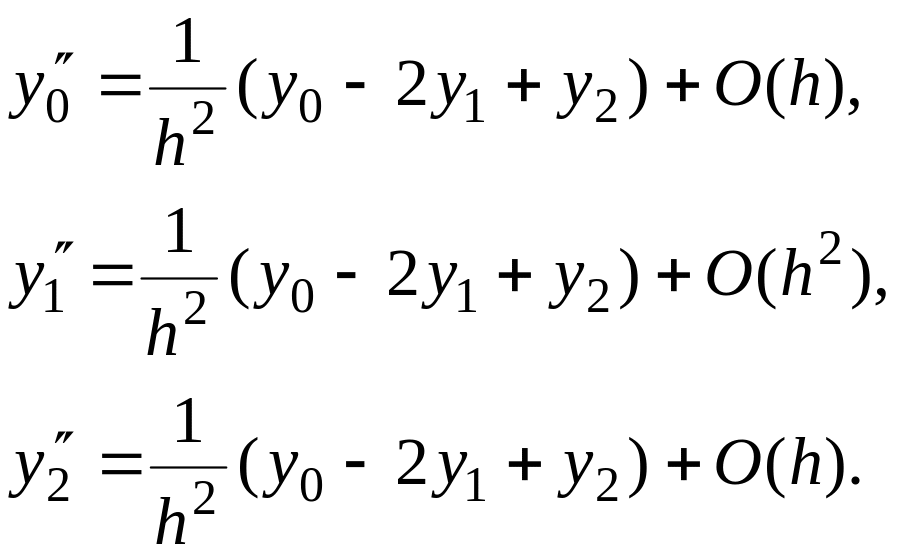
(12)
В
случае четырех узлов (![]()
)
имеем

(13)
В
случае пяти узлов (![]()
)
имеем

(14)
3.
Улучшение аппроксимации производной.
Метод Рунге-Ромберга. Сущность метода
Рунге – Ромберга. Пусть
![]()
– производная, которая подлежит
аппроксимации;
![]()
– конечно–разностная аппроксимация
этой производной на равномерной сетке
с шагом h;
R
– погрешность (остаточный член)
аппроксимации, главный член которой
можно записать в виде
![]()
т.е.
![]()
![]()
.
(15).
Формула
(15) позволяет по результатам двух
расчетов значений производной
и
![]()
(с шагом h
и kh)
с порядком точности p
найти её уточненное значение с порядком
точности p+1.
Пример.
Вычислить производную функции
![]()
в точке x=1.
Очевидно, что
![]()
,
поэтому
![]()
Найдем эту производную численно. Составим
таблицу значений функции:
|
x |
0.8 |
0.9 |
1.0 |
|
y |
0.512 |
0.729 |
1.0 |
Воспользуемся
аппроксимацией производной с помощью
левых разностей, имеющей первый порядок
(p=1).
Примем шаг равным 0.1 и 0.2, т.е. k=2.
Получим

По
формуле Рунге найдем уточненное значение
производной:
![]()
Задачи
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
30.04.2022611.84 Кб432.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При делении приближенного числа на точное в частном получается столько’ верных значащих цифр, сколько их содержится в делимом. Например, в частном 35,7:25= 1,428 (делимое — приближенное число, делитель — точное) следует оставить три цифры, т. е. 1,43.
При делении приближенного числа на приближенное в частном получается столько верных знаков, сколько их в числе с меньшим количеством верных цифр. Поэтому при делении приближенных чисел с разным количеством верных знаков последние уравниваются по числу знаков менее точного числа. Например, если требуется разделить 65,268 на 21,8, то достаточно сохранить в делимом три первые цифры 65,3 (с округлением). Частное от деления 65,3 на 21,8 равно 2,99. Если в качестве делимою возьмем число 65,268, то результат получим в виде числа 2,99394, т. е. верными цифрами будут те же три знака 2,99 и, стало быть, вычисления, относящиеся к получению остальных трех знаков, в данном случае оказались практически совершенно бесполезными.
Если делимое и делитель даны о большим количеством знаков, а в частном желают получить ограниченное число их (2—4 знака), то в делимом и делителе сохраняют на один знак больше (т. е. соответственно 3—5 знаков) против желаемого количества знаков в частном.
Соблюдение этого правила особенно важно в том случае, когда первая значащая цифра делимого меньше первой значащей цифры делителя.
Не лишне также запомнить весьма полезное для практических вычислений следующее правило: если в приближенном делителе первая цифра больше или равна 5, то в делителе можно сохранить только то количество знаков, какое желают получить в частном.
Покажем теперь на примере часто применяемый способ сокращенного деления приближенных чисел.
Пусть требуется найти частное от деления 4,2872 на 6,724 с четырьмя верными цифрами.
В данном примере делимое меньше делителя, значит, в частном будет нуль целых. Заметив это, ‘будем производить деление, не обращая пока внимания на запятые в делимом и делителе.
6724
2528 2016
672 3
Первую значащую цифру частного и первый остаток находим обычным способом:
42872 40344
2528
Далее, вместо раздробления первого остатка в десятичные доли отбросим крайнюю цифру делителя справа и будем делить первый остаток на оставшиеся три цифры делителя:
Повторяем тот же прием со вторым остатком, отбрасывая крайнюю цифру делителя:
512 67
469 7
43
Наконец, повторяем тот же прием с третьим остатком, отбрасывая следующую цифру делителя и округляя оставшуюся:
43 42
1
Деление закончено, в частном имеем четыре знака — 0,6376.
Ход решения этого примера можно короче представить в таком виде:
6724
42872 40344
2528 2016
6376
(: на 672) (: на 67) (:>на 7)
512 469
43 42
1
Решение того же примера обычным способом имеет такой вид:
42872 40344
25280 20172
51080 47068
40120 33620
6724
63759
65000 60516
Сопоставляя указанные способы деления, нетрудно видеть, насколько первый из них проще второго. Выполнение деления сокращенным способом требует в несколько раз меньше времени, нежели обычным путем.
Очень удобным и практически весьма ценным оказывается этот способ при делении на счетах, в чем легко можно убедиться на практике.
Добавить комментарий
1) надо посчитать относительные погрешности трех исходных чисел
и сложить их. Это будет отн погр результата.
Как найти отн погр исходных чисел?
По соглашению абсолютная погрешность исходных чисел равна половине
единицы разряда последнего знака, т. е.
а_1= 0.05 д_1 = 0.05 / 25.1 = 0.0020
а_2= 0.0005 значит д_2 = 0.0005/1.173 = 0.00043
а_3 = 0.005 д_3 = 0.005 / 5.91 = 0.00085
д=д_1+д_2+д_3 = 0. 00328
округляем относительную погрешность до двух значащих цифр
всегда вверх
получаем д = 0.0033 или 0.004 если до одной значащей цифры
Теперь вычисляем результат деления
25,1 : 1,173 : 5,91. = 3.6207 пока оставим лишние цифры
вычислим теперь абсолютную погрешность
3.6207 * 0.0033 = 0.012
мы видим, что абсолютная погрешность меньше половины одной десятой,
но больше половины одной сотой
значит абсолютную погрешность надо округлить до сотых
а=0.02
Значит последняя верная цифра в результате будет разряд десятых
Ответ: 3.6 все цифры верные
или 3.62 +- 0.02 (все погрешности округляются вверх! )
после округления абсолютной погрешности подрастает относительная
и становится равной 0.0055
вот такие мучения делить приближенные числа!
Тема
урока: «Приближение суммы, разности, произведения и частного двух чисел»
Теоретический
материал
Зачастую
необходимо быстро прикинуть результат, который получается при сложении,
вычитании, умножении или делении двух десятичных дробей. Если дроби имеют много
знаков после запятой, выполнить эти действия быстро довольно сложно. Для этого
используют правила приближения суммы, разности, произведения и частного двух
чисел.
Сумма (разность, произведение, частное) двух
чисел считается приближённо равной сумме (разности, произведению, частному) их
приближений.
Поясню на примере.
1,45 + 2,32
Округлим данные числа до десятых.
1,45 ≈ 1,5
2,32 ≈ 2,3
Сложим приближённые значения дробей.
1,5 + 2,3 = 3,8
Проверим с исходными числами.
1,45 + 2,32 = 3,77
Округлим сумму до десятых.
3,77 ≈ 3,8
Получили тот же результат.
Итак, чтобы
вычислить приближённую сумму или разность двух чисел, надо округлить эти числа
с одинаковой точностью, то есть до одного и того же разряда. Затем сложить или
вычесть полученные приближения.
Рассмотрим пример.
23,184567 + 4,4486
Округлим эти числа с точностью до одной
сотой.
23,184567 ≈ 23,18
4,4486 ≈ 4,45
Найдём сумму приближённых значений.
23,18 + 4,45 = 27,63
23,184567 + 4,4486 ≈ 27,63
Теперь рассмотрим умножение и деление.
Чтобы вычислить
приближённое произведение или частное двух чисел, надо округлить эти числа с
точностью до одной и той же значащей цифры, перемножить или разделить
полученные приближения и результат округлить до той же значащей цифры.
Пусть даны числа.
246,76556 и 0,0078653
Найдём их произведение и частное.
Округлим числа до трёх значащих цифр.
246,76556 ≈ 247
0,0078653 ≈ 0,00787
Вычислим произведение их приближений.
247·0,00787 = 1,94389
Округлим результат также до трёх значащих
цифр.
1,94389 ≈ 1,94
Получаем, что
246,76556 · 0,0078653 ≈ 1,94
Вычислим частное приближений этих чисел и
тоже округлим его до трёх значащих цифр.
247 : 0,00787 = 31385,00635… ≈ 31400
Получаем, что
246,76556 : 0,0078653 ≈ 31400
Точность вычислений находится в противоречии
с простотой вычислений. Чем большим количеством цифр мы пользуемся, тем точнее
наш результат.
Разбор заданий.
В
рабочей тетради решить задания № 911, 912(2 столбик), 913(2 столбик), 914(а, б).
Проверьте
правильность вашего решения:
№
911.
а)
а = 3,28 » 3,3;
b = 0,11 » 0,1;
a
+ b = 3,3 + 0,1 = 3,4.
a
– b = 3,3 – 0,1 = 3,2
б)
а
= -1,256 » -1,3;
b = 2,555 » 2,6;
a
+ b = -1,3 + 2,6 = 1,3;
a
– b = -1,3 – 2,6 = -3,9.
в)
а
= 0,010010 » 0;
b = 0,2 » 0,2;
a
+ b = 0 + 0,2 = 0,2;
a
– b = 0 – 0,2 = -0,2.
г)
а
= -1,256 » -1,3;
b = -3,42426 » – 3,4;
a
+ b = 2,7 = (-3,4) = -0,7;
a
– b = 2,7 + 3,4 = 6,1.
г)
а = 0,5642 » 0,56;
b = -3,573 »
-3,57;
a
+ b = 0,56 + (-3,57) = -3,01;
a
– b = 0,56 – (-3,57) = 4,13.
е)
а
= -9,5273 » -9,53;
b = -11,1928 » -11,19;
a
+ b = -9,53 + (– 11,19) = -20,72;
a
– b = -9,53 – (-11,19) = 1,66.
№
913
б)
а = 2,1456 » 2,15;
b = 0,78788 »
0,788;
a
∙ b = 2,15 ∙ 0,788 = 1,6942
»
1,69; – умножаем обязательно в столбик!!!
a
: b = 2,15 : 0,788 = 2150 : 788 = 2,7284….» 2,73.
– делим в столбик!!!!!
г)
а = 0,03531 » 0,0353;
b = 357,693 »
358;
a
∙ b = 0,0353 ∙ 358 = 12,6374
»
12,6; – в тетради должно быть умножение в столбик!
a
: b =
0,0353 : 358 = 0,000098603….» 0,0000986. – в тетради
должно быть деление в столбик.
Домашнее задание: Выучить параграф
4.11 страница 171 – 173; письменно выполнить в тетради: № 912(1
столбик), 913(1 столбик).
