Как найти частное решение линейного неоднородного уравнения

Данная статья раскрывает вопрос о решении линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Будет рассмотрена теория вместе с примерами приведенных задач. Для расшифровки непонятных терминов необходимо обращаться к теме об основных определениях и понятиях теории дифференциальных уравнений.

Рассмотрим линейное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами вида y”+p·y’+q·y=f(x), где произвольными числами являются p и q, а имеющаяся функция f(х) непрерывная на интервале интегрирования x.

Перейдем к формулировке теоремы общего решения ЛНДУ.

Теорема общего решения ЛДНУ

Общим решением, находящимся на интервале х, неоднородного дифференциального уравнения вида y(n)+fn-1(x)·y(n-1)+…+f0(x)·y=f(x) с непрерывными коэффициентами интегрирования на x интервале f0(x), f1(x),…, fn-1(x) и непрерывной функцией f(x) равняется сумме общего решения y0, которое соответствует ЛОДУ и каким-нибудь частным решением y~, где исходным неоднородным уравнением является y=y0+y~.

Отсюда видно, что решение такого уравнения второго порядка имеет вид y=y0+y~. Алгоритм нахождения  y0 рассмотрен в статье о линейных однородных дифференциальных уравнениях второго порядка с постоянными коэффициентами. После чего следует переходить к определению y~.

Выбор частного решения ЛНДУ зависит от вида имеющейся функции f(x), располагающейся в правой части уравнения. Для этого необходимо рассмотреть отдельно решения линейных неоднородных дифференциальных уравнений второго порядка при постоянных коэффициентах.

Когда f(x) считается за многочлен n-ой степени f(x) = Pn(x), отсюда следует, что частное решение ЛНДУ находим по формуле вида y~=Qn(x)·xγ, где Qn(x) является многочленом степени n, r – это количество нулевых корней характеристического уравнения. Значение y~ является частным решением y~”+p·y~’+q·y~=f(x), тогда имеющиеся коэффициенты, которые определены многочленом
Qn(x), отыскиваем при помощи метода неопределенных коэффициентов из равенства y~”+p·y~’+q·y~=f(x).

Когда функция f(x) представляется  в виде произведения многочлена со степенью n и экспоненты f(x)=Pn(x)·eax, тогда отсюда получаем, что  частным решением ЛНДУ второго порядка будет уравнение вида y~=eax·Qn(x)·xγ, где Qn(x) является многочленом n-ой степени, а r – количеством корней характеристического уравнения, равняющиеся α.

Коэффициенты, принадлежащие Qn(x) находятся по равенству  y~”+p·y~’+q·y~=f(x).

Когда функция записывается как f(x)=A1cos(βx)+B1sinβx, а А1 и В1 являются числами, тогда частным решением ЛНДУ считается уравнение вида y~=Acosβx+Bsinβx·xγ, где А и В считаются неопределенными коэффициентами, а r числом комплексно сопряженных корней, относящихся к характеристическому уравнению, равняющимся ±iβ. В этом случае поиск коэффициентов проводится по равенству y~”+p·y~’+q·y~=f(x).

Когда f(x)=eax·Pn(x)sin(βx)+Qk(x)cos(βx), тогда y~=eax·(Lm(x)sin(βx)+Nm(x)cos(βx)·xγ. Имеем, что r – это число комплексно сопряженных пар корней, относящихся к характеристическому уравнению, равняются α±iβ, где Pn(x), Qk(x), Lm(x) и Nm(x) являются многочленами степени n, k, т, m, где m=max(n, k). Нахождение коэффициентов Lm(x) и Nm(x) производится, исходя из равенства y~”+p·y~’+q·y~=f(x).

Алгоритм решения ЛДНУ

116
117

дифференциальные уравнения

второго порядка

с постоянными
коэффициентами

13.1. Структура решения неоднородного
линейного

дифференциального уравнения второго
порядка

с постоянными коэффициентами

Уравнение вида

,

где pиq– вещественные числа, называется
линейным неоднородным уравнением
второго порядка с постоянными
коэффициентами.

Общее решение этого уравнения
представляет собой сумму частного
решения неоднородного уравнения y_ч.н.и общего решения соответствующего
однородного уравненияy_о.о.,
то естьy=y_ч.н.+y_о.о.. Это
утверждение составляет содержание
теоремы о структуре общего решения
неоднородного линейного дифференциального
уравнения второго порядка с постоянными
коэффициентами.

Напомним, уравнение является однородным,
если f(x)
равно нулю. Для того чтобы решить
однородное дифференциальное уравнение,
необходимо составить характеристическое
уравнение.
При его решении возможны следующие три
случая.

Случай 1. Если корни k₁,k₂ различны, то
общее решение однородного уравнения
имеет вид:

.

Случай 2. Если k₁ =k₂ =k,
то общее решение однородного уравнения
имеет вид:

.

Случай 3. Если
,
то общее решение однородного уравнения
имеет вид:

,

где
,.

13.2. Нахождение частных решений неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами

Частное решение линейного неоднородного
уравнения зависит от вида правой части
уравнения, то есть от функции
.

Если
,
где–данный многочлен степени,
то частное решение линейного неоднородного
уравнения имеет вид:

,

где
– многочлен степенис неизвестными коэффициентами, которые
нужно найти,

– число корней характеристического
уравнения, равных нулю.

Если
,
то частное решение линейного неоднородного
уравнения имеет вид:

,

где
– многочлен степенис неизвестными коэффициентами,

– кратность корня характеристического
уравнения.

Если
,
где,и– известные числа, то частное решение
линейного неоднородного уравнения
имеет вид:

где
,– неизвестные коэффициенты,

– число корней характеристического
уравнения, равных.

13.3. Примеры решений неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами

Рассмотрим примеры решения неоднородных
дифференциальных уравнений второго
порядка с постоянными коэффициентами.

Пример 1.Найти общее решение уравнения.

Решение.Характеристическое уравнениеимеет корниk₁ =
0,k₂ = 1. Общее
решение однородного уравнения тогда
имеет вид:

.

Найдем частное решение неоднородного
уравнения. Так как 0 является корнем
характеристического уравнения кратности
т = 1, то частное решение имеет вид:

.

Найдем
и:,.

Теперь подставим производные в исходное
уравнение, получим:

.

Приравнивая коэффициенты при одинаковых
степенях
,
получим систему алгебраических уравнений:

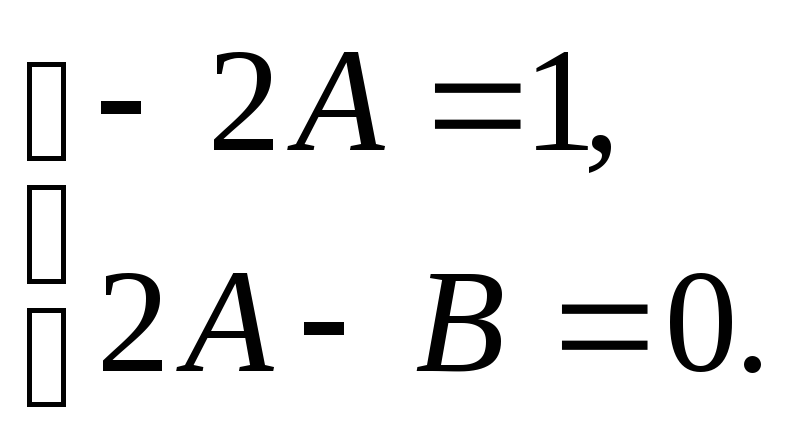
Решая систему, находим, что
,.
Итак,.
Тогда общее решение неоднородного
уравнения примет вид:

.

Пример 2.Найти общее решение уравнения.

Решение. Характеристическое уравнение
имеет вид:,
которое имеет корниk₁
= 2,k₂ = 3.
Следовательно, общее решение однородного
уравнения примет вид:

.

Так как
= 1 не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения необходимо искать в виде:.
Подставив
ив исходное уравнение, получим:

;

;

;

.

Приравняем коэффициенты при одинаковых
степенях
,
получим систему уравнений:

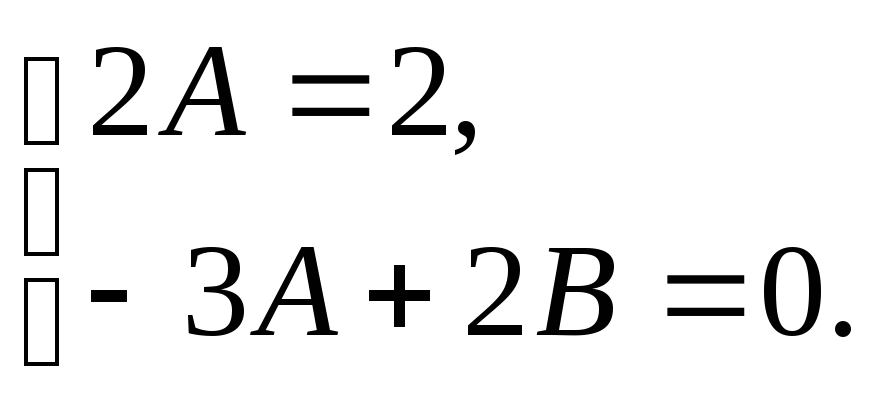
Откуда находим, что
,.

Находим общее решение неоднородного
уравнения:

Пример 3.Найти частное решение
уравнения,
удовлетворяющее начальным условиям,.

Решение. Характеристическое уравнениеk²+ 1 = 0 действительных
корней не имеет. Найдеми:

,.

Общее решение однородного уравнения
имеет вид:

.

Найдем частное решение неоднородного
уравнения. Так как 2 не является корнем
характеристического уравнения, то

;

;

.

Подставим
ив исходное уравнение, получим:

;

.

Из последнего равенства получим систему
уравнений:

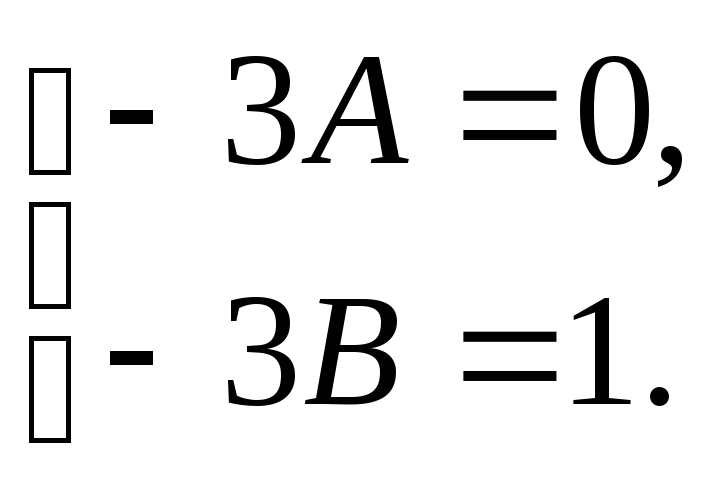
Откуда следует, что
,.

Тогда общее решение неоднородного
уравнения имеет вид:

.

Для того чтобы найти частное решение
исходного уравнения, подставим начальные
условия в полученное решение. Имеем:

,.

,

,.

Тогда получаем, что частное решение,
удовлетворяющее начальным условиям
,,
имеет вид:

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.

Как найти общее и частное решение линейных дифференциальных уравнений

Линейное дифференциальное уравнение – это уравнение, в котором все $y$ и его производные, входят только в первой степени и не перемножаются между собой.

В этой статье рассмотрим решение таких уравнений первого и второго порядка с неоднородной правой частью. В зависимости от порядка диффура выбирается метод его решения. Хотя есть универсальный метод вариации произвольных постоянных. Разберем все методы.

Линейное ДУ первого порядка

Линейные дифференциальные уравнения первого порядка имеют следующий вид $$y’+g(x)y=f(x),$$ где $g(x)$ и $f(x)$ некоторые функции. Для решения такого типа уравнений можно применить метод Бернулли, либо метод Лагранжа (вариация произвольной постоянной).

Метод Бернулли

1. Выполняем подстановку $y=uv, y’=u’v+uv’$, где $u(x),v(x)$ некоторые функции
2. Строим систему уравнений, чтобы найти $u(x)$ и $v(x)$
3. Подставляем $u(x), v(x)$ в $y=uv$, чтобы получить общее решение.

Пример 1

Найти частное решение линейного дифференциального уравнения первого порядка $$y’-y tg x=frac{1}{cos x}, y(0)=0.$$

Решение

Первым шагом делаем подстановку $y=uv, y’=u’v+uv’$ и получаем $$u’v+uv’-uv tg x=frac{1}{cos x}.$$ Теперь выносим за скобки функцию $u$ и составляем систему уравнений: $$u’v+u(v’-v tg x)=frac{1}{cos x}$$ $$begin{cases} v’-v tg x = 0 \ u’v=frac{1}{cos x} end{cases}.$$ Сначала решаем первое уравнение методом разделяющихся переменных, чтобы из него получить $v(x)$: $$begin{cases} frac{dv}{v} = tg x dx \ u’v=frac{1}{cos x} end{cases} Rightarrow begin{cases} ln|v| = -int frac{d(cos x)}{cos x} \ u’v = frac{1}{cos x} end{cases}$$ $$begin{cases} ln|v| = -ln|cos x| \ u’v=frac{1}{cos x} end{cases} Rightarrow begin{cases} v=frac{1}{cos x} \ u’ = 1 end{cases} Rightarrow begin{cases} v=frac{1}{cos x} \ u=x+C end{cases}.$$ Таким образом подставляем найденные $u$ и $v$ в подстановку $y=uv$, чтобы получить общее решение линейного дифференциального уравнения $$y=frac{x+C}{cos x}.$$ Но по условию требуется найти частное решение, поэтому используя дополнительное условие $y(0)=0$ находим константу $C$ $$frac{0+C}{cos 0} = 0 Rightarrow C = 1.$$ Теперь зная значение $C=1$ подставляем его в общее решение и получаем ответ в виде частного решения линейного дифференциального уравнения $$y = frac{x}{cos x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y = frac{x}{cos x}$$

Метод Лагранжа (вариация произвольной постоянной)

1. Находим общее решение однородного уравнения
2. В общем решении заменяем постоянную $C$ на функцию $C(x)$
3. Находим $y’$ и подставляем его вместе с $y$ в исходное уравнение
4. Получаем чему равно $C(x)$ из последнего равенства
5. Подставляем $C(x)$ в ранее полученное общее решение и записываем ответ

Пример 2

Решить линейное дифференциальное уравнение первого порядка $$y’ cos^2 x + y = tg x, quad y(0)=0.$$

Решение

Сначала приведем уравнение к виду $y’+g(x)=f(x)$ путем деления обеих частей диффура на квадрат косинуса $$y’ + frac{y}{cos^2 x} = frac{sin x}{cos^3 x}.$$ Теперь находим общее решение однородного дифференциального уравнения $$y’+frac{y}{cos^2 x} = 0.$$ Разделяем переменные по разные стороны и интегрируем обе части: $$frac{dy}{dx}=-frac{y}{cos^2 x}$$ $$int frac{dy}{y}=-int frac{dx}{cos^2 x}$$ $$ln|y|=-tg x + C$$ $$y = Ce^{-tg x}.$$ Теперь найдем частное решение неоднородного уравнения методом Лагранжа варьируя произвольную постоянную. А именно, заменяем в полученном общем решении константу $C$ на функцию $C(x)$ $$y = C(x)e^{-tg x}.$$ Находим производную функции $$y’ = C'(x)e^{-tg x} – C(x)e^{-tg x} frac{1}{cos^2 x}.$$ Подставляем общее решение и его производную в исходное линейное дифференциальное уравнение, чтобы получить $C'(x)$ $$(C'(x)e^{-tg x} – C(x)e^{-tg x} frac{1}{cos^2 x}) cos^2 x + C(x)e^{-tg x} = tg x.$$ После упрощения получаем, что $$C'(x)e^{-tg x} cos^2 x = tg x.$$ Умножаем уравнение на $e^{tg x}$ и делим на $cos^2 x$ $$C'(x) = frac{tg x}{cos^2 x} e^{tg x}.$$ Теперь, можно получить $C(x)$, просто проинтегрировав правую часть уравнения $$C(x) = int frac{tg x}{cos^2 x} e^{tg x} dx. $$ Выполняем подведение под знак дифференциала $frac{1}{cos^2 x}$ $$C(x) = int tg x e^{tg x} d(tg x).$$ Для комфорта взятия интеграла сделаем замену $tg x = t$, а затем применяя метод интегрирования по частям найдем решение интеграла $$C(x)=int t e^t dt = begin{vmatrix} u = t qquad du=dt \ dv=e^t qquad v=e^t end{vmatrix} = te^t – int e^t dt = te^t – e^t + C.$$ Возвращаемся назад к иксам $$C(x) = te^t – e^t + C = tg x e^{tg x} – e^{tg x} + C.$$ Итак, теперь можно записать общее решение линейного дифференциального уравнения неоднородного $$ytext{о.н.} = ( tg x e^{tg x} – e^{tg x} + C)e^{-tg x} = tg x – 1 + Ce^{-tg x}.$$ По условию задачи требуется найти частное решение, значит применяем условие $y(0)=0$ и находим значение постоянной $C$ $$0 – 1 + C = 0 Rightarrow C=1.$$ Теперь можно записать окончательный ответ $$y = e^{-tg x} + tg x – 1.$$

Ответ

$$y = e^{-tg x} + tg x – 1$$

Линейное ДУ второго порядка

Обычно в контрольных работах дают задачи на решение линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. Поэтому разберем как решать именно такие уравнения $$y”+py’+qy=f(x).$$

Метод подбора по правой части

Общее решение линейного неоднородного уравнения складывается из общего решения однородного и частного решения неоднородного уравнений $$y_text{о.н.} = y_text{о.о.}+y_text{ч.н.}.$$ Поэтому первым делом нужно решить однородное уравнение (т.е. f(x)=0), а затем найти частное решение подобрав правую часть по таблице.

Для того, чтобы найти общее решение линейного однородного уравнения, требуется составить характеристический многочлен и найти его корни $$lambda^2 + plambda + q = 0.$$ В зависимости от получившихся корней общее решение однородного уравнения выглядит следующим образом:

1. $lambda_1 neq lambda_2$, то $y_text{о.о.} = C_1 e^{lambda_1 x} + C_2 e^{lambda_2 x}$
2. $lambda_1 = lambda_2$, то $y_text{о.о.} = C_1 e^{lambda_1 x} + C_2 xe^{lambda_1 x}$
3. $lambda_{1,2} = alpha pm beta i$, то $y_text{о.о.} = C_1e^{alpha x}cos beta x + C_2 e^{alpha x} sin beta x$.

Далее необходимо по виду правой части подобрать частное решение $y_text{ч.н.}$. Для этого нужно воспользоваться таблицей.

№	Правая часть	Корни характеристического многочлена	Вид частного решения
1	$$P_n (x)$$	Число 0 не является корнем характеристического уравнения.	$$tilde{P_n}(x)$$
Число 0 – корень характеристического уравнения кратности $S$.	$$x^s tilde{P_n}(x)$$
2	$$P_n (x) e^{alpha x}$$	Число $alpha$ не является корнем характеристического уравнения.	$$tilde{P_n} (x) e^{alpha x}$$
Число $alpha$ является корнем характеристического уравнения кратности $S$.	$$x^s tilde{P_n} (x) e^{alpha x}$$
3	$$P_n (x) cos beta x + Q_m (x) sin beta x$$	Число $pm ibeta$ не является корнем характеристического уравнения.	$$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$
Число $pm ibeta$ является корнем характеристического уравнения кратности $S$.	$$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$
4	$$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$	Число $alpha pm ibeta$ не является корнем характеристического уравнения.	$$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$
Число $alpha pm ibeta$ является корнем характеристического уравнения.	$$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$

Где $P_n(x)$ и $Q_m(x)$ многочлены.

Пример 3

Найти общее решение линейного дифференциального уравнения второго порядка $$y”+y’-2y=8sin 2x.$$

Решение

Первым делом находим общее решение однородного дифференциального уравнения $$y”+y’-2y=0.$$ Для этого составляем характеристический многочлен и находим его корни по общей формуле решения квадратных уравнений: $$lambda^2+lambda-2=0$$ $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, quad lambda_2 = 1.$$ Теперь, используя корни, записывам $$y_text{о.о.} = C_1e^{-2 x} + C_2e^{x}.$$ Теперь нужно найти частное решение неоднородного уравнения $y_text{ч.н.}$ методом подбора правой части. Смотрим на неё и видим, что в нее входит произведение многочлена нулевой степени на косинус. Значит, частное решение будет подбирать в виде $$y_text{ч.н.} = Acos 2x + Bsin 2x,$$ где $A$ и $B$ неизвестные коэффициенты, которые требуется найти на следующем этапе решения. Найдем первую и вторую производную от частного решения: $$y’_text{ч.н.} = -2Asin 2x + 2Bcos 2x$$ $$y”_text{ч.н.} = -4Acos 2x – 4Bsin 2x$$ Теперь подставим полученные производные от $y_text{ч.н.}$ и его само в исходное дифференциальное уравнение, чтобы получить значения $A$ и $B$ методом неопределенных коэффициентов: $$-4Acos 2x – 4Bsin 2x -2Asin 2x + 2Bcos 2x – 2Acos 2x -2Bsin 2x = 8sin 2x$$ $$(2B – 6A)cos 2x + (-6B – 2A)sin 2x = 8sin 2x.$$ Теперь необходимо составить систему уравнений. Справа видим только синус, значит все что перед косинусом слева равно нулю. А всё что перед синусом равно восьми $$begin{cases} 2B-6A = 0 \ -6B-2A = 8 end{cases} Leftrightarrow begin{cases} B-3A=0 \ 3B+A=-4 end{cases} Leftrightarrow begin{cases} B = frac{6}{5} \ A=-frac{2}{5} end{cases}$$ Теперь частное решение неоднородного уравнения выглядит следующим образом $$y_text{ч.н.} = -frac{2}{5} cos 2x – frac{6}{5}sin 2x.$$ Подставляем все найденные данные в окончательную формулу, чтобы записать ответ $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.} = C_1e^{-2 x} + C_2e^{x} -frac{2}{5} cos 2x – frac{6}{5}sin 2x.$$

Ответ

$$y = C_1e^{-2 x} + C_2e^{x} -frac{2}{5} cos 2x – frac{6}{5}sin 2x$$

Пример 4

Решить линейное дифференциальное уравнение $$y”-4y=e^{2x}sin 2x.$$

Решение

Сначала получим общее решение однородного уравнения $$y”-4y=0.$$ Составляем характеристическое уравнение и найдем его корни: $$lambda^2 – 4 = 0$$ $$(lambda – 2)(lambda + 2) = 0$$ $$lambda_1 = -2, quad lambda_2 = 2.$$ Записываем теперь решение $$y_text{о.о.} = C_1 e^{2x} + C_2 e^{-2x}.$$ Теперь выполним подбор частного решения неоднородного уравнения, основываясь на типе правой части. Она состоит из произведение экспоненты на синус, перед которым многочлен. По таблице находим, что частное решение нужно искать в виде $$y_text{ч.н.} = Ae^{2x}cos 2x + Be^{2x}sin 2x.$$ Необходимо найти коэффициенты $A$ и $B$. Для этого нужно найти вторую производную частного решения и подставить в исходное уравнение $$y’_text{ч.н.} = 2Ae^{2x}cos 2x – 2Ae^{2x}sin 2x + 2Be^{2x}sin 2x + 2Be^{2x}cos 2x = $$ $$ = (2A+2B)e^{2x}cos 2x + (2B-2A)e^{2x}sin 2x$$ $$y”_text{ч.н.} = 2(2A+2B)e^{2x}cos 2x – 2(2A+2B)e^{2x}sin 2x + 2(2B-2A)e^{2x}sin 2x + 2(2B-2A)e^{2x}cos 2x = $$ $$ = 8Be^{2x}cos 2x – 8Ae^{2x}sin 2x.$$ Подставляем в исходное ДУ: $$8Be^{2x}cos 2x – 8Ae^{2x}sin 2x – 4Ae^{2x}cos 2x – 4Be^{2x}sin 2x = e^{2x} sin 2x$$ $$(8B-4A)e^{2x}cos 2x + (-8A-4B)e^{2x}sin 2x = e^{2x}sin 2x.$$ Теперь составляем систему уравнений путем сопоставления левой и правой части. То, что слева перед синусом приравниваем к тому, что справа перед синусом. А справа косинуса нет, значит там ноль. Поэтому приравниваем скобки перед косинусом слева к нулю $$begin{cases} 8B-4A=0 \ -8A-4B = 1 end{cases} Rightarrow begin{cases} 2B-A=0 \ -8A-4B=1 end{cases} Rightarrow begin{cases} A = -frac{1}{10} \ B = -frac{1}{20} end{cases}.$$ Теперь частное решение приобретает вид $$y_text{ч.н.} = -frac{1}{10}e^{2x}cos 2x – frac{1}{20} e^{2x} sin 2x,$$ и можно записать окончательный ответ к задаче $$y_text{о.н.} = y_text{о.о.}+y_text{ч.н.} = C_1 e^{2x} + C_2 e^{-2x}-frac{1}{10}e^{2x}cos 2x – frac{1}{20} e^{2x} sin 2x.$$

Ответ

$$y = C_1 e^{2x} + C_2 e^{-2x}-frac{1}{10}e^{2x}cos 2x – frac{1}{20} e^{2x} sin 2x$$

Метод Лагранжа (вариация произвольной постоянной)

Данный метод удобно применять тогда, когда правая часть не подходит под формулы из таблицы. Таким образом, метод Лагранжа становится универсальной палочкой-выручалочкой при решении данного типа задач. Алгоритм следующий:

1. Находим общее решение однородного уравнения $y_text{о.о.} = C_1 y_1 + C_2 y_2$
2. Заменяем константы $C_1,C_2$ на функции $C_1(x)$ и $C_2(x)$
3. Решаем систему методом Крамера $begin{cases} C_1 ‘(x)y_1 + C_2 ‘(x)y_2 = 0 \ C_2 ‘(x)y’_1 + C_2 ‘(x) y’_2 = f(x) end{cases}$
4. Интегрируем полученные $C’_1 (x)$ и $C’_2 (x)$
5. Подставляем $C_1(x)$ и $C_2(x)$ в общее решение $y_text{о.о.}$

Пример 5

Найти общее решение линейного дифференциального уравнения второго порядка $$y”+y=frac{1}{sin x}.$$

Решение

Первым делом находим общее решение однородного уравнения $$y”+y=0, $$ составив характериcтический многочлен $$lambda^2 + 1 = 0, $$ и вычислив его корни $$lambda_{1,2} = pm i.$$ Записываем решение $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Далее заменяем в нём постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и соответственно $C_2(x)$. И сразу замечаем, что $y_1 = cos x$ и $y_2 = sin x$. Это пригодится для дальнейшего решения задачи при построении системы уравнений. А сейчас записываем, что $$y_text{о.о.} = C_1 (x) cos x + C_2(x) sin x.$$ Перед тем как составим систему уравнений найдем производные: $$y’_1 = -sin x$$ $$y’_2 = cos x.$$ Теперь получаем систему и решаем её методом Крамера $$begin{cases} C_1 ‘(x)cos x+C_2(x)sin x = 0 \ -C’_1 (x)sin x + C’_2(x) cos x = frac{1}{sin x} end{cases}.$$ Находим значение главного определителя $$Delta = begin{vmatrix} cos x & sin x \ -sin x & cos x end{vmatrix} = cos^2 x + sin^2 x = 1.$$ Найдем значение первого дополнительного определителя $$Delta_1 = begin{vmatrix} 0 & sin x \ frac{1}{sin x} & cos x end{vmatrix} = -1 .$$ Найдем значение второго дополнительного определителя $$Delta_2 = begin{vmatrix} cos x & 0 \ -sin x & frac{1}{sin x} end{vmatrix} = frac{cos x}{sin x}.$$ Теперь можно получить производные от искомых функций: $$C’_1(x) = frac{Delta_1}{Delta} = -1$$ $$C’_2(x) = frac{Delta_2}{Delta} = frac{cos x}{sin x}.$$ А затем путем интегрирования находим первообразные последних функций: $$C_1(x)=int (-1) dx = -x + tilde{C_1}$$ $$C_2(x)=int frac{cos x}{sin x} dx = int frac{d(sin x)}{sin x} = ln|sin x| + tilde{C_2}.$$ Теперь получим общее решение неоднородного линейного дифференциального уравнения путем подстановки найденных $C_1(x)$ и $C_2(x)$ в $y_text{о.о.}$ $$y_text{о.о.} = (-x + tilde{C_1})cos x + (ln|sin x|+tilde{C_2})sin x.$$

Ответ

$$y = (-x + tilde{C_1})cos x + (ln|sin x|+tilde{C_2})sin x$$