Данная статья раскрывает вопрос о решении линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Будет рассмотрена теория вместе с примерами приведенных задач. Для расшифровки непонятных терминов необходимо обращаться к теме об основных определениях и понятиях теории дифференциальных уравнений.
Рассмотрим линейное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами вида y”+p·y’+q·y=f(x), где произвольными числами являются p и q, а имеющаяся функция f(х) непрерывная на интервале интегрирования x.
Перейдем к формулировке теоремы общего решения ЛНДУ.
Теорема общего решения ЛДНУ
Общим решением, находящимся на интервале х, неоднородного дифференциального уравнения вида y(n)+fn-1(x)·y(n-1)+…+f0(x)·y=f(x) с непрерывными коэффициентами интегрирования на x интервале f0(x), f1(x),…, fn-1(x) и непрерывной функцией f(x) равняется сумме общего решения y0, которое соответствует ЛОДУ и каким-нибудь частным решением y~, где исходным неоднородным уравнением является y=y0+y~.
Отсюда видно, что решение такого уравнения второго порядка имеет вид y=y0+y~. Алгоритм нахождения y0 рассмотрен в статье о линейных однородных дифференциальных уравнениях второго порядка с постоянными коэффициентами. После чего следует переходить к определению y~.
Выбор частного решения ЛНДУ зависит от вида имеющейся функции f(x), располагающейся в правой части уравнения. Для этого необходимо рассмотреть отдельно решения линейных неоднородных дифференциальных уравнений второго порядка при постоянных коэффициентах.
Когда f(x) считается за многочлен n-ой степени f(x) = Pn(x), отсюда следует, что частное решение ЛНДУ находим по формуле вида y~=Qn(x)·xγ, где Qn(x) является многочленом степени n, r – это количество нулевых корней характеристического уравнения. Значение y~ является частным решением y~”+p·y~’+q·y~=f(x), тогда имеющиеся коэффициенты, которые определены многочленом
Qn(x), отыскиваем при помощи метода неопределенных коэффициентов из равенства y~”+p·y~’+q·y~=f(x).
Вычислить по теореме Коши y”-2y’=x2+1, y(0)=2, y'(0)=14.
Решение
Иначе говоря, необходимо перейти к частному решению линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами y”-2y’=x2+1, которое будет удовлетворять заданным условиям y(0)=2, y'(0)=14.
Общим решением линейного неоднородного уравнения является сумма общего решения, которое соответствует уравнению y0 или частному решению неоднородного уравнения y~, то есть y=y0+y~.
Для начала найдем общее решение для ЛНДУ, а после чего – частное.
Перейдем к нахождению y0. Запись характеристического уравнения поможет найти корни. Получаем, что
k2-2k=0k(k-2)=0k1=0, k2=2
Получили, что корни различные и действительные. Поэтому запишем
y0=C1e0x+C2e2x=C1+C2e2x.
Найдем y~. Видно, что правая часть заданного уравнения является многочленом второй степени, тогда один из корней равняется нулю. Отсюда получим, что частным решением для y~ будет
y~=Q2(x)·xγ=(Ax2+Bx+C)·x=Ax3+Bx2+Cx, где значения А, В, С принимают неопределенные коэффициенты.
Найдем их из равенства вида y~”-2y~’=x2+1.
Тогда получим, что:
y~”-2y~’=x2+1(Ax3+Bx2+Cx)”-2(Ax3+Bx2+Cx)’=x2+13Ax2+2Bx+C’-6Ax2-4Bx-2C=x2+16Ax+2B-6Ax2-4Bx-2C=x2+1-6Ax2+x(6A-4B)+2B-2C=x2+1
Приравняв коэффициенты с одинаковыми показателями степеней x, получим систему линейных выражений -6A=16A-4B=02B-2C=1. При решении любым из способов найдем коэффициенты и запишем: A=-16, B=-14, C=-34 и y~=Ax3+Bx2+Cx=-16×3-14×2-34x.
Эта запись называется общим решением исходного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.
Для нахождения частного решения, которое удовлетворяет условиям y(0)=2, y'(0)=14, требуется определить значения C1 и C2 , исходя из равенства вида y=C1+C2e2x-16×3+14×2+34x.
Получаем, что:
y(0)=C1+C2e2x-16×3+14×2+34xx=0=C1+C2y'(0)=C1+C2e2x-16×3+14×2+34x’x=0==2C2e2x-12×2+12x+34x=0=2C2-34
Работаем с полученной системой уравнений вида C1+C2=22C2-34=14, где C1=32, C2=12.
Применив теорему Коши, имеем, что
y=C1+C2e2x-16×3+14×2+34x==32+12e2x-16×3+14×2+34x
Ответ: 32+12e2x-16×3+14×2+34x.
Когда функция f(x) представляется в виде произведения многочлена со степенью n и экспоненты f(x)=Pn(x)·eax, тогда отсюда получаем, что частным решением ЛНДУ второго порядка будет уравнение вида y~=eax·Qn(x)·xγ, где Qn(x) является многочленом n-ой степени, а r – количеством корней характеристического уравнения, равняющиеся α.
Коэффициенты, принадлежащие Qn(x) находятся по равенству y~”+p·y~’+q·y~=f(x).
Найти общее решение дифференциального уравнения вида y”-2y’=(x2+1)·ex.
Решение
Уравнение общего вида y=y0+y~. Указанное уравнение соответствует ЛОДУ y”-2y’=0. По предыдущему примеру видно, что его корни равняются k1=0 и k2=2 и y0=C1+C2e2x по характеристическому уравнению.
Видно, что правой частью уравнения является x2+1·ex. Отсюда ЛНДУ находится через y~=eax·Qn(x)·xγ, где Qn(x), являющимся многочленом второй степени, где α=1 и r=0, потому как у характеристического уравнения отсутствует корень, равный 1. Отсюда получаем, что
y~=eax·Qn(x)·xγ=ex·Ax2+Bx+C·x0=ex·Ax2+Bx+C.
А, В, С являются неизвестными коэффициентами, которые можно найти по равенству y~”-2y~’=(x2+1)·ex.
Получили, что
y~’=ex·Ax2+Bx+C’=ex·Ax2+Bx+C+ex·2Ax+B==ex·Ax2+x2A+B+B+Cy~”=ex·Ax2+x2A+B+B+C’==ex·Ax2+x2A+B+B+C+ex·2Ax+2A+B==ex·Ax2+x4A+B+2A+2B+C
Значит
y~”-2y~’=(x2+1)·ex⇔ex·Ax2+x4A+B+2A+2B+C–2ex·Ax2+x2A+B+B+C=x2+1·ex⇔ex·-Ax2-Bx+2A-C=(x2+1)·ex⇔-Ax2-Bx+2A-C=x2+1⇔-Ax2-Bx+2A-C=1·x2+0·x+1
Показатели при одинаковых коэффициентах приравниваем и получаем систему линейных уравнений. Отсюда и находим А, В, С:
-A=1-B=02A-C=1⇔A=-1B=0C=-3
Ответ: видно, что y~=ex·(Ax2+Bx+C)=ex·-x2+0·x-3=-ex·x2+3 является частным решением ЛНДУ, а y=y0+y=C1e2x-ex·x2+3 – общим решением для неоднородного дифуравнения второго порядка.
Когда функция записывается как f(x)=A1cos(βx)+B1sinβx, а А1 и В1 являются числами, тогда частным решением ЛНДУ считается уравнение вида y~=Acosβx+Bsinβx·xγ, где А и В считаются неопределенными коэффициентами, а r числом комплексно сопряженных корней, относящихся к характеристическому уравнению, равняющимся ±iβ. В этом случае поиск коэффициентов проводится по равенству y~”+p·y~’+q·y~=f(x).
Найти общее решение дифференциального уравнения вида y”+4y=cos(2x)+3sin(2x).
Решение
Перед написанием характеристического уравнения находим y0. Тогда
k2+4=0k2=-4k1=2i, k2=-2i
Имеем пару комплексно сопряженных корней. Преобразуем и получим:
y0=e0·(C1cos(2x)+C2sin(2x))=C1cos2x+C2sin(2x)
Корни из характеристического уравнения считаются сопряженной парой ±2i, тогда f(x)=cos(2x)+3sin(2x). Отсюда видно, что поиск y~ будет производиться из y~=(Acos(βx)+Bsin(βx)·xγ=(Acos(2x)+Bsin(2x))·x. Неизвестные коэффициенты А и В будем искать из равенства вида y~”+4y~=cos(2x)+3sin(2x).
Преобразуем:
y~’=((Acos(2x)+Bsin(2x)·x)’==(-2Asin(2x)+2Bcos(2x))·x+Acos(2x)+Bsin(2x)y~”=((-2Asin(2x)+2Bcos(2x))·x+Acos(2x)+Bsin(2x))’==(-4Acos(2x)-4Bsin(2x))·x-2Asin(2x)+2Bcos(2x)–2Asin(2x)+2Bcos(2x)==(-4Acos(2x)-4Bsin(2x))·x-4Asin(2x)+4Bcos(2x)
Тогда видно, что
y~”+4y~=cos(2x)+3sin(2x)⇔(-4Acos(2x)-4Bsin(2x))·x-4Asin(2x)+4Bcos(2x)++4(Acos(2x)+Bsin(2x))·x=cos(2x)+3sin(2x)⇔-4Asin(2x)+4Bcos(2x)=cos(2x)+3sin(2x)
Необходимо приравнять коэффициенты синусов и косинусов. Получаем систему вида:
-4A=34B=1⇔A=-34B=14
Следует, что y~=(Acos(2x)+Bsin(2x)·x=-34cos(2x)+14sin(2x)·x.
Ответ: общим решением исходного ЛНДУ второго порядка с постоянными коэффициентами считается
y=y0+y~==C1cos(2x)+C2sin(2x)+-34cos(2x)+14sin(2x)·x
Когда f(x)=eax·Pn(x)sin(βx)+Qk(x)cos(βx), тогда y~=eax·(Lm(x)sin(βx)+Nm(x)cos(βx)·xγ. Имеем, что r – это число комплексно сопряженных пар корней, относящихся к характеристическому уравнению, равняются α±iβ, где Pn(x), Qk(x), Lm(x) и Nm(x) являются многочленами степени n, k, т, m, где m=max(n, k). Нахождение коэффициентов Lm(x) и Nm(x) производится, исходя из равенства y~”+p·y~’+q·y~=f(x).
Найти общее решение y”+3y’+2y=-e3x·((38x+45)sin(5x)+(8x-5)cos(5x)).
Решение
По условию видно, что
α=3, β=5, Pn(x)=-38x-45, Qk(x)=-8x+5, n=1, k=1
Тогда m=max(n,k)=1. Производим нахождение y0, предварительно записав характеристическое уравнение вида:
k2-3k+2=0D=32-4·1·2=1k1=3-12=1, k2=3+12=2
Получили, что корни являются действительными и различными. Отсюда y0=C1ex+C2e2x. Далее необходимо искать общее решение, исходя из неоднородного уравнения y~ вида
y~=eαx·(Lm(x)sin(βx)+Nm(x)cos(βx)·xγ==e3x·((Ax+B)cos(5x)+(Cx+D)sin(5x))·x0==e3x·((Ax+B)cos(5x)+(Cx+D)sin(5x))
Известно, что А, В, С являются коэффициентами, r=0, потому как отсутствует пара сопряженных корней, относящихся к характеристическому уравнению с α±iβ=3±5·i. Данные коэффициенты находим из полученного равенства:
y~”-3y~’+2y~=-e3x((38x+45)sin(5x)+(8x-5)cos(5x))⇔(e3x((Ax+B)cos(5x)+(Cx+D)sin(5x)))”–3(e3x((Ax+B)cos(5x)+(Cx+D)sin(5x)))=-e3x((38x+45)sin(5x)+(8x-5)cos(5x))
Нахождение производной и подобных слагаемых дает
-e3x·((15A+23C)·x·sin(5x)++(10A+15B-3C+23D)·sin(5x)++(23A-15C)·x·cos(5x)+(-3A+23B-10C-15D)·cos(5x))==-e3x·(38·x·sin(5x)+45·sin(5x)++8·x·cos(5x)-5·cos(5x))
После приравнивания коэффициентов получаем систему вида
15A+23C=3810A+15B-3C+23D=4523A-15C=8-3A+23B-10C-15D=-5⇔A=1B=1C=1D=1
Из всего следует, что
y~=e3x·((Ax+B)cos(5x)+(Cx+D)sin(5x))==e3x·((x+1)cos(5x)+(x+1)sin(5x))
Ответ: теперь получено общее решение заданного линейного уравнения:
y=y0+y~==C1ex+C2e2x+e3x·((x+1)cos(5x)+(x+1)sin(5x))
Алгоритм решения ЛДНУ
Любой другой вид функции f(x) для решения предусматривает соблюдение алгоритма решения:
- нахождение общего решения соответствующего линейного однородного уравнения, где y0=C1⋅y1+C2⋅y2, где y1 и y2 являются линейно независимыми частными решениями ЛОДУ, С1 и С2 считаются произвольными постоянными;
- принятие в качестве общего решения ЛНДУ y=C1(x)⋅y1+C2(x)⋅y2;
- определение производных функции через систему вида C1′(x)+y1(x)+C2′(x)·y2(x)=0C1′(x)+y1′(x)+C2′(x)·y2′(x)=f(x), а нахождение функций C1(x) и C2(x) посредствам интегрирования.
Найти общее решение для y”+36y=24sin(6x)-12cos(6x)+36e6x.
Решение
Переходим к написанию характеристического уравнения, предварительно записав y0, y”+36y=0. Запишем и решим:
k2+36=0k1=6i, k2=-6i⇒y0=C1cos(6x)+C2sin(6x)⇒y1(x)=cos(6x), y2(x)=sin(6x)
Имеем, что запись общего решения заданного уравнения получит вид y=C1(x)·cos(6x)+C2(x)·sin(6x). Необходимо перейти к определению производных функций C1(x) и C2(x) по системе с уравнениями:
C1′(x)·cos(6x)+C2′(x)·sin(6x)=0C1′(x)·(cos(6x))’+C2′(x)·(sin(6x))’=0⇔C1′(x)·cos(6x)+C2′(x)·sin(6x)=0C1′(x)(-6sin(6x)+C2′(x)(6cos(6x))==24sin(6x)-12cos(6x)+36e6x
Необходимо произвести решение относительно C1′(x) и C2′(x) при помощи любого способа. Тогда запишем:
C1′(x)=-4sin2(6x)+2sin(6x)cos(6x)-6e6xsin(6x)C2′(x)=4sin(6x)cos(6x)-2cos2(6x)+6e6xcos(6x)
Каждое из уравнений следует проинтегрировать . Тогда запишем получившиеся уравнения:
C1(x)=13sin(6x)cos(6x)-2x-16cos2(6x)++12e6xcos(6x)-12e6xsin(6x)+C3C2(x)=-16sin(6x)cos(6x)-x-13cos2(6x)++12e6xcos(6x)+12e6xsin(6x)+C4
Отсюда следует, что общее решение будет иметь вид:
y=13sin(6x)cos(6x)-2x-16cos2(6x)++12e6xcos(6x)-12e6xsin(6x)+C3·cos(6x)++-16sin(6x)cos(6x)-x-13cos2(6x)++12e6xcos(6x)+12e6xsin(6x)+C4·sin(6x)==-2x·cos(6x)-x·sin(6x)-16cos(6x)++12e6x+C3·cos(6x)+C4·sin(6x)
Ответ: y=y0+y~=-2x·cos(6x)-x·sin(6x)-16cos(6x)++12e6x+C3·cos(6x)+C4·sin(6x)
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Как решать дифференциальные уравнения
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Основные понятия и определения
-
- Определения
- Типы уравнений
- Алгоритм решения
- Дифференциальные уравнения первого порядка
-
- ДУ с разделяющимися переменными
- Однородные ДУ
- Линейные неоднородные ДУ
- ДУ Бернулли
- ДУ в полных дифференциалах
- Дифференциальные уравнения второго порядка
-
- ДУ допускающие понижение порядка
- Линейные однородные ДУ с постоянными коэффицентами
- Линейные неоднородные ДУ с постоянными коэффициентами
- Метод Лагранжа
Введите уравнение
Условия к задаче (необязательно)
Пример 1 Пример 2 Правила ввода
Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.
Основные понятия и определения
Определения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).
Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y” = 1 $$
Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y”(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.
Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.
В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y”(x)$, поэтому это ДУ второго порядка.
Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.
Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.
Типы уравнений
- ДУ первого порядка
– с разделяющимися переменными
– однородные
– линейные неоднородные
– уравнение Бернулли - ДУ второго порядка
– уравнения допускающие понижение порядка
– однородные с постоянными коэффициентами
– неоднородные с постоянными коэффициентами
Алгоритм решения
- По старшей производной функции $y(x)$ определить порядок ДУ
- Зная порядок, определить тип уравнения
- Узнав тип, подобрать подходящий метод решения
- Используя метод, найти общее решение
- Получить частное решение из общего путем вычисления неизвестной $C$
В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$
ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!
| Пример 1 |
| Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$ |
| Решение |
|
Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$ Теперь подставим $y’$ и $y$ в исходное уравнение. $$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$ Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ. |
| Ответ |
| $$y = Ce^{frac{x^2}{2}} $$ |
Дифференциальные уравнения первого порядка
ДУ с разделяющимися переменными
Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$
СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.
Алгоритм нахождения общего решения:
- Переписываем производные через $y’ = frac{dy}{dx}$
- Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
- Интегрируем обе части уравнения
| Пример 2 |
| Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$ |
| Решение |
|
Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка. Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить “игрики” от “иксов” по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$ После замены производной игрека исходное уравнение приобретает такой формат: $$frac{dy}{dx} = xy$$ Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$. $$ frac{dy}{y} = xdx $$ Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения. $$ int frac{dy}{y} = int xdx $$ Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$. $$ ln|y| = frac{x^2}{2} + C $$ Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем. $$ y = e^{frac{x^2}{2} + C} $$ Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения. Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением. $$ y = Ce^{frac{x^2}{2}} $$ |
| Ответ |
| $$ y = Ce^{frac{x^2}{2}} $$ |
| Пример 3 |
| Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$. |
| Решение |
|
Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$: $$ frac{dy}{dx} = frac{2x}{1+x^2} $$ Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$: $$ dy = frac{2x}{1+x^2} dx $$ Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы: $$ int dy = int frac{2x}{1+x^2} dx $$ $$ y = int frac{2x}{1+x^2} dx $$ Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл: $$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$ Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$: $$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$ Теперь заменив в общем решении $C$ на ноль, получаем частное решение: $$y = ln(1+x^2)$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = ln(1+x^2)$$ |
Однородные ДУ
Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.
Решается по следующему алгоритму:
- Проверить уравнение на однородность с помощью $lambda$
- Привести уравнение к виду $y’ = f(frac{y}{x})$
- Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
- Решить уравнение методом разделяющихся переменных
| Пример 4 |
| Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} – 1$$ |
| Решение |
|
Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$: $$y’ = frac{lambda y}{lambda x} – 1$$ Выполняем сокращение $lambda$ в числителе и знаменателе: $$y’ = frac{y}{x} – 1$$ После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$: $$ t’x + t = t – 1$$ Переносим $t$ в одну сторону и тем самым уничтожаем его: $$ t’x = -1 $$ Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$ Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства: $$dt = -frac{dx}{x}$$ Интегрируем обе части: $$int dt = – int frac{dx}{x}$$ $$t = -ln|x|+C$$ Выполняем назад замену $t = frac{y}{x}$: $$frac{y}{x} = -ln|x|+C$$ Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения: $$y = -xln|x| +Cx$$ |
| Ответ |
| $$y = -xln|x| +Cx$$ |
| Пример 5 |
| Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$ |
| Решение |
|
Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$. $$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$ После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения. Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$ Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$ Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$ Интегрируем обе части уравнения $$int frac{2+t}{t}dt = – int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$ Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y^2 = Cxe^frac{-y}{x}$$ |
Линейные неоднородные ДУ
Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$
Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$.
Алгоритм метода Бернулли:
- Выполняем замену $y=uv$ и $y’ = u’v+uv’$
- Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
- Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ
Алгоритм метода вариации произвольной постоянной:
- Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
- В полученном общем решении заменяем константу $C$ на функцию $C(x)$
- Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
- Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ
| Пример 6 |
| Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$. |
| Решение |
|
Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$ Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$ Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ – 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$ Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$ Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$ Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$ В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$ С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 – x^2.$$ |
| Ответ |
| $$y = x^4 – x^2$$ |
| Пример 7 |
| Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$. |
| Решение |
|
Перепишем уравнение в виде $$ y’ – y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ – y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$ Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$ Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$ Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x – C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$ В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$ Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x – cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x – cos x$. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = Csin x – cos x$$ |
ДУ Бернулли
Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$
Алгоритм решения:
- Выполняем подстановку $y = z^frac{1}{1-alpha}$
- После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
- Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$
| Пример 8 |
| Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$. |
| Решение |
|
Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$ Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ. Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$ Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$ Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$ Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} – int e^{-x} dx = xe^{-x} +e^{-x} + C$$ Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$ |
| Ответ |
| $$y = frac{1}{Ce^x + x + 1}$$ |
ДУ в полных дифференциалах
Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.
Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:
- Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
- Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$
- Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$
| Пример 9 |
| Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$ |
| Решение |
|
Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$. Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$ Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$ Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$ Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$ Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x^2+5xy+y^3 = C.$$ |
Дифференциальные уравнения второго порядка
ДУ допускающие понижение порядка
Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:
- Без функции $y$: $F(x,y’,y”)=0$
- Без переменной $x$: $F(y,y’,y”)=0$
Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.
| Пример 10 |
| Найти частное решение дифференциального уравнения второго порядка $xy”+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$. |
| Решение |
|
Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$ Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$ Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$ Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$ Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$ Записываем частное решение дифференциального уравнения $$y = ln|x|.$$ |
| Ответ |
| $$y = ln|x|$$ |
| Пример 11 |
| Найти частное решение дифференциального уравнения второго порядка $$yy”+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$ |
| Решение |
|
Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y” = p'(y)cdot y’ = p'(y)p$. Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$ В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$ Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$ Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 – Cfrac{1}{y^2}$$ $$(y’)^2 = 1 – Cfrac{1}{y^2}.$$ Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 – Cfrac{1}{1^2} Rightarrow C = 0.$$ Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 – Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$ Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$ |
| Ответ |
| $$y = x + 1$$ |
Линейные однородные ДУ с постоянными коэффицентами
Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y”+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y” Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$
В зависимости от получившихся корней имеем общее решение в различных видах:
- Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
- Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
- Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.
| Пример 12 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’-2y = 0$. |
| Решение |
|
Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$ Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$ Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = C_1 e^{-2x} + C_2 e^{x}$$ |
Линейные неоднородные ДУ с постоянными коэффициентами
Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y”+py’+q = f(x).$$
Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$
Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.
| № | Правая часть | Корни характеристического многочлена | Вид частного решения |
| 1 | $$P_n (x)$$ | Число 0 не является корнем характеристического уравнения. | $$tilde{P_n}(x)$$ |
| Число 0 – корень характеристического уравнения кратности $S$. | $$x^s tilde{P_n}(x)$$ | ||
| 2 | $$P_n (x) e^{alpha x}$$ | Число $alpha$ не является корнем характеристического уравнения. | $$tilde{P_n} (x) e^{alpha x}$$ |
| Число $alpha$ является корнем характеристического уравнения кратности $S$. | $$x^s tilde{P_n} (x) e^{alpha x}$$ | ||
| 3 | $$P_n (x) cos beta x + Q_m (x) sin beta x$$ | Число $pm ibeta$ не является корнем характеристического уравнения. | $$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$ |
| Число $pm ibeta$ является корнем характеристического уравнения кратности $S$. | $$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$ | ||
| 4 | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ | Число $alpha pm ibeta$ не является корнем характеристического уравнения. | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Число $alpha pm ibeta$ является корнем характеристического уравнения. | $$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Пример 13 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y = 4xcos x$. |
| Решение |
|
Сначала находим общее решение однородного уравнения $$y” + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$ Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y”_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y”_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$ Подставляем найденные $y_text{ч.н.}$ и $y”_text{ч.н.}$ в исходный диффур из “дано” задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$ Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$ |
| Ответ |
| $$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$ |
| Пример 14 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’=5x+2e^x$. |
| Решение |
|
Сначала найдем общее решение однородного дифференциального уравнения $$y”+y’=5x+2e^x.$$ Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$ Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$ Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y”=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y”$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$ Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$ Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 – 5x + e^x.$$ Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x.$$ |
| Ответ |
| $$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x$$ |
Метод Лагранжа
Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.
- Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
- Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
- Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
- Получаем $C_1(x)$ и $C_2(x).$
| Пример 15 |
| Найти частное решение дифференциального уравнения $$y”-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$ |
| Решение |
|
Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y”-2y’+y=0.$$ Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$ Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений. Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$ Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$ Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$ Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$ |
| Ответ |
| $$y = xe^x(1+ln|x|)$$ |
Этот метод
применим к решению ЛНДУ
с постоянными коэффициентами вида (3)
только в случаях, когда его правая часть
:
-
многочлен;
-
показательная
функция; -
тригонометрические
функции
(или одна
из них); -
линейная
комбинация перечисленных функций; -
произведение
перечисленных функций.
Таким образом,
рассматриваемый метод применяется при
следующем виде правой части ЛНДУ:
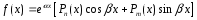
(2)
где

многочлен степени

а

многочлен степени


числа. Возможны разновидности этого
вида правой части в зависимости от
того, содержатся или нет в
тригонометрические функции.
Сущность
метода
состоит в том , что :
.
Рассмотрим
два различных вида ( и их частные случаи)
правой части
ЛНДУ (3)
и соответствующие им виды частного
решения

таблицу 3).
Таблица
3.
Частное решение
линейных неоднородных дифференциальных
уравнений по виду его правой части
|
Вид |
Вид |
|
|
I |
|
Примеры |
|
Случай |
|
|
|
Случай
|
|
|
|
II |
где |
|
|
Случай
т.е.
степени, т.е. |
|
|
|
Случай |
|
Рассмотрим
сущность метода подбора частного
решения ЛНДУ
по виду правой части на примерах.
I
вид. Правая
часть ЛНДУ

(1)
где

многочлен

степени,

постоянное число. Тогда общий вид
частного решения:

где

та же самая показательная функция, что
и в


многочлен той же степени, что и


число корней характеристического
уравнения, равных

Далее путем
подстановки общего вида
в линейное неоднородное дифференциальное
уравнение находятся неопределённые
коэффициенты многочлена
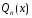
Пример 3.
Найти общее
решение дифференциального уравнения:

Решение.
-
Находим общее
решение
соответствующего линейного однородного
дифференциального уравнения:

Характеристическое
уравнение :

Его корни

Общее решение ЛОДУ:

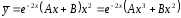
-
Найдем неизвестные
коэффициенты А
и В.
Для этого подставим в данное
дифференциальное уравнение
.
Предварительно найдем их, а затем
умножим соответственно на 4, 4 и 1:
Сложим левые и
правые части этих равенств, получим
алгебраическое уравнение с тремя
неизвестными
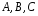
Разделим обе части полученного уравнения
на
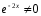
Приравниваем коэффициенты слева и
справа при одинаковых степенях
:

Решение системы:

-
Подставим A
и B
в общий вид
,
получим

-
Найдем общее
решение ЛНДУ:

Ответ:

Замечание.
Следует
обратить внимание на то, что полученное
в данном примере значение r=2
(кратность корней) привело к двум не
информативным алгебраическим уравнениям
(*).
В практике решения
ЛНДУ
распространены следующие частные
случаи I-го
вида правой части f(x).
Случай 1.
Правая часть
ЛНДУ:
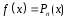
где
– многочлен n-ой
степени, т.е.

Таким образом, в

Тогда общий вид
частного решения:

где

многочлен той же степени, что и

r
– число корней характеристического
уравнения, равных нулю.
Далее, дифференцируя
функцию
и подставляя выражения
в ЛНДУ,
находим неопределенные коэффициенты
многочлена

Подставляя эти
коэффициенты в общий вид

находим частное решение ЛНДУ.
Напомним общий
вид многочленов:
-
третьей степени
(n=3):;
-
второй степени
(n=2):;
-
первой степени
(n=1):;
-
нулевой степени
(n=0):.
Пример 4.
Найти общее решение ДУ:

Решение.
-
Находим общее
решение
соответствующего
ЛОДУ:
Характеристическое
уравнение:

Его корни:

Общее решение
ЛОДУ:

-
Правая часть
,
следовательно общий вид частного
решения ЛНДУ:
,
,
т.к. один корень характеристического
уравнения равен 0). -
Найдем неизвестные
коэффициенты A
и B.
Для этого подставим в данное ДУ
:

Тогда

Приравниваем
коэффициенты при одинаковых степенях


-
Подставим A
и B
в общий вид
,
получим

-
Найдем общее
решение ЛНДУ:

:

Ответ:

Случай
2.
Правая
часть ЛНДУ:

где
– постоянное число, т.е. в (20)
– многочлен нулевой степени (
Тогда общий вид
частного решения:

где
– та же показательная функция;
– постоянное число (в общем случае

которое находится методом неопределенных
коэффициентов;
– число корней характеристического
уравнения, равных
Возможен и еще
один, наиболее простой, частный случай
(вернее, подслучай) вида правой части

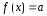
т.е. в (20)
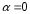
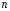
Тогда общий вид частного решения:
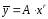
где
– постоянное число, которое находится
методом неопределенных коэффициентов,
– число корней характеристического
уравнения, равных нулю. Рассмотрим
второй вид
правой части

в котором содержатся тригонометрические
функции
и

т.е. наиболее общий вид (19) и его частные
случаи.
II
вид. Правая
часть ЛНДУ
содержит тригонометрические функции
и

с полными многочленами перед ними:

(19)
где
– многочлен

степени,
– многочлен

степени.
Тогда общий вид
частного решения:

где
и
– многочлены
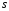
степени,

и
– те же тригонометрические функции, что
и в правой части
ДУ;
– та же показательная функция;
– число корней характеристического
уравнения, совпадающих с

Далее применяется метод неопределенных
коэффициентов.
Пример 5. Найти
общее решение ДУ:

Решение.
-
Находим общее
решение
соответствующего
ЛОДУ:
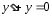
Характеристическое
уравнение

Его корни комплексные

Общее решение ЛОДУ:


– многочлен 0-ой степени,
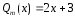
многочлен 1-й
степени,

т.к. множитель

в записи
он отсутствует).
Тогда этому виду
правой части соответствует частное
решение вида

т.к.

т.е. при


1-й степени,
(т.к.
совпадает с корнем характеристического
уравнения).
-
Найдем неизвестные
коэффициенты A,
B,
C,
D.
Для этого подставим
в данное ДУ
Предварительно найдем их, а затем
умножим соответственно на 1, 0, 1:

Сложив соответственно
левые и правые части этих равенств,
получим алгебраическое уравнение с
неизвестными А, В, С, D.
Аналогично
предыдущим примерам приравниваем
коэффициенты при одинаковых функциях
соответственно левой и правой частей
уравнения:
-
Подставим А, B,
C,
D
в общий вид
:
-
Найдем общее
решение ЛНДУ:

Ответ:

В практике решения
ЛНДУ
распространены следующие частные
случаи II-го
вида правой части
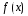
Случай
1.
Правая часть
ЛНДУ:

где

известные действительные числа. Таким
образом, в (19)

т.е.
и

многочлены 0-ой степени.
Тогда общий вид
частного решения:

где
и

неизвестные действительные числа,
которые находятся методом неопределенных
коэффициентов;
и

те же тригонометрические функции, что
и в


та же показательная функция;

число корней характеристического
уравнения, совпадающих с

Пример 6.
Найти общее решение ДУ:
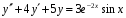
Решение.
-
Находим общее
решение
соответствующего ЛОДУ:

Характеристическое
уравнение:

Его корни комплексные:

Общее решение
ЛОДУ:

-
Правая часть
соответствует первому
частному случаю II
вида правой части:

(
т.к.
совпадает с корнем характеристического
уравнения).
Сложим соответственно
левые и правые части этих равенств,
получим алгебраическое уравнение с
двумя неизвестными
и

Разделим обе части
полученного уравнения на

Аналогично предыдущему примеру,
приравниваем коэффициенты при одинаковых
функциях соответственно левой и правой
частей уравнения:
(*)
Вновь (как это
было в примере 3) два уравнения с
неизвестными коэффициентами в (*) не
информативны. Из оставшихся уравнений
имеем:


-
Найдем общее
решение ЛНДУ:

Ответ:

Случай
2.
Правая часть
ЛНДУ:

где
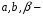
действительные числа. Таким образом,
в (19) многочлены 0-ой степени, т.е.

Тогда общий вид
частного решения:

где
и

неизвестные действительные числа,
которые находятся методом неопределенных
коэффициентов;
и

те же тригонометрические функции, что
и в


число корней характеристического
уравнения, совпадающих с

Пример7. Определить
общий вид частного решения ДУ

Решение.
-
Составим
характеристическое уравнение
соответствующего ЛНДУ:
.
Его корни
.
-
Правая часть
соответствует второму частному случаю
II
вида, следовательно

где
(т.к.

совпадает с одним корнем характеристического
уравнения).
Таким образом,

общий вид частного решения.
Ответ:

общий вид частного решения.
Обобщением всех
рассмотренных случаев правой части
при нахождении частного решения
ЛНДУ
является (19) (в таблице 3 вида II)
Завершая рассмотрение
решения ЛНДУ
методом неопределенных коэффициентов,
представим общую схему (Рис.1)
|
1-й |
|
2-й |
|
что |
ЛОДУ |
ЛНДУ |
|
как |
(см. табл.2).
|
в
|
|
3-й |
Найти общее |
Рис. 1 Общая схема
решения ЛНДУ
методом неопределенных коэффициентов
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример частного решения линейного дифференциального уравнения
Задание. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям (xo = 0).
y″ + 6y' + 13y = 8e-x, yo = 2/3, y'o = 2.
Решение находим с помощью калькулятора. Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение:
r2 +6 r + 13 = 0
D = 62 – 4·1·13 = -16
Корни характеристического уравнения: r1 = -3 + 2i, r1 = -3 – 2i
Следовательно, фундаментальную систему решений составляют функции:
y1=e-3x·cos(2x), y2=e-3x·sin(2x)
Общее решение однородного уравнения имеет вид: y=C1·e-3x·cos(2x)+C2·e-3x·sin(2x)
Найдем частное решение при условии:y(0) = 2/3, y'(0) = 2
Поскольку y(0) = c1, то получаем первое уравнение:
c1 = 2/3
Находим первую производную:
y’ = -3·c2·e-3·x·sin(2·x)-2·c1·e-3·x·sin(2·x)-3·c1·cos(2·x)·e-3·x+2·c2·cos(2·x)·e-3·x
Поскольку y'(0) = -3·c1+2·c2, то получаем второе уравнение:
-3·c1+2·c2 = 2
В итоге получаем систему из двух уравнений:
c1 = 2/3
-3·c1+2·c2 = 2
т.е.:
c1 = 2/3, c2 = 2
Тогда частное решение при заданных начальных условиях можно записать в виде:
Рассмотрим правую часть: f(x) = 8·e-x
Поиск частного решения. Уравнение имеет частное решение вида: y* = Ae-x. Вычисляем производные онлайн:
Первая производная: y’ = -A·e-x
Вторая производная: y″ = A·e-x
Найденные производные подставляем в исходное дифференциальное уравнение: y″ + 6y' + 13y = (A·e-x) + 6(-A·e-x) + 13(Ae-x) = 8·e-x
или 8·A·e-x = 8·e-x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений: 8A = 8
Откуда, A = 1
Частное решение имеет вид: y* = e-x
Таким образом, общее решение дифференциального уравнения имеет вид:
Рассмотрим тоже самое уравнение, но решим методом вариации произвольной постоянной.
Для нахождения производных C’i составляем систему уравнений:
C’1·e-3x·cos(2x)+C’2·e-3x·sin(2x)=0
C’1(-2·e-3x·sin(2x)-3·cos(2x)·e-3x) + C’2(-3·e-3x·sin(2x)+2·cos(2x)·e-3x) = 8*exp(-x)
Выразим C’1 из первого уравнения:
C’1 = -c2·sin(2x)/(cos(2x))
и подставим во второе. В итоге получаем:
C’1 = -4·e2x·sin(2x)
C’2 = 4·cos(2x)·e2x
Интегрируем полученные функции C’i:
C1 = -e2x·sin(2x)+cos(2x)·e2x + C*1
C2 = e2x·sin(2x)+cos(2x)·e2x + C*2
Записываем полученные выражения в виде:
C1 = (-e2x·sin(2x)+cos(2x)·e2x)·cos(2x)·e-3x + C*1e-3x·cos(2x)
C2 = (e2x·sin(2x)+cos(2x)·e2x)·e-3x·sin(2x) + C*2e-3x·sin(2x)
или
C1 = -cos(2x)·e-x·sin(2x)+cos2(2x)·e-x + C*1e-3x·cos(2x)
C2 = cos(2x)·e-x·sin(2x)+sin2(2x)·e-x + C*2e-3x·sin(2x)
y = C1 + C2
Таким образом, общее решение дифференциального уравнения имеет вид:
Скачать пример решения Скачать
Перейти к онлайн решению своей задачи
Пример. y″ + 5y' + 6 = 12cos(2x)
Cоставляем характеристическое уравнение дифференциального уравнения: r2 +5 r + 6 = 0
Находим дискриминант: D = 52 – 4·1·6 = 1
Корни характеристического уравнения: r1 = -2, r2 = -3. Следовательно, фундаментальную систему решений составляют функции: y1 = e-2x, y2 = e-3x
Общее решение однородного уравнения имеет вид: y=C1·e-2x+C2·e-3x
Найдем частное решение при условии:y(0) = 1, y'(0) = 3
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = 1
Находим первую производную: y’ = -3·c2·e-3·x-2·c1·e-2·x
Поскольку y'(0) = -3·c2-2·c2, то получаем второе уравнение:
-3·c2-2·c2 = 3
В итоге получаем систему из двух уравнений:
c1+c2 = 1
-3·c2-2·c2 = 3
которую решаем или методом обратной матрицы или методом исключения переменных.
c1 = 6, c2 = -5
Тогда частное решение при заданных начальных условиях можно записать в виде: y=6·e-2x-5·e-3x
Рассмотрим правую часть: f(x) = 12·cos(2·x)
Уравнение имеет частное решение вида: y* = Acos(2x) + Bsin(2x)
Вычисляем производные: y’ = -2·A·sin(2x)+2·B·cos(2x); y″ = -4·A·cos(2x)-4·B·sin(2x)
которые подставляем в исходное дифференциальное уравнение: y″ + 5y’ + 6y = (-4·A·cos(2x)-4·B·sin(2x)) + 5(-2·A·sin(2x)+2·B·cos(2x)) + 6(Acos(2x) + Bsin(2x)) = 12·cos(2·x) или -10·A·sin(2x)+2·A·cos(2x)+2·B·sin(2x)+10·B·cos(2x) = 12·cos(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему линейных уравнений:
-10A + 2B = 0
2A + 10B = 12
СЛАУ решаем методом Крамера:
A = 3/13;B = 15/13;
Частное решение имеет вид:
y* = 3/13cos(2x) + 15/13sin(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:
см. также диф уравнения онлайн
Пример 2. y’’ + y = cos(x)
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами. Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r2 + 1 = 0
D = 02 - 4·1·1 = -4
Корни характеристического уравнения:
(комплексные корни):
r1 = i, r2 = -i
Следовательно, фундаментальную систему решений составляют функции:
y1 = e0xcos(x) = cos(x)
y2 = e0xsin(x) = sin(x)
Общее решение однородного уравнения имеет вид: y=C1·cos(x)+C2·sin(x)
Рассмотрим правую часть: f(x) = cos(x)
Найдем частное решение. Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) – некоторые полиномы
имеет частное решение
y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
где k – кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) – полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 0, α = 0, β = 1.
Следовательно, число α + βi = 0 + 1i является корнем характеристического уравнения кратности k = 1(r1).
Уравнение имеет частное решение вида:
y* = x (Acos(x) + Bsin(x))
Вычисляем производные:
y' = sin(x)(B-A·x)+cos(x)(A+B·x)
y″ = cos(x)(2·B-A·x)-sin(x)(2·A+B·x)
которые подставляем в исходное дифференциальное уравнение:
y″ + y = (cos(x)(2·B-A·x)-sin(x)(2·A+B·x)) + (x (Acos(x) + Bsin(x))) = cos(x)
или
2·B·cos(x)-2·A·sin(x) = cos(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
2B = 1
-2A = 0
Следовательно:
A = 0; B = 1/2;
Частное решение имеет вид: y* = x (0cos(x) + ½ sin(x)) = ½ x sin(x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Скачать пример решения
см. также решение диф уравнения в онлайн.
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Определение
Уравнение
(*)
где
и
– непрерывные
функция в интервале
называется
неоднородным линейным дифференциальным уравнение второго порядка, функции
и
– его
коэффицинентами. Если
в
этом интервале, то уравнение принимает вид:
(**)
и называется однородным
линейным дифференциальным уравнением второго порядка. Если уравнение (**) имеет
те же коэффициенты
и
, как уравнение (*), то оно называется
однородным уравнением, соответствующим неоднородному уравнению (*).
Однородные дифференциальные линейные уравнения второго порядка
Пусть в линейном уравнении
и
– постоянные
действительные числа.
Частное решение уравнения
будем искать в виде функции
, где
– действительное
или комплексное число, подлежащее определению. Дифференцируя по
, получаем:
Подставляя в исходное дифуравнение, получаем:
Отсюда, учитывая, что
, имеем:
Это уравнение называется
характеристическим уравнением однородного линейного дифуравнения. Характеристическое уравнение и дает
возможность найти
. Это уравнение второй степени, поэтому
имеет два корня. Обозначим их через
и
. Возможны три случая:
Корни действительные и разные
В этом случае общее решение уравнения:
Пример 1
Решение
Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Корни действительные и равные
В этом случае общее решение уравнения:
Пример 2
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Корни комплексные
В этом случае общее решение уравнения:
Пример 3
Решение
Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Неоднородные дифференциальные линейные уравнения второго порядка
Рассмотрим теперь решение некоторых
типов линейного неоднородного уравнения второго порядка с постоянными
коэффициентами
где
и
– постоянные
действительные числа,
– известная непрерывная
функция в интервале
. Для нахождения общего решения такого
дифференциального уравнения необходимо знать общее решение соответствующего
однородного дифференциального уравнения
и частное
решение
. Рассмотрим
некоторые случаи:
Правая часть дифференциального уравнения имеет вид:
Частное решение дифференциального
уравнения ищем также в форме квадратного трехчлена:
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициенты.
Если нуль – однократный корень
характеристического уравнения, то
Если нуль – двухкратный корень
характеристического уравнения, то
Аналогично обстоит дело, если
– многочлен
произвольной степени
Пример 4
Решение
Решим соответствующее однородное уравнение.
Характеристическое уравнение:
Общее решение однородного уравнения:
Найдем частное решение неоднородного
дифуравнения:
Подставляя найденные производные в исходное дифуравнение, получаем:
Искомое частное решение:
Общее решение исходного дифуравнения:
Правая часть дифференциального уравнения имеет вид:
Частное решение ищем в виде
, где
– неопределенный
коэффициент.
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициент.
Если
– корень
характеристического уравнения, то частное решение исходного дифференциального
уравнения ищем в виде
, когда
– однократный
корень, и
, когда
– двукратный
корень.
Пример 5
Решение
Характеристическое
уравнение:
Общее
решение соответствующего однородного дифференциального уравнения:
Найдем
частное решение соответствующего неоднородного дифференциального уравнения:
Подставляя
в исходное дифуравнение, получаем:
Общее
решение дифуравнения:
Правая часть дифференциального уравнения имеет вид:
В этом случае частное решение
ищем в форме тригонометрического двучлена:
где
и
– неопределенные коэффициенты
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициенты.
Эти уравнения определяют коэффициенты
и
кроме случая, когда
(или когда
– корни характеристического уравнения). В
последнем случае частное решение дифференциального уравнения ищем в виде:
Пример 6
Решение
Характеристическое
уравнение:
Общее
решение соответствующего однородного дифуравнения:
Найдем
частное решение неоднородного дифуравнения
Подставляя
в исходное дифуравнение, получаем:
Общее
решение исходного дифуравнения:





 ,
, -многочлен
-многочлен -ой
-ой -постоянное
-постоянное ,
, –
– ;
; –
– –
– ,
,



 ,
, –
– ;
; –
– ;
; где
где
 ,
, –
– –
– .
.

 ,
, –
–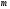

 ,
, и
и –
– ,
,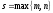 ).
). –
– ;
; –
– –
–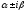 ,
,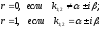
 ,
, –
–
 ,
,
 или
или ).
). ,
, –
– –
–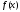 ;
; –
–
 ,
, ,
, ,
,
 ,
, –
– ;
; –
– .
.

 .
.
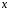

 ,
,



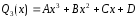 ;
; ;
;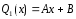 ;
; .
. соответствующего
соответствующего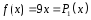 ,
, ,
, ,
,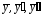 :
: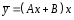 ,
,

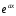









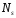


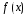


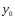 соответствующего
соответствующего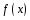
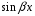





 :
: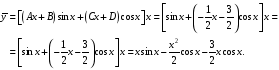



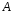










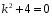 .
.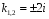 .
.





 ЛОДУ
ЛОДУ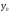 -общее
-общее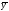 –
–





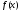 ;
;


 .
.