Как
и в общем случае исследования системы
неоднородных
линейных уравнений, использование
теоремы
Кронекера–Капелли в частном случае
исследования системы линейных однородных
уравнений также плодотворно. Общая
схема решения:
A1*:
Вычисляем
![]() :
:
ранг матрицы
![]() .
.
Так
как для однородной системы уравнений
![]() =
=![]() ,
,
то всегда выполняется
![]()
![]()
![]() .
.
Однородная система уравнений всегда
совместна. Пусть
![]() =
=![]() .
.
Это значит, что определён базовый
минор:
M![]()
матрицы
![]() .
.
A2*:
В системе уравнений оставляем только
те
![]()
уравнения-строки, которые попали
в базовый минор:
остальные являются следствием выделенных.
A3*:
В левой части каждого из оставшихся для
дальнейшего решения уравнений оставляем
те
![]()
столбцов с неизвестными, которые попали
в базовый минор:
остальные неизвестные объявляем
свободными
и соответствующие столбцы с ними
переносим в правую часть.
A4*:
Находим решения преобразованной системы
уравнений, применяя формулы Крамера:
определитель
преобразованной системы не
равен нулю!
A5*:
Полученное решение системы называют
общим:
вычисленные по формулам Крамера
неизвестные выражаются
через свободные
неизвестные. Присваивая свободным
неизвестным произвольные значения,
получаем частные
решения.
Замечание:
отметим ещё раз, что свободных неизвестных
![]() :
:
их можно воспринимать как число степеней
свободы процесса; вычисляемых неизвестных
–
![]() .
.
☺☺
Пример
8–04:
Исследовать систему уравнений:

Найти общее решение и одно частное.
Решение:
1). Составим матрицу:
![]() =
= и найдём её ранг. Выделим для окаймления
и найдём её ранг. Выделим для окаймления
минор (не равен нулю), расположенный в
правом верхнем углу матрицы:
-
3
4
1
2
6
8
2
5
1
9
12
3
10
2
1
3). Окаймляющие
миноры будем обозначать:
![]() ,
,
где![]() –
–
указывает номер отмеченной для окаймления
строки,![]() –
–
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
![]() =
= =4·
=4·![]() –8·
–8·![]() +12·
+12·![]() =m1·(5)–h1·(4)+g1·(1)=4·(5)–8·(4)+12·(1)
=m1·(5)–h1·(4)+g1·(1)=4·(5)–8·(4)+12·(1)
=0;
Замечание:
параметры: m1,
h1,
g1
изменяются при переходе к минорам
![]() ,
,![]() ,
,
числа:(5),
(4),
(1)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
![]() =
= =
=
m2·(5)–h2·(4)+g2·(1)=
3·(5)–6·(4)+9·(1)
=0;
4).
Так как все миноры 3-го порядка
оказались равными нулю, то
![]() =2.
=2.
5). Учитывая
расположение не равного нулю минора,
3-е уравнение отбрасываем и свободными
неизвестными объявляем
![]() и
и![]() :
:

далее применяем
правило Крамера:
![]() =1;
=1; ![]() =
=
![]() =
=![]() ;
;
![]() =
=![]() =0.
=0.
6). Общее решение
системы:
![]() =
=![]() =
=![]() ;
;
![]() =
=![]() =0;
=0;
частное решение получим при значениях:![]() =1,
=1,![]() =–1,
=–1,
→![]() =1,
=1,![]() =0.
=0.
Ответ:
общее решение:![]() =
=![]() =
=![]() ;
;
![]() =
=![]() =0;
=0;
частное решение: (1,–1,1,0).
Пример
8–05:
Исследовать
систему уравнений:

Найти
общее и частное решение.
Решение:
1). Применим пошаговый
процесс метода Гаусса:
-
4
-3
2
-1
1
–1
-1
2
3
-2
1
-3
1
–1
1
2
2
-1
0
-5
=(1)→
1
-1
1
2
=(2)→
5
-3
1
-8
1
0
-1
-7
-
1
–1
-1
2
1
0
0
-7
0
0
-2
0
0
0
1
0
0
0
-2
0
=(3)→
0
0
0
0
=(4)→
0
1
0
–9
0
1
0
–9
Выполнены
операции:
(1):
[R4]–[R1];
[R1]–[R2];
[R2]–[R3];
[R3]–[R4].
(2):
[R2]–[R1];
[R3]–[R1];
[R4]–[R1].
(3):
[R3]–[R1];
[R2]
делим на (–2); [R1]–[R2];
[R1]–[R4].
(4):
раскрываем
полученный результат.
2).
Видим:
![]() =3.
=3.
Свободной неизвестной объявляем![]() =
=![]() .
.
3). Из уравнения-строки
[R4] запишем:![]() =9
=9![]() ;
;
из строки [R2]:![]() =0;
=0;
[R4] запишем:![]() =7
=7![]() .
.
Произвольная величина![]() определяет бесчисленное множество
определяет бесчисленное множество
решений заданного уравнения.
Ответ: общее
решение: (7![]() ;9
;9![]() ;0;
;0;![]() )=
)=![]() (7,9,
(7,9,
0;1).
Замечание:
видим,
что и применение фундаментальных
результатов теоремы Кронекера-Капелли
не продвинуло нас в понимании системы
решений
системы ЛОУ!
☻
Соседние файлы в папке ЛА и АГ пособие
- #
- #
- #
- #
- #
- #
- #
- #
Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.
Метод Гаусса
- Метод Гаусса
- Пример 1
- Пример 2
- Несовместность системы (нет решений)
- Пример 3
- Общее и частное решение системы (бесконечное множество решений)
- Пример 4
Пусть задана система линейных алгебраических уравнений: $$begin{cases} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 = b_1 \ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 = b_2 \ a_{31} x_1 + a_{32} x_2 + a_{33} x_3 = b_3 end{cases}. $$
- Запишем систему уравнений в виде расширенной матрицы, состоящей из коэффициентов и столбца свободных членов. Вертикальная черта используется для удобства оформления. $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ a_{21} & a_{22} & a_{23} & | & b_2 \ a_{31} & a_{32} & a_{33} & | & b_3 end{pmatrix} $$
- С помощью элементарных преобразований матрицы (вычитание одной строки из другой, умноженной на коэффициент, удаление одинаковых и нулевых строк, деление строки на число отличное от нуля) получаем нули под главной диагональю $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ 0 & a_{22} & a_{23} & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$
- Используя элементарные преобразования, изложенные в пункте 2, приводим матрицу к виду содержащему нули везде, кроме главной диагонали $$ begin{pmatrix} a_{11} & 0 & 0 & | & b_1 \ 0 & a_{22} & 0 & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$
| Пример 1 |
| Решить систему уравнений методом Гаусса $$begin{cases} x_1 + 2 x_2 + x_3 = 5 \ -x_1 + 3 x_2 -2 x_3 = 3 \ – x_1 -7 x_2 + 4 x_3 = -5 end{cases}. $$ |
| Решение |
|
Запишем расширенную матрицу, состоящую из коэффициентов при неизвестных $x_1, x_2, x_3$ и отдельно столбец свободных членов $b_1, b_2, b_3$. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ -1 & 3 & -2 & | & 3 \ -1 & -7 & 4 & | & -5 end{pmatrix} $$ Приведем матрицу к нижнетреугольному виду (под главной диагональю должны быть нули) с помощью элементарных преобразований. Прибавим ко второй строке первую. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ -1 & -7 & 4 & | & -5 end{pmatrix} $$ Далее прибавляем к третьей строке первую. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & -5 & 5 & | & 0 end{pmatrix}$$ Теперь осталось к третьей строке прибавить вторую строку, чтобы под главной диагональю были только нули. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & 0 & 4 & | & 8 end{pmatrix}$$ Замечаем, что в третьей строке стоят числа, которые можно сократить на четыре. Для этого выполняем деление всей третьей строки на 4. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Теперь выполняем обратный ход Гаусса снизу вверх. Прибавляем ко второй строке третью строку. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & 0 & | & 10 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Сразу замечаем, что вторую строку можно сократить на 5. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Продолжаем обратный ход, вычитаем третью строку из первой. $$begin{pmatrix} 1 & 2 & 0 & | & 3 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Осталось из первой строки вычесть вторую строку, умноженную на 2, для того, чтобы в первой строке появился ноль. $$begin{pmatrix} 1 & 0 & 0 & | & -1 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Теперь перепишем получившуюся матрицу в виде системы уравнений, чтобы в дальнейшем получить чему равны неизвестные $x_1, x_2, x_3$. $$begin{cases} x_1 = -1 \ x_2 = 2 \ x_3 = 2 end{cases}$$ |
| Ответ |
| $$x_1 = -1, x_2 = 2, x_3 = 2$$ |
| Пример 2 |
| Решить систему линейных алгебраических уравнений методом Гаусса $$begin{cases} 2x_1 + 5 x_2 + 4x_3 + x_4 = 20 \ x_1 + 3 x_2 + 2x_3 +x_4 = 11 \ 2x_1 +10 x_2 + 9 x_3 + 7x_4 = 40 \ 3x_1 + 8x_2 + 9x_3 + 2x_4 = 37 end{cases}. $$ |
| Решение |
|
Записываем расширенную матрицу $$ begin{pmatrix} 2&5&4&1&|&20 \ 1&3&2&1&|&11 \ 2&10&9&7&|&40 \ 3&8&9&2&|&37 end{pmatrix}.$$ Умножаем вторую строку на 2 и вычитаем из неё первую строчку. Из третьей строки просто вычитаем первую. Умножаем четвертую строку на 2 и вычитаем из неё первую строку, умноженную на 3. Получаем матрицу $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&5&5&6&|&20 \ 0&1&6&1&|&14 end{pmatrix}.$$ Берем вторую строку, умноженную на 5 и вычитаем из третьей. Затем вторую строку вычитаем из четвертой. $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&6&0&|&12 end{pmatrix}$$ Теперь умножаем третью строку на 6 и вычитаем её из четвертой строки, умноженной на 5. $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&0&-6&|&0 end{pmatrix}$$ Получили нижнетреугольную матрицу, то есть ниже главной диагонали расположены нули. Теперь проделываем элементарные преобразования снизу вверх, так называемый обратный ход Гаусса. Но прежде замечаем, что появилась строка, в которой можно выполнить сокращение. А именно в четвертой строке можно разделить все числа на (-6). И получаем $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Вот теперь вычитаем четвертую строчку из третьей, второй и первой. $$begin{pmatrix} 2&5&4&0&|&20 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Из второй строки мы не будем вычить третью, потому что там итак стоит ноль, ради которого мы проводим элементарные преобразования, поэтому пропускаем этот шаг. Умножаем на 4 третью строку и вычитаем её из первой, умноженной на 5. $$begin{pmatrix} 10&25&0&0&|&60 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Замечаем, что в первой строке можно все числа сократить на 5. $$begin{pmatrix} 2&5&0&0&|&12 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Теперь остался последний шаг это умножить вторую строку на 5 и вычесть из первой. $$begin{pmatrix} 2&0&0&0&|&2 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Замечаем, что первую строку можно сократить на 2, а третью строку на 5. $$begin{pmatrix} 1&0&0&0&|&1 \ 0&1&0&0&|&2 \ 0&0&1&0&|&2 \ 0&0&0&1&|&0 end{pmatrix}$$ Переписываем матрицу в виде привычной системы уравнений и получаем ответ $$begin{pmatrix} 1&0&0&0&|&1 \ 0&1&0&0&|&2 \ 0&0&1&0&|&2 \ 0&0&0&1&|&0 end{pmatrix} sim begin{cases} x_1 = 1 \ x_2 = 2 \ x_3 = 2 \ x_4 = 0 end{cases}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x_1 = 1, x_2 = 2, x_3 = 2, x_4 = 0$$ |
Несовместность системы (нет решений)
Если в результате элементарных преобразований появилась нулевая строка вида $$begin{pmatrix} 0&0&0&|&b end{pmatrix} text{ где } b neq 0,$$то система уравнений не имеет решений. На этом алгоритм Гаусса заканчивает свою работу и можно записывать ответ, что система несовместна, то есть нет решений.
| Пример 3 |
| Найти решение системы линейных уравнений методом Гаусса $$begin{cases} 7x_1 – 2x_2 – x_3 = 2 \ 6x_1 – 4x_2 – 5x_3 = 3 \ x_1 + 2x_2 + 4x_3 = 5 end{cases}.$$ |
| Решение |
|
Как обычно пишем расширенную матрицу по коэффициентам при неизвестных переменных и столбцу свободных членов $$begin{pmatrix} 7&-2&-1&|&2 \ 6&-4&-5&|&3 \ 1&2&4&|&5 end{pmatrix}.$$ Запускаем алгоритм Гаусса. Идём сверху вниз. Умножаем вторую строку на 7 и вычитаем из неё первую строчку умноженную на 6. Затем первую строку вичитаем из третьей, умноженной на 7. $$begin{pmatrix} 7&-2&-1&|&2 \ 0&-16&-29&|&9 \ 0&16&29&|&33 end{pmatrix}$$ Далее по алгоритму прибавляем вторую строку к третьей. $$begin{pmatrix} 7&-2&-1&|&2 \ 0&-16&-29&|&9 \ 0&0&0&|&42 end{pmatrix}$$ Видим, что в результате элементарных преобразований появилась строка в которой все нули, кроме свободного члена. Это означает, что система несовместа, то есть у системы уравнений нет решения. |
| Ответ |
| Нет решений, так как система несовместна. |
Общее и частное решение системы (бесконечное множество решений)
Часто после элементарных преобразований в расширенной матрице появляются нулевые строки вида $$begin{pmatrix} 0&0&0&|&0 end{pmatrix}.$$ Такую строку нужно вычеркивать из матрицы и система уравнений будет иметь бесконечное множество решений. Разберем это на практике.
| Пример 4 |
| Найти общее и два частных решения системы линейных алгебраических уравнений методом Гаусса $$begin{cases} x_1+x_2-x_3=4 \ 3x_1+2x_2-5x_3=7 \ 3x_1+x_2-7x_3=2 end{cases}.$$ |
| Решение |
|
Составляем расширенную матрицу $$begin{pmatrix} 1&1&-1&|&4 \ 3&2&-5&|&7 \ 3&1&-7&|&2 end{pmatrix}.$$ Из второй и третьей строки вычетаем первую, умноженную на 3. $$begin{pmatrix} 1&1&-1&|&4 \ 0&-1&-2&|&-5 \ 0&-2&-4&|&-10 end{pmatrix}$$ Из третьей строки вычитаем вторую, домноженную на 2. $$begin{pmatrix} 1&1&-1&|&4 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix}$$ Теперь согласно обратному ходу Гаусса вторую строку прибавляем к первой. $$begin{pmatrix} 1&0&-3&|&-1 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix}$$ По окочанию элементарных преобразований получилась строка, в которой все элементы равны нулю. Значит, система имеет бесконечное множество решений. Для его записи понадобится отличать базисные и свободные переменные. Обычно за базисные берут переменные, которые стоят на главной диагонали, а остальные свободные. В нашем случае базисными будут $x_1, x_2$, а свободной $x_3$. Переписываем матрицу в виде системы $$begin{pmatrix} 1&0&-3&|&-1 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix} sim begin{cases} x_1-3x_3 = -1 \ -x_2-2x_3 = -5 end{cases}.$$ Так как $x_1, x_2$ являются базисными переменными, то их переносим в левую часть равенства, а всё остальное в правую часть. Получившееся называют общим решением решением системы уравнений $$begin{cases} x_1-3x_3 = -1 \ -x_2-2x_3 = -5 end{cases} sim begin{cases} x_1 = 3x_3-1 \ x_2 = 5-2x_3 end{cases}.$$ Чтобы получить частное решение системы уравнений нужно вместо свободного $x_3$ подставить любое число, например $x_3 = 0$. Тогда получаем, что $$begin{cases} x_1 = -1 \ x_2 = 5 end{cases}.$$ Возьмем ещё например $x_3 = 1$ и получаем $$begin{cases} x_1 = 2 \ x_2 = 3 end{cases}.$$ Можно брать различные числа вместо $x_3$ и получать бесконечное множество решений. |
| Ответ |
|
Общее решение системы уравнений $$begin{cases} x_1 = 3x_3-1 \ x_2 = 5-2x_3 end{cases}.$$ Частные решения системы уравнений $$begin{cases} x_1 = -1 \ x_2 = 5 end{cases}, begin{cases} x_1 = 2 \ x_2 = 3 end{cases}.$$ |
Как найти общее и частное решение системы линейных уравнений
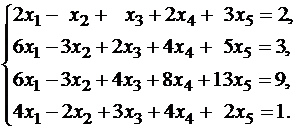

Пример 2. Исследовать совместность, найти общее и одно частное решение системы

Решение. Переставим первое и второе уравнения, чтобы иметь единицу в первом уравнении и запишем матрицу B.

Получим нули в четвертом столбце, оперируя первой строкой:

Теперь получим нули в третьем столбце с помощью второй строки:

 Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третью строку умножим на (–2) и прибавим к четвертой:

Видим, что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
-x1=-3 → x1=3; x2=3-x1 → x2=0; x3=1-2x1 → x3=5.
x4 = 10- 3x1 – 3x2 – 2x3 = 11.
Пример 3. Исследовать систему на совместность и найти решение, если оно существует.

Решение. Составляем расширенную матрицу системы.

 Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Умножая первую строку на (-1), складываем ее с третьей:

Умножим вторую строку на (-2) и прибавим к третьей:

Система несовместна, так как в основной матрице получили строку, состоящую из нулей, которая вычеркивается при нахождении ранга, а в расширенной матрице последняя строка останется, то есть rB > rA.
Задание. Исследовать данную систему уравнений на совместность и решить ее средствами матричного исчисления.
Решение
Пример. Доказать совместимость системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) методом Крамера. (ответ ввести в виде: x1,x2,x3)
Решение:doc:doc:xls
Ответ: 2,-1,3.
Пример. Дана система линейных уравнений. Доказать ее совместность. Найти общее решение системы и одно частное решение.
Решение
Ответ:x3 = — 1 + x4 + x5; x2 = 1 — x4; x1 = 2 + x4 — 3x5
Задание. Найти общее и частное решения каждой системы.
Решение. Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x1 | x2 | x3 | x4 | x5 |
Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-3). Добавим 3-ую строку к 2-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2,x3, значит, неизвестные x1,x2,x3 – зависимые (базисные), а x4,x5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x1 | x2 | x3 | x4 | x5 |
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
27x3 =
— x2 + 13x3 = — 1 + 3x4 — 6x5
2x1 + 3x2 — 3x3 = 1 — 3x4 + 2x5
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x1,x2,x3 через свободные x4,x5, то есть нашли общее решение:
x3 = 0
x2 = 1 — 3x4 + 6x5
x1 = — 1 + 3x4 — 8x5
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.
Задание. Решить систему уравнений.
Ответ😡2 = 2 — 1.67x3 + 0.67x4
x1 = 5 — 3.67x3 + 0.67x4
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной
Пример. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.
Решение: Проверяем совместность системы с помощью теоремы Кронекера — Капелли. Согласно теореме Кронекера — Капелли, из того, что следует несовместность исходной системы.
Ответ: система не совместна.
Решение
Решение систем линейных уравнений — примеры общих и частных методов вычислений

Понятия и обозначения
Для измерения геометрических или физических величин в математике используют действительное число — вещественное. В уравнении под ним понимают все свободные члены или неизвестные переменные. Вычисление линейных алгебраических уравнений играет важную роль в различных математических задачах: численных методах, программировании, эконометрике.
Общий вид системы линейных уравнений (СЛАУ) в классическом понимании представляют следующим образом:
a11 * n 1 + a 12 * n 2 + …+a 1x n x = c 1.
a21 * n 1 + a 22 * n 2 + …+a 2x n x = c 2.
as1 * n 1 + a 12 * n 2 + …+a 1x n x = c s.
В этой записи s — это количество уравнений, x — число переменных, а n — переменная которую необходимо вычислить. Предполагается что a и b это известные свободные члены. Индексы обозначают порядковый номер уравнения. Первый символ — расположение строчки, а второй — позиция произведения переменной и свободного члена.
Если эти члены отличные от нуля, то система называется неоднородной, в ином же случае однородной. Квадратной системой называется совокупность уравнений, когда их число совпадает с количеством неизвестных. Существует понятие и неопределённой системы. Это совокупность, при которой неизвестных больше числа уравнений. Если наоборот, то система считается переопределенной. В литературе её ещё часто называют прямоугольной.
Система считается решаемой, когда множество членов X соответствует такому набору чисел, что при их подстановке вместо n вся система обратится в тождество. Если существует хотя бы одно решение, система называется совместной. Ответы, превращающие уравнения в равенства, при которых переменные не совпадают, считаются различными.
Существует четыре способа развязывания системы уравнений:
- способ подстановки;
- использование новых переменных;
- алгебраическое сложение;
- матричный метод.
Вид используемого алгоритма зависит от типа примера. Метод алгебраического сложения применяют, когда в задании лишь одно неизвестное, а коэффициенты противоположны или равны. Если же хотя бы в одной из формул коэффициент равен единице, то удобнее будет решить систему уравнений методом подстановки. В иных случаях используют матрицы.
Алгебраическое сложение
Способ заключается в сложении или вычитании выражений. Это довольно простой способ и в то же время эффективный. Алгоритм нахождения ответа для равенств с двумя переменными n и m сводится к следующему:

- уравниванию модулей коэффициентов при любом из неизвестных;
- сложению или вычитанию равенства;
- вычисления составленного выражения;
- прогонки каждого найденного корня через первую или вторую строчку системы уравнений;
- нахождению второго неизвестного.
То есть после выполнения арифметических действий с уравнениями должно получиться одно выражение с одним неизвестным. Затем находят значение этой переменной и в него подставляют полученный корень. Например, нужно узнать, какие корни системы, состоящей из двух строчек, превращают её в тождество:
В первую очередь необходимо сложить равенства между собой. В итоге получится:
Подставив поочерёдно в каждое равенство найденные корни можно найти второе неизвестное. Для корня n = – 5 ответом будет:
- (-5) 2 + m 2 = 29;
- 25 + m 2 = 29;
- m 2 = 29 – 25;
- m 2 = 4.
Соответственно, корнями будут числа два и минус два. Аналогичные действия необходимо выполнить и для корня другого знака n = 5. В итоге получится, что пары (− 5; − 2), (− 5; 2), (5; − 2), (5 ; 2) являются нужным ответом. При достаточном опыте подробно описывать решение не обязательно.
Существуют системы, требующие подготовительного этапа. Например, такого вида:
Исключить здесь сразу переменную не выйдет. Если умножить все члены первой строчки на тройку, а второй на четвёрку, получится запись:
9 * n – 12 * m = 15.
8 * n + 12 * m = 28.
Теперь равенства можно сложить, тем самым исключив переменную m. Затем система решается по базисному алгоритму. Чтобы понять, можно ли решить систему этим методом, следует предварительно её проанализировать. Необходимое условие заключается в том, что коэффициенты второй переменной должны быть одинаковыми по модулю, но противоположными по знаку.
Метод подстановки
Систему равенств возможно решить и способом подстановки. Используя любое из уравнений, можно выразить любую из неизвестных переменных, а затем подставить её в другое равенство. Алгоритм использования метода следующий:

- через n в одном из уравнений выражают m;
- подставляют полученное равенство вместо n в другое тождество;
- решают уравнение и находя m;
- поочерёдно подставляют найденные корни и получают ответ.
Например, нужно проверить, все ли целые корни могут быть у системы:
10 * n + 3 * m = 17.
Выразив m через n можно записать равенство: n = (8* m + 16) / 5. Так как n одинаково в обоих уравнениях, то следует подставить полученное тождество и записать: 10* n + 3*(8* n +16) / 5 = 17. Отсюда уже просто найти корень. Он будет равен дроби 1/2. Подставив его вместо n легко вычислить и второй корень: m = (8 * n + 16) / 5 = 4. Таким образом, у системы будет только один целый корень. При желании проверить ответ можно решить систему другим методом.
Использование матриц

Для систем с произвольным числом уравнений и неизвестных используют другие методы. Если система состоит из нелинейных дифференциальных уравнений с постоянными коэффициентами, то используют матричный способ. Этот метод предполагает применение обратной матрицы.
Пусть дана система с тремя неизвестными х1, х2, х3. Нужно найти значения, при которых равенства станут верными. Для нахождения решений используют три матрицы:
- Коэффициент системы. При этом её определитель не должен быть равным нулю.
- Вектора неизвестных. Именно его понадобится найти.
- Столбца свободных членов.

Базисное решение строят на произведении первой и второй матрицы. В результате получают матрицу размером три на один. То есть вектор-столбец с тремя элементами. После выполнения действия получится, что системный вектор будет равен левой части системы и соответствовать третьей матрице. Таким образом, обозначив матрицы буквами А, Б, В, можно записать выражение А * Б = В и найти необходимую Б.
При умножении на А -1 (обратную матрицу) получают равенство: Е * Б = А -1 * В, где Е – единичная матрица получена из совместимости прямой и обратной. Так как при произведении с единичной матрицей значения не изменяются, то решением системы будет формула: Б = А -1 * В.
Способ Гаусса-Жордана
Частным случаем решения системы является Метод Гаусса — Жордана. Суть решения основана на составлении специальной таблицы. В первый столбец заносятся известные значения, то есть величины, расположенные после равно, а в три других коэффициенты, стоящие после неизвестных. Чтобы приступить к решению, необходимо выполнить три шага:
- выбрать ключевой элемент из первых трёх столбцов;
- переписать строчку с ключевым значением, предварительно разделив все элементы на это значение;
- переписать оставшиеся элементы, при этом вычитая из него произведение соответствующих ему чисел.

В полученной новой матрице снова выбирают ключевой элемент и выполняют все действия снова. Шаги повторяют до тех пор, пока не получится матрица, состоящая из нулей и единиц. Значения корней системы будут находиться на пересечении столбцов со строчками напротив единиц.
Этот метод используют только при выполнении условия совместности. Его ещё называют способом простой итерации. Он был доказан и оптимизирован Зейделем. С помощью итерационного метода можно посчитать систему А* Б = В с точностью “е”. Составляют n уравнение на сходимость, а затем на точность. Затем из первого уравнения выражают n1, второго n2, третьего n3 и так далее. Новые n с индексом i +1 считаются через старые i. Зейдель предложил расширить решение и добавить снова для счёта индекс i+1.
Это фундаментальные способы решения сложных систем уравнений. Они трудные, требуют опыта и внимательности. Поэтому существуют специальные онлайн-калькуляторы по методу Гаусса с подробным решением, помогающие исследовать систему любой численности.
Теорема Кронекера — Капелли
Применяется она при проведении исследований без непосредственного решения. То есть для записи эквивалентной совокупности алгебраических уравнений с их минимальным числом. Теорема говорит о следующем: система уравнений А * Б = В имеет решение только тогда, когда ранг А равен (А, В), где последнее расширенная матрица, полученная из первого члена путём приписывания столбца В.
Это утверждение обобщает различные виды СЛАУ:
- Несовместные – которые определяют при условии, что их ранг меньше ранга расширенной матрицы. Существование корней невозможно.
- Совместные неопределённые – системы, имеющие бесконечное множество решений. В этом случае ранги равны, а количество неизвестных будет меньше.
- Совместно определённые – в этом случае ранг равен расширенной матрице и количеству неизвестных. Точное решение будет одно.
Выводом из этой теоремы является то, что число главной переменной совокупности будет всегда равно рангу системы. При этом столбец свободных членов представляет собой линейную комбинацию столбцов матрицы А.
Решение Крамера

Пожалуй, это один из самых простых способов нахождения корней уравнений. Для решения строят несколько матриц. Основная получается из коэффициентов, стоящих при неизвестных. Она обозначается символом дельта. Вторую, дельта-икс, образуют из основной матрицы заменой первого столбца на ответы уравнений. Следующая, дельта-игрек, строится с заменой в основной матрице второго столбца на значения ответов и так далее.
Затем вычисляют дискриминант этих матриц, то есть их определитель. Для его поиска можно использовать способ треугольника или разложения. Первый подходит для простых матриц. Находят его как разницу умножения чисел, стоящих в матрице крест-накрест. Второй же применим для матриц, содержащих три и более строк. При нахождении выбирают одну из них и раскладывают матрицу.
Как только все дискриминанты найдены, используют правило Крамера: n = Δn/ Δ. Подставляют значения, находят ответ. Стоит отметить, что много интернет-порталов, предлагающих услугу расчётов СЛАУ, используют для вычислений онлайн-метод Крамера.
Удобные онлайн-калькуляторы

В некоторых случаях решение СЛАУ онлайн будет хорошим подспорьем для того, чтобы разобраться в различных правилах, используемых при решениях. Из популярных интернет-сервисов, позволяющих найти корни систем, можно отметить: kontrolnaya-rabota, mathsolution, planetcalc, allcalc. Использовать эти сайты-решатели смогут даже слабо подготовленные пользователи, имеющие общее представление о методах решений.
Для выполнения расчёта необходимо ввести параметры системы и нажать кнопку «Рассчитать». При этом можно выбрать метод, на базе которого будут проводиться вычисления. Удобным является и то, что полученный расчёт сопровождается объяснениями.
На этих порталах также можно посмотреть примеры и правила решений. Некоторые калькуляторы могут построить и график системы. Например, kontrolnaya-rabota. Для этого на сайте нужно выбрать раздел «Графическое решение уравнений онлайн» и ввести исследуемую систему равенств.
Исследование СЛАУ. Общие сведения
В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Пример 1
Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.
Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .
Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
- когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .
Пример 2
А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0
r ( A 1 ) = 1 , r ( B 1 ) = 1
А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6
источники:
http://nauka.club/matematika/algebra/resheniye-sistem-lineynykh-uravnenii.html
http://zaochnik.com/spravochnik/matematika/issledovanie-slau/slau/
Рассмотрим произвольную СЛАУ Ax = b. Заменив столбец b свободных членов нулевым, получим однородную СЛАУ Ax = 0, соответствующую неоднородной СЛАУ Ax = b. Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.
Теорема 14.4. Пусть столбец x° — некоторое решение СЛАУ Ax = b. Произвольный столбец x является решением этой СЛАУ тогда и только тогда, когда он имеет представление x = x° + у, где y — решение соответствующей однородной СЛАУ Ay = 0.
◄ Если x — решение СЛАУ Ax = b, то A(x — x°) = Ax — Ax° = b — b = 0. Поэтому столбец y = x — x° является решением соответствующей однородной СЛАУ, и мы получаем представление x = x° + y.
Наоборот, если y — произвольное решение соответствующей однородной системы, то x = x° + y — решение системы Ax = b, так как A(x° + y) = Ax° + Ay = b + 0 = b. ►
Следствие 14.3. Пусть x’ и x” — решения неоднородной системы Ax = b. Тогда их разность y = x’ — x” является решением соответствующей однородной системы Ay = 0.
Теорема 14.4 сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно знать одно ее решение (частное решение) и все решения соответствующей однородной СЛАУ.
Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (на-пример, по теореме 13.1 Кронекера — Капелли), а во-вторых, найти частное решение x° этой системы, чтобы свести ее к однородной системе.
Следствием теорем 14.3 и 14.4 является теорема о структуре общего решения неоднородной СЛАУ.
Теорема 14.5. Пусть x° — частное решение СЛАУ Ax = b и известна фундаментальная система решений x(1), …, x(k) соответствующей однородной системы Ax = 0. Тогда любое решение СЛАУ Ax = b можно представить в виде
x = x° + c1x(1) + c2x(2) + … + ckx(k), (14.8)
где ci ∈ R, i = 1,k. #
Как и в случае однородной СЛАУ, название теоремы отражает то, что формула
x = x° + xoo, xoo = c1x(1) + … + ckx(k), (14.9)
при произвольных постоянных ci ∈ R, i = 1,k, описывает все множество решений СЛАУ Ax = b. Формулу (14.9) называют общим решением СЛАУ.
Как найти частное решение неоднородной СЛАУ Ax = b? Пусть для соответствующей однородной системы Ax = 0 выбраны базисные и свободные неизвестные. Базисный минор матрицы A является базисным и для расширенной матрицы (A | b), если СЛАУ Ax = b совместна.
Поэтому строки базисного минора определяют те уравнения СЛАУ Ax = b, из которых следуют остальные. Эти остальные можно отбросить. Итак, пусть есть СЛАУ
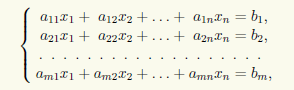
и базисный минор матрицы СЛАУ сосредоточен вверху слева:

Тогда исходная система эквивалентна следующей:
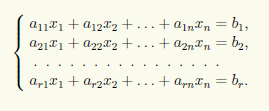
Зададим нулевые значения xr+1 = … = xn = 0 для свободных неизвестных и получим СЛАУ с невырожденной матрицей
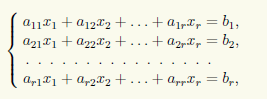
имеющей единственное решение. Решая последнюю систему, находим значения x°1, …, x°r. Тогда частным решением будет столбец (x°1, …, x°r, 0, …, 0)T .
