Как решать дифференциальные уравнения
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Основные понятия и определения
-
- Определения
- Типы уравнений
- Алгоритм решения
- Дифференциальные уравнения первого порядка
-
- ДУ с разделяющимися переменными
- Однородные ДУ
- Линейные неоднородные ДУ
- ДУ Бернулли
- ДУ в полных дифференциалах
- Дифференциальные уравнения второго порядка
-
- ДУ допускающие понижение порядка
- Линейные однородные ДУ с постоянными коэффицентами
- Линейные неоднородные ДУ с постоянными коэффициентами
- Метод Лагранжа
Введите уравнение
Условия к задаче (необязательно)
Пример 1 Пример 2 Правила ввода
Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.
Основные понятия и определения
Определения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).
Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y” = 1 $$
Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y”(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.
Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.
В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y”(x)$, поэтому это ДУ второго порядка.
Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.
Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.
Типы уравнений
- ДУ первого порядка
– с разделяющимися переменными
– однородные
– линейные неоднородные
– уравнение Бернулли - ДУ второго порядка
– уравнения допускающие понижение порядка
– однородные с постоянными коэффициентами
– неоднородные с постоянными коэффициентами
Алгоритм решения
- По старшей производной функции $y(x)$ определить порядок ДУ
- Зная порядок, определить тип уравнения
- Узнав тип, подобрать подходящий метод решения
- Используя метод, найти общее решение
- Получить частное решение из общего путем вычисления неизвестной $C$
В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$
ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!
| Пример 1 |
| Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$ |
| Решение |
|
Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$ Теперь подставим $y’$ и $y$ в исходное уравнение. $$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$ Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ. |
| Ответ |
| $$y = Ce^{frac{x^2}{2}} $$ |
Дифференциальные уравнения первого порядка
ДУ с разделяющимися переменными
Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$
СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.
Алгоритм нахождения общего решения:
- Переписываем производные через $y’ = frac{dy}{dx}$
- Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
- Интегрируем обе части уравнения
| Пример 2 |
| Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$ |
| Решение |
|
Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка. Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить “игрики” от “иксов” по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$ После замены производной игрека исходное уравнение приобретает такой формат: $$frac{dy}{dx} = xy$$ Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$. $$ frac{dy}{y} = xdx $$ Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения. $$ int frac{dy}{y} = int xdx $$ Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$. $$ ln|y| = frac{x^2}{2} + C $$ Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем. $$ y = e^{frac{x^2}{2} + C} $$ Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения. Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением. $$ y = Ce^{frac{x^2}{2}} $$ |
| Ответ |
| $$ y = Ce^{frac{x^2}{2}} $$ |
| Пример 3 |
| Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$. |
| Решение |
|
Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$: $$ frac{dy}{dx} = frac{2x}{1+x^2} $$ Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$: $$ dy = frac{2x}{1+x^2} dx $$ Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы: $$ int dy = int frac{2x}{1+x^2} dx $$ $$ y = int frac{2x}{1+x^2} dx $$ Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл: $$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$ Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$: $$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$ Теперь заменив в общем решении $C$ на ноль, получаем частное решение: $$y = ln(1+x^2)$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = ln(1+x^2)$$ |
Однородные ДУ
Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.
Решается по следующему алгоритму:
- Проверить уравнение на однородность с помощью $lambda$
- Привести уравнение к виду $y’ = f(frac{y}{x})$
- Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
- Решить уравнение методом разделяющихся переменных
| Пример 4 |
| Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} – 1$$ |
| Решение |
|
Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$: $$y’ = frac{lambda y}{lambda x} – 1$$ Выполняем сокращение $lambda$ в числителе и знаменателе: $$y’ = frac{y}{x} – 1$$ После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$: $$ t’x + t = t – 1$$ Переносим $t$ в одну сторону и тем самым уничтожаем его: $$ t’x = -1 $$ Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$ Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства: $$dt = -frac{dx}{x}$$ Интегрируем обе части: $$int dt = – int frac{dx}{x}$$ $$t = -ln|x|+C$$ Выполняем назад замену $t = frac{y}{x}$: $$frac{y}{x} = -ln|x|+C$$ Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения: $$y = -xln|x| +Cx$$ |
| Ответ |
| $$y = -xln|x| +Cx$$ |
| Пример 5 |
| Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$ |
| Решение |
|
Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$. $$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$ После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения. Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$ Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$ Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$ Интегрируем обе части уравнения $$int frac{2+t}{t}dt = – int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$ Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y^2 = Cxe^frac{-y}{x}$$ |
Линейные неоднородные ДУ
Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$
Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$.
Алгоритм метода Бернулли:
- Выполняем замену $y=uv$ и $y’ = u’v+uv’$
- Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
- Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ
Алгоритм метода вариации произвольной постоянной:
- Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
- В полученном общем решении заменяем константу $C$ на функцию $C(x)$
- Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
- Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ
| Пример 6 |
| Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$. |
| Решение |
|
Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$ Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$ Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ – 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$ Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$ Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$ Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$ В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$ С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 – x^2.$$ |
| Ответ |
| $$y = x^4 – x^2$$ |
| Пример 7 |
| Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$. |
| Решение |
|
Перепишем уравнение в виде $$ y’ – y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ – y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$ Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$ Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$ Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x – C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$ В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$ Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x – cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x – cos x$. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = Csin x – cos x$$ |
ДУ Бернулли
Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$
Алгоритм решения:
- Выполняем подстановку $y = z^frac{1}{1-alpha}$
- После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
- Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$
| Пример 8 |
| Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$. |
| Решение |
|
Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$ Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ. Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$ Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$ Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$ Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} – int e^{-x} dx = xe^{-x} +e^{-x} + C$$ Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$ |
| Ответ |
| $$y = frac{1}{Ce^x + x + 1}$$ |
ДУ в полных дифференциалах
Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.
Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:
- Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
- Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$
- Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$
| Пример 9 |
| Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$ |
| Решение |
|
Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$. Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$ Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$ Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$ Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$ Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x^2+5xy+y^3 = C.$$ |
Дифференциальные уравнения второго порядка
ДУ допускающие понижение порядка
Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:
- Без функции $y$: $F(x,y’,y”)=0$
- Без переменной $x$: $F(y,y’,y”)=0$
Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.
| Пример 10 |
| Найти частное решение дифференциального уравнения второго порядка $xy”+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$. |
| Решение |
|
Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$ Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$ Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$ Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$ Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$ Записываем частное решение дифференциального уравнения $$y = ln|x|.$$ |
| Ответ |
| $$y = ln|x|$$ |
| Пример 11 |
| Найти частное решение дифференциального уравнения второго порядка $$yy”+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$ |
| Решение |
|
Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y” = p'(y)cdot y’ = p'(y)p$. Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$ В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$ Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$ Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 – Cfrac{1}{y^2}$$ $$(y’)^2 = 1 – Cfrac{1}{y^2}.$$ Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 – Cfrac{1}{1^2} Rightarrow C = 0.$$ Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 – Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$ Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$ |
| Ответ |
| $$y = x + 1$$ |
Линейные однородные ДУ с постоянными коэффицентами
Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y”+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y” Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$
В зависимости от получившихся корней имеем общее решение в различных видах:
- Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
- Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
- Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.
| Пример 12 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’-2y = 0$. |
| Решение |
|
Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$ Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$ Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = C_1 e^{-2x} + C_2 e^{x}$$ |
Линейные неоднородные ДУ с постоянными коэффициентами
Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y”+py’+q = f(x).$$
Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$
Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.
| № | Правая часть | Корни характеристического многочлена | Вид частного решения |
| 1 | $$P_n (x)$$ | Число 0 не является корнем характеристического уравнения. | $$tilde{P_n}(x)$$ |
| Число 0 – корень характеристического уравнения кратности $S$. | $$x^s tilde{P_n}(x)$$ | ||
| 2 | $$P_n (x) e^{alpha x}$$ | Число $alpha$ не является корнем характеристического уравнения. | $$tilde{P_n} (x) e^{alpha x}$$ |
| Число $alpha$ является корнем характеристического уравнения кратности $S$. | $$x^s tilde{P_n} (x) e^{alpha x}$$ | ||
| 3 | $$P_n (x) cos beta x + Q_m (x) sin beta x$$ | Число $pm ibeta$ не является корнем характеристического уравнения. | $$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$ |
| Число $pm ibeta$ является корнем характеристического уравнения кратности $S$. | $$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$ | ||
| 4 | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ | Число $alpha pm ibeta$ не является корнем характеристического уравнения. | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Число $alpha pm ibeta$ является корнем характеристического уравнения. | $$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Пример 13 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y = 4xcos x$. |
| Решение |
|
Сначала находим общее решение однородного уравнения $$y” + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$ Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y”_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y”_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$ Подставляем найденные $y_text{ч.н.}$ и $y”_text{ч.н.}$ в исходный диффур из “дано” задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$ Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$ |
| Ответ |
| $$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$ |
| Пример 14 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’=5x+2e^x$. |
| Решение |
|
Сначала найдем общее решение однородного дифференциального уравнения $$y”+y’=5x+2e^x.$$ Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$ Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$ Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y”=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y”$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$ Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$ Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 – 5x + e^x.$$ Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x.$$ |
| Ответ |
| $$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x$$ |
Метод Лагранжа
Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.
- Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
- Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
- Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
- Получаем $C_1(x)$ и $C_2(x).$
| Пример 15 |
| Найти частное решение дифференциального уравнения $$y”-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$ |
| Решение |
|
Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y”-2y’+y=0.$$ Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$ Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений. Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$ Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$ Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$ Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$ |
| Ответ |
| $$y = xe^x(1+ln|x|)$$ |
I. Обыкновенные дифференциальные
уравнения
1.1. Основные понятия и определения
Дифференциальным уравнением называется
уравнение, связывающее между собой
независимую переменную x, искомую
функцию y и её производные или
дифференциалы.
Символически дифференциальное уравнение
записывается так:
F(x,y,y’)=0, F(x,y,y”)=0, F(x,y,y’,y”,.., y(n))=0
Дифференциальное уравнение называется
обыкновенным, если искомая функция зависит
от одного независимого переменного.
Решением дифференциального уравнения
называется такая функция ![]() ,
,
которая обращает это уравнение в тождество.
Порядком дифференциального уравнения
называется порядок старшей производной,
входящей в это уравнение
Примеры.
1. Рассмотрим дифференциальное уравнение
первого порядка
![]()
Решением этого уравнения является
функция y = 5 ln x. Действительно, ![]() ,
,
подставляя y’ в уравнение, получим ![]()
– тождество.
А это и значит, что функция y = 5 ln x– есть
решение этого дифференциального уравнения.
2. Рассмотрим дифференциальное уравнение
второго порядка y” – 5y’ +6y = 0. Функция ![]()
– решение этого уравнения.
Действительно, ![]() .
.
Подставляя эти выражения в уравнение,
получим: ![]() ,
,
![]()
– тождество.
А это и значит, что функция ![]()
– есть решение этого дифференциального
уравнения.
Интегрированием дифференциальных
уравнений называется процесс нахождения
решений дифференциальных уравнений.
Общим решением дифференциального
уравнения называется функция вида ![]() ,в
,в
которую входит столько независимых
произвольных постоянных, каков порядок
уравнения.
Частным решением дифференциального
уравнения называется решение, полученное
из общего решения при различных числовых
значениях произвольных постоянных.
Значения произвольных постоянных
находится при определённых начальных
значениях аргумента и функции.
График частного решения
дифференциального уравнения называется интегральной
кривой.
Примеры
1.Найти частное решение дифференциального
уравнения первого порядка
xdx + ydy = 0, если y = 4 при x = 3.
Решение. Интегрируя обе части уравнения,
получим ![]()
Замечание. Произвольную постоянную С,
полученную в результате интегрирования,
можно представлять в любой форме, удобной
для дальнейших преобразований. В данном
случае, с учётом канонического уравнения
окружности произвольную постоянную С
удобно представить в виде ![]() .
.
![]()
– общее решение дифференциального
уравнения.
Частное решение уравнения,
удовлетворяющее начальным условиям y =
4 при x = 3 находится из общего
подстановкой начальных условий в общее
решение: 32 + 42= C2; C=5.
Подставляя С=5 в общее решение, получим x2
+y2 = 52.
Это есть частное решение
дифференциального уравнения, полученное из
общего решения при заданных начальных
условиях.
2. Найти общее решение дифференциального
уравнения ![]()
Решением этого уравнения является всякая
функция вида ![]() ,
,
где С – произвольная постоянная.
Действительно, подставляя в уравнения ![]() ,
,
получим: 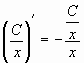 ,
,
![]() .
.
Следовательно, данное дифференциальное
уравнение имеет бесконечное множество
решений, так как при различных значениях
постоянной С равенство ![]()
определяет различные решения уравнения ![]() .
.
Например, непосредственной подстановкой
можно убедиться, что функции ![]()
являются решениями уравнения ![]() .
.
Задача, в которой требуется найти частное
решение уравнения y’ = f(x,y)
удовлетворяющее начальному условию y(x0)
= y0, называется задачей Коши.
Решение уравнения y’ = f(x,y),
удовлетворяющее начальному условию, y(x0)
= y0, называется решением задачи Коши.
Решение задачи Коши имеет простой
геометрический смысл. Действительно,
согласно данным определениям, решить
задачу Коши y’ = f(x,y) при условии y(x0)
= y0,, означает найти интегральную
кривую уравнения y’ = f(x,y) которая
проходит через заданную точку M0(x0,y0).
II. Дифференциальные уравнения первого
порядка
2.1. Основные понятия
Дифференциальным уравнением первого
порядка называется уравнение вида F(x,y,y’) =
0.
В дифференциальное уравнение первого
порядка входит первая производная и не
входят производные более высокого порядка.
Уравнение y’ = f(x,y) называется
уравнением первого порядка, разрешённым
относительно производной.
Общим решением дифференциального
уравнения первого порядка называется
функция вида ![]() ,
,
которая содержит одну произвольную
постоянную.
Пример. Рассмотрим дифференциальное
уравнение первого порядка ![]() .
.
Решением этого уравнения является
функция ![]() .
.
Действительно, заменив в данном уравнении,
![]()
его значением, получим
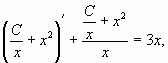
![]()
то есть 3x=3x
Следовательно, функция ![]()
является общим решением уравнения![]()
при любом постоянном С.
Найти частное решение данного уравнения,
удовлетворяющее начальному условию y(1)=1
Подставляя начальные условия x = 1, y =1
в общее решение уравнения ![]() ,
,
получим ![]()
откуда C = 0.
Таким образом, частное решение получим из
общего ![]()
подставив в это уравнение, полученное
значение C = 0 ![]()
![]()
– частное решение.
2.2. Дифференциальные уравнения с
разделяющимися переменными
Дифференциальным уравнением с
разделяющимися переменными называется
уравнение вида: y’=f(x)g(y) или через
дифференциалы ![]() ,
,
где f(x) и g(y)– заданные функции.
Для тех y, для которых ![]() ,
,
уравнение y’=f(x)g(y) равносильно уравнению,
![]()
в котором переменная y присутствует
лишь в левой части, а переменная x- лишь в
правой части. Говорят, «в уравнении y’=f(x)g(y
разделим переменные».
Уравнение вида ![]()
называется уравнением с разделёнными
переменными.
Проинтегрировав обе части уравнения ![]()
по x, получим G(y) = F(x) + C– общее
решение уравнения, где G(y) и F(x) –
некоторые первообразные соответственно
функций ![]()
и f(x), C произвольная постоянная.
Алгоритм решения дифференциального
уравнения первого порядка с разделяющимися
переменными
- Производную функции переписать через её
дифференциалы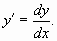
- Разделить переменные.
- Проинтегрировать обе части равенства,
найти общее решение. - Если заданы начальные условия, найти
частное решение.
Пример 1
Решить уравнение y’ = xy
Решение. Производную функции y’
заменим на ![]()
![]()
разделим переменные ![]()
![]()
проинтегрируем обе части равенства:
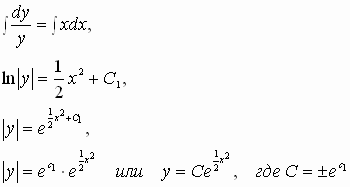
Ответ: ![]()
Пример 2
Найти частное решение уравнения
2yy’ = 1- 3x2,
если y0 = 3 при x0 = 1
Это—уравнение с разделенными
переменными. Представим его в
дифференциалах. Для этого перепишем данное
уравнение в виде ![]()
Отсюда ![]()
Интегрируя обе части последнего
равенства, найдем ![]()
Подставив начальные значения x0 = 1,
y0 = 3 найдем С 9=1-1+C, т.е. С = 9.
Следовательно, искомый частный интеграл
будет ![]()
или ![]()
Пример 3
Составить уравнение кривой, проходящей
через точку M(2;-3) и имеющей касательную с угловым
коэффициентом ![]()
Решение. Согласно условию ![]()
Это уравнение с разделяющимися
переменными. Разделив переменные, получим: ![]()
Проинтегрировав обе части уравнения,
получим: 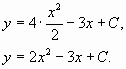
Используя начальные условия, x = 2 и y
= – 3 найдем C:
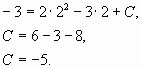
Следовательно, искомое уравнение имеет
вид ![]()
2.3. Линейные дифференциальные уравнения
первого порядка
Линейным дифференциальным уравнением
первого порядка называется уравнение вида y’
= f(x)y + g(x)
где f(x) и g(x) – некоторые заданные функции.
Если g(x)=0 то
линейное дифференциальное уравнение
называется однородным и имеет вид: y’ = f(x)y
Если ![]()
то уравнение y’ = f(x)y + g(x) называется неоднородным.
Общее решение линейного однородного
дифференциального уравнения y’ = f(x)y задается формулой: ![]()
где С – произвольная постоянная.
В частности, если С =0, то решением
является y = 0 Если линейное однородное уравнение имеет
вид y’ = ky где k – некоторая постоянная, то его общее решение
имеет вид: ![]() .
.
Общее решение линейного неоднородного
дифференциального уравнения y’ = f(x)y + g(x) задается формулой ![]() ,
,
т.е. равно сумме общего решения
соответствующего линейного однородного
уравнения и частного решения ![]()
данного уравнения.
Для линейного неоднородного уравнения
вида ![]() y’
y’
= kx + b,
где k и b–
некоторые числа и ![]() частным
частным
решением будет являться постоянная функция
![]() .
.
Поэтому общее решение имеет вид ![]() .
.
Пример. Решить уравнение y’ + 2y +3 = 0
Решение. Представим уравнение в виде y’
= -2y – 3 где k = -2, b= -3 Общее решение задается формулой ![]()
![]() .
.
Следовательно, ![]()
где С – произвольная постоянная.
Ответ: ![]()
2.4. Решение линейных дифференциальных
уравнений первого порядка методом Бернулли
Нахождение общего решения линейного
дифференциального уравнения первого
порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных
уравнений с разделенными переменными с
помощью подстановки y=uv,
где u и v – неизвестные функции от x.
Этот метод решения называется методом
Бернулли.
Алгоритм решения линейного дифференциального
уравнения первого порядка
y’ = f(x)y + g(x)
1. Ввести подстановку y=uv.
2. Продифференцировать это равенство y’ =
u’v + uv’
3. Подставить y и y’ в данное уравнение:
u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).
4. Сгруппировать члены уравнения так, чтобы
u вынести
за скобки: ![]()
![]()
5. Из скобки, приравняв ее к нулю, найти
функцию ![]()
![]()
Это уравнение с разделяющимися
переменными: ![]()
Разделим переменные и получим: ![]()
Откуда ![]() .
.
![]() .
.
6. Подставить полученное значение v в уравнение ![]()
(из п.4):
![]()
и найти функцию ![]()
Это уравнение с разделяющимися переменными:
![]()
![]()
7. Записать общее решение в виде: ![]()
![]() ,
,
т.е. ![]() .
.
Пример 1
Найти частное решение уравнения y’ = -2y
+3 = 0 если y =1 при x = 0
Решение. Решим его с помощью
подстановки y=uv, .y’ = u’v + uv’
Подставляя y и y’
в данное уравнение, получим ![]()
Сгруппировав второе и третье слагаемое
левой части уравнения, вынесем общий
множитель u за
скобки![]()
Выражение в скобках приравниваем к нулю и,
решив полученное уравнение, найдем функцию v
= v(x)![]()
Получили уравнение с разделенными
переменными. Проинтегрируем обе части
этого уравнения: ![]()
Найдем функцию v:
![]()
Подставим полученное значение v в уравнение ![]()
Получим: ![]()
Это уравнение с разделенными переменными.
Проинтегрируем обе части уравнения:![]()
Найдем функцию u = u(x,c) ![]()
Найдем общее решение: ![]()
Найдем частное решение уравнения,
удовлетворяющее начальным условиям y = 1 при
x = 0:
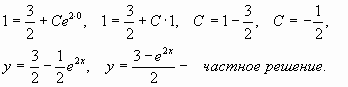
Ответ: ![]()
III. Дифференциальные уравнения высших
порядков
3.1. Основные понятия и определения
Дифференциальным уравнением второго
порядка называется уравнение, содержащее
производные не выше второго порядка. В
общем случае дифференциальное уравнение
второго порядка записывается в виде: F(x,y,y’,y”)
= 0
Общим решением дифференциального
уравнения второго порядка называется
функция вида ![]()
![]() ,
,
в которую входят две произвольные
постоянные C1 и C2.
Частным решением дифференциального
уравнения второго порядка называется
решение, полученное из общего ![]()
при некоторых значениях произвольных
постоянных C1 и C2.
3.2. Линейные однородные дифференциальные
уравнения второго порядка с
постоянными коэффициентами.
Линейным однородным дифференциальным
уравнением второго порядка с постоянными
коэффициентами называется уравнение вида
y” + py’ +qy = 0, где pи q–
постоянные величины.
Алгоритм решения однородных дифференциальных
уравнений второго порядка с постоянными
коэффициентами
1. Записать дифференциальное уравнение в
виде: y” + py’ +qy = 0.
2. Составить его характеристическое
уравнение, обозначив y” через r2,
y’ через r, yчерез
1:![]()
r2 + pr +q = 0
3.Вычислить дискриминант D = p2 -4q
и найти корни характеристического
уравнения; при этом если:
а) D > 0; следовательно,
характеристическое уравнение имеет два
различных действительных корня ![]() .
.
Общее решение дифференциального уравнения
выражается в виде ![]() ,
,
где C1 и C2 – произвольные постоянные.
б) D = 0; следовательно,
характеристическое уравнение имеет равные
действительные корни ![]() .
.
Общее решение дифференциального уравнения
выражается в виде ![]()
в) D < 0; следовательно,
характеристическое уравнение имеет
комплексные корни, ![]()
Общее решение дифференциального уравнения
выражается, в виде
![]()
Примеры.
1. Найти частное решение дифференциального
уравнения
![]()
Решение. Составим характеристическое
уравнение ![]()
![]()
D>0,
![]()
Общее решение ![]()
Дифференцируя общее решение, получим ![]()
Составим систему из двух уравнений 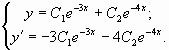
Подставим вместо ![]() ,
,![]() и
и
![]()
заданные начальные условия:
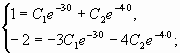
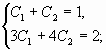
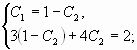
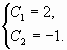
![]()
Таким образом, искомым частным решением
является функция
![]() .
.
2. Найти частное решение уравнения
![]()
Решение
![]() <0,
<0,
![]()
Общее решение ![]()
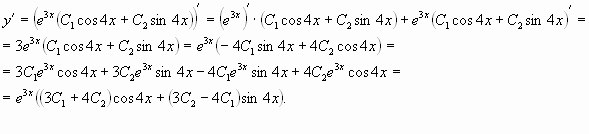
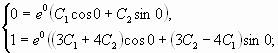
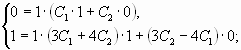
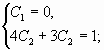
![]() –
–
частное решение.
IV. Практическая работа
Вариант 1
1. Составить уравнение кривой, проходящей
через точку M(1;2) и имеющей угловой коэффициент ![]() .
.
2. Найти частные решения дифференциальных
уравнений:
а)![]()
б) ![]()
в) ![]()
г) ![]()
Вариант 2
1. Составить уравнение кривой, проходящей
через точку M(2;1) и имеющей угловой коэффициент ![]()
2. Найти частные решения дифференциальных
уравнений:
а)![]()
б) ![]()
в) ![]()
г) ![]()
V. Ответы
|
Вариант 1 |
Вариант 2 |
|
1. |
1. |
|
2. а) |
2. а) |
|
б) |
б) |
|
в) |
в) |
|
г) |
г) |
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Определение
Уравнение
(*)
где
и
– непрерывные
функция в интервале
называется
неоднородным линейным дифференциальным уравнение второго порядка, функции
и
– его
коэффицинентами. Если
в
этом интервале, то уравнение принимает вид:
(**)
и называется однородным
линейным дифференциальным уравнением второго порядка. Если уравнение (**) имеет
те же коэффициенты
и
, как уравнение (*), то оно называется
однородным уравнением, соответствующим неоднородному уравнению (*).
Однородные дифференциальные линейные уравнения второго порядка
Пусть в линейном уравнении
и
– постоянные
действительные числа.
Частное решение уравнения
будем искать в виде функции
, где
– действительное
или комплексное число, подлежащее определению. Дифференцируя по
, получаем:
Подставляя в исходное дифуравнение, получаем:
Отсюда, учитывая, что
, имеем:
Это уравнение называется
характеристическим уравнением однородного линейного дифуравнения. Характеристическое уравнение и дает
возможность найти
. Это уравнение второй степени, поэтому
имеет два корня. Обозначим их через
и
. Возможны три случая:
Корни действительные и разные
В этом случае общее решение уравнения:
Пример 1
Решение
Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Корни действительные и равные
В этом случае общее решение уравнения:
Пример 2
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Корни комплексные
В этом случае общее решение уравнения:
Пример 3
Решение
Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Неоднородные дифференциальные линейные уравнения второго порядка
Рассмотрим теперь решение некоторых
типов линейного неоднородного уравнения второго порядка с постоянными
коэффициентами
где
и
– постоянные
действительные числа,
– известная непрерывная
функция в интервале
. Для нахождения общего решения такого
дифференциального уравнения необходимо знать общее решение соответствующего
однородного дифференциального уравнения
и частное
решение
. Рассмотрим
некоторые случаи:
Правая часть дифференциального уравнения имеет вид:
Частное решение дифференциального
уравнения ищем также в форме квадратного трехчлена:
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициенты.
Если нуль – однократный корень
характеристического уравнения, то
Если нуль – двухкратный корень
характеристического уравнения, то
Аналогично обстоит дело, если
– многочлен
произвольной степени
Пример 4
Решение
Решим соответствующее однородное уравнение.
Характеристическое уравнение:
Общее решение однородного уравнения:
Найдем частное решение неоднородного
дифуравнения:
Подставляя найденные производные в исходное дифуравнение, получаем:
Искомое частное решение:
Общее решение исходного дифуравнения:
Правая часть дифференциального уравнения имеет вид:
Частное решение ищем в виде
, где
– неопределенный
коэффициент.
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициент.
Если
– корень
характеристического уравнения, то частное решение исходного дифференциального
уравнения ищем в виде
, когда
– однократный
корень, и
, когда
– двукратный
корень.
Пример 5
Решение
Характеристическое
уравнение:
Общее
решение соответствующего однородного дифференциального уравнения:
Найдем
частное решение соответствующего неоднородного дифференциального уравнения:
Подставляя
в исходное дифуравнение, получаем:
Общее
решение дифуравнения:
Правая часть дифференциального уравнения имеет вид:
В этом случае частное решение
ищем в форме тригонометрического двучлена:
где
и
– неопределенные коэффициенты
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициенты.
Эти уравнения определяют коэффициенты
и
кроме случая, когда
(или когда
– корни характеристического уравнения). В
последнем случае частное решение дифференциального уравнения ищем в виде:
Пример 6
Решение
Характеристическое
уравнение:
Общее
решение соответствующего однородного дифуравнения:
Найдем
частное решение неоднородного дифуравнения
Подставляя
в исходное дифуравнение, получаем:
Общее
решение исходного дифуравнения:
75
|
−4A + 2C =1, |
|
|
A −4B + 4C + 2D = 0, |
|
|
2A + 4C = 0, |
|
|
−4A −2B +C −4D = 0. |
|
|
Из первого и третьего уравнений системы следует: A = −0,2, |
|
|
C = 0,1. |
Поэтому из второго и четвертого уравнений находим |
|
B = 0,13, |
D = 0,16. Таким образом, искомое частное решение за- |
пишется в виде
y = (−0,2x +0,13)cos 2x +(0,1x +0,16)sin 2x.
Складывая его с общим решением однородного уравнения, окончательно получим общее решение исходного уравнения
y= C1 +C2e−x + (−0,2x +0,13)cos 2x +(0,1x +0,16)sin 2x.
2.4.2.Метод вариации произвольных постоянных
Если известно общее решение однородного линейного дифференциального уравнения, соответствующего заданному неоднородному, то его частное решение может быть найдено методом вариации произвольных постоянных (методом Лагранжа).
Рассмотрим его реализацию для линейных дифференциальных уравнений второго порядка:
|
y′′+ a1 y′+ a2 y = f (x). |
(2.59) |
Сначала находим общее решение соответствующего линейного однородного уравнения L(y) = 0 в виде
|
y0 = C1 y1 + C2 y2, |
(2.60) |
|
где C1 и C2 – произвольные постоянные, y1 , |
y2 – частные линейно |
независимые решения однородного уравнения.
Далее ищем решение неоднородного уравнения (2.59), аналогичное по структуре (2.60), но произвольные постоянные в (2.60) заменяем неизвестными функциями, а именно принимаем
|
y = C1 (x)y1 + C2 (x)y2. |
(2.61) |
Тогда y′ = C1′(x)y1 +C1 (x)y1′ +C2′(x)y2 +C2(x)y2′.

76
Так как функции C1 (x) и C2(x) произвольны, то можно принять,
|
что они должны удовлетворять условию: |
|
|
C1′(x)y1 +C2′(x)y2 = 0. |
(2.62) |
|
Тогда y′ = C1 (x)y1′ +C2(x)y2′ и, следовательно, |
|
|
y′′ = C1′(x)y1′ +C1 (x)y1′′+C2′(x)y2′ +C2(x)y2′′. |
(2.63) |
Подставляя теперь значения производных в уравнение (2.59), получим
|
C1 (x)(y1′′+ a1 y1′ + a2 y1 )+C2(x)(y2′′ + a1 y2′ + a2 y2 )+ |
(2.64) |
||
|
+C1′(x)y1′ +C2′(x)y2′ = f (x). |
|||
|
Учитывая, что функции y1 |
и y2 являются решениями одно- |
||
|
родного уравнения (2.59), и, следовательно, |
|||
|
y1′′+ a1 y1′ + a2 y1 = 0, |
y2′′ + a1 y2′ + a2 y2 = 0, |
||
|
приходим к равенству |
C1′(x)y1′ +C2′(x)y2′ = f (x).
Таким образом, чтобы выражение (2.61) было решением неоднородного уравнения (2.59), неизвестные функции C1 (x) и
C2(x) должны удовлетворять следующей системе дифференциальных уравнений
|
C′(x)y |
+C′ |
(x)y |
= 0, |
(2.65) |
||||
|
1 |
1 |
2 |
2 |
= f (x). |
||||
|
C1′(x)y1′ +C2′(x)y2′ |
||||||||
|
Определитель этой системы – определитель Вронского |
||||||||
|
W = |
y1 |
y2 |
≠ 0, |
|||||
|
y2′ y2′ |
||||||||
|
так как функции y1 и y2 |
линейно независимы. Поэтому система |
(2.65), рассматриваемая как система линейных алгебраических уравнений относительно С1′(x), С2′(x), имеет решение и притом
единственное. Применяя формулы Крамера11, его можно предста-
11 К р а м е р Габриэль (31.07.1704 – 04.01.1752) – швейцарский математик.
77
вить в виде
|
C1′(x) = − |
y2 f (x) |
, |
C2′(x) = |
y1 f (x) |
. |
(2.66) |
|
|
W |
|||||||
|
W |
Интегрируя дифференциальные уравнения первого порядка (2.66), находим
|
С (x) = − |
∫ |
y2 f (x) |
dx +C , |
C (x) = |
∫ |
y1 f (x) |
dx + C . |
(2.67) |
||||||
|
1 |
W |
1 |
2 |
W |
2 |
|||||||||
|
Подставляя (2.67) |
в (2.61), |
получим общее решение неод- |
||||||||||||
|
нородного уравнения в виде |
||||||||||||||
|
∫ |
y2 f (x) |
∫ |
y1 f (x) |
|||||||||||
|
y = C1 y1 + C2 y2 |
− y1 |
W |
dx + y2 |
W |
dx. |
(2.68) |
||||||||
Последние два слагаемых в правой части формулы (2.67) определяют частное решение неоднородного уравнения (2.59).
Таким образом, если известна фундаментальная система решений соответствующего линейного однородного уравнения y1 , y2, то общее решение неоднородного уравнения может быть
найдено с помощью квадратур (то есть неопредёленных интегралов от этих решений).
Замечание. Метод вариации произвольных постоянных является общим методом, пригодным для построения решения линейных неоднородных дифференциальных уравнений (как с переменными, так и с постоянными коэффициентами) при произвольной непрерывной правой части. Но он является принципиально более сложным, чем метод подбора, так как его реализация связана с интегрированием дифференциальных уравнений первого порядка. Поэтому для линейных неоднородных уравнений с постоянными коэффициентами и с правыми частями специального вида, указанными в таблице 2, проще применять метод подбора частного решения.
Пример. Решить уравнение
|
′′ |
′ |
e−2x |
||||
|
y |
+ 4 y |
+ 4 y = x . |
(2.69) |
|||
1). Находим общее решение соответствующего однородного уравнения
78
y′′+ 4 y′+ 4 y = 0.
Составляем характеристическое уравнение k 2 + 4k + 4 = 0.
|
Его корни k1 = k2 = −2. |
Следовательно, частные линейно незави- |
||||
|
симые решения равны |
y = e−2x , |
y |
2 |
= xe−2x , |
а общее решение |
|
1 |
y0 = C1e−2x +C2xe−2x .
2). Так как правая часть неоднородного уравнения (2.69) не относится ни к одному из рассмотренных в таблице 2 случаев, то частное решение находим методом вариации произвольных постоянных. Принимаем
|
y = C (x)e−2x + C |
2 |
(x)xe−2x , |
(2.70) |
|
1 |
где C1 (x) и C2 (x) – неизвестные (варьируемые) функции. Тогда
их производные C1′ (x) и C2′(x) могут быть найдены из решения системы (2.65):
|
′ |
(x)e |
−2x |
′ |
−2x |
= 0, |
|||||||||
|
C1 |
+ C2 (x)xe |
|||||||||||||
|
−2x |
||||||||||||||
|
− 2C1′(x)e−2x + C2′(x)(e−2x − 2xe−2x ) = e |
x |
. |
||||||||||||
Определитель этой системы |
||||||||||||||
|
W = |
e−2x |
xe |
−2x |
= e−4 x . |
||||||||||
|
− |
2e−2x |
e−2x |
− 2xe−2x |
|||||||||||
|
Поэтому для определения варьируемых функций согласно |
||||||||||||||
|
(2.66) получаем дифференциальные уравнения вида |
||||||||||||||
|
C1′(x) = − xe−2xe−2x |
= −1, |
C2′(x) = e−2xe−2x |
= |
1 . |
(2.71) |
|||||||||
|
xe−4 x |
xe−4 x |
x |
||||||||||||
Интегрируя уравнения (2.71), находим |
||||||||||||||
|
C1 (x) = −x + C1 , |
C2 (x) = ln x + C2. |
(2.72) |
Подставляя (2.72) в (2.70), получим общее решение уравнения в виде
y = e−2x [C1 + C2x + x(lnx −1)].
79
2.5.Вынужденные колебания линейной системы
содной степенью свободы без учета сил сопротивления
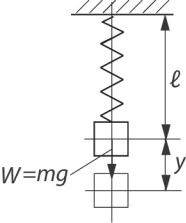
Клинейным дифференциальным уравнениям с постоянными коэффициентами сводятся многие задачи о механических и электрических колебаниях.
1) В качестве первого практического примера применения изложенной теории рассмотрим задачу о вынужденных колебаниях линейной системы с одной степенью свободы без учета сил сопротивления. Такой системой моделируются вертикальные перемещения груза массой m на пружине (см. рис. I.8). Массой пружины по сравнению с массой груза пренебрегается.
Если сообщить грузу некоторую начальную скорость и начальное отклонение, то под действием восстанавливающей силы упругости пружины система будет совершать колебания относительно положения статического равновесия, называемые собст-
венными или свободными колебаниями.
Рис. I.8
Удлинение пружины при действии статически приложенного груза W = mg равно
где k – коэффициент жëсткости пружины (груз, вызывающий ëе удлинение, равное единице) [16].
Если y – вертикальное перемещение колеблющегося груза
относительно положения статического равновесия (оно считается положительным, если направлено вниз), то уравнение движения
80
груза при его свободных колебаниях согласно второму закону Ньютона запишется в виде
|
m d 2 y = mg −k(y +δст ) |
||||||||
|
dt2 |
||||||||
|
или после подстановки выражения (2.73) |
||||||||
|
d 2 y + p2 y = 0, |
(2.74) |
|||||||
|
где |
dt2 |
|||||||
|
k |
g |
|||||||
|
t – время, а |
p2 = |
= |
– квадрат круговой частоты собственных |
|||||
|
m |
||||||||
|
δст |
колебаний системы.
Пусть кроме силы веса и силы натяжения пружины на груз действует периодическая возмущающая сила P(t) = F sin ωt , вы-
зывающая вынужденные колебания системы (F – амплитуда, ω – частота вынужденных колебаний),
Тогда дифференциальное уравнение движения груза запишется в виде
md 2 y = mg −k(y +δст )+ F sin ωt dt2
или
m d 2 y + ky = F sin ωt. dt2
Полагая q = mF , получим окончательно уравнение вынуж-
денных колебаний одномассовой системы в виде линейного неоднородного дифференциального уравнения с постоянными коэффициентами второго порядка:
|
y′′+ p2 y = q sin ωt. |
(2.75) |
|
|
Решаем сначала однородное уравнение |
y′′+ p2 y = 0. |
Ха- |
|
рактеристическое уравнение, ему соответствующее: k 2 + p2 |
= 0, |
|
имеет мнимые корни k1,2 |
= ±pi . Поэтому общее решение одно- |
|
|
родного уравнения запишется в виде |
||
|
y0 |
= C1 cos pt +C2 sin pt. |
(2.76) |

81
Полагая C1 = Asinϕ, C2 = Acosϕ, можно представить решение (2.76) в виде
y0 = Asin(pt +ϕ).
Это решение описывает собственные колебания массы m относительно положения статического равновесия. Как видно, колебания являются незатухающими и происходят по синусои-
дальному закону с амплитудой A, периодом τ = 2pπ = 2π 
 mk и на-
mk и на-
чальной фазой ϕ. При этом величина, обратная периоду – так на-
зываемая техническая частота колебаний (число колебаний в секунду), равна
ν=τ1 = 2pπ
иизмеряется в герцах. Тогда число колебаний в 1 мин. будет рав-
но
|
60p |
60 |
300 |
, |
||||||||
|
n = |
= |
g |
= |
||||||||
|
2π |
2π |
δст |
|||||||||
|
fст |
где fст – в см. Этой формулой пользуются в расчëтах в тех случа-
ях, когда система может быть сведена к системе с одной степенью свободы.
Частное решение уравнения (2.75) ищем методом подбора в
виде
y = B cosωt +C sin ωt.
Находя неопределëнные коэффициенты B и C, получим
|
y |
= |
F sin ωt |
= |
q sin ωt |
(2.77) |
|||||||||
|
ω |
2 |
ω2 |
||||||||||||
|
mp2 |
− |
p2 |
− |
|||||||||||
|
1 |
2 |
1 |
2 |
|||||||||||
|
p |
p |
|||||||||||||
и окончательно, общее решение уравнения колебаний запишется в виде
|
y = C1 cos pt +C2 sin pt + |
q |
sin ωt. (2.78) |
|||||
|
p2 |
ω2 |
||||||
|
1− |
2 |
||||||
|
p |
|||||||
Последнее слагаемое описывает так называемый установив-

82
шийся режим вынужденных колебаний системы с частотой ω.
|
Подставляя в (2.77) выражения для p2 |
и |
q, получим |
|||||||||||||||||||||
|
F |
|||||||||||||||||||||||
|
y = |
q sin ωt |
= |
m sin ωt |
= |
F |
1 |
sin ωt. (2.79) |
||||||||||||||||
|
ω2 |
k |
ω2 |
|||||||||||||||||||||
|
p |
2 |
k |
ω2 |
1 |
− |
||||||||||||||||||
|
− |
2 |
− |
2 |
2 |
|||||||||||||||||||
|
1 |
p |
1 |
p |
p |
|||||||||||||||||||
|
m |
|||||||||||||||||||||||
|
Множитель |
F |
характеризует перемещение, которое вызы- |
|||||||||||||||||||||
|
k |
вает максимальная возмущающая сила, если она приложена ста-
|
тически, а множитель kдин = |
1 |
характеризует динамич- |
|
1−ω2 / p2 |
ность действия этой силы. Абсолютная величина этого множите-
ля называется коэффициентом динамичности.
Как видно из полученного решения, когда отношение ω / p →1, коэффициент динамичности и амплитуда колебаний
неограниченно возрастают. Это явление совпадения частоты возмущающей силы с частотой собственных колебаний системы на-
зывается резонансом.
2) Вынужденные колебания упруго подвешенного груза могут быть вызваны также другим способом, например, если верхнему концу пружины задать в вертикальном направлении простое гармоническое движение (см. рис. I.8)
Решение этой задачи дано С.П.Тимошенко12 [16].
Тогда удлинение пружины в произвольный момент времени будет равно y +δст − y1, а соответствующая сила упругости пру-
жины: mg + k(y − y1 ) (перемещение груза y при этом в любой
момент времени отсчитывается от положения равновесия, в котором y1 = 0). Поэтому уравнение движения подвешенного на пру-
жине груза запишется в виде
12Т и м о ш е н к о Степан Прокофьевич (22.12.1878 –29.05.1972)
–российский ученый и инженер в области механики деформируемого твердого тела.
83
|
m d 2 y = mg −k(y +δ |
ст |
− y ) |
|||||||
|
dt2 |
1 |
||||||||
|
или |
|||||||||
|
d 2 y |
|||||||||
|
m |
+ k(y − y )= 0. |
(2.81) |
|||||||
|
dt |
2 |
1 |
|||||||
|
k |
|||||||||
|
Подставляя y |
в уравнение |
(2.81) и обозначая |
q = C |
, полу- |
|||||
|
1 |
m |
||||||||
|
чим |
|||||||||
|
d 2 y |
|||||||||
|
+ p2 y = q sin ωt. |
(2.82) |
||||||||
|
dt2 |
Уравнение (2.82) совпадает с уравнением (2.75) при F = Ck. Следовательно, заданное гармоническое перемещение верхнего конца пружины C sin ωt можно рассматривать как эквивалентное
приложению возмущающей силы Ck sin ωt. Поэтому установив-
шийся режим вынужденных колебаний при перемещении верхнего конца пружины по принятому гармоническому закону будет описываться равенством, аналогичным равенству (2.79):
|
y = |
F 1 |
sin ωt = C |
1 |
sin ωt. |
(2.83) |
|||||
|
k 1− |
ω2 |
1− |
ω2 |
|||||||
|
p2 |
p2 |
Используя решение задачи 2), легко получить решение следующей задачи [16]:
3) Пусть колесо катится с постоянной горизонтальной скоростью V =18 м/ с по неровной дороге, профиль которой задан
|
уравнением y = C sin |
πx |
, где C = 2,5см, а |
l = 90см (см. рис. I.9). |
|
l |
Найти амплитуду вынужденных вертикальных колебаний груза W = mg , связанного пружиной с осью колеса, если статическое
удлинение пружины под действием груза составляет δст = 9,8см.
|
Рассматривая свободные |
вертикальные колебания груза |
|||||
|
W на пружине, найдем квадрат угловой частоты этих колебаний |
||||||
|
p2 = |
g |
= |
981=100 |
1 |
. |
|
|
сек2 |
||||||
|
δст |
9,8 |
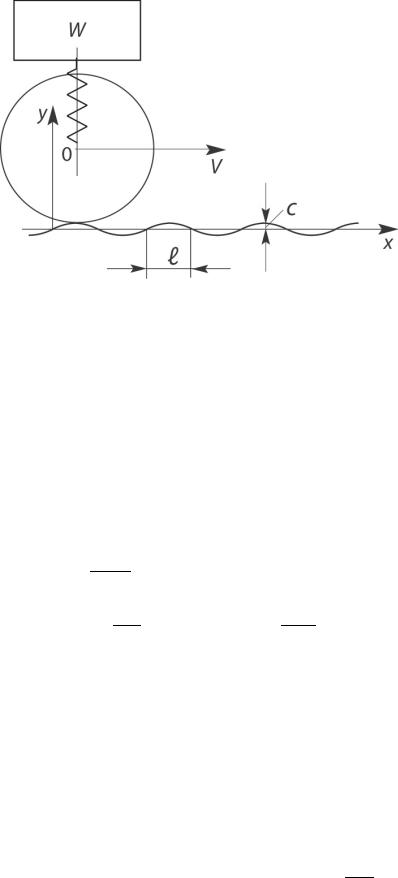
84
Рис. I.9
Центр O катящегося колеса совершает вертикальные колебания ввиду неровности профиля дороги.
Пусть в начальный момент времени t = 0 точка касания колеса с дорогой находится в начале координат y = 0. Тогда, учи-
тывая, что y =Vt , получим для вертикальных колебаний этой точки равенство y = C sin πVtl . Поэтому вынужденные колебания груза можно определить из равенства (2.83) после подстановки в него значений p2 =100 сек1 2 , C = 2,5см,
ω= πlV =180090π = 20π сек1 ..
Врезультате амплитуда вынужденных колебаний колеса
будет равна (в этих вычислениях масса колеса не учитывается)
|
ymax = |
2,5 |
= 0,066см. |
|||||
|
1− |
(20π)2 |
||||||
|
100 |
Как видно, при заданной скорости движения вертикальные колебания колеса лишь в очень малой степени передаются грузу.
При уменьшении скорости V , в конце концов, при πlV = p можно

85
придти к резонансу; при этом будут очень сильные колебания груза.
2.6.Вынужденные колебания линейной системы
содной степенью свободы с учетом сил сопротивления
Если колеблющееся тело при движении испытывает сопротивление, пропорциональное скорости (это простейший случай так называемого вязкого трения, при котором сила трения
R = c dydt ), и кроме того, на него действует возмущающая сила
F sin ωt , то уравнение вынужденных колебаний системы с одной степенью свободы записывается в виде [16]
|
d 2 y |
+ 2n dy |
+ p2 y = |
F sin ωt , |
(2.84) |
||||
|
dt2 |
dt |
m |
||||||
|
где |
k |
c |
||||||
|
p2 = |
, |
2n = |
. |
(2.85) |
||||
|
m |
m |
В (2.85) c–постоянная, равная величине демпфирующей силы при скорости, равной единице.
Однородное уравнение, соответствующее уравнению (2.85), описывает малые свободные колебания с учетом вязкого трения.
Характеристическое уравнение λ2 + 2nλ + p2 = 0 имеет кор-
|
ни λ |
= −n ± |
n2 − p2 |
. Будем различать три случая. |
|
|
1,2 |
n > p (случай большого сопротивления), то оба |
|||
|
1) |
Если |
корня действительны и отрицательны. Общее решение однородного уравнения запишется в виде
y0 = C1eλ1t +C2eλ2t = C1e(−n+
 n2−p2 ) t +C2e(−n−
n2−p2 ) t +C2e(−n−
 n2−p2 ) t =
n2−p2 ) t =
=e−nt (C1e
 n2−p2 t +C2e−
n2−p2 t +C2e−
 n2−p2 t ).
n2−p2 t ).
Сростом времени t отклонение y0 → 0, то есть система
асимптотически приближается к исходному невозмущëнному равновесному состоянию. Движение при этом не будет колебательным, а носит так называемый апериодический характер, хотя может реализовываться по – разному (см. рис. I.10).
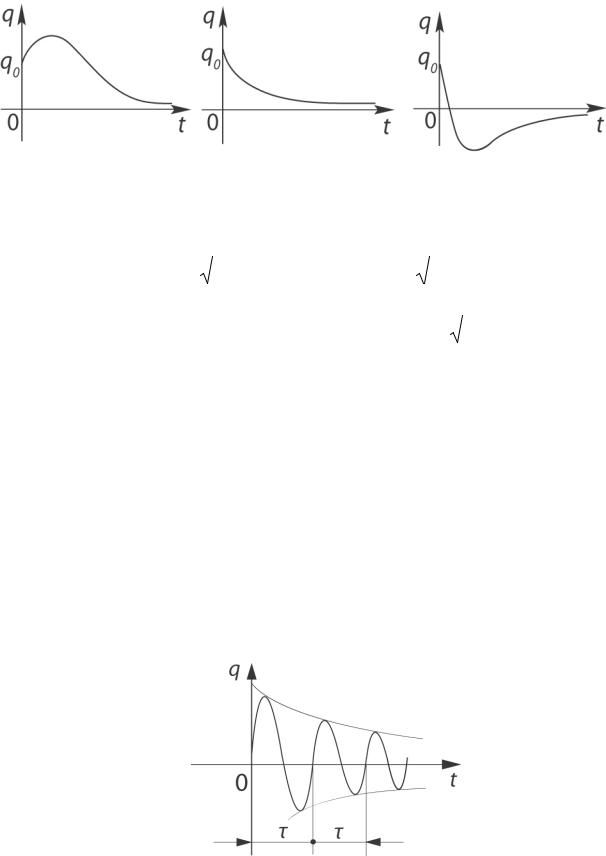
86
Рис. I.10
2) Если n < p (случай малого сопротивления), то корни характеристического уравнения будут комплексно сопряжëнными:
|
λ = −n +i p2 −n2 , |
λ |
2 |
= −n −i p2 |
−n2 |
||||||||
|
1 |
||||||||||||
|
или |
||||||||||||
|
λ = −n +ir, |
λ |
2 |
= −n −ir, |
где |
r = |
p2 −n2 |
. (2.86) |
|||||
|
1 |
||||||||||||
|
Общее решение уравнения (2.86) |
при этом будет |
|||||||||||
|
y |
0 |
= C e−nt cos rt +C |
e−nt sin rt , |
(2.87) |
||||||||
|
1 |
2 |
|||||||||||
|
и если принять C1 = Asinϕ, C2 = Acosϕ, (где |
A,ϕ – постоянные), |
|||||||||||
|
оно может быть приведено к виду |
y0 |
= Ae−nt sin(rt +ϕ). |
Множитель e−nt убывает со временем, поэтому при малом трении происходят собственные колебания с амплитудой, убывающей со временем, так называемые затухающие колебания (см.
рис. I.11).
Частное решение неоднородного уравнения (2.84) находим методом подбора. Принимаем
|
y = M sin ωt + N cosωt, |
(2.88) |
Рис. I.11

87
|
где M и |
N – неопределëнные коэффициенты. Подставляя (2.88) |
|||||||
|
в уравнение (2.84) и приравнивая коэффициенты при |
sin ωt и |
|||||||
|
cosωt, получим |
||||||||
|
M = |
P |
p2 −ω2 |
N = − |
P |
2nω |
. (2.89) |
||
|
, |
||||||||
|
m |
(p2 −ω2 )2 + 4n2ω2 |
m |
(p2 −ω2 )2 + 4n2ω2 |
Поэтому общее решение уравнения вынужденных колебаний линейной системы при гармоническом возмущении с учетом (2.87), (2.89) запишется в виде
y= y0 + y = e−nt (C1 cos rt +C2 sin rt)+ M sin ωt + N cosωt.
2.7.Колебания независимой подвески13
Построить график вертикального смещения оси колеса легкового автомобиля массой mк = 30 кг, если для его крепления ис-
пользуется независимая рычажная подвеска со следующими характеристиками: коэффициент демпфирования амортизатора
k = 3 103 н сек/ м; жесткость пружины c =1,7 105 н/ м. Пред-
полагается, что внешняя сила, действующая на колесо, изменяются по закону:
P(t) = P0 + Pc cosωt, где P0 =850кг, Pс = 58кг, ω = 33 гц.
При этом P0 – постоянная (статическая) составляющая силы (реакция от дороги), а Pc cosωt – зависящая от времени динамиче-
ская составляющая нагрузки (обусловленная неровностями дороги).
В расчетах не учитывать упругость шины и инерционные характеристики подвески колеса.
Схематично независимая подвеска колеса показана на рис.I.12.
13 Общая задача о вертикальных колебаниях автомобиля и его агрегатов подробно рассмотрена Е.А.Лопаницыным (см. “Избранные проблемы прикладной механики и математики”. Сб. научных работ кафедры “Прикладная и вычислительная математика”, посвященный 80-летию чл.-корр. РАН Э.И.Григолюка. М.: МГТУ
“МАМИ”, 2003. 320 с.).

88
Пренебрегая вращательными движениями колеса вокруг оси подвески, будем учитывать только вертикальные перемещения колеса yк = yп . Массу подвески отнесëм к массе колеса.
Подвеска (рессора) моделируется линейно – упругим элементом (пружиной) жесткостью c, а амортизатор – демпфером с коэффициентом демпфирования k. Поэтому сила, действующая на колесо со стороны подвески, складывается из силы, пропор-
Рис. I.12
циональной перемещению (это сила упругости пружины cyп ) и
силы, пропорциональной скорости (силы демпфирования амортизатора: kdyп / dt). Следовательно, суммарное усилие, передаю-
щееся от подвески на колесо, будет равно
Fп = cyп + k dydtп .
Дифференциальное уравнение движения колеса под действием сил, действующих со стороны подвески и шины (см. рис. ), запишется в виде
mк d 2 yк = P(t)− Fп −mк g. dt2
Если масса колеса измеряется в кг, перемещение – в см, а силы P(t) и Fп – в кг, то уравнение приводится к виду
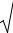
|
89 |
||||
|
d 2 yк = g |
1 |
[P(t)− F |
] −1 , |
|
|
dt2 |
п |
|||
|
mк |
где g = 981см/ сек2.
Подставляя в для усилий P(t) и
d 2 yк dt2
это уравнение приведенные выше выражения Fп , получим
|
= g |
1 |
P + P cosωt −cy |
−k dyк |
−1 . |
||
|
к |
||||||
|
0 |
c |
|||||
|
mк |
dt |
После элементарных преобразований приходим к неоднородному линейному дифференциальному уравнению второго порядка:
|
d 2 y |
к +b |
dy |
к +b y |
к |
= b cosωt +b , |
||
|
dt2 |
|||||||
|
1 |
dt |
2 |
3 |
4 |
коэффициенты которого равны
|
kg |
cg |
Pc g |
P0 |
|||||||
|
b1 = m |
, |
b2 = m |
, |
b3 = |
, |
b4 |
||||
|
m |
= g m |
−1 . |
||||||||
|
к |
к |
к |
к |
Характеристическое уравнение для соответствующего однородного уравнения при заданных значениях параметров имеет комплексные сопряжëнные корни
|
k =α ± βi, где |
α = − |
b |
, β = |
b12 −4b2 |
. |
|||
|
1 |
||||||||
|
12 |
2 |
2 |
||||||
Частное решение неоднородного уравнения колебаний находится методом подбора.
В результате общее решение уравнения колебаний колеса запишется в виде
|
αt |
αt |
b3 |
2 |
||||||
|
yк (t) = C1e |
cos βt +C2e |
sin βt + |
[(b2 −ω |
)cosωt + |
|||||
|
(b ω)2 |
+(b |
−ω2)2 |
|||||||
|
1 |
2 |
+b1ωsin ωt] +b2−1b4 .
Определяя далее произвольные постоянные C1 и C2 из начальных условий:
yк (0) = 0, yк′(0) = 0,
представим окончательно точное решение задачи в виде
yк (t) = a0 + a1 cosωt + a2 sin ωt +eαt (a3 cos βt + a4 sin βt),
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
