Как найти частное решение разностного уравнения - Сайт, где вы сможете решить свои вопросы

Решения разностных уравнений

Разностные уравнения для чайников

На этой странице мы рассмотрим примеры решения типовых задач, встречающихся в курсе дифференциальных и разностных уравнений, а именно нахождение общего или частного решения линейного разностного уравнения с постоянными коэффициентами. Чаще всего в контрольных встречаются уравнения второго или третьего порядка:

$$
a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)=f(x), \ a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)+ a_3 y(x+3)=f(x).
$$

Здесь $a_i$ – постоянные коэффициенты, $f(x)$ – правая часть (неоднородность уравнения), $y(x)$ – искомая неизвестная функция.

Решение разностных уравнений практически полностью аналогично решению линейных дифференциальных уравнений с постоянными коэффициентами (см. тут примеры): ищется решение однородного уравнения через составление характеристического уравнения, и частное решение неоднородного уравнения по виду правой части.

Лучшее спасибо – порекомендовать эту страницу

Примеры решений разностных уравнений

Задача 1. Решить разностное уравнение: $y(x+2)-4y(x+1)+4y(x)=2^x$

Задача 2. Найти общее решение линейного разностного неоднородного уравнения второго порядка с постоянными коэффициентами.

$$ y(i+2)-4y(i+1)-12y(i)=6cdot 6^i.$$

Задача 3. Решить разностное уравнение третьего порядка

$$ y(x+3)-16y(x+2)+83y(x+1)-140y(x)=0, quad y(0)=3, y(1)=18, y(2)=120. $$

Задача 4. Найти частное решение однородного разностного уравнения:

$$ y(x+3)-6y(x+2)+11y(x+1)-6y(x)=0, quad y(0)=0, y(1)=2, y(2)=8. $$

Помощь с разностными уравнениями

Если вам нужна помощь с решением задач и контрольных по дифференциальным и разностным уравнениям (и другим разделам математического анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей, оформление производится в Word, срок от 1 дня.

Поможем с решением задач и уравнений

Дополнительная информация

Задачи по дифференциальным уравнениям с решениями
Онлайн-помощь на контрольной
Почему МатБюро?

Источник

Решения разностных уравнений

Разностные уравнения для чайников

$$ a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)=f(x), \ a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)+ a_3 y(x+3)=f(x). $$

Примеры решений разностных уравнений

Задача 1. Решить разностное уравнение: $y(x+2)-4y(x+1)+4y(x)=2^x$

Задача 3. Решить разностное уравнение третьего порядка

$$ y(x+3)-16y(x+2)+83y(x+1)-140y(x)=0, quad y(0)=3, y(1)=18, y(2)=120. $$

Задача 4. Найти частное решение однородного разностного уравнения:

Помощь с разностными уравнениями

Если вам нужна помощь с решением задач и контрольных по дифференциальным и разностным уравнениям (и другим разделам математического анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Пример частного решения линейного дифференциального уравнения

Рассмотрим тоже самое уравнение, но решим методом вариации произвольной постоянной.
Для нахождения производных C’_i составляем систему уравнений:
C’₁·e -3x ·cos(2x)+C’₂·e -3x ·sin(2x)=0
C’₁(-2·e -3x ·sin(2x)-3·cos(2x)·e -3x ) + C’₂(-3·e -3x ·sin(2x)+2·cos(2x)·e -3x ) = 8*exp(-x)
Выразим C’₁ из первого уравнения:
C’₁ = -c2·sin(2x)/(cos(2x))
и подставим во второе. В итоге получаем:
C’₁ = -4·e 2x ·sin(2x)
C’₂ = 4·cos(2x)·e 2x
Интегрируем полученные функции C’_i:
C₁ = -e 2x ·sin(2x)+cos(2x)·e 2x + C * ₁
C₂ = e 2x ·sin(2x)+cos(2x)·e 2x + C * ₂
Записываем полученные выражения в виде:
C₁ = (-e 2x ·sin(2x)+cos(2x)·e 2x )·cos(2x)·e -3x + C * ₁e -3x ·cos(2x)
C₂ = (e 2x ·sin(2x)+cos(2x)·e 2x )·e -3x ·sin(2x) + C * ₂e -3x ·sin(2x)
или
C₁ = -cos(2x)·e -x ·sin(2x)+cos 2 (2x)·e -x + C * ₁e -3x ·cos(2x)
C₂ = cos(2x)·e -x ·sin(2x)+sin 2 (2x)·e -x + C * ₂e -3x ·sin(2x)
y = C₁ + C₂
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример . y″ + 5y’ + 6 = 12cos(2x)
Cоставляем характеристическое уравнение дифференциального уравнения: r 2 +5 r + 6 = 0
Находим дискриминант: D = 5 2 – 4·1·6 = 1

Корни характеристического уравнения: r₁ = -2, r₂ = -3. Следовательно, фундаментальную систему решений составляют функции: y₁ = e -2x , y₂ = e -3x
Общее решение однородного уравнения имеет вид: y =C₁·e -2x +C₂·e -3x
Найдем частное решение при условии:y(0) = 1, y'(0) = 3
Поскольку y(0) = c₁+c2, то получаем первое уравнение:
c₁+c2 = 1
Находим первую производную: y’ = -3·c₂·e -3·x -2·c1·e -2·x
Поскольку y'(0) = -3·c₂-2·c₂, то получаем второе уравнение:
-3·c₂-2·c₂ = 3
В итоге получаем систему из двух уравнений:
c₁+c2 = 1
-3·c₂-2·c₂ = 3
которую решаем или методом обратной матрицы или методом исключения переменных.
c₁ = 6, c₂ = -5
Тогда частное решение при заданных начальных условиях можно записать в виде: y =6·e -2x -5·e -3x
Рассмотрим правую часть: f(x) = 12·cos(2·x)
Уравнение имеет частное решение вида: y * = Acos(2x) + Bsin(2x)
Вычисляем производные: y’ = -2·A·sin(2x)+2·B·cos(2x); y″ = -4·A·cos(2x)-4·B·sin(2x)
которые подставляем в исходное дифференциальное уравнение: y″ + 5y’ + 6y = (-4·A·cos(2x)-4·B·sin(2x)) + 5(-2·A·sin(2x)+2·B·cos(2x)) + 6(Acos(2x) + Bsin(2x)) = 12·cos(2·x) или -10·A·sin(2x)+2·A·cos(2x)+2·B·sin(2x)+10·B·cos(2x) = 12·cos(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему линейных уравнений:
-10A + 2B = 0
2A + 10B = 12
СЛАУ решаем методом Крамера:
A = 3 /₁₃;B = 15 /₁₃;
Частное решение имеет вид:
y * = 3 /₁₃cos(2x) + 15 /₁₃sin(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример 2 . y’’ + y = cos(x)
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами. Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:

r 2 + 1 = 0
D = 0 2 – 4·1·1 = -4

Корни характеристического уравнения:
(комплексные корни):
r₁ = i, r₂ = -i
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 0 x cos(x) = cos(x)
y₂ = e 0 x sin(x) = sin(x)

Общее решение однородного уравнения имеет вид: y =C₁·cos(x)+C₂·sin(x)

Рассмотрим правую часть: f(x) = cos(x)

Найдем частное решение. Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) – некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k – кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) – полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 0, α = 0, β = 1.
Следовательно, число α + βi = 0 + 1i является корнем характеристического уравнения кратности k = 1(r₁).

Уравнение имеет частное решение вида:
y * = x (Acos(x) + Bsin(x))
Вычисляем производные:
y’ = sin(x)(B-A·x)+cos(x)(A+B·x)
y″ = cos(x)(2·B-A·x)-sin(x)(2·A+B·x)
которые подставляем в исходное дифференциальное уравнение:
y″ + y = (cos(x)(2·B-A·x)-sin(x)(2·A+B·x)) + (x (Acos(x) + Bsin(x))) = cos(x)
или
2·B·cos(x)-2·A·sin(x) = cos(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
2B = 1
-2A = 0
Следовательно:
A = 0; B = 1 /₂;
Частное решение имеет вид: y * = x (0cos(x) + ½ sin(x)) = ½ x sin(x)

Таким образом, общее решение дифференциального уравнения имеет вид:

Разностные уравнения

Содержание:

Разностные уравнения

Понятие разницы и разностного уравнения

Если для значений переменной x₁, x₂, x₃, . функция f (x) принимает значения f (x₁), f (x₂), f (x₃) . , то приращения функции составляют f (x₂) – f (x₁), f (x₃) – f (x₂), .

Приращение функции при переходе от значения x_i к значению x_i+1 будем обозначать: В частности можно взять в качестве значения независимых переменных x и x + 1 . Разность Δf (x) = f (x + 1) – f (x) называется первой разностью или разностью первого порядка. Она может рассматриваться в свою очередь как функция от x, а потому и для нее можно определить разницу:

Введем обозначения ΔΔf (x) = Δ 2 f (x), тогда Δ 2 f (x) = f (x + 2) – 2 f (x + 1) + f (x) и называется разностью второго порядка.

Аналогично можно найти разности третьего, четвертого и т. д. порядков.

Определим разности некоторых важнейших функций.

1) Если f (x) = С, где С — постоянная величина, то
Δf (x) = f (x + 1) – f (x) = С – С = 0.

Понятно, что и все разности следующих порядков будут также равняться нулю.

2) Если f (x) = ax + b, то
Δf = Δf (x + 1) – f (x) = a (x + 1) + b – ax – b = a.

Разница первого порядка линейной функции равна постоянной, а все остальные будут равны нулю.

3) Если f (x) = ax 2 + bx + c, то

Поскольку разница первого порядка является линейной функцией, то разница второго порядка — постоянная, а все последующие разности равны нулю.

4) Если f (x) = a x , то

В экономических исследованиях часто встречаются задачи, в которых время t является независимой переменной, а зависимая переменная определяется для времени t, t + 1, t + 2 и т. д.

Обозначим y_t — значение функции y в момент времени t; y_t+1 — значение функции в момент, сдвинутый на одну единицу, например, на следующий час, на следующую неделю и т. д., y_t+2 — значение функции y в момент, сдвинутый на две единицы и т. д.

Очевидно, что

Откуда:

За разность второго порядка, имеем или
поэтому

Аналогично можно доказать, что

Итак, любую функцию

можно представить в виде: (7.50)
и наоборот.

Определение. Уравнение
(7.51)
называется разностным уравнением n-го порядка.

Решить разностное уравнение n-го порядка — это значит найти такую функцию y_t, которая превращает уравнение (7.50) или (7.51) в тождество.

Решение, в котором есть произвольная постоянная, называется общим; решение, в котором постоянная отсутствует, называется частным.

Определение. Уравнение
(7.52)
где a₀, a₁, . a_n — постоянные числа, называется неоднородным разностным
уравнением n-го порядка с постоянными коэффициентами.

Если в уравнении (7.52) f (t) = 0, то уравнение называется однородным разностным уравнением n-го порядка с постоянными коэффициентами:
(7.53)

Уравнение есть однородное разностное уравнение первого порядка с постоянными коэффициентами a и b, а уравнение — неоднородное разностное уравнение второго порядка с постоянными коэффициентами a, b, c.

ТЕОРЕМА 1. Если решениями однородного разностного уравнения (7.53) является y₁ (t) и y₂ (t), то его решением будет также функция y₁ (t) + y₂ (t).

ТЕОРЕМА 2. Если y (t) является решением однородного разностного уравнения (7.53), то его решением будет также функция Ay (t), где А — произвольная постоянная.

ТЕОРЕМА 3. Если y (t) — частное решение неоднородного уравнения (7.52) и y (t, A₁, A₂, . A_n) — общее решение однородного уравнения (7.53), то общим решением неоднородного разностного уравнения будет функция: y (t) + y (t, A₁, A₂, . A_n).

Эти теоремы схожи с теоремами для дифференциальных уравнений, которые были приведены нами в предыдущем разделе.

Разностные уравнения первого порядка с постоянными коэффициентами

Рассмотрим неоднородное разностное уравнение
(7.54)

Соответствующее ему однородное уравнение будет:
(7.55)

Возьмем функцию и убедимся, что она будет решением уравнения (7.55). Поскольку , тогда . Подставим y_t и y_t-1 в уравнение (7.55):
Итак, является решением уравнения (7.55).

По теореме (2) общее решение однородного разностного уравнения (7.55) является функция , где А — произвольная постоянная.

Пусть — частное решение неоднородного разностного уравнения (7.54). По теореме (3) общим решением неоднородного разностного уравнения (7.54) будет функция

Частное решение найти нетрудно, если f (t) = α, где α — некоторая постоянная. На самом деле, если где u — постоянная. Подставим в уравнение (7.54), имеем: u – au = α, откуда
Итак, общее решение уравнения (7.54) запишем в виде: .

Разностные уравнения второго порядка с постоянными коэффициентами

Пусть задано неоднородное разностное уравнение второго порядка с постоянными коэффициентами:
(7.56)
и соответствующее ему однородное уравнение
(7.57)

Убедимся, что функция будет решением уравнения (7.58). Подставим в уравнение (7.57) (λ ≠ 0), получим Поскольку λ ≠ 0, то поделим на λ t-2 , имеем λ 2 + aλ + b = 0 (7.58)

Это уравнение называется характеристическим уравнением для уравнения (7.57).

Здесь могут иметь место следующие три случая:

1. D = a 2 – 4b > 0, тогда уравнение (7.58) будет иметь два действительных различных корня.
Общее решение уравнения (7.57) запишется в виде:

а общее решение неоднородного уравнения (7.56) запишется так:

2. D = a 2 – 4b = 0, тогда и и

В этом случае однородное уравнение (7.57) примет вид:
(7.59)
Тогда

Легко убедиться, что решением уравнения (7.59) является также функция
Поэтому общим решением уравнения (7.59) является функция а общим решением неоднородного уравнения (7.56) функция

3. D = a 2 – 4b 2 – 5λ + 6 = 0 будет иметь действительные разные корни (D = 25 – 24 = 1 > 0), λ1 =2, λ2 = 3.
Общим решением однородного уравнения является функция

Далее положим, что y_t = y — частное решение неоднородного уравнения, тогда

Таким образом, общим решением неоднородного уравнения является функция Постоянные A₁ и A₂ определим из начальных условий: y₀ = 5, y₁ = 9. Тогда для t = 0 и t = 1 соответственно будем иметь:

Решим эту систему уравнений относительно A₁ и A₂:

Откуда

Итак, — общее решение заданного в условии разностного уравнения.

Примеры применения разностных уравнений в экономических задачах

Пример 1. Пусть некоторая сумма средств выдается под сложный процент p, то к концу t-го года ее размер будет составлять:
Это однородное разностное уравнение первого порядка. Его решением будет функция , где A — некоторая постоянная, которую можно найти из начальных условий.

Если положить y₀ = F , то A = F, откуда

Это известная формула величины фонда F, который выдается под сложный процент.

Пример 2. Пусть величина предложения сельскохозяйственной продукции в t-м году есть функция цены прошлого года а спрос на эту продукцию есть функция цены в этом году. Следовательно, спрос: а предложение

Цена равновесия для данной продукции определяется равенством:
а это разностное уравнение первого порядка.

Положим, что функция спроса определяется формулой а функция предложения — формулой

Цена равновесия запишется: то есть Решением этого уравнения является функция Постоянная A определяется из начальных условий, для t = 0 цена составляет p₀.

Тогда p₀ = A и решением уравнения является функция
Если начальная цена p₀ = 0, то p_t = 0 для всех значений t.

Следовательно, цена не подлежит изменению.

Вообще говоря, функция предложения — возрастающая, а потому b > 0; а функция спроса — убывающая, и поэтому a

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

[spoiler title=”источники:”]

http://math.semestr.ru/math/example-differential.php

http://natalibrilenova.ru/raznostnyie-uravneniya/

[/spoiler]

Источник

Содержание:

Разностные уравнения
Разностные уравнения первого порядка с постоянными коэффициентами
Разностные уравнения второго порядка с постоянными коэффициентами

Разностные уравнения

Понятие разницы и разностного уравнения

Если для значений переменной x₁, x₂, x₃, … функция f (x) принимает значения f (x₁), f (x₂), f (x₃) … , то приращения функции составляют f (x₂) – f (x₁), f (x₃) – f (x₂), …

Введем обозначения ΔΔf (x) = Δ² f (x), тогда Δ² f (x) = f (x + 2) – 2 f (x + 1) + f (x) и называется разностью второго порядка.

Аналогично можно найти разности третьего, четвертого и т. д. порядков.

Определим разности некоторых важнейших функций.

1) Если f (x) = С, где С — постоянная величина, то
Δf (x) = f (x + 1) – f (x) = С – С = 0.

Понятно, что и все разности следующих порядков будут также равняться нулю.

2) Если f (x) = ax + b, то
Δf = Δf (x + 1) – f (x) = a (x + 1) + b – ax – b = a.

Разница первого порядка линейной функции равна постоянной, а все остальные будут равны нулю.

3) Если f (x) = ax² + bx + c, то

4) Если f (x) = a^x, то

В экономических исследованиях часто встречаются задачи, в которых время t является независимой переменной, а зависимая переменная определяется для времени t, t + 1, t + 2 и т. д.

Очевидно, что

Откуда:

За разность второго порядка, имеем или
поэтому

Аналогично можно доказать, что

Итак, любую функцию

можно представить в виде: (7.50)
и наоборот.

Определение. Уравнение
(7.51)
называется разностным уравнением n-го порядка.

Определение. Уравнение
(7.52)
где a₀, a₁, …, a_n — постоянные числа, называется неоднородным разностным
уравнением n-го порядка с постоянными коэффициентами.

ТЕОРЕМА 3. Если y (t) — частное решение неоднородного уравнения (7.52) и y (t, A₁, A₂, …, A_n) — общее решение однородного уравнения (7.53), то общим решением неоднородного разностного уравнения будет функция: y (t) + y (t, A₁, A₂, …, A_n).

Разностные уравнения первого порядка с постоянными коэффициентами

Рассмотрим неоднородное разностное уравнение
(7.54)

Соответствующее ему однородное уравнение будет:
(7.55)

Разностные уравнения второго порядка с постоянными коэффициентами

Убедимся, что функция будет решением уравнения (7.58). Подставим в уравнение (7.57) (λ ≠ 0), получим Поскольку λ ≠ 0, то поделим на λ^t-2, имеем λ² + aλ + b = 0 (7.58)

Это уравнение называется характеристическим уравнением для уравнения (7.57).

Здесь могут иметь место следующие три случая:

1. D = a² – 4b > 0, тогда уравнение (7.58) будет иметь два действительных различных корня.
Общее решение уравнения (7.57) запишется в виде:

а общее решение неоднородного уравнения (7.56) запишется так:

2. D = a² – 4b = 0, тогда и и

В этом случае однородное уравнение (7.57) примет вид:
(7.59)
Тогда

3. D = a² – 4b < 0, тогда характеристическое уравнение (7.58) имеет два комплексных сопряженных корня:

Обозначим тогда общим решением однородного уравнения (7.57) будет функция а неоднородного уравнения (7.56) — функция

Пример 1. Решить разностное уравнение:

Решение. Запишем соответствующее ему однородное уравнение:

Характеристическое уравнение λ² – 5λ + 6 = 0 будет иметь действительные разные корни (D = 25 – 24 = 1 > 0), λ1 =2, λ2 = 3.
Общим решением однородного уравнения является функция

Далее положим, что y_t = y — частное решение неоднородного уравнения, тогда

Таким образом, общим решением неоднородного уравнения является функция Постоянные A₁ и A₂ определим из начальных условий: y₀ = 5, y₁ = 9. Тогда для t = 0 и t = 1 соответственно будем иметь:

Решим эту систему уравнений относительно A₁ и A₂:

Откуда

Итак, — общее решение заданного в условии разностного уравнения.

Примеры применения разностных уравнений в экономических задачах

Если положить y₀ = F , то A = F, откуда

Это известная формула величины фонда F, который выдается под сложный процент.

Цена равновесия для данной продукции определяется равенством:
а это разностное уравнение первого порядка.

Положим, что функция спроса определяется формулой а функция предложения — формулой

Тогда p₀= A и решением уравнения является функция
Если начальная цена p₀= 0, то p_t= 0 для всех значений t.

Следовательно, цена не подлежит изменению.

Вообще говоря, функция предложения — возрастающая, а потому b > 0; а функция спроса — убывающая, и поэтому a < 0. Откуда Знак выражения зависит от номера года t, следовательно, цена колеблется.

Здесь имеют место три случая:

1) Если то и соответственно
Тогда говорят, что колебания цены сдерживается.

2) Если то последовательные колебания цены составляют
В этом случае говорят, что колебания цены периодические.

3) Если то и p_t бесконечно растет.
Говорят, что колебания цены растет.

Лекции:

Случайная вероятность
Эквивалентные бесконечно малые функции. Сравнение бесконечно больших функций
Решение определённых интегралов
Параллельные прямые
Кривизна и кручение пространственной кривой. Формулы Френе
Пределы в математике
Дифференциал функции
Объемы подобных фигур
Алгебра логики
Эластичность функции

Источник

В
общем случае линейное разностное
уравнение порядка M
с постоянными коэффициентами имеет вид

,
(8.16)

где
описывают конкретную систему, причем.

8.2.3.1. Решение разностных уравнений методом прямой подстановки

Уравнение
(8.16) записано в виде, удобном для решения
методом прямой
подстановки.
Имея набор начальных условий (например,

дляi=-1,
-2, …, –M)
и входную последовательность
по формуле (8.16)т можно непосредственно
вычислить выходную последовательностьдля.

Пример.

Дана
последовательность

Разностное
уравнение имеет вид

(8.17)

с
начальными условиями.

Данное
уравнение можно решить подстановкой,
что дает:

8.2.3.2. Решение разностных уравнений в
явном виде

Хотя
решение разностного уравнения
подстановкой
и целесообразно
в некоторых случаях, значительно полезнее
получить решения в явном
виде.

Основная
идея сводится к получению двух решений
разностного уравнения: однородного
и частного.

Однородное
уравнение получается путем подстановки
нулей вместо всех членов, содержащих
элементы входной последовательности
и определение отклика при нулевой
входной последовательности.

Частное
решение
получается из подбора вида последовательности
навыходе
при заданной входной
последовательности
.
Для определения произвольных постоянных
однородного решения используются
начальные условия.

Пример.

Решить
уравнение (8.17) этим методом.

Однородное
уравнение имеет вид

(8.18)

Известно,
что характеристическими
решениями однородных уравнений,
соответствующих линейным разностным
уравнениям с постоянными коэффициентами,
является решение вида
.
Поэтому, подставляя вместов (8.18),получим

Отсюда
однородное решение имеет вид

.
(8.19)

Частное
решение, соответствующее входной
последовательности
,
попробуем найти в виде

.
(8.20)

Из
уравнения (8.16) получаем

Поскольку
коэффициенты при равных степенях
в левой и правой частях уравнения должны
совпадать, то из получаемой системы
(трех уравнений) находим три искомых
коэффициента:.

Таким
образом, общее решение имеет вид:

,
(8.21)

В этом выражении
коэффициент
находится из начального условия.

Тогда
из (8.21) получим

(8.22)

Проверка
решения (8.22) при
показывает полное совпадение с приведенным
выше прямым решением.

Преимущество
решения (8.22) заключается в том, что оно
позволяет весьма просто определить
для любого конкретного.

8.2.3.3. Схемы реализации цифровых систем

Важное
значение разностных уравнений состоит
в том, что они непосредственно определяют
способ
построения цифровой системы.

Так,
разностное уравнение первого
порядка
самого общего вида

(8.23)

м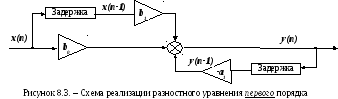ожно
реализовать с помощью схемы

Блок
“задержки” осуществляет задержку
сигнала на один отсчет.

Разностное
уравнение второго
порядка самого общего вида

(8.24)

м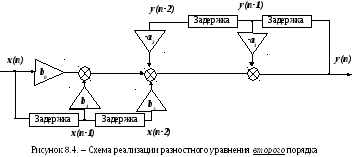ожет
быть реализовано при помощи схемы,
приведенной на рисунке 8.4.

Системы
первого и второго порядка могут быть
использованы при реализации систем
более высокого поряджка, т.к. последние
могут быть представлены в виде
последовательного или параллельного
соединения систем первого и второго
порядка.

8.2.4. Z – преобразование

Одним
из методов представления последовательностей
является Z-преобразование.

Для
последовательности
,
заданной при всех,Z-преобразование
определяется следующим степенным
рядом

.
(8.25)

где

– комплексная переменная.

8.2.4. 1. Последовательности конечной
длины

Если
отлична от нуля только в интервале,
где–конечны, то
сходится в– плоскости везде, за исключением, может
быть, точкиили.

Линейную
систему с постоянными параметрами,
импульсная характеристика которой
является последовательностью конечной
длины, называют системой с конечной
импульсной характеристикой, или, что
то же самое, КИХ-фильтром.

Типичная
импульсная характеристикаконечной длины изображена на рисунке
8.5.

Системой
(фильтром) с бесконечной импульсной
характеристикой (БИХ) называется
система (фильтр), длина импульсной
характеристики которой не ограничена
слева
или справаили с обеих сторон.

8.2.4. 2. Примеры Z-преобразования.

Найти
Z-преобразование
единичного импульса.

Решение.

Так
как
при любых,
кроме,
при котором,
то согласно (8.25) имеем

.
(8.26)

Найти
Z-преобразование
единичного
скачка.

Так
как
везде, кроме,
где,
то из (8.25) получим

.
(8.27)

Бесконечный
ряд сходится при
,
т.к.имеет единственную особую точку.

(Примечание.
Результат (8.27) вытекает из формулы суммы
геометрической прогрессии

Найти
Z-преобразование
комплексной
экспоненты.

.
(8.28)

сходится при
,
т.к. единственной особой точкой является.

Найти
Z-преобразование
простой экспоненциальной
последовательности.

В
этом случае
приипри.

Тогда
согласно (8.25) получаем

.
(8.29)

сходится при
,
т.к. единственной особой точкой является.

8.2.4. 3. Свойства Z
– преобразования

Линейность.

Z
– преобразование линейно.

Пусть

– z
– преобразования
последовательностей
.

Тогда
справедливо

.
(8.30)

Задержка.

Если
,

то

. (8.31)

Это
свойство полезно при переходе от
представления линейной системы с
постоянными переменными к представлению
ее z
– преобразованием
и наоборот.

Пример.

Пусть
имеется разностное уравнение

Представим
его в виде z
– преобразования

или

где

Свертка
последовательностей

Пусть

входные и выходные последовательности
дискретной линейной системы с постоянными
параметрами,– импульсная характеристика системы,– их соответствующиеz
– преобразования.

Тогда
имеет место

,
(8.32)

или

Как
следует из рассмотрения (8.32), операция
свертки последовательностей сводится
к перемножению их z
– преобразований.

8.2.4.4. Решение разностных уравнений
с применением одностороннего z
– преобразования

Разностные
уравнения обычно определены при
и имеют набор начальных условий.

Разностное
уравнение первого
порядка

,
(8.33)

начальное
условие
.

Пусть
на вход поступает последовательность

Чтобы
найти одностороннее z
– преобразование, умножим обе части
равенства (8.33) на
и просуммируем отдо

Из
свойства задержки

Отсюда

Поскольку

то

Разложив
второе слагаемое на простые дроби,
получим

Обратное
z
– преобразование дает последовательность
– решение разностного уравнения

Соседние файлы в папке НОВИКОВ_2013-14

Источник

Как решать дифференциальные уравнения

СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ

Основные понятия и определения
1. Определения
2. Типы уравнений
3. Алгоритм решения
Дифференциальные уравнения первого порядка
1. ДУ с разделяющимися переменными
2. Однородные ДУ
3. Линейные неоднородные ДУ
4. ДУ Бернулли
5. ДУ в полных дифференциалах
Дифференциальные уравнения второго порядка
1. ДУ допускающие понижение порядка
2. Линейные однородные ДУ с постоянными коэффицентами
3. Линейные неоднородные ДУ с постоянными коэффициентами
4. Метод Лагранжа

Введите уравнение

Условия к задаче (необязательно)

Пример 1 Пример 2 Правила ввода

Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.

Основные понятия и определения

Определения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).

Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y” = 1 $$

Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y”(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.

Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.

В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y”(x)$, поэтому это ДУ второго порядка.

Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.

Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.

Типы уравнений

ДУ первого порядка
– с разделяющимися переменными
– однородные
– линейные неоднородные
– уравнение Бернулли
ДУ второго порядка
– уравнения допускающие понижение порядка
– однородные с постоянными коэффициентами
– неоднородные с постоянными коэффициентами

Алгоритм решения

По старшей производной функции $y(x)$ определить порядок ДУ
Зная порядок, определить тип уравнения
Узнав тип, подобрать подходящий метод решения
Используя метод, найти общее решение
Получить частное решение из общего путем вычисления неизвестной $C$

В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$

ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!

Пример 1

Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$

Решение

Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$

Теперь подставим $y’$ и $y$ в исходное уравнение.

$$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$

Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ.

Ответ

$$y = Ce^{frac{x^2}{2}} $$

Дифференциальные уравнения первого порядка

ДУ с разделяющимися переменными

Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$

СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.

Алгоритм нахождения общего решения:

Переписываем производные через $y’ = frac{dy}{dx}$
Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
Интегрируем обе части уравнения

Пример 2

Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$

Решение

Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка. Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить “игрики” от “иксов” по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$

После замены производной игрека исходное уравнение приобретает такой формат:

$$frac{dy}{dx} = xy$$

Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$.

$$ frac{dy}{y} = xdx $$

Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения.

$$ int frac{dy}{y} = int xdx $$

Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$.

$$ ln|y| = frac{x^2}{2} + C $$

Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем.

$$ y = e^{frac{x^2}{2} + C} $$

Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения.
$$ y = e^{frac{x^2}{2}} cdot e^C $$

Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением.

$$ y = Ce^{frac{x^2}{2}} $$

Ответ

$$ y = Ce^{frac{x^2}{2}} $$

Пример 3

Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$.

Решение

Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$:

$$ frac{dy}{dx} = frac{2x}{1+x^2} $$

Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$:

$$ dy = frac{2x}{1+x^2} dx $$

Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы:

$$ int dy = int frac{2x}{1+x^2} dx $$

$$ y = int frac{2x}{1+x^2} dx $$

Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл:

$$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$

Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$:

$$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$

Теперь заменив в общем решении $C$ на ноль, получаем частное решение:

$$y = ln(1+x^2)$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y = ln(1+x^2)$$

Однородные ДУ

Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.

Решается по следующему алгоритму:

Проверить уравнение на однородность с помощью $lambda$
Привести уравнение к виду $y’ = f(frac{y}{x})$
Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
Решить уравнение методом разделяющихся переменных

Пример 4

Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} – 1$$

Решение

Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$:

$$y’ = frac{lambda y}{lambda x} – 1$$

Выполняем сокращение $lambda$ в числителе и знаменателе:

$$y’ = frac{y}{x} – 1$$

После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$:

$$ t’x + t = t – 1$$

Переносим $t$ в одну сторону и тем самым уничтожаем его:

$$ t’x = -1 $$

Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$

Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства:

$$dt = -frac{dx}{x}$$

Интегрируем обе части:

$$int dt = – int frac{dx}{x}$$

$$t = -ln|x|+C$$

Выполняем назад замену $t = frac{y}{x}$:

$$frac{y}{x} = -ln|x|+C$$

Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения:

$$y = -xln|x| +Cx$$

Ответ

$$y = -xln|x| +Cx$$

Пример 5

Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$

Решение

Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$.

$$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$

После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения.

Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$

Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$

Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$

Интегрируем обе части уравнения $$int frac{2+t}{t}dt = – int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$

Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$

Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате.

Ответ

$$y^2 = Cxe^frac{-y}{x}$$

Линейные неоднородные ДУ

Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$

Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$.

Алгоритм метода Бернулли:

Выполняем замену $y=uv$ и $y’ = u’v+uv’$
Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ

Алгоритм метода вариации произвольной постоянной:

Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
В полученном общем решении заменяем константу $C$ на функцию $C(x)$
Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ

Пример 6

Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$.

Решение

Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$

Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$

Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ – 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$

Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$

Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$

Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$

В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$

С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 – x^2.$$

Ответ

$$y = x^4 – x^2$$

Пример 7

Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$.

Решение

Перепишем уравнение в виде $$ y’ – y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ – y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$

Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$

Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$

Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x – C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$

В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$

Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x – cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x – cos x$.

Ответ

$$y = Csin x – cos x$$

ДУ Бернулли

Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$

Алгоритм решения:

Выполняем подстановку $y = z^frac{1}{1-alpha}$
После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$

Пример 8

Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$.

Решение

Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$

Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ.

Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$

Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$

Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$

Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} – int e^{-x} dx = xe^{-x} +e^{-x} + C$$

Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$

Ответ

$$y = frac{1}{Ce^x + x + 1}$$

ДУ в полных дифференциалах

Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.

Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:

Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$
Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$

Пример 9

Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$

Решение

Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$.

Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$

Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$

Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$

Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$

Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$

Ответ

$$x^2+5xy+y^3 = C.$$

Дифференциальные уравнения второго порядка

ДУ допускающие понижение порядка

Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:

Без функции $y$: $F(x,y’,y”)=0$
Без переменной $x$: $F(y,y’,y”)=0$

Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.

Пример 10

Найти частное решение дифференциального уравнения второго порядка $xy”+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$.

Решение

Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$

Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$

Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$

Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$

Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$

Записываем частное решение дифференциального уравнения $$y = ln|x|.$$

Ответ

$$y = ln|x|$$

Пример 11

Найти частное решение дифференциального уравнения второго порядка $$yy”+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$

Решение

Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y” = p'(y)cdot y’ = p'(y)p$.

Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$

В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$

Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$

Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 – Cfrac{1}{y^2}$$ $$(y’)^2 = 1 – Cfrac{1}{y^2}.$$

Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 – Cfrac{1}{1^2} Rightarrow C = 0.$$

Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 – Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$

Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$

Ответ

$$y = x + 1$$

Линейные однородные ДУ с постоянными коэффицентами

Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y”+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y” Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$

В зависимости от получившихся корней имеем общее решение в различных видах:

Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.

Пример 12

Найти общее решение дифференциального уравнения второго порядка $y”+y’-2y = 0$.

Решение

Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$

Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$

Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$

Ответ

$$y = C_1 e^{-2x} + C_2 e^{x}$$

Линейные неоднородные ДУ с постоянными коэффициентами

Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y”+py’+q = f(x).$$

Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$

Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.

`№`	`Правая часть`	`Корни характеристического многочлена`	`Вид частного решения`
1	$$P_n (x)$$	Число 0 не является корнем характеристического уравнения.	$$tilde{P_n}(x)$$
Число 0 – корень характеристического уравнения кратности $S$.	$$x^s tilde{P_n}(x)$$
2	$$P_n (x) e^{alpha x}$$	Число $alpha$ не является корнем характеристического уравнения.	$$tilde{P_n} (x) e^{alpha x}$$
Число $alpha$ является корнем характеристического уравнения кратности $S$.	$$x^s tilde{P_n} (x) e^{alpha x}$$
3	$$P_n (x) cos beta x + Q_m (x) sin beta x$$	Число $pm ibeta$ не является корнем характеристического уравнения.	$$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$
Число $pm ibeta$ является корнем характеристического уравнения кратности $S$.	$$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$
4	$$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$	Число $alpha pm ibeta$ не является корнем характеристического уравнения.	$$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$
Число $alpha pm ibeta$ является корнем характеристического уравнения.	$$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$

Пример 13

Найти общее решение дифференциального уравнения второго порядка $y”+y = 4xcos x$.

Решение

Сначала находим общее решение однородного уравнения $$y” + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$

Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$

Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y”_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y”_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$

Подставляем найденные $y_text{ч.н.}$ и $y”_text{ч.н.}$ в исходный диффур из “дано” задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$

Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$

Ответ

$$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$

Пример 14

Найти общее решение дифференциального уравнения второго порядка $y”+y’=5x+2e^x$.

Решение

Сначала найдем общее решение однородного дифференциального уравнения $$y”+y’=5x+2e^x.$$

Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$

Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$

Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y”=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y”$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$

Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$

Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 – 5x + e^x.$$

Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x.$$

Ответ

$$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x$$

Метод Лагранжа

Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.

Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
Получаем $C_1(x)$ и $C_2(x).$

Пример 15

Найти частное решение дифференциального уравнения $$y”-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$

Решение

Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y”-2y’+y=0.$$

Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$

Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений.

Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$

Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$

Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$

Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$

Ответ

$$y = xe^x(1+ln|x|)$$

Источник

Решения разностных уравнений

Разностные уравнения для чайников

Примеры решений разностных уравнений

Помощь с разностными уравнениями

Дополнительная информация

Решения разностных уравнений

Разностные уравнения для чайников

Примеры решений разностных уравнений

Помощь с разностными уравнениями

Пример частного решения линейного дифференциального уравнения

Разностные уравнения

Разностные уравнения

Разностные уравнения первого порядка с постоянными коэффициентами

Разностные уравнения второго порядка с постоянными коэффициентами

Разностные уравнения

Разностные уравнения первого порядка с постоянными коэффициентами

Разностные уравнения второго порядка с постоянными коэффициентами

8.2.3.1. Решение разностных уравнений методом прямой подстановки

Как решать дифференциальные уравнения

Основные понятия и определения

Определения

Типы уравнений

Алгоритм решения

Дифференциальные уравнения первого порядка

ДУ с разделяющимися переменными

Однородные ДУ

Линейные неоднородные ДУ

ДУ Бернулли

ДУ в полных дифференциалах

Дифференциальные уравнения второго порядка

ДУ допускающие понижение порядка

Линейные однородные ДУ с постоянными коэффицентами

Линейные неоднородные ДУ с постоянными коэффициентами

Метод Лагранжа

Вам также может понравиться

Как найти пароль для инстаграм

Клянчить что это за ошибка как исправить

Как составить функцию по графику функции y

Добавить комментарий Отменить ответ