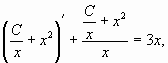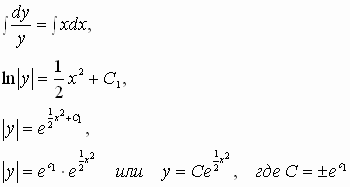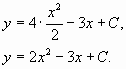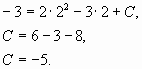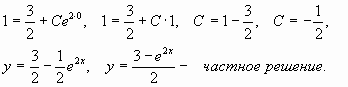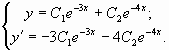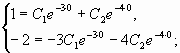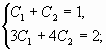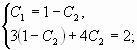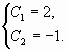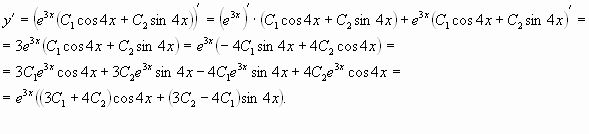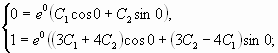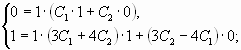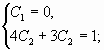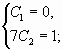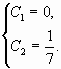Как найти частное решение задачи коши

При постановке
задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до

включительно (где
-порядок дифференциального уравнения), заданные в одной и той же точке
.

Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения:

удовлетворяющее начальным условиям:

Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:

Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого,
находим производную
функции

полученной ранее:

Далее, поставляем начальные условия в функцию

и её производную
:

Решая полученную
систему уравнений получаем значения произвольных постоянных

и
:

Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение:

Задача Коши. Общее и частное решения

При
решении многих задач требуется найти
не все решения уравнения (1.3), а только
такое, которое принимает заданное
значение при заданном значении независимой
переменной, а именно, требуется найти
решение
удовлетворяющее условию

(1.4)

где
илюбые числа, для которых определена
функцияУсловие (1.4) называютначальным
условием,
числа
и–начальными
значениями
решения уравнения (1.3), а саму задачу –
задачей Коши
или
начальной задачей.
С геометрической точки зрения задача
Коши состоит в нахождении интегральной
кривой, проходящей через данную точку

На
вопрос о существовании и единственности
решения задачи Коши отвечает следующая
теорема, которую мы приводим без
доказательства и в упрощенной формулировке.

Теорема
1.1. Если в
уравнении
функцияи ее частная производнаянепрерывны в некоторой областина плоскости,
то какова бы ни была точкаобласти,
существует единственное решениеуравнения (1.3), определенное в некотором
интервале, содержащем точкуи удовлетворяющее условию

В
частности, если два решения
иуравнения (1.3) совпадают хотя бы для
одного значения,
то эти решения тождественно равны для
всех тех значений,
для которых они оба определены.

Геометрический
смысл этой теоремы состоит в том, что
через каждую точку
областипроходит одна и только одна интегральная
кривая уравнения (1.3) или, другими словами,
вся областьпокрыта интегральными кривыми уравнения
(1.3), которые нигде не пересекаются между
собой.

Общее,
частное и особое решения.
Если закрепить начальное значение
абсциссы
,
а начальному значениюпридавать различные допустимые значениято каждому такому значению будет
соответствовать единственная интегральная
кривая (рис. 1.1) и, следовательно, в областимножество всех интегральных кривых
образует семейство кривых, зависящих
от одного параметра, который может
изменяться в определенных пределах и
который принято обозначать через,
так что все семейство интегральных
кривых может быть описано уравнением

Определение.
Функция

(1.5)

непрерывно
дифференцируемая по
называетсяобщим
решением уравнения (1.3)
в области

,
если она удовлетворяет следующим двум
условиям:

1)
равенство (1.5) разрешимо в области
относительно произвольной постоянной

(1.6)

2)
функция
является решением уравнения (1.3) для
всякого значения постоянной,
полученной из формулы (1.6), в которой
точка– любая точка из области.

Естественно,
что знание общего решения (1.5) дает
возможность решить задачу Коши для
любых начальных значений
из области.
Для этого достаточно заменить в формуле
(1.5) переменныеичисламии,
решить полученное уравнениеотносительно,
т.е. получить соотношениеи подставить найденное значение в общее
решение (1.5). Полученная функцияи есть искомое решение. Общее решение
уравнения (1.3), записанное в виде, не
разрешенном относительно искомой
функции, т.е. в виде

или
,

называют
общим
интегралом этого уравнения.

Решение,
которое получается из общего решения
если в последнем произвольной постояннойпридать конкретное (допустимое) значение,
называетсячастным
решением.
Аналогично определяются частные
интегралы.

Решение,
которое не может быть получено из общего
решения (общего интеграла) ни при каком
конкретном значении произвольной
постоянной, называется особым
решением.
Геометрически особому решению
соответствует интегральная кривая, не
содержащаяся в семействе интегральных
кривых, составляющих общее решение
(общий интеграл). Особое решение
примечательно тем, что через каждую
точку изображающей его интегральной
кривой проходит, по крайней мере, еще
одна интегральная кривая того же
уравнения, имеющая в этой точке ту же
касательную.

Если
правая часть уравнения (1.3) удовлетворяет
в области
условиям теоремы 1.1, то это уравнение
не имеет в областиособых решений.

Пример
1.1. Рассмотрим
уравнение

(1.7)

Так
как правая часть уравнения (1.7) и ее
частная производная
удовлетворяют условиям теоремы 1.1 во
всех точках плоскостиза исключением точек оси,
то через любую точкуприпроходит единственная интегральная
кривая уравнения (1.7). Для отыскания
общего решения запишем уравнение (1.7) в
виде

В
левой части равенства стоит дифференциал
функции
,
а в правой – дифференциал функции.
Из равенства дифференциалов этих функций
следует, что сами эти функции могут
отличаться лишь на произвольное
постоянное слагаемое,
так что можем написатьили в таком виде

(1.8)

Функция
(1.8) является общим решением уравнения
(1.7) всюду на плоскости
за исключением оси.

Непосредственно
видно, что, подставив функцию
в уравнение (1.7), получим тождество, т.е.является решением данного уравнения,
притом особым решением, так как оно не
может быть получено из общего решенияни при каком значении постоянной.
Заметим, что через каждую точкуосипроходит криваясовпадающая прис общим решением (1.8) и касательной к
которой в этой точке является сама ось(рис. 1.2).

В
дальнейшем слова решить
(проинтегрировать) дифференциальное
уравнение
будут означать одно из двух:

а)
найти его общее решение (общий интеграл),
если начальные условия не заданы;

б)
найти частное решение (частный интеграл),
удовлетворяющее заданным начальным
условиям.

Далее
будут рассмотрены типы дифференциальных
уравнений первого порядка, интегрируемых
в квадратурах, и указаны пути получения
общего решения (общего интеграла).

Соседние файлы в папке УМК Математика 3-й сем

• #
• #
• #
• #
• #
• #
• #
• #
• #

Дано неоднородное ДУ второго порядка с постоянными коэффициентами. Общее решение которого будет иметь вид $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$. Для начала находим общее решение однородного уравнения $y_{o.o.}$, затем частное решение неоднородного уравнения $y_text{ч.н.}$ с помощью метода подбора правой части уравнения.

На первом этапе решаем уравнение в качестве однородного без правой части, то есть меняем её на ноль. Заменяем все $y$ на новую переменную $lambda$, показатель степени которой будет равен порядку производной. $$y”-y=0,$$ $$lambda^2 – 1 = 0,$$ $$(lambda-1)(lambda+1)=0,$$ $$lambda_1 = -1, lambda_2 = 1.$$ Теперь можно записать общее решение однородного ДУ. $$y_text{о.о.} = C_1e^{lambda x}+C_2e^{-lambda x} = C_1e^{x}+C_2e^{-x}$$

Переходим к получению $y_text{ч.н.}$. Смотрим на правую часть уравнения, данного в условии задачи. В неё входят синус и косинус, умноженные на многочлены нулевой степени. Значит, частное решение ищем в виде $y_text{ч.н.} = Asin x – Bcos x$. Находим вторую производную данного выражения. $$y’ = Acos x + Bsin x,$$ $$y”=-Asin x + Bcos x.$$ Подставляем $y$ и $y”$ в исходное уравнение из условия задачи, чтобы найти неизвестные коэффициенты $A$ и $B$. $$-Asin x + Bcos x – Asin x + Bcos x = 2sin x – 4cos x$$ После приведения подобных получаем $$-2Asin x + 2Bcos x = 2sin x – 4cos x.$$ Далее составляем систему из двух уравнений благодаря коэффициентам перед синусом и косинусом левой и правой части уравнения. $$begin{cases} -2A = 2 \ 2B = -4 end{cases} Leftrightarrow begin{cases} A = -1 \ B = -2 end{cases}$$ Благодаря полученным коэффициентам $A$ и $B$ записываем $$y_text{ч.н.} = -sin x + 2cos x$$

Итак, общее решение неоднородного дифференциального уравнения в итоге будет иметь вид $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.} = C_1e^{x}+C_2e^{-x} -sin x + 2cos x.$$

Так как требуется найти решение задачи Коши, то ход действий на этом не закончен. Переходим к вычислению коэффициентов $C_1$ и $C_2$.

Берём первую производную $y’ = C_1e^x – C_2e^{-x} – cos x – 2sin x$.

Теперь можно составить систему уравнений $$begin{cases} y'(0)=0 \ y(0) = 0 end{cases} Leftrightarrow begin{cases} C_1 – C_2 – 1 = 0 \ C_1 + C_2 + 2 = 0 end{cases}.$$ Решаем систему уравнений. $$begin{cases} C_1 = C_2 + 1 \ C_2 + 1 + C_2 + 2 = 0 end{cases} Leftrightarrow begin{cases} C_1 = C_2 + 1 \ C_2 = -frac{3}{2} end{cases} Leftrightarrow begin{cases} C_1 = -frac{1}{2} \ C_2 = -frac{3}{2} end{cases}.$$

Теперь подставляя полученные константы в общее решение дифференциального уравнения записываем решение задачи Коши в окончательном виде $$y = -frac{1}{2}e^x – frac{3}{2}e^{-x} -sin x + 2cos x.$$

I. Обыкновенные дифференциальные
уравнения

1.1. Основные понятия и определения

Дифференциальным уравнением называется
уравнение, связывающее между собой
независимую переменную x, искомую
функцию y и её производные или
дифференциалы.

Символически дифференциальное уравнение
записывается так:

F(x,y,y’)=0, F(x,y,y”)=0, F(x,y,y’,y”,.., y⁽ⁿ⁾)=0

Дифференциальное уравнение называется
обыкновенным, если искомая функция зависит
от одного независимого переменного.

Решением дифференциального уравнения
называется такая функция ,
которая обращает это уравнение в тождество.

Порядком дифференциального уравнения
называется порядок старшей производной,
входящей в это уравнение

Примеры.

1. Рассмотрим дифференциальное уравнение
первого порядка

Решением этого уравнения является
функция y = 5 ln x. Действительно, ,
подставляя y’ в уравнение, получим
– тождество.

А это и значит, что функция y = 5 ln x– есть
решение этого дифференциального уравнения.

2. Рассмотрим дифференциальное уравнение
второго порядка y” – 5y’ +6y = 0. Функция
– решение этого уравнения.

Действительно, .

Подставляя эти выражения в уравнение,
получим: ,

– тождество.

А это и значит, что функция
– есть решение этого дифференциального
уравнения.

Интегрированием дифференциальных
уравнений называется процесс нахождения
решений дифференциальных уравнений.

Общим решением дифференциального
уравнения называется функция вида ,в
которую входит столько независимых
произвольных постоянных, каков порядок
уравнения.

Частным решением дифференциального
уравнения называется решение, полученное
из общего решения при различных числовых
значениях произвольных постоянных.
Значения произвольных постоянных
находится при определённых начальных
значениях аргумента и функции.

График частного решения
дифференциального уравнения называется интегральной
кривой.

Примеры

1.Найти частное решение дифференциального
уравнения первого порядка

xdx + ydy = 0, если y = 4 при x = 3.

Решение. Интегрируя обе части уравнения,
получим

Замечание. Произвольную постоянную С,
полученную в результате интегрирования,
можно представлять в любой форме, удобной
для дальнейших преобразований. В данном
случае, с учётом канонического уравнения
окружности произвольную постоянную С
удобно представить в виде .

– общее решение дифференциального
уравнения.

Частное решение уравнения,
удовлетворяющее начальным условиям y =
4 при x = 3 находится из общего
подстановкой начальных условий в общее
решение: 3² + 4²= C²; C=5.

Подставляя С=5 в общее решение, получим x²
+y² = 5².

Это есть частное решение
дифференциального уравнения, полученное из
общего решения при заданных начальных
условиях.

2. Найти общее решение дифференциального
уравнения

Решением этого уравнения является всякая
функция вида ,
где С – произвольная постоянная.
Действительно, подставляя в уравнения ,
получим: ,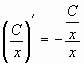
.

Следовательно, данное дифференциальное
уравнение имеет бесконечное множество
решений, так как при различных значениях
постоянной С равенство
определяет различные решения уравнения .

Например, непосредственной подстановкой
можно убедиться, что функции
являются решениями уравнения .

Задача, в которой требуется найти частное
решение уравнения y’ = f(x,y) 
удовлетворяющее начальному условию y(x₀)
= y₀, называется задачей Коши.

Решение уравнения y’ = f(x,y),
удовлетворяющее начальному условию, y(x₀)
= y₀, называется решением задачи Коши.

Решение задачи Коши имеет простой
геометрический смысл. Действительно,
согласно данным определениям, решить
задачу Коши y’ = f(x,y)  при условии y(x₀)
= y₀,, означает найти интегральную
кривую уравнения y’ = f(x,y)  которая
проходит через заданную точку M₀(x₀,y₀).

II. Дифференциальные уравнения первого
порядка

2.1. Основные понятия

Дифференциальным уравнением первого
порядка называется уравнение вида F(x,y,y’) =
0.

В дифференциальное уравнение первого
порядка входит первая производная и не
входят производные более высокого порядка.

Уравнение y’ = f(x,y) называется
уравнением первого порядка, разрешённым
относительно производной.

Общим решением дифференциального
уравнения первого порядка называется
функция вида ,
которая содержит одну произвольную
постоянную.

Пример. Рассмотрим дифференциальное
уравнение первого порядка .

Решением этого уравнения является
функция .

Действительно, заменив в данном уравнении,

его значением, получим

то есть 3x=3x

Следовательно, функция
является общим решением уравнения
при любом постоянном С.

Найти частное решение данного уравнения,
удовлетворяющее начальному условию y(1)=1
Подставляя начальные условия x = 1, y =1 
в общее решение уравнения ,
получим
откуда C = 0.

Таким образом, частное решение получим из
общего
подставив в это уравнение, полученное
значение C = 0

– частное решение.

2.2. Дифференциальные уравнения с
разделяющимися переменными

Дифференциальным уравнением с
разделяющимися переменными называется
уравнение вида: y’=f(x)g(y) или через
дифференциалы ,
где f(x)  и g(y)– заданные функции.

Для тех y, для которых ,
уравнение y’=f(x)g(y) равносильно уравнению,

в котором переменная y присутствует
лишь в левой части, а переменная x- лишь в
правой части. Говорят, «в уравнении y’=f(x)g(y
разделим переменные».

Уравнение вида
называется уравнением с разделёнными
переменными.

Проинтегрировав обе части уравнения
по x, получим G(y) = F(x) + C– общее
решение уравнения, где G(y) и F(x) –
некоторые первообразные соответственно
функций
и f(x), C произвольная постоянная.

Алгоритм решения дифференциального
уравнения первого порядка с разделяющимися
переменными

1. Производную функции переписать через её
   дифференциалы
2. Разделить переменные.
3. Проинтегрировать обе части равенства,
   найти общее решение.
4. Если заданы начальные условия, найти
   частное решение.

Пример 1

Решить уравнение y’ = xy

Решение. Производную функции y’
заменим на

разделим переменные

проинтегрируем обе части равенства:

Ответ:

Пример 2

Найти частное решение уравнения

2yy’ = 1- 3x²,
если y₀ = 3 при x₀ = 1

Это—уравнение с разделенными
переменными. Представим его в
дифференциалах. Для этого перепишем данное
уравнение в виде
Отсюда

Интегрируя обе части последнего
равенства, найдем

Подставив начальные значения x₀ = 1,
y₀ = 3 найдем С 9=1-1+C, т.е. С = 9.

Следовательно, искомый частный интеграл
будет
или

Пример 3

Составить уравнение кривой, проходящей
через точку M(2;-3) и имеющей касательную с угловым
коэффициентом

Решение. Согласно условию

Это уравнение с разделяющимися
переменными. Разделив переменные, получим:

 Проинтегрировав обе части уравнения,
получим:

Используя начальные условия, x = 2  и y
= – 3 найдем C:

Следовательно, искомое уравнение имеет
вид

2.3. Линейные дифференциальные уравнения
первого порядка

Линейным дифференциальным уравнением
первого порядка называется уравнение вида y’
= f(x)y + g(x)

где f(x) и g(x) – некоторые заданные функции.

Если g(x)=0 то
линейное дифференциальное уравнение
называется однородным и имеет вид:  y’ = f(x)y

Если
то уравнение y’ = f(x)y + g(x) называется неоднородным.

Общее решение линейного однородного
дифференциального уравнения y’ = f(x)y задается формулой:
где С – произвольная постоянная.

В частности, если С =0, то решением
является  y = 0 Если линейное однородное уравнение имеет
вид y’ = ky где k – некоторая постоянная, то его общее решение
имеет вид: .

Общее решение линейного неоднородного
дифференциального уравнения y’ = f(x)y + g(x) задается формулой ,

т.е. равно сумме общего решения
соответствующего линейного однородного
уравнения и частного решения
данного уравнения.

Для линейного неоднородного уравнения
вида y’
= kx + b,

где k и b–
некоторые числа и частным
решением будет являться постоянная функция
.
Поэтому общее решение имеет вид .

Пример. Решить уравнение y’ + 2y +3 = 0

Решение. Представим уравнение в виде y’
= -2y – 3 где k = -2, b= -3 Общее решение задается формулой .

Следовательно,
где С – произвольная постоянная.

Ответ:

2.4. Решение линейных дифференциальных
уравнений первого порядка методом Бернулли

Нахождение общего решения линейного
дифференциального уравнения первого
порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных
уравнений с разделенными переменными с
помощью подстановки y=uv,
где u и v – неизвестные функции от x.
Этот метод решения называется методом
Бернулли.

 Алгоритм решения линейного дифференциального
уравнения первого порядка

y’ = f(x)y + g(x)

1. Ввести подстановку y=uv.

2. Продифференцировать это равенство y’ =
u’v + uv’

3. Подставить y и y’ в данное уравнение:  
u’v + uv’ = f(x)uv + g(x) или u’v + uv’ +  f(x)uv = g(x).

4. Сгруппировать члены уравнения так, чтобы
u вынести
за скобки:

5. Из скобки, приравняв ее к нулю, найти
функцию

Это уравнение с разделяющимися
переменными:

Разделим переменные и получим:

Откуда .
.

6. Подставить полученное значение v в уравнение
(из п.4):

и найти функцию
Это уравнение с разделяющимися переменными:

7. Записать общее решение в виде: ,
т.е. .

Пример 1

Найти частное решение уравнения y’ = -2y
+3 = 0  если y =1  при x = 0

Решение. Решим его с помощью
подстановки y=uv, .y’ = u’v + uv’

Подставляя y и y’
в данное уравнение, получим

Сгруппировав второе и третье слагаемое
левой части уравнения, вынесем общий
множитель u за
скобки

Выражение в скобках приравниваем к нулю и,
решив полученное уравнение, найдем функцию v
= v(x)

Получили уравнение с разделенными
переменными. Проинтегрируем обе части
этого уравнения:
Найдем функцию v:

Подставим полученное значение v в уравнение
Получим:

Это уравнение с разделенными переменными.
Проинтегрируем обе части уравнения:
Найдем функцию u = u(x,c)
Найдем общее решение:
Найдем частное решение уравнения,
удовлетворяющее начальным условиям y = 1 при
x = 0:

Ответ:

III. Дифференциальные уравнения высших
порядков

3.1. Основные понятия и определения

Дифференциальным уравнением второго
порядка называется уравнение, содержащее
производные не выше второго порядка. В
общем случае дифференциальное уравнение
второго порядка записывается в виде: F(x,y,y’,y”)
= 0

Общим решением дифференциального
уравнения второго порядка называется
функция вида ,
в которую входят две произвольные
постоянные C₁ и C₂.

Частным решением дифференциального
уравнения второго порядка называется
решение, полученное из общего
при некоторых значениях произвольных
постоянных C₁ и C₂.

3.2. Линейные однородные дифференциальные
уравнения второго порядка с



постоянными коэффициентами.

Линейным однородным дифференциальным
уравнением второго порядка с постоянными
коэффициентами называется уравнение вида
y” + py’ +qy = 0, где pи q–
постоянные величины.

Алгоритм решения однородных дифференциальных
уравнений второго порядка с постоянными
коэффициентами

1. Записать дифференциальное уравнение в
виде: y” + py’ +qy = 0.

2. Составить его характеристическое
уравнение, обозначив y” через r²,
y’  через r, yчерез
1:
r² + pr +q = 0

3.Вычислить дискриминант  D = p² -4q
и найти корни характеристического
уравнения; при этом если:

а) D > 0; следовательно,
характеристическое уравнение имеет два
различных действительных корня .
Общее решение дифференциального уравнения
выражается в виде ,
где C₁ и C₂ – произвольные постоянные.

б) D = 0; следовательно,
характеристическое уравнение имеет равные
действительные корни .
Общее решение дифференциального уравнения
выражается в виде

в) D < 0; следовательно,
характеристическое уравнение имеет
комплексные корни,
Общее решение дифференциального уравнения
выражается, в виде 

Примеры.

1. Найти частное решение дифференциального
уравнения

Решение. Составим характеристическое
уравнение

D>0,

Общее решение

Дифференцируя общее решение, получим

Составим систему из двух уравнений

Подставим вместо ,и

заданные начальные условия:

Таким образом, искомым частным решением
является функция

.

2. Найти частное решение уравнения

Решение

<0,

Общее решение

–
частное решение.

IV. Практическая работа

Вариант 1

1. Составить уравнение кривой, проходящей
через точку M(1;2) и имеющей угловой коэффициент .

2. Найти частные решения дифференциальных
уравнений:

а)

б)

в)

г)

Вариант 2

1. Составить уравнение кривой, проходящей
через точку M(2;1) и имеющей угловой коэффициент

2. Найти частные решения дифференциальных
уравнений:

а)

б)

в)

г)

V. Ответы