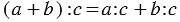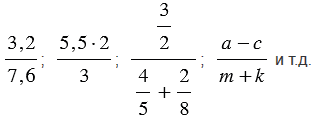В данной публикации мы рассмотрим, каким образом можно обыкновенную (простую) дробь разделить на число или другую дробь, и как найти частное от деления смешанных дробей. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
-
Деление дроби
- На число
- На другую дробь
-
Деление смешанных дробей
- Примеры задач
Деление дроби
На число
Результатом деления обыкновенной дроби на число n является дробь, знаменатель которой равняется произведению знаменателя исходной дроби и этого числа n. Числитель при этом остается тем же.
Примечание: после выполнения деления не забываем проверить, можно ли сократить новую дробь.
На другую дробь
Чтобы разделить одну дробь на другую, переворачиваем дробь-делитель (меняем местами числитель и знаменатель) и умножаем ее на дробь-делимое, которое оставляем без изменений.
a/b
:
c/d
=
a/b
⋅
d/c
=
a ⋅ d/b ⋅ c
Деление смешанных дробей
Чтобы найти частное от деления смешанных дробей, для начала их нужно представить в виде неправильных дробей, и только после этого выполнить деление.
X
a/b
: Y
c/d
=
X ⋅ b + a/b
:
Y ⋅ d + c/d
=
X ⋅ b + a/b
⋅
d/Y ⋅ d + c
=
(X ⋅ b + a) ⋅ d/(Y ⋅ d + c) ⋅ b
Примеры задач
Задание 1
Разделите дробь
5/6
на число 5.
Решение
5/6
: 5 =
5/6⋅5
=
5/30
=
1/6
Задание 2
Разделите дробь
4/15
на
2/9
.
Решение
4/15
:
2/9
=
4/15
⋅
9/2
=
4⋅9/15⋅2
=
36/30
=
6/5
= 1
1/5
Задание 3
Найдите частное от деления дроби 6
1/4
на дробь 4
2/3
.
Решение
Т.к. даны смешанные дроби, сначала запишем их в виде неправильных, потом выполним требуемое действие.
6
1/4
: 4
2/3
=
6⋅4+1/4
:
4⋅3+2/3
=
25/4
:
14/3
=
25/4
⋅
3/14
=
25⋅3/4⋅14
=
75/56
=1
19/56
Содержание
- Деление и дроби
- Дробные выражения
- —>Сайт учителя математики А.В.Капитановой —>
- Умножение дроби на натуральное число
- Пример: Найти произведение дроби и натурального числа:
- Пример: Найти произведение двух смешанных чисел:
- Пример: Найти частное от деления дроби на натуральное число:
- Пример: Найти частное от деления дробей:
- Пример: Найти частное от деления смешанных чисел:
Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 

Пример:
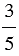
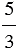
В результате деления двух натуральных чисел может получится натуральное число или дробное число.
Пример:
20 : 4 = 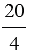
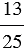
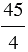
Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем.
Пример:
а) 1 = 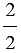
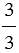
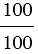
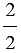
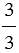
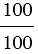
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
б) 7 = 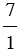
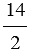
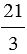
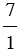
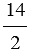
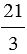
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
Частное от деления одного выражения на другое можно записать с помощью черты дроби. Например, выражение (3,5 — 1,1) : (7,3 + 2,7) можно записать в виде 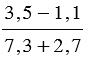
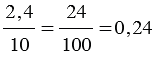
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
К дробным выражениям относятся:
Числитель дробного выражения — выражение, стоящее над чертой.
Знаменатель дробного выражения — выражение, стоящее под чертой.
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
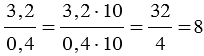
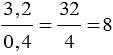
То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
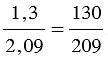
Поделись с друзьями в социальных сетях:
Источник
—>Сайт учителя математики А.В.Капитановой —>
Умножение дроби на натуральное число
Пример: Найти произведение дроби и натурального числа:
Умножение обыкновенных дробей
- перемножить числители и знаменатели дробей;
- сократить полученную дробь.
| 3 | · | 2 | = | 3 · 2 | = | 6 |
| 7 | 5 | 7 · 5 | 35 |
Умножение смешанных чисел
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Пример: Найти произведение двух смешанных чисел:
| 2 | 1 | · | 1 | 2 | = | 2 · 2 + 1 | · | 1 · 3 + 2 | = | 5 | · | 5 | = | 5 · 5 | = | 25 | = | 6 · 4 + 1 | = 4 | 1 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 · 3 | 6 | 6 | 6 |
Пример: Найти произведение смешанного числа и целого числа:
| 4 | 1 | · | 6 | = | 4 · 3 + 1 | · | 6 | = | 13 · 6 | = | 26 |
| 3 | 3 | 3 |
Пример: Найти произведение смешанного числа и обыкновенной дроби:
| 2 | 1 | · | 3 | = | 2 · 7 + 1 | · | 3 | = | 15 | · | 3 | = | 15 · 3 | = | 5 · 9 | = | 9 | = | 7 + 2 | = 1 | 2 |
| 7 | 5 | 7 | 5 | 7 | 5 | 7 · 5 | 7 · 5 | 7 | 7 | 7 |
Деление дроби на натуральное число
Пример: Найти частное от деления дроби на натуральное число:
Определение: Чтобы получить дробь, обратную данной, следует поменять местами числитель и знаменатель.
Деление натурального числа на дробь
Пример: Найти частное от деления натурального числа на дробь:
| 2: | 4 | = | 2· | 5 | = | 2 · 5 | = | 2 · 5 | = | 5 | = | 2 · 2 + 1 | = 2 | 1 |
| 5 | 4 | 4 | 2 · 2 | 2 | 2 | 2 |
Деление обыкновенных дробей
Пример: Найти частное от деления дробей:
| 3 | : | 4 | = | 3 | · | 5 | = | 3 · 5 | = | 15 |
| 7 | 5 | 7 | 4 | 7 · 4 | 28 |
Деление смешанных чисел
- преобразовать смешанные дроби в неправильные;
- умножить первую дробь на дробь, обратную второй;
- сократить полученную дробь;
- если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Пример: Найти частное от деления смешанных чисел:
| 1 | 1 | : | 2 | 2 | = | 1 · 2 + 1 | : | 2 · 3 + 2 | = | 3 | : | 8 | = | 3 | · | 3 | = | 3 · 3 | = | 9 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 | 8 | 2 · 8 | 16 |
Пример: Найти частное от деления смешанного числа на дробь:
Источник
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:
Найдём частное двух обыкновенных дробей.
При необходимости дробь сокращают.
Пример:
.
В случае деления целого числа на обыкновенную дробь целое число можно умножить на дробь, обратную делителю, или сначала представить целое число в виде неправильной дроби, а затем выполнить деление обыкновенных дробей:
8:45=8⋅54=82⋅541=2⋅51=101=10;8:45=81:45=81⋅54=82⋅541=2⋅51=101=10.
Чтобы найти частное смешанных чисел, смешанные числа представляют в виде неправильных дробей и выполняют деление по правилу деления обыкновенных дробей:
325:15=3⋅5+25:15=175:15=175⋅51=17⋅5151⋅1=17⋅11⋅1=171=17;412:634=92:274=92⋅427=91⋅4221⋅273=1⋅21⋅3=23.
Деление дробей онлайн
Чтобы разделить дробь на дробь нужно умножить первую дробь на дробь обратную второй.
Правила деления дробей
Чтобы разделить дробь на дробь, нужно делимое умножить на дробь обратную делителю
Как делить обыкновенные дроби
Чтобы разделить обыкновенную дробь на обыкновенную дробь, нужно вторую дробь сделать обратной затем умножить на вторую дробь по правилам умножения дробей.
Разберём пример: разделим дробь 1/4 на 1/3. Для этого развернём вторую дробь 3/1. Получится выражение 1/4 × 3/1. Перемножим числители 1 × 3 = 3 и знаменатели 4 × 1 = 4 в итоге у нас получится дробь 3/4
Как разделить натуральное число на дробь
Чтобы разделить натуральное число на дробь, нужно сделать дробь обратной. Числитель обратной дроби умножить на натуральное число а знаменатель обратной дроби останется без изменения.
Как разделить смешанную дробь на целое число
Чтобы разделить смешанную дробь на целое число нужно смешанную дробь перевести в неправильную. Затем целое число представить в виде обратной дроби и умножить на неправильную дробь. После чего выполнить умножение обыкновенных дробей.
Разберём пример: разделим смешанную дробь 3 целые 3/4 на целое число 7.
Перед делением нужно смешанную дробь перевести в неправильную 3 целые 3/4 = 15/4. Представим целое число в виде обратной дроби7 это 1/7. Умножим дроби 15/4 и 1/7. Перемножим числители 15*1 = 15, перемножим знаменатели4*7 = 28
Как разделить смешанную дробь на смешанную дробь
Для деления смешанной дроби ра смешанную дробь нужно обе дроби представить в виде неправильных. Затем вторую дробь преобразовать в обратную. После чего перемножить обе дроби по правилам умножения обыкновенных дробей.
Разберём пример: разделим смешанную дробь 2 целые 3/5 на смешанную дробь 3 целые 1/2
Преобразуем обе дроби в неправильные
Развернём вторую дробь и изменим знак деления на умножение
Перемножим дроби по правилам умножения обыкновенных дробей
Похожие калькуляторы
Математика
6 класс
Урок № 46
Умножение и деление смешанных дробей произвольного знака
Перечень рассматриваемых вопросов:
- умножение смешанных дробей произвольного знака;
- деление смешанных дробей произвольного знака.
Тезаурус
Натуральные числа – это числа, которые используются при подсчёте предметов.
Правильная дробь – это дробь, у которой числитель меньше знаменателя.
Положительная смешанная дробь есть сумма натурального числа и правильной дроби.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
«Математика – царица наук, арифметика – царица математики», – сказал К. Ф. Гаусс. Следуя за царицей математики, продолжим изучать арифметические действия со смешанными дробями. И сегодня поговорим об умножении и делении смешанных чисел любого знака.
Как выделять целую часть из положительной неправильной дроби и как приводить положительную смешанную дробь к виду неправильной мы вспоминали на прошлом уроке. Поэтому сразу переходим к алгоритму умножения смешанных чисел:
Чтобы найти произведение смешанных дробей произвольного знака, их выражают в виде неправильных дробей и применяют правила умножения дробей. При необходимости результат упрощают (сокращают и выражают в виде смешанной дроби).
Найдём произведение
Количество отрицательных множителей нечётное, значит, произведение будет отрицательным.
Приведём смешанные дроби к виду неправильных.
Представим данную неправильную дробь в виде смешанного числа.
Чтобы найти частное смешанных дробей произвольного знака, их выражают в виде неправильных дробей и применяют правила деления дробей. При необходимости результат упрощают (сокращают и выражают в виде смешанной дроби).
Найдём частное
Количество отрицательных дробей в выражении нечётное, значит, частное будет отрицательным.
Приведём смешанные дроби к виду неправильных.
Перемножим отдельно числитель и знаменатель.
Сравнение значений выражений.
Сравним значения выражений, не вычисляя их.
Решение
Для сравнения достаточно посмотреть на знаки, которые будут получаться при вычислениях. Так как в первом выражении две отрицательные дроби, то произведение будет положительным.
Во втором выражении две дроби с разными знаками, следовательно, частное будет отрицательным. Значит, значение первого выражения больше, чем второго.
Разбор заданий тренировочного модуля
№ 1. Какой знак имеет выражение?
Решение
Так как числа в выражении имеют разные знаки, то знак частного будет отрицательным.
Ответ: знак “”.
№ 2. Выберите число x, для которого верно равенство.
Решение
Чтобы определить значение х, нужно выполнить арифметические действия в правой части равенства. Но для начала приведём дроби к общему знаменателю 15.
Далее применим правило сложения и вычитания смешанных дробей.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Ответ: