Деление столбиком используют, когда нужно разделить простые или сложные многозначные числа. Оно помогает найти ответ за счёт разбивания решения на ряд более простых шагов. В статье объясним на примерах, как делить в столбик и дадим пошаговый алгоритм.
Какие арифметические действия используют при делении в столбик
При знакомстве с делением в столбик у школьника могут возникнуть трудности и недопонимания. Отчасти потому, что при сложении в столбик мы только складываем, а при вычитании только вычитаем. Когда же мы делим в столбик, то по очереди выполняем: деление, умножение и вычитание. Кроме того, нужно знать таблицу умножения, уметь делить с остатком и аккуратно писать цифры, каждую в своей клетке, чтобы не ошибиться в расчётах.
Термины «делимое», «делитель», «частное», «неполное делимое»


Деление двузначного числа на однозначное
Разделим 86 на 2
1. Для начала определим первое неполное делимое и узнаем, сколько будет цифр в частном. 8 можем разделить на 2, значит, 8 — первое неполное делимое, в частном будет первая цифра. После 8 есть ещё одна цифра, значит, и в частном будет ещё одна цифра — всего две цифры.
2. Разделим первое неполное делимое 8 на делитель 2, получим первую цифру частного — 4.
3. Умножим делитель 2 на цифру частного 4, получим ответ — 8. Этот результат записываем под первым неполным делимым.
4. Находим остаток 8 — 8 = 0. Остаток 0 меньше делителя 2, значит, продолжаем вычисления. Остаток 0 можно не писать.
5. Сносим (переписываем) цифру 6 — это новое неполное делимое.
6. Делим неполное делимое 6 на делитель 2, получаем — 3. Результат записываем в частное.
7. Умножаем делитель 2 на новую цифру частного 3, получаем 6. Результат записываем под вторым неполным делимым.
8. Записываем последний остаток 0. Больше мы не можем снести ни одной цифры, значит, неполных делимых не осталось. Деление в столбик закончено.
Деление трёхзначного числа на однозначное
Разделим 486 на 3
1. Сначала определим, сколько цифр в частном: первая цифра делимого — 4, мы можем разделить 4 на 3, значит, в частном будет первая цифра. После первого неполного делимого ещё две цифры, значит, и в частном будет ещё две цифры — всего три.
2. Затем разделим первое неполное делимое 4 на делитель 3. В результате получим 1.
3. Далее умножим делитель на полученную цифру частного: 3 · 1 = 3. Запишем 3 под первым неполным делителем.
4. Теперь нужно найти остаток при помощи вычитания.
5. Остаток 1 меньше делителя 3, значит, продолжаем вычисления. Рядом с цифрой остатка 1 пишем следующую цифру делимого — 8. Следующее неполное делимое — 18.
6. Разделим 18 на 3 и получим вторую цифру частного — 6.
7. Теперь умножим делитель на полученную цифру частного: 3 · 6 = 18 и найдём остаток — 0. Его можно не писать.
8. Сносим цифру 6 — это последнее неполное делимое. Делим 6 на 3 и получаем — 2. В частное пишем 2.
9. Далее умножим делитель на полученную цифру частного: 3 · 2 = 6 и найдём остаток — 0. Вычисления закончены.
Пример деления с нулём в частном, или сколько раз можно сносить цифру делимого, чтобы получить одно новое неполное делимое
Разделим 816 на 8
1. Первое неполное делимое 8, а за ним ещё две цифры. Значит, в частном будет 3 цифры.
2. Разделим первое неполное делимое 8 на делитель 4 и запишем в частное ответ — 2.
3. Умножим делитель 4 на цифру частного 2, получим 8. Запишем число под первым неполным делимым.
4. Сносим цифру 1 — это новое неполное делимое. Остаток 0 не пишем.
5. Вспомним деление с остатком и разделим 1 на 4. В результате получим 0, остаток — 1. Цифру 0 записываем в частное.
6. Умножим делитель 4 на цифру частного 0, результат 0 запишем под вторым неполным делимым. Остаток 1.
7. Сносим 6 и получаем новое неполное делимое 16. Делим 16 на 4, получаем цифру частного 4.
8. Умножаем делитель 4 на цифру частного 4 и пишем результат под неполным делимым.
9. Записываем последний остаток 0 — деление выполнено.
Как можно сократить запись деления
Когда мы получили неполное делимое 1, которое меньше делителя 4, сносим вторую цифру делимого, чтобы новое неполное делимое было больше делителя. А в частное ставим 0. И далее выполняем деление в установленном порядке.
В этом примере мы дважды сносили цифру делимого, чтобы получить неполное делимое, которое больше делителя.

Надеемся, что теперь у вашего ребёнка не возникнет трудностей с делением в столбик. А если вдруг они есть, наши репетиторы с удовольствием готовы вам помочь!
Влюбляем в обучение на уроках в онлайн-школе Тетрика
Оставьте заявку и получите бесплатный вводный урок
В данной публикации мы рассмотрим правила и практические примеры того, каким образом натуральные числа (двузначные, трехзначные и многозначные) можно делить столбиком – с остатком и без него.
-
Правила деления в столбик
- Без остатка
- С остатком
- Примеры деления в столбик
Правила деления в столбик
Без остатка
Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.
Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:
1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок. Результат будем записывать под делителем.

2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.

Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.
3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица. Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления.

Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.
4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.

Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.
5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.

На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.
С остатком
В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.
Например, остаток от деления 112 на 5 равняется двум. То есть 112 : 5 = 22 (2).

Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.
Примеры деления в столбик
Пример 1
Разделим трехзначное число на двузначное, например 378 на 21.

Ответ: 378 : 21 = 18.
Пример 2
Найдем частное от деления чисел 1537 и 35.

Пояснение: в данном случае в делимом нужно сразу отсчитать слева не две, а три цифры, т.к. числа 1 и 15 меньше 35.
Ответ: 1537 : 35 = 43 (32)
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Деление в столбик
Поддержать сайт![]()
Для деления чисел из двух и более цифр (знаков) применяют деление в столбик.
По традиции, разбираться как делить столбиком будем на примере.
Вычислить:
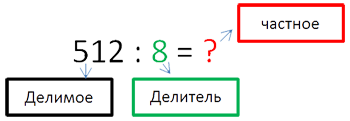
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
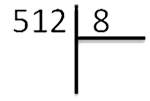
Их частное (результат) будем записывать под делителем. У нас это цифра «8».
Начинаем делить «512» на «8» следующим образом:
- Определяем неполное частное. Для этого слева направо сравниваем
цифры делимого и делитель.

Берём «5».
Цифра «5» меньше «8», значит нужно взять еще одну цифру из делимого.
- «51» больше «8». Значит это неполное частное. Ставим точку в частном (под уголком делителя).

Запомните!

Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас
после «51» стоит только одно цифра
«2». Значит и добавляем в результат ещё одну точку.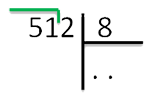
-
Приступаем к делению. Вспоминая таблицу умножения на
«8», находим ближайшее к
«51» произведение.
«6 · 8 = 48»
Записываем цифру «6» в частное.

Записываем «48» под «51».
Запомните!

При записи под неполном частным самая правая цифра неполного
частного должна стоять над самой правой цифрой произведения.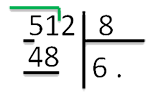
Между «51» и «48» слева поставим «−» (минус). Вычтем по правилам
вычитания в столбик «48» и под чертой запишем результат.
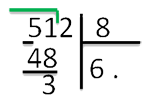
- В остатке получилось «3».
Сравним остаток с делителем. «3» меньше «8».Запомните!

Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение
более близкое, чем то, которое взяли мы.Спишем из делимого «512» цифру «2» к «3».
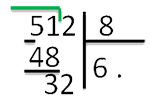
Число «32» больше «8».
И опять по таблице умножения на «8», найдем ближайшее произведение.8 · 4 = 32
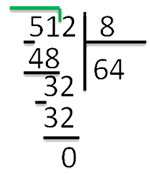
В остатке получился ноль. Значит числа разделились нацело (без остатка).
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
16 ноября 2016 в 10:04
Ирина Винницкая

Профиль
Благодарили: 0
Сообщений: 1

Ирина Винницкая
Профиль
Благодарили: 0
Сообщений: 1
Добрый день. Как правильно объяснить ребенку писменное деление 150720/60. Можно ли сократить нули? Спасибо.
0
Спасибо
Ответить
2 июня 2017 в 22:42
Ответ для Ирина Винницкая
Валентин Новиков

Профиль
Благодарили: 0
Сообщений: 1

Валентин Новиков
Профиль
Благодарили: 0
Сообщений: 1
150720/60
0
Спасибо
Ответить
22 марта 2016 в 20:47
Таня Матвиенко

Профиль
Благодарили: 0
Сообщений: 1

Таня Матвиенко
Профиль
Благодарили: 0
Сообщений: 1
в столбик 3456 разделить на 36
0
Спасибо
Ответить
19 сентября 2016 в 13:12
Ответ для Таня Матвиенко
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В этой теме подробно описано.
0
Спасибо
Ответить
17 января 2016 в 21:26
Женя Ковтун

Профиль
Благодарили: 0
Сообщений: 1

Женя Ковтун
Профиль
Благодарили: 0
Сообщений: 1
сколько будеть подилить 624 на 3?
0
Спасибо
Ответить
18 января 2016 в 9:51
Ответ для Женя Ковтун
Аида Горбунова

Профиль
Благодарили: 0
Сообщений: 1

Аида Горбунова
Профиль
Благодарили: 0
Сообщений: 1
208)
0
Спасибо
Ответить
21 января 2016 в 16:11
Ответ для Женя Ковтун
Сергей Фадеев

Профиль
Благодарили: 0
Сообщений: 6

Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
208
0
Спасибо
Ответить
24 января 2016 в 13:45
Ответ для Женя Ковтун
Инна Шабрашина

Профиль
Благодарили: 0
Сообщений: 5

Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
208
0
Спасибо
Ответить
27 октября 2015 в 18:18
Даниил Питора

Профиль
Благодарили: 0
Сообщений: 1

Даниил Питора
Профиль
Благодарили: 0
Сообщений: 1
Разделить число 140 в отношении
а)1 к 6 б)2 к 5
Люди помогите срочно!!! Плиз![]()
0
Спасибо
Ответить
15 сентября 2016 в 11:03
Ответ для Даниил Питора
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Если я правильно понимаю задачу, то решение такое:
1) 140 · = 23
2) 140 · = 56
0
Спасибо
Ответить
9 июня 2015 в 10:19
Полина Данилова

Профиль
Благодарили: 0
Сообщений: 1

Полина Данилова
Профиль
Благодарили: 0
Сообщений: 1
учащиеся посадили на пришкольном участке 64саженца яблонь и груш.Причем, яблонь было посажено в 3 раза больше, чем груш.Сколько саженцев яблонь и сколько груш было посажено?
0
Спасибо
Ответить
30 мая 2016 в 12:32
Ответ для Полина Данилова
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
обозначим количество саженцев груш за X. тогда саженцев яблок будет 3 · X. Т.к. известно, что всего было посажено 64 саженца можем составить уравнение:
х +3 · x = 64
4 · x = 64
x = 64: 4
x= 16 — саженцев груш
3 · x = 3 · 16 = 48 — саженцев яблок
Проверка:
16 + 48 = 64
64 = 64.
Ответ: 16 саженцев груш и 48 саженцев яблок.
0
Спасибо
Ответить
8 июня 2015 в 16:01
Валик Софиев

Профиль
Благодарили: 0
Сообщений: 1

Валик Софиев
Профиль
Благодарили: 0
Сообщений: 1
1:2:3:4:5 ставте сколько хотите и где хотите скобок и получите наебольший ответ!!!
0
Спасибо
Ответить
12 июня 2016 в 3:11
Ответ для Валик Софиев
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
1:(((2:3):4):5) = 30.
0
Спасибо
Ответить
27 апреля 2015 в 12:13
Витя Азаров

Профиль
Благодарили: 0
Сообщений: 1

Витя Азаров
Профиль
Благодарили: 0
Сообщений: 1
820 · 430 ? 196049 в столбик
0
Спасибо
Ответить
11 мая 2015 в 11:04
Ответ для Витя Азаров
Ярослава Фесенко

Профиль
Благодарили: 0
Сообщений: 3

Ярослава Фесенко
Профиль
Благодарили: 0
Сообщений: 3
820 · 430=353600-196049=156551
0
Спасибо
Ответить
15 апреля 2015 в 21:45
Светлана Черновицкая

Профиль
Благодарили: 0
Сообщений: 2

Светлана Черновицкая
Профиль
Благодарили: 0
Сообщений: 2
как правильно записать и решить столбиком пример 1000 разделить на 4
0
Спасибо
Ответить
19 апреля 2015 в 14:19
Ответ для Светлана Черновицкая
Маша Галлямова

Профиль
Благодарили: 0
Сообщений: 2

Маша Галлямова
Профиль
Благодарили: 0
Сообщений: 2
1000:4
10:4=2(остаток 2)
10-8=2
20:4=5
получается 250
0
Спасибо
Ответить
Содержание статьи
- Как правильно делить в столбик?
- Что нужно знать ребенку для понимания деления столбиком?
- Методика обучения детей делению столбиком
- Работа с многозначными числами
- Как объяснить деление с остатком?
Чтобы упростить деление чисел, традиционно используется метод деления в столбик. Не все дети понимают принцип с первого раза, а многие взрослые уже успели его забыть. Давайте разберемся, как без лишних слов объяснить ребенку деление «уголком», чтобы он научился решать примеры с двузначными, трехзначными и даже четырехзначными числами.

Как правильно делить в столбик?
Удобнее рассмотреть сам процесс на несложной иллюстрации (№1).
Как найти частное двух чисел – 35 и 5?
- Пишем числа, участвующие в делении, так:

Делимое в данном случае – 35, делитель – 5. Под делителем пишется частное. - Находим неполное частное. Посмотрим на первую цифру слева. В нашем случае это 3, и оно меньше 5 – значит, добавляем следующую цифру слева и будем работать с этой величиной (у нас 35).
- Определяем, какое количество пятерок (5) поместится в 35. Вспоминаем таблицу умножения и заключаем, что в 35 поместиться 7 пятерок. Значит, в графе частное записываем 7.

- Проверяем правильность действий путем умножения: 7 X 5=35. Все верно, решение выполнено точно.

Что нужно знать ребенку для понимания деления столбиком?
Чтобы любимое чадо освоило, как делить уголком (в столбик), нужно два условия:
- отличное знание таблицы умножения;
- умение быстро считать в уме.
В конце 3 класса ученики усваивают, как разделить простые двузначные числа.
При переходе в 4 класс дети учатся делить многозначные числа (больше, чем 100). Также происходит обучение делению уголком чисел с двузначным и трехзначным делителем, решение примеров с остатком.

Методика обучения детей делению столбиком
Если школьник пропустил занятия по математике либо не смог усвоить знания на уроке, то родители должны сами донести до него нужную информацию. Спешка в таком деле неуместна – быстро не значит хорошо. Следует проявить терпение. Деление чисел – простое дело для взрослого, а для школьника задача весьма сложная.
Проверьте знание таблицы умножения. Если ребенок не умножает «автоматически», позвольте подсматривать в табличку.
Первый пример можно взять простейший, с делением без остатка на однозначное число (как в иллюстрации №1).
Когда малыш понял принцип и успешно справился с несложным заданием, пора научить его делению трехзначных чисел. Выполним пример №2.
Работа с многозначными числами
Задание 2: разделим 372 на 6. Для этого на листке бумаги производим следующие действия:
- Определяем делимое (372) и делитель (6), оформляем запись в уголок:

- Неполное частное в нашем варианте, конечно, 37 (т. к. в 3 не поместится 6 ни разу, берем следующую цифру).
- Считаем, много ли шестерок уместится в 37. Если 36:6, то получим 6. Получившееся 6 пишем в графе «частное», а 36 пишем под делителем.
- Вычитаем из 37-36=1. Пишем единичку слева внизу под чертой:

- В единичке не поместится ни одной шестерки, значит, берем оставшуюся цифру из делимого (2). Получилось 12. Нужно определить, сколько в 12 поместится 6 (12 больше 6 ровно в два раза). Получаем 2. Записываем в частное получившуюся величину:

Пример решен, можно проверить правильность путем умножения: 62X6=372.
Как объяснить деление с остатком?
Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:
В группе 8 учеников, на обед им выдали 18 ватрушек на подносе. Когда каждый получит по 2 ватрушки (18:8=2 и ост. 2), на подносе останутся лишние 2 штуки. Это и есть остаток.
Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).
Обучение школьника должно проходить поэтапно, от простых примеров к более сложным. Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.
Прием деления столбиком
Когда мы говорим о делении, то подразумеваем, что надо нечто целое поделить на несколько одинаковых частей. Допустим, мы хотим поделить торт на восемь человек поровну. Для этого надо порезать торт так, чтобы все восемь кусков оказались одинакового размера.
Источник: paulinecakeclub.ru
Сначала мы режем торт пополам (делим на 2 одинаковые части). После этого каждую половинку режем еще раз пополам (получаем 4 одинаковых куска). И, наконец, делим на 2 одинаковые части каждую четвертинку. В результате получаем 8 одинаковых кусков торта.
Так знание математической операции «деление» помогло нам не обидеть никого из гостей. В повседневной жизни вам придется часто сталкиваться с делением. Например, вы всемером заказали две пиццы, и надо их стоимость поделить на всех.
Мы подскажем, как легко и просто сделать это без помощи взрослых и разных умных гаджетов. Разберемся с операцией деления на примерах для учащихся начальной школы — учеников третьего и четвертого классов. Покажем, как делить числа состоящие из двух или трех знаков.
Как делить «с остатком»
При делении большого числа на маленькое не всегда получается сделать это так, чтобы не было остатка. При этом остаток, получившийся в результате деления, не может быть равен делителю или больше него. Он всегда меньше.
Допустим, мы хотим поделить 18 конфет поровну на 2-х человек. Понятно, что каждому достанется по 9 конфет (18 : 2 = 9). Это пример деления без остатка.
Если же мы захотим поделить 18 конфет на 4-х человек, то каждый получит по 4 конфеты (4 × 4 = 16). И у нас останется еще 2 конфеты — это и будет остаток.
2 < 4. Остаток не превышает делитель и не равен ему — значит, мы поделили конфеты правильно.
18 : 4 = 4 (2). Ответ: 4 и остаток 2.
Что было бы, если бы мы решили дать каждому из четверых человек по 3 конфеты, а не по 4? 4 × 3 = 12. Тогда у нас бы осталось еще 6 конфет (18 − 12 = 6).
Но 6 > 4. Получилось бы, что наш остаток превышает делитель — значит, мы поделили бы неправильно.
Разберем еще два примера.
- Разделим 22 на 5. Какое число меньше, чем 22, и при этом делится на 5 без остатка? Это числа 5, 10, 15, 20. Нам нужно выбрать из них самое большое — число 20. Если его поделим на 5, то получим 4. Делаем проверку: 5 × 4 = 20, 22 − 20 = 2. Ответ: 4 и остаток 2. Принято записывать так: 22 : 5 = 4 (2).
- Разделим 39 на 6. Самое большое число, кратное 6 и при этом меньше, чем 39 — это 36. 36 : 6 = 6, 39 – 36 = 3. Разделив 39 на 6, мы получим 6 и в остатке будет 3. Запишем решение в виде: 39 : 6 = 6 (3).
Что значит «делить столбиком»
Если вы умеете делить одно число на другое в уме, это замечательно. Но когда числа большие, даже взрослые могут затрудниться это сделать. Чтобы не запутаться при делении больших чисел, математики придумали способ деления столбиком с помощью бумаги и ручки или карандаша.
Мы познакомим вас с алгоритмом деления в столбик. Он очень простой и легко запоминается. После небольшой тренировки вы без затруднения сможете решать похожие примеры самостоятельно.
Делим трехзначное число на однозначное
Давайте разберем, как делить в столбик многозначное число на простом примере: в качестве делимого возьмем трехзначное число 322, а в качестве делителя — однозначное число 7. Необходимо найти частное.
322 : 7 = ?
Приступаем к алгоритму. Каждое действие обозначим отдельными шагами — этапами.
Этап 1. Делимое 322 записываем с левой стороны. Затем рисуем знак уголка. Справа от него записываем делитель. Должно получиться как на картинке внизу.
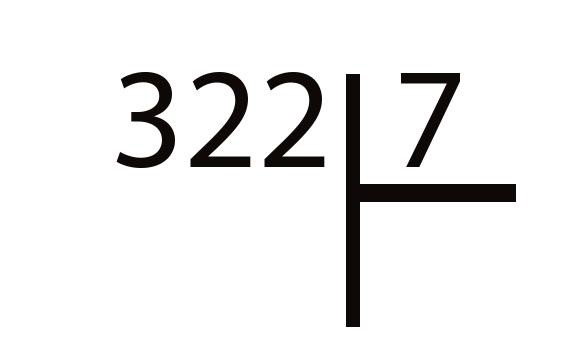
Этап 2. Внимательно изучаем делимое: из скольких сотен, десятков и единиц оно состоит. Нам надо найти число, которое называется «неполным делимым». Оно может оказаться равным делителю или быть больше него.
Число сотен в нашем примере равно 3. Его нельзя поделить на 7, так как 3 < 7. Значит, его мы отбрасываем.
Число десятков у нас — 32. При этом 32 > 7. Значит, оно и будет нашим искомым «неполным делимым».
Делим 32 на 7. Поделить без остатка не получится. Делитель 7 целиком входит 4 раза в делимое 32. Значит, мы нашли неполное частное 4: 7 × 4 = 28, но при этом получили и в остатке 4: 32 − 28 = 4.
Вот как это будет выглядеть в вашей тетради.
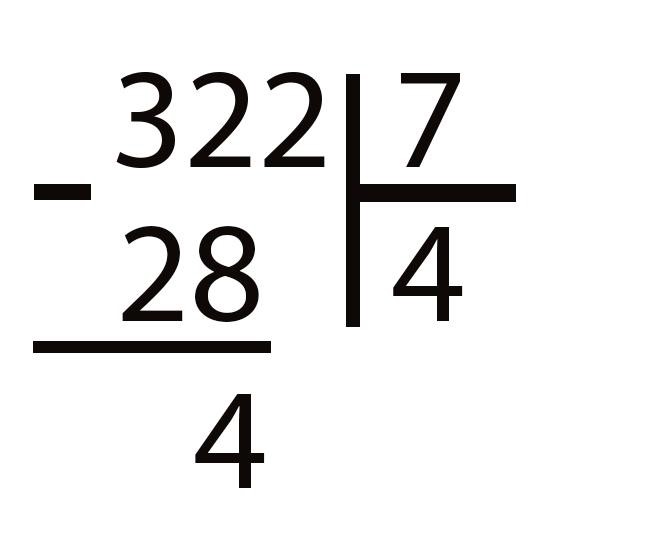
Если бы в качестве неполного частного мы взяли число 5, то нам пришлось бы от 32 отнимать 7 × 5 = 35. Мы не можем отнять 35 от 32, так как вычитаемое не может быть больше уменьшаемого.
Если бы мы рассматривали как неполное частное число 3, то при вычитании мы получили бы в остатке число большее, чем делитель: 7 × 3 = 21, 32 − 21 = 11, 11 > 7. Это решение также было бы ошибочным. Остаток не может быть больше делителя.
Этап 3.
Припишем к полученному остатку с правой стороны следующую цифру делимого. В математике принято обозначать это действие словами «снести двойку». У нас получилось число 42, которое нам нужно продолжить делить на наше делимое 7.
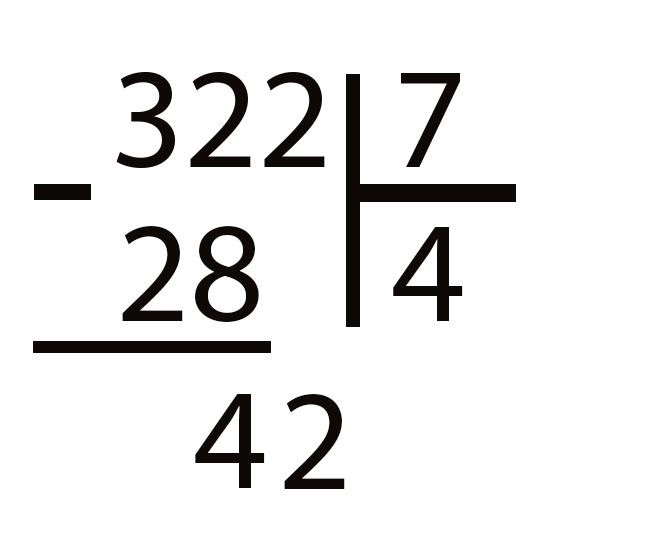
Этап 4. Пробуем получившееся число 42 поделить на 7. Вспоминаем таблицу умножения: 7 × 6 = 42. Значит, 42 делится на 7 без остатка. Пишем рядом с неполным частным 4 (справа от него) цифру 6. Получаем полное частное в виде числа 46.
Пишем внизу: 42 − 42 = 0. Это означает, что число 322 поделилось на 7 нацело, без остатка.
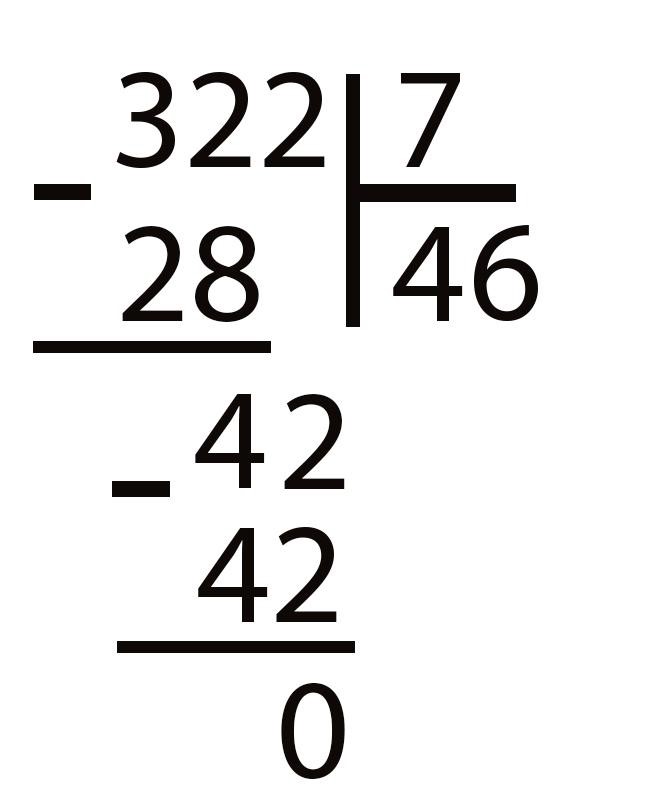
Источник: googleusercontent.com
Ответ: 322 : 7 = 46
Если в результате деления большего числа на меньшее вместо нуля в остатке вы получите какое-то другое число (меньшее, чем делитель), значит оно делится не нацело, а с остатком. И получившееся вместо нуля число и будет этим остатком.
В конце статьи вы найдете задания с ответами, потренировавшись на которых вы легко сможете перейти к следующему уровню.
Делим трехзначное число на двузначное
Если вы достаточно натренировались в делении на однозначные числа, то пора переходить к двузначным, взятым в качестве делителя.
Сначала потренируемся: научимся делить двузначное числа на аналогичное. Попробуем поделить 84 на 14.
84 : 14 = ?
Этап 1. Запишем делимое 84 слева, потом знак уголка, затем справа от него — делитель 14.
Этап 2. Анализируем наше делимое: 8 на 14 поделить нельзя. Будем действовать методом подбора. Найдем, на какое число надо умножить 14, чтобы в результате получилось 84.
14 × ? = 84
Этап 3. По очереди перебираем возможные варианты ответа:
- 14 × 2 = 28;
- 14 × 3 = 42:
- 14 × 4 = 56;
- 14 × 5 = 70;
- 14 × 6 = 84.
Последний вариант нас устраивает.
Запишем цифру 6 в качестве частного под знаком уголка с правой стороны:
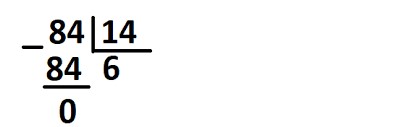
Источник: gstatic.com
Ответ: 84 : 14 = 6.
Теперь рассмотрим более сложный пример: попробуем разделить трехзначное число 273 на число 13, которое является двузначным.
Итак, наше делимое — 273, делитель — 13. Необходимо найти частное.
273 : 13 = ?
Этап 1. Делимое 273 записываем с левой стороны. Затем рисуем знак уголка. Справа от него записываем делитель.
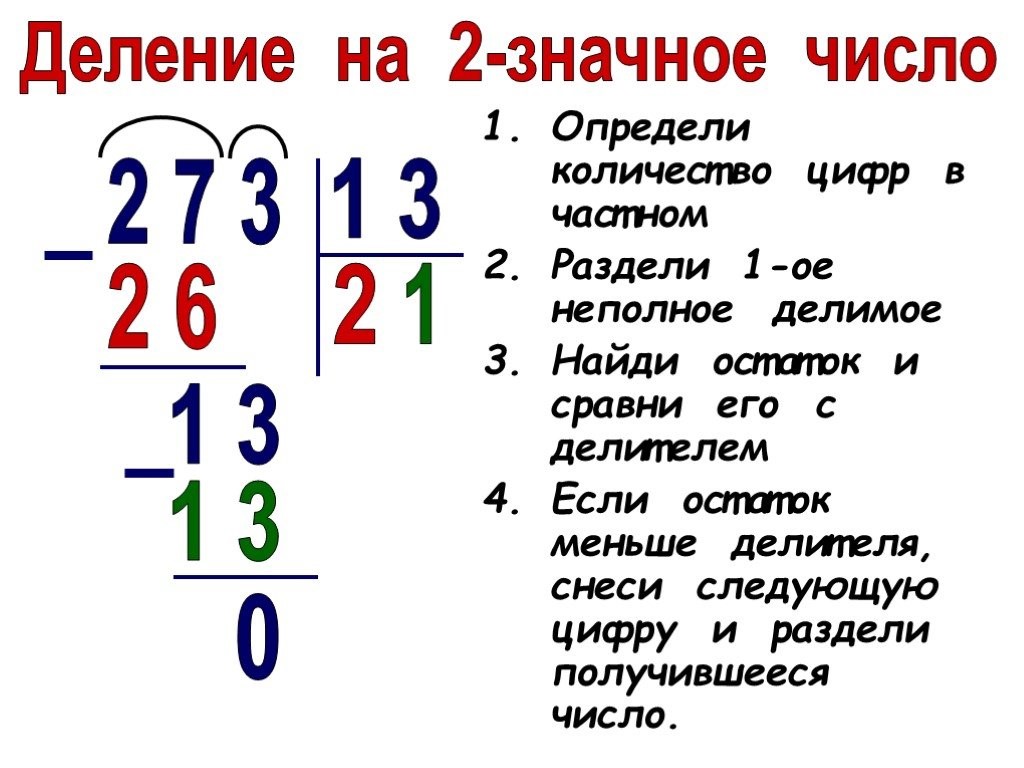
Этап 2. Анализируем наше делимое, как и в предыдущем случае, слева направо. Число 2 на 13 не делится. А вот число 27 нам подходит: 27 > 13. Значит, оно и будет нашим искомым «неполным делимым».
Делим 27 на 13. Поделить без остатка мы не можем. Делитель 13 дважды укладывается целиком в делимое 27. Таким образом, мы нашли неполное частное 2: 13 × 2 = 26, но при этом получаем в остатке единицу: 27 − 26 = 1. Остаток не превышает делитель и не равен ему (1 < 13), значит все в порядке.
Этап 3. Приписываем к полученной единице справа следующую цифру делимого. В нашем случае это цифра 3. Говоря другими словами, «сносим тройку». В результате нас получилось число 13.
Этап 4. Теперь для нас не представляет никакого труда разделить 13 на 13. Любое число делится само на себя без остатка: 13 : 13 = 1. Записываем с правой стороны от неполного частного 2 цифру 1. Получаем полное частное — число 21.
Дописываем наш столбик в самом низу: 13 − 13 = 0. Таким образом, число 273 поделилось на 13 нацело, без остатка.
Возьмем другой пример:
Попробуем поделить трехзначное число 410 на двузначное 82.
410 : 82 = ?
Этап 1. Запишем делимое 410 слева, потом знак уголка, затем справа от него — делитель 82.
Этап 2. Анализируем наше делимое: 4 на 82 поделить невозможно, но и 41 тоже меньше, чем наш делитель 82. Получается, что способ деления столбиком здесь не подходит. Придется действовать методом подбора.
Этап 3. По очереди перебираем возможные варианты ответа:
- 82 × 2 = 164;
- 82 × 3 = 246:
- 82 × 4 = 328;
- 82 × 5 = 410.
Мы нашли искомое частное путем подбора. Ответ: 410 : 82 = 5.
Делим число столбиком с остатком
Возьмем трехзначное число 764 и вместе попробуем поделить его на однозначное число 5.
Делимое — 764, делитель — 5. Наша задача — найти частное и проверить, что будет в остатке.
764 : 5 = ?
Действуем по отработанному алгоритму.
Этап 1. Слева записываем делимое 764, рядом с ним рисуем знак уголка, после которого чуть правее записываем делитель 5.
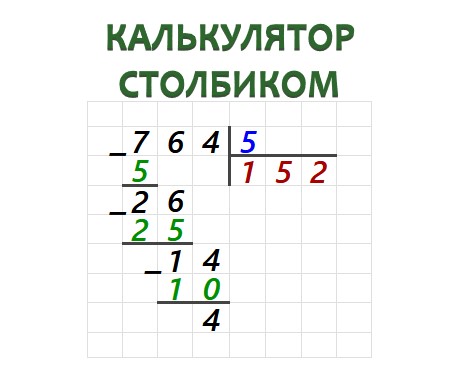
Источник: findhow.org
Этап 2. Анализируем делимое 764 в уже известной нам последовательности. Число сотен 7 больше, чем наш делитель 5. Значит, 7 — наше начальное «неполное делимое».
Делим 7 на 5. Получаем неполное частное 1 и остаток, равный «двойке»: 7 − 5 = 2. Остаток не больше делителя (2 < 5), как и должно быть.
Этап 3. Приписываем к полученной двойке справа следующую цифру делимого. В данном примере это цифра 6. Получаем число 26.
Этап 4. Проделываем всю процедуру еще раз. Ищем самое большее из чисел, делящихся на 5, но при этом меньше, чем 26. Таким числом будет 25 — наш делитель 5 укладывается в него целиком ровно 5 раз: 5 × 5 = 25. Записываем пятерку справа от единицы. 26 − 25 = 1. Все верно — остаток 1 меньше, чем делитель 5.
Этап 5. К полученной в качестве остатка единице сносим четверку — крайнюю из цифер делимого. Получаем число 14, которое надо продолжить делить на 5.
Этап 6. Ближайшее к 14 число, чуть меньше его и делящееся на 5 — это 10. Делим 10 на 5 и получаем 2. Проверяем: 5 × 2 = 10. Двойку приписываем справа в окошке для частного. 14 − 10 = 4. Делаем проверку: остаток 4 < 5. У нас не осталось больше неиспользованных цифр в делимом. Значит, 4 — это конечный искомый остаток. А в окошке для частного — окончательный ответ, искомое частное.
Ответ: 764 : 5 = 152 (4)
Теперь разберем пример деления с остатком трехзначного числа на двузначное.
В качестве делимого возьмем 255, в качестве делителя — 10. Найдем частное вместе с остатком.
255 : 10 = ?
Этап 1. Пишем привычным образом делимое 255 и после знака уголка справа записываем делитель 10.
Этап 2. Рассмотрим делимое 255. Число 2 не подходит по определению (нам нужно число, состоящее не менее чем из двух знаков). Следующее число 25 больше, чем наш делитель 10. Следовательно, оно нам подходит.
Делим 25 на 10. Ближайшее кратное к 10 число — 20. Оно дважды содержит число 10. Таким образом, кроме неполного частного 2 мы получили остаток, равный пяти: 25 − 20 = 5. Остаток не превышает делитель (5 < 10), все верно.
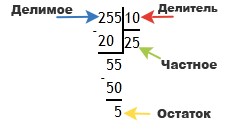
Источник: binary2hex.ru
Этап 3. Сносим вниз к полученной пятерке справа цифру 5, стоящую самой последней в делимом. Мы получили число 55, которое надо разделить на 10.
Этап 4. Продолжаем деление. Наибольшее число, кратное 10, и при этом меньше, чем 55 — это число 50. Наш делитель 10 входит в него 5 раз: 10 × 5 = 50. Записываем пятерку справа от двойки в окошке для записи частного. Проверяем: 55 − 50 = 5. Значит, остаток мы нашли правильно (5 < 10). А число 25 будет искомым частным.
Ответ: 255 : 10 = 25 (5)
Упражнения для самостоятельного деления в столбик
Чтобы убедиться в том, правильно ли вы усвоили материал, стоит немного поупражняться. Попробуйте решить столбиком примеры, приведенные ниже, а потом сверьтесь с нашими ответами.
Начните с легкого (1) уровня:
- 32 : 4 = ?
- 65 : 5 = ?
- 54 : 9 = ?
- 72 : 6 = ?
- 81 : 3 = ?
Решили? Тогда переходите к среднему (2) уровню сложности:
- 192 : 12 = ?
- 245 : 5 = ?
- 221 : 13 = ?
- 432 : 9 = ?
- 928 : 8 = ?
Если вы и с этим успешно справились, попробуйте более сложный (3) уровень, где в качестве делимого выступают четырехзначные числа.
- 7485 : 3 = ?
- 3105 : 23 = ?
- 5538 : 26 = ?
- 6344 : 61 = ?
- 1423 : 25 = ?
Самые отважные могут попробовать свои силы в делении столбиком пятизначного числа (уровень *)
- 48633 : 39 = ?
Ответы:
- примеры 1 уровня: 8; 13; 6; 12; 27;
- примеры 2 уровня: 16; 49; 17; 48; 116.
Посмотреть процесс решения примеров более сложного уровня вы можете на иллюстрации, нажав на ссылку:
- 7485 : 3 = 2495;
- 3105 : 23 = 135;
- 5538 : 26 = 213;
- 6344 : 61 = 104;
- 1423 : 25 = 56 (23);
- 48633 : 39 = 1247.
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
