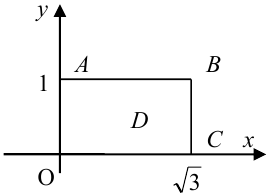
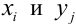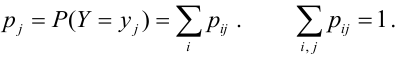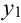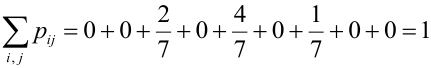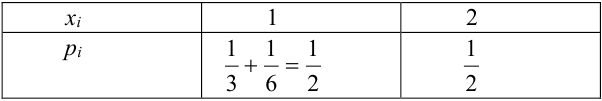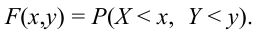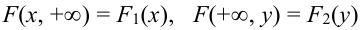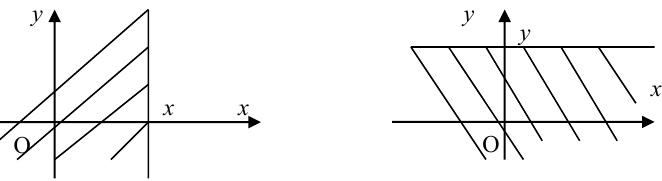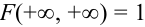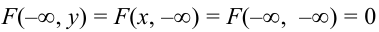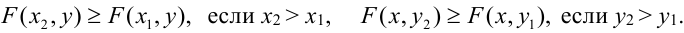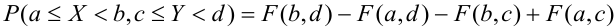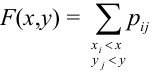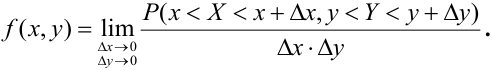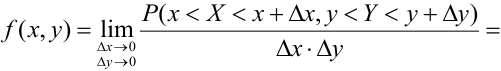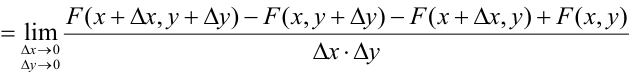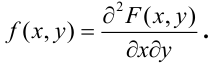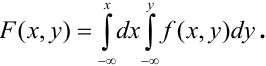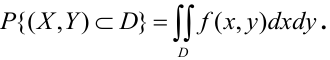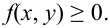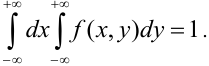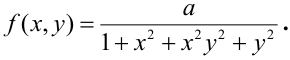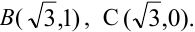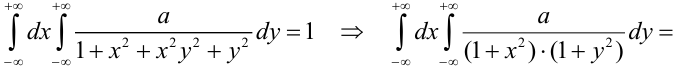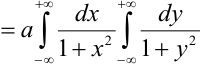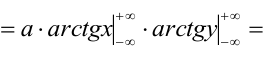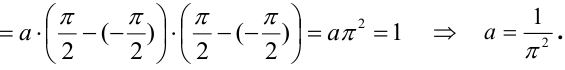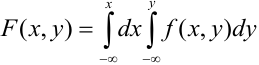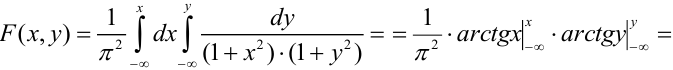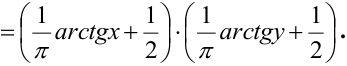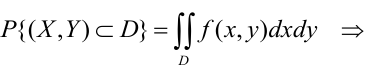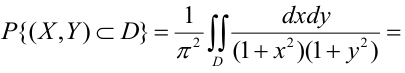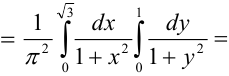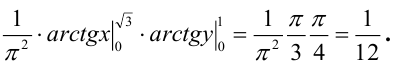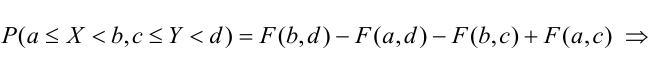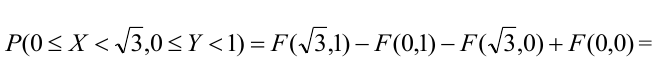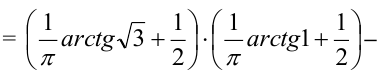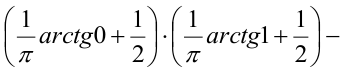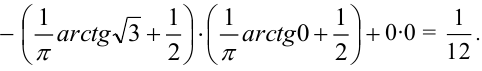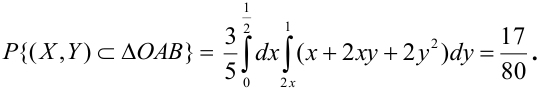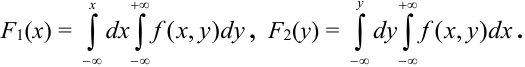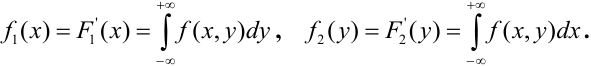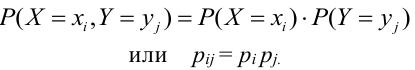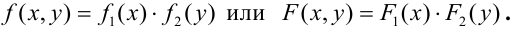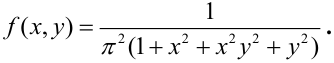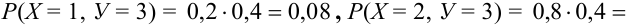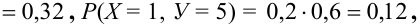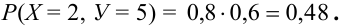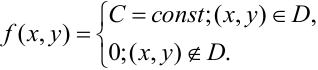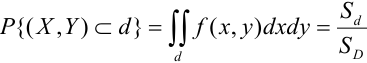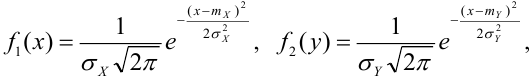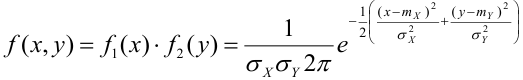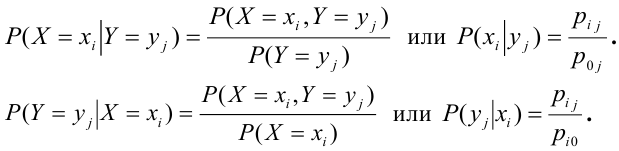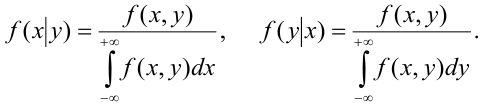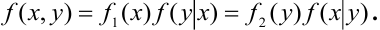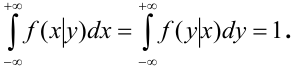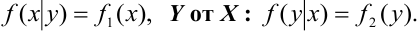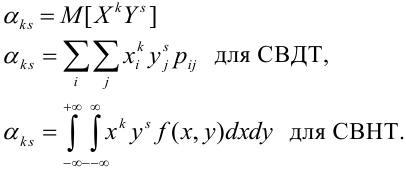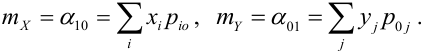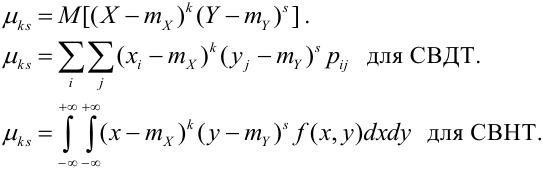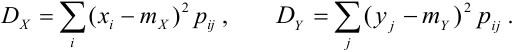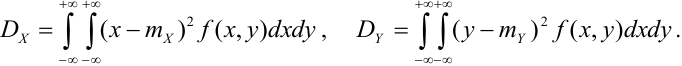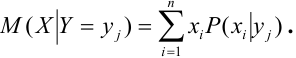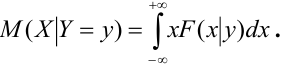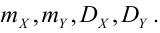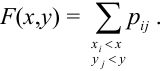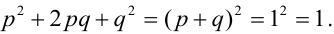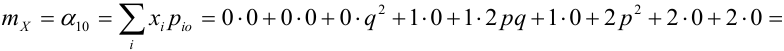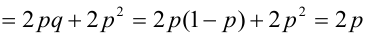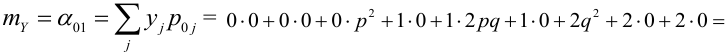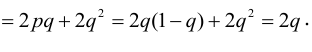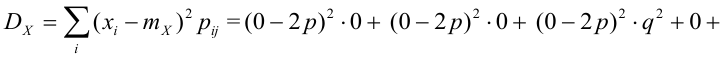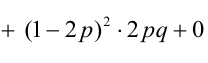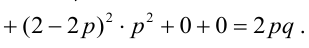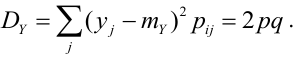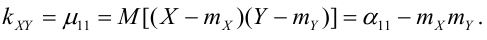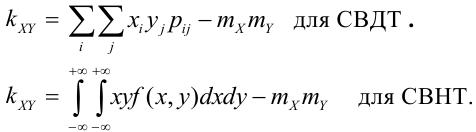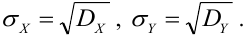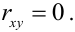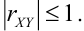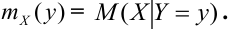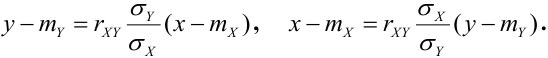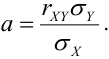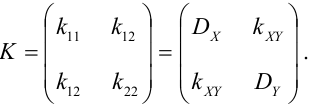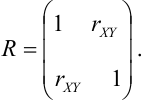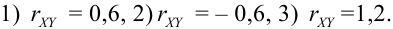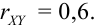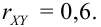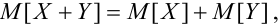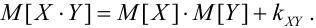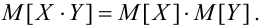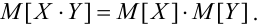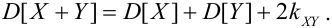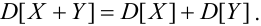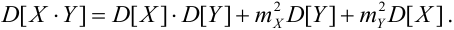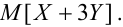Функцией распределения
случайной величины называют
вероятность того, что случайная величина
примет частное значение меньшее
некоторого фиксированного,
т.е.
P(X<x)
=F(x).
Геометрически это
равенство можно истолковать так: функция
распределения F(x)
есть вероятность того, что случайная
величина X
примет значение, которое изображается
точкой, лежащей левее точки x.
Так как случайная
дискретная величина может принимать
значения
то функция распределения для нее будет
.
Свойства функции
распределения
1)
Функция
распределения F(x)
является неубывающей функцией своего
аргумента, т.е.
,
если
.
2) Функция распределения
F(x)есть
неотрицательная функция, значения
которой принадлежат отрезку (0,1), т.е.
.
График
функции
распределения
А) Случайная дискретная
величина.
Таблица 2
-
x
0
1
2
p
0,3
0,5
0,2
F(0
)=0;
F(1)=0,3;
F(2)=P(X=0)+P(X=1)=0,3+0,5=0,8;
F(3)=
P(X=0)+P(X=1)+P(X=2)= 0,3+0,5+0,2=1.
Для случайной
дискретной величины функция распределения
F(x)
имеет ступенчатый график (Рис. 2),
количество ступенек равно числу частных
значений случайной величины, а высота
ступеньки равна значению вероятности
появления этого частного значения
случайной величины.
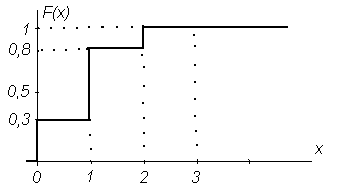
Рисунок 2 График
функции распределения случайной
дискретной величины
Б) Случайная
непрерывная величина.
Функция распределения
этой случайной величины представляет
собой непрерывную кривую (Рис.3).
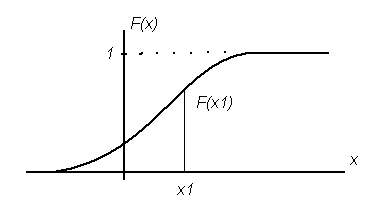
Рисунок 3 График
функции распределения случайной
непрерывной величины
13 Плотность распределения случайной величины и ее свойства.
Функция распределения
случайной непрерывной величины
дополнительно обладает еще одним
свойством, которое заключается в том,
что вероятность того, что случайная
непрерывная величина примет одно
определенное значение, равна нулю.
Пусть случайная
непрерывная величина X
может принять
частное значение в интервале
,
причем известна ее функция распределения
F(x).
Требуется найти вероятность попадания
ее в этот интервал, т.е.
при условии, что
.
Используя предел
вероятности попадания величины в
заданный интервал, получаем
.
Этот результат
означает, что пользоваться формулой
(2.1) для определения вероятности попадания
случайной непрерывной величины в
заданный интервал, близкий нулю, нельзя.
Задание закона
распределения не является единственным
способом. Очень часто его задают так
называемой дифференциальной функцией
распределения или плотностью вероятности.
Дифференциальной
функцией распределения (плотностью
вероятности) f(x)
случайной непрерывной величины X
называют первую производную от функции
распределения случайной непрерывной
величины X:
.
Дифференциальная
функция f(x)
характеризует плотность распределения
значений случайной непрерывной величины,
что и определило ее второе название.
Действительно, так
как вероятность попадания случайной
величины X
в интервал
равна приращению функции на этом
интервале, т.е.
,
то отношение этого
приращения к приращению аргумента
будет характеризовать
среднюю плотность вероятности на этом
интервале.
В пределе при
стремлении
к нулю получим (предполагается, что
функция f(x)
дифференцируема):
.
График дифференциальной
функции f(x)
называется кривой распределения.
Установим, как можно
найти по известной плотности вероятности
f(x):
1) вероятность
попадания случайной непрерывной величины
в заданный интервал; 2) функцию распределения
F(x).
Пусть случайная
непрерывная величина X
задана плотностью вероятности, график
которой изображен на рис. 6.
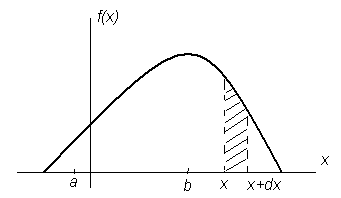
Рисунок 6 График
плотности вероятности
Дифференциал функции
dF(x)=f(x)dx
представляет
собой вероятность того, что случайная
величина X
примет значение
в интервале (x,
x+
dx).
Произведение f(x)dx
называется
элементом
вероятности.
Геометрически это площадь элементарного
прямоугольника с основанием dx
и высотой f(x).
Для того чтобы найти
вероятность
попадания случайной величины X
в интервал (a,
b)
по известной плотности вероятности
f(x)
необходимо просуммировать элементы
вероятности f(x)dx
в этом интервале:
.
Исходя из определения
функции распределения F(x)
и последнего выражения, получим
.
Геометрически
функции распределения F(x)
есть не что иное, как площадь бесконечной
фигуры, ограниченной кривой распределения
и осью абсцисс, лежащей левее точки x.
Свойства плотности
вероятности:
а) плотность
вероятности есть функция неотрицательная;
б) распределение
имеет размерность обратную размерности
случайной величины;
в) интеграл в
бесконечных пределах от плотности
вероятности равен единице, т.е.
.
плотность вероятности
применяется только для случайных
непрерывных величин.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Функции от случайной величины
- Закон распределения суммы двух случайных величин
Функции случайных величин
В приложениях часто приходится рассматривать случайные величины, которые являются некоторыми функциями случайных величин. Например, необходимо рассмотреть квадрат случайной величины или произведение двух случайных величин. При этом часто необходимо выяснить закон распределения получающейся случайной величины. В данной главе мы рассматриваем задачи, связанные с решением такого типа проблем.
Функции от случайной величины
Понятие функции случайной величины уже рассматривалось. Там же мы установили, что для непрерывной функции
будет снова случайной величиной.
В данном параграфе мы будем рассматривать задачу нахождения функции плотности 



По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Примеры с решением
Пример 8.1.
Пусть 


Решение:
Пусть 




Подставляя выражение (8.1) в (8.2), получим
Возможны два случая. Если 





Если 


откуда формула для плотности:
Возможно вам будут полезны данные страницы:
Формулы (8.5), (8.6) можно записать единообразно с использованием абсолютной величины. Это легко запомнить, если сообразить, что так как левая часть принимает только положительные значения, то и числовой множитель в правой части должен быть положительным. Итак, заключительная формула для искомой плотности имеет вид:
В качестве следствия получим следующее утверждение.
Теорема 8.1. Если 


Тогда согласно (8.8) имеем 


Пример 8.2.
Пусть 


Решение:
Найдем сначала функцию распределения 
где 

Рассмотренные примеры служат двум целям: во-первых, дать подход к нахождению функции плотности в типичных случаях и, во-вторых, использовать полученные формулы в дальнейших приложениях.
Закон распределения суммы двух случайных величин
Пусть дана система двух случайных величин 

Заметим, что для любой непрерывной функции 


Теорема 8.2. Если система случайных величин 



Доказательство. Найдем функцию распределения случайной величины 




Тогда функцию распределения для случайной величины 
Дифференцируя no 
Поскольку выражение для плотности симметрично относительно переменных 
Тем самым мы получили искомое выражение (8.11) и доказательство теоремы закончено полностью.
Особого внимания заслуживает случай, когда случайные величины 
где 


Отвлекаясь от существа решаемой задачи, можно заметить, что полученная нами формула (8.14) определяет весьма интересную операцию над функциями: каждой паре функций 



Пример 8.3.
Даны две независимые случайные величины 

Решение:
Поскольку 



При 




При 

И наконец, при 

Итак,
На рис. 8.2 изображен график соответствующей функции плотности, который называется законом распределения Сэмпсона.
Если 

Следующий пример связан с нахождением закона распределения величины
где все 
Формула (8.10) 
поскольку
Заметим, что свойство нормированности плотности (8.17) следует из определения 
Свойство 1.
Свойство 2.
Свойство 3.
Свойство 1 выводится с помощью формулы (8.14) и замены переменной 
К последнему интегралу применим формулу интегрирования по частям. Положим
Тогда получим
Первое выражение в скобках равно нулю, поскольку 
Интеграл от функции плотности равен единице по свойству нормированности, и мы получаем искомую формулу.
Свойство 3 доказывается совершенно аналогично, только интегрировать по частям придется дважды. Вывод предлагаем провести читателю.
Пример 8.4.
Найти закон распределения случайной величины 
Решение:
Случайная величина 


По свойству 2 

Теорема 8.3. Функция плотности случайной величины 
Математическое ожидание и дисперсия равны соответственно


Из рисунка видно, что графики плотности не являются симметричными относительно математического ожидания, однако с ростом числа степеней свободы они становятся все более симметричными.
Наряду с суммой случайных величин в приложениях часто приходится иметь дело с частным непрерывных случайных величин. Для нахождения функции плотности частного сделаем сначала предварительное замечание.
Пусть 

Отметим следующие свойства
Свойство 1. 
Действительно, производная 
где 


Очевидно, что 

по свойству функции плотности.
Свойство 3. Если функция 


Для проверки этого свойства достаточно доказать свойство нормированности. Иными словами, надо проверить, что
Имеем
Доказанные свойства позволяют рассматривать функцию 
Теорема 8.4. Пусть даны непрерывные случайные величины 








Рассматривая параметр 




Следующая теорема использует формулу (8.23), чтобы найти функцию плотности, которая будет использована для описания распределения Фишера.
Теорема 8.5. Если случайные величины 


Доказательство. Подставляя в формулу (8.23) выражения для плотностей (8.17), получим
В последнем интеграле произведем замену 

П0ЛУЧИМ ИСКОМУЮ Формулу для плотности.
Определение. Распределением Фишера называется распределение случайной величины


Применяя теорему 8.5, получим выражение для плотности величины, распределенной по закону Фишера.
Теорема 8.6. Случайная величина 
Графики функций плотности для трех случаев: а) 




Определение. Случайная величина подчинена закону распределения Стьюдента с 
где 
Плотность распределения Стьюдента с 

В частности, 





Лекции:
- Случайный вектор распределения
- Системы случайных величин
- Условное нормальное распределение
- Нормальное распределение на плоскости
- Многомерный нормальный закон
- Математическое ожидание: пример решения
- Законы распределения случайных величин
- Моменты случайной величины
- Моменты высших порядков
- Метод моментов
Содержание:
Системы случайных величин или случайные векторы:
При изучении случайных явлений в зависимости от их сложности приходится использовать два, три и большее число случайных величин.
Например, 1) попадание снаряда в цель определяется не одной, а двумя случайными величинами: абсциссой и ординатой точки попадания, 2) случайное отклонение точки разрыва снаряда при дистанционной стрельбе определяется комплексом трех случайных величин: тремя координатами этой точки.
Определение 57. Совместное рассмотрение двух или нескольких случайных величин приводит к системе случайных величин или к случайному вектору.
(X, Y) – двумерный случайный вектор или система двух СВ.
Изучать систему – значит изучать сами случайные величины, ее составляющие; связи и зависимости между ними.
Геометрическая интерпретация системы: 1) систему двух случайных величин (X, У) рассматривают как случайную точку на плоскости (Охх) или как случайный вектор с составляющими X, У; 2) систему трех случайных величин (X, У, Z) рассматривают как случайную точку на плоскости (Оxyz) или как случайный вектор с составляющими X, У; Z и т.д.
В зависимости от типа случайных величин, образующих систему, могут быть дискретные, непрерывные и смешанные системы.
Определение 58. Двумерный случайный вектор (X, У) называется вектором дискретного типа (СВДТ), если множество его возможных значений не более, чем счетно.
Определение 59. (первое определение) Двумерный случайный вектор (X, У) называется вектором непрерывного типа (СВНТ), если множество его возможных значений непрерывно заполняет некоторую область плоскости (Оху)-
Определение 60. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Законы распределения СВДТ и СВНТ
Таблица распределения – закон распределения СВДТ:
Рассмотрим двумерный случайный вектор (X, У), где X и У – дискретные случайные величины с возможными значениями
Пример:
Из цифр 1, 2, 3, 4, 6, 8, 9 наудачу отбирают две цифры. Х – число четных цифр в выборке, Y – число нечетных. Описать закон распределения.
Решение.
X (четные) – 2, 4, 6, 8; Y ( нечетные) – 1, 3, 9. Следовательно, возможные значения X 
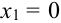
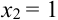
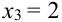
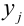
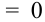
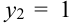
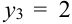
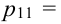
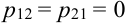
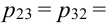
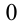
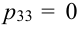
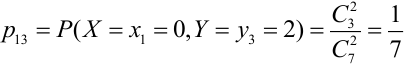
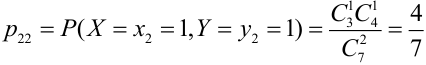
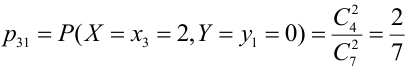
Таблица распределения имеет вид:
Проверка:
Пример:
Дана таблица распределения случайного вектора (X, Y). Получить ряды распределения для Х и Y отдельно.
Решение.
Проверка:
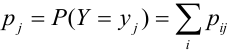
Проверка:
Функция распределения – закон распределения СВДТ и СВНТ
Функция распределения – универсальный закон распределения случайных векторов как дискретного, так и непрерывного типа.
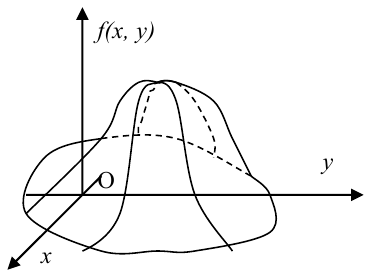
Определение 61. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x,y), равная вероятности совместного выполнения двух неравенств: X < х, Y < у, т.е.
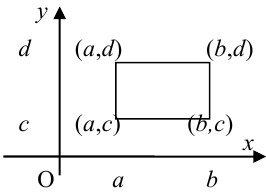
Геометрически F(x,y) представляет вероятность попадания случайной точки (X,Y) в левый нижний бесконечный квадрант плоскости с вершиной в точке (х,у).
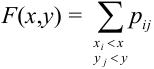
Свойства F(x;y).
1. Условие согласованности:
Пояснение. Отодвигая одну из границ квадранта в бесконечность, получаем полуплоскость, вероятность попадания в которую есть функция распределения одной случайной величины.
2.
Пояснение. Квадрант обращается во всю координатную плоскость, попадание случайной точки в которую есть достоверное событие.
3.
Пояснение. Отодвигая ту или иную границу квадранта в (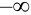
4. F(x, у) – неубывающая функция по каждому аргументу.
5. Вероятность попадания случайной точки (X, У) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
Определение 62. (второе определение) Двумерный случайный вектор называется случайным вектором непрерывного типа (СВНТ), если его функция распределения непрерывна на всей плоскости и существует неотрицательная и интегрируемая по Риману в бесконечных пределах по х, у функция 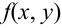
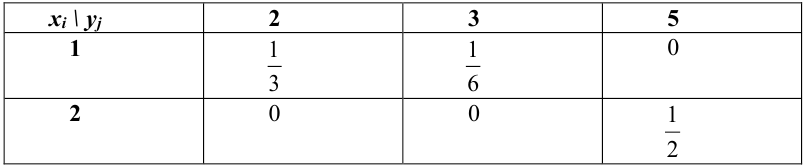
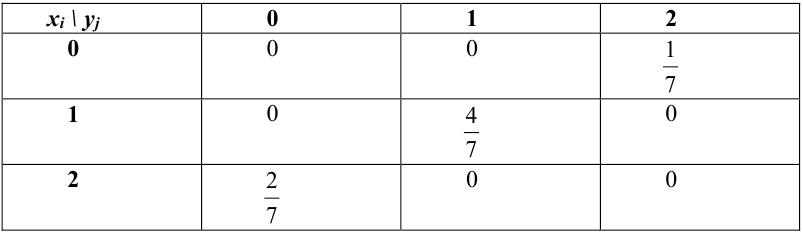
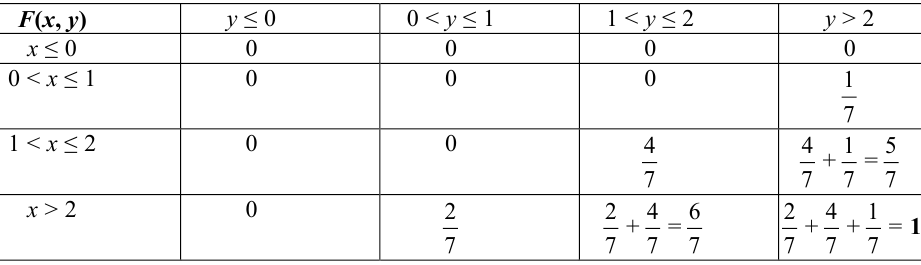
Пример №1
Найти функцию распределения, если случайный вектор задан таблицей распределения:
Решение.
Случайный вектор дискретного типа, следовательно,
Плотность распределения (Для СВНТ)
Определение 63. (первое определение) Плотностью распределения системы двух непрерывных случайных величин называется предел отношения вероятности попадания случайной точки (X, Y) в элементарный прямоугольник к площади прямоугольника, когда оба его размера стремятся к нулю:
Распишем интервальную вероятность с помощью функции распределения:
Правая часть равенства – определение смешанной производной функции двух переменных F(x, у), отсюда следует
Определение 64. (второе определение) Плотностью распределения системы двух непрерывных случайных величин называется смешанная частная производная от функции распределения системы:
Отсюда,
Геометрически 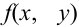
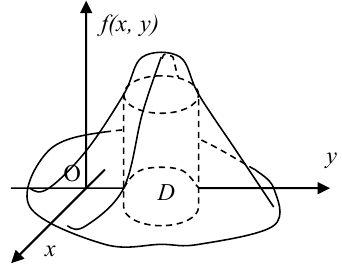
Вероятность попадания случайной точки в некоторую область D плоскости (Oxy) находится по формуле:
Геометрически вероятность попадания случайной точки в область D плоскости (Oxy) изображается объемом цилиндрического тела, ограниченного поверхностью распределения и опирающегося на эту область.
Свойства плотности
1. 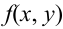
2. Условие нормировки:
Пример №2
Дана плотность распределения непрерывного вектора
Найти: 1) коэффициент а, 2) функцию распределения F(x, у), 3) вероятность попадания случайной точки в прямоугольник с вершинами в точках O(0,0), A(0,1),
Решение.
1) Для вычисления коэффициента а применим условие нормировки:
2) По определению
3) Вероятность попадания в прямоугольник.
1 способ:
2 способ (по 5 свойству):
Пример №3
Дана плотность распределения непрерывного вектора 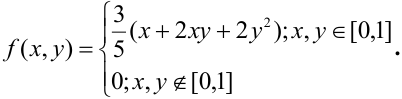
Решение.
Плотность распределения задана в квадрате. Область пересечения квадрата с заданным треугольником заштрихованный треугольник, ограниченный снизу прямой 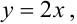
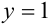
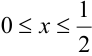
Плотности распределения отдельных величин, входящих в систему
Пусть известна плотность распределения 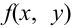
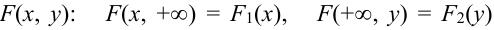
Отсюда, дифференцированием первого равенства по х, а второго по у, получим, что плотности распределения одной из величин равны интегралу от плотности распределения системы в бесконечных пределах по аргументу, соответствующему другой случайной величине:
Ставится вопрос, как по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. В общем случае эта задача не разрешима, но, с другой стороны, закон распределения системы должен содержать все сведения о величинах, входящих в систему, в том числе и сведения о том, как они связаны между собой.
Определение 65. Случайные величины X и Y, входящие в систему, называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае, они называются зависимыми.
Теорема. Для того, чтобы дискретные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
Для того, чтобы непрерывные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
Пример №4
Дана плотность распределения непрерывного вектора:
Зависимы или независимы случайные величины, входящие в систему?
Решение.
Представим плотность в виде произведения:
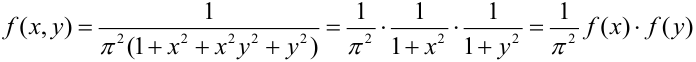
Пример №5
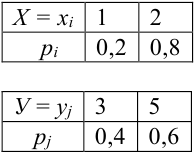
Дано распределение дискретных независимых случайных величин Х и Y:
Записать закон распределения случайного вектора (Х + Y).
Решение.
Найдем возможные значения случайного вектора (Х+ Y): 1 + 3 = 4, 2 + 3 =5, 1+5 = 6, 2 + 5 = 7.
Найдем их вероятности, пользуясь условием независимости:
Следовательно, ряд распределения случайного вектора (Х + Y) имеет вид:
Замечание. Одним из наиболее простых распределений системы двух непрерывных величин является равномерное распределение.
Определение 66. Система двух непрерывных случайных величин имеет равномерное распределение в области D плоскости (Оху), если плотность распределения в точках области D постоянна и равна нулю в остальных точках плоскости:
В силу свойства 2 плотности имеем, что 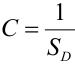
Определение 67. Пусть Х и Y независимые величины, распределенные по нормальному закону, их плотности распределения имеет вид:
Следовательно, плотность распределения системы (Х,Y) на основании теоремы умножения плотностей распределения для случая независимых величин получим в виде
Если X и Y зависимы между собой, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему, что привело к введению условных законов распределения.
Определение 68. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.
Обозначим G (х,у) – множество возможных значений случайного вектора (X, Y).
Рассмотрим СВДТ.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у называется совокупность возможных значений 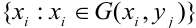
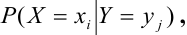
Рассмотрим CBHT.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у :
Теорема (умножения законов распределения):
Условие нормировки:
Условие независимости Х от Y:
Числовые характеристики системы
Определение 69. Начальным моментом 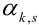
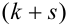
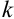
Математическое ожидание дискретных случайных величин Х и Y, входящих в систему:
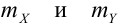
Определение 70. Центральным моментом 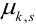
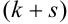
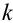
Дисперсия случайных величин X и Y, входящих в систему – характеристика рассеивания случайной точки в направлении осей (ох) и (оу):
Дисперсия дискретных случайных величин Х и Y, входящих в систему:
Дисперсия непрерывных случайных величин Х и Y, входящих в систему:
Замечание. Для краткого описания условных законов распределения используются различные характеристики, наиболее важной из которых является математическое ожидание:
Определение 71. Условным математическим ожиданием дискретной случайной величины X при условии, что Y принимает одно из своих возможных значений 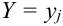
Для непрерывной случайной величины X:
Аналогично, вводится понятие условного мат. ожидания для СВ Y.
Пример №6
По некоторой цели производится два выстрела. Вероятность попадания при одном выстреле равна р. Рассмотрим две случайные величины: X – число попаданий в цель, Y – число промахов. Составить таблицу распределения, записать функцию распределения системы F(x,y) и найти числовые характеристики
Решение.
Случайный вектор дискретного типа, следовательно,
Пояснение:
Ковариация, корреляция и линии регрессии
Особую роль при исследовании системы играет второй смешанный центральный момент.
Определение 72. Второй смешанный центральный момент 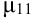
Теория корреляции решает две задачи: 1) установление формы связи между случайными величинами, 2) определение тесноты и силы этой связи.
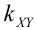
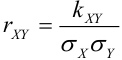
(Иногда его обозначают как 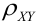
Средние квадратические отклонения случайных величин X и Y равны
Определение 17. X и Y называются некоррелированными случайными величинами, если их коэффициент корреляции 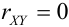
Свойства коэффициента корреляции
Свойства коэффициента корреляции 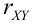
1. Если X и Y – независимые СВ, то 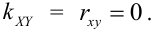
2.
3. В случае 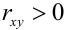
4. В случае 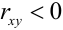
Взаимная связь двух случайных величин, помимо 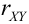
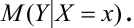
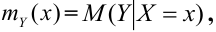
Аналогично, зависимость Х от Y описывает функция
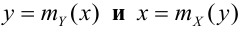
Линии, определенные этими уравнениями, называются кривыми или линиями регрессии. (Вводятся лишь для непрерывных СВ, для ДСВ линии будут состоять из точек.)
Если обе линии регрессии – прямые, то корреляционную зависимость называют линейной (линейная корреляция). Для нормально распределенного случайного вектора (X,Y) уравнения регрессии линейные:
Связь коэффициента корреляции и линий регрессии
1) Если 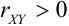
2) Если 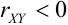
3) Если 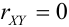
4) Если, 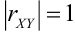
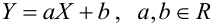
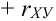
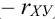
Часто пишут уравнение в виде: 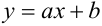
Определение 73. Ковариационной матрицей случайного вектора называется симметрическая действительная матрица, элемент которой представляет собой ковариации соответствующих пар компонент:
Определение 74. Корреляционной матрицей случайного вектора называется нормированная ковариационная матрица
Пример №7
Дано уравнение парной регрессии 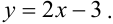
Решение.
Из рассмотрения исключаем 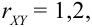
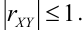
Замечание. Можно было знак 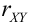
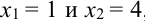
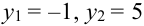
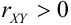
Пример №8
Дано уравнение парной регрессии 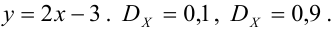
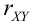
Решение.
Из формулы 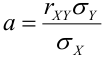
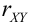
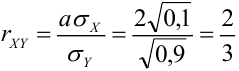
Свойства математического ожидания и дисперсии
1. X, Y как зависимые, так и независимые случайные величины, тогда
2.
Если X, Y – некоррелированные, то
Если X, Y- независимые, то
3.
Если X, Y- некоррелированные, то
4. Если X, Y-независимые, то
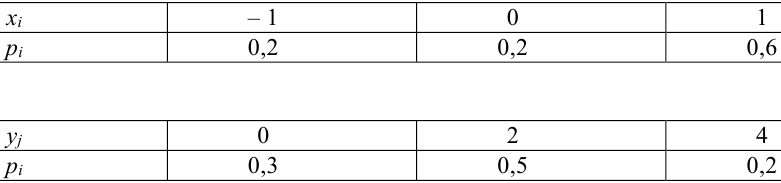
Пример №9
Даны законы распределения случайных величин X, Y:
Найти
Решение.
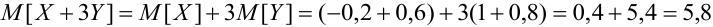
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
- Точечные оценки, свойства оценок
- Алгебра событий – определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Случайные события – определение и вычисление
 будет снова случайной величиной.
будет снова случайной величиной.