Дифференцирование функции, заданной неявно
Известно, что функция
![]() может быть задана неявно уравнением,
может быть задана неявно уравнением,
связывающим переменные![]() и
и![]() :
:
![]() .
.
Например, уравнение
![]() определяет функцию
определяет функцию![]() ,
,
при этомD![]() E
E![]() R.
R.
Уравнение
![]() выполняется только при
выполняется только при![]() и задает точку
и задает точку![]() .
.
Уравнение![]() не определяет никакой функции наR,
не определяет никакой функции наR,
так как оно не имеет действительных
корней, а значит, нельзя рассматривать![]() как функцию от
как функцию от![]() .
.
Итак, уравнение вида
![]() не всегда задает функцию
не всегда задает функцию![]() .
.
Пусть уравнение
![]() определяет
определяет![]()
как некоторую функцию от![]() .
.
Если в это уравнение подставить вместо
у функцию![]() ,
,
то получим тождество
![]() .
.
Придадим
![]() приращение
приращение![]() ,
,
тогда значению аргумента будет
соответствовать значение функции![]() ,
,
но с другой стороны
![]() .
.
Разность
![]() также равна нулю:
также равна нулю:
![]() .
.
Как было показано выше, ее полное
приращение в этой точке можно представить
в виде
![]() .
.
Разделим последнее равенство на
![]() :
:
![]() .
.
Откуда
![]() .
.
Перейдя к пределу, получим формулу
вычисления производной функции, заданной
неявно:
![]() .
.
Аналогично можно вычислить частные
производные неявной функции
![]() переменных по всем ее аргументам.
переменных по всем ее аргументам.
Например, для функции
![]() справедливо:
справедливо:
![]() ,
,![]() .
.
Пример. Вычислить производную
неявной функции, заданной уравнением![]() .
.
Решение.Обозначим левую часть
данного уравнения через![]() .
.
![]() ,
,![]() .
.
Следовательно,
![]() .
.
Пример. Вычислить производную
неявной функции, заданной уравнением![]() .
.
Решение.Обозначим левую часть
данного уравнения через![]() .
.
![]() ,
,![]() .
.
Следовательно,
![]() .
.
Пример. Найти частные производные
неявной функции![]() ,
,
заданной уравнением![]() .
.
Решение.![]() ,
,![]() ,
,![]() .
.
Следовательно,
![]() ,
,
![]() .
.
Частные производные и дифференциалы высших порядков
Частные производные высших порядков.
Пусть функция![]()
имеет непрерывные частные производные![]() и
и![]()
в точке![]()
![]() D(
D(![]() ).
).
Эти производные, в свою очередь,
являются функциями двух переменных![]()
и![]() .
.
Будем называть![]()
и![]() частными производными первого порядка.
частными производными первого порядка.
Частные производные по
![]()
и по![]()
от частных производных первого
порядка, если они существуют, называются
частными производными второго порядка
от функции![]()
в точке![]()
и обозначаются
![]() ,
,![]() ,
,![]() ,
,![]()
(если
![]() дифференцируется последовательно два
дифференцируется последовательно два
раза по![]() );
);
![]() ,
,![]() ,
,![]() ,
,![]()
(если
![]() дифференцируется сначала по
дифференцируется сначала по![]() ,
,
а затем по![]() );
);
![]() ,
,![]() ,
,![]() ,
,![]()
(если
![]() дифференцируется сначала по
дифференцируется сначала по![]() ,
,
а затем по![]() );
);
![]() ,
,![]() ,
,![]() ,
,![]()
(если
![]() дифференцируется последовательно два
дифференцируется последовательно два
раза по![]() ).
).
Производные второго порядка можно снова
дифференцировать как по
![]() ,
,
так и по![]() .
.
В результате получим восемь частных
производных третьего порядка:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Аналогично, частная производная от
производной
![]() -го
-го
порядка называется частной производной![]() -го
-го
порядка и обозначается
![]() ,
,![]() ,
,![]() и т. д.
и т. д.
Частные производные высших порядков
функции
![]() ,
,
взятые по различным переменным,
например,![]() ,
,![]() ,
,![]() ,
,![]() и т.д., называются смешанными производными.
и т.д., называются смешанными производными.
Среди частных производных второго
порядка функции
![]() имеются две смешанные производные
имеются две смешанные производные![]() и
и![]() .
.
Возникает вопрос: зависит ли результат
дифференцирования функций нескольких
переменных от порядка дифференцирования
по разным переменным.
Справедлива следующая
Теорема. Если функция![]() и ее частные производные
и ее частные производные![]() ,
,![]() ,
,![]() и
и![]() определены и непрерывны в точке
определены и непрерывны в точке![]() и в некоторой ее окрестности, то
и в некоторой ее окрестности, то![]() .
.
Замечание.Данная теорема, а также
все приведенные выше рассуждения имеют
место и для функции любого числа
переменных.
Пример. Найти частные производные
второго порядка функции
![]() .
.
Решение.Функция определена и
непрерывна наR2.
Найдем частные производные первого
порядка
![]() ,
,![]() .
.
Они определены и непрерывны на R2.
Найдем частные производные второго
порядка
![]() ,
,![]() ,
,
![]() .
.
Дифференциалы высших порядков. Пусть![]() — функция двух независимых переменных
— функция двух независимых переменных![]() и
и![]() ,
,
дифференцируемая в областиD(![]() ).
).
Придавая![]() и
и![]() приращения
приращения![]() ,
,![]() ,
,
в любой точке![]()
![]() D
D![]() можно найти полный дифференциал
можно найти полный дифференциал
![]() ,
,
который называют дифференциалом
первого порядка функции
![]() .
.
Дифференциал от дифференциала первого
порядка в любой точке
![]()
![]() D
D![]() ,
,
если он существует, называется
дифференциалом второго порядка и
обозначается
![]() .
.
Найдем аналитическое выражение для
![]() ,
,
считая![]() и
и![]() постоянными:
постоянными:
![]()
![]() .
.
Поступая аналогично, получаем аналитическое
выражение для дифференциала третьего
порядка
![]() :
:
![]() .
.
Замечание.Приведенные выше формулы
дифференциалов не обладают свойствами
инвариантности для сложных функций.
Пример. Найти![]() и
и
![]() ,
,
если![]() .
.
Решение.Используем формулу для
вычисления полного дифференциала
![]() .
.
![]() ,
,![]()
![]() .
.
Для определения
![]() вычислим предварительно частные
вычислим предварительно частные
производные второго порядка:
![]() ,
,![]() ,
,![]()
![]() .
.
Соседние файлы в папке Высшая математика
- #
- #
- #
- #
- #
- #
- #
- #
![]()
Частные
производные неявной функции нескольких переменных
Если в уравнении вида ![]()
каждой паре чисел ![]()
и ![]()
из некоторой области соответствует одно или несколько значений ![]() ,
,
удовлетворяющих этому уравнению, то уравнение ![]()
неявно определяет одну или несколько однозначных функций ![]()
от ![]()
и ![]() .
.
В этом случае говорят, что ![]()
есть неявная функция от![]()
и ![]() .
.
Частные производные ![]()
и ![]()
неявной функции находятся по формулам (предполагается, что 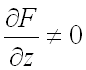 ):
):
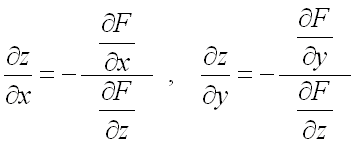
.
Примеры
решения задач
Пример 1.
Найти частные производные первого порядка функции ![]() ,
,
заданной уравнением: 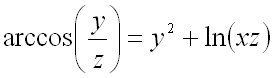 .
.
Решение.
Как известно, частные производные
![]()
и ![]()
неявной функции ![]() ,
,
заданной уравнением вида ![]() ,
,
находятся по формулам:
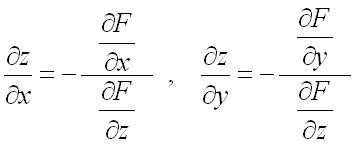 ,
,
где предполагается, что 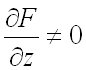 .
.
В нашем случае для решения задачи сначала необходимо преобразовать формулу,
задающую функцию ![]() ,
,
к виду ![]() :
:
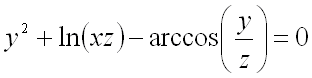 .
.
Найдем частную производную
![]() :
:
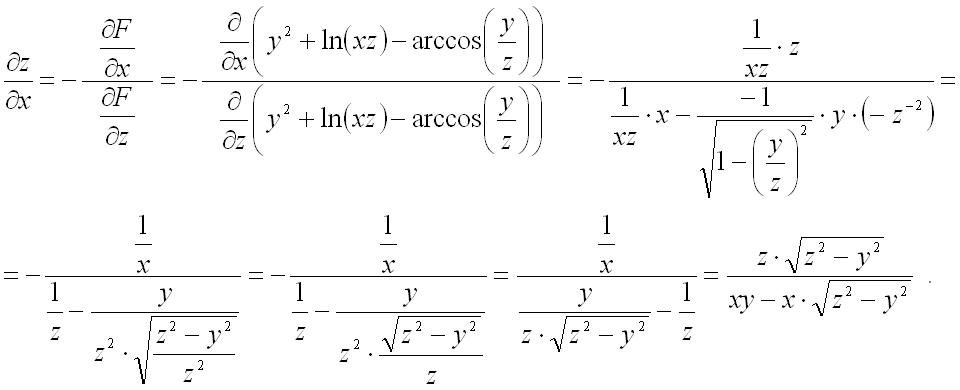
При вычислении второй частной
производной первого порядка в знаменателе дроби сразу подставим результат, полученный
для ![]()
из первой частной производной с учетом смены знака:
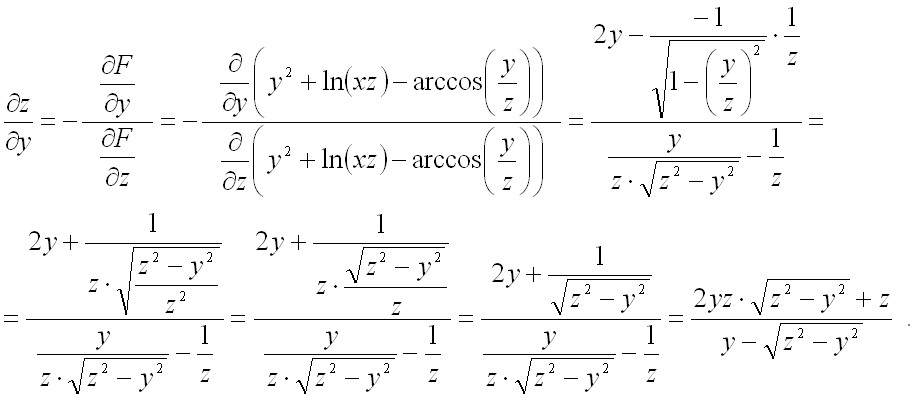
Ответ: 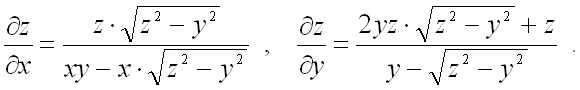
![]()
![]()
Производная неявной функции онлайн
Неявная функция – это функция, например , заданная в виде уравнения:
F ( x , y ( x ) ) = 0
Как правило, вместо уравнения F ( x , y ( x ) ) = 0 пишут просто F ( x , y ) = 0 подразумевая, что есть функция от .
В качестве примера неявного задания функции, можно привести уравнение окружности:
уравнение декартового листа:
x 3 + y 3 = 3 ∙ a ∙ x ∙ y ( a = const ≠ 0 ) ,
и т.д. Все эти примеры можно записать в виде уравнения F ( x , y ) = 0 : уравнение окружности: F ( x , y ) = x 2 + y 2 − a 2 = 0 , уравнение декартового листа: F ( x , y ) = x 3 + y 3 − 3 ∙ a ∙ x ∙ y = 0 .
В связи с тем, что для исследования любой функции (в том числе и заданной неявно) необходимо вычислять производную, задача нахождения производной функции заданной неявно возникает довольно часто. Так, как же найти производную неявной функции? Исчерпывающий ответ на этот вопрос вы получите, воспользовавшись нашим онлайн калькулятором.
Для того, чтобы решить вашу задачу, для начала перепишите свою функцию в виде уравнения F ( x , y ) = 0 . Как это сделать, подробно описано выше (нужно просто перенести все слагаемые в левую часть уравнения, оставив справа ). Далее вам необходимо определиться, как у вас обозначается переменная и как обозначается функция, которая зависит от этой переменной. В приведенных выше примерах, – переменная, – функция, зависящая от .
Затем, вам необходимо ввести свое уравнение F ( x , y ) в наш онлайн калькулятор и получить решение вашей задачи.
Частные производные
Назначение сервиса . Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word .
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
- Примеры
x 2 +xy ≡ x^2+x*y .
cos 2 (2x+y) ≡ (cos(2*x+y))^2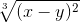 ≡ (x-y)^(2/3)
≡ (x-y)^(2/3)
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
- Примеры
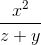 ≡ x^2/(z+y)
≡ x^2/(z+y)
cos 2 (2x+zy) ≡ (cos(2*x+z*y))^2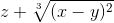 ≡ z+(x-y)^(2/3)
≡ z+(x-y)^(2/3)
Частные производные функции нескольких переменных
Пример 1 . z=2x 5 +3x 2 y+y 2 –4x+5y-1
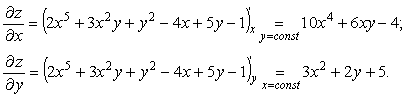
Пример 2 . Найти частные производные 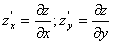 функции z = f(x;y) в точке A(x0;y0).
функции z = f(x;y) в точке A(x0;y0).

Находим частные производные:


Найдем частные производные в точке А(1;1)


Находим вторые частные производные:
Производная функции, заданной неявно
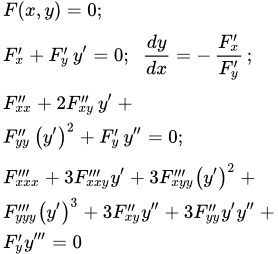
Производная первого порядка
Пусть функция задана неявным образом с помощью уравнения
(1) .
И пусть это уравнение, при некотором значении , имеет единственное решение . Пусть функция является дифференцируемой функцией в точке , причем
.
Тогда, при этом значении , существует производная , которая определяется по формуле:
(2) .
Доказательство
Для доказательства рассмотрим функцию как сложную функцию от переменной :
.
Применим правило дифференцирования сложной функции и найдем производную по переменной от левой и правой частей уравнения
(3) :
.
Поскольку производная от постоянной равна нулю и , то
(4) ;
.
Производные высших порядков
Перепишем уравнение (4), используя другие обозначения:
(4) .
При этом и являются сложными функциями от переменной :
;
.
Зависимость определяет уравнение (1):
(1) .
Поскольку производная правой части уравнения (4) равна нулю, то
(5) .
Подставив сюда производную , получим значение производной второго порядка в неявном виде.
Дифференцируя, аналогичным образом, уравнение (5), мы получим уравнение, содержащее производную третьего порядка :
.
Подставив сюда найденные значения производных первого и второго порядков, найдем значение производной третьего порядка.
Продолжая дифференцирование, можно найти производную любого порядка.
Примеры
Пример 1
Найдите производную первого порядка от функции, заданной неявно уравнением:
(П1) .
Решение по формуле 2
Находим производную по формуле (2):
(2) .
Перенесем все переменные в левую часть, чтобы уравнение приняло вид .
.
Отсюда .
Находим производную по , считая постоянной.
;
;
;
.
Находим производную по переменной , считая переменную постоянной.
;
;
;
.
По формуле (2) находим:
.
Мы можем упростить результат если заметим, что согласно исходному уравнению (П.1), . Подставим :
.
Умножим числитель и знаменатель на :
.
Решение вторым способом
Решим этот пример вторым способом. Для этого найдем производную по переменной левой и правой частей исходного уравнения (П1).
Подставим (из уравнения (П1)):
.
Умножим на :
.
Пример 2
Найти производную второго порядка от функции , заданной неявно с помощью уравнения:
(П2.1) .
Дифференцируем исходное уравнение, по переменной , считая что является функцией от :
;
.
Применяем формулу производной сложной функции.
.
Дифференцируем исходное уравнение (П2.1):
;
.
Из исходного уравнения (П2.1) следует, что . Подставим :
.
Раскрываем скобки и группируем члены:
;
(П2.2) .
Находим производную первого порядка:
(П2.3) .
Чтобы найти производную второго порядка, дифференцируем уравнение (П2.2).
;
;
;
.
Подставим выражение производной первого порядка (П2.3):
.
Умножим на :
;
.
Отсюда находим производную второго порядка.
Пример 3
Найти производную третьего порядка при от функции , заданной неявно с помощью уравнения:
(П3.1) .
Дифференцируем исходное уравнение по переменной считая, что является функцией от .
;
;
;
;
;
;
(П3.2) ;
Дифференцируем уравнение (П3.2) по переменной .
;
;
;
;
;
(П3.3) .
Из уравнений (П3.2), (П3.3) и (П3.4) находим значения производных при .
;
;
.
Автор: Олег Одинцов . Опубликовано: 16-02-2017
[spoiler title=”источники:”]
http://math.semestr.ru/math/derivatives.php
http://1cov-edu.ru/mat_analiz/proizvodnaya/nayti/neyavnoy-funktsii/
[/spoiler]
Явные и неявные
В этой статье мы познакомимся с неявными функциями и техникой их дифференцирования. Вспомним для начала, как выглядят функции, заданные явно. Это “обычные” функции вида y=f(x)y=f(x), с которыми вы уже имели дело и умеете вычислять их производные. Запись y=f(x)y=f(x) обозначает, что мы функцию yy смогли выразить (явно представить) через её аргумент xx. З неявными функциями дело обстоит иначе. Здесь мы не можем “перетащить” yy в левую сторону выражения, а все что содержит xx — в правую. Такие функциональные зависимости в общем виде можно записать так:
F(x,y)=0F(x, y)=0
Эта запись означает, что величины xx и yy как-то связанны между собой, но ничего не говорится о том, как yy выражается через xx (и можно ли это вообще сделать). Одну и ту же функцию (но не каждую) можно записать как в явном так и в неявном виде. Например, неявно заданную функцию F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x} можно записать явно: y(x)=−53x2y(x)=-frac{5}{3x^2}. В этом случае нам удалось выразить yy через xx. Или, если:
F(x,y)=x2+y2−1=0F(x, y)=x^2+y^2-1=0
то
y=±1−x2y=pm sqrt{1-x^2}
Здесь функция получилась многозадачной (именно двузначной, отвечающей двум знакам), но это не страшно. Мы все-равно представили yy как выражение зависящее от xx. В правой стороне у нас присутствует только xx.
Но существуют случаи, когда этого сделать нельзя. Можно навести множество примеров таких функций. Например:
F(x,y)=ylnx+eyy2F(x, y)=yln x+e^yy^2
Ну попробуйте выразить отсюда yy через xx. То есть запишите эту функцию в виде y=f(x)y=f(x). Вот вам и пример неявной заданной функции. Ещё пример:
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
Здесь, мы хотя и не можем выразить yy через xx, но мы все-равно можем считать yy функцией от аргумента xx. Так как каждому значению xx будут соответствовать какие-то значения yy.
Естественно, возникает вопрос о дифференцировании подобных функций. Вы уже понимаете, что эта операция очень важна, и было бы тяжело поверить, что математики ничего не придумали на этот счет.
Дифференцирование неявно заданных функций
Оказывается, что для того чтобы посчитать производную от yy по xx нам не обязательно решать уравнение:
F(x,y)=0F(x, y)=0
Теоретически можно доказать (пользуюсь определением производной, производя предельный переход и т. д.), что:
dydx=−∂F(x,y)∂x∂F(x,y)∂yfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}
Обозначение ∂partial обозначает частную производную. Мы здесь имеем дело с двумя переменными xx и yy и берем производные от функции F(x,y)F(x, y) по этим величинам. Так, выражение:
∂F(x,y)∂xfrac{partial F(x, y)}{partial x}
говорит, что берется производная от F(x,y)F(x, y) по xx, при этом величина yy считается постоянной. Следует обратить внимание на знак “минус” перед дробью, а также на то, что мы не можем сократить числитель и знаменатель на ∂F(x,y)partial F(x, y), так как производные берутся по разным величинам. Вооружившись этой главной формулой вычисления производных от неявных функций, перейдем к разбору нескольких примеров.
Примеры
F(x,y)=x2+y2−1F(x, y)=x^2+y^2-1
∂F(x,y)∂x=2x, ∂F(x,y)∂y=2yfrac{partial F(x, y)}{partial x}=2x, frac{partial F(x, y)}{partial y}=2y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−2x2y=−xyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{2x}{2y}=-frac{x}{y}
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
∂F(x,y)∂x=sinx+xcosx, ∂F(x,y)∂y=siny+ycosyfrac{partial F(x, y)}{partial x}=sin x+x cos x, frac{partial F(x, y)}{partial y}=sin y+y cos y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−sinx+xcosxsiny+ycosyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{sin x+xcos x}{sin y+ycos y}
- F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x}
∂F(x,y)∂x=3y−5×2, ∂F(x,y)∂y=3xfrac{partial F(x, y)}{partial x}=3y-frac{5}{x^2}, frac{partial F(x, y)}{partial y}=3x
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−3y−5x23x=−3yx2−53x3frac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{3y-frac{5}{x^2}}{3x}=-frac{3yx^2-5}{3x^3}
Но здесь мы можем выразить yy через xx явно:
y=−53x2y=-frac{5}{3x^2}
Подставим это выражение в формулу для производной выше:
dydx=103x3frac{dy}{dx}=frac{10}{3x^3}
А теперь поступим так, как будто нам с самого начала была известна явная зависимость y=f(x)y=f(x). То есть продифференцируем функцию y(x)=−53x2y(x)=-frac{5}{3x^2} по xx:
dydx=ddx(−53×2)=−53(−2)1×3=103x3frac{dy}{dx}=frac{d}{dx}Big(-frac{5}{3x^2}Big)=-frac{5}{3}(-2)frac{1}{x^3}=frac{10}{3x^3}
Получили то же самое. Значит мы все сделали правильно.
Частные производные
Частные производные применяются в заданиях с функциями нескольких переменных. Правила нахождения точно такие же как и для функций одной переменной, с разницей лишь в том, что одну из переменных нужно считать в момент дифференцирования константой (постоянным числом).
Формула
Частные производные для функции двух переменных $ z(x,y) $ записываются в следующем виде $ z’_x, z’_y $ и находятся по формулам:
Частные производные первого порядка
$$ z’_x = frac{partial z}{partial x} $$
$$ z’_y = frac{partial z}{partial y} $$
Частные производные второго порядка
$$ z”_{xx} = frac{partial^2 z}{partial x partial x} $$
$$ z”_{yy} = frac{partial^2 z}{partial y partial y} $$
Смешанная производная
$$ z”_{xy} = frac{partial^2 z}{partial x partial y} $$
$$ z”_{yx} = frac{partial^2 z}{partial y partial x} $$
Частная производная сложной функции
а) Пусть $ z (t) = f( x(t), y(t) ) $, тогда производная сложной функции определяется по формуле:
$$ frac{dz}{dt} = frac{partial z}{partial x} cdot frac{dx}{dt} + frac{partial z}{partial y} cdot frac{dy}{dt} $$
б) Пусть $ z (u,v) = z(x(u,v),y(u,v)) $, тогда частные производные функции находится по формуле:
$$ frac{partial z}{partial u} = frac{partial z}{partial x} cdot frac{partial x}{partial u} + frac{partial z}{partial y} cdot frac{partial y}{partial u} $$
$$ frac{partial z}{partial v} = frac{partial z}{partial x} cdot frac{partial x}{partial v} + frac{partial z}{partial y} cdot frac{partial y}{partial v} $$
Частные производные неявно заданной функции
а) Пусть $ F(x,y(x)) = 0 $, тогда $$ frac{dy}{dx} = -frac{f’_x}{f’_y} $$
б) Пусть $ F(x,y,z)=0 $, тогда $$ z’_x = – frac{F’_x}{F’_z}; z’_y = – frac{F’_y}{F’_z} $$
Примеры решений
| Пример 1 |
| Найти частные производные первого порядка $ z (x,y) = x^2 – y^2 + 4xy + 10 $ |
| Решение |
|
Для нахождения частной производной по $ x $ будем считать $ y $ постоянной величиной (числом): $$ z’_x = (x^2-y^2+4xy+10)’_x = 2x – 0 + 4y + 0 = 2x+4y $$ Для нахождения частной производной функции по $ y $ определим $ y $ константой: $$ z’_y = (x^2-y^2+4xy+10)’_y = -2y+4x $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ z’_x = 2x+4y; z’_y = -2y+4x $$ |
| Пример 2 |
| Найти частные производные функции второго порядка $ z = e^{xy} $ |
| Решение |
|
Сперва нужно найти первый производные, а затем зная их можно найти производные второго порядка. Полагаем $ y $ константой: $$ z’_x = (e^{xy})’_x = e^{xy} cdot (xy)’_x = ye^{xy} $$ Положим теперь $ x $ постоянной величиной: $$ z’_y = (e^{xy})’_y = e^{xy} cdot (xy)’_y = xe^{xy} $$ Зная первые производные аналогично находим вторые. Устанавливаем $ y $ постоянной: $$ z”_{xx} = (z’_x)’_x = (ye^{xy})’_x = (y)’_x e^{xy} + y(e^{xy})’_x = 0 + ye^{xy}cdot (xy)’_x = y^2e^{xy} $$ Задаем $ x $ постоянной: $$ z”_{yy} = (z’_y)’_y = (xe^{xy})’_y = (x)’_y e^{xy} + x(e^{xy})’_y = 0 + x^2e^{xy} = x^2e^{xy} $$ Теперь осталось найти смешанную производную. Можно продифференцировать $ z’_x $ по $ y $, а можно $ z’_y $ по $ x $, так как по теореме $ z”_{xy} = z”_{yx} $ $$ z”_{xy} = (z’_x)’_y = (ye^{xy})’_y = (y)’_y e^{xy} + y (e^{xy})’_y = ye^{xy}cdot (xy)’_y = yxe^{xy} $$ |
| Ответ |
| $$ z’_x = ye^{xy}; z’_y = xe^{xy}; z”_{xy} = yxe^{xy} $$ |
| Пример 3 |
| Найти частную производную сложной функции $ z = x^2 + y^2, x = sin t, y = t^3 $ |
| Решение |
|
Находим $ frac{partial z}{partial x} $: $$ frac{partial z}{partial x} = (x^2+y^2)’_x = 2x $$ Находим $ frac{partial z}{partial y} $: $$ frac{partial z}{partial y} = (x^2+y^2)’_y = 2y $$ Теперь ищем $ frac{dx}{dt} $ и $ frac{dy}{dt} $: $$ frac{dx}{dt} = frac{d(sin t)}{dt} = cos t $$ $$ frac{dy}{dt} = frac{d(t^3)}{dt} = 3t^2 $$ Подставляем всё это в формулу и записываем ответ: $$ frac{dz}{dt} = frac{partial z}{partial x} cdot frac{dx}{dt} + frac{partial z}{partial y} cdot frac{dy}{dt} $$ $$ frac{dz}{dt} = 2x cdot cos t + 2y cdot 3t^2 $$ |
| Ответ |
| $$ frac{dz}{dt} = 2x cdot cos t + 2y cdot 3t^2 $$ |
| Пример 4 |
| Пусть $ 3x^3z – 2z^2 + 3yz^2-4x+z-5 = 0 $ задаёт неявную функцию $ F(x,y,z) = 0 $. Найти частные производные первого порядка. |
| Решение |
|
Записываем функцию в формате: $ F(x,y,z) = 3x^3z – 2z^2 + 3yz^2-4x+z-5 = 0 $ и находим производные: $$ z’_x (y,z – const) = (x^3 z – 2z^2 + 3yz^2-4x+z-5)’_x = 3 x^2 z – 4 $$ $$ z’_y (x,y – const) = (x^3 z – 2z^2 + 3yz^2-4x+z-5)’_y = 3z^2 $$ |
| Ответ |
| $$ z’_x = 3x^2 z – 4; z’_y = 3z^2; $$ |
