Частные производные
Частные производные применяются в заданиях с функциями нескольких переменных. Правила нахождения точно такие же как и для функций одной переменной, с разницей лишь в том, что одну из переменных нужно считать в момент дифференцирования константой (постоянным числом).
Формула
Частные производные для функции двух переменных $ z(x,y) $ записываются в следующем виде $ z’_x, z’_y $ и находятся по формулам:
Частные производные первого порядка
$$ z’_x = frac{partial z}{partial x} $$
$$ z’_y = frac{partial z}{partial y} $$
Частные производные второго порядка
$$ z”_{xx} = frac{partial^2 z}{partial x partial x} $$
$$ z”_{yy} = frac{partial^2 z}{partial y partial y} $$
Смешанная производная
$$ z”_{xy} = frac{partial^2 z}{partial x partial y} $$
$$ z”_{yx} = frac{partial^2 z}{partial y partial x} $$
Частная производная сложной функции
а) Пусть $ z (t) = f( x(t), y(t) ) $, тогда производная сложной функции определяется по формуле:
$$ frac{dz}{dt} = frac{partial z}{partial x} cdot frac{dx}{dt} + frac{partial z}{partial y} cdot frac{dy}{dt} $$
б) Пусть $ z (u,v) = z(x(u,v),y(u,v)) $, тогда частные производные функции находится по формуле:
$$ frac{partial z}{partial u} = frac{partial z}{partial x} cdot frac{partial x}{partial u} + frac{partial z}{partial y} cdot frac{partial y}{partial u} $$
$$ frac{partial z}{partial v} = frac{partial z}{partial x} cdot frac{partial x}{partial v} + frac{partial z}{partial y} cdot frac{partial y}{partial v} $$
Частные производные неявно заданной функции
а) Пусть $ F(x,y(x)) = 0 $, тогда $$ frac{dy}{dx} = -frac{f’_x}{f’_y} $$
б) Пусть $ F(x,y,z)=0 $, тогда $$ z’_x = – frac{F’_x}{F’_z}; z’_y = – frac{F’_y}{F’_z} $$
Примеры решений
| Пример 1 |
| Найти частные производные первого порядка $ z (x,y) = x^2 – y^2 + 4xy + 10 $ |
| Решение |
|
Для нахождения частной производной по $ x $ будем считать $ y $ постоянной величиной (числом): $$ z’_x = (x^2-y^2+4xy+10)’_x = 2x – 0 + 4y + 0 = 2x+4y $$ Для нахождения частной производной функции по $ y $ определим $ y $ константой: $$ z’_y = (x^2-y^2+4xy+10)’_y = -2y+4x $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ z’_x = 2x+4y; z’_y = -2y+4x $$ |
| Пример 2 |
| Найти частные производные функции второго порядка $ z = e^{xy} $ |
| Решение |
|
Сперва нужно найти первый производные, а затем зная их можно найти производные второго порядка. Полагаем $ y $ константой: $$ z’_x = (e^{xy})’_x = e^{xy} cdot (xy)’_x = ye^{xy} $$ Положим теперь $ x $ постоянной величиной: $$ z’_y = (e^{xy})’_y = e^{xy} cdot (xy)’_y = xe^{xy} $$ Зная первые производные аналогично находим вторые. Устанавливаем $ y $ постоянной: $$ z”_{xx} = (z’_x)’_x = (ye^{xy})’_x = (y)’_x e^{xy} + y(e^{xy})’_x = 0 + ye^{xy}cdot (xy)’_x = y^2e^{xy} $$ Задаем $ x $ постоянной: $$ z”_{yy} = (z’_y)’_y = (xe^{xy})’_y = (x)’_y e^{xy} + x(e^{xy})’_y = 0 + x^2e^{xy} = x^2e^{xy} $$ Теперь осталось найти смешанную производную. Можно продифференцировать $ z’_x $ по $ y $, а можно $ z’_y $ по $ x $, так как по теореме $ z”_{xy} = z”_{yx} $ $$ z”_{xy} = (z’_x)’_y = (ye^{xy})’_y = (y)’_y e^{xy} + y (e^{xy})’_y = ye^{xy}cdot (xy)’_y = yxe^{xy} $$ |
| Ответ |
| $$ z’_x = ye^{xy}; z’_y = xe^{xy}; z”_{xy} = yxe^{xy} $$ |
| Пример 3 |
| Найти частную производную сложной функции $ z = x^2 + y^2, x = sin t, y = t^3 $ |
| Решение |
|
Находим $ frac{partial z}{partial x} $: $$ frac{partial z}{partial x} = (x^2+y^2)’_x = 2x $$ Находим $ frac{partial z}{partial y} $: $$ frac{partial z}{partial y} = (x^2+y^2)’_y = 2y $$ Теперь ищем $ frac{dx}{dt} $ и $ frac{dy}{dt} $: $$ frac{dx}{dt} = frac{d(sin t)}{dt} = cos t $$ $$ frac{dy}{dt} = frac{d(t^3)}{dt} = 3t^2 $$ Подставляем всё это в формулу и записываем ответ: $$ frac{dz}{dt} = frac{partial z}{partial x} cdot frac{dx}{dt} + frac{partial z}{partial y} cdot frac{dy}{dt} $$ $$ frac{dz}{dt} = 2x cdot cos t + 2y cdot 3t^2 $$ |
| Ответ |
| $$ frac{dz}{dt} = 2x cdot cos t + 2y cdot 3t^2 $$ |
| Пример 4 |
| Пусть $ 3x^3z – 2z^2 + 3yz^2-4x+z-5 = 0 $ задаёт неявную функцию $ F(x,y,z) = 0 $. Найти частные производные первого порядка. |
| Решение |
|
Записываем функцию в формате: $ F(x,y,z) = 3x^3z – 2z^2 + 3yz^2-4x+z-5 = 0 $ и находим производные: $$ z’_x (y,z – const) = (x^3 z – 2z^2 + 3yz^2-4x+z-5)’_x = 3 x^2 z – 4 $$ $$ z’_y (x,y – const) = (x^3 z – 2z^2 + 3yz^2-4x+z-5)’_y = 3z^2 $$ |
| Ответ |
| $$ z’_x = 3x^2 z – 4; z’_y = 3z^2; $$ |
Дифференцирование функции, заданной неявно
Известно, что функция
![]() может быть задана неявно уравнением,
может быть задана неявно уравнением,
связывающим переменные![]() и
и![]() :
:
![]() .
.
Например, уравнение
![]() определяет функцию
определяет функцию![]() ,
,
при этомD![]() E
E![]() R.
R.
Уравнение
![]() выполняется только при
выполняется только при![]() и задает точку
и задает точку![]() .
.
Уравнение![]() не определяет никакой функции наR,
не определяет никакой функции наR,
так как оно не имеет действительных
корней, а значит, нельзя рассматривать![]() как функцию от
как функцию от![]() .
.
Итак, уравнение вида
![]() не всегда задает функцию
не всегда задает функцию![]() .
.
Пусть уравнение
![]() определяет
определяет![]()
как некоторую функцию от![]() .
.
Если в это уравнение подставить вместо
у функцию![]() ,
,
то получим тождество
![]() .
.
Придадим
![]() приращение
приращение![]() ,
,
тогда значению аргумента будет
соответствовать значение функции![]() ,
,
но с другой стороны
![]() .
.
Разность
![]() также равна нулю:
также равна нулю:
![]() .
.
Как было показано выше, ее полное
приращение в этой точке можно представить
в виде
![]() .
.
Разделим последнее равенство на
![]() :
:
![]() .
.
Откуда
![]() .
.
Перейдя к пределу, получим формулу
вычисления производной функции, заданной
неявно:
![]() .
.
Аналогично можно вычислить частные
производные неявной функции
![]() переменных по всем ее аргументам.
переменных по всем ее аргументам.
Например, для функции
![]() справедливо:
справедливо:
![]() ,
,![]() .
.
Пример. Вычислить производную
неявной функции, заданной уравнением![]() .
.
Решение.Обозначим левую часть
данного уравнения через![]() .
.
![]() ,
,![]() .
.
Следовательно,
![]() .
.
Пример. Вычислить производную
неявной функции, заданной уравнением![]() .
.
Решение.Обозначим левую часть
данного уравнения через![]() .
.
![]() ,
,![]() .
.
Следовательно,
![]() .
.
Пример. Найти частные производные
неявной функции![]() ,
,
заданной уравнением![]() .
.
Решение.![]() ,
,![]() ,
,![]() .
.
Следовательно,
![]() ,
,
![]() .
.
Частные производные и дифференциалы высших порядков
Частные производные высших порядков.
Пусть функция![]()
имеет непрерывные частные производные![]() и
и![]()
в точке![]()
![]() D(
D(![]() ).
).
Эти производные, в свою очередь,
являются функциями двух переменных![]()
и![]() .
.
Будем называть![]()
и![]() частными производными первого порядка.
частными производными первого порядка.
Частные производные по
![]()
и по![]()
от частных производных первого
порядка, если они существуют, называются
частными производными второго порядка
от функции![]()
в точке![]()
и обозначаются
![]() ,
,![]() ,
,![]() ,
,![]()
(если
![]() дифференцируется последовательно два
дифференцируется последовательно два
раза по![]() );
);
![]() ,
,![]() ,
,![]() ,
,![]()
(если
![]() дифференцируется сначала по
дифференцируется сначала по![]() ,
,
а затем по![]() );
);
![]() ,
,![]() ,
,![]() ,
,![]()
(если
![]() дифференцируется сначала по
дифференцируется сначала по![]() ,
,
а затем по![]() );
);
![]() ,
,![]() ,
,![]() ,
,![]()
(если
![]() дифференцируется последовательно два
дифференцируется последовательно два
раза по![]() ).
).
Производные второго порядка можно снова
дифференцировать как по
![]() ,
,
так и по![]() .
.
В результате получим восемь частных
производных третьего порядка:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Аналогично, частная производная от
производной
![]() -го
-го
порядка называется частной производной![]() -го
-го
порядка и обозначается
![]() ,
,![]() ,
,![]() и т. д.
и т. д.
Частные производные высших порядков
функции
![]() ,
,
взятые по различным переменным,
например,![]() ,
,![]() ,
,![]() ,
,![]() и т.д., называются смешанными производными.
и т.д., называются смешанными производными.
Среди частных производных второго
порядка функции
![]() имеются две смешанные производные
имеются две смешанные производные![]() и
и![]() .
.
Возникает вопрос: зависит ли результат
дифференцирования функций нескольких
переменных от порядка дифференцирования
по разным переменным.
Справедлива следующая
Теорема. Если функция![]() и ее частные производные
и ее частные производные![]() ,
,![]() ,
,![]() и
и![]() определены и непрерывны в точке
определены и непрерывны в точке![]() и в некоторой ее окрестности, то
и в некоторой ее окрестности, то![]() .
.
Замечание.Данная теорема, а также
все приведенные выше рассуждения имеют
место и для функции любого числа
переменных.
Пример. Найти частные производные
второго порядка функции
![]() .
.
Решение.Функция определена и
непрерывна наR2.
Найдем частные производные первого
порядка
![]() ,
,![]() .
.
Они определены и непрерывны на R2.
Найдем частные производные второго
порядка
![]() ,
,![]() ,
,
![]() .
.
Дифференциалы высших порядков. Пусть![]() — функция двух независимых переменных
— функция двух независимых переменных![]() и
и![]() ,
,
дифференцируемая в областиD(![]() ).
).
Придавая![]() и
и![]() приращения
приращения![]() ,
,![]() ,
,
в любой точке![]()
![]() D
D![]() можно найти полный дифференциал
можно найти полный дифференциал
![]() ,
,
который называют дифференциалом
первого порядка функции
![]() .
.
Дифференциал от дифференциала первого
порядка в любой точке
![]()
![]() D
D![]() ,
,
если он существует, называется
дифференциалом второго порядка и
обозначается
![]() .
.
Найдем аналитическое выражение для
![]() ,
,
считая![]() и
и![]() постоянными:
постоянными:
![]()
![]() .
.
Поступая аналогично, получаем аналитическое
выражение для дифференциала третьего
порядка
![]() :
:
![]() .
.
Замечание.Приведенные выше формулы
дифференциалов не обладают свойствами
инвариантности для сложных функций.
Пример. Найти![]() и
и
![]() ,
,
если![]() .
.
Решение.Используем формулу для
вычисления полного дифференциала
![]() .
.
![]() ,
,![]()
![]() .
.
Для определения
![]() вычислим предварительно частные
вычислим предварительно частные
производные второго порядка:
![]() ,
,![]() ,
,![]()
![]() .
.
Соседние файлы в папке Высшая математика
- #
- #
- #
- #
- #
- #
- #
- #
![]()
Частные
производные неявной функции нескольких переменных
Если в уравнении вида ![]()
каждой паре чисел ![]()
и ![]()
из некоторой области соответствует одно или несколько значений ![]() ,
,
удовлетворяющих этому уравнению, то уравнение ![]()
неявно определяет одну или несколько однозначных функций ![]()
от ![]()
и ![]() .
.
В этом случае говорят, что ![]()
есть неявная функция от![]()
и ![]() .
.
Частные производные ![]()
и ![]()
неявной функции находятся по формулам (предполагается, что 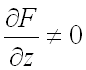 ):
):
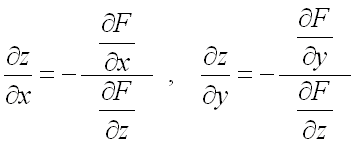
.
Примеры
решения задач
Пример 1.
Найти частные производные первого порядка функции ![]() ,
,
заданной уравнением: 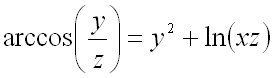 .
.
Решение.
Как известно, частные производные
![]()
и ![]()
неявной функции ![]() ,
,
заданной уравнением вида ![]() ,
,
находятся по формулам:
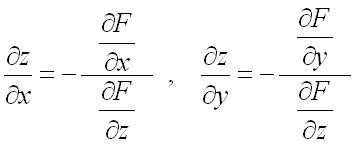 ,
,
где предполагается, что 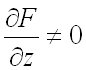 .
.
В нашем случае для решения задачи сначала необходимо преобразовать формулу,
задающую функцию ![]() ,
,
к виду ![]() :
:
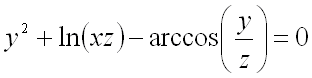 .
.
Найдем частную производную
![]() :
:
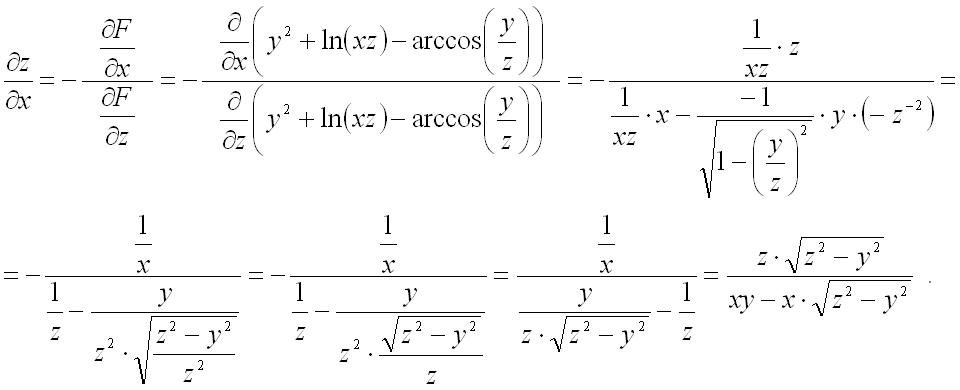
При вычислении второй частной
производной первого порядка в знаменателе дроби сразу подставим результат, полученный
для ![]()
из первой частной производной с учетом смены знака:
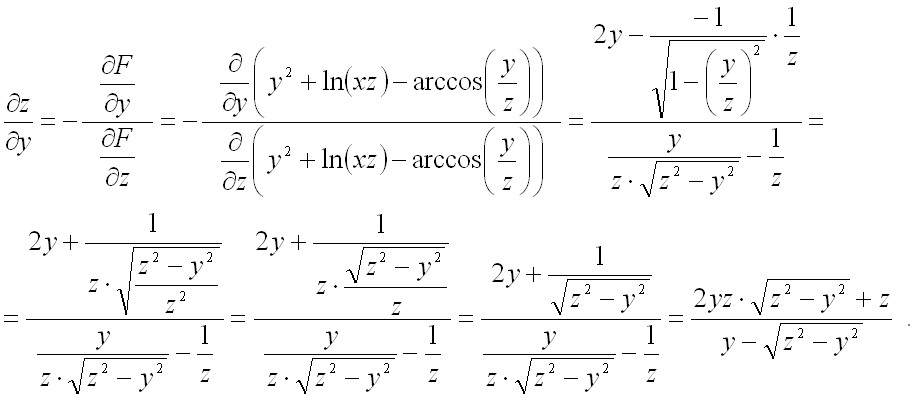
Ответ: 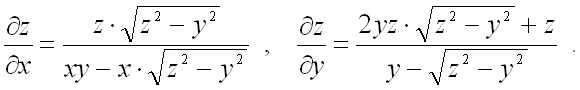
![]()
![]()
Чтобы понять частные производные, сначала нужно разобраться с обычными. И не нужно ничего искать: в нашей отдельной статье мы уже подготовили все для того, чтобы у вас это получилось. А сейчас речь пойдет о частных производных.
Добро пожаловать на наш телеграм-канал за полезной рассылкой и актуальными студенческими новостями.
Функция двух и более переменных
Прежде чем говорить о частных производных, нужно затронуть понятие функции нескольких переменных, без которого нет смысла в частной производной. В школе мы привыкли иметь дело с функциями одной переменной:
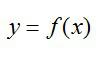
Производными таких функций мы и считали раньше. График функции одной переменной представляет собой линию на плоскости: прямую, параболу, гиперболу и т.д.
А что, если добавить еще одну переменную? Получится такая функция:
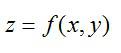
Это – функция двух независимых переменных x и y. График такой функции представляет собой поверхность в трехмерном пространстве: шар, гиперболоид, параболоид или еще какой-нибудь сферический конь в вакууме. Частные производные функции z по иксу и игреку соответственно записываются так:
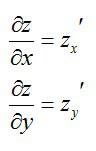
Существуют также функции трех и более переменных. Правда, график такой функции нарисовать невозможно: для этого понадобилось бы как минимум четырехмерное пространство, которое невозможно изобразить.
Частная производная первого порядка
Запоминаем главное правило:
При вычислении частной производной по одной из переменных, вторая переменная принимается за константу. В остальном правила вычисления производной не меняются.
То есть, частная производная по сути ничем не отличается от обычной. Так что, держите перед глазами таблицу производных элементарных функций и правила вычисления обычных производных. Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции:
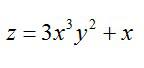
Сначала возьмем частную производную по иксу, считая игрек обычным числом:
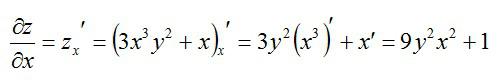
Теперь считаем частную производную по игреку, принимая икс за константу:
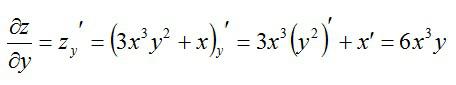
Как видите, ничего сложного в этом нет, а успех с более сложными примерами – лишь дело практики.
Частная производная второго порядка
Как находится частная производная второго порядка? Так же, как и первого. Чтобы найти частные производные второго порядка, нужно просто взять производную от производной первого порядка. Вернемся к примеру выше и посчитаем частные производные второго порядка.
По иксу:
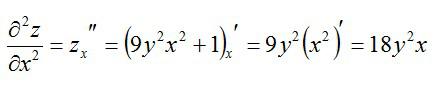
По игреку:
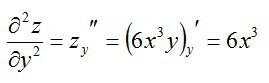
Частные производные третьего и высших порядков не отличаются по принципу вычисления. Систематизируем правила:
- При дифференцировании по одной независимой переменной, вторая принимается за константу.
- Производная второго порядка – это производная от производной первого порядка. Третьего порядка – производная от производной второго порядка и т.д.
Частные производные и полный дифференциал функции
Частый вопрос в практических заданиях – нахождение полного дифференциала функции. Для функции нескольких переменных полный дифференциал определяется, как главная линейная часть малого полного приращения функции относительно приращений аргументов.
Определение звучит громоздко, но с буквами все проще. Полный дифференциал первого порядка функции нескольких переменных выглядит так:
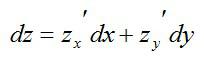
Зная, как считаются частные производные, нет никакой проблемы вычислить и полный дифференциал.
Частные производные – не такая уж и бесполезная тема. Например, дифференциальные уравнения в частных производных второго порядка широко используются для математического описания реальных физических процессов.
Здесь мы дали лишь общее, поверхностное представление о частных производных первого и второго порядка. Вас интересует эта тема или остались конкретные вопросы? Задавайте их в комментариях и обращайтесь к экспертам профессионального студенческого сервиса за квалифицированной и скорой помощью в учебе. С нами вы не останетесь один на один с проблемой!
![]()
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Частные производные
Частной производной по x функции z = f(x,y) в точке A(x0,y0) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.
Частные производные функции z(x,y) находятся по следующим формулам: ![]()
Вторые частные производные функции z(x,y) находятся по формулам:
![]()
Смешанные частные производные функции z(x,y) находятся по формулам: ![]()
Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
x2+xy ≡ x^2+x*y.
cos2(2x+y) ≡ (cos(2*x+y))^2
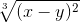 ≡ (x-y)^(2/3)
≡ (x-y)^(2/3)
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
Примеры
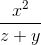 ≡ x^2/(z+y)
≡ x^2/(z+y)
cos2(2x+zy) ≡ (cos(2*x+z*y))^2
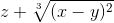 ≡ z+(x-y)^(2/3)
≡ z+(x-y)^(2/3)
Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.
Частные производные функции нескольких переменных
Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δxz=f(x+Δx,y)-f(x,y) – это частное приращение функции z по аргументу x; Δyz=f(x,y+Δy)-f(x,y) – это частное приращение функции z по аргументу у.
Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:
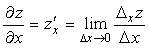 – это частная производная функции z по аргументу x;
– это частная производная функции z по аргументу x;
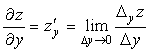 – это частная производная функции z по аргументу у.
– это частная производная функции z по аргументу у.
Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.
Пример 1. z=2x5+3x2y+y2–4x+5y-1
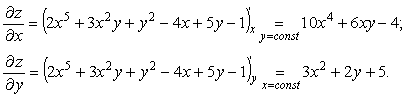
Пример 2. Найти частные производные ![]() функции z = f(x;y) в точке A(x0;y0).
функции z = f(x;y) в точке A(x0;y0).

Находим частные производные:


Найдем частные производные в точке А(1;1)


Находим вторые частные производные:


Найдем смешанные частные производные:

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
