
Чтобы вычислить производную порядка выше 5-го численно, можно последовательно применить несколько раз оператор N-й производной (листинг 3.10), подобно тому, как производится отыскание кратных интегралов (см. разд. 4.3.4). Однако следует помнить о том, что численное определение производных высших порядков производится тем же вычислительным методом Риддера, что и для первых производных. Поскольку, как уже было сказано, для первой производной этот метод обеспечивает точность до 7—8 значащих разрядов числа, при повышении порядка производной на каждую единицу точность падает примерно на один разряд.
ВНИМАНИЕ!
Из сказанного ясно, что падение точности при численном расчете высших производных может быть очень существенно. В частности, если попытаться определить шестую производную функции 1/x, то в качестве результата будет выдан ноль, в то время как истинное значение девятой производной может быть найдено при помощи символьного процессора (листинг 3.10).
Листинг 3.10. Попытка численного поиска шестой производной функции в точке дает неправильный результат
1
|
f(x) |
||||||||
|
x |
||||||||
|
x |
0.1 |
|||||||
|
d |
d5 |
5f(x) |
0 |
|||||
|
dx |
dx |
|||||||
|
d6 |
f(x) 7.20 109 |
|||||||
|
dx6 |
||||||||
С помощью обоих процессоров Mathcad можно вычислять производные функций не только одного, но и любого количества аргументов. Как известно, производные функции нескольких аргументов по одному из них называются частными. Чтобы вычислить частную производную, необходимо, как обычно, ввести оператор производной с панели Математический анализ (Calculus) и в соответствующем местозаполнителе напечатать имя переменной, по которой должно быть осуществлено дифференцирование.
3.4.1. Частные производные
Примеры отыскания частных производных функции двух переменных приведены в листингах 3.11 и 3.12. В первой строке обоих листингов определяется сама функция, а в последующих (символьным или численным образом) рассчитываются ее производные по обеим переменным — x и k. Чтобы определить частную производную в точке, необходимо предварительно задать значения всех аргументов, что и

сделано в следующих строках листинга 3.12. Обратите внимание, что для символьного поиска производной функции нет необходимости задавать значения всех ее аргументов (третья строка листинга 3.12), а вот для численного дифференцирования (последняя строка листинга) должны быть предварительно определены все аргументы функции, иначе вместо результата появится сообщение об ошибке.
Листинг 3.11. Аналитическое вычисление частных производных
f(x  k)
k)  k
k  sin(x)
sin(x)
|
f(x |
k) |
k cos(x) |
||
|
x |
||||
|
f(x |
k) |
sin(x) |
||
|
k |
Листинг 3.12. Символьное и численное вычисления частных производных в точке
f(x  k)
k)  k
k  sin(x) x
sin(x) x  10
10
f(x  k) k
k) k  cos(10)
cos(10)
x
k  1
1
f(x k) 0.839
x
Частные производные высших порядков рассчитываются точно так же, как и обычные производные высших порядков (см. разд. 3.3). Листинг 3.13 иллюстрирует расчет вторых производных функции по переменным x и y, а также смешанной производной.
Листинг 3.13. Вычисление второй частной производной
f(x  y)
y)  y2
y2  x3
x3  y
y  x2
x2
|
2 |
6 y2 x |
||||||
|
f(x |
y) |
2 y |
|||||
|
x2 |
|||||||
|
2 |
2 x3 |
||||||
|
f(x |
y) |
||||||
|
y2 |
|||||||
|
f(x |
y) |
6 y x2 |
2 x |
||||
|
x y |

Возможно, вы обратили внимание, что во всех трех листингах 3.11—3.13 оператор дифференцирования записан в традиционной форме частной производной (с округлыми символами дифференциала). Запись оператора не влияет на вычисления, а служит лишь более привычной формой представления расчетов.
Для того чтобы изменить вид оператора дифференцирования на представление частной производной, следует:
1.Вызвать контекстное меню из области оператора дифференцирования нажатием правой кнопки мыши.
2.Выбрать в контекстном меню верхний пункт Отображать производную как
(View Derivative As).
3.В появившемся подменю (рис. 3.8) выбрать пункт Частную производную
(Partial Derivative).
Рис. 3.8. Изменение вида оператора дифференцирования
Чтобы вернуть вид производной, принятый по умолчанию, выберите в подменю пункт По умолчанию (Default) либо, для представления ее в обычном виде, —
пункт Производную (Derivative).
3.4.2. Примеры: градиент, дивергенция и ротор
Завершим разговор о частных производных несколькими примерами векторного анализа, которые нередко встречаются в вычислительной практике. Программная реализация первого из них, посвященная вычислению градиента функции двух переменных, приведена в листинге 3.14. В качестве примера взята функция f(x,y), определяемая в первой строке листинга, график которой показан на рис. 3.9, в виде линий уровня. Как известно, градиент функции f(x,y) является векторной функцией тех же аргументов, что и f(x,y), определенной через ее частные производные, согласно второй строке листинга 3.14. В его третьей строке производится аналити-

ческое вычисление градиента, а в оставшейся части листинга задаются ранжированные переменные и матрицы, необходимые для подготовки графика линий уровня самой функции и графика векторного поля ее градиента (рис. 3.10).
 ПРИМЕЧАНИЕ
ПРИМЕЧАНИЕ
В Mathcad 14 появился оператор вычисления градиента функции, который записывается следующим образом:
|
y |
0.24 x |
|
x y f(x y) |
( 0.04) y3 |
|
x |
Таким образом, вычисления, приведенные в листинге 3.14, можно записать проще и нагляднее, заменив приведенной формулой вторую и третью строку листинга.
Листинг 3.14. Вычисление градиента функции двух переменных
|
f(x |
y) |
0.12 x2 |
x y |
0.01 y4 |
||||||||
|
f(x |
y) |
|||||||||||
|
x |
||||||||||||
|
grad (x |
y) |
|||||||||||
|
f(x |
y) |
|||||||||||
|
y |
||||||||||||
|
.24 x |
y |
|||||||||||
|
grad(x |
y) |
-2 y3 |
||||||||||
|
x |
4. 10 |
|||||||||||
|
N |
5 |
|||||||||||
|
i |
0 |
2 N |
j |
0 |
2 N |
|||||||
|
Fi |
j |
f(i N j |
N) |
Vi |
j |
grad(i N j N) |
||||||
|
Xi j |
Vi j |
0 |
Yi j |
Vi j |
1 |
|||||||
Как можно убедиться, сравнив графики на рис. 3.9 и 3.10, математический смысл градиента состоит в задании в каждой точке (x,y) направления на плоскости, в котором функция f(x,y) растет наиболее быстро.
Абсолютное значение градиента (т. е. длина вектора в каждой точке) определяет локальную скорость изменения f(x,y). Из сопоставления графиков ясно, что в центре показанной на них области (x,y) сама функция f(x,y) меняется медленно (соответственно, значения ее градиента являются малыми), а в углах — быстро (там значения градиента максимальны).
Очень важно заметить, что градиент является не скалярной, а векторной функцией переменных x,y, поскольку фактически представляет собой комбинацию двух функций, задающих соответствующие проекции (горизонтальную и вертикальную) вектора в каждой точке. До сих пор в данной главе мы рассматривали дифференцирование скалярных функций, однако в математике часто приходится иметь дело и

|
112 |
Глава 3 |
|
Рис. 3.9. Модельная функция двух переменных (продолжение листинга 3.14)
Рис. 3.10. Векторное поле градиента функции двух переменных (продолжение листинга 3.14)
с вычислением производных векторных функций. Рассмотрим эти действия на примере операции поиска дивергенции (листинг 3.15 и рис. 3.11), применимой к векторному полю, т. е. векторной функции, зависящей от пространственных координат (на плоскости, как в нашем примере, или в трехмерном пространстве).

|
Дифференцирование |
113 |
|||||||||||||
|
Листинг 3.15. Вычисление дивергенции векторной функции |
||||||||||||||
|
0.24 x |
y |
|||||||||||||
|
f(x y) |
4 10-2 y3 |
|||||||||||||
|
x |
||||||||||||||
|
div (x |
y) |
f(x |
y)0 |
f(x y)1 |
||||||||||
|
x |
y |
|||||||||||||
|
3 |
2 |
|||||||||||||
|
div(x |
y) |
.24 |
y |
|||||||||||
|
25 |
||||||||||||||
Рис. 3.11. График дивергенции векторной функции (продолжение листинга 3.15)
Если, как принято в математике, обозначить оператор взятия градиента символом , то дивергенцию вектор-функции можно формально определить как скалярное произведение f, а еще одну распространенную операцию векторного анализа — ротор (или, по-другому, вихрь или завихренность) — как векторное произведение f. Рисунок 3.11 иллюстрирует пример векторной функции f(x,y) (определяемой в первой строке листинга) и вычисление ее дивергенции (которое производится
аналитически в третьей строке). Обратите внимание, что в качестве исходной век- тор-функции взят результат предыдущих расчетов, показанный (в форме векторного поля) на рис. 3.10. Строки кода в верхней части рис. 3.11 нужны для подготовки графика вычисленной дивергенции (в виде трехмерной поверхности и линий уровня, соответственно, сверху и снизу).

Точно такую же структуру имеют расчеты ротора той же векторной функции f(x,y) в листинге 3.16, причем определение операции взятия ротора приводится в его второй строке (как и в случае дивергенции для листинга 3.15). Читателю, знакомому с векторным анализом, предлагается догадаться самому, почему в рассматриваемом примере (листинги 3.14—3.16) ротор получается тождественно равным нулю (последняя строка листинга 3.16).
Листинг 3.16. Вычисление ротора векторной функции
0.24  x
x  y
y
f(x y)
x 4  10-2
10-2 y3
y3
|
rot(x |
y) |
f(x y)1 |
f(x y)0 |
||
|
x |
y |
||||
|
rot(x |
y) |
0 |
В заключение разговора о векторном анализе функций подчеркнем, что примеры в листингах 3.14—3.16 относились к функциям двух переменных, т. е. описывали двумерный случай. Еще два листинга — 3.17 и 3.18 — показывают, как действуют перечисленные операции векторного анализа в трехмерном (пространственном) случае.
Листинг 3.17. Градиент функции трех переменных
f(x  y
y  z)
z)  z
z  sin(x
sin(x  y)
y)
|
f(x |
y |
z) |
||||
|
x |
||||||
|
grad(x y z) |
f(x |
y |
z) |
|||
|
y |
z cos(x y) y |
|||||
|
f(x |
y |
z) |
grad(x y z) |
z cos(x y) x |
||
|
z |
sin(x y) |
Листинг 3.18. Дивергенция и ротор в трехмерном пространстве
|
x y |
|||||||
|
f(x y |
z) |
z |
|||||
|
x |
2z |
||||||
|
div(x |
y z) |
f(x y z)0 |
f(x y z)1 |
f(x y z)2 |
|||
|
x |
y |
z |

|
Дифференцирование |
115 |
||||||||||
|
f(x |
y |
z)2 |
f(x |
y |
z)1 |
||||||
|
y |
z |
||||||||||
|
rot(x |
y |
z) |
f(x |
y |
z)0 |
f(x |
y |
z)2 |
|||
|
z |
x |
||||||||||
|
f(x |
y |
z)1 |
f(x |
y |
z)0 |
||||||
|
x |
y |
||||||||||
|
div(x |
y |
z) y |
2 |
||||||||
|
1 |
|||||||||||
|
rot(x |
y |
z) |
1 |
x
3.4.3. Пример: якобиан
Еще одна задача, связанная с нахождением частных производных векторной функции, заключается в вычислении якобиана (или определителя матрицы Якоби) — матрицы, составленной из частных производных векторной функции по всем ее аргументам. Эта задача встречается в различных областях математики, например, применительно к жестким дифференциальным уравнениям (см. разд. 9.4). Приемы вычисления якобиана векторной функции f(x) векторного аргумента x демонстрируются в листинге 3.19. В нем для определения частных производных якобиана каждый i-й скалярный компонент f(x)i дифференцируется символьным процессо-
ром Mathcad.
Листинг 3.19. Вычисление якобиана векторной функции векторного аргумента
|
x0 x1 |
|||||||||||||
|
f(x) |
x0 |
||||||||||||
|
x1 |
|||||||||||||
|
x1 x2 |
|||||||||||||
|
x |
x |
x |
|||||||||||
|
f |
y |
0 |
f |
y |
0 |
f |
y |
0 |
|||||
|
x |
z |
y |
z |
z |
z |
||||||||
|
x |
x |
x |
|||||||||||
|
J(x y |
z) |
f |
y |
1 |
f |
y |
1 |
f |
y |
1 |
|||
|
x |
z |
y |
z |
z |
z |
||||||||
|
x |
x |
x |
|||||||||||
|
f |
y |
2 |
f |
y |
2 |
f |
y |
2 |
|||||
|
x |
z |
y |
z |
z |
z |
||||||||

|
116 |
Глава 3 |
|||||
|
y |
x |
0 |
||||
|
J(x y z) |
x |
x |
x |
|||
|
y |
ln(y) y |
0 |
||||
|
y |
||||||
|
0 |
z |
y |
Тот же самый якобиан можно вычислить и несколько по-другому, если определить функцию не одного векторного, а трех скалярных аргументов f(x,y,z) (листинг 3.20). Не забывайте, что для численного определения якобиана необходимо сначала определить точку, в которой он будет рассчитываться, т. е. вектор x в терминах листинга 3.19, или все три переменных x,y,z в обозначениях листинга 3.20.
Листинг 3.20. Вычисление якобиана векторной функции трех скалярных аргументов
f(x  y
y  z)
z)
J(x  y
y  z)
z)
J(x  y
y  z)
z)
x y yx
y yx
y z
z
|
f(x |
y |
z)0 |
f(x |
y |
z)0 |
f(x |
y |
z)0 |
||||||
|
x |
y |
z |
||||||||||||
|
f(x |
y |
z)1 |
f(x |
y |
z)1 |
f(x |
y |
z)1 |
||||||
|
x |
y |
z |
||||||||||||
|
f(x |
y |
z)2 |
f(x |
y |
z)2 |
f(x |
y |
z)2 |
||||||
|
x |
y |
z |
||||||||||||
|
y |
x |
0 |
||||||||||||
|
y |
x |
ln(y) |
y |
x x |
0 |
|||||||||
|
y |
||||||||||||||
|
0 |
z |
y |
 ПРИМЕЧАНИЕ
ПРИМЕЧАНИЕ
В Mathcad 14 предусмотрена новая функция вычисления якобиана Jacob (листинг 3.21).
 Листинг 3.21. Вычисление якобиана при помощи встроенной функции
Листинг 3.21. Вычисление якобиана при помощи встроенной функции
Mathcad 14
|
x0 |
x1 |
x1 |
x0 |
0 |
|
|
Jacob |
x1 |
x0 x |
x0 |
x0 |
1 |
|
ln x1 x1 |
x0 x1 |
0 |
|||
|
x1 |
x2 |
0 |
x2 |
x1 |
Соседние файлы в папке сведения
- #
- #
- #
- #
- #
- #
- #
- #
- #
В прошлый раз мы с вами научились использовать возможности мощнейшей математической среды MathCAD для вычисления различных вещей, относящихся к дифференциальному исчислению: пределов, производных, сумм сходящихся числовых и функциональных рядов. Сегодня мы с вами продолжим знакомство с тем, как в MathCAD вычислять многие важные вещи из ВУЗовского курса математического анализа. Надеюсь, что это будет для вас достаточно интересно.
Вычисление частных производных
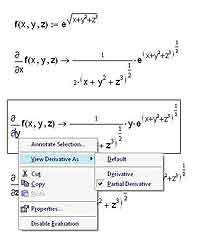
Напомню на всякий случай, что частными называются производные от функций нескольких переменных, берущиеся по одной или нескольким переменным. Для вычисления частных производных в MathCAD’е используются те же самые операторы, которые мы с вами уже весьма успешно применяли для вычисления полных производных. Единственное отличие — это, конечно же, оформление оператора взятия производной. В математическом анализе для отличия частных производных от полных используется специальная запись, в которой буква d, обозначающая производную, и сверху, и снизу пишется наклонной. MathCAD, как и во всех остальных случаях, позволяет пользователю применять привычную запись. Для того, чтобы изменить внешний вид оператора производной, выделите выражение и кликните по нему правой кнопкой мыши. В появившемся контекстном меню нужно выбрать пункт View Derivative As (Показывать производную как…), а в нем — Partial Derivative (Частная производная). Вы всегда можете вернуться к обычному отображению оператора производной, выбрав в том же самом меню пункт Derivative (Производная), который устанавливает для оператора производной вид оператора полной производной. Обратите внимание на то, что установка вида одного оператора взятия производной никак не влияет на все остальные операторы, как уже имеющиеся в вашей рабочей области, так и на те, которые будут добавлены в нее позднее.
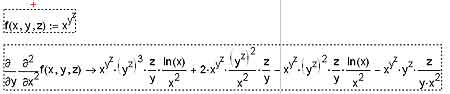
Что касается такой весьма и весьма немаловажной вещи, как взятие смешанных производных, то она реализуется с помощью последовательного взятия частных производных по разным переменным. Хотя, конечно, в результате могут получаться и довольно громоздкие выражения, как, например, на иллюстрации, демонстрирующей применение нескольких операторов взятия производной для вычисления смешанных производных.
Неопределенные интегралы
Дифференцирование в математическом анализе неразрывно связано с интегрированием. Эти обратные друг другу действия — две стороны одной медали, а потому и мы с вами, поговорив об одном из них, перейдем к разговору о втором. У математиков есть шутка, что дифференцирование — это ремесло, а интегрирование — это искусство. MathCAD позволяет и интегрирование свести к уровню ремесла — если, конечно же, представлять себе, что в принципе может быть решаемо с помощью этой программы, а что нужно довести до того вида, в котором задачу уже можно “скармливать” MathCAD’у. Задача вычисления неопределенного интеграла обратна задаче нахождения производной функции. Неопределенный интеграл имеет также название первообразной, которое по ряду причин используется реже. Для вычисления неопределенных интегралов в среде MathCAD используется оператор, который можно легко найти на панели Calculus. Под знаком интеграла пользователь должен ввести функцию, для которой он хочет найти первообразную, а после знака дифференциала — переменную, по которой будет производиться интегрирование. Как видите, и здесь MathCAD верен себе, то есть дает пользователю возможность использовать, опять-таки, знакомые по математическому анализу обозначения неопределенных интегралов. Нужно отметить также, что для неопределенных интегралов необходимо применять символьное вычисление выражений, то есть знак “стрелочки”, а не знак равенства.
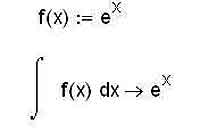
Следует, впрочем, помнить, что многие интегралы просто принципиально не выражаются в элементарных функциях. В том случае, если вы подсунули MathCAD’у один из таких весьма распространенных интегралов, ситуация может иметь два различных финала: либо MathCAD успешно проинтегрирует выражение и выдаст результат с использованием каких-либо специальных функций, либо же честно признается, что его такое интегрировать не учили. Во втором случае вы увидите после “стрелочки”, стоящей за интегралом, запись вида indef_int(f(x), x). Естественно, вместо f(x) и x будут соответственно стоять подынтегральная функция и та переменная, по которой вы хотели провести интегрирование. Оба возможных варианта продемонстрированы на иллюстрации ниже.
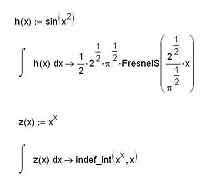
Со специальными функциями тоже все не так просто. Синтаксис, используемый для их записи в MathCAD’е, все же несколько отличается от принятого в математике, а потому, вполне вероятно, для того, чтобы разобраться в том, что за специальные функции скрываются за той или иной записью, придется воспользоваться справочной системой среды MathCAD. Для этого нажмите F1, в появившемся окне выберите вкладку Search, в поле рядом с кнопкой Go введите имя функции, информацию по которой вам нужно найти, а затем нажмите эту самую кнопку. Среди результатов поиска может оказаться и несколько разделов, и имеет смысл просмотреть их все.
В общем-то, даже в том случае, если MathCAD поднимает белый флаг при виде неопределенного интеграла, это не значит, что его вовсе невозможно вычислить в элементарных или специальных функциях. Вполне возможно, что с помощью каких-либо преобразований вам удастся привести его к виду, пригодному для решения в MathCAD. Также имеет смысл поискать решение в старых печатных справочниках или “погуглить” в интернете. Вполне возможно, что у MathCAD’а просто не хватило творческого воображения на то, чтобы до конца “раскрутить” ваш сложный интеграл.
Определенные интегралы
Неопределенные интегралы — это, конечно же, хорошо, но все же на практике куда как чаще используются интегралы определенные. И, думаю, для вас не окажется неожиданностью тот факт, что MathCAD прекрасно умеет справляться и с этим видом интегралов. Определенный интеграл, как вы понимаете, отличается от неопределенного наличием пределов интегрирования. Фактически неопределенный интеграл — это функция (первообразная подынтегральной функции), в то время как определенный интеграл — это просто какое-то число. То есть его мы можем вычислить не только аналитически, но и численно, что позволяет нам рассчитывать значения определенных интегралов даже тогда, когда первообразная рассчитана быть не может. Оператор для расчета определенных интегралов в MathCAD’е находится на панели Calculus недалеко от оператора расчета неопределенных интегралов и отличается от него, как я уже совсем недавно говорил, наличием пределов сверху и снизу от символа интеграла. После того, как вы запишете подынтегральное выражение, переменную интегрирования и собственно пределы, можно ставить знак равенства или стрелочку для вычисления определенного интеграла. В первом случае интеграл будет вычислен численно, во втором — аналитически.
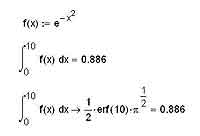
Вопрос о том, какой способ вычисления интегралов использовать: численный или аналитический, — не такой надуманный и праздный, как может сначала показаться. Дело в том, что аналитически определенные интегралы вычисляются, во-первых, точнее, а во-вторых, быстрее, нежели численно. Правда, может возникнуть ситуация, аналогичная той, которую вы можете увидеть на иллюстрации выше — то есть символьный процессор не доведет процесс вычислений до конца, а оставит интеграл в виде смеси численных значений и функций. Впрочем, с этим всегда довольно просто справиться, как видите. Для вычисления кратных интегралов используется тот же прием, что и для вычисления смешанных частных производных для функций многих переменных. То есть мы последовательно интегрируем несколько раз функцию с заданными пределами, и в результате получаем именно то, что, в общем- то, и рассчитывали получить. Стоит отметить, что, поскольку при интегрировании кратных интегралов мы теряем при численном интегрировании особенно много времени, то здесь особенно желательно использовать именно аналитический способ вычисления интегралов.
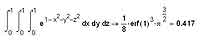
В применении системы MathCAD для расчета определенных интегралов есть немало тонких моментов, которые не возникали при расчете интегралов неопределенных. Особенно это касается численных методов расчета интегралов. Как я уже говорил, эти методы позволяют рассчитать даже такие интегралы, которые не поддаются аналитическому вычислению. Однако за все надо платить, а потому использование численных методов интегрирования способно приводить к значительным погрешностям в результате, что, сами понимаете, при решении весьма значительного по своей распространенности класса задач не просто нежелательно, а часто даже совершенно недопустимо. О погрешностях при численном интегрировании в MathCAD’е и о том, как избежать того, чтобы они стали совсем уж гигантскими, мы с вами поговорим в следующий раз. А пока что давайте подведем итоги тому, о чем мы говорили сегодня.
Как видите, MathCAD с легкостью справляется с интегралами — пусть не со всеми, но с их значительной частью. Тех возможностей этой великолепной среды, о которых мы с вами уже успели поговорить в цикле статей “MathCAD — это просто!”, на мой взгляд, как раз достаточно для того, чтобы прибавить вам энтузиазма в дальнейшем изучении этой программы.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 26 за 2008 год в рубрике soft
Помогаю со студенческими работами здесь
 Производная в точке
Производная в точке
Написал кусочную функцию в маткаде, хочу высчитать производную в точке, в учебнике тот же пример, в…
 Производная от функции
Производная от функции
Есть достаточно большая функция f2(f1), для простоты представим:…
Странно считается производная
необходимо найти экстремумы функции, для этого нужно приравнять к нулю производную. Но маткад…
Производная высших порядков
Помогите пожалуйста разобраться, нашла пример решения в справке:
по условию мне дано…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
2
Решение дифференциальных уравнений в частных производных mathcad
При решении дифференциального уравнения искомой величиной является функция. Для ОДУ неизвестная функция — функция одной переменной. Дифференциальные уравнения в частных производных — это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. Mathcad имеет ряд встроенных функций, предназначенных для решения ОДУ. Каждая из этих функций предназначена для численного решения дифференциального уравнения. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений). Для каждого алгоритма, который используется при решении дифференциальных уравнений, Mathcad имеет различные встроенные функции. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы по крайней мере следующие величины, необходимые для поиска решения:
- Начальные условия.
- Набор точек, в которых нужно найти решение.
- Само дифференциальное уравнение, записанное в некотором специальном виде, который будет детально описан в этой главе.
В этом разделе описано, как решить ОДУ, используя функцию rkfixed. Раздел начинается с примера того, как решить простейшее дифференциальное уравнение первого порядка. Затем будет показано, как можно решать дифференциальные уравнения более высокого порядка.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:
с начальными условиями: y(0) = 4
Функция rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:
- Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.
- Второй столбец содержит значения найденного решения в соответствующих точках.
Рисунок 1: Решение дифференциального уравнения первого порядка.
Функция rkfixed имеет следующие аргументы:
| y = | Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y0 = y(x1). |
| x1, x2 = | Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1. |
| npoints = | Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed. |
| D (x, y) = | Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций. |
Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого команду Решить относительно переменной из меню Символика.
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.
Дифференциальные уравнения второго порядка
Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:
- Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.
- Функция D(t, y) является теперь вектором с двумя элементами:
Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:
Рисунок 3: Решение дифференциального уравнения второго порядка.
Уравнения более высокого порядка
Методика решения дифференциальных уравнений более высокого порядка является развитием методики, которая применялась для решения дифференциальных уравнений второго порядка. Основное различие состоит в следующем:
- Вектор начальных значений y теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y’ , y”. y (n-1)
- Функция D является теперь вектором, содержащим n элементов:
Пример, приведенный на Рисунке 4, показывает, как решить следующее дифференциальное уравнение четвертого порядка:
с начальными условиями:
Рисунок 4: Решение дифференциального уравнения более высокого порядка.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
MathCAD — это просто! Часть 23. Внутренняя кухня решения дифференциальных уравнений. Дифференциальные уравнения в частных производных
Хотя мы с вами говорим о решении дифференциальных уравнений в среде MathCAD уже, в общем-то, довольно-таки давно, тем не менее, тема эта по- прежнему остается не до конца раскрытой. Почему? Потому, что дифференциальным уравнениям и их решению в мире посвящено гигантское количество различных научных работ и книг — пожалуй, столько их не посвящалось больше ни одному вопросу прикладного применения математики.
Дифференциальные уравнения сегодня — это, прежде всего, основа для всех физических и химических расчетов, применяемых в промышленности и науке. И потому без дифференциальных уравнений не может обойтись в рамках своей профессиональной деятельности ни один специалист технического или естественнонаучного профиля. И чем лучше мы с вами научимся решать дифференциальные уравнения с помощью MathCAD, тем легче вам будет разбираться с ними в тот момент, когда они понадобятся вам для выполнения какой-либо порученной вам работы. Разговор о дифференциальных уравнениях в MathCAD просто не может быть полным без двух вещей. Первая из них — это краткий, слишком краткий для того, чтобы быть действительно полезным, рассказ о внутренних механизмах решения дифференциальных уравнений в этой мощной математической среде, то есть об используемых MathCAD’ом алгоритмах их численного интегрирования. Увы, объем газетной статьи ограничен, и рассказывать подробно настолько, насколько хотелось бы, у меня нет возможности. Вторая же такая вещь — рассказ о решении дифференциальных уравнений в частных производных, к которым относятся практически все уравнения математической и теоретической физики. Конечно, вещи это довольно сложные, но я постараюсь сделать их понятными для каждого из читателей серии “MathCAD — это просто”. Ну, а судить, насколько хорошо у меня это выйдет, уже дело ваше.
Численное интегрирование обыкновенных дифференциальных уравнений методом Рунге-Кутта четвертого порядка
Для того, чтобы понять, как именно работают алгоритмы численного решения дифференциальных уравнений, нужно вспомнить, что именно мы делаем, решая дифференциальное уравнение в MathCAD’е. Вспомнили? Правильно, мы интегрируем. Значит, мы находим первообразную некоторой функции, которую в простейшем случае можем записать как f(x,y), где y и будет решением нашего дифференциального уравнения. Для того, чтобы объяснять дальше, нужно напомнить, что же такое производная — ведь именно ею является наша функция f(x, y) по отношению к своей искомой первообразной. Производная — это предел приращения функции к пределу приращения своего аргумента (или своих аргументов, если таковых имеется больше, чем один). Однако пределы — это всего лишь математическая абстракция, какой бы хорошей и удобной она ни была. То есть мы не можем в реальном мире оперировать бесконечно малым приращением ни функции, ни ее аргументов, если хотим с их помощью вычислить саму производную. Выход из этой ситуации напрашивается самый простой и логичный — перейти от бесконечно малого приращению к малому, но все же конечному. Говорят, что дифференциальное уравнение при этом заменяется на разностное, и для его решения применяются специальные разностные методы.
Самым распространенным методом решения дифференциальных уравнений в численном виде является метод Рунге-Кутта четвертого порядка, который из-за его повсеместной распространенности обычно называют просто методом Рунге-Кутта. Этот метод разработан еще в начале XX века немецкими математиками Карлом Рунге и Мартином Вильгельмом Куттом и с тех пор, как появились первые вычислительные машины, используется для численного решения дифференциальных уравнений самым что ни на есть активным образом. В MathCAD’е метод Рунге-Кутта в его классическом виде реализован в функции rkfixed. Ограничения, накладываемые ею на решаемые с ее помощью уравнения, — это те самые ограничения, которые на них накладывает метод Рунге-Кутта. Алгоритм Рунге-Кутта итерационный, то есть для вычисления значения функции с заданной точностью нужно выполнить вычисления несколько раз, и для каждого следующего вычисления используются результаты предыдущего. Записать это в виде формул можно следующим образом:
Самая нижняя из всех формул — это исходное уравнение, которое мы решаем указанным методом, а коэффициенты k называются прогоночными коэффициентами. Как видите, для того, чтобы вычислить по этим формулам хоть одно значение y, нужно воспользоваться начальным (нулевым) значением y. То есть этот метод очень хорошо подходит для решения задачи Коши, а вот если встретится краевая задача, то здесь уже надо искать другой метод. Как можно понять из формул, h — это величина шага интегрирования. Об этой величине я рассказывал тогда, когда приоткрывал завесу тайны над “кухней” численного интегрирования в MathCAD’е, а потому останавливаться на ней повторно и рисовать графики, иллюстрирующие ее геометрическую интерпретацию, я не буду. Почему рассмотренный нами алгоритм называется алгоритмом четвертого порядка? Дело в том, что суммарная погрешность при вычислении функции по записанным выше формулам составляет величину порядка h4. При достаточно малых h это очень хорошая точность, и именно поэтому метод Рунге-Кутта получил такое широкое распространение. Конечно, рассмотренный нами метод численного решения дифференциальных уравнений не настолько универсален, насколько нам того хотелось бы, но разработчики MathCAD существенно упростили нам задачу, реализовав удобную и мощную функцию Odesolve, комбинирующую в себе возможности нескольких разных алгоритмов численного решения обыкновенных дифференциальных уравнений. Если вдруг вы решите проникнуть глубже в тайны методов численного решения дифференциальных уравнений, то делать это лучше всего с помощью соответствующих учебников, которых в библиотеках и в интернете можно найти великое множество.
Решение дифференциальных уравнений в частных производных
Что ж, давайте уже перейдем к завершающему наш разговор о дифференциальных уравнениях в MathCAD’е вопросу — решению дифференциальных уравнений в частных производных. Дифференциальным уравнением в частных производных называется уравнение относительно функции нескольких переменных (обязательно более чем одной), содержащее саму эту функцию (что, впрочем, необязательно) и ее частные производные по различным аргументам (вот это уже необходимо). Классическими уравнениями в частных производных являются уравнения математической физики — например, такие, как уравнение колебаний мембраны или даже струны; уравнение теплопроводности, описывающее перенос тепловой энергии в веществах; уравнение Шредингера, на котором построена вся квантовая механика. Решать уравнения в частных производных обычно еще сложнее, чем обыкновенные дифференциальные уравнения, однако, как вы сами сможете убедиться, это утверждение можно не считать справедливым в тех случаях, когда вам на помощь приходит такая мощная математическая среда, как MathCAD. Давайте попробуем решить с помощью MathCAD’а уже упоминавшееся буквально пару строчек назад уравнение теплопроводности, которое можно записать в следующем виде:
Решать его будем с помощью уже частично знакомого вам блока Given…Pdesolve. Он весьма схож с блоком Given. Odesolve, который мы использовали для обыкновенных дифференциальных уравнений, но имеются некоторые отличия. Так, например, производные для этого блока нужно задавать в индексной форме записи. То есть первая производная от y по x будет записана как yx. В MathCAD’е для записи производных в нижнем регистре нажмите кнопку “.” (“ю” на русской клавиатуре). Вот таким образом будет выглядеть наше решение дифференциального уравнения в частных производных:
То, что стоит сразу непосредственно после Given, думаю, в каких-либо подробных прояснениях не нуждается, потому что это, собственно говоря, и есть то самое дифференциальное уравнение, которое мы с вами усиленно решаем. Сразу же следом за ним идут начальные условия по времени и граничные условия по координате — такие условия называются условиями Дирихле. Но самое важное, в общем-то, не они, а та функция, с помощью которых наш набор условий превращается в решенное дифференциальное уравнение — это функция Pdesolve. Первый ее параметр — это название функции или вектор функций, которые заданы в блоке Given. Второй и третий параметры — это один из аргументов функции и вектор из его начального и конечного значений. Здесь нужно внимательно следить за тем, чтобы эти значения в блоке Given обязательно совпадали с параметрами самой Pdesolve — в случае их взаимного несоответствия система MathCAD выдаст ошибку. Следующие два (или четыре, или шесть — все зависит от исходной функции и решаемого уравнения) параметра также обозначают аргумент и его граничные значения. Ну, а завершают список параметров функции Pdesolve количество шагов по каждой из переменных. Совсем не обязательно делать их равными для всех переменных — надо смотреть на особенности самого уравнения, а также начальных и граничных условий. Чтобы визуализировать результаты решения, можно воспользоваться нашими знаниями о построении графиков в MathCAD’е и построить трехмерный график (см. соответствующий рисунок). Вопрос на засыпку: какая из осей изображает время? Вот и проверим, насколько вы разобрались в свое время с графиками.
Конечно, для таких уравнений, где одна из переменных является временем, лучше строить не трехмерные графики, а двумерные, но анимированные. Как они делаются, я вам уже имел удовольствие рассказывать, а потому вы, безо всяких сомнений, успешно справитесь с их созданием.
Что ж, как видите, и в глубинах MathCAD’а, в которых идет решение дифференциальных уравнений численными методами, все оказалось вовсе не так уж и сложно. Конечно, мы с вами разобрали только самый простой случай, но ведь перед нами, согласитесь, и не стоит задачи написать собственную математическую среду наподобие MathCAD, а потому мы можем позволить себе не разбираться в тонкостях реализации разных методов, а просто предоставить MathCAD’у самому разбираться с подсунутыми нами уравнениями. С дифференциальными уравнениями в частных производных тоже все оказалось не так уж сложно, потому что разработчики MathCAD постарались максимально унифицировать процесс их решения с процессом решения обыкновенных дифференциальных уравнений. Так что не нужно бояться дифференциальных уравнений, если под рукой есть MathCAD. Рано или поздно, так или иначе, но они падут под натиском этого грозного математического “оружия”.
Компьютерная газета. Статья была опубликована в номере 37 за 2008 год в рубрике soft
Решение дифференциальных уравнений в частных производных mathcad
Глава 5. Решение дифференциальных уравнений
5.8 Функции решения параболических и гиперболических уравнений
Дифференциальные уравнения в частных производных требуют нахождение функции не одной, а нескольких переменных. MathCAD имеет очень ограниченные возможности для решения таких уравнений, ведь для решения каждого вида уравнений в частных производных требуется свой метод решения.
Уравнения в частных производных можно разделить на три типа:
1) параболические, содержащие первую производную по одной переменной и вторую – по другой, причем все производные входят в уравнение с одинаковым знаком;
2) гиперболические, содержащие первую производную по одной переменной и вторую – по другой, входящие в уравнение с разными знаками;
3) эллиптические, содержащие вторые производные, причем одного знака.
Функции решения параболических и гиперболических уравнений
MathCAD 11 включает в себя две функции для решения параболических и гиперболических уравнений, pdesolve и numol .
Функция pdesolve используется в составе вычислительного блока Given – pdesolve для решения параболических и гиперболических уравнений (или систем уравнений) в частных производных, имеющих в качестве аргументов, как правило, время t и пространственную координату x .
Обращение к этой функции:
возвращает скалярную (для одного уравнения) или векторную (для системы уравнений) функцию, являющуюся решением уравнения (или системы уравнений). Здесь u –явно заданный вектор имен функций (без указания имен аргументов), подлежащих вычислению. Эти функции, а также граничные условия должны быть определены внутри вычислительного блока Given – pdesolve ; х – пространственная координата; x range – вектор значений аргумента х для граничных условий. Он должен состоять из двух чисел, представляющих две границы расчетного интервала; t – время (имя второго аргумента неизвестной функции); t range – вектор значений аргумента t для граничных условий, состоящих из двух чисел, представляющих две границы расчетного интервала; x pts – количество пространственных точек дискретизации (может не указываться); t pts – количество временных слоев (может не указываться).
Пример использования функции pdesolve приведен на рис. 5.19 запись вычислительного блока с функцией pdesolve аналогична записи блока с функцией Odesolve . Результаты расчета показаны на рис. 5.20.
Решение одномерного волнового уравнения
Здесь w -перемещение, v -скорость перемещения
где тогда
Представим первое уравнение как систему двух
уравнений первого порядка
Given
граничные условия
Рис. 5.1 9 Пример использования функции pdesolve
Единичное решение волнового уравнения
Сетка решений волнового уравнения на временном и пространственном интервалах
Рис. 5. 20 Результаты решения волнового уравнения
Обратите внимание на то, что уравнения внутри вычислительного блока должны записываться с аргументами. Для идентификации частных производных следует использовать нижний индекс, например, – вторая производная функции u по пространственной координате х.
Недостатком функции pdesolve (как и функции Odesolve ) является невозможность ее использования в составе выражения – программы для многократного решения дифференциального уравнения. При необходимости многократного решения обыкновенных дифференциальных уравнений в состав программного модуля можно включать функции Rkadapt или Bulstoer.
При необходимости многократного решения дифференциальных уравнений в частных производных в состав программного модуля можно включать функцию numol , которая, как и pdesolve , появилась в MathCAD 11.
Функция numol предназначена для решения тех же уравнений, что и функция pdesolve .
Обращение к этой функции:
возвращает матрицу решения дифференциального уравнения в частных производных в каждой точке по пространственной (по строкам) и временной (по столбцам) координате. Если решается не одно уравнение, а система уравнений, то результатом решения является составная матрица, образованная путем слияния (слева направо) со значениями каждой искомой сеточной функции. Здесь x range – вектор значений аргумента х для граничных условий. Он должен состоять из двух чисел, представляющих две границы расчетного интервала; t range – вектор значений аргумента t для граничных условий, состоящих из двух чисел, педставляющих две границы расчетного интервала; x pts – количество пространственных точек дискретизации (может не указываться); t pts – количество временных слоев (может не указываться); N pde – количество дифференциальных уравнений в частных производных в системе; N ae – количество дополнительных алгебраических уравнений, входящих в систему; rhs – вектор правых частей уравнений; init – векторная функция, определяющая начальные условия для каждой неизвестной функции; bc – функциональная матрица граничных условий.
Вектор граничных условий может иметь значения трех типов:
– rhs содержит вторые пространственные производные: граничные условия (или Дирихле « D », или Неймана « N ») требуются по одному с каждой стороны интервала интегрирования;
– rhs содржит первые пространственные производные: граничные условия Дирихле на левой или правой границе интервала, на другой стороне NA ;
– нет пространственных производных – граничные условия не требуются.
Функциональная матрица bc содержит три столбца, имеющих ледующий вид:
– ( init _ left ( t ) init _ right ( t ) ” D “) – для граничных условий Дирихле;
– ( init _ left ( t ) init _ right ( t ) ” N “) – для граничных условий Неймана.
Пользоваться функцией numol намного сложнее, чем функцией pdesolve .
Граничное условие называется условием Дирихле, если задано значение функции, или Неймана, если задана первая производная функции.
[spoiler title=”источники:”]
http://nestor.minsk.by/kg/2008/37/kg83705.html
http://www.math.mrsu.ru/text/courses/mcad/5.8.htm
[/spoiler]
