Частные производные и дифференциал функции
Частной производной
функции нескольких переменных по
одной из этих переменных называется
предел отношения соответствующего
частного приращения функции к приращению
данной переменной, когда последнее
стремится к нулю (если этот предел
существует).
Для функции
![]() имеем:
имеем:
![]() (частная производная
(частная производная
по переменной х);
![]() (частная производная
(частная производная
по переменной y).
Из
определения частных производных следует,
что для нахождения производной
![]() надо считать постоянной переменнуюy,
надо считать постоянной переменнуюy,
а для нахождения
![]() – переменнуюx.
– переменнуюx.
При
нахождении частной производной пользуются
правилами дифференцирования
функции одной переменной, считая все
другие аргументы постоянными.
Полным дифференциалом
функции называется
сумма произведений частных производных
этой функции на приращения соответ-
ствующих
независимых переменных, т. е.
![]()
Для независимых
переменных x
и y
любые приращения x
и y
будем считать их дифференциалами, т. е.
![]() и
и![]()
Тогда полный
дифференциал функции
z
= f(x;
y)
вычисляется по следующей формуле:
![]()
а для функции трех
переменных u
= f(x;
y;
x):
![]()
Полный дифференциал
часто используется для приближенных
вычислений
значений функции, т. е.
![]()
Существование
частных производных является лишь
необходимым,
но недостаточным условием дифференцируемости
функции.
Следующая теорема
выражает достаточное
условие дифференцируемости функции
двух переменных.
Теорема.
Для того
чтобы функция z
= f(x;
y)
была дифференцируемой в данной точке,
достаточно, чтобы она обладала частными
производными, непрерывными в этой точке.
Пример 11. Вычислить
частные производные и полный дифференциал
функции
![]()
Решение
Считая
![]() постоянным, найдем производную поx
постоянным, найдем производную поx
![]()
![]()
Считая
![]() постоянным и дифференцируя поy,
постоянным и дифференцируя поy,
находим
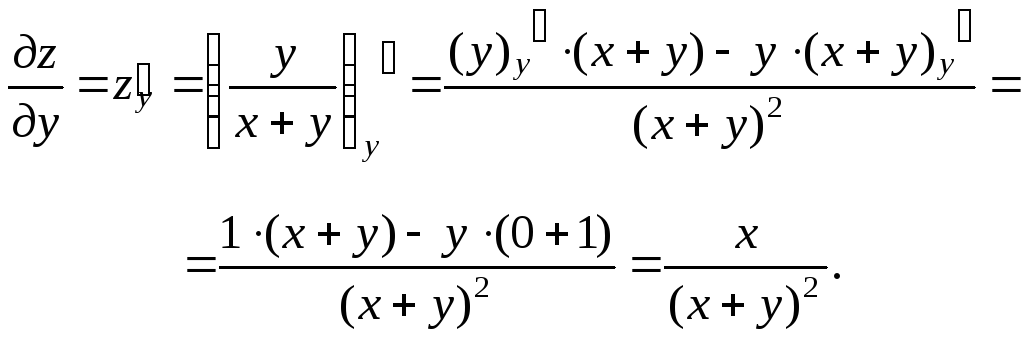
Полный дифференциал:
![]()
Пример 12.
Вычислить
1,073,97.
Решение
Число
![]() есть частное значение функцииf(x;
есть частное значение функцииf(x;
y)
= xy
при x
= 1,07, y
= 3,97. Известно, что f(1;
4) = 1. Поэтому принимаем x0
= 1, y0
= 4. Тогда
![]() y
y
= y
– y0
= 3,97 – 4 = –0,03.
Так как
![]()
![]()
![]()
![]() то
то![]()
Тест 7.
Частная
производная
![]() функции
функции![]() равна:
равна:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
Тест 8. Полный
дифференциал
![]() функцииz
функцииz
= x2
– 4y
равен:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
Частные производные и дифференциалы высших порядков
Частными
производными второго порядка называют
частные производные,
взятые от частных производных первого
порядка
![]()
![]()
![]()
![]()
Аналогично
определяются частные производные
третьего и более высоких порядков.
Запись
![]() означает, что функцияz
означает, что функцияz
k
раз продифференцирована по переменной
x
и
![]() раз по переменнойy.
раз по переменнойy.
Частные производные
![]() и
и![]() называютсясмешанными.
называютсясмешанными.
Значения
смешанных производных равны в тех
точках, в которых эти производные
непрерывны.
Полный дифференциал
второго порядка d 2z
функции z
= f(x;
y)
выражается формулой
![]()
Дифференциалы
высших порядков
определяются по аналогии
![]()
Пример 13.
Найти
частные производные второго порядка
функции
![]()
Решение
Вначале найдем
частные производные первого порядка
![]()
![]()
Продифференцировав
их еще раз, получим
![]()
![]()
![]()
![]()
Сравнивая последние
два выражения, видим, что
![]()
Пример 14.Найти полный
дифференциал второго
порядка функции
![]()
Решение
Находим частные
производные второго порядка
![]()
![]()
![]()
![]()
![]()
Следовательно,
![]()
Тест 9. Частная
производная второго порядка
![]() функции
функции
![]()
равна:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
Тест 10. Частная
производная второго порядка
![]() функцииz
функцииz
= 7x2y
– 4y2
равна:
1)
0;
2) 14xy;
3) 14x;
4) 7x2y;
5) –8y.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы понять частные производные, сначала нужно разобраться с обычными. И не нужно ничего искать: в нашей отдельной статье мы уже подготовили все для того, чтобы у вас это получилось. А сейчас речь пойдет о частных производных.
Добро пожаловать на наш телеграм-канал за полезной рассылкой и актуальными студенческими новостями.
Функция двух и более переменных
Прежде чем говорить о частных производных, нужно затронуть понятие функции нескольких переменных, без которого нет смысла в частной производной. В школе мы привыкли иметь дело с функциями одной переменной:
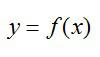
Производными таких функций мы и считали раньше. График функции одной переменной представляет собой линию на плоскости: прямую, параболу, гиперболу и т.д.
А что, если добавить еще одну переменную? Получится такая функция:
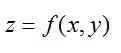
Это – функция двух независимых переменных x и y. График такой функции представляет собой поверхность в трехмерном пространстве: шар, гиперболоид, параболоид или еще какой-нибудь сферический конь в вакууме. Частные производные функции z по иксу и игреку соответственно записываются так:
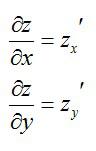
Существуют также функции трех и более переменных. Правда, график такой функции нарисовать невозможно: для этого понадобилось бы как минимум четырехмерное пространство, которое невозможно изобразить.
Частная производная первого порядка
Запоминаем главное правило:
При вычислении частной производной по одной из переменных, вторая переменная принимается за константу. В остальном правила вычисления производной не меняются.
То есть, частная производная по сути ничем не отличается от обычной. Так что, держите перед глазами таблицу производных элементарных функций и правила вычисления обычных производных. Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции:
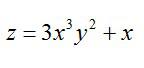
Сначала возьмем частную производную по иксу, считая игрек обычным числом:
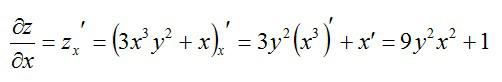
Теперь считаем частную производную по игреку, принимая икс за константу:
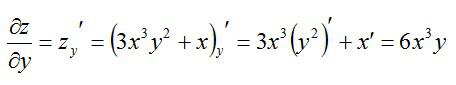
Как видите, ничего сложного в этом нет, а успех с более сложными примерами – лишь дело практики.
Частная производная второго порядка
Как находится частная производная второго порядка? Так же, как и первого. Чтобы найти частные производные второго порядка, нужно просто взять производную от производной первого порядка. Вернемся к примеру выше и посчитаем частные производные второго порядка.
По иксу:
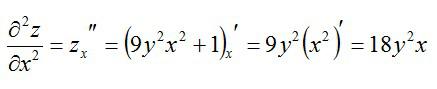
По игреку:
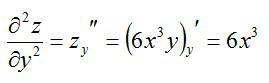
Частные производные третьего и высших порядков не отличаются по принципу вычисления. Систематизируем правила:
- При дифференцировании по одной независимой переменной, вторая принимается за константу.
- Производная второго порядка – это производная от производной первого порядка. Третьего порядка – производная от производной второго порядка и т.д.
Частные производные и полный дифференциал функции
Частый вопрос в практических заданиях – нахождение полного дифференциала функции. Для функции нескольких переменных полный дифференциал определяется, как главная линейная часть малого полного приращения функции относительно приращений аргументов.
Определение звучит громоздко, но с буквами все проще. Полный дифференциал первого порядка функции нескольких переменных выглядит так:
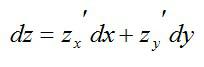
Зная, как считаются частные производные, нет никакой проблемы вычислить и полный дифференциал.
Частные производные – не такая уж и бесполезная тема. Например, дифференциальные уравнения в частных производных второго порядка широко используются для математического описания реальных физических процессов.
Здесь мы дали лишь общее, поверхностное представление о частных производных первого и второго порядка. Вас интересует эта тема или остались конкретные вопросы? Задавайте их в комментариях и обращайтесь к экспертам профессионального студенческого сервиса за квалифицированной и скорой помощью в учебе. С нами вы не останетесь один на один с проблемой!
![]()
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Содержание:
- Дифференцирование функций многих переменных
- Полный дифференциал и дифференцируемость функции
- Эластичность функции многих переменных
- Частные производные высших порядков
- Дифференциальное вычисление функции многих переменных
- Экстремум функции двух переменных
- Метод наименьших квадратов
- Экономические задачи, что приводятся к использованию функций многих переменных
- Функции нескольких переменных и их вычисление
- Основные понятия и область определения функции
- Граница и непрерывность функции двух переменных
- Приросты функции двух переменных
- Частные производные
- Геометрическая интерпретация частных производных
- Частные дифференциалы и полный дифференциал. Использование в приближенных вычислениях
- Производная по направлению
- Градиент функции и линии уровня
- Локальный экстремум функции двух переменных
- Условный экстремум
- Метод сведения к экстремума функции одной переменной
- Метод множителей Лагранжа
- Наименьшее и наибольшее значение функции в замкнутой области
Дифференцирование функций многих переменных
Ограничимся случаем функций двух переменных. Все дальнейшее справедливо, однако, и в том случае, когда число переменных равно трем, четырем и т.д.
Итак, пусть в некоторой окрестности точки  определена функция
определена функция  . Определим приращения переменных
. Определим приращения переменных  и
и  формулами:
формулами:
 .
.
Тогда любая точка ( ) из окрестности точки (
) из окрестности точки ( ) может быть представлена как
) может быть представлена как
 .
.
При изменении  от
от  до
до  – (и постоянном
– (и постоянном  ) функция
) функция  изменяется на величину
изменяется на величину
 .
.
Эта разность называется частным приращением функции  по
по  . Частное приращение по
. Частное приращение по  определяется аналогично:
определяется аналогично:
 .
.
Определение 1. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремиться к нулю.
Частные производные по  функции
функции  обозначают, как
обозначают, как  , по
, по  – как
– как  . Если частная производная вычисляется в конкретной точке, то пишут
. Если частная производная вычисляется в конкретной точке, то пишут  . Согласно определению 1, имеем
. Согласно определению 1, имеем
 , (1)
, (1)
 . (2)
. (2)
Из определения следует, что для нахождения частной производной  можно использовать правила дифференцирования функции одной переменной, считая переменную
можно использовать правила дифференцирования функции одной переменной, считая переменную  константой.
константой.
Пример №72
Найти частные производные функций: a)  ; б)
; б)  .
.
Решение:
а) Считая  , находим
, находим  . Считая
. Считая  , находим
, находим  .
.
б) Частная производная  вычисляется как производная степенной функции, а частная производная
вычисляется как производная степенной функции, а частная производная  вычисляется как производная показательной функции.
вычисляется как производная показательной функции.
Полный дифференциал и дифференцируемость функции
Рассмотрим одновременное изменение независимых переменных  и
и  . Тогда функция
. Тогда функция  изменится на величину
изменится на величину
 . (3)
. (3)
Величина Az, заданная формулой (3.20), называется полным приращением функции z в точке (д’0,у0). Так же, как и случае функции одной переменной возникает задача о
приближенной замене приращения Az (которое как правило, является нелинейной функцией от Ay и Ау) на линейную функцию от Ay и Ау. Роль линейного приближения выполняет полный дифференциал функции, который определяется как сумма произведений частных производных функции на приращения независимых переменных. Так, в случае функции двух переменных, полный дифференциал определяется равенством
 . (4)
. (4)
В формуле (4) точка ( ) явно не указана, однако, следует помнить, что в различных точках (
) явно не указана, однако, следует помнить, что в различных точках ( ) дифференциал будет различным.
) дифференциал будет различным.
Дифференциалами независимых переменных  и
и  назовем их приращения
назовем их приращения  . Поэтому (4) можно записать так:
. Поэтому (4) можно записать так:
 . (5)
. (5)
Пример №73
Найти полный дифференциал функции  и вычислить его в точках: а) (0:2), б) (1:1).
и вычислить его в точках: а) (0:2), б) (1:1).
Решение:
Запишем полный дифференциал в общем виде
 .
.
Подставив координаты точек, получим

Определение 2. Функция  называется дифференцируемой в точке (
называется дифференцируемой в точке ( ), если ее полное приращение можно представить в виде
), если ее полное приращение можно представить в виде
 , (6)
, (6)
или, короче,
 ,
,
где  – расстояние от точки (
– расстояние от точки ( ) до точки (
) до точки ( );
);  – функция, бесконечно малая при
– функция, бесконечно малая при  , т.е.
, т.е.
 .
.
Теорема 1. Если функция  дифференцируема в точке (
дифференцируема в точке ( ), то она непрерывна в этой точке.
), то она непрерывна в этой точке.
Теорема 2. (достаточное условие дифференцируемости). Если частные производные  и
и  определены в окрестности точки (
определены в окрестности точки ( ) и эти производные непрерывны в самой точке (
) и эти производные непрерывны в самой точке ( ), то функция
), то функция  дифференцируема в этой точке.
дифференцируема в этой точке.
Эластичность функции многих переменных
Ранее было введено понятие эластичности функции одной переменной. Аналогично вводится это понятие и для функции нескольких неременных. Пусть, например,  – функция двух переменных;
– функция двух переменных;

 – ее частные приращения.
– ее частные приращения.
Определение 3. Эластичностью функции  в точке (
в точке ( ) по переменной
) по переменной  называется предел
называется предел

Эластичностью  по
по  в той же точке:
в той же точке:

Говорят, что  – коэффициент эластичности
– коэффициент эластичности  по
по  , а
, а  – коэффициент эластичности
– коэффициент эластичности  по
по  (обозначение точки часто опускается). Из определения вытекают следующие формулы:
(обозначение точки часто опускается). Из определения вытекают следующие формулы:
 ,
,  . (7)
. (7)
Пример №74
Найти коэффициенты эластичности по  и
и  производственной функции Кобба-Дугласа
производственной функции Кобба-Дугласа  в точке (
в точке ( ).
).
Решение:
Согласно формулам (7) имеем

 ,
,
 .
.
Следовательно, в любой точке ( ) коэффициенты производственной функции Кобба-Дугласа постоянны и равны:
) коэффициенты производственной функции Кобба-Дугласа постоянны и равны:  .
.
Частные производные высших порядков
Пусть  – открытое множество в
– открытое множество в  ,
,  – определенная на множестве
– определенная на множестве  функция. Предположим, что в каждой точке
функция. Предположим, что в каждой точке  существуют частные производные
существуют частные производные  и
и  . Тогда частные производные
. Тогда частные производные  и
и  естественно считать функциями с областью определения
естественно считать функциями с областью определения  . Они называются частными производными первого порядка. Частные производные от функций
. Они называются частными производными первого порядка. Частные производные от функций  и
и  называются частными производными второго порядка от функции
называются частными производными второго порядка от функции  . Частные производные от частных производных второго порядка называются частными производными третьего порядка и т.д.
. Частные производные от частных производных второго порядка называются частными производными третьего порядка и т.д.
Если первая производная функции  была взята, скажем, по переменной
была взята, скажем, по переменной  , то ее частные производные в точке (
, то ее частные производные в точке ( ) обозначаются так:
) обозначаются так:
 ,
,  ,
,
или
 ,
,  Аналогичные обозначения используются и для других частных производных. Например.
Аналогичные обозначения используются и для других частных производных. Например.  и т.д.
и т.д.
Частные производные второго порядка  и
и  называются смешанными частными производными.
называются смешанными частными производными.
Пример №75
Найти все частные производные второго порядка от функций: a)  ; б)
; б)  .
.
Решение:
а) Имеем  ,
,  . Следовательно,
. Следовательно,  .
.
б) Имеем  ,
,  . Следовательно,
. Следовательно,  ,
,  ,
, 
Обратим внимание на то, что в примере 4 смешанные частные производные от одной и той же функции  совпадают. Являются ли данные совпадения случайными, или они – следствия какого-то общего правила? Следующая теорема дает ответ на этот вопрос.
совпадают. Являются ли данные совпадения случайными, или они – следствия какого-то общего правила? Следующая теорема дает ответ на этот вопрос.
Теорема 3. Если производные  и
и  существуют в некоторой окрестности точки
существуют в некоторой окрестности точки  и непрерывны в самой точке
и непрерывны в самой точке  , то они равны между собой:
, то они равны между собой:
 .
.
Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
Другие темы которые вам помогут понять высшую математику:
Дифференциальное вычисление функции многих переменных
Проиллюстрируем основные понятия и формулы для функции двух переменных, поскольку переход к большему числу переменных не вызывает трудностей. Если  то частичные приросты с переменными
то частичные приросты с переменными  и полный прирост функции обозначаются уравнениями:
и полный прирост функции обозначаются уравнениями:

Если существует  то эта граница называется производной функции
то эта граница называется производной функции  с переменной
с переменной  и обозначается одним из символов:
и обозначается одним из символов: Аналогично обозначается часть производной с переменной
Аналогично обозначается часть производной с переменной  Частичная производная с одной из переменных находится с правилами дифференцированная функция одной переменной, причем вторая переменная считается при этом постоянной.
Частичная производная с одной из переменных находится с правилами дифференцированная функция одной переменной, причем вторая переменная считается при этом постоянной.
Решение примеров:
Найти частичные производные функций двух переменных.
Пример 5.1

Решение

Пример 5.2

Решение

Пример 5.3

Решение

Главная линейная относительно  и
и  часть полного прироста функции называется полным дифференциалом функции. который обозначается
часть полного прироста функции называется полным дифференциалом функции. который обозначается  и вычисляется по формуле:
и вычисляется по формуле:

Принимая  и
и  найти полный дифференциал функций двух переменных.
найти полный дифференциал функций двух переменных.
Пример 5.4

Решение

Пример 5.5

Решение

Пример 5.6

Решение

Частичными производными второго порядка от функции  называются частичные производные от ее первых производных.
называются частичные производные от ее первых производных.

Остальные две производные называются смешанными и они равны между собой по условию их непрерывности.
Дифференциал второго порядка  обозначается по формуле
обозначается по формуле  и вычисляется при условии непрерывности смешанных производных по формуле
и вычисляется при условии непрерывности смешанных производных по формуле

Производная  функции
функции  с направлением
с направлением  вычисляется по формуле
вычисляется по формуле

и вычислена в точке  дает скорость изменения функции в направлении в точке
дает скорость изменения функции в направлении в точке 
Вектор  называется градиентом функции в точке
называется градиентом функции в точке  от направлен в сторону скорейшего изменения функции и обозначается так:
от направлен в сторону скорейшего изменения функции и обозначается так:

Геометрическое уравнение  задает некоторую поверхность. Чтобы выявить вид поверхности пересечем ее плоскостью
задает некоторую поверхность. Чтобы выявить вид поверхности пересечем ее плоскостью  (постоянная) и такое уравнение
(постоянная) и такое уравнение  задается в плоскости
задается в плоскости  кривая, которая в экономике называется изоквантой. Если на изокванте взять некоторую точку
кривая, которая в экономике называется изоквантой. Если на изокванте взять некоторую точку  то вектор – градиент в этой точке будет перпендикулярной к изокванте.
то вектор – градиент в этой точке будет перпендикулярной к изокванте.
Задача 5.37
 Найти
Найти  в точке
в точке  в направление
в направление 
Решение.

Задача 5.38
Пусть  и
и  Найти
Найти  в точке
в точке  и нарисовать этот вектор.
и нарисовать этот вектор.
Решение



Задача 5.39
 точка
точка  Найти изокванту, которая проходим через данную точку
Найти изокванту, которая проходим через данную точку  и
и 
Решение.

Уравнение изокванты в общем виде  Выберем
Выберем  таким образом, чтобы изокванта проходила через точку
таким образом, чтобы изокванта проходила через точку 

тогда  Изоквантой будет круг с центром в точке
Изоквантой будет круг с центром в точке  и радиусом
и радиусом 
Экстремум функции двух переменных
Если функция  имеет частичные производные, то критические точки, или точки подозрительные на экстремум, ищутся среди решений системы:
имеет частичные производные, то критические точки, или точки подозрительные на экстремум, ищутся среди решений системы:

Пусть  – критическая точка. Обозначим через
– критическая точка. Обозначим через  соответственно значение:
соответственно значение:
 в точке
в точке 
Если
 то функция достигает
то функция достигает 
 то экстремума нет,
то экстремума нет,
 – сомнительный случай, нужны дополнительные исследования.
– сомнительный случай, нужны дополнительные исследования.
Важными являются задачи на условный экстремум, когда ищется экстремум функции  при условии, что переменные
при условии, что переменные  и
и  связаны уравнением связи
связаны уравнением связи 
Такая задача приводится к исследованию на безусловный экстремум функции Лагранжа 

где число  называется множителем Лагранжа.
называется множителем Лагранжа.
После исключения  исследуем на экстремум функцию Лагранжа, как функцию двух переменных
исследуем на экстремум функцию Лагранжа, как функцию двух переменных 
Решение примеров:
Пример 5.50
Исследовать на экстремум функцию

Решение. Находим частичные производные функции

Рассмотрим систему двух уравнений с двумя неизвестными

Решением этой системы будут числа  Точка
Точка  называется критической.
называется критической.
Находим частичные производные второго порядка в точке 


 следует. существует
следует. существует  функции в точке
функции в точке 
Пример 5.51
Исследовать на экстремум функцию двух переменных

Решение. Запишем первые производные функции

Рассмотрим систему двух уравнений с двумя переменными.

Решением этой системы являются числа 
находим вторые частичные производные функции:

Найдем значение вторых частичных переменных в точке 

 следует, существует
следует, существует  функции
функции 
Пример 5.52
Исследовать на экстремум функцию двух переменных

Решение. Находим первые частичные производные функции 

Запишем систему двух уравнений с двумя переменными

Видим, что эта система имеет решения
 и
и 
находим вторые частичные производные функции:

Найдем значение вторых частичных переменных в точке 

Преобразуем точку 

Существует  функции
функции

Пример 5.53
Найти экстремум функции  при условии
при условии 
Функция Лагранжа будет иметь вид

Напишем необходимые условия существования экстремума:

Отсюда получим:
 и
и 
Критическая точка будет иметь координаты:


тогда 
следует, существует  функции
функции 
Метод наименьших квадратов
Пусть зависимость между двумя переменными  и
и  задана в виде таблицы, полученный опытным путем. Это могут быть результаты исследования или наблюдение. статистические обработки материала.
задана в виде таблицы, полученный опытным путем. Это могут быть результаты исследования или наблюдение. статистические обработки материала.

Таблицу можно интерпретировать как множество  точек на плоскости
точек на плоскости 
Нужно подобрать функцию  которая в определенном смысле “кратчайшим образом” была бы вписана в множество данных точек. Если функция линейная, то есть имеет вид
которая в определенном смысле “кратчайшим образом” была бы вписана в множество данных точек. Если функция линейная, то есть имеет вид  то используя метод исследования на экстремум функции двух переменных
то используя метод исследования на экстремум функции двух переменных  получим систему двух линейных уравнений относительно
получим систему двух линейных уравнений относительно  и
и 

Такую систему называют системой нормальных уравнений.
Решение примеров:
Задача 5.64
Имеет данные про цену нефти  (ден. ед) и индекс акций нефтяных компаний
(ден. ед) и индекс акций нефтяных компаний  (ден. ед):
(ден. ед):

Предполагая, что между переменными  и
и  существует линейная зависимость найти эмпиричную формулу вида
существует линейная зависимость найти эмпиричную формулу вида  используя метод наименьших квадратов.
используя метод наименьших квадратов.
Решение. Найдем необходимые на расчетов суммы 
 сложим вспомогательную таблицу:
сложим вспомогательную таблицу:

Система нормальных уравнений имеет вид:

Решив систему, найдем

Тогда

Таким образом, из увеличения цены нефти на 1 денежную единицу индекс акций нефтяных компаний в среднем возрастет на 12, 078 денежных единиц.
Экономические задачи, что приводятся к использованию функций многих переменных
Приведем экономическое толкование понятия частичных производных.
Рассмотрим производственную функцию  которая выражает затраты производства в зависимости от количества двух видов продукции
которая выражает затраты производства в зависимости от количества двух видов продукции  и
и  что выпускается. Пусть фактор
что выпускается. Пусть фактор  изменился на
изменился на  тогда производственная функция изменится на
тогда производственная функция изменится на  Выражение
Выражение  выражает средний прирост производственной функции на единицу прироста фактора
выражает средний прирост производственной функции на единицу прироста фактора  , или средние затраты производства на единицу продукции
, или средние затраты производства на единицу продукции  . Осуществим граничный переход при
. Осуществим граничный переход при  Получим граничные затраты производства на единицу продукции
Получим граничные затраты производства на единицу продукции .
.

Проверив аналогичные вычисления с фактором  получим:
получим:

Эластичность производственной функции  относительно факторов производства
относительно факторов производства  и
и  устанавливается так:
устанавливается так:
 указывает приблизительно процентный прирост производственной функции (снижения) соответственно к приросту фактора
указывает приблизительно процентный прирост производственной функции (снижения) соответственно к приросту фактора  на 1% при условии, что фактор
на 1% при условии, что фактор  не изменяется;
не изменяется;
 указывает приблизительно процентный прирост производственной функции соответственно к приросту фактора
указывает приблизительно процентный прирост производственной функции соответственно к приросту фактора  на 1% при условии, что фактор
на 1% при условии, что фактор  не изменяется;
не изменяется;
Если производственная функция устанавливает зависимость выпуска  от
от  производственных факторов
производственных факторов  в виде
в виде  то дифференциальной характеристикой такой функции будет:
то дифференциальной характеристикой такой функции будет:
 – граничная эффективность фактора
– граничная эффективность фактора 
 – эластичность выпуска
– эластичность выпуска  относительно фактора
относительно фактора 
Решение примеров:
Пример 5.69.
Поток пассажиров  выражается функцией
выражается функцией  где
где  – число жителей,
– число жителей,  – расстояние между городами. Найти частичные производные и объяснить их смысл.
– расстояние между городами. Найти частичные производные и объяснить их смысл.
Решение. Производная  показывает, что при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей. Производная
показывает, что при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей. Производная  показывает, что при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами.
показывает, что при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами.
Пример 5.70
Для выпуска некоторого товара обозначена производственная функция  где
где  и
и  – факторы производства. Обозначить: а) закон изменения производственной функции; б) эластичность функции по каждому фактору; в) коэффициент эластичности по факторам при
– факторы производства. Обозначить: а) закон изменения производственной функции; б) эластичность функции по каждому фактору; в) коэффициент эластичности по факторам при 
Решение.
а) чтобы обозначить изменение производственной функции по факторам  и
и  нужно найти частичные производные
нужно найти частичные производные  и
и 

б) Используем определение эластичности функции по фактору, найдем:

где 
в) Вычислим коэффициенты эластичности при 
найдем сначала значение производственной функции при 

Следует, с возрастанием фактора  на 1% происходит относительно возрастания заданного производственной функции приблизительно на 0,89%. При возрастании фактора
на 1% происходит относительно возрастания заданного производственной функции приблизительно на 0,89%. При возрастании фактора  на 1% и неизменности фактора
на 1% и неизменности фактора  производственная функция возрастает приблизительно на 0.26%. Таким образом, наиболее влияет на производственную функцию
производственная функция возрастает приблизительно на 0.26%. Таким образом, наиболее влияет на производственную функцию  фактор
фактор  .
.
Заметим, что отрицательное значение коэффициента эластичности показывает уменьшение производственной функции при возрастании соответственного фактора. например, если  и
и  – функция выпуска продукции, то возрастание фактора
– функция выпуска продукции, то возрастание фактора  на 1% приводит к снижению выпуска продукции на 0,08%.
на 1% приводит к снижению выпуска продукции на 0,08%.
Пример 5.71
Пусть производственная функция  где
где  – затраты живого труда,
– затраты живого труда,  – затраты автоматизированной работы. Найти
– затраты автоматизированной работы. Найти  и
и  в точке
в точке 
Решение. Приблизительный процентный прирост функции  что соответствует приросту независимых переменных
что соответствует приросту независимых переменных  и
и  на 1% обозначим по формулам:
на 1% обозначим по формулам:
 и
и 
Вычислим частичные производные функции  к
к  и к
и к 

тогда

Найдем значение  и
и  в заданной точке
в заданной точке 

С возрастанием затрат живого труда на 1% объем производства увеличиться приблизительно на 1,67%, а из возрастания затрат автоматизированной работы на 1% объем производства увеличится приблизительно на 1,33%.
Пример 5.72
Фирма изготовляет два вида товаров  и
и  и продает их по цене 1000 рублей и 800 рублей соответственно. Объемы выпуска товаров
и продает их по цене 1000 рублей и 800 рублей соответственно. Объемы выпуска товаров  и
и  Функция затрат имеет вид:
Функция затрат имеет вид:

найти такие значения  и
и  по которым прибыль, полученная фирмой, максимальная. Найти эту прибыль.
по которым прибыль, полученная фирмой, максимальная. Найти эту прибыль.
Решение. Суммарная прибыль от продажи товаров  и
и  будет:
будет:

Прибыль, которую получает фирма, обозначим  Она собой представляет разницу между прибылью
Она собой представляет разницу между прибылью  и затратами
и затратами  а именно:
а именно:

Нужно найти максимум этой функции. Для нахождения стационарных точек находим частичные производные первого порядка от функции  и приравниваем их к нулю:
и приравниваем их к нулю:

решив систему, получим: 
Следует, стационарная точка 

Потому точка  является точкой максимума. Максимальная прибыль достигается при объемах производства
является точкой максимума. Максимальная прибыль достигается при объемах производства 
Найдем сумму максимальной прибыли:

 (рублей).
(рублей).
В экономических исследованиях часто ставиться задача уравнения факторов и показателя, принятого как функцию. В этом случае целесообразно зависимость между функциональным признаком и факторами – аргументами  выразить в виде степенной функции
выразить в виде степенной функции

тогда показатель степени  является показателем эластичности
является показателем эластичности  к
к  Например, объем производства в тысячах рублей в зависимости от некоторых производственной факторов
Например, объем производства в тысячах рублей в зависимости от некоторых производственной факторов  представленных функцией
представленных функцией

Коэффициенты эластичности  показывают,что на темп повышения объема производства наиболее влияет фактор
показывают,что на темп повышения объема производства наиболее влияет фактор  В случае увеличения
В случае увеличения  на 1% выпуск продукции возрастает на 0,48%. Увеличение же
на 1% выпуск продукции возрастает на 0,48%. Увеличение же  на 1% приведет к снижению выпуска продукции на 0,09%.
на 1% приведет к снижению выпуска продукции на 0,09%.
Функции нескольких переменных и их вычисление
На развитие экономических процессов и явлений, как правило, влияет большое количество факторов, часть из которых связана между собой определенными соотношениями, а другие являются независимыми друг от друга. Итак, для построения математической модели этих процессов возникает потребность в использовании рядом с функциями одной переменной функций, зависящих от нескольких переменных.
После изучения данной темы вы сможете:
- ● использовать функции нескольких переменных для формализации экономических процессов;
- ● понимать экономическое содержание частных производных функции нескольких переменных
- ● знать методы дифференцирования функций нескольких переменных
- ● использовать дифференциал функции нескольких переменных для приближенных вычислений экономических показателей;
- ● уметь вычислять производную по направлению и градиент функции и применять их в экономических моделях;
- ● уметь вычислять экстремум функции нескольких переменных
- ● знать понятия эмпирических формул и метода наименьших квадратов;
- ● уметь применять инструменты дифференциального исчисления
- функции нескольких переменных к решению реальных экономических задач;
- ● применять эмпирические формулы и метод наименьших квадратов к обработке данных;
- ● уметь находить эластичность функций нескольких переменных и проводить исследования экономических процессов с ее применением и интерпретировать полученные результаты.
Основные понятия и область определения функции
Функцией нескольких переменных  называется переменная
называется переменная  , если каждому набору значений
, если каждому набору значений  из множества
из множества  по определенному правилу или закону ставится в соответствие одно определенное значение величины
по определенному правилу или закону ставится в соответствие одно определенное значение величины  с множества
с множества  . Переменные
. Переменные  называют независимыми переменными, или аргументами, функции,
называют независимыми переменными, или аргументами, функции,  – зависимой переменной, или функцией. Количество независимых переменных может быть произвольной. Множество наборов
– зависимой переменной, или функцией. Количество независимых переменных может быть произвольной. Множество наборов  которым соответствует определенное значение
которым соответствует определенное значение  , называется областью определения функции, или ее областью существования
, называется областью определения функции, или ее областью существования  . Соответствующее множество значений переменной
. Соответствующее множество значений переменной  называют областью значений функции
называют областью значений функции  .
.
Для простоты изложения материала ограничимся рассмотрением основных понятий и положений о функции нескольких переменных на примере функции двух переменных:  .
.
Как и функция одной переменной, функция двух независимых переменных может быть задана несколькими способами: табличным (с помощью таблицы значений аргументов и функции), аналитическим (с помощью одной или нескольких формул) или графическим способом. В табл. 18.1 приведены табличный способ задания функции двух переменных.
Табличный способ задания функции двух переменных Таблица 18.1

Если для функции одной переменной  областью определения чаще всего является интервал числовой оси (конечный или бесконечный), то в случае функции двух переменных
областью определения чаще всего является интервал числовой оси (конечный или бесконечный), то в случае функции двух переменных  совокупность пар
совокупность пар  , которые образуют область определения функции
, которые образуют область определения функции  , определяет множество точек плоскости, то есть
, определяет множество точек плоскости, то есть  . Областью определения функции двух переменных может быть некоторая ограниченная или неограниченная часть плоскости. В первом случае линию, ограничивающую область, называют пределом области определения. Точки области определения функции, которые не относятся к пределам, называют внутренними точками области. В случае, когда предел принадлежит области определения, имеем замкнутую область. Область, которая содержит только внутренние точки, называется открытой.
. Областью определения функции двух переменных может быть некоторая ограниченная или неограниченная часть плоскости. В первом случае линию, ограничивающую область, называют пределом области определения. Точки области определения функции, которые не относятся к пределам, называют внутренними точками области. В случае, когда предел принадлежит области определения, имеем замкнутую область. Область, которая содержит только внутренние точки, называется открытой.
В случае, когда функция задана формулой, областью определения считается область существования соответствующего математического выражения. Нахождение области определения (для) функции  базируется на знании областей существования основных элементарных функций одной переменной и сводится к решению неравенств (или их систем) относительно переменных
базируется на знании областей существования основных элементарных функций одной переменной и сводится к решению неравенств (или их систем) относительно переменных  и
и  .
.
Найдем область определения некоторых функций.
1) Для функции  областью определения является вся плоскость
областью определения является вся плоскость  , поскольку выражение имеет смысл для произвольных
, поскольку выражение имеет смысл для произвольных  и
и  .
.
2) Для функции  математическое выражение имеет смысл при условии
математическое выражение имеет смысл при условии  , то есть
, то есть  . Это неравенство удовлетворяют все точки, которые находятся в середине круга радиусом 4, центр которого содержится в начале координат. Точки окружности также принадлежат области определения, то есть область определения функции является замкнутой (рис. 18.1).
. Это неравенство удовлетворяют все точки, которые находятся в середине круга радиусом 4, центр которого содержится в начале координат. Точки окружности также принадлежат области определения, то есть область определения функции является замкнутой (рис. 18.1).

Рис. 18.1
3) Аналитическое выражение, определяющее функцию  , имеет смысл, когда
, имеет смысл, когда . Последнее неравенство описывает часть плоскости, расположенной над параболой
. Последнее неравенство описывает часть плоскости, расположенной над параболой  , а точки самой параболы в область определения не относятся. Это пример открытой области определения (рис. 18.2).
, а точки самой параболы в область определения не относятся. Это пример открытой области определения (рис. 18.2).

Рис. 18.2
Алгоритм нахождения области определения функции предусматривает следующие этапы:
1) записывают неравенство или систему неравенств, которая соответствует области определения элементарных функций, которые образуют аналитическое выражение функции  ;
;
2) с помощью графического или аналитического решения полученной неровности или системы неравенств находят область определения.
Каждая пара значений  из множества
из множества  определяет точку
определяет точку  на плоскости
на плоскости  , а значение функции
, а значение функции  является аппликатой точки
является аппликатой точки  в пространстве.
в пространстве.
Графиком функции двух переменных  называют множество точек трехмерного пространства
называют множество точек трехмерного пространства  , аппликанта которых связана с абсциссой
, аппликанта которых связана с абсциссой  и ординатой
и ординатой  функциональной зависимостью
функциональной зависимостью  . Следовательно, графиком функции двух непрерывных переменных является некоторая поверхность в трехмерном пространстве.
. Следовательно, графиком функции двух непрерывных переменных является некоторая поверхность в трехмерном пространстве.
Например, областью определения функции  является все множество точек плоскости
является все множество точек плоскости  , а ее графиком, как известно из аналитической геометрии, является параболоид вращения. Он изображен на рис. 18.3.
, а ее графиком, как известно из аналитической геометрии, является параболоид вращения. Он изображен на рис. 18.3.

Рис. 18.3
Как правило, построение графика функции двух переменных является сложной задачей. Поэтому для определения характера поведения функции очень часто пользуются понятием линии уровня функции.
Линией уровня функции двух переменных  называют такое множество точек на плоскости
называют такое множество точек на плоскости  , что во всех точках этой линии значения функции одинаковое и равно некоторой постоянной величине
, что во всех точках этой линии значения функции одинаковое и равно некоторой постоянной величине  . Число
. Число  в этом случае называется уровнем функции (рис. 18.4).
в этом случае называется уровнем функции (рис. 18.4).

Рис. 18.4
Примером применения функций нескольких переменных в экономике является производственная функция  , которая устанавливает зависимость величины созданного общественного продукта
, которая устанавливает зависимость величины созданного общественного продукта  от различных факторов: расходы (живого) труда
от различных факторов: расходы (живого) труда  , объем производственных фондов
, объем производственных фондов  , энергоемкость производства
, энергоемкость производства и т.д.; параметры
и т.д.; параметры  удовлетворяют условию:
удовлетворяют условию: 
Примером производственной функции является функция Кобба-Дугласа, которая устанавливает функциональную зависимость между объемом основных фондов  , затратами труда
, затратами труда  и объему
и объему  , где
, где  – характеристика производительности выбранной технологии,
– характеристика производительности выбранной технологии,  ;
;  – коэффициент эластичности по труду
– коэффициент эластичности по труду  .
.
В задачах потребительского выбора используется так называемая функция полезности, описывающая количественную характеристику  целесообразности приобретения того или иного набора
целесообразности приобретения того или иного набора  различных товаров (благ)
различных товаров (благ)  , где
, где  – количество
– количество  -го блага в натуральных единицах. Примерами таких функций являются:
-го блага в натуральных единицах. Примерами таких функций являются:
логарифмическая функция
 где
где  – параметры
– параметры 
функция постоянной эластичности
 где
где  – постоянные
– постоянные 
Конечно, в основу модели поведения потребителей возлагают гипотезу: каждый из них, осуществляя выбор наборов благ при заданных ценах и имеющемся доходе, стремится максимизировать уровень удовлетворения своих потребностей.
Граница и непрерывность функции двух переменных
Рассмотрим понятие  –окрестности точки
–окрестности точки  , под которым будем понимать совокупность всех точек
, под которым будем понимать совокупность всех точек  , которые находятся внутри круга радиусом
, которые находятся внутри круга радиусом  с центром в точке
с центром в точке  то есть это множество точек, координаты которых удовлетворяют неравенство
то есть это множество точек, координаты которых удовлетворяют неравенство

Понятие границы функции двух переменных сложнее, чем понятие границы для функции одной переменной. Это объясняется тем, что при определении предела одной переменной направлений, по которым может приближаться аргумент в избранное значения, только два: вдоль оси  слева или справа от заданной точки. При определении пределов функции двух переменных существует множество направлений, по которым может осуществляться приближения точки
слева или справа от заданной точки. При определении пределов функции двух переменных существует множество направлений, по которым может осуществляться приближения точки  до точки
до точки  .
.
Общепринятым является требование: значение предела  при
при  равно
равно  только тогда, когда величина
только тогда, когда величина  не будет зависеть от пути, по которому происходит приближения точки
не будет зависеть от пути, по которому происходит приближения точки  к точке
к точке  . Сформулируем следующее определение предела.
. Сформулируем следующее определение предела.
Постоянная величина  называется пределом функции
называется пределом функции  в точке
в точке  (при приближении точки
(при приближении точки  к точке
к точке  ), если любом наперед заданном положительном числу
), если любом наперед заданном положительном числу  можно поставить в соответствие такое число
можно поставить в соответствие такое число  , которое зависит от
, которое зависит от  , что для всех точек
, что для всех точек  с
с  -окрестности точки
-окрестности точки  выполняется неравенство
выполняется неравенство

Такое определение предела функции двух (и большего числа) переменных называют определением «языком  », или определением по Коши.
», или определением по Коши.
Предел функции двух переменных обозначают так:

Число  не зависит от того, каким путем происходит приближения точки
не зависит от того, каким путем происходит приближения точки  к точке
к точке  .
.
Основные теоремы о пределах функций одной переменной распространяются и на случай функций двух переменных, а именно:
1. Граница постоянной величины равна самой постоянной:

2. Граница алгебраической суммы конечного числа функций равен алгебраической сумме границ этих функций, если существуют эти границы:

3. Граница произведения конечного числа функций, границы которых существуют, равна произведению границ этих функций:

4. Граница доли двух функций равна доле границ этих функций, если существуют границы этих функций и граница знаменателю не равна нулю:

Установим существование предела  при
при  y
y
Пусть точка  приближается к точке
приближается к точке  вдоль прямой
вдоль прямой  , где
, где  – угловой коэффициент. Тогда
– угловой коэффициент. Тогда

Таким образом, мы получили, что граница зависит от углового коэффициента  , то есть от того, каким путем приближается точка
, то есть от того, каким путем приближается точка  к точке
к точке  . Это означает, что граница функции в точке
. Это означает, что граница функции в точке  не существует.
не существует.
Функция f является непрерывной в точке
является непрерывной в точке  , если выполняются следующие условия:
, если выполняются следующие условия:
1) функция определена в этой точке;
2) существует конечная граница при  и
и 
3) эта граница равна значению функции в точке 
Если в какой-то точке  крайней мере одна из указанных выше условий не выполняется, эта точка является точкой разрыва.
крайней мере одна из указанных выше условий не выполняется, эта точка является точкой разрыва.
Приведенные выше определения описывают непрерывность функции  , по совокупности переменных. Если зафиксировать одну из переменных, например,
, по совокупности переменных. Если зафиксировать одну из переменных, например,  , то получим функцию от одной переменной
, то получим функцию от одной переменной  . Если эта функция
. Если эта функция  является непрерывной в точке
является непрерывной в точке  , то говорят, что функция
, то говорят, что функция  является непрерывной в точке
является непрерывной в точке  по переменной
по переменной  . Аналогично вводится определение непрерывности функции
. Аналогично вводится определение непрерывности функции  в точке
в точке  по переменной
по переменной  .
.
Если функция  непрерывна в каждой внутренней точке области и на ее границе, то такая функция является непрерывной в замкнутой области.
непрерывна в каждой внутренней точке области и на ее границе, то такая функция является непрерывной в замкнутой области.
Для функций нескольких переменных выполняются теоремы о непрерывности суммы, произведения и частного, установленные ранее для функции одной переменной. Справедливы также свойства функции, непрерывной в замкнутой области. Приведем одну из этих свойств о наибольшее и наименьшее значения функции в замкнутой области, которое будет использовано в последующих главах.
Если функция определена и непрерывна в замкнутой области
определена и непрерывна в замкнутой области  , то внутри этой области найдется по крайней мере одна такая точка
, то внутри этой области найдется по крайней мере одна такая точка  , что для всех остальных точек области выполняется неравенство
, что для всех остальных точек области выполняется неравенство

и по крайней мере одна такая точка  , что для всех остальных точек выполняется неравенство
, что для всех остальных точек выполняется неравенство

Значение  является наибольшим значением функции
является наибольшим значением функции  в области
в области  , а значение
, а значение  – ее наименьшим значением в этой области. Доказательство выходит за пределы данного учебника.
– ее наименьшим значением в этой области. Доказательство выходит за пределы данного учебника.
Приросты функции двух переменных
Пусть задана функция  . Выберем произвольную точку
. Выберем произвольную точку  с области ее определения.
с области ее определения.
Зафиксируем значение одной из независимых переменных, например, переменной  , и предоставим другой независимой переменной
, и предоставим другой независимой переменной  прирост
прирост  . Тогда функция
. Тогда функция  получит прирост, который называют частным приростом
получит прирост, который называют частным приростом  по
по  в точке
в точке  и обозначают
и обозначают  . Иными словами, частное прирост – это разница между значениями функции в точке
. Иными словами, частное прирост – это разница между значениями функции в точке  и в исходной точке
и в исходной точке  :
:

Аналогично, зафиксировав значение переменной  и предоставив прирост независимой переменной y, то есть, если с точки
и предоставив прирост независимой переменной y, то есть, если с точки  перейти в точку
перейти в точку  , получим частное прирост
, получим частное прирост  по
по  :
:

Если независимой переменной  предоставить прирост
предоставить прирост  и одновременно независимой переменной y предоставить прирост
и одновременно независимой переменной y предоставить прирост  , рассмотрев разницу между значениями функции в точке
, рассмотрев разницу между значениями функции в точке  и в точке
и в точке  , то получим полный прирост функции в точке
, то получим полный прирост функции в точке  :
:
Проиллюстрируем сказанное на примере функции 
Найдем частные приросты и полный прирост этой функции:

Отсюда видно, что 
Частные производные
Частной производной функции  по переменной
по переменной  называется предел отношения частного прироста функции по соответствующей переменной
называется предел отношения частного прироста функции по соответствующей переменной  к приросту самой независимой переменной
к приросту самой независимой переменной  при условии, что приращение аргумента стремится к нулю
при условии, что приращение аргумента стремится к нулю  произвольным образом. Частная производная по переменной
произвольным образом. Частная производная по переменной  от функции
от функции  имеет ряд обозначений:
имеет ряд обозначений: 
 Согласно определению можно записать:
Согласно определению можно записать:

Аналогично определяется частная производная по переменной y от функции 

Эти производные являются аналогами производных функций одной переменной, но существенно отличаются от них тем, что как сама функция, так и ее производные зависят от двух переменных. Из того, что частные приросты были получены в предположении постоянства одной из независимых переменных, следует, что правила нахождения частных производных не отличаются от правил дифференцирования функций одной переменной.
При нахождении частных производных функции двух переменных одна независимая переменная считается постоянной величиной и дифференцировки происходит с использованием таблицы производных основных элементарных функций одной переменной и правил дифференцирования.
Например, найдем частные производные функции 
Дифференцируем заданную функцию сначала по переменной  , при этом переменная
, при этом переменная  считаем постоянной. По правилу дифференцирования сложной функции получим:
считаем постоянной. По правилу дифференцирования сложной функции получим:

Теперь найдем производную от заданной функции по переменной  , считая постоянной переменную
, считая постоянной переменную  :
:

Геометрическая интерпретация частных производных
Напомним, что графиком функции  является поверхность
является поверхность  в трехмерном пространстве (рис. 18.5).
в трехмерном пространстве (рис. 18.5).

Рис. 18.5
Возьмем на плоскости  точку
точку  и проведем через нее плоскость, которая описывается уравнением
и проведем через нее плоскость, которая описывается уравнением , где
, где  . При фиксированном значении y частная производная
. При фиксированном значении y частная производная  равна тангенсу угла
равна тангенсу угла  , который образует касательная, проходящей через точку
, который образует касательная, проходящей через точку  , к линии пересечения графика функции и плоскости с положительным направлением оси
, к линии пересечения графика функции и плоскости с положительным направлением оси  .
.

Аналогично получаем, что

где  – угол между положительным направлением оси
– угол между положительным направлением оси  и касательной к линии пересечения поверхности
и касательной к линии пересечения поверхности  с плоскостью
с плоскостью  .
.
Поскольку частные производные от функции  являются функциями независимых переменных
являются функциями независимых переменных  и
и  , то их, в свою очередь, можно дифференцировать.
, то их, в свою очередь, можно дифференцировать.
Как известно, второй производной функции является первая производная от первой производной этой функции. Потому как результат дифференцирования частных производных первого порядка от функции нескольких переменных мы получим частные производные второго порядка функции  . Рассмотрим эти производные. Так, если дифференцировки и первый, и второй раз осуществляется по переменной
. Рассмотрим эти производные. Так, если дифференцировки и первый, и второй раз осуществляется по переменной  , то мы получаем частную производную второго порядка по переменной
, то мы получаем частную производную второго порядка по переменной  :
:

Аналогично получаем частную производную второго порядка по переменной  :
:

а также смешанные производные:

и

Для смешанных производных справедлива теорема, которую предоставим без доказательства.
Теорема 18.1 (о равенстве смешанных частных производных). Если функция  и ее частные производные
и ее частные производные  определенные и непрерывные в некоторой области, то смешанные производные не зависящие от порядка дифференцирования, то есть
определенные и непрерывные в некоторой области, то смешанные производные не зависящие от порядка дифференцирования, то есть

Таким образом, функция двух переменных  , которая удовлетворяет определенным требованиям непрерывности, имеет только три различных частных производных второго порядка.
, которая удовлетворяет определенным требованиям непрерывности, имеет только три различных частных производных второго порядка.
Найдем частные производные второго порядка функции 

Отметим, что функция  определена и непрерывна для любых пар
определена и непрерывна для любых пар  , поскольку образована добавлением и умножением непрерывных функций.
, поскольку образована добавлением и умножением непрерывных функций.
Сначала найдем частные производные первого порядка:

Они также являются определенными и непрерывными на  . Теперь найдем частные производные второго порядка:
. Теперь найдем частные производные второго порядка:

Следовательно, мы получили

Частные дифференциалы и полный дифференциал. Использование в приближенных вычислениях
Найдя полный прирост 
 функции
функции  при переходе от точки
при переходе от точки  к точке
к точке  , остановимся на анализе его структуры.
, остановимся на анализе его структуры.
Функция называется дифференцируемой в точке, если ее прирост  можно представить в виде суммы линейной (относительно
можно представить в виде суммы линейной (относительно  и
и  ) части и слагаемых высокого порядка малость
) части и слагаемых высокого порядка малость

где  – бесконечно малые при
– бесконечно малые при  и
и  – некоторые постоянные.
– некоторые постоянные.
Выражение  , который является главной частью прироста функции, линейно зависит от приростов ее аргументов, называется полным дифференциалом функции и обозначается
, который является главной частью прироста функции, линейно зависит от приростов ее аргументов, называется полным дифференциалом функции и обозначается  или
или  :
:

Теорема 18.2 (первое необходимое условие диффренцируемости). Если функция  является дифференцируемой в точке
является дифференцируемой в точке  , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство. Если в соотношении (18.12) перейти к пределу при  и
и  , получим
, получим

поэтому функция  является непрерывной в точке
является непрерывной в точке  , что и требовалось доказать.
, что и требовалось доказать.
Теорема 18.3 (второе необходимое условие дифференцируемости). Если функция  является дифференцируемой в точке
является дифференцируемой в точке  , то есть выполняется условие (18.12), то в этой точке существуют обе ее частные производные, причем
, то есть выполняется условие (18.12), то в этой точке существуют обе ее частные производные, причем

Доказательство. По условию теоремы функция  является дифференцируемой в точке
является дифференцируемой в точке  , то есть в этой точке выполняется соотношение (18.12).
, то есть в этой точке выполняется соотношение (18.12).
Предположим, что  . Тогда
. Тогда  . Поделив последнее выражение на
. Поделив последнее выражение на  , перейдем к границе при
, перейдем к границе при  получим
получим

Следовательно,

Аналогично можно доказать, что

Необходимое условие дифференцируемости не является достаточным.
Теорема 18.4 (достаточное условие дифференцируемости). Если функция  в окрестности точки
в окрестности точки  имеет непрерывные частные производные
имеет непрерывные частные производные  и
и  , то она дифференцируемой в этой точке (без доказательства).
, то она дифференцируемой в этой точке (без доказательства).
Аналогично тому как было введено понятие дифференциала для функции одной переменной, рассмотрим это понятие для функции нескольких переменных. Вернемся к формуле (18.12). По теореме 18.3 коэффициент  равен значению частной производной первого порядка от функции
равен значению частной производной первого порядка от функции  по аргументу
по аргументу  для точки
для точки  , а коэффициент
, а коэффициент  – значению частной производной первого порядка от функции
– значению частной производной первого порядка от функции  по аргументу y для точки
по аргументу y для точки  . Следовательно, полный прирост функции
. Следовательно, полный прирост функции  в точке
в точке  имеет вид
имеет вид

где  – бесконечно малые при
– бесконечно малые при 
Выражение  которое является главной линейной частью полного приращения функции, называется полным дифференциалом функции
которое является главной линейной частью полного приращения функции, называется полным дифференциалом функции  .
.
Поскольку для независимых переменных их приросты и дифференциалы совпадают, то есть  то формула для полного дифференциала примет вид
то формула для полного дифференциала примет вид

Каждый из слагаемых формулы (18.13) является главной частью приращения функции, линейно зависит от прироста данного аргумента при условии, что второй аргумент является постоянным. Каждый из этих слагаемых (18.13) называется частичным дифференциалом по соответствующим аргументом:  , где
, где
 – частичный дифференциал функции
– частичный дифференциал функции  по аргументу
по аргументу  ;
;
 – частичный дифференциал функции
– частичный дифференциал функции  по аргументу
по аргументу  .
.
Основным свойством дифференциала является инвариантность формы первого дифференциала, то есть равенство (18.13) выполняется независимо от того, являются переменные  и
и  независимыми, или они являются функциями других аргументов.
независимыми, или они являются функциями других аргументов.
Заметим, что дифференциал  (18.13) называют дифференциалом первого порядка. Если функции
(18.13) называют дифференциалом первого порядка. Если функции  и
и  дифференцируемыми в точке
дифференцируемыми в точке  , можно ввести понятие дифференциала второго порядка как дифференциала от дифференциала первого порядка
, можно ввести понятие дифференциала второго порядка как дифференциала от дифференциала первого порядка  . Следовательно, согласно формуле (18.13) получим:
. Следовательно, согласно формуле (18.13) получим:

Аналогично можно найти дифференциалы третьего порядка и высших порядков.
Полный дифференциал первого порядка  является главной линейной частью приращения функции, поэтому с его помощью можно осуществлять приближенное вычисление значений функции, отбрасывая в выражении для
является главной линейной частью приращения функции, поэтому с его помощью можно осуществлять приближенное вычисление значений функции, отбрасывая в выражении для  слагаемые, бесконечно малыми большего порядка по сравнению с
слагаемые, бесконечно малыми большего порядка по сравнению с  и
и  . Для этого преобразуем формулу для полного приращения функции с учетом соотношения (18.12) следующим образом:
. Для этого преобразуем формулу для полного приращения функции с учетом соотношения (18.12) следующим образом:

Разница между полным приростом функции  и ее полным дифференциалом в точке
и ее полным дифференциалом в точке  при
при  и
и  является величиной бесконечно малой высшего порядка по сравнению с приростом ее аргументов. Отсюда следует, что для достаточно малых
является величиной бесконечно малой высшего порядка по сравнению с приростом ее аргументов. Отсюда следует, что для достаточно малых  и
и  значение функции в точке
значение функции в точке  приближенно равен значению функции в точке
приближенно равен значению функции в точке  , к которому добавлено выражение
, к которому добавлено выражение  , то есть дифференциал функции в точке
, то есть дифференциал функции в точке  . Итак, имеем формулу для приближенных вычислений значений функции:
. Итак, имеем формулу для приближенных вычислений значений функции:

Таким образом, получаем значение функции

или приближенно

Для приближенного вычисления значения функции в точке применяется следующий алгоритм:
1) найти точку  , координаты которой близки к координатам данной точки
, координаты которой близки к координатам данной точки , а значение функции
, а значение функции  в точке
в точке  легко вычисляется;
легко вычисляется;
2) определить частные производные первого порядка в точке  ;
;
3) воспользоваться формулой (18.16).
Вычислить приближенно 
Рассмотрим функцию  . Пусть
. Пусть  , тогда определяем
, тогда определяем  . Считая, что
. Считая, что 
 , получим
, получим  . Находим частные производные первого порядка:
. Находим частные производные первого порядка:

и вычислим полный дифференциал в точке 

Воспользуемся формулой (18.16):

Вычисления на калькуляторе дает результат: 4,9987398. Как видно, абсолютная погрешность составляет 0,0007398.
Для иллюстрации точности вычисления с помощью дифференциала приведем еще один пример. Пусть общая прибыль от реализации определенной продукции описывается соотношением:  где
где  – прибыль от реализации единицы продукции,
– прибыль от реализации единицы продукции,  – количество реализованной продукции. В определенный момент времени прибыль от реализации составляет
– количество реализованной продукции. В определенный момент времени прибыль от реализации составляет  Определим, как изменится общая прибыль, если выручка от реализации единицы продукции возрастет на величину
Определим, как изменится общая прибыль, если выручка от реализации единицы продукции возрастет на величину  , а количество реализованной продукции – на
, а количество реализованной продукции – на  .
.
Приращение функции, описывающей прибыль от реализации, определяется формулой:

поскольку для данной функции

Численно функция  равна площади прямоугольника со сторонами
равна площади прямоугольника со сторонами  и
и  Тогда прирост функции
Тогда прирост функции  можно рассматривать как прирост площади прямоугольника при условии, что сторона, которая имела длину
можно рассматривать как прирост площади прямоугольника при условии, что сторона, которая имела длину  , получит прирост
, получит прирост  , а сторона длиной
, а сторона длиной  – прирост
– прирост  (рис. 18.6).
(рис. 18.6).
Так, площадь выходного прямоугольника равна  (на рис. 18.6 этот прямоугольник не имеет штриховки).
(на рис. 18.6 этот прямоугольник не имеет штриховки).

Рис. 18.6
Если предоставить прирост лишь одной из сторон прямоугольника, а длину другой оставить постоянной, то площадь выходного прямоугольника увеличится на величину, соответствующую частичном дифференциалу функции  по этой переменной (эта доля прироста функции на рис. 18.6 соответствует одному из прямоугольников, имеют штриховку под одним наклоном), а сумма площадей этих двух прямоугольников – полному дифференциалу функции. Тогда полный прирост функции (вся заштрихованная площадь) отличается от ее полного дифференциала на величину
по этой переменной (эта доля прироста функции на рис. 18.6 соответствует одному из прямоугольников, имеют штриховку под одним наклоном), а сумма площадей этих двух прямоугольников – полному дифференциалу функции. Тогда полный прирост функции (вся заштрихованная площадь) отличается от ее полного дифференциала на величину  (на рис. 18.6 это площадь маленького прямоугольника, имеет двойную штриховку). Так как по условию задачи
(на рис. 18.6 это площадь маленького прямоугольника, имеет двойную штриховку). Так как по условию задачи  и
и  , то величина
, то величина  является бесконечно малой более высокого порядка по сравнению с бесконечно малыми
является бесконечно малой более высокого порядка по сравнению с бесконечно малыми  и
и  . В данном примере величина
. В данном примере величина  и является абсолютной погрешностью при замене полного приращения функции ее дифференциалом. Поскольку относительная погрешность равна отношению абсолютной погрешности к значению функции, то в рассматриваемом примере относительная погрешность равна
и является абсолютной погрешностью при замене полного приращения функции ее дифференциалом. Поскольку относительная погрешность равна отношению абсолютной погрешности к значению функции, то в рассматриваемом примере относительная погрешность равна

Производная по направлению
Пусть функция  задана в некоторой окрестности точки
задана в некоторой окрестности точки  . Рассмотрим направление (рис. 19.1), заданный единичным вектором
. Рассмотрим направление (рис. 19.1), заданный единичным вектором  , где
, где  .
.

Рис. 19.1
Перейдем вдоль направления этого вектора от точки  до точки
до точки  . Функция получит полный прирост:
. Функция получит полный прирост:

Вектор  , координатами которого является приросты аргументов, назовем вектором приростов:
, координатами которого является приросты аргументов, назовем вектором приростов:  . Его длина равна
. Его длина равна 
 . Проекция вектора приростов на направление
. Проекция вектора приростов на направление  , которую обозначим через
, которую обозначим через  , положительная, если его направление совпадает с направлением вектора
, положительная, если его направление совпадает с направлением вектора  , и отрицательная – в противном случае:
, и отрицательная – в противном случае:

Производной функции  по направлению
по направлению  называется предел отношения
называется предел отношения  при условии, что
при условии, что  , и обозначается символом
, и обозначается символом 
Следовательно,

Теорема 19.1 (о производной по направлению). Если функция  определена в окрестности точки
определена в окрестности точки  и имеет в ней непрерывные частные производные, то в этой точке существует производная по направлению произвольного вектора
и имеет в ней непрерывные частные производные, то в этой точке существует производная по направлению произвольного вектора  , которую можно найти по формуле
, которую можно найти по формуле

где  и
и  – направляющие косинусы.
– направляющие косинусы.
Доказательство. Возьмем на луче, выходящий из точки  в направлении вектора
в направлении вектора  , точку
, точку  Поскольку функция
Поскольку функция  имеет непрерывные частные производные в точке
имеет непрерывные частные производные в точке  то ее полный прирост, соответствует приросту ее аргументов
то ее полный прирост, соответствует приросту ее аргументов  и
и  , можно записать в виде:
, можно записать в виде:

Запишем вектор приростов:  . На рис. 19.1 видно, что
. На рис. 19.1 видно, что 
 Тогда:
Тогда:

Если точка  направляется в точки
направляется в точки  вдоль заданного луча и при этом
вдоль заданного луча и при этом  и
и  , то
, то 
В этих условиях перейдем в последнем выражении до предела. Поскольку  бесконечно малые при
бесконечно малые при  и
и  , а направляющие косинусы и частные производные в точке
, а направляющие косинусы и частные производные в точке  являются постоянными, то получим:
являются постоянными, то получим:

Отсюда:

Градиент функции и линии уровня
Рассмотрим функцию  , которая определена в области
, которая определена в области  и является дифференцируемой в точке
и является дифференцируемой в точке 
Градиентом функции  в точке
в точке  называется вектор, координатами которого являются частные производные первого порядка функции
называется вектор, координатами которого являются частные производные первого порядка функции  в этой точке. Градиент обозначается символом
в этой точке. Градиент обозначается символом  . Следовательно, если разложить градиент по единичным базисом, то его можно записать в векторной форме:
. Следовательно, если разложить градиент по единичным базисом, то его можно записать в векторной форме:

или в координатной форме: 
Выберем в точке  направление, которое определяется единичным вектором
направление, которое определяется единичным вектором  . Найдем скалярное произведение градиента функции в данной точке и направляющего вектора
. Найдем скалярное произведение градиента функции в данной точке и направляющего вектора 

С учетом (19.1) имеем

Отсюда по определению скалярного произведения получим:

где  – угол между векторами
– угол между векторами  и
и 
Отметим два основных свойства  , вытекающие из полученной формулы (19.3):
, вытекающие из полученной формулы (19.3):
1) производная по направлению в данной точке достигает наибольшего значения, если направление вектора  совпадает с направлением
совпадает с направлением  , то есть направление градиента функции является направлением, по которому функция меняется с максимальной скоростью;
, то есть направление градиента функции является направлением, по которому функция меняется с максимальной скоростью;
2) градиент в выбранной точке образует прямой угол с касательной к линии уровня функции, проходящей через эту точку 
Рассмотрим пример. Пусть задано функцию

Определим ее градиент в точке  и убедимся, что градиент перпендикулярен линии уровня, проходящей через эту точку. Для этого сначала определим частные производные первого порядка от функции
и убедимся, что градиент перпендикулярен линии уровня, проходящей через эту точку. Для этого сначала определим частные производные первого порядка от функции 

и вычислим их в точке 

Следовательно, можем записать, что 
Теперь найдем уравнение линии уровня, проходящей через точку  Значение функции
Значение функции  (ее уровень), что соответствует этой линии уровня, составляет
(ее уровень), что соответствует этой линии уровня, составляет  Следовательно, уравнением линии уровня при
Следовательно, уравнением линии уровня при  будет
будет  Сведем его к каноническому виду:
Сведем его к каноническому виду:

Следовательно, получили каноническое уравнение окружности с центром в точке с координатами  , радиус которого равен
, радиус которого равен  . Чтобы убедиться, что градиент функции перпендикулярно к линии уровня, найдем угловой коэффициент касательной к линии уровня в точке
. Чтобы убедиться, что градиент функции перпендикулярно к линии уровня, найдем угловой коэффициент касательной к линии уровня в точке 
Уравнение линии уровня определяется функцией, заданной неявно. По формуле производной от такой функции имеем:

Следовательно, в точке  угловой коэффициент касательной к линии уровня функции
угловой коэффициент касательной к линии уровня функции  равна 0,2. Градиент
равна 0,2. Градиент  образует с осью
образует с осью  угол, тангенс которого определяем как отношение координат градиента:
угол, тангенс которого определяем как отношение координат градиента:  Тогда произведение угловых коэффициентов касательной и градиента равен
Тогда произведение угловых коэффициентов касательной и градиента равен  Следовательно, градиент функции в точке
Следовательно, градиент функции в точке  является перпендикуляром к касательной линии уровня функции в выбранной точке. На рис. 19.2 изображена линию уровня функции
является перпендикуляром к касательной линии уровня функции в выбранной точке. На рис. 19.2 изображена линию уровня функции  6 при уровне
6 при уровне  , а также градиент этой функции в точке
, а также градиент этой функции в точке 

Рис. 19.2
Локальный экстремум функции двух переменных
Пусть функция  определена на множестве
определена на множестве  и точка
и точка  . Говорят, что функция
. Говорят, что функция  в точке
в точке  имеет локальный максимум (минимум), если вокруг этой точки существует такой
имеет локальный максимум (минимум), если вокруг этой точки существует такой  -окрестность, что для всех точек этого окрестности выполняется неравенство:
-окрестность, что для всех точек этого окрестности выполняется неравенство:

Теорема 19.2 (необходимое условие экстремума). Если функция двух переменных  дифференцированная в точке
дифференцированная в точке  и имеет в этой точке экстремум, то обе частные производные первого порядка в этой точке равны нулю:
и имеет в этой точке экстремум, то обе частные производные первого порядка в этой точке равны нулю:

Как и в случае функции одной переменной, точки, где первые производные равны нулю или не существуют, называются критическими. Критические точки, в которых первые производные равны нулю, называются стационарными.
Выполнение условия (19.4) является необходимым условием экстремума, однако не является достаточным условием экстремума. Решив систему этих уравнений, определим координаты точек, в которых функция может иметь экстремум.
Чтобы сформулировать достаточное условие экстремума, рассмотрим определитель, элементами которого являются производные второго порядка функции 

Матрица, элементами которой являются частные производные второго порядка функции нескольких переменных, называется матрицей Гессе, а ее определитель – гессиан. Для функции двух переменных гессиан является определителем второго порядка.
Теорема 19.3 (достаточное условие экстремума). Если функция  в стационарной точке
в стационарной точке  и некоторой ее окрестности имеет все частные производные второго порядка и гессиан в этой точке положительный, то функция
и некоторой ее окрестности имеет все частные производные второго порядка и гессиан в этой точке положительный, то функция  имеет в точке
имеет в точке  локальный экстремум. При этом, если в этой точке
локальный экстремум. При этом, если в этой точке  , то в стационарной точке функция имеет минимум, если
, то в стационарной точке функция имеет минимум, если  , то – максимум.
, то – максимум.
Следовательно, достаточное условие экстремума для функции двух переменных можно записать в виде:

В случае, когда в стационарной точке определитель (19.5) отрицательный, то функция локального экстремума в этой точке не имеет. Если в стационарной точке гессиан равен нулю, то приведенная выше теорема не отвечает на вопрос о существовании экстремума, и нужны дополнительные исследования.
Проведем исследование функции  на локальный экстремум. За необходимым условием экстремума проверим, имеет ли функция стационарные точки. Для этого найдем ее производные первого порядка:
на локальный экстремум. За необходимым условием экстремума проверим, имеет ли функция стационарные точки. Для этого найдем ее производные первого порядка:

Положив эти производные равными нулю, получим систему уравнений для вычисления координат стационарной точки:

Отсюда получим, что стационарная точка  имеет координаты:
имеет координаты:

За достаточным условием проверим, является ли эта стационарная точка точкой локального экстремума. Для этого найдем все производные второго порядка и вычислим их значения в стационарной точке:

Теперь составим матрицу Гессе и вычислим ее определитель.
Получаем:

Поскольку гессиан является положительным, то функция в стационарной точке имеет экстремум. Теперь определяем характер экстремума. Имеем  отсюда следует, что стационарная точка является точкой локального минимума.
отсюда следует, что стационарная точка является точкой локального минимума.
Вычислим значение функции в точке 

Проведем исследование функции  на локальный экстремум. Сначала определим первые производные функции и по системе уравнений, которую получаем необходимым условием экстремума, вычислим координаты стационарной точки:
на локальный экстремум. Сначала определим первые производные функции и по системе уравнений, которую получаем необходимым условием экстремума, вычислим координаты стационарной точки:

Найдем производные второго порядка:

Проверим, выполняется достаточное условие экстремума:

Поскольку гессиан отрицательный, то функция не имеет экстремума.
Условный экстремум
Пусть функция  определена в области
определена в области  , и на координаты точек области наложено соотношение
, и на координаты точек области наложено соотношение  , которое называется уравнением связи. Это означает, что на области определения функции рассматриваются только точки, для которых выполняется равенство
, которое называется уравнением связи. Это означает, что на области определения функции рассматриваются только точки, для которых выполняется равенство  Множество всех таких точек обозначать через
Множество всех таких точек обозначать через  и точка
и точка  то есть
то есть 
Можно считать, что в этом случае аргументы функции  не являются независимыми, а связаны между собой соотношением
не являются независимыми, а связаны между собой соотношением  Рассмотрим задачу о нахождении экстремума такой функции. В этом случае применяют термин условный экстремум.
Рассмотрим задачу о нахождении экстремума такой функции. В этом случае применяют термин условный экстремум.
Точка  называется точкой условного максимума (минимума) функции
называется точкой условного максимума (минимума) функции  если существует такая
если существует такая  -окрестность этой точки, для всех точек
-окрестность этой точки, для всех точек  сечения этого окрестности с множеством
сечения этого окрестности с множеством  выполняется неравенство:
выполняется неравенство:

Для решения задачи на условный экстремум применяются метод сведения к экстремума функции одной переменной или метод множителей Лагранжа.
Метод сведения к экстремума функции одной переменной
Если уравнение  можно решить относительно одной из переменных, то есть представить в явном виде эту переменную как функцию другой переменной, то, подставив ее в функцию
можно решить относительно одной из переменных, то есть представить в явном виде эту переменную как функцию другой переменной, то, подставив ее в функцию  , получим новую функцию, которая зависит только от одной переменной. Локальный экстремум этой новой функции и будет условным экстремумом исходной функции
, получим новую функцию, которая зависит только от одной переменной. Локальный экстремум этой новой функции и будет условным экстремумом исходной функции  . Следовательно, задачу поиска условного экстремума можно свести к решению задачи о нахождении локального экстремума функции одной переменной.
. Следовательно, задачу поиска условного экстремума можно свести к решению задачи о нахождении локального экстремума функции одной переменной.
Найдем условный экстремум функции  , если
, если  .
.
В данном случае можно из уравнения связи одну из переменных выразить через другую и подставить в функцию, а затем исследовать полученную функцию одной переменной на локальный экстремум. Следовательно, получим  , подставим в исходную функцию и получим
, подставим в исходную функцию и получим  . Далее будем исследовать на экстремум полученную функцию от одной переменной.
. Далее будем исследовать на экстремум полученную функцию от одной переменной.
Находим ее первую производную  По необходимым условием экстремума определяем абсциссу стационарной точки
По необходимым условием экстремума определяем абсциссу стационарной точки  . Эта точка является точкой максимума, так как при переходе через эту точку слева направо производная меняет знак с
. Эта точка является точкой максимума, так как при переходе через эту точку слева направо производная меняет знак с  на
на (достаточное условие экстремума). Теперь для
(достаточное условие экстремума). Теперь для  из уравнения связи определяем ординату точки максимума:
из уравнения связи определяем ординату точки максимума:  . Находим значение функции:
. Находим значение функции:

Метод множителей Лагранжа
Если уравнение связи нельзя решить относительно одной из переменных, то для нахождения условного экстремума функции  при наличии соотношения
при наличии соотношения применяют метод неопределенных множителей Лагранжа. Суть метода заключается в том, чтобы перейти от задачи поиска условного экстремума функции двух переменных к задаче поиска безусловного экстремума функции трех переменных.
применяют метод неопределенных множителей Лагранжа. Суть метода заключается в том, чтобы перейти от задачи поиска условного экстремума функции двух переменных к задаче поиска безусловного экстремума функции трех переменных.
Согласно этому методу составляют функцию Лагранжа

где  – неопределенная постоянная, называется множителем Лагранжа.
– неопределенная постоянная, называется множителем Лагранжа.
Множитель  еще одной переменной, рядом со сменными
еще одной переменной, рядом со сменными  и
и  является аргументом функции Лагранжа, и именно функция Лагранжа, которая в этом случае является функцией трех переменных, исследуется на экстремум.
является аргументом функции Лагранжа, и именно функция Лагранжа, которая в этом случае является функцией трех переменных, исследуется на экстремум.
Теорема 19.4 (необходимое условие экстремума). Пусть функции  и
и  непрерывные в области
непрерывные в области  , имеют непрерывные частные производные первого порядка по переменным
, имеют непрерывные частные производные первого порядка по переменным  и
и  , а точка
, а точка  является точкой условного локального экстремума функции
является точкой условного локального экстремума функции  при наличии уравнения связи
при наличии уравнения связи  и пусть
и пусть  . Тогда существует такое единственное число
. Тогда существует такое единственное число  , что координаты точки
, что координаты точки  , которая является стационарной точкой функции Лагранжа
, которая является стационарной точкой функции Лагранжа  , удовлетворяют системе уравнений:
, удовлетворяют системе уравнений:

Теорема подается без доказательства.
Система равенств (19.9) является необходимым условием локального экстремума функции трех переменных, следовательно, если точка  является точкой условного локального экстремума функции
является точкой условного локального экстремума функции  при наличии условия
при наличии условия  то точка
то точка  является стационарной точкой функции Лагранжа.
является стационарной точкой функции Лагранжа.
Поскольку  а
а  то два последних уравнения условия (19.9) можно записать в векторной форме:
то два последних уравнения условия (19.9) можно записать в векторной форме:

Тогда для стационарной точки функции Лагранжа имеем:

Это значит, что в точке  которая является точкой условного экстремума, градиенты функций
которая является точкой условного экстремума, градиенты функций  и
и  принадлежат одной прямой.
принадлежат одной прямой.
Геометрическая интерпретация условного экстремума представим на рис. 19.3

Рис. 19.3
Функции  соответствуют несколько линий уровня, среди которых выделено именно ту, на которой функция достигает экстремального значения
соответствуют несколько линий уровня, среди которых выделено именно ту, на которой функция достигает экстремального значения  тогда как для функции
тогда как для функции  приведено только линию уровня, для которой выполняется условие
приведено только линию уровня, для которой выполняется условие  Линии уровня функций
Линии уровня функций  и
и  в точке экстремума
в точке экстремума  касаются друг к другу.
касаются друг к другу.
Фрагмент карты линий уровня, изображенной на рис. 19.3, является типичным для задач экономического содержания. Например, такой вид имеют линии установившегося значения производственных функций – изокванты. Если производственная функция является функцией двух аргументов (чаще всего, это расходы и капитал), то изокванты отражают возможные комбинации факторов производства для достижения определенного уровня производства. Следовательно, изоквант определяет возможность замещения одного фактора производства другим.
Если приросту  соответствует такое значение
соответствует такое значение  , что переход от одних условий производства в другие осуществляется при изокванте, то дифференциал производственной функции (на изокванте) равнен нулю.
, что переход от одних условий производства в другие осуществляется при изокванте, то дифференциал производственной функции (на изокванте) равнен нулю.
Вернемся к вопросу о условном экстремуме функции. Итак, из системы (19.9) находим координаты стационарной точки  . Однако соотношение (19.9) является необходимым, но не является достаточным условием условного экстремума.
. Однако соотношение (19.9) является необходимым, но не является достаточным условием условного экстремума.
Теорема 19.5 (достаточное условие экстремума). Пусть для функции  точка
точка  является стационарной. Если функция в этой точке имеет производные второго порядка и второй дифференциал при фиксированном
является стационарной. Если функция в этой точке имеет производные второго порядка и второй дифференциал при фиксированном  :
:

то при  функция достигает минимума, а при
функция достигает минимума, а при  – максимума (без доказательства).
– максимума (без доказательства).
Схема исследования на экстремум функции Лагранжа:
1) составить функцию Лагранжа (19.8)
2) записать систему уравнений (19.9), то есть необходимые условия экстремума;
3) найти стационарные точки функции, для чего решить систему (19.9)
4) проверить достаточное условие экстремума в каждой стационарной точке;
5) сделать выводы.
Исследование на экстремум функции Лагранжа эквивалентно решению задачи на условный экстремум (19.7), а именно: если точка  является точкой экстремума функции Лагранжа, то точка
является точкой экстремума функции Лагранжа, то точка  является точкой условного экстремума функции
является точкой условного экстремума функции  . Обоснование этого факта требует дополнительных сведений из раздела «Функции многих переменных», которые в данном учебнике не рассматриваются.
. Обоснование этого факта требует дополнительных сведений из раздела «Функции многих переменных», которые в данном учебнике не рассматриваются.
Например, найдем экстремум функции  при условии, что на ее переменные наложено ограничение :
при условии, что на ее переменные наложено ограничение : 
Перепишем уравнение связи в виде:  . Отсюда
. Отсюда  . Составим функцию Лагранжа:
. Составим функцию Лагранжа:

и найдем ее частные производные первого порядка:

Согласно необходимого условия экстремума функции Лагранжа (19.9) получаем систему уравнений для определения координат стационарных точек:

Решив первое уравнение системы, найдем, что  Следовательно, для функции
Следовательно, для функции  имеем стационарные точки
имеем стационарные точки  и
и  Соответственно для исходной функции точки
Соответственно для исходной функции точки  и
и  являются стационарными точками условного экстремума.
являются стационарными точками условного экстремума.
Для проверки выполнения достаточного условия экстремума для функции Лагранжа надо определить знак второго дифференциала  в точках
в точках  и
и 
Найдем частные производные второго порядка:

Следовательно, второй дифференциал функции Лагранжа (19.11) имеет вид: 

Как видим, знак  совпадает со знаком множителя Лагранжа
совпадает со знаком множителя Лагранжа 
Таким образом, в точке M имеем  и функция Лагранжа в этой точке достигает минимума. Следовательно, функция
и функция Лагранжа в этой точке достигает минимума. Следовательно, функция  в точке
в точке  достигает условного минимума,
достигает условного минимума,  В точке
В точке  имеем
имеем  , следовательно, функция Лагранжа достигает максимума, а функция
, следовательно, функция Лагранжа достигает максимума, а функция  в соответствующей точке
в соответствующей точке  достигает условного максимума,
достигает условного максимума, 
Этот пример можно проиллюстрировать геометрически (рис. 19.4). На графике приведены линии уровня функции  и
и  проходящих через точку
проходящих через точку  где функция
где функция  достигает условного максимума. Поскольку функция
достигает условного максимума. Поскольку функция
 описывает эллипс с центром симметрии в начале координат, то в точке
описывает эллипс с центром симметрии в начале координат, то в точке  для функции
для функции  будет наблюдаться условный минимум.
будет наблюдаться условный минимум.

Рис. 19.4
График не просто иллюстрирует приведенный пример, но позволяет предложить простой способ ее решения. Так, для определения стационарной точки функции Лагранжа найдем проекции градиента функции 

С учетом этого по соотношению (19.10) для точки  относительно проекций градиента функции
относительно проекций градиента функции  можно записать:
можно записать:

Подставив эти соотношения условию ограничения, получим уравнение относительно  :
:

Теперь определяем координаты стационарных точек функции Лагранжа. Понятно, что мы получили те же точки  и
и 
Наименьшее и наибольшее значение функции в замкнутой области
При нахождении экстремума функции нескольких переменных, которая непрерывная на замкнутом множестве, возникает вопрос об исчислении наибольшего и наименьшего значений, которые приобретает функция на этом множестве, то есть о нахождении глобального максимума и глобального минимума. Поскольку функция может достигать глобального экстремума на границе области, то одной из составляющих задач на глобальный экстремум является нахождение стационарных точек при исследовании функции на условный экстремум; уравнением связи в этом случае выступает уравнение границы области. Установления стационарных точек осуществляется рассмотренными выше методом сведения к нахождению экстремума функции одной переменной и методом множителей Лагранжа.
При нахождении наибольшего и наименьшего значений функции на замкнутой области  необходимо осуществить следующие шаги:
необходимо осуществить следующие шаги:
1) найти стационарные точки функции и проверить, относятся ли они к замкнутой области, для которой проводится исследование;
2) найти стационарные точки функции на кривой, которая описывает пределы области;
3) вычислить значения функции в найденных стационарных точках на замкнутой области и ее границы;
4) сравнить найденные значения функции и выбрать из них наименьшее и наибольшее.
Например, на области  найдем наибольшее и наименьшее значения функции
найдем наибольшее и наименьшее значения функции  Исходной неровности соответствует круг, радиус которого равен единице, а центр находится в точке
Исходной неровности соответствует круг, радиус которого равен единице, а центр находится в точке 
Сначала проверим, имеет функция стационарные точки, принадлежащие области, которая определена неравенством  Следовательно, найдем стационарные точки:
Следовательно, найдем стационарные точки:

Стационарная точка  является внутренней точкой области определения и является центром круга. Находим значение функции в этой точке:
является внутренней точкой области определения и является центром круга. Находим значение функции в этой точке:  Теперь надо исследовать поведение функции на границе области определения. По сути это исследование на условный экстремум, где уравнением связи является уравнение границы области определения функции
Теперь надо исследовать поведение функции на границе области определения. По сути это исследование на условный экстремум, где уравнением связи является уравнение границы области определения функции  В данном примере нет необходимости применять метод множителей Лагранжа, поскольку уравнения связи можно решить относительно любой из переменных. Из уравнения
В данном примере нет необходимости применять метод множителей Лагранжа, поскольку уравнения связи можно решить относительно любой из переменных. Из уравнения  получаем
получаем  Подставляя это выражение в исходную функцию, получим функцию одной переменной
Подставляя это выражение в исходную функцию, получим функцию одной переменной 
 Найдем ее стационарные точки, используя необходимое условие экстремума для функции одной переменной:
Найдем ее стационарные точки, используя необходимое условие экстремума для функции одной переменной:

Находим значение функции в этой точке  и значения на концах промежутка
и значения на концах промежутка 

Таким образом, для функции  следует сравнить ее значении в точках:
следует сравнить ее значении в точках: 
 Соответствующие значения функции в этих точках равны:
Соответствующие значения функции в этих точках равны: 
 Сравним полученные значения по величине. Отсюда следует, что наименьшее значение функция принимает в точках
Сравним полученные значения по величине. Отсюда следует, что наименьшее значение функция принимает в точках  и
и  и равно оно числу
и равно оно числу  , а самого большого – в точках
, а самого большого – в точках  и
и  и оно равно числу
и оно равно числу  . Следовательно,
. Следовательно,

Лекции:
- Дифференцирование суммы, произведения и частного
- Система логарифмических уравнений
- Криволинейный интеграл: примеры решения
- Вычислить объем тела
- Метод наименьших квадратов
- Контрольная производная и ее геометрический смысл
- Иррациональные уравнении
- Методы решения тригонометрических уравнений
- Свойства непрерывного отображения множеств
- Линейные дифференциальные уравнения
Частные производные
Частной производной по x функции z = f(x,y) в точке A(x0,y0) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.
Частные производные функции z(x,y) находятся по следующим формулам: ![]()
Вторые частные производные функции z(x,y) находятся по формулам:
![]()
Смешанные частные производные функции z(x,y) находятся по формулам: ![]()
Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
x2+xy ≡ x^2+x*y.
cos2(2x+y) ≡ (cos(2*x+y))^2
 ≡ (x-y)^(2/3)
≡ (x-y)^(2/3)
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
Примеры
 ≡ x^2/(z+y)
≡ x^2/(z+y)
cos2(2x+zy) ≡ (cos(2*x+z*y))^2
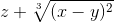 ≡ z+(x-y)^(2/3)
≡ z+(x-y)^(2/3)
Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.
Частные производные функции нескольких переменных
Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δxz=f(x+Δx,y)-f(x,y) – это частное приращение функции z по аргументу x; Δyz=f(x,y+Δy)-f(x,y) – это частное приращение функции z по аргументу у.
Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:
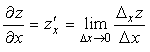 – это частная производная функции z по аргументу x;
– это частная производная функции z по аргументу x;
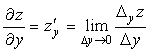 – это частная производная функции z по аргументу у.
– это частная производная функции z по аргументу у.
Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.
Пример 1. z=2x5+3x2y+y2–4x+5y-1
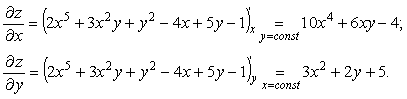
Пример 2. Найти частные производные ![]() функции z = f(x;y) в точке A(x0;y0).
функции z = f(x;y) в точке A(x0;y0).

Находим частные производные:


Найдем частные производные в точке А(1;1)


Находим вторые частные производные:


Найдем смешанные частные производные:

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Содержание:
Дифференцируемость функции нескольких переменных:
Рассмотрим функцию 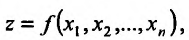
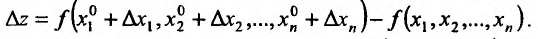
Определение 16.1.1. Функция 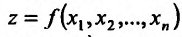 называется дифференцируемой в точке
называется дифференцируемой в точке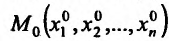 если ее полное приращение в этой точке может быть представлено в виде:
если ее полное приращение в этой точке может быть представлено в виде: 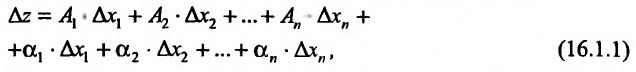
где 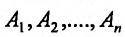 – постоянные величины, а
– постоянные величины, а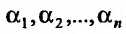 – бесконечно малые при
– бесконечно малые при 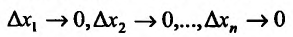 функции, равные нулю при
функции, равные нулю при 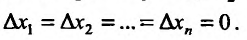
Равенство (16.1.1) называется условием дифференцирусмости функции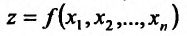 в точке
в точке 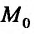 . Это условие можно записать и в следующем виде:
. Это условие можно записать и в следующем виде:
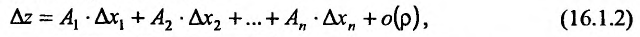
где 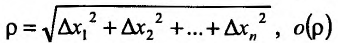 – бесконечно малая функция более высокого порядка малости по сравнению с
– бесконечно малая функция более высокого порядка малости по сравнению с  . Справедлива следующая теорема.
. Справедлива следующая теорема.
Теорема 16.1.1. Если функция 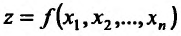 дифференцируема в точке
дифференцируема в точке  то в этой точке существуют частные производные по всем аргументам, причем
то в этой точке существуют частные производные по всем аргументам, причем 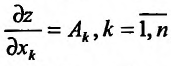 , где
, где 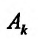 определяются из условия (16.1.1) или (16.1.2) дифференцируемости функции.
определяются из условия (16.1.1) или (16.1.2) дифференцируемости функции.
Доказательство. Пусть функция 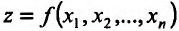 дифференцируема в точке
дифференцируема в точке 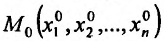 . Тогда выполняется равенство (16.1.2), из которого следует, что частное приращение
. Тогда выполняется равенство (16.1.2), из которого следует, что частное приращение 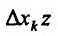 функции
функции 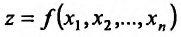 в этой точке равно
в этой точке равно 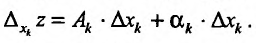 . Разделив все члены этого равенства на
. Разделив все члены этого равенства на 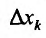 и, перейдя к пределу при
и, перейдя к пределу при 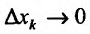 , последовательно получим:
, последовательно получим: 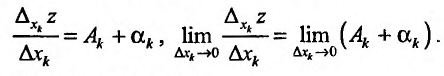
Откуда следует, что
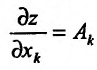 , так как
, так как 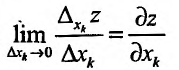
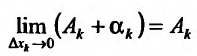 , так как
, так как 
Теорема доказана.
Из доказанной теоремы следует, что условие дифференцируемости (16.1.2) можно записать в следующей форме:
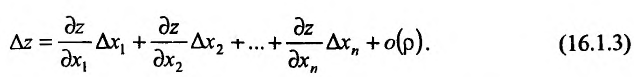
Так как коэффициенты 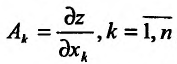 определяются единственным образом, то дифференцируемую функцию можно представить единственным образом в форме (16.1.1) или (16.1.2).
определяются единственным образом, то дифференцируемую функцию можно представить единственным образом в форме (16.1.1) или (16.1.2).
Кроме того, из дифференцируемое функции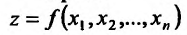 в точке
в точке  следует ее непрерывность в этой точке.
следует ее непрерывность в этой точке.
Сформулируем теперь достаточные условия дифференцируемости функции.
Теорема 16.1.2. Если функция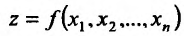 имеет частные производные по всем аргументам в некоторой окрестности точки
имеет частные производные по всем аргументам в некоторой окрестности точки 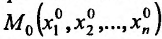 непрерывные в самой точке
непрерывные в самой точке 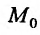 , то она дифференцируема в точке
, то она дифференцируема в точке 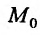
Доказательство. Для простоты доказательство приведем для функции z = f(x,y) двух переменных. Предположим, что функция z = f(x,y) имеет непрерывные частные производные в рассматриваемой точке 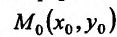 . Выразим полное приращение
. Выразим полное приращение 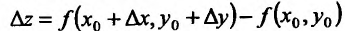 через частные производные. Для этого в правой части равенства прибавим и вычтем
через частные производные. Для этого в правой части равенства прибавим и вычтем 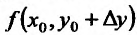 :
:
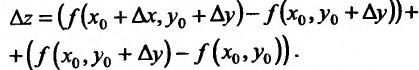
Выражение 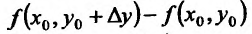 – приращение по у, a
– приращение по у, a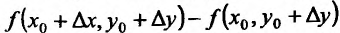 приращение по х. Применяя к каждому из приращений теорему Лагранжа (применить теорему Лагранжа можем, так как частные производные непрерывны в точке
приращение по х. Применяя к каждому из приращений теорему Лагранжа (применить теорему Лагранжа можем, так как частные производные непрерывны в точке  ), получим:
), получим:
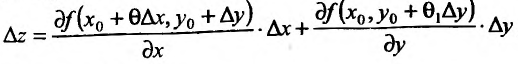
где 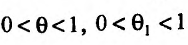
Так как частные производные, по предположению, непрерывны, то
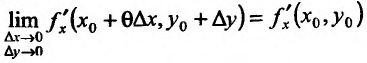
и
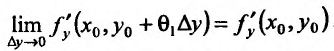
Тогда, используя представления, для функции, имеющей предел, получим.
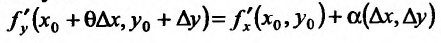
и
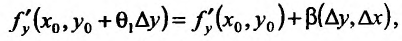
где 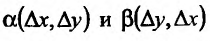 – бесконечно малые функции порядка малости выше по сравнению с
– бесконечно малые функции порядка малости выше по сравнению с 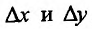 , и, следовательно,
, и, следовательно, 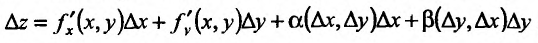
Приращение функции представлено в форме (16.1.2), значит, функция z = f(x,y) дифференцируема в точке 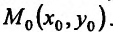 . Теорема доказана.
. Теорема доказана.
Дифференциал функции первого и высших порядков
Главную линейную относительно приращений аргументов часть приращения функции 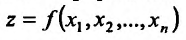 в точке
в точке
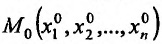 называют полным дифференциалом dz дифференцируемой функции:
называют полным дифференциалом dz дифференцируемой функции:
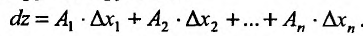
Используя (16.1.3), это равенство можно переписать в виде:
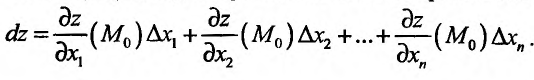
Под дифференциалом 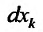 независимой переменной хк будем понимать число, равное приращению
независимой переменной хк будем понимать число, равное приращению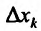 . Тогда полный дифференциал будет определяться равенством:
. Тогда полный дифференциал будет определяться равенством:
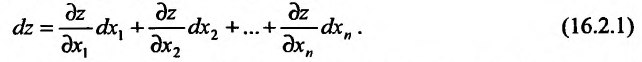
Формула (16.2.1) дифференциала функции  установлена для случая, когда аргументы
установлена для случая, когда аргументы  являются независимыми переменными. Эта же формула справедлива и в том случае, когда аргументы
являются независимыми переменными. Эта же формула справедлива и в том случае, когда аргументы 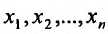 сами являются дифференцируемыми функциями некоторых новых аргументов
сами являются дифференцируемыми функциями некоторых новых аргументов 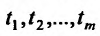 , которые можно считать независимыми. Это свойство первого дифференциала называют свойством инвариантности его формы.
, которые можно считать независимыми. Это свойство первого дифференциала называют свойством инвариантности его формы.
Для функции z = f(x,y) двух переменных дифференциал определяется по формуле:

Ясно, что если функция z = f(x,y) дифференцируема в точке, то она имеет единственный дифференциал, так как частные производные определяются однозначно.
Полный дифференциал применяется в приближенных вычислениях. Для этого формулу полного приращения 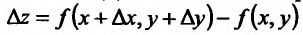 представим в виде:
представим в виде:
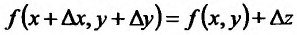
Из предыдущего ясно, что, с точностью до бесконечно малых высшего порядка относительно 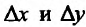 , можно написать равенство:
, можно написать равенство:
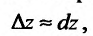 , где
, где 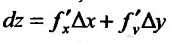 .
.
Поэтому
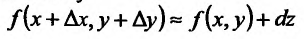
или 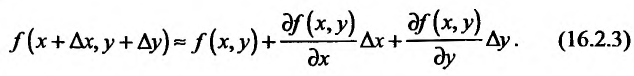
Формула (16.2.3) используется в приближенных вычислениях.
Пример:
Вычислить дифференциал функции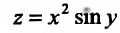
Решение:
Из рассуждений, приведенных выше, следует, что для вычисления дифференциала функции z = f(x,y), нужно вычислить частные производные и подставить их в формулу (46.2.2). Вычислив частные производные:
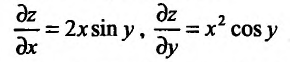
и подставив их в формулу полного дифференциала, получим:
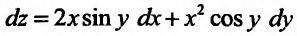
Пример:
Вычислить значение выражения
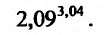
Решение:
Введем в рассмотрение функцию 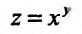 и выделим
и выделим 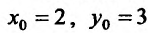 . Тогда
. Тогда 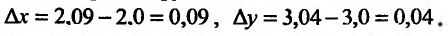 . Вычислим:
. Вычислим:
а) частные производные функции 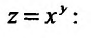
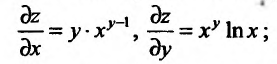
б) значения функции и частных производных в точке (2;3):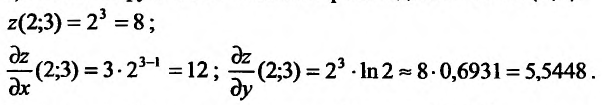
Подставив найденные значения в формулу (16.2.3), получим: 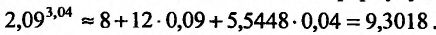 .
.
Предположим, что величина, стоящая в правой части (16.2.2), представляет собой функцию аргументов 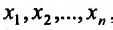 , дифференцируемую в данной точке
, дифференцируемую в данной точке 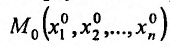 . Тогда сама функция
. Тогда сама функция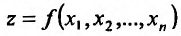 должна быть дважды дифференцируемой в точке
должна быть дважды дифференцируемой в точке 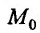 , а аргументы являлись независимыми переменными или два раза дифференцируемыми функциями некоторых независимых переменных
, а аргументы являлись независимыми переменными или два раза дифференцируемыми функциями некоторых независимых переменных 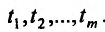 . При этих предположениях можно рассматривать дифференциал
. При этих предположениях можно рассматривать дифференциал
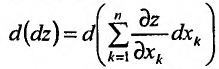
который называется вторым дифференциалом или дифференциалом второго порядка функции 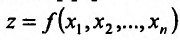 и обозначается
и обозначается 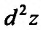 .
.
Дифференциал 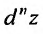 любого порядка п вводится по индукции, го есть
любого порядка п вводится по индукции, го есть
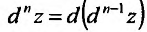
В случае, когда аргументы 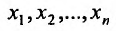 являются независимыми переменными, для дифференциала второго порядка справедливо представление:
являются независимыми переменными, для дифференциала второго порядка справедливо представление:
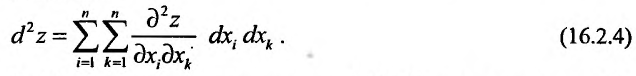
Дифференциал второго порядка (16.2.4) представляет собой симметричную (так как 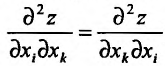 ) квадратичную форму от переменных
) квадратичную форму от переменных , коэффициенты которой равны соответствующим частным производным второго порядка функции
, коэффициенты которой равны соответствующим частным производным второго порядка функции  . В частности, дифференциал второго порядка функции z= f(x,y) определяется равенством:
. В частности, дифференциал второго порядка функции z= f(x,y) определяется равенством:
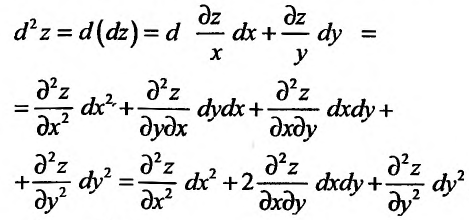
так как

Если аргументы 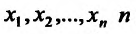 раз дифференцируемой функции
раз дифференцируемой функции 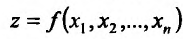 в точке
в точке 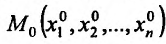 являются независимыми переменными, для дифференциала n-го порядка этой функции справедливо представление:
являются независимыми переменными, для дифференциала n-го порядка этой функции справедливо представление:
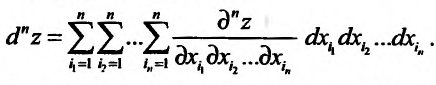
Другой вид имеют представления для второго и последующих дифференциалов функции 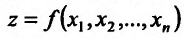 в случае, когда аргументы
в случае, когда аргументы 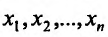 являются функциями переменных
являются функциями переменных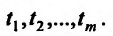
Пример:
Вычислить дифференциал второго порядка функции
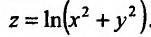
Решение:
Применим формулу (16.2.5) предварительно вычислив последовательно частные производные первого и второго порядков:
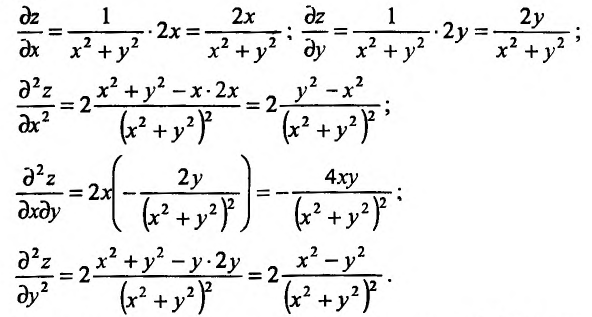
Подставив значения частных производных в (16.2.5), получим искомое выражение дифференциала второго порядка заданной функции:
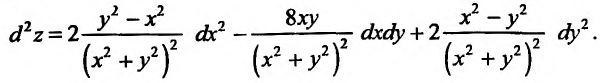
Геометрический смысл условия
Рассмотрим функцию двух переменных z= f(x,y) и предположим, что она дифференцируема в точке  . Тогда (16.1.2) можно записать в виде:
. Тогда (16.1.2) можно записать в виде:
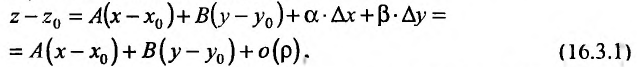
где А и В – постоянные величины, равные частным производным в точке 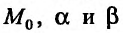 – бесконечно малые при
– бесконечно малые при 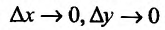 функции,
функции, 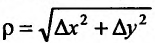 .
.
Из аналитической геометрии известно, что уравнение  определяет некоторую плоскость, проходящую через точку
определяет некоторую плоскость, проходящую через точку 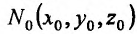 и имеющую нормальный вектор
и имеющую нормальный вектор 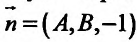 .
.
С геометрической точки зрения, графиком функции z = f(x,y) является поверхность в системе прямоугольных декартовых координат (x,y,z), проектирующаяся на плоскость Оху в область определения функции.
Назовем плоскость, проходящую через точку  поверхности, касательной плоскостью в этой точке, если угол между этой плоскостью и секущей плоскостью, проходящей через точку
поверхности, касательной плоскостью в этой точке, если угол между этой плоскостью и секущей плоскостью, проходящей через точку  и любую другую точку
и любую другую точку поверхности, стремятся к нулю, если точка
поверхности, стремятся к нулю, если точка 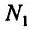 стремится к точке
стремится к точке 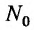 .
.
Очевидно, что плоскость (16.3.2) проходит через точку 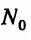 поверхности. Так как координаты вектора
поверхности. Так как координаты вектора 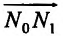 секущей плоскости равны
секущей плоскости равны 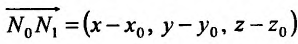 , то угол между векторами
, то угол между векторами 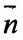 и
и 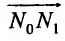 определяется по формуле:
определяется по формуле:
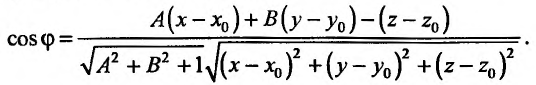
Из условия дифференцируемое™ (16.1.2) следует, что разность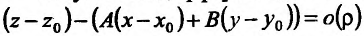 является величиной бесконечно малой, при
является величиной бесконечно малой, при  . Значит
. Значит  когда
когда  , то есть
, то есть 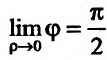 . Следовательно, плоскость
. Следовательно, плоскость 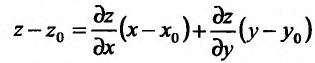 касательная к поверхности z = f(x,y).
касательная к поверхности z = f(x,y).
Таким образом, с геометрической точки зрения, дифференцируемость функции z = f(x,y) в точке  означает наличие касательной плоскости (16.3.3) к поверхности функции z = f(x,y) в точке
означает наличие касательной плоскости (16.3.3) к поверхности функции z = f(x,y) в точке  (см. рис. 16.1).
(см. рис. 16.1).
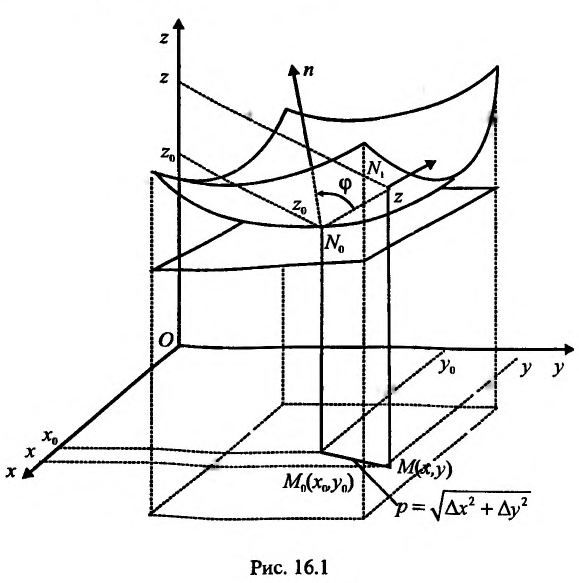
Производная по направлению
Рассмотрим функцию z=f(x,y), определенную в некоторой окрестности точки  и дифференцируемую в точке
и дифференцируемую в точке  , и всевозможные лучи, выходящие из точки М0. Направление каждого луча задается единичным вектором
, и всевозможные лучи, выходящие из точки М0. Направление каждого луча задается единичным вектором  с направляющими косинусами, где
с направляющими косинусами, где 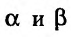 углы, которые составляет вектор
углы, которые составляет вектор 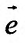 с осями координат Ох и Оу.
с осями координат Ох и Оу.
Фиксируем некоторый луч, выходящий из точки 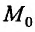 , выберем на нем произвольную точку М(х,у) и рассмотрим вектор
, выберем на нем произвольную точку М(х,у) и рассмотрим вектор 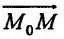 , обозначив его величину через l (см. рис. 16.2). Тогда координаты этого вектора
, обозначив его величину через l (см. рис. 16.2). Тогда координаты этого вектора  определяются его величиной l и направлением фиксированного луча, которое совпадает с направлением единичного вектора
определяются его величиной l и направлением фиксированного луча, которое совпадает с направлением единичного вектора 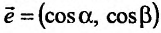 :
:
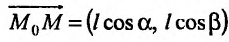
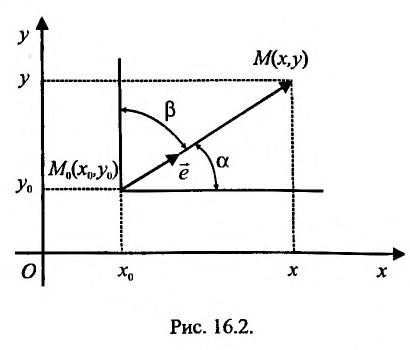
С другой стороны, координаты вектора 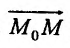 равны разностям координат конечной и начальной точек вектора:
равны разностям координат конечной и начальной точек вектора:
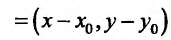 Сопоставляя два соотношения для координат вектора
Сопоставляя два соотношения для координат вектора  , получим равенства:
, получим равенства: 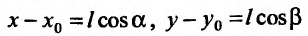 или
или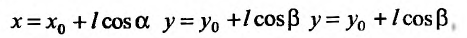 Подставив, значения координат х и у в функцию z = f(x,y), получим, что на луче, выходящем из точки
Подставив, значения координат х и у в функцию z = f(x,y), получим, что на луче, выходящем из точки  , направление которого определяется единичным вектором
, направление которого определяется единичным вектором 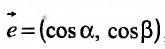 , функция z = f(x,y) представляет собой сложную функцию одной переменной l вида
, функция z = f(x,y) представляет собой сложную функцию одной переменной l вида 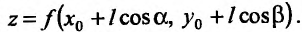 .
.
Определение 16.4.1. Производная сложной функции 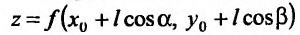 по переменной l, в точке 1 = 0, называется производной функции z = f(x,y) в точке
по переменной l, в точке 1 = 0, называется производной функции z = f(x,y) в точке 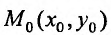 по направлению, определяемому единичным вектором
по направлению, определяемому единичным вектором  , и обозначаемой символом
, и обозначаемой символом 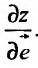 .
.
Так как вдоль луча 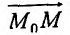 функция z = f{x.y) является функцией одной переменной l, то производную по направлению можно рассматривать как предел отношения прирашения функции z = f(x,y) к величине l вектора
функция z = f{x.y) является функцией одной переменной l, то производную по направлению можно рассматривать как предел отношения прирашения функции z = f(x,y) к величине l вектора 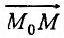 , когда эта величина стремиться к нулю:
, когда эта величина стремиться к нулю:
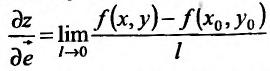
Из определения 16.4.1 получим формулу для вычисления производной по направлению, определяемому вектором 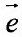
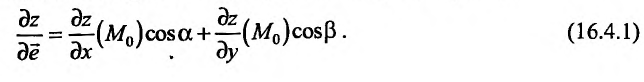
Пример №1
Вычислить производную функции 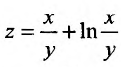 в точке
в точке 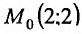 по направлению, определяемому вектором
по направлению, определяемому вектором  , который составляет с осью Ох угол равный 45°.
, который составляет с осью Ох угол равный 45°.
Решение:
Воспользуемся формулой (16.4.1) и вычислим частные производные заданной функции:
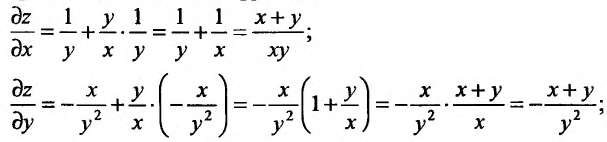
и их значения в точке  :
:
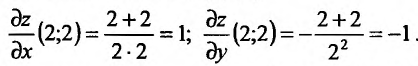
Подставив эти значения в формулу (16.4.1), получим:

Это означает, что заданная функция в указанном направлении является постоянной.
В практических приложениях особый интерес представляет вопрос о направлении быстрейшего возрастания функции в точке. С этой целью вводится понятие градиента дифференцируемой в данной точке  функции z = f(x,y).
функции z = f(x,y).
Определение 16.4.2. Градиентом функции z = f(x,y) в данной точке 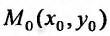 называется вектор, имеющий своим началом эту точку, координатами которого являются частные производные этой функции в точке
называется вектор, имеющий своим началом эту точку, координатами которого являются частные производные этой функции в точке  .
.
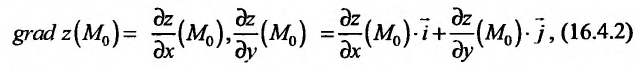
где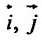 – единичные векторы координатных осей Ох и Оу.
– единичные векторы координатных осей Ох и Оу.
Воспользовавшись тем, что, скалярное произведение векторов равно сумме произведений одноименных координат этих векторов, выражение (16.4.1) для производной по направлению, определяемому вектором 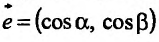 , можно рассматривать как скалярное произведение векторов
, можно рассматривать как скалярное произведение векторов 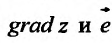 :
:

Скалярное произведение двух векторов равно произведению длин этих векторов на косинус угла между ними. Поэтому выражение (16.4.3) можно переписать в виде:
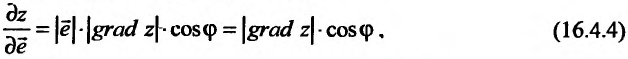
где 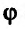 – угол между векторами
– угол между векторами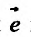 и
и 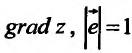 . Из равенства (16.4.4) следует теорема.
. Из равенства (16.4.4) следует теорема.
Теорема 16.4.1. Градиент функции z = f(x,y) в точке 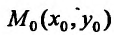 характеризует направление и величину максимального роста этой функции в точке
характеризует направление и величину максимального роста этой функции в точке 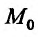 .
.
Действительно, производная 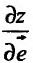 достигает максимального значения при
достигает максимального значения при  , то есть если
, то есть если  . Это означает, что направление вектора
. Это означает, что направление вектора 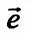 совпадает с направлением вектора
совпадает с направлением вектора 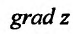 , причем производная
, причем производная 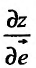 в этом направлении равна
в этом направлении равна 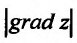 .
.
Очевидно, что направление противоположное градиенту, будет являться направлением быстрейшего убывания функции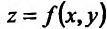 .
.
Пример №2
Найти направление быстрейшего возрастания функции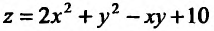 в точке
в точке  и вычислить значение производной в этом направлении.
и вычислить значение производной в этом направлении.
Решение:
Как доказано выше, направление и величину максимального роста функции определяет градиент этой функции. Поэтому вычислим частные производные этой функции: 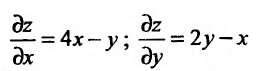 и их значения в точке
и их значения в точке 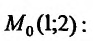
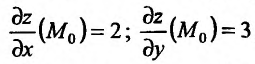 и подставим в выражение (16.4.2):
и подставим в выражение (16.4.2): 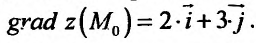
Следовательно, искомое направление составляет угол 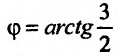 осью Ох. Производная по направлению, определяемая градиентом этой функции в данной точке, равна
осью Ох. Производная по направлению, определяемая градиентом этой функции в данной точке, равна 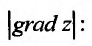
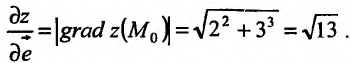
Выясним геометрический смысл вектора grad z. Для этого рассмотрим линии уровня функции z = f(x,y), понимая под этим термином те линии, на которых функция z = f(x,y) сохраняет постоянное значение, то есть удовлетворяет соотношению f(х,у)=с. Построим касательную к линии уровня, угловой коэффициент которой равен-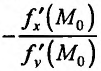 . Угловой коэффициент grad z в точке
. Угловой коэффициент grad z в точке  равен
равен 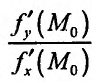 . Произведение угловых коэффициентов касательной и grad z равно — 1. Следовательно, вектор grad z в каждой точке линии уровня имеет направление перпендикулярное к
. Произведение угловых коэффициентов касательной и grad z равно — 1. Следовательно, вектор grad z в каждой точке линии уровня имеет направление перпендикулярное к  линии уровня.
линии уровня.
Аналогично определяется производная по направлению и градиент для дифференцируемой в данной точке 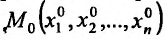 функции
функции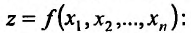
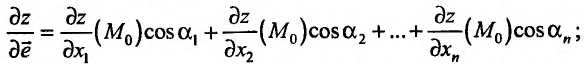
Производная по направлению, определяемому вектором 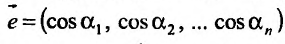 , также равна скалярному произведению вектора
, также равна скалярному произведению вектора 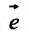 и grad z:
и grad z:
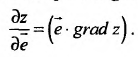
Определение экстремума функции двух переменных
Пусть функция n переменных 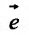 определена в некоторой окрестности точки
определена в некоторой окрестности точки 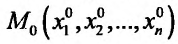 пространства
пространства  . Функция z = f(м) будет иметь в точке
. Функция z = f(м) будет иметь в точке  локальный максимум (минимум), если существует такая
локальный максимум (минимум), если существует такая 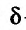 -окрестность точки
-окрестность точки 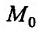 , что для всех точек М из этой окрестности значение
, что для всех точек М из этой окрестности значение 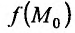 является наибольшим (наименьшим) среди всех значений
является наибольшим (наименьшим) среди всех значений 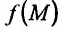 этой функции. Точки локального максимума или локального минимума называются точками экстремума.
этой функции. Точки локального максимума или локального минимума называются точками экстремума.
Рассмотрим функцию двух переменных z = f(x, у) и определим необходимые условия экстремума. Функция z = f(x,y) достигает максимума в точке 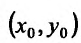 , если значение
, если значение 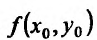 не меньше всех смежных значений функции, то есть
не меньше всех смежных значений функции, то есть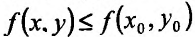 Для всех точек (х,у) из некоторой
Для всех точек (х,у) из некоторой  -окрестности точки
-окрестности точки 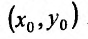 достаточно близких к точке и отличных от нее.
достаточно близких к точке и отличных от нее.
Функция z = f(x,y) достигает минимума в точке 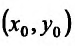 , если
, если 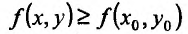 для всех (х,y) из некоторой
для всех (х,y) из некоторой 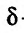 -окрестности точки
-окрестности точки 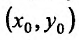 . Максимум и минимум функции называются экстремумами функции.
. Максимум и минимум функции называются экстремумами функции.
Итак, пусть точка 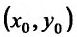 – является точкой локального максимума либо минимума, то есть точкой локального экстремума. Фиксируем у функции
– является точкой локального максимума либо минимума, то есть точкой локального экстремума. Фиксируем у функции 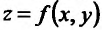 аргумент
аргумент 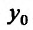 , то есть, положим
, то есть, положим 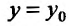 . Рассмотрим функцию
. Рассмотрим функцию 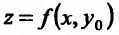 одной независимой переменной X. По предположению она должна достигать локального максимума при
одной независимой переменной X. По предположению она должна достигать локального максимума при 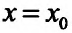 , и поэтому ее производная по X должна или превращаться в нуль или не существовать. Но производная функции
, и поэтому ее производная по X должна или превращаться в нуль или не существовать. Но производная функции 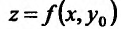 – это частная производная по X функции
– это частная производная по X функции 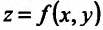 и, следовательно, она должна или равняться нулю или не существовать. Аналогичным рассуждением убедимся, что и производная функции
и, следовательно, она должна или равняться нулю или не существовать. Аналогичным рассуждением убедимся, что и производная функции 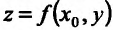 по у должна или обращаться в нуль или не существовать при
по у должна или обращаться в нуль или не существовать при 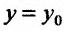 – Итак, мы приходим к следующей теореме.
– Итак, мы приходим к следующей теореме.
Теорема 17.1.1. Функция z = f(x,y) может достигать локального максимума либо минимума лишь при тех значениях х и у, при которых частные производные первого порядка 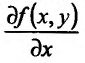 и
и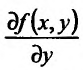 обращаются в нуль либо не существуют.
обращаются в нуль либо не существуют.
Аналогичное утверждение справедливо и для функции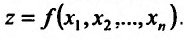
Если функция 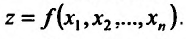 имеет в точке
имеет в точке  частные производные и точка
частные производные и точка 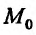 является точкой локального экстремума, то все частные производные первого порядка обращаются в нуль в точке
является точкой локального экстремума, то все частные производные первого порядка обращаются в нуль в точке  :
:
Равенства (17.1.1) являются лишь необходимыми и не являются достаточными условиями локального экстремума. Например, у функции z = ху частные производные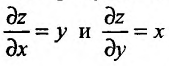 обращаются в нуль в точке
обращаются в нуль в точке 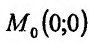 , но экстремума в этой точке функция z = xy не имеет, так как в как угодно малой
, но экстремума в этой точке функция z = xy не имеет, так как в как угодно малой 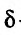 -окрестности этой точки функция принимает как положительные, так и отрицательные значения.
-окрестности этой точки функция принимает как положительные, так и отрицательные значения.
Точки, в которых обращаются в нуль все частные производные первого порядка функции z= f(x,y), называются стационарными точками.
Отметим, что если функция дифференцируема в точке
дифференцируема в точке 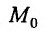 и имеет в этой точке локальный экстремум, то дифференциал dz этой функции в точке
и имеет в этой точке локальный экстремум, то дифференциал dz этой функции в точке  равен нулю:
равен нулю:
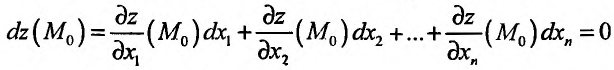
при любых 
Пример №3
Исследовать функцию 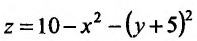 на экстремум.
на экстремум.
Решение:
Функция определена при 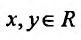 . Вычислим частные производные заданной функции
. Вычислим частные производные заданной функции 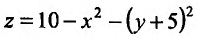 :
:
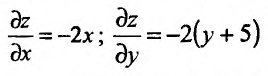
и приравняем их к нулю. Получим систему:
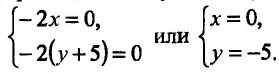
Итак, точка 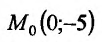 может быть точкой экстремума Наличие экстремума можно установить лишь с помощью достаточного условия.
может быть точкой экстремума Наличие экстремума можно установить лишь с помощью достаточного условия.
Достаточное условие экстремума
При формулировке достаточного условия локального экстремума функции n переменных 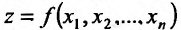 важную роль играет дифференциал второго порядка этой функции:
важную роль играет дифференциал второго порядка этой функции:

который представляет собой квадратичную форму относительно дифференциалов аргументов 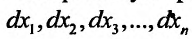 . Введем обозначение
. Введем обозначение
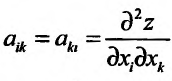 (в частности,
(в частности,
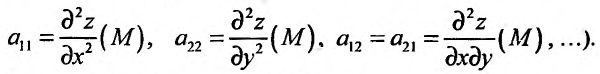
Тогда матрица квадратичной формы

может бьггь записана в виде:
где 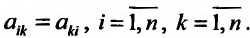 Используя критерий Сильвестра: «Для того, чтобы квадратичная форма (17.2.2) была положительно определенной (отрицательно определенной), необходимо и достаточно, чтобы все главные миноры матрицы (17.2.3) были положительные, то есть чтобы
Используя критерий Сильвестра: «Для того, чтобы квадратичная форма (17.2.2) была положительно определенной (отрицательно определенной), необходимо и достаточно, чтобы все главные миноры матрицы (17.2.3) были положительные, то есть чтобы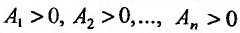 (чтобы знаки главных миноров матрицы (17.2.3) чередовались, то есть
(чтобы знаки главных миноров матрицы (17.2.3) чередовались, то есть 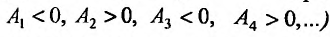 можно сформулировать достаточные условия экстремума функции двух переменных.
можно сформулировать достаточные условия экстремума функции двух переменных.
Теорема 17.2.1. Пусть функция двух переменных z = f(x,y) один раз дифференцируема в окрестности точки 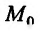 и два раза дифференцируема в самой точке
и два раза дифференцируема в самой точке 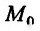 и пусть
и пусть 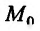 является стационарной точкой. Тогда, если в точке
является стационарной точкой. Тогда, если в точке 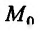 выполнено условие
выполнено условие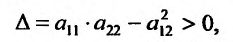 , то функция z = f(x, у) имеет в точке
, то функция z = f(x, у) имеет в точке 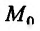 локальный экстремум (максимум при
локальный экстремум (максимум при 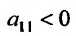 и минимум при
и минимум при 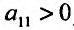 ). Если же в точке
). Если же в точке 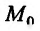
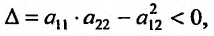 , то функция z = f(x, у) не имеет в этой точке локального экстремума. Случай
, то функция z = f(x, у) не имеет в этой точке локального экстремума. Случай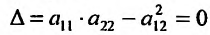 требует дополнительного исследования.
требует дополнительного исследования.
Справедливость первой части теоремы вытекает из критерия Сильвестра, так как главные миноры матрицы (17.2.3) квадратичной формы равны
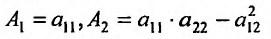 и если
и если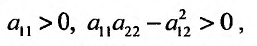
то дифференциал второго порядка является положительно определенной квадратичной формой, а если
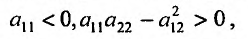 то отрицательно определенной квадратичной формой.
то отрицательно определенной квадратичной формой.
Знак разности  определяется дифференциалом второго порядка, что следует из формулы Тейлора:
определяется дифференциалом второго порядка, что следует из формулы Тейлора:
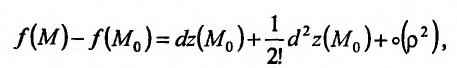
где 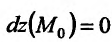 . Тогда если
. Тогда если 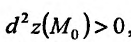 , то разность
, то разность 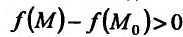 , и тогда
, и тогда 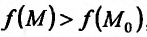 , следовательно, точка
, следовательно, точка 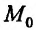 является точкой минимума. Если же
является точкой минимума. Если же 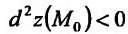 , то
, то 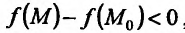 и тогда
и тогда 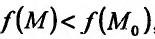 , следовательно, точка
, следовательно, точка 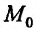 является точкой максимума. Если же в точке
является точкой максимума. Если же в точке 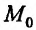
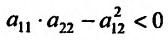 , то дифференциал второго порядка
, то дифференциал второго порядка 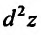 представляет собой знакопеременную квадратичную форму и, следовательно, не сохраняется знак разности
представляет собой знакопеременную квадратичную форму и, следовательно, не сохраняется знак разности 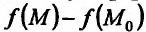 , что свидетельствует об отсутствии экстремума в точке
, что свидетельствует об отсутствии экстремума в точке 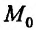 .
.
Пример №4
Исследовать функцию 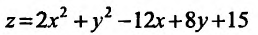 на экстремум.
на экстремум.
Решение:
Функция определена на всей плоскости. Вычислим частные производные заданной функции: 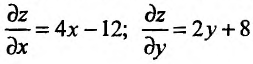 и приравняем их к нулю:
и приравняем их к нулю: 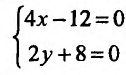
Решив систему, найдем стационарную точку М(3; -4), которая может быть точкой экстремума функции. Для определения существования экстремума функции в этой точке, вычислим частные производные второго порядка:
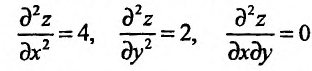
и подставим их значения в выражение: 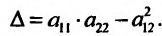 Так как
Так как 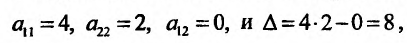 то в точке
то в точке 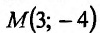 функция имеет минимум.
функция имеет минимум.
Определение экстремума функции широко применяется в экономических исследованиях. Рассмотрим следующий пример.
Пример №5
Фирма имеет два филиала, издержки производства в которых описываются функциями 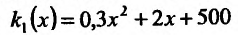 и
и 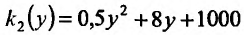 соответственно, где х и у- объемы производимой продукции. Общий спрос на товар фирмы определяется ценой р за единицу продукции, зависящей от объема выпускаемой продукции z = х + у и определяемой функцией z=5000 – 4р. Рассчитать оптимальный объем выпуска продукции для производителя, оптимальную цену в целом и распределение производственной про-граммы по филиалам.
соответственно, где х и у- объемы производимой продукции. Общий спрос на товар фирмы определяется ценой р за единицу продукции, зависящей от объема выпускаемой продукции z = х + у и определяемой функцией z=5000 – 4р. Рассчитать оптимальный объем выпуска продукции для производителя, оптимальную цену в целом и распределение производственной про-граммы по филиалам.
Решение:
Оптимальный выпуск продукции определяется максимальной прибылью фирмы, которая равна разности дохода фирмы от реализуемой продукции по цене р и издержек, то есть функцией прибыли:
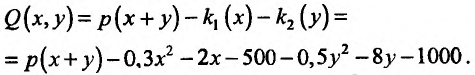 .
.
Найдем значение функции цены р из равенства
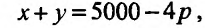
решив которое получим:
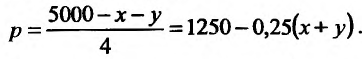
Подставим значение цены в функцию прибыли:
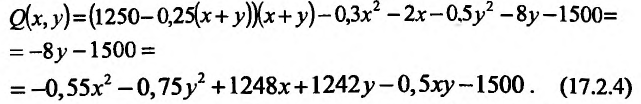
Определим экстремум функции прибыли (17.2.4). Для этого вычислим частные производные первого порядка:
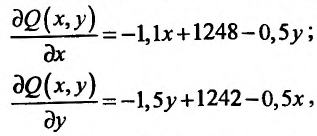
приравняем их к нулю и решим систему: 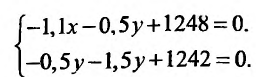
Получим значения: 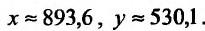 . Характер экстремума в стационарной точке (893,6;530,l) определим, вычислив значение частных производных второго порядка:
. Характер экстремума в стационарной точке (893,6;530,l) определим, вычислив значение частных производных второго порядка:
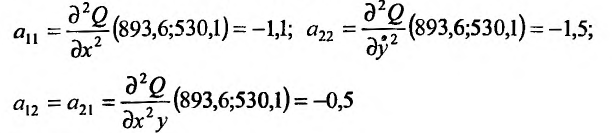
и значение выражения:
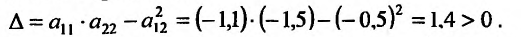 .
.
Так как 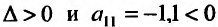 , то точка (893,6;530,l) является точкой максимума и при найденных значениях х и у функция прибыли получает наибольшее значение.
, то точка (893,6;530,l) является точкой максимума и при найденных значениях х и у функция прибыли получает наибольшее значение.
Таким образом, если фирма в первом филиале произведет примерно 894 единицы продукции, а во втором – 530 единиц, то продав ее по цене р = 1250-0,25(894 + 530) = 894 денежных единиц за единицу, она получит максимальную прибыль, равную:
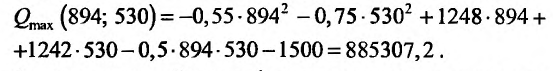
Аналогичным образом формулируются достаточные условия локального экстремума функции n переменных.
Теорема 17.2.2. Пусть функция  один раз дифференцируема в некоторой окрестности точки и два раза дифференцируема в самой точке
один раз дифференцируема в некоторой окрестности точки и два раза дифференцируема в самой точке и точка
и точка 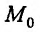 является стационарной точкой функции
является стационарной точкой функции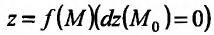 . Тогда, если дифференциал второго порядка
. Тогда, если дифференциал второго порядка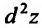 представляет собой положительно определенную (отрицательно определенную) квадратичную форму от переменных
представляет собой положительно определенную (отрицательно определенную) квадратичную форму от переменных 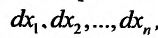 то функция
то функция 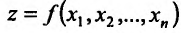 имеет в точке
имеет в точке 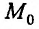 локальный минимум (локаланый максимум)- Если же дифференциал второго порядка (17.2.1), представляет cобой знакопеременную квадратичную фор-щ'( 17.2.2), то функция z = f(м) не имеет локального экстремума точке
локальный минимум (локаланый максимум)- Если же дифференциал второго порядка (17.2.1), представляет cобой знакопеременную квадратичную фор-щ'( 17.2.2), то функция z = f(м) не имеет локального экстремума точке 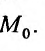
Наибольшее и наименьшее значения функции
В предыдущих параграфах рассмотрены методы определения локального экстремума функции п переменных. Пусть требуется найти наибольшее (наименьшее) значение функции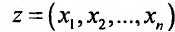 в определенной области D, то есть требуется найти точки глобального экстремума функции.
в определенной области D, то есть требуется найти точки глобального экстремума функции.
Вначале находим точки локального экстремума внутри заданной области D, методами, указанными в предыдущих параграфах. Затем находим экстремумы функции на границе области D и сравниваем ее максимумы (минимумы) внутри области со значениями на границе области. Наибольшее (наименьшее) из всех этих значений и будет наибольшим (наименьшим) значением функции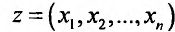 в данной области D.
в данной области D.
Пример №6
Найти наименьшее и наибольшее значение функции 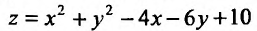 в замкнутой области, ограниченной окружностью
в замкнутой области, ограниченной окружностью 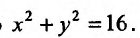
Решение:
Определим вначале локальные экстремумы внутри круга 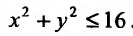 Для этого последовательно вычислим частные производные, приравняем их к нулю, найдем стационарные точки, решив соответствующую систему, и определим характер стационарных точек:
Для этого последовательно вычислим частные производные, приравняем их к нулю, найдем стационарные точки, решив соответствующую систему, и определим характер стационарных точек:
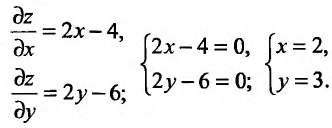
Точка А(2;3) принадлежит кругу 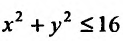 Так как
Так как 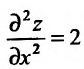 ,
,
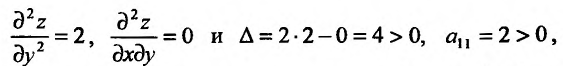 то в точке
то в точке
А(2,3) функция достигает минимума, min z = f(2;3) = -3.
Найдем экстремумы на границе области, то есть на окружности 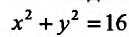 Воспользуемся параметрическими уравнениями этой окружности
Воспользуемся параметрическими уравнениями этой окружности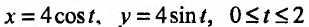 Подставив их в заданную функцию, получим функцию одной переменной t:
Подставив их в заданную функцию, получим функцию одной переменной t: 
Исследуем функцию  на экстремум:
на экстремум:
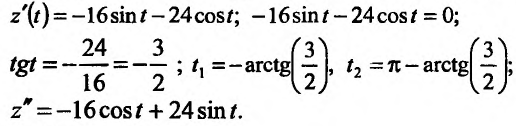
Так как
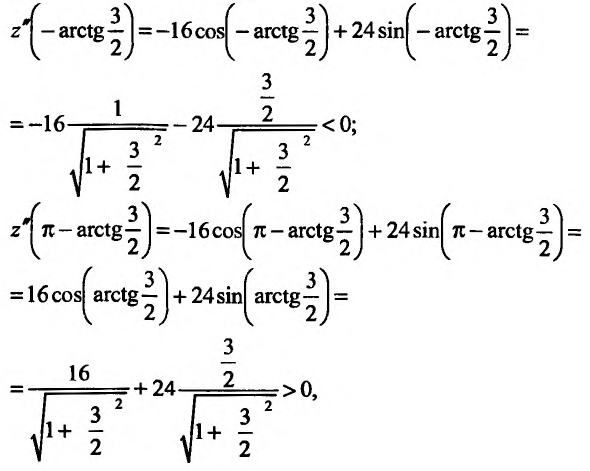
то  – точка максимума, a
– точка максимума, a  – точка минимума, причем
– точка минимума, причем
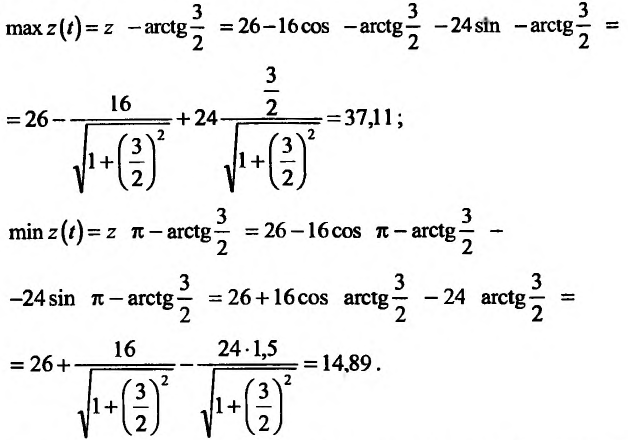
Сравнивая, полученные экстремальные значения функции, замечаем, что в круге 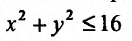 наименьшее значение функции равно «-3», и достигается оно внутри круга в точке А(2;3). а наибольшее значение функции равно 37,11 и достигается оно на окружности
наименьшее значение функции равно «-3», и достигается оно внутри круга в точке А(2;3). а наибольшее значение функции равно 37,11 и достигается оно на окружности 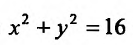 в точке
в точке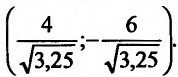
Метод наименьших квадратов
Понятие об эмпирических формулах. При изучении различных процессов и явлений мы почти всегда сталкиваемся с задачей: «Функциональная зависимость между переменными величинами л: и у задана, исходя из тех или иных теоретических соображений Формула, выражающая эту зависимость, содержит постоянные величины, которые необходимо определить по результатам наблюдений.»
Отметим, что нередко при обработке результатов наблюдений (опыта) приходится встречаться и с более сложной задачей, то есть с задачей вида: «В результате наблюдений получен ряд значений переменных х и у, однако характер функциональной зависимости между ними остается неизвестным. Требуется, по наблюденным данным, найти аналитическое выражение зависимости между x и y. Такие формулы, принято называть эмпирическими формулами, то есть формулами, полученными в результате опыта (наблюдений).
Совершенно ясно, что однозначно установить функциональную зависимость между х и у по конечному числу измеренных значений было бы невозможно даже в том случае, если бы они не обладали ошибками, свойственными наблюденным величинам.
Следует поэтому отчетливо представлять, что математическая обработка результатов наблюдений не может ставить перед собой задачу разгадать истинный характер зависимости между имеющимися переменными. Речь идет лишь о том, чтобы охватить результаты опыта наиболее простой формулой, которая позволит применять методы математического анализа к дальнейшему изучению наблюденных данных.
Метод наименьших квадратов. Пусть в результате некоторого опыта мы получили числовые значения, которые дают возможность установить взаимосвязь между исследуемыми величинами в математической форме. Исходя из теоретических соображений, выберем вид этой зависимости:

Функция (17.4.1) — это функция независимой переменной х и (m + l)-ro параметра 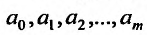 . Эти параметры постоянны и неизвестны, так как они не поддаются непосредственным измерениям заранее. Для их определения производится ряд измерений величин х и у. Подставляя поочередно их в равенство (17.4.1), мы получаем уравнения между параметрами
. Эти параметры постоянны и неизвестны, так как они не поддаются непосредственным измерениям заранее. Для их определения производится ряд измерений величин х и у. Подставляя поочередно их в равенство (17.4.1), мы получаем уравнения между параметрами 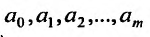 вида:
вида:
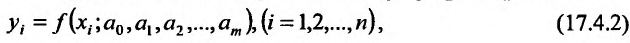
где 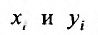 , соответствующие друг другу измерения, а n – число измерений. Если бы значения х и у находились точно, то для отыскания m +1 параметра достаточно было бы произвести m+1 измерение. На самом же деле, значения х и у содержат ошибки и никакие m +1 измерений не позволят определить истинные значения параметров. Поэтому обычно производится большее число измерений (n > m + l), в результате чего число уравнений (17.4.2) будет больше числа неизвестных параметров. Полученная система будет, вообще говоря, несовместной, то есть точные решения каких-либо m + 1 из уравнений системы могут не удовлетворять остальным уравнениям. Наша задача состоит в том, чтобы найти такие значения неизвестных параметров, которые будут удовлетворять этим уравнениям наилучшим образом, хотя и не точно.
, соответствующие друг другу измерения, а n – число измерений. Если бы значения х и у находились точно, то для отыскания m +1 параметра достаточно было бы произвести m+1 измерение. На самом же деле, значения х и у содержат ошибки и никакие m +1 измерений не позволят определить истинные значения параметров. Поэтому обычно производится большее число измерений (n > m + l), в результате чего число уравнений (17.4.2) будет больше числа неизвестных параметров. Полученная система будет, вообще говоря, несовместной, то есть точные решения каких-либо m + 1 из уравнений системы могут не удовлетворять остальным уравнениям. Наша задача состоит в том, чтобы найти такие значения неизвестных параметров, которые будут удовлетворять этим уравнениям наилучшим образом, хотя и не точно.
Так как уравнения (17.4.2) удовлетворяются не точно, то будем иметь:
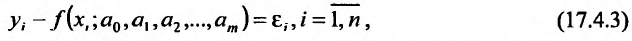
где 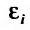 — отклонения измеренных значений yj от вычисленных по формуле (17.4.1). В методе наименьших квадратов утверждается, что наилучшими значениями параметров будут такие, при которых сумма квадратов отклонений
— отклонения измеренных значений yj от вычисленных по формуле (17.4.1). В методе наименьших квадратов утверждается, что наилучшими значениями параметров будут такие, при которых сумма квадратов отклонений 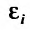 , будет наименьшей, то есть
, будет наименьшей, то есть
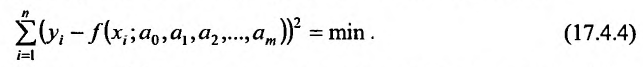
Замечание. Мы не рассматриваем сумму самих отклонений (невязок), так как сумма 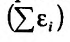 может быть очень малой и тогда, когда отдельные отклонения
может быть очень малой и тогда, когда отдельные отклонения 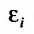 очень велики, но имеют разные знаки и взаимно компенсируют друг друга.
очень велики, но имеют разные знаки и взаимно компенсируют друг друга.
Из минимума суммы квадратов отклонений автоматически вытекает, что все невязки е, в своей совокупности должны быть минимальными.
Рассматривая теперь правую часть выражения (17.4.4) как некоторую функцию независимых переменных  , применим необходимые условия экстремумов для нахождения минимума этой функции. Для этого вычислим частные производные по этим переменным
, применим необходимые условия экстремумов для нахождения минимума этой функции. Для этого вычислим частные производные по этим переменным  и приравняем их к нулю. Получим в точности m +1 уравнение с m +1 неизвестными. Составление и решение этой системы особенно просто в том случае, когда функция
и приравняем их к нулю. Получим в точности m +1 уравнение с m +1 неизвестными. Составление и решение этой системы особенно просто в том случае, когда функция 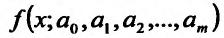 линейна относительно параметров, то есть если она имеет вид:
линейна относительно параметров, то есть если она имеет вид:
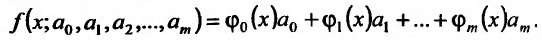
Тогда дифференцируя сумму квадратов отклонений
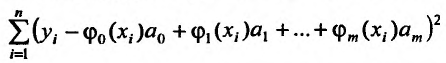
по 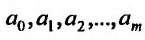 и приравнивая к нулю частные производные, получим:
и приравнивая к нулю частные производные, получим: 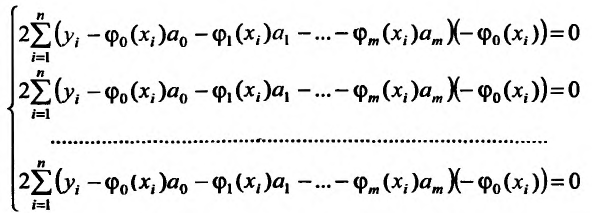
Или после преобразования будем иметь линейную неоднородную систему:
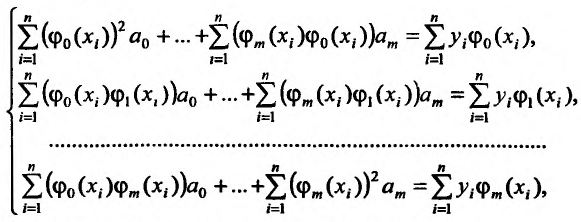
которую решаем любым известным нам способом.
Применим теперь общие выводы в некоторых конкретных случаях.
а) Выравнивание по прямой. Пусть 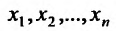 – последовательность значений независимой переменной, а
– последовательность значений независимой переменной, а 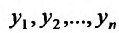 – последовательность соответствующих значений зависимой переменной, полученных из опыта. Требуется подобрать прямую, которая наилучшим образом отображала бы зависимость между х и у, то есть, чтобы отклонения фактических значений функции от подобранной прямой были бы минимальными.
– последовательность соответствующих значений зависимой переменной, полученных из опыта. Требуется подобрать прямую, которая наилучшим образом отображала бы зависимость между х и у, то есть, чтобы отклонения фактических значений функции от подобранной прямой были бы минимальными.
Для решения этой задачи применим метод наименьших квадратов. В этом случае функция 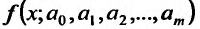 зависит от двух параметров, которые обозначим а и b, и имеет вид:
зависит от двух параметров, которые обозначим а и b, и имеет вид: 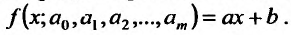 .
.
Отклонения от фактических значений функции составляют: 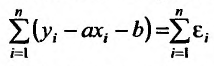
Согласно метода наименьших квадратов, искомыми параметрами а и b будут те, для которых
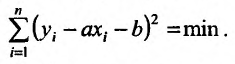
Необходимое условие существования минимума состоит в том, чтобы
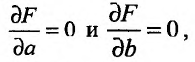
где 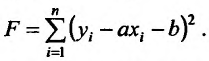
Вычислив частные производные и приравняв их нулю, получим два уравнения для определения а и b:
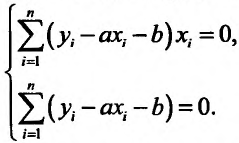
Раскрывая скобки и производя суммирование, получаем систему линейных уравнений: 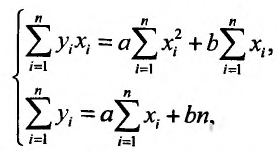
решая которую находим значения а и b: 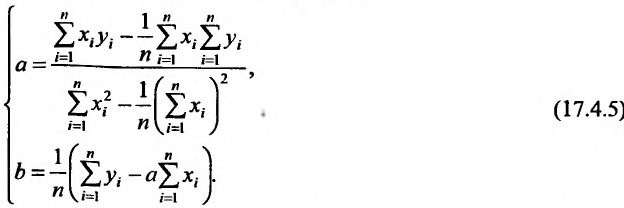
Значения а и b, найденные по формулам (17.4.5), определяют прямую наилучшим образом, в смысле метода наименьших квадратов, описывающую изучаемую зависимость.
Пример:
В течение четырех последовательных лет переменные х и у принимали значения, указанные в таблице 17.1. 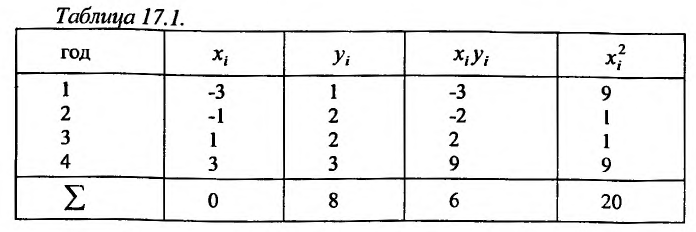
Найти прямую, выражающую зависимость величины у от величины х.
Решение:
Для определения эмпирической прямой у = ах + b, составим систему (17.4.5).Так как
то система (17.4.5) будет иметь вид: 
Решив систему, находим: b = 2, а = 0,3.
Тогда искомая прямая, имеет вид: y = 0,Зх + 2.
б) Выравнивание но параболе. Пусть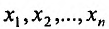 – последовательность значений независимой переменной, а
– последовательность значений независимой переменной, а 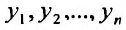 последовательность соответствующих значений зависимой переменной.
последовательность соответствующих значений зависимой переменной.
Предположим, что точки 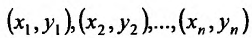 расположены вдоль некоторой параболы. Применим метод наименьших квадратов для определения параметров квадратичной функции, то есть параболы второго порядка:
расположены вдоль некоторой параболы. Применим метод наименьших квадратов для определения параметров квадратичной функции, то есть параболы второго порядка: 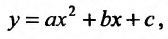
соответствующей наблюденной экспериментальной зависимости, таким образом, чтобы сумма квадратов отклонений эмпирических данных от действительных значений функции была минимальной, то есть 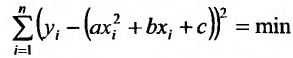 где
где  – наблюденные значения, а
– наблюденные значения, а  – значения функции в точках
– значения функции в точках 
Необходимые условия существования минимума функции 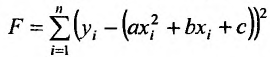 определяют систему уравнений:
определяют систему уравнений:
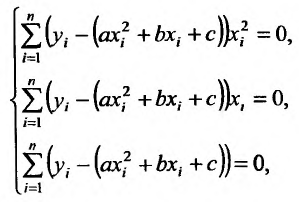
которую можно преобразовать к виду: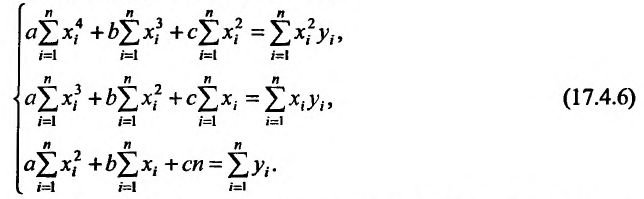
Решая эту систему одним из известных методов, вычисляем неизвестные коэффициенты a, b и с.
в) Выравнивание с помощью гиперболы. Пусть  -последовательность значений независимой переменной, а
-последовательность значений независимой переменной, а 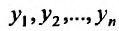 – последовательность соответствующих значений зависимой переменной. Предположим, что эмпирические данные
– последовательность соответствующих значений зависимой переменной. Предположим, что эмпирические данные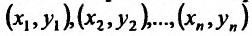 описываются гиперболой
описываются гиперболой
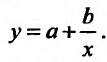
Эта гипербола подобрана наилучшим образом, в смысле способа наименьших квадратов, если функция
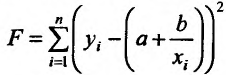
достигает минимума. Необходимые условия минимума функции F определяют систему:
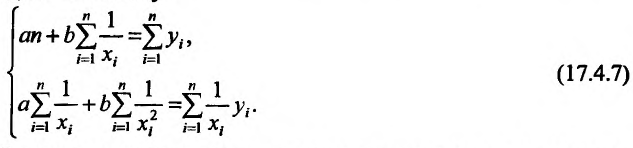
Решая эту систему, находим значения неизвестных параметров а и b.
Зависимость между удельными затратами и объемом производства можно описать гиперболой. Действительно, если переменные издержки составляют а, а постоянные издержки b, то полные затраты определяются уравнением К(х) = ах + b, где х – объем (производства) выпуска продукции. Тогда удельные затраты равны отношению полных затрат к объему производства, т. е.
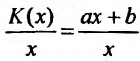
и, следовательно:
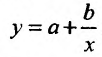
Применяя метод наименьших квадратов, мы можем определить а и b, если за у принять удельные затраты.
г) Выравнивание по показательной функции. Пусть  – последовательность значений независимой переменной, а
– последовательность значений независимой переменной, а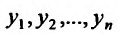 – последовательность соответствующих значений зависимой переменной. Предположим, что точки
– последовательность соответствующих значений зависимой переменной. Предположим, что точки 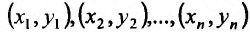 расположены вдоль показательной кривой
расположены вдоль показательной кривой
вида 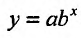 . Найдем параметры а и b, используя метод наименьших квадратов, то есть найдем такую кривую
. Найдем параметры а и b, используя метод наименьших квадратов, то есть найдем такую кривую 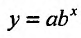 , которая бы наилучшим образом отражала зависимость между переменными х и у.
, которая бы наилучшим образом отражала зависимость между переменными х и у.
Представим уравнение показательной кривой 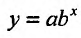 в виде
в виде
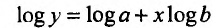 , или, вводя обозначения logа=А, logb = B,
, или, вводя обозначения logа=А, logb = B,
получим:
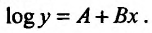
Отсюда следует, что функция у, представленная на графике в системе прямоугольных координат, где ось ординат разделена по логарифмической шкале, а ось абсцисс – по обычной шкале, определяет прямую с угловым коэффициентом В и расстоянием по оси Оу, равным А.
Согласно методу наименьших квадратов, найдем минимум
функции 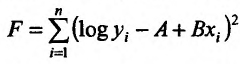 .Применяя необходимые условия
.Применяя необходимые условия
существования минимума, получим:
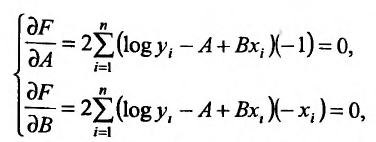
или, раскрывая скобки и производя суммирование, будем иметь систему:
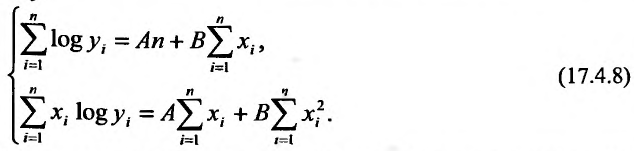
Решая, полученную систему (17.4.8), известными методами, найдем параметры А и В. Потенцируя равенства log а = А и log b = B, находим а и Ь, которые определяют показательную кривую 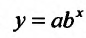 , наилучшим образом описывающую изучаемую зависимость.
, наилучшим образом описывающую изучаемую зависимость.
Необходимые условия условного экстремума
В предыдущем параграфе мы рассмотрели локальный экстремум функции, аргументы которой не связаны никакими дополнительными условиями. Вместе с тем в приложениях математики (в экономических исследованиях) часто встречается задача об отыскании экстремума функции, аргументы которой удовлетворяют дополнительным условиям связи.
Приведем пример задачи об отыскании условного экстремума:
«Пусть требуется найти экстремум функции 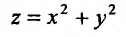 при условии, что аргументы этой функции удовлетворяют условию связи Зх + у —2 = 0.»
при условии, что аргументы этой функции удовлетворяют условию связи Зх + у —2 = 0.»
Таким образом, экстремумы функции ищутся не на всей плоскости Оху , а лишь на прямой Зх + у – 2 = 0. Для решения поставленной задачи подставим значение у (определяемое из условия связи 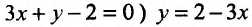 , в функцию z:
, в функцию z:
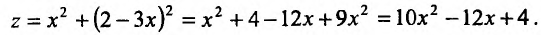
Получили функцию аргумента х и свели поставленную задачу к отысканию безусловного экстремума функции 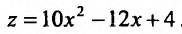
Так как 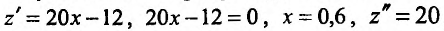 , то функция
, то функция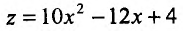 имеет минимум в точке х = 0,6, равный
имеет минимум в точке х = 0,6, равный 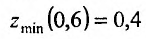 . Таким образом, функция
. Таким образом, функция 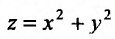 с условием связи Зх + у – 2 = 0 имеет условный минимум
с условием связи Зх + у – 2 = 0 имеет условный минимум 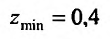 в точке (0,6;0,2). Отметим, что безусловный минимум функции
в точке (0,6;0,2). Отметим, что безусловный минимум функции 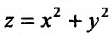 достигается в точке (0;0) и равен z = 0. Это значит, что минимум функции
достигается в точке (0;0) и равен z = 0. Это значит, что минимум функции 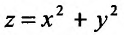 на всей плоскости не совпадает с ее минимумом на прямой
на всей плоскости не совпадает с ее минимумом на прямой 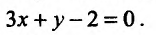
Рассмотрим общую постановку задачи об отыскании условного экстремума.
Пусть требуется найти экстремум функции двух переменных

при условии, что аргументы х и у удовлетворяют уравнению:
F(x,y) = a. (17.5.2)
Определение 17.5.1. Функция z = f(x,y) при условии F(x,y) = а имеет условный максимум (минимум) в точке 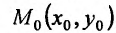 , координаты которой удовлетворяют условиям связи И7.5.2), если существует такая окрестность
, координаты которой удовлетворяют условиям связи И7.5.2), если существует такая окрестность  , что для всех точек
, что для всех точек , координаты которых удовлетворяют условиям связи (17.5.2).
, координаты которых удовлетворяют условиям связи (17.5.2).
Геометрическая задача на условный экстремум может быть истолкована следующим образом. Дана поверхность Q с уравнением  и линия L на этой поверхности, являющаяся линией пересечения поверхности Q с цилиндрической поверхностью F(x,y) = a. (рис. 17.1)
и линия L на этой поверхности, являющаяся линией пересечения поверхности Q с цилиндрической поверхностью F(x,y) = a. (рис. 17.1)
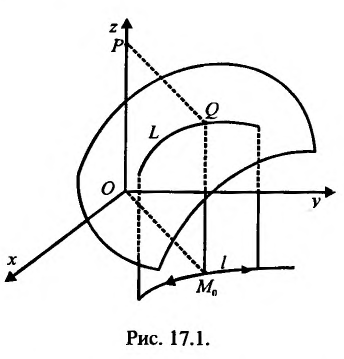
У точек линии L надо найти экстремальную аппликату. Точки поверхности Q, не принадлежащие линии L, не рассматриваются. На рис. 17.1 точка Р имеет максимальную в этом смысле аппликату. Спроектировав линию L на плоскость хОу, получим кривую l с уравнением F(x,y) = a. Точка 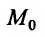 линии I (проекция точки Р-поверхности Q) называется точкой условного экстремума (в данном случае точкой условного максимума) функции z = f(x,y). а аппликата
линии I (проекция точки Р-поверхности Q) называется точкой условного экстремума (в данном случае точкой условного максимума) функции z = f(x,y). а аппликата  точки Р – условным экстремумом (максимумом).
точки Р – условным экстремумом (максимумом).
Дня нахождения условного экстремума функции z = f(x,y) при наличии связи F(x,y)= а, предположим, что F дифференцируема в окрестности точки  , непрерывна в точке
, непрерывна в точке  и производная
и производная 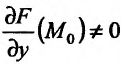 . Тогда существует окрестность точки
. Тогда существует окрестность точки 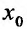 , в которой определена единственная функция
, в которой определена единственная функция 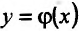 , дифференцируемая в этой окрестности. Подставляя найденную функцию в (17.5.1), сведем вопрос о существовании условного экстремума в точке
, дифференцируемая в этой окрестности. Подставляя найденную функцию в (17.5.1), сведем вопрос о существовании условного экстремума в точке  у функции
у функции 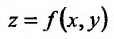 при наличии связи (17.5.2) к вопросу о существовании безусловного экстремума в точке х0 у сложной функции
при наличии связи (17.5.2) к вопросу о существовании безусловного экстремума в точке х0 у сложной функции 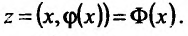
Установим теперь необходимые условия существования условного экстремума в точке  таким образом, чтобы не решать уравнения связи. Итак, пусть функция
таким образом, чтобы не решать уравнения связи. Итак, пусть функция 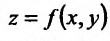 дифференцируема в точке
дифференцируема в точке  и имеет в этой точке условный экстремум при наличии связи (17.5.2) или (что то же самое) функция
и имеет в этой точке условный экстремум при наличии связи (17.5.2) или (что то же самое) функция 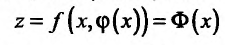 (17.5.3) имеет в точке
(17.5.3) имеет в точке  безусловный экстремум. Необходимым условием безусловного экстремума функции (17.5.3) в точке
безусловный экстремум. Необходимым условием безусловного экстремума функции (17.5.3) в точке  является равенство нулю производной этой функции
является равенство нулю производной этой функции 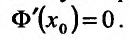 Так как функция Ф сложная неявно заданная функция, то, применяя правило дифференцирования неявно заданной функции, получим:
Так как функция Ф сложная неявно заданная функция, то, применяя правило дифференцирования неявно заданной функции, получим: 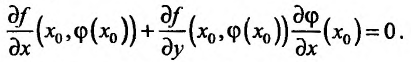 (17.5.4) Подставив в (17.5.2) решение этого уравнения
(17.5.4) Подставив в (17.5.2) решение этого уравнения 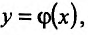 получим тождество. Тогда, дифференцируя это тождество, получим:
получим тождество. Тогда, дифференцируя это тождество, получим: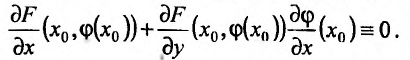 (17.5.5) Умножим, далее, равенство (17.5.5) на произвольный (и пока неизвестный) постоянный множитель
(17.5.5) Умножим, далее, равенство (17.5.5) на произвольный (и пока неизвестный) постоянный множитель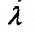 и сложим с (17.5.4). В результате получим следующее равенство:
и сложим с (17.5.4). В результате получим следующее равенство: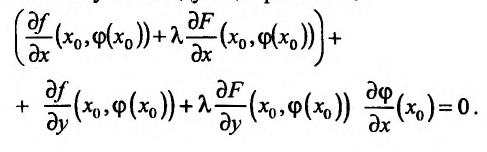 (17.5.6)
(17.5.6)
Пусть
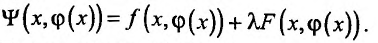
Тогда равенство (17.5.6) можно записать в виде:
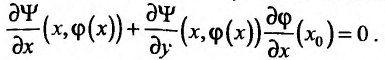
Выберем 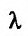 таким, чтобы выполнялось равенство:
таким, чтобы выполнялось равенство:
–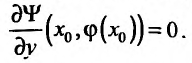
Так как функция 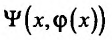 сложная функция, то, применив правило дифференцирования сложной функции, получим:
сложная функция, то, применив правило дифференцирования сложной функции, получим:
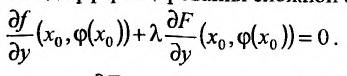 (17.5.8)
(17.5.8)
Так как 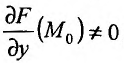 , то из (17.5.8) можно найти
, то из (17.5.8) можно найти  Тогда из (17.5.7) следует:
Тогда из (17.5.7) следует:
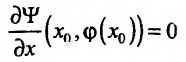 или
или
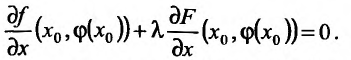 (17.5.9)
(17.5.9)
Присоединив к (17.5.8) и (17.5.9) условие связи (17.5.2), мы получим систему:
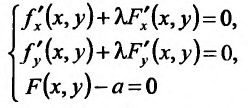
для определения координат точек возможного условного экстремума и 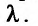
Практически поступают следующим образом составляют функцию Лагранжа
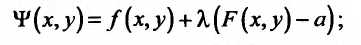 находят точки возможного безусловного экстремума; для исключения множителя
находят точки возможного безусловного экстремума; для исключения множителя 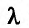 привлекают условие связи (17.5.2).
привлекают условие связи (17.5.2).
Достаточное условие условного экстремума
Рассмотрим далее достаточное условие условного экстремума функции 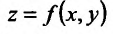 в точке
в точке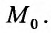 Мы должны определить знак разности
Мы должны определить знак разности 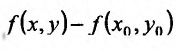 при всех
при всех 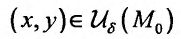 и удовлетворяющих уравнению связи
и удовлетворяющих уравнению связи 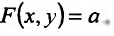 Из уравнения связи непосредственно следует, что вместо разности
Из уравнения связи непосредственно следует, что вместо разности 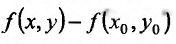 можно рассматривать разность
можно рассматривать разность  составленную для функции Лагранжа и исследовать ее знак. Разлагая эту функцию
составленную для функции Лагранжа и исследовать ее знак. Разлагая эту функцию 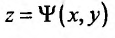 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  с остаточным членом в форме Пеано при
с остаточным членом в форме Пеано при 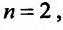 получим:
получим:
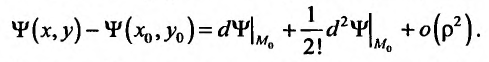
Так как 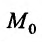 – стационарная точка, то дифференциал первого порядка
– стационарная точка, то дифференциал первого порядка 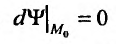 и знак разности определяется знаком второго дифференциала
и знак разности определяется знаком второго дифференциала 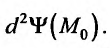 При этом, в точке
При этом, в точке будет минимум, если при наличии связи
будет минимум, если при наличии связи 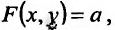 дифференциал второго порядка
дифференциал второго порядка 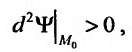 и максимум, если
и максимум, если 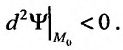 Дифференциал второго порядка
Дифференциал второго порядка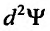 в точке
в точке  возможного экстремума можно вычислять, гак как если бы переменные
возможного экстремума можно вычислять, гак как если бы переменные 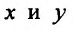 были бы независимыми, то есть по формуле:
были бы независимыми, то есть по формуле: 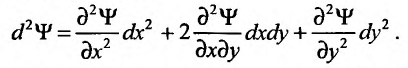 (17.6.1)
(17.6.1)
Однако при проведении вычислений, следует в формулу (17.6.1) подставить вместо дифференциала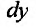 его значение, определяемое из равенства:
его значение, определяемое из равенства:
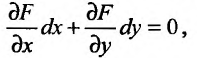 то есть
то есть
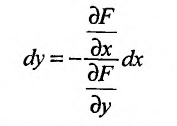
и изучить вопрос о знакоопределенности 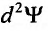 в данной точке
в данной точке 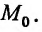 . После подстановки значения
. После подстановки значения 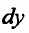 в (17.6.1), получим*
в (17.6.1), получим* 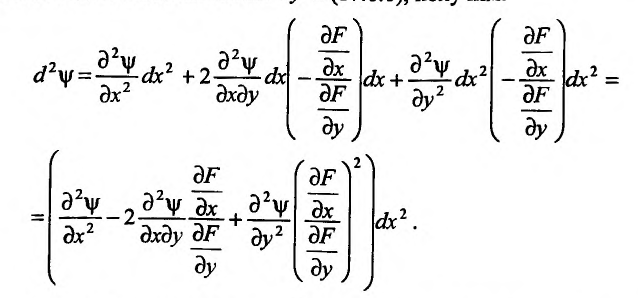
Откуда следует, что знак 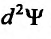 определяется знаком выражения:
определяется знаком выражения: 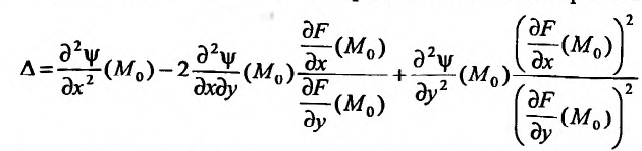 Если
Если то
то  что означает, что в точке
что означает, что в точке  условный минимум, если же
условный минимум, если же 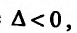 то
то 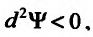 тогда в точке
тогда в точке 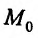 условный максимум.
условный максимум.
Выражение 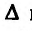 можно записать в матричном виде:
можно записать в матричном виде:
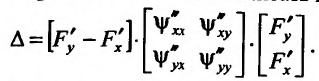 Все элементы матриц вычисляются в точке
Все элементы матриц вычисляются в точке 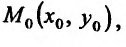 для заданного
для заданного 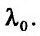
Пример №7
В данный полукруг радиуса R вписать прямоугольник наибольшей площади.
Решение:
Площадь прямоугольника со сторонами х и у (см. рис. 17.2.) выражается формулой:
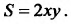
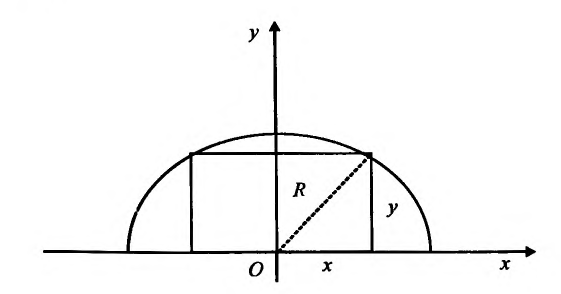
рис.17.2.
Координаты  удовлетворяют уравнению
удовлетворяют уравнению 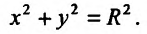 Найдем максимум функции
Найдем максимум функции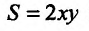 при условии
при условии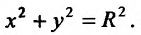 Составляем функцию Лагранжа:
Составляем функцию Лагранжа:
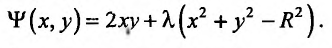
Вычисляем частные производные первого порядка функции 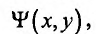 приравниваем их к нулю и, присоединив уравнение связи, получим систему для нахождения точек возможного условного экстремума:
приравниваем их к нулю и, присоединив уравнение связи, получим систему для нахождения точек возможного условного экстремума:
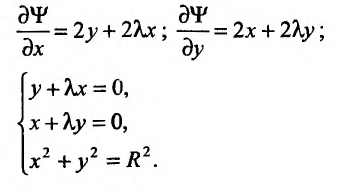 (17.6.2)
(17.6.2)
Из системы (17.6.2) находим:
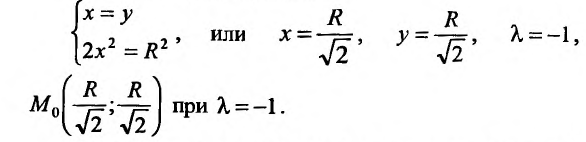 то есть
то есть
Мы получили единственный ответ, и так как наибольшее значение должно существовать, то ему должны соответствовать найденные значения переменных: 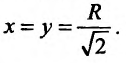 Подставляя эти значения в формулу, получаем:
Подставляя эти значения в формулу, получаем: 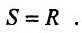
Пример №8
Некоторый цех завода выпускает два вида изделий, причем изделие каждого вида обрабатывается на двух разных станках А и В. Каждая единица первого изделия требует 3-х часов обработки на станке А и 2-х часов – на станке В. Для второго изделия время обработки соответственно 2 и 3 часа. Станок А можно использовать не более 8 часов, станок В – не более 7 часов. Прибыль, получаемая от продажи каждого вида изделия, равна 20 денежных единиц. Составить план работы цеха, обеспечивающий получение максимальной прибыли.
Решение:
Обозначим через 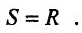 резерв времени работы станков А и В, а через
резерв времени работы станков А и В, а через 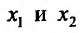 количество изделий первого и второго вида, который должен выпустить цех. Тогда, для составления плана, обеспечивающего максимальную прибыль, нужно найти максимум функции
количество изделий первого и второго вида, который должен выпустить цех. Тогда, для составления плана, обеспечивающего максимальную прибыль, нужно найти максимум функции 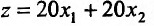 при ограничениях:
при ограничениях:
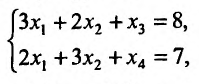
где 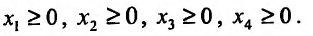
Составляем функцию Лагранжа:
Вычисляем частные производные, приравниваем их к нулю и составляем систему:
Находим решение системы:
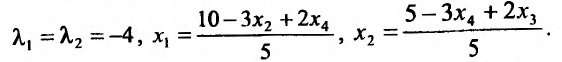 Подставив найденные значения
Подставив найденные значения  в функцию Лагранжа, получим функцию:
в функцию Лагранжа, получим функцию:
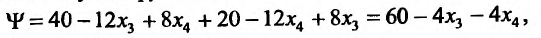
которая достигает максимума, когда  достигают минимума, то есть
достигают минимума, то есть 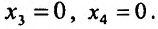 Подставив значения
Подставив значения 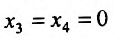 в решение системы, найдем:
в решение системы, найдем:
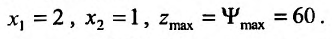
Пример №9
Имеется два технологических процесса производства некоторого продукта. Обозначим через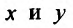 количество продукта, произведенного соответственно первым и вторым способом. Издержки производства при каждом технологическом процессе производства выражаются функциями:
количество продукта, произведенного соответственно первым и вторым способом. Издержки производства при каждом технологическом процессе производства выражаются функциями:
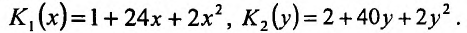
За некоторое время нужно произвести 100 единиц продукта, то есть 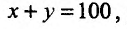 распределив их так, чтобы минимизировать общие издержки.
распределив их так, чтобы минимизировать общие издержки.
Решение:
Составим функцию, характеризующую издержки производства:
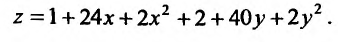
При этом количества продукта удовлетворяю! равенству 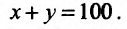 Итак, задача сводится к нахождению минимума функции, описывающей издержки производства при условии, что объемы продукта связаны условием. Это значит, что нужно найти условный минимум функции двух переменных. Для этого составим функцию Лагранжа:
Итак, задача сводится к нахождению минимума функции, описывающей издержки производства при условии, что объемы продукта связаны условием. Это значит, что нужно найти условный минимум функции двух переменных. Для этого составим функцию Лагранжа:
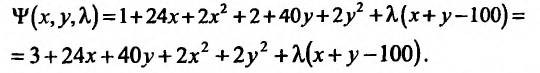
Вычислим частные производные и приравняем их к нулю:
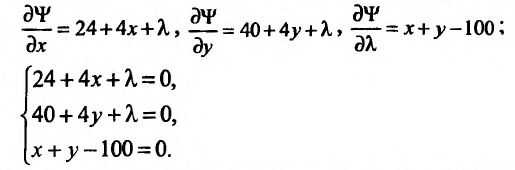
Решив систему (17.6.3), находим 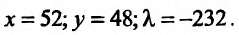
Вычисляем частные производные второго порядка функции Лагранжа:
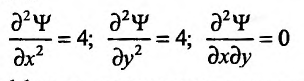
и дифференциал второго порядка при выполнении условий связи, то есть когда 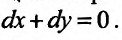 Имеем:
Имеем: 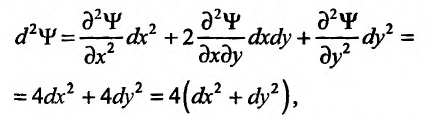 и, значит, при выполнении условий связи
и, значит, при выполнении условий связи При
При  функция
функция 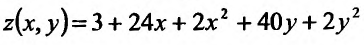 имеет условный минимум.
имеет условный минимум.
Таким образом, если 52 единицы продукта произвести первым технологическим способом, а 48 единиц продукта вторым технологическим способом, то общие издержки производства 100 единиц продукта будут минимальными.
Дифференциальное исчисление функции нескольких переменных
Ранее мы изучали функции одной независимой переменной. Однако многим явлениям, в том числе экономическим, присуща многофакторная зависимость. Исследование таких зависимостей привело к необходимости расширения известного понятия функциональной зависимости и введению понятия функции нескольких переменных.
Будем рассматривать функции двух переменных, т.к. все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. Эти факты обобщаются на случай большего числа переменных. Кроме того, для функций двух переменных можно дать наглядную геометрическую интерпретацию.
Определение. Пусть дано множество D упорядоченных пар чисел  Если каждой паре (х,.у) значений двух, независимых друг от друга, переменных величин х и у, принадлежащих множеству D, соответствует определенное значение величины Z, то говорят, что Z есть функция двух переменных хиу, определенная на множестве D .
Если каждой паре (х,.у) значений двух, независимых друг от друга, переменных величин х и у, принадлежащих множеству D, соответствует определенное значение величины Z, то говорят, что Z есть функция двух переменных хиу, определенная на множестве D .
Символическое обозначение  или Z = f(x,y). При этом х и у называются независимыми переменными (аргументами), a Z – зависимой переменной (функцией).
или Z = f(x,y). При этом х и у называются независимыми переменными (аргументами), a Z – зависимой переменной (функцией).
Определение. Совокупность пар (х,y) значений х и у, при которых определяется функция Z = f(х,у) называется областью определения или областью существования этой функции. Множество значений, принимаемых Z в области определения, называется областью изменения этой функции, обозначается  или Е.
или Е.
Пара (х,у) определяет точку M(х,у) в области существования, т.е. область определения – часть плоскости 
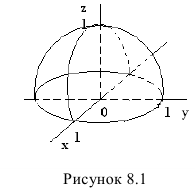
Область определения функции 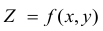 в простейших случаях представляет собой:
в простейших случаях представляет собой:
- либо часть плоскости, ограниченную замкнутой кривой, причем точки этой кривой (границы области) могут принадлежать или не принадлежать области определения,
- либо всю плоскость,
- либо, наконец, совокупность нескольких частей плоскости
Геометрически изображением функции Z = f(х,у) в системе координат 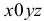 является некоторая поверхность.
является некоторая поверхность.
Примеры:
1. Примером функции двух переменных может служить формула площади прямоугольника S со сторонами, длины которых равны х и у: S = ху. Областью определения этой функции является множество 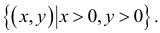
2. Область определения функции Z = 2x-y является вся плоскость.
3. Область определения функции 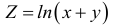 – точки правее (выше) прямой
– точки правее (выше) прямой
у=-х.
4. Для функции, описывающей площадь треугольника S = xy/2, область определения х>0 и у>0. Заметим, что естественной областью определения является вся плоскость.
5. Функция 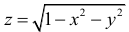 имеет областью определения круг
имеет областью определения круг 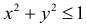 и
и
изображается верхней полусферой с центром в точке O(0,0,0) и радиусом R = 1 (Рисунок 8.1).
Аналогично определяется функция любого конечного числа независимых переменных и 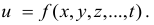
6. Объём параллелепипеда V = xyz .
В области D существует множество точек, в которых функция 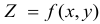 принимает одинаковые значения. Если Z = C = const, тогда уравнение f(х,у) = С определяет линию в плоскости
принимает одинаковые значения. Если Z = C = const, тогда уравнение f(х,у) = С определяет линию в плоскости 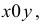 во всех точках которой Z = С. Такая линия называется линией уровня.
во всех точках которой Z = С. Такая линия называется линией уровня.
Если задана функция трех переменных 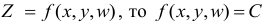 определяет поверхность уровня, во всех точках которой Z = С.
определяет поверхность уровня, во всех точках которой Z = С.
Линию, ограничивающую данную область, будем называть границей области. Точки области, не лежащие на границе области, называются внутренними точками области.
Область, состоящая из одних внутренних точек, называется открытой или незамкнутой.
Область с присоединенной к ней границей называется замкнутой, обозначается 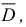 примером замкнутой области является круг с окружностью.
примером замкнутой области является круг с окружностью.
Область называется ограниченной, если существует такое постоянное С, что расстояние любой точки М области от начала координат O меньше С.
Функция двух переменных, как и функция одной переменной, может быть задана разными способами: табличным, аналитическим (с помощью формулы), графическим (например, полусфера – для функции двух аргументов, см. Рисунок 12).
Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично функции одной переменной.
Предел и непрерывность
Введем понятие окрестности точки. Множество всех точек М(х,у) плоскости, координаты которых удовлетворяют неравенству 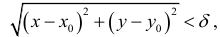 называется
называется 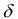 – окрестностью точки
– окрестностью точки 
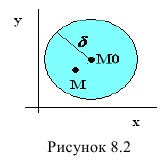
Другими словами  – окрестность точки – это все внутренние точки круга с центром
– окрестность точки – это все внутренние точки круга с центром  и радиусом
и радиусом 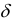 (Рисунок 8.2).
(Рисунок 8.2).
Пусть функция 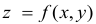 определена в некоторой окрестности точки
определена в некоторой окрестности точки 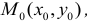 кроме, быть может, самой этой точки.
кроме, быть может, самой этой точки.
Определение. Число А называется пределом функции z = f(x,y) при 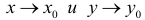 (или, что то же самое, при
(или, что то же самое, при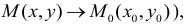 если для любого сколь угодно малого положительного числа
если для любого сколь угодно малого положительного числа 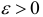 существует
существует  такое, что для всех
такое, что для всех  и удовлетворяющих неравенству
и удовлетворяющих неравенству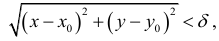 выполняется неравенство
выполняется неравенство 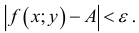
Записывают это так:
Геометрический смысл предела функции двух переменных состоит в следующем.
Каково бы ни было число 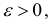 найдется
найдется 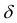 – окрестность точки
– окрестность точки 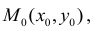 что во всех ее точках М(х,у), отличных от
что во всех ее точках М(х,у), отличных от 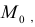 аппликаты соответствующих точек поверхности z = f(x,y) отличаются от числа А по модулю меньше, чем на
аппликаты соответствующих точек поверхности z = f(x,y) отличаются от числа А по модулю меньше, чем на 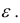
Вычисление пределов функций двух переменных оказывается существенно более трудной задачей по сравнению со случаем одной переменной. Причина заключается в том, что из определения предела следует, что если предел существует, то он не зависит от пути, по которому М стремится к 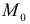 (число таких направлений бесконечно! Для функции одной переменной
(число таких направлений бесконечно! Для функции одной переменной 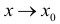 по двум направлениям – справа и слева!). На плоскости – таких направлений – бесконечное множество, и пределы функции по разным направлениям могут не совпадать.
по двум направлениям – справа и слева!). На плоскости – таких направлений – бесконечное множество, и пределы функции по разным направлениям могут не совпадать.
Определение. Функция z = f(x,y) называется непрерывной в точке 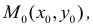 если она:
если она:
а) определена в этой точке и некоторой ее окрестности;
б) имеет предел 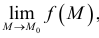
в) этот предел равен значению функции z = f(x,y) в точке  т.е.
т.е.
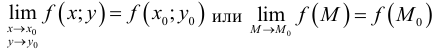
Определение. Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области.
Частные и полное приращение функции нескольких переменных
Пусть дана функция двух переменных z = f(x,у). Полагая у = const, дадим независимой переменной х приращение 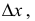 тогда z получит приращение, которое называют частным приращением z по х и обозначают
тогда z получит приращение, которое называют частным приращением z по х и обозначают 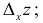
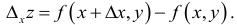
Аналогично, 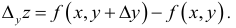
Наконец, сообщив аргументу х приращение 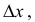 а аргументу у – приращение
а аргументу у – приращение 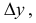 получим для z приращение
получим для z приращение 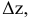 которое называется полным приращением функции z и определяется формулой
которое называется полным приращением функции z и определяется формулой
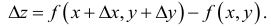
Заметим, что в общем случае 
Пример:
Пусть z = ху.
Тогда приращения этой функции будут иметь вид 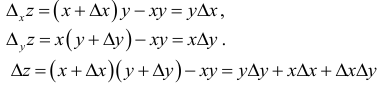
При 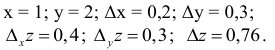
Аналогичным образом определяются частные и полные приращения функции любого количества переменных.
Рассмотрим примеры использования функции нескольких переменных в экономике.
Пример:
Пусть предметами потребления будут два товара: А и В, с соответствующими ценами 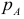 и
и 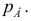 Если цены на другие товары постоянны, а доходы потребителей и структура потребностей на изменяются, то спрос и предложение каждого из товаров зависит от их цен.
Если цены на другие товары постоянны, а доходы потребителей и структура потребностей на изменяются, то спрос и предложение каждого из товаров зависит от их цен.
Запишем несколько функций:
1) Спрос на товар A: 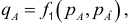
2) Спрос на товар В: 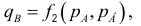
3) Предложение товара А: 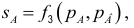
4) Предложение товара В: 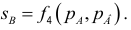
Частные производные
Определение. Частной производной по х от функции z = f(x,y) называется предел отношения частного приращения  по х к приращению
по х к приращению 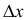 при стремлении
при стремлении 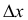 к нулю. Частная производная обозначается одним из символов
к нулю. Частная производная обозначается одним из символов
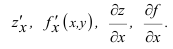
Таким образом, по определению
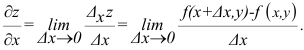
Аналогично определяется частная производная по у.
Заметив, что 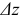 вычисляется при неизменном у, мы можем определить правило нахождения частной производной:
вычисляется при неизменном у, мы можем определить правило нахождения частной производной:
частная производная по одной переменной вычисляется в предположении, что остальные переменные являются величинами постоянными.
- Заказать решение задач по высшей математике
Полный дифференциал функции нескольких переменных
Полным приращением функции z =f(х,у)в точке M(х,у) называют разность
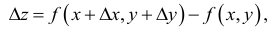
где  – произвольные приращения аргументов.
– произвольные приращения аргументов.
Функцию  называют дифференцируемой в точке (х,у), если в этой точке полное приращение можно представить в виде
называют дифференцируемой в точке (х,у), если в этой точке полное приращение можно представить в виде
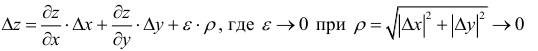
Полным дифференциалом функции z = f(x,y) называют главную часть
полного приращения  линейную относительно приращений аргументов
линейную относительно приращений аргументов  т.е.
т.е.
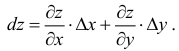
Пусть
1) z = х, найдем: 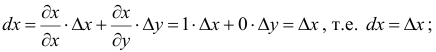
2) z = у, найдем: 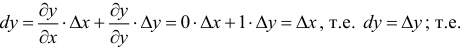
дифференциалы независимых переменных совпадают с их приращениями.
Поэтому полный дифференциал функции z = f(х, у) определяется по формуле
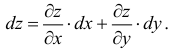
Полный дифференциал равен сумме произведений частных производных на дифференциалы соответствующих независимых переменных.
Из этого следует, что (при достаточно малом 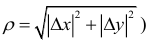 для дифференцируемой функции z = f(x,y) справедливы приближенные равенства
для дифференцируемой функции z = f(x,y) справедливы приближенные равенства
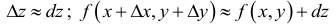
т.е. полное приращение функции приближенно равно ее полному дифференциалу.
Функция f(x,y) называется дифференцируемой в точке (х,у), если она имеет в этой точке полный дифференциал.
Пример №10
Вычислить приближенно 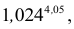 исходя из значения функции
исходя из значения функции 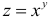 при x = 1,у = 4 и заменяя ее приращение дифференциалом.
при x = 1,у = 4 и заменяя ее приращение дифференциалом.
Решение. Искомое число есть наращенное значение функции z при 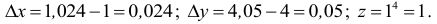
Найдем приращение функции:
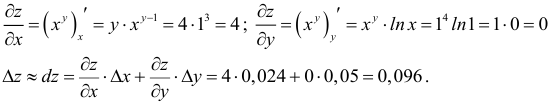
Итак, 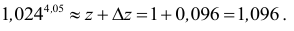
Частные производные и дифференциалы высших порядков
Пусть имеется функция двух переменных 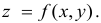
Частными производными второго порядка функции 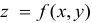 называются частные производные от ее частных производных первого порядка.
называются частные производные от ее частных производных первого порядка.
Частные производные 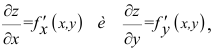 вообще говоря, являются функциями переменных х и у. Поэтому от них можно снова находить частные производные. Следовательно, можно получить четыре частных производных второго порядка:
вообще говоря, являются функциями переменных х и у. Поэтому от них можно снова находить частные производные. Следовательно, можно получить четыре частных производных второго порядка:
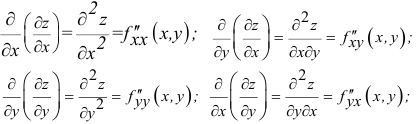
Производные второго порядка можно снова дифференцировать как по х, так и по у. Получим восемь частных производных третьего порядка, и т.д..
Пример №11
Вычислить четвертую производную если
если 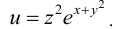
Последовательно дифференцируя заданную функция, получаем
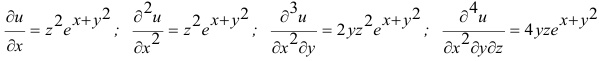
Возникает естественный вопрос – зависит ли результат дифференцирования от порядка (последовательности) дифференцирования?
Теорема. Если функция z = f(x,y) и её частные производные 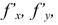
 определены и непрерывны в точке М(х,у) и в некоторой её окрестности, то в этой точке смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой:
определены и непрерывны в точке М(х,у) и в некоторой её окрестности, то в этой точке смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой:
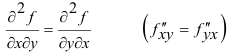
Теорема имеет место и для функции любого числа переменных.
Дифференциалом второго порядка функции 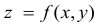 называют
называют
дифференциал от ее полного дифференциала, т.е. 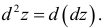 Аналогично определяются дифференциалы третьего
Аналогично определяются дифференциалы третьего 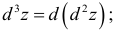 и высших порядков:
и высших порядков:
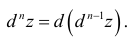
Если х и у-независимые переменные и функция z = f(x,y) имеет непрерывные частные производные, то дифференциалы второго и третьего порядков вычисляются по формулам
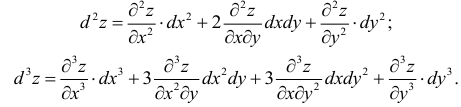
Вообще, имеет место символическая формула, 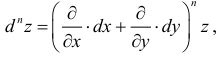
которая формально раскрывается по биномиальному закону.
Дифференцирование сложной функции
а) Пусть 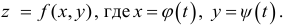 Функции
Функции  и
и 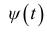
– дифференцируемы. Тогда производная сложной функции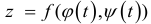 вычисляется по формуле:
вычисляется по формуле:
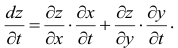
б) Предположим, что в уравнении 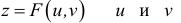 являются функциями независимых переменных х и у:
являются функциями независимых переменных х и у: 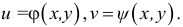 В этом случае z есть сложная функция от аргументов х и у.
В этом случае z есть сложная функция от аргументов х и у.
Предположим, что функции 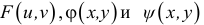 имеют непрерывные частные производные по всем своим аргументам, и поставим задачу:
имеют непрерывные частные производные по всем своим аргументам, и поставим задачу:
вычислить 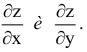
Дадим аргументу х приращение  сохраняя значение у неизменным. Тогда
сохраняя значение у неизменным. Тогда 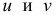 получат приращения, соответственно получит приращение и функция
получат приращения, соответственно получит приращение и функция 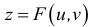
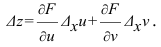
Разделим всё на 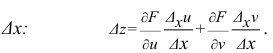
Переходя к пределу при 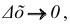 получим
получим
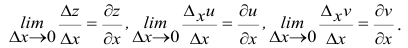
Следовательно, 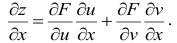
Аналогично получим 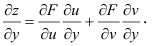
Дифференцирование неявных функций
Функция 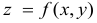 называется неявной, если она задается уравнением F(x,y,z)=0, неразрешенным относительно z.
называется неявной, если она задается уравнением F(x,y,z)=0, неразрешенным относительно z.
Найдем частные производные 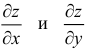 неявной функции z, заданной уравнением F(x,y,z) = 0. Для этого подставим в уравнение вместо z
неявной функции z, заданной уравнением F(x,y,z) = 0. Для этого подставим в уравнение вместо z
функцию f(х,у), получим тождество 
Частные производные по х и по у функции, тождественно равной нулю, также равны нулю:
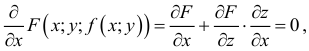 , (у – считаем постоянным),
, (у – считаем постоянным),
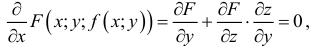 (х – считаем постоянным),
(х – считаем постоянным),
Откуда 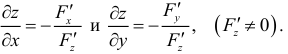
Пример №12
Найти частные производные функции z, заданной уравнением
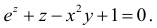
Решение: 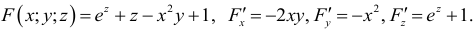
По формуле производной неявной функции имеем:
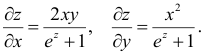
Производная в заданном направлении
Пусть функция z = f(x,y) определена в некоторой окрестности точки М(х,у), L – некоторое направление, задаваемое единичным вектором
 – косинусы углов, образуемых вектором
– косинусы углов, образуемых вектором  с осями координат и называемые направляющими косинусами.
с осями координат и называемые направляющими косинусами.
При перемещении в данном направлении L точки М(х,у) в точку 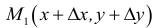 функция z получит приращение
функция z получит приращение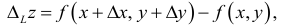 называемое приращением функции z в данном направлении L (рисунок 8.3).
называемое приращением функции z в данном направлении L (рисунок 8.3).
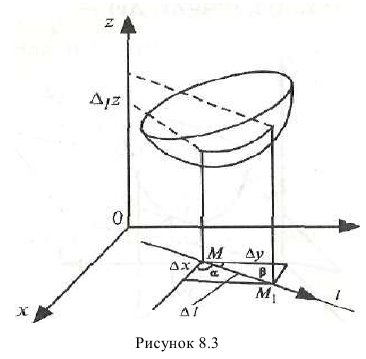
Если  то, очевидно, что
то, очевидно, что 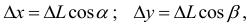 следовательно,
следовательно, 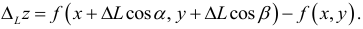
Определение. Производной  по направлению L функции двух переменных z=f(х,у) называется предел отношения приращения функции в этом направлении к величине перемещения
по направлению L функции двух переменных z=f(х,у) называется предел отношения приращения функции в этом направлении к величине перемещения  при стремлении последней к
при стремлении последней к
нулю, т.е.
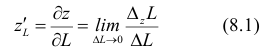
Производная  характеризует скорость изменения функции в направлении L.
характеризует скорость изменения функции в направлении L.
Очевидно, что рассмотренные ранее частные производные  представляют производные по направлениям, параллельным соответственно осям Ох и Оу.
представляют производные по направлениям, параллельным соответственно осям Ох и Оу.
Нетрудно показать, что
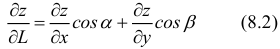
Градиент функции
Определение. Градиентом 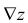 функции z = f(x,y) называется вектор с началом в точке М(х,у), координатами которого являются частные производные функции z = f(x,y).
функции z = f(x,y) называется вектор с началом в точке М(х,у), координатами которого являются частные производные функции z = f(x,y).
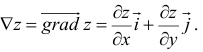
Рассмотрим скалярное произведение векторов 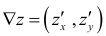 и единичного вектора
и единичного вектора 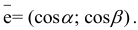 Получим
Получим
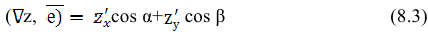
Сравнивая равенства (8.2) и (8.3), получим, что 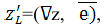 т.е. производная по направлению есть скалярное произведение градиента
т.е. производная по направлению есть скалярное произведение градиента  и единичного вектора, задающего направление L.
и единичного вектора, задающего направление L.
Известно, что скалярное произведение двух векторов максимально, если они одинаково направлены. Следовательно, градиент функции  в данной точке характеризует направление максимальной скорости изменения функции в этой точке.
в данной точке характеризует направление максимальной скорости изменения функции в этой точке.
Производная 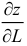 в направлении градиента имеет наибольшее значение, которое определяется по формуле
в направлении градиента имеет наибольшее значение, которое определяется по формуле
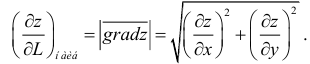
Теорема. Пусть задана дифференцируемая функция z = f(x,y) и пусть в точке, величина градиента отлична от нуля. Тогда градиент перпендикулярен линии уровня, проходящей через данную точку.
Экстремумы функций нескольких переменных
Будем рассматривать функцию двух переменных. Как и в случае одной переменной, функция z = f(x,y) имеет узловые, определяющие структуру графика, точки. В первую очередь это точки экстремума.
Определение. Точка  называется точкой максимума (минимума) функции z = f(x,у), если существует такая окрестность, что для всех точек
называется точкой максимума (минимума) функции z = f(x,у), если существует такая окрестность, что для всех точек  из этой окрестности, удовлетворяющих условию
из этой окрестности, удовлетворяющих условию 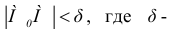 достаточно малое положительное число, выполняется неравенство:
достаточно малое положительное число, выполняется неравенство: 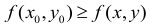
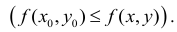
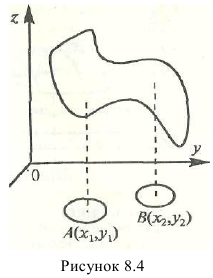
Максимум или минимум функции называется ее экстремумом. Точка 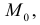 в которой функция имеет экстремум, называется точкой экстремума.
в которой функция имеет экстремум, называется точкой экстремума.
На рисунке 8.4: точка 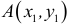 — есть точка минимума, а точка
— есть точка минимума, а точка 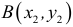 —точка максимума.
—точка максимума.
Следует обратить внимание на локальный характер экстремума (максимума и минимума) функции, так как речь идет о максимальном и минимальном значении лишь в достаточно малой окрестности точки 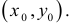
Теорема (необходимый признак существования экстремума).
Если  есть точка экстремума функции z = f(x,y), то ее частные производные первого порядка в этой точке равны нулю, т.е.
есть точка экстремума функции z = f(x,y), то ее частные производные первого порядка в этой точке равны нулю, т.е.
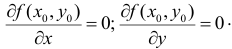
в предположении, что указанные частные производные существуют в точке 
Этот признак — необходимый, т.е. функция может иметь экстремум также в тех точках, где хотя бы одна из частных производных не существует. Точки, в которых первые частные производные обращаются в ноль, или не существуют, называются критическими (стационарными) точками этой функции.
Например, у функции z = xy первые частные производные обращаются в нуль в точке (0;0), однако экстремума у этой функции в этой точке нет.
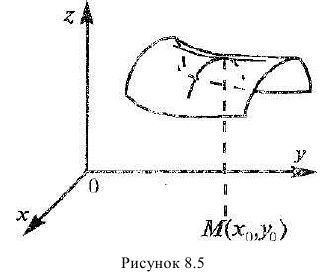
На рисунке 8.5 изображена так называемая седловая точка 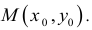 Частные производные
Частные производные 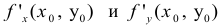 равны нулю, но, очевидно, никакого экстремума в точке
равны нулю, но, очевидно, никакого экстремума в точке 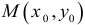 нет. Такие седловые точки являются
нет. Такие седловые точки являются
двумерными аналогами точек перегиба функций одной переменной. Задача заключается в том, чтобы отделить их от точек экстремума. Иными, словами, требуется знать достаточное условие экстремума.
Теорема (достаточное условие экстремума функции двух переменных).
Пусть функция z = f(x,y):
а) определена в некоторой окрестности критической точки 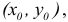 в которой ее частные производные первого порядка равны нулю, т.е.
в которой ее частные производные первого порядка равны нулю, т.е.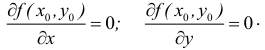
б) имеет в этой точке непрерывные частные производные второго порядка
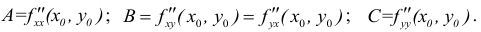
Возможны следующие случаи:
1. 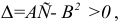 в точке
в точке  функция
функция 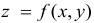 имеет экстремум, причем, если А<0 — максимум; если А>0 — минимум.
имеет экстремум, причем, если А<0 — максимум; если А>0 — минимум.
2. 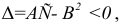 в окрестности точки
в окрестности точки 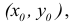 функция
функция 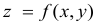 экстремума не имеет, но может быть минимакс (форма «седла», рисунок 17).
экстремума не имеет, но может быть минимакс (форма «седла», рисунок 17).
3. 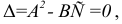 требуется дополнительное исследование.
требуется дополнительное исследование.
Пример №13
Найти экстремумы функции 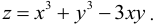
Решение. 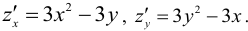 Приравнивая первые частные
Приравнивая первые частные
производные нулю, найдем стационарные точки:
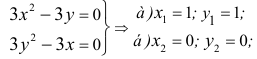
Найдем частные производные второго порядка 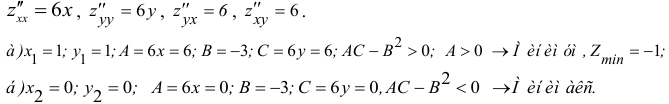
Пример №14
Пусть производится два вида товаров, обозначим их количества через х и у. Пусть цены на эти товары 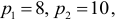 а функция затрат
а функция затрат 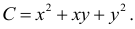 Найти максимум прибыли.
Найти максимум прибыли.
Для решения задачи выразим функцию прибыли /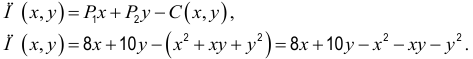
Условия локального экстремума приводят к решению системы двух алгебраических уравнений:
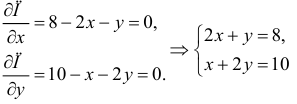
Решение системы дает точку (2,4).
Определим вид экстремума, для этого найдем значения вторых производных функции прибыли:
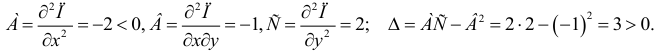
Поскольку 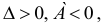 то найденная точка определяет локальный максимум функции прибыли
то найденная точка определяет локальный максимум функции прибыли 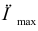 (2,4) = 28.
(2,4) = 28.
Наибольшее и наименьшее значение функции в замкнутой области
Пусть функция z = f(x,y) непрерывна в замкнутой ограниченной области и дифференцируема внутри этой области. Тогда она имеет в этой области наибольшее и наименьшее значения, которые достигаются либо внутри области, либо на её границе. Если наибольшее или наименьшее значение функция принимает во внутренних точках области, то, очевидно, что эти точки являются точками экстремума функции.
Правило нахождения наибольшего и наименьшего значений функции двух переменных:
- найти все критические точки функции, принадлежащие замкнутой области и вычислить значения функции в этих точках;
- найти наибольшее и наименьшее значения функции на границах области;
- сравнить все найденные значения функции, выбрать из них наибольшее и наименьшее.
Замечание. Иногда границу области удобно разбить на части, каждая из которых задается своим уравнением.
Пример №15
Найти наибольшее и наименьшее значения функции 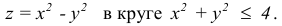
Решение.
Найдем частные производные первого порядка 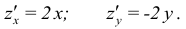
Приравняем их нулю 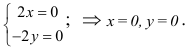
Получаем критическую точку 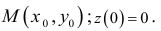 Окружность
Окружность 
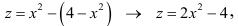 причем
причем 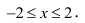
Задача свелась к нахождению наибольшего и наименьшего значений
функции одной переменной 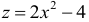 на отрезке
на отрезке 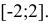 Получаем
Получаем 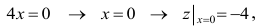 на концах отрезка:
на концах отрезка:
Условный экстремум
Рассмотрим задачу, специфическую для функций нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторому условию.
Пусть рассматривается функция z = f(x,y), аргументы х и у которой удовлетворяют условию g(x,y) = С, называемому уравнением связи.
Определение. Точка  называется точкой условного максимума (минимума), если существует такая окрестность этой точки, что для всех точек (х,у) из этой окрестности удовлетворяющих условию g(x,y) = C, выполняется
называется точкой условного максимума (минимума), если существует такая окрестность этой точки, что для всех точек (х,у) из этой окрестности удовлетворяющих условию g(x,y) = C, выполняется
неравенство
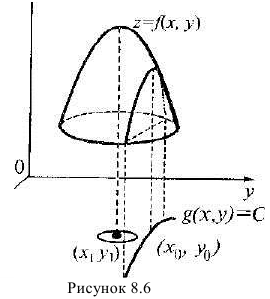
На рис. 18 изображена точка условного максимума 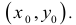 Очевидно, что она не является точкой безусловного экстремума функции z = f(x,y) (на рис. 8.6 это точка
Очевидно, что она не является точкой безусловного экстремума функции z = f(x,y) (на рис. 8.6 это точка 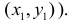
Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Допустим уравнение связи g(x,y) = C удалось разрешить относительно одной из переменных, например, выразить t через х:  Подставив полученное выражение в функцию двух переменных, получим
Подставив полученное выражение в функцию двух переменных, получим 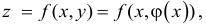 т.е. функцию одной переменной. Ее экстремум и будет условным экстремумом функции z = f(х,у).
т.е. функцию одной переменной. Ее экстремум и будет условным экстремумом функции z = f(х,у).
Пример №16
Найти точки максимума и минимума функции 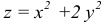 при условии Зх+2у =11.
при условии Зх+2у =11.
Решение. Выразим из уравнения Зх +2у = 11 переменную у через переменную х и подставим полученное выражение 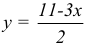 в функцию z.
в функцию z.
Получим 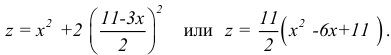 Эта функция имеет единственный минимум
Эта функция имеет единственный минимум 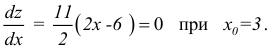 Соответствующее значение функции
Соответствующее значение функции 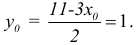 Таким образом, (3; 1) — точка условного экстремума (минимума).
Таким образом, (3; 1) — точка условного экстремума (минимума).
В рассмотренном примере уравнение связи g(x,y) = C оказалось линейным, поэтому его легко удалось разрешить относительно одной из переменных. Однако в более сложных случаях сделать это не удается.
Метод множителей Лагранжа
Для отыскания условного экстремума часто используется метод множителей Лагранжа.
Рассмотрим функцию трех переменных
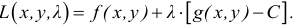
Эта функция называется функцией Лагранжа, а 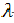 — неопределенным множителем Лагранжа.
— неопределенным множителем Лагранжа.
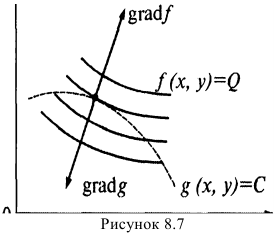
Теорема. Если точка 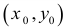 является точкой условного экстремума функции
является точкой условного экстремума функции 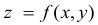 при условии
при условии 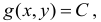 то существует значение
то существует значение 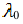 такое,
такое,
что точка 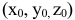 является точкой экстремума функции
является точкой экстремума функции 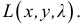
Таким образом, для нахождения условного экстремума функции 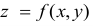 при условии g(x,y) = C требуется найти решение системы
при условии g(x,y) = C требуется найти решение системы
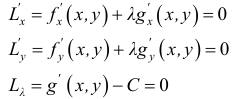
Последнее из этих уравнений совпадает с уравнением связи.
Первые два уравнения системы можно переписать в виде
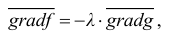
т.е. в точке условного экстремума градиенты функций f(x,y) и g(x,y) коллинеарные.
На рисунке 8.7 показан геометрический смысл условий Лагранжа. Линия 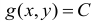 пунктирная, линии уровня
пунктирная, линии уровня 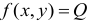 функции z = f(x,y)
функции z = f(x,y)
сплошные.
Пример №17
Найти точки экстремума функции 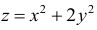 при условии Зх + 2у = 11, используя метод множителей Лагранжа.
при условии Зх + 2у = 11, используя метод множителей Лагранжа.
Решение. Составим функцию Лагранжа 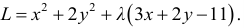 Приравнивая нулю ее частные производные, получим систему уравнений
Приравнивая нулю ее частные производные, получим систему уравнений
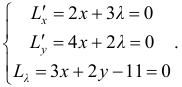
Ее единственное решение 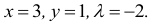 Таким образом, точкой условного экстремума может быть только точка (3;1). Нетрудно убедиться в том, что в этой точке функция z = f(x,y) имеет условный минимум.
Таким образом, точкой условного экстремума может быть только точка (3;1). Нетрудно убедиться в том, что в этой точке функция z = f(x,y) имеет условный минимум.
В случае если число переменных более двух, может рассматриваться и несколько уравнений связи. Соответственно в этом случае будет и несколько множителей Лагранжа.
Мы не рассматриваем здесь достаточные условия условного экстремума. Отметим только, что во многих задачах критическая точка функции Лагранжа оказывается единственной и соответствует не только локальному, но и глобальному условному минимуму или максимуму.
Метод наименьших квадратов
Пусть 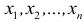 – последовательность значений независимой
– последовательность значений независимой
переменной, а 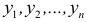 последовательность соответствующих значений зависимой переменной.
последовательность соответствующих значений зависимой переменной.
Требуется подобрать прямую, которая «наилучшим» образом изображала бы зависимость между х и у. Это означает, что отклонения фактических значений функций от «подобранной» прямой должны быть минимальными. Пусть
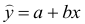
есть уравнение этой прямой. Имеем 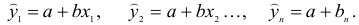
Отклонения от фактических значений функции составляют:
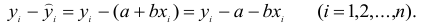
Эти отклонения могут быть положительными или отрицательными; Поэтому прямая подбирается так, чтобы сумма квадратов отклонений
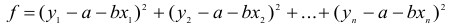 была наименьшей.
была наименьшей.
Следовательно, нужно определить а и b так, чтобы f достигала минимума. Необходимое условие существования минимума состоит в том, чтобы
Имеем:
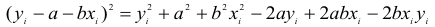
следовательно, 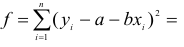
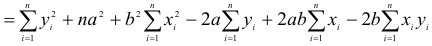
Вычислим 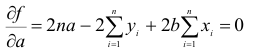
Откуда 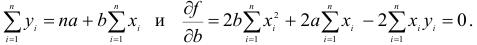
Откуда 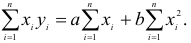
Так мы получаем два уравнения с двумя неизвестными а и b; 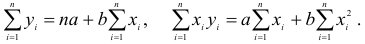
Решение этих двух уравнений дает значения а и b, которые определяют прямую, наилучшим образом отражающую ход изменений функции.
Пример №18
В течении 4-х последних лет переменные х и у принимали следующие значения: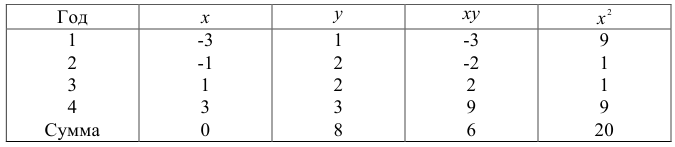
Найти уравнение прямой линии, выражающее зависимость величины у от величины х.
Имеем:
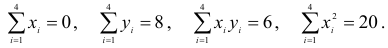
Следовательно, необходимое условие существования минимума суммы квадратов отклонений есть
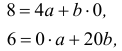
откуда
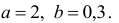
Следовательно, искомая прямая есть
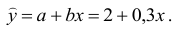
y = a + bx = 2 + 0,3x.
Для сравнения, на рисунке 8.8 изображены точки с координатами, равными значениям х и y пo данным таблицы, а также прямая линия 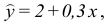 построенная с помощью метода наименьших квадратов.
построенная с помощью метода наименьших квадратов.
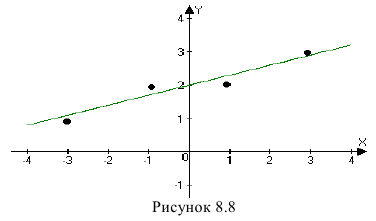
Понятие двойного интеграла
Пусть функция f(x,y) определена в ограниченной замкнутой области D плоскости 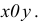 Разобьем область D произвольным образом на п элементарных областей, имеющих площади
Разобьем область D произвольным образом на п элементарных областей, имеющих площади  и диаметры
и диаметры  (диаметром области называют наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку
(диаметром области называют наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку 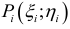 и умножим значение функции в точке
и умножим значение функции в точке 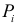 на площадь этой области.
на площадь этой области.
Интегральной суммой для функции f(х,у) по области D называют сумму вида
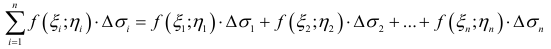
Если при стремлении наибольшего диаметра к нулю, т.е. при max  интегральная сумма имеет определенный конечный предел
интегральная сумма имеет определенный конечный предел
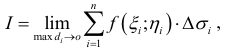 не зависящий от способа разбиения области D на элементарные области и от выбора точек
не зависящий от способа разбиения области D на элементарные области и от выбора точек  в пределах каждой из них, то этот предел называют двойным интегралом от функции
в пределах каждой из них, то этот предел называют двойным интегралом от функции  в области D и обозначают следующим образом:
в области D и обозначают следующим образом:
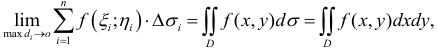
где: D – область интегрирования, 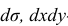 – элемент площади.
– элемент площади.
Геометрический смысл двойного интеграла
Если 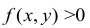 в области D, то двойной интеграл
в области D, то двойной интеграл 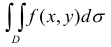 равен объему D цилиндрического тела, ограниченного сверху поверхностью,
равен объему D цилиндрического тела, ограниченного сверху поверхностью,
сбоку цилиндрической поверхностью с образующими параллельными оси Oz и снизу областью D плоскости 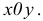
Основные свойства двойного интеграла
Пусть функции 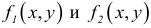 интегрируемы в области D.
интегрируемы в области D.
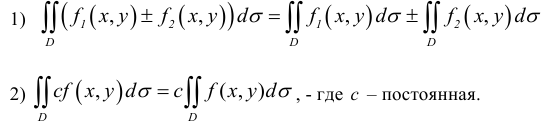
3) Если область интегрирования D разбита на две области  и в каждой из этих областей функция f(x,y) интегрируема, то
и в каждой из этих областей функция f(x,y) интегрируема, то
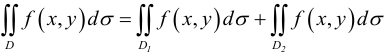
4) Оценка двойного интеграла. Если 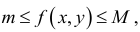 то
то
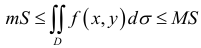
где S — площадь области D, а m и М — соответственно наименьшее и наибольшее значения функции f(x,y) в области D .
Вычисление двойного интеграла
При вычислении двойного интеграла его сводят к повторному, т.е. дважды применяют процесс обычного интегрирования.
Различают два основных вида области интегрирования.
1. Область интегрирования D ограничена слева и справа прямыми
х = а и х = b (а каждая из которых пересекается вертикальной прямой только в одной точке (рисунок 8.9).
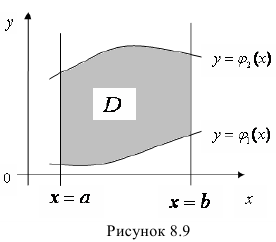
Для такой области двойной интеграл вычисляют по формуле
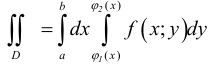
Причем сначала вычисляют внутренний интеграл 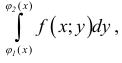 в котором х считают постоянным.
в котором х считают постоянным.
2. Область интегрирования D ограничена снизу и сверху прямыми у = с и y = d (с каждая из которых пересекается
горизонтальной прямой только в одной точке (рисунок 8.10).
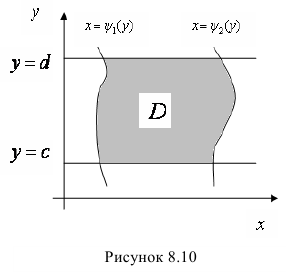
Для такой области двойной интеграл вычисляют по формуле
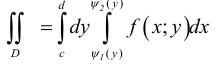
Причем сначала вычисляют внутренний интеграл
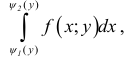
в котором у считают постоянным.
Правые части указанных формул называют двукратными (или повторными) интегралами.
В общем случае область интегрирования с помощью разбиения на части сводят к основным областям.
Пример №19
Вычислить двойные интегралы по указанным областям:
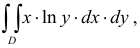 где область D – прямоугольник
где область D – прямоугольник 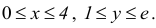
Решение: 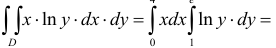
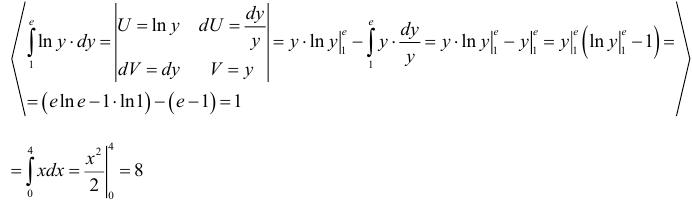
Пример №20
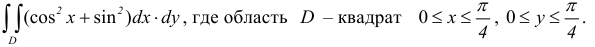
Решение:
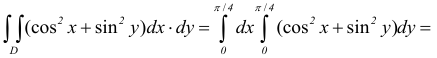
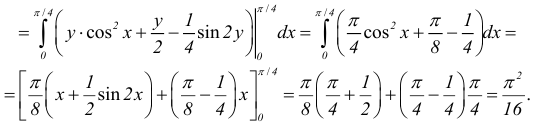
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Исследование поведения функций
- Предел и непрерывность функции двух переменны
