Как найти частотный интервал

Часто́тный интерва́л — безразмерная физическая величина, выражающая в логарифмическом виде соотношение двух частот или ширину полосы частот. Частотный интервал равен логарифму отношений большей частоты к меньшей, основание логарифма зависит от выбранной единицы. Это понятие широко используется в акустике, радиотехнике и музыке.

Единицы частотного интервала[править | править код]

• Октава — 1 окт = log₂(f₂/f₁) при f₂/f₁ = 2
• Цент — 1 цент = окт/1200
• Декада — 1 дек = lg(f₂/f₁) при f₂/f₁ = 10
• Савар — 1 Савар = log_1,0023(f₂/f₁) при f₂/f₁ = 1,0023
• Мокт — 1 мокт = 1,2005 цента = 0,3012 Савара

См. также[править | править код]

• Интервал (музыка)
• Логарифмический масштаб
• Частота периодического процесса
• Электромагнитный спектр

Литература[править | править код]

• Бурдун Г. Д., Базакуца В. А. Единицы физических величин. — Харьков: Вища школа, 1984.

Это статья-заготовка о единицах измерения. Помогите Википедии, дополнив эту статью, как и любую другую.

Частотный интервал

Полезное

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

НАУКА. ИННОВАЦИИ ТЕХНОЛОГИИ, №3, 2016

УДК 621.39 Жиляков Е.Г. [Zhilyakov E.G.],

Белов С.П. [Belov S.P.], Медведева А.А. [Medvedeva А.А.], Курлов А.В. [Kurlov A.V.], Лихолоб П.Г. [Likholob P.G.]

ОБ ОДНОМ АЛГОРИТМЕ ОПРЕДЕЛЕНИЯ

ИНФОРМАЦИОННЫХ

ЧАСТОТНЫХ ИНТЕРВАЛОВ*

About one algorithm of determining the frequency intervals information

Рассматривается задача анализа отрезков речевых сигналов, с целью выявления их особенностей. Необходимость решения таких задач возникает в области сегментации и распознавания речи, ее сжатия и очистки от шумов. Анализ литературных источников показывает, что наиболее часто при решении таких задач используются частотные представления. При этом наиболее эффективным является использование субполосного частотного анализа, суть которого заключается в соотнесении свойств отрезков сигналов с некоторым разбиением оси частот на интервалы конечной ширины. В рамках данной статьи представлены результаты исследования метода определения информационных частотных интервалов в речевых сигналах, полученные на основе применения субполосного частотного анализа. Определена зависимость вероятности ошибочного определения информационных частотных интервалов от уровня энергии накладываемого шума. Результаты исследования алгоритма определения информационных частотных интервалов свидетельствуют о целесообразности использования адаптивного порога для определения информационных частотных интервалов в задачах анализа речевых сигналов.

Ключевые слова: речевые сигналы, информационные частотные интервалы в речевых сигналах, субполосный частотный анализ, распределение энергии речевых сигналов в частотной области.

Considers the problem of analysis of speech signals, with the aim of identifying their characteristics. The needs to solve these problems arise in the field of speech recognition and segmentation, its compression and removal of noise. Analysis of the literature shows that the most commonly used frequency representation in solving such problems. The most effective is the use of sub-band frequency analysis, the essence of which lies in the correlation properties of the signal segments with some splitting the frequency axis into intervals of finite width. In this article the results of research method for determining the frequency domain information in the speech signals obtained on the basis of sub-band frequency analysis. The dependence of the probability of an erroneous definition of frequency intervals information on the energy level of noise overlay. Results of the study algorithm for determining the frequency intervals of information indicate the feasibility of using an adaptive threshold to determine the frequency intervals of information for the analysis of speech signals.

Keywords: speech signals, information of frequency intervals in the speech signals, subpolicy frequency analysis, energy distribution of speech signals in the frequency domain.

* Работа подготовлена в рамках II Международной конференции «Параллельная компьютерная алгебра и ее приложения в новых инфоком-муникационных системах»

При решении различных задач обработки речевых сигналов (таких как сегментация, распознавание речи, сжатие, очистка речи от шума и др.) возникает необходимость предварительного анализа отрезков речевых сигналов, с целью выявления их особенностей. Анализ литературных источников показывает, что наиболее эффективным является анализ особенностей распределения энергии речевых сигналов в частотной области. При этом наиболее эффективным является использование субполосного анализа [1], суть которого заключается в соотнесении свойств отрезков сигналов с некоторым разбиением оси частот на интервалы конечной ширины.

Для вычисления энергии, сосредоточенной в заданном частотном интервале предлагается использовать субполосные матрицы А,, с элементами вида [1]:

а;к=(*т(У2г(1-к))-*т(Г1г(1~к)))/(х(1-к)) а^(У2г-У1г)/л:

где V и V – соответственно нижняя и верхняя частоты г-го частотного интервала.

Использование соотношения:

Рг{Х]у) = ХхАгХн, (2)

позволяет вычислить точное значение энергии анализируемого отрезка речевого сигнала хм = (хг.., х,;)7. сосредоточенной в г-ом частотном интервале, не переходя в частотную область.

В выражении (2) N – длительность анализируемого отрезка сигнала в отсчетах, Т обозначает операцию транспонирования.

Использование данного математического аппарата позволяет проводить анализ особенностей распределения энергии отрезков речевых сигналов, соответствующих различным звукам речи (рис. 1-4).

Рис. 1. Фрагмент речевого сигнала, порожденного звуком «а»

(Га= 16 кГц, N = 256).

Длительность сигнала, отсчетов

Рис. 2. Фрагмент речевого сигнала, порожденного звуком «ш»

16 кГц, N = 256).

Как видно из представленных рисунков для различных звуков русской речи характерно разное распределение энергии в области частот.

При решении ряда задач обработки речевых сигналов интерес представляет определение в автоматическом режиме частотных интервалов, которые несут основную информацию о характере звука, так называемых информационных частотных интервалов.

Очевидно, что к информационным частотным интервалам необходимо отнести интервалы, в которых сосредоточена большая энергия, превышающая некоторое пороговое значение.

0.25

0.15

0 05 –

0 1000 2000 3000 4000 5000 6000 7000 8000 Частота, Гц

Рис. 3.

Распределение энергии фрагмента речевого сигнала, порожденного звуком «а» 16 кГц, N = 256,А? = 128).

0.045 0.04 0.035

та

1 0.03

г

о

2 0.025

та ш

ё 0.02 сх

| 0.015 о

0 01 0.005 0

0

1000 2000

3000 4000 5000 6000 Частота, Гц

7000 8000

Рис. 4.

Распределение энергии фрагмента речевого сигнала, порожденного звуком «ш» 16 кГц, N = 256, Я = 128)

№3, 2016

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

Об одном алгоритме определения информационных частотных интервалов

27

Рис. 5. Фрагмент речевого сигнала, порожденного звуком «а»

(fd= 16 кГц, N = 256).

О 03

_I_I_l_I_I_

О 50 100 150 200 250 300

Длительность сигнала, отсчетов

Рис. 6.

Фрагмент речевого сигнала, порожденного звуком «ш» (fd= 16 кГц, N = 256).

В качестве порогового значения предлагается выбирать среднее значение энергии, приходящейся на анализируемый частотный интервал. Таким образом, решение о принадлежности частотного интервала к информационным будет приниматься при выполнении условия [2]:

Рг(хм)>\хм ||2 (Г2г-Г1г)/я:. (3)

Все остальные интервалы в этом случае представляют собой неинформационные частотные интервалы. На рисунках 5-8 представлены результаты определения информационных частотных интервалов в соответствии с выражением (3) для некоторых звуков русской речи.

Как видно из представленных рисунков, использование предложенного алгоритма позволяет выделить информационные частотные интервалы с преобладающей энергией. Интерес представляет устойчивость определения информационных частотных интервалов к воздействию аддитивных шумов.

Для выявления чувствительности определения информационных частотных интервалов к воздействию аддитивного шума были оценены вероятности ошибочного определения информационных частотных интервалов для различных звуков русской речи при разных отношениях шум/сигнал. При этом оценивались две вероятности: вероятность ошибок первого и второго рода:

=инф ■ ^все_неинф- *

‘°ои<2 — -— ^инф ^все инф- Р.»

где Нинф- количество частотных интервалов, ошибочно отнесенных к информационным; ^все_неинф – количество неинформационных частотных интервалов, использованных для исследования; ^шф ~ количество частотных интервалов, верно отнесенных к

информационным; N все _инф – количество информационных частотных интервалов, использованных для исследования.

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

. Об одном алгоритме определения информационных частотных интервалов .

Рис. 7. Распределение энергии фрагмента речевого сигнала, по-

рожденного звуком «а» с указанием информационных частотных интервалов 16 кГц, N = 256, Я = 128).

Рис. 8. Распределение энергии фрагмента речевого сигнала, по-

рожденного звуком «ш» с указанием информационных частотных интервалов 16 кГц, Л/= 256, /? = 128).

Информационные и неинформационные частотные интервалы, используемые для исследования, определялись при отсутствии шумов. В таблице 1 представлены результаты оценки вероятностей первого и второго рода для различных длительностей отрезков анализа.

Табл. 1. ЗНАЧЕНИЯ ВЕРОЯТНОСТЕЙ ОШИБОЧНОГО ПРИНЯТИЯ

РЕШЕНИЯ ПРИ РАЗЛИЧНЫХ ЗНАЧЕНИЯХ ОТНОШЕНИЯ ШУМ/СИГНАЛ 16 кГц)

Отношение Рош1 Рош2

шум/сигнал N = 128 N = 256 N = 128 N = 256

0,1 0,0132 0,0142 0,0026 0,0028

0,2 0,0287 0,0289 0,0052 0,0058

0,3 0,0424 0,0447 0,0083 0,0088

0,4 0,0559 0,0605 0,0119 0,0124

0,5 0,0689 0,0762 0,0164 0,0170

0,6 0,0815 0,0916 0,0235 0,0242

0,7 0,0939 0,1065 0,0362 0,0367

0,8 0,1061 0,1210 0,0553 0,0555

0,9 0,1182 0,1349 0,0794 0,0791

1,0 0,1299 0,1485 0,1060 0,1053

Из таблицы видно, что вероятности ошибочного принятия решения при различных длительностях отрезка анализа отличаются незначительно и не превышают 0,15.

Таким образом, использование предлагаемого подхода позволяет определить информационные частотные интервалы даже при высоком отношении шум/сигнал, что позволяет говорить о целесообразности использования данного метода в задачах анализа и обработки речевых сигналов.

Работа выполнена при поддержке гранта РФФИ № 15-0701463 “Разработка методов и алгоритмов автоматического распознавания устной речи с использованием субполосного анализа речевых сигналов”.

Библиографический список

1. Жиляков, Е.Г. Вариационные методы анализа сигналов на основе частотных представлений [Текст] / Е.Г. Жиляков, С.П. Белов, A.A. Черноморец // Вопросы радиоэлектроники, сер. ЭВТ, вып. 1. Москва: Электроника, 2010. 185 с.

2. Жиляков Е.Г О сегментации речевых сигналов на однородные отрезки [Текст] / Жиляков Е.Г, Белов С.П., Белов A.C., Фирсо-ва A.A. // Научные ведомости Белгородского государственного университета, Серия Экономика Информатика, №7(204), вып. 34/1, 2015, с. 194-199.

Пусть Ах, Лг, Аз… — положения компоненты с частотой V в последовательных порядках интерферограммы (рис. 29), В], Взг Вз… — положения компоненты V в тех же порядках, Дь Да, Дз–— расстояния между компонентами, Д1А, Дзл, Дза… и Ахв, Дгв, Дзв— — расстояния между соседними порядками. Для порядков, достаточно удаленных от центра картины, частотный интервал между компонентами с хорошим приближением может быть определен по. формуле  [c.81]

Действительно, при определении функции v, Т) в соответствии с выражением (73) на дискретных частотах частотный интервал составляет  [c.83]

Результаты проведенных исследований позволяют сделать следующие выводы относительно последовательности решения прикладной задачи проектирования линейной колебательной системы составляется точное математическое описание системы (модель), затем методами декомпозиции эта система по ряду признаков разбивается на определенное число подсистем меньшей размерности, далее каждая подсистема подвергается анализу на ЭЦВМ или АВМ с использованием методики планируемого эксперимента, в частности метода ПЛП-поиска. На основе такого эксперимента строятся упрощенные математические зависимости. Таким образом, для целого класса колебательных систем, описываемых линейными дифференциальными уравнениями, проектировщик получает зависимости, позволяющие ему сразу принять то или иное проектное решение. В частности, проектировщик может подобрать такие сочетания параметров, при которых собственные частоты системы будут находиться вне требуемого частотного интервала или амплитуды колебаний в этом интервале будут существенно уменьшены,  [c.23]

Как уже указывалось ранее, контур спектральной линии значительно шире частотного интервала между модами резонатора, поэтому в полосу усиления попадает обычно большое количество мод, которые генерируются одновременно. В результате интерференции мод появляются флюктуации интенсивности. Если создать такие условия, когда в процессе генерации участвуют все моды, но с определенным соотношением фаз присущих им колебаний, то при этом происходит генерация весьма коротких импульсов исключительно большой мощности.  [c.32]

В выражении (5.15) неявно предполагается, что p(v)—константа во всем частотном интервале взаимодействия атомной системы, в которой происходит испускание и поглощение. Тем самым ограничивается применимость вырал<ения (5.15), так как монохроматичность сигналов лазера настолько велика, что плотность энергии на единицу частотного интервала нельзя считать точно определенной величиной. Если ввести понятие формы атомной линии и заменить p(v) интенсивностью, выраженной в виде дельта-функции Дирака, то приведенное выражение для индуцированного испускания будет верно.  [c.230]

Продолжительность состояния поляризации. Предположим, что одновременно возбуждается много атомов. Пусть все они сосредоточены в небольшой области у начала координат х — у = г = 0 и наблюдатель, смотрящий на источник по оси г, регистрирует электромагнитные волны, которые являются суперпозицией волн, испущенных отдельными атомами. Будем называть мгновением интервал времени, который мал по сравнению со средним временем высвечивания т, но содержит много периодов колебаний Т = 2л/с1)о. Далее, пусть наблюдатель описывает излучение, используя понятия амплитуд Ех и Еу и разности фаз между колебаниями по осям х я у. В любой момент поле Ех представляет собой суперпозицию полей от колебаний всех атомов, излучающих в соответствующие моменты. То же справедливо и для Еу. Все атомы колеблются с одинаковой частотой Юо, но с различными амплитудами и фазовыми константами. Поэтому результирующее излучение занимает определенный частотный интервал. Несмотря на это, мы можем говорить о доминирующей частоте о и об амплитуде и фазовой постоянной, которые зависят от амплитуд и фаз всех вкладов. (То же справедливо и лля Еу.)В течение любого временного интервала, малого по сравнению с т, все колеблющиеся атомы теряют лишь небольшую часть своей энергии и фазовые постоянные остаются неизменными. Поэтому амплитуда и фазовая постоянная суперпозиции, определяющей Ех (или Еу), не изменяются значительно в течение интервала времени, много меньшего т. Поляризация электромагнитного излучения в течение такого интервала времени остается постоянной. В частности, не меняется и разность фаз между Е и Еу. Теперь предположим, что через относительно большой интервал времени, равный многим т, мы проверяем поляризацию результирующей волны. Атомы, которые излучали (в начале интервала), теперь перестанут излучать, и их излучение будет заменено излучением новых атомов. (Не имеет значения, возбуждены ли новые атомы или снова возбуждены старые.) Движение электронов во вновь возбуждаемых атомах не связано с движением электронов в старых атомах (за исключением того, что для простоты можно считать среднюю энергию возбуждения новых и старых атомов одинаковой). Сложив л -компоненты излучения всех атомов, получим х-компоненту Ех общей волны. Она должна иметь примерно такую же амплитуду, что и компонента Ех, полученная из старого набора возбужденных атомов. Однако фазовая постоянная нового поля Ех никак не связана с фазовой постоянной старого поля Ех- То же справедливо и для составляющей поля по оси у. Далее, поскольку разность фаз движений по осям х я у нового набора атомов никак не коррели-рована с разностью фаз движений по х я у для старого набора, то поведение разности фаз Ех и Еу полностью непредсказуемо и носит характер случайного события, если наш временной интервал т.  [c.385]

Каждая катушка в генераторе должна перекрывать определенный частотный интервал, необходимый для проведения измерений.  [c.123]

Интервал At можно выбирать различным путем в зависимости от допускаемой ошибки воспроизведения исходной функции. Некоторые критерии выбора отсчетов при определенных моделях исходных функций и способов воспроизведения могут обеспечить нулевую или близкую к нулю ошибку воспроизведения. Это, во-первых, частотный критерий Котельникова [69], при котором интервалы между отсчетами выбираются с учетом частотного спектра дискретизируемой функции. Известная теорема Котельникова гласит Функция с ограниченным спектром полностью определяется своими значениями, отсчитанными через интервал Ai 1/2F, где F — ширина спектра .  [c.91]

Система ограничения перемещения с использованием инфракрасных лучей 164] по сравнению с фотоэлектрической имеет то преимущество, что исключает влияние на нее посторонних источников света. Излучаемый с определенной частотной модуляцией через оптическое устройство одного крана инфракрасный луч отражается от другого крана и попадает на приемный экран первого крана, где сравнивается с излучаемым сигналом. В качестве отражателя на кранах, работающих на расстоянии до 10 м, используется соответствующим образом отраженная часть металлоконструкции, при больших расстояниях — специальные отражатели. Система позволяет настраивать излучатель на два интервала расстояний между кранами — от 2,5 до 30 м при большем расстоянии включается сигнализация или снижается скорость передвижения, при меньшем расстоянии кран затормаживается. Система снабжена устройством самоконтроля, которое обеспечивает остановку крана при выходе из строя лампы, нарушении системы сравнения, отсутствии напряжения и т. д.  [c.199]

Остановимся теперь на особенностях определения собственных значений и собственных форм составных систем, включающих подсистемы с сосредоточенными и сосредоточенно-распределенными параметрами (см. рис. 76). При отсутствии нулевых значений i согласно (13.23) и кратных элементов со,- матрицы Q системы (13.22), как указывалось в 13, можно обоснованно усекать бесконечномерную модель (13.22). Будем полагать, что для рассматриваемого ограниченного частотного интервала (О, % ) выполняется неравенство (13.24). Тогда проблема собственных спектров эквивалентной усеченной модели (13.22) на указанном частотном интервале решается на базе дихотомического алгоритма (14.10), (14.11) и вычислительной схемы (14.44). Возможные дополпительпые модификации расчетной модели (13.22), связанные с наличием нулевых Сг или кратных сог, рассмотрены выше.  [c.240]

Рассмотренный ниже пример гелий-неонового лазера, работающего на длине волны 1,15 мк, показывает, что применение интерферометра Фабри — Перо обеспечивает практически необходимое разрежение мод для возникновения генерации на одной или нескольких оптических частотах, а также оптическую обратную связь, которая необходима в случае переходов с низким усилением. Ширина допплеровской линии для перехода на длине волны 1,15 мк приблизительно равна Avd = 800 Мгц, тогда как естественная ширина, определенная по времени жизни спонтанного излучения с помощью уравнения (5.48), приблизительно равна Avjv = 80 Мгц. Частотный интервал между осевыми модами лазера при расстоянии между зеркалами 1 м ( l2d == = 150 Мгц) превышает естественную ширину линии, что обеспечивает попадание пяти или шести основных мод в полную ширину линии для резонатора без проводящих стенок. Если бы стенки резонатора были металлическими, то, как следует из выражения (5.5), число мод приближалось бы к 10 .  [c.300]

Параметр вырождения лазерного излучения можно вычислить на основе следуюш их соображений. Пусть — число фотонов, испуш енных световым источником по нормали к поверхности с единицы плош ади за единицу времени в единичный телесный угол в пределах малого частотного интервала Av со средней частотой v. Если излучаюш ая плош,адь источника равна 5, то можно показать [22], что в зависимости от определенной степени когерентности у будет суш ествовать плош,адь Л, нахо-дяш аяся на расстоянии R (по нормали от 5), такая, что на частоте V выполняется соотношение  [c.465]

С р,ествует два вида акустических величин 1) величины, характеризующие звук как физическое явление волнообразного распространения колебаний частиц упругой среды. К ним относятся скорость звука, звуковое давление, звуковая энергия, плотность звуковой энергии и др. 2) величины, характеризующие звук как специфическое ощущение, вызываемое действием звуковых волн на орган слуха. К ним относятся уровень громкости, частотный интервал и др. Между теми и другими вev ичинaми существует определенная зависимость. Например, частотный интервал связан с ча-  [c.102]

Как мы видел и, для адекватного описания интерференции частично когерентного света, вообще говоря, необходимо знать взаимную функцию когерентности Г1г(т) или, что эквивалентно этому, обычные интенсивиости /1 и /2 и комплексную степень когерентности 712(1). Здесь мы ограничимся важным случаем квазимонохроматического свега, т. е. света, состоящего из спектральных компонент, которые занимают частотный интервал Дv, малый но сравнению со средней частотой V. Мы покажем, что в этом случае теория принимает более простой вид. В частности, мы найдем, что при определенном дополнительном предположении, которое выполняегся во многих цриложениях, вместо Г1г(т) и 712(1) можно применять корреляционные функции, не зависящие от параметра 1.  [c.463]

Несмотря на большой диапазон применяемых частот и разнообразие изучаемых явлений, некоторые характерные особенности радиоспектроскопии, имеющие важные следствия для теории, выделяют ее как единое целое. Необходимое электромагнитное излучение может создаваться с помощью электронных генераторов, работающих на определенных частотах, которые могут быть измерены с высокой точностью. В противо-подожность инфракрасной, оптической и 7″Спектроскопии, неточность Аг частоты излучения будет, как правило, меньше ширины уровней АЕ 1к (в единицах частоты), между которыми индуцируется переход. Вследствие малости энергии ку каждого фотона и узости частотного интервала Дг, в котором они излучаются, для создания астрономически большого числа фотонов (скажем, 10 ) на единицу частотного интервала достаточны очень малые мощности. Из квантовой теории излучения хорошо известно, что в присутствии такого большого числа фотонов индуцированные излучение и поглощение значительно преобладают над спонтанным излучением, которое в радиоспектроскопии оказывается пренебрежимо малым. Индуцированное излучение или поглощение (в противоположность спонтанному излучению) не требует квантовомеха-нического описания, что значительно упрощает рассмотрение.  [c.13]

С другой стороны, величину /г/2 = РоТо можно рассматривать как произведение длительности сигнала на полосу частот, называя полосой частот минимальный частотный интервал, в котором содержатся все ненулевые частотные компоненты амплитудного спектра сигнала, а его длительностью — интервал времени, в течение которого он отличен от нуля. Следует, однако, указать, что эти понятия имеют много различных определений, большинство из которых таково, что произведение длительности на полосу частот оказывается для широкого класса сигналов близким к единице [19].  [c.229]

Поскольку интересно знать зависимость демпфирования от действительной средней скорости, то суммирование производится в отдельных интересующих исследователя частотных диапазонах. При этом следует иметь в виду, что при увеличении частоты ширина полосы резонансных форм колебаний становится равной интервалу частот или большей, чем интервал частот, расположенных между последовательными формами колебаний. Следовательно, в спектре реакции системы с определенными граничными условиями существует некоторая критическая частота, ниже которой отдельные реакции форм будут отчетливо разлцчаться и выше которой реакции форм сливаются в плавную кривую. Эта частота определяется как = Ао) , где — интервал частот, расположенный между последовательными формами A(o —ширина полосы п формы колебания на уровне половинной мощности. Так как ширина полосы формы для достаточно малого демпфирования 1) равна т)(й , то критическая частота определяется по формуле ( )кр = – частот возбуждения  [c.228]

Вместе с тем реальный приемник и усилительно-регистри])ую-щие блоки спектрометра обладают определенными частотными характеристиками, указывающими тот интервал частот ) А/, в котором спгнал можно усилить и зарегистрировать. Поэтому уровень шума, непосредственно регистрируемого па выходе спектрометра, зависит от соотиошеиия между А/ и б/. Если А/ 6/, то шумовые импульсы регистрируются практически без изменения своей формы и мощности. Если же Д/ < 6/, то величина регистрируемого шума,  [c.309]

Интервал частот Дсо (или для циклических частот Дл ), в котором по определению энергия колебаний составляет половину энергии на резонансной частоте (т. е. на частоте (Оо), называют шириной резонансной кривой. Таким образом, добротность колебательной системы равна отношению ее собственной частоты к ширине энергетической резонансной кривой, откуда добротность (а вместе с нею и другие характеристики затухания) легко определяется экспериментально из частотной зависимости какойчшбудь акустической величины. Если измеряется интенсивность ультразвука (плотность энергии, мощность и т. д.), то добротность находится непосредственно из полученной кривой частотной зависимости. Если же измеряемой величиной является, например, амплитуда давления (колебательной скорост , смещения и т. д.), то для использования формулы (УИЬбб) полученную частотную зависимость данной величины нужно предварительно пересчитать на частотную зависимость квадрата этой величины. В свою очередь, добротность системы определяет ее избирательность по частоте, или полосу пропускания, т. е тот интервал частот, в котором энергия вынужденных колебаний составляет не менее 50% от энергии на резонансной частоте. Это означает, например, что пластинка с добротностью Q , используемая в качестве преобразователя, может излучать ультразвук с интенсивностью более 50% от максимальной в полосе частот Дл = Vo/Qд. Это означает также, что плоскопараллельный слой, на который падают плоские ультразвуковые волны, обладает коэффициентом пропускания ф более 0,5 от максимального в интервале частот vJQ . Поскольку добротность нагруженного слоя на основной частоте его колебаний определяется отношением волновых сопротивлений слоя и внешней среды рс/(р1С1), то для полосы пропускания слоя вблизи основной частоты это дает Av =  [c.196]

Как видно из рассмотренного примера, при записи импульсных частотных сигалов на разных дорожках необходимо записывать на отдельную дорожку импульсы сигнала эталонной частоты. При воспроизведении этот сигнал используется для формирования интервала опроса и для подсчета импульсов в интервале измерения при использовании счетных методов определения частоты.  [c.161]

Детектор с низким частотным разрешением. Пусть частотная полоса детектора сигнала много больше частотной полосы синхронизма, тогда, очевидно, его показания пропорциональны интегралу от (2) по (Й1 = I где Ра йР/сШ, Р а = = аР/йасЮ (предполагается, что интервал интегрирования, равный полосе детектора, включает только одну частоту со (Й ), принадлежащую поверхности синхронизма в направлении Й ). Из определения дельта-функции следует, что  [c.183]

Эта задача объясняет частотный спектр электромагнитного излучения, называемого синхротронным. Его источником является релятивистский электрон, совершающий равномерное круговое движение с частотой Vj. Можно показать (см. главу 7), что, если такое движение совершает нерелятивистский электрон, то он испускает электромагнитное излучение одной частоты Vj. Причина в том, что электрическое поле в излучении нерелятивистского электрона пропорционально той компоненте ускорения заряда, которая перпендикулярна радиусу-вектору от заряда к наблюдателю. При круговом движении эта проекция ускорения представляет собой гармоническое движение. Поэтому, для нерелятивистского электрона излучаемое поле пропорционально os oi или sin oi. Для релятивистского электрона вpeмeннaя зависимость излучаемого поля не определяется os (x>ii. Вместо этого интенсивность излучения сильно сконцентрирована по направлению мгновенной скорости заряда. Когда электрон движется прямо на наблюдателя, он испускает излучение, которое будет обнаружено наблюдателем позже. Излучение, испускаемое в другие моменты времени, не достигнет наблюдателя. Таким образом, электрическое поле, измеренное наблюдателем, имеет определенную величину в течение короткого интервала At однажды за каждый период Ti и будет близко к нулю в остальную часть периода. Поэтому наблюдаемый спектр состоит из частот Vj= 1/Tj и гармоник 2v,, Sv и т. д. до максимальной (главной) частоты, близкой к I/At. Покажите, что временной интервал At определяется из приблизительного равенства At/Tit AQ/2n, где А0 — полная угловая ширина .  [c.101]

Спектры величин q и х были непосредственно измерены Гурвичем и Цвангом (1960) и Гурвичем (1961) исходя из следующего определения этих спектров. Пусть ы(Дш), ге (До) и 7 (Дш) — пульсации и, w и Т, пропущенные через частотный фильтр с узкой полосой пропускания Дш около частоты . Тогда среднее произведение —ы(Дш)ге (Дш) будет вкладом интервала Дш осн частот в значение и = т/р вертикального турбулентного потока количества движения (нормированного на единицу массы), а W (Дш) Т (Дш) — вкладом интервала Дш в значение i / pP нормированного вертикального турбулентного потока тепла. Соответственно этому функции  [c.459]

ДНИ при частотах, лежащих ниже порога разрушения пар 2Д/Л, в магнитном поле, параллельном цилиндрическому участку поверхности Ферми, и обнаружили линейную частотную зависимость ш Я. Кох и Пинкус [117] интерпретировали этот факт как возбуждение из магнитных поверхностных состояний в БКШ-континуум. Автор думает, что четко определенные. состояния Пинкуса соответствуют неявному предположению о зеркальном граничном условии для волнового уравнения боголюбовских пар [114]. С другой стороны, Будзинский и Гарфункель [118] наблюдали широкий интервал полос поглощения в алюминии, которые Гарфункель [118] интерпретирует с помощью диффузного граничного условия для сверхпроводящей волновой функции.  [c.145]

Данным, представленным на рис. 94, можно дать еще одну трактовку. Основываясь на них, можно считать, что ширина полосы эффективной звукоизоляции решетки из упругих элементов в определенной мере пропорциональна частотному интервалу между первой и второй собственными частотами. Из этого следует вывод о том, что одним из возможных путей улучше1шя диапазонных свойств решетки является использование таких конструкций и способов закрепления упругпх пластин, которые обеспечивают увеличение интервала между собственными частотами. Возможности для практического использования таких рекомендаций будут рассмотрены в последующих параграфах.  [c.181]

На основе этого описания могут быть впределены временньге и частотные характеристики системы. Первым шагом в вычислении переходных характеристик является определение временного интервала. В комплексе TRL- для этого используют оператор двоеточие . Команда [> t=0 . 1 10  [c.109]

---

Измерение
частоты. В
частотно-измерительной технике главной
величиной периодического сигнала
является период
– наименьший
интервал времени, через который
повторяется произвольно выбранное
мгновенное значение периодического
сигнала, а частота
определяется как величина, обратная
этому периоду.

Для
измерения промышленной частоты могут
применяться стрелочные приборы
электродинамической системы. На низких
частотах применяют электронно-счетные
частотомеры и осциллографы. На высоких
и сверхвысоких частотах применяют
резонансные частотомеры.

Приборы
для измерения частоты (в обозначении
типа имеют букву Ч):

Ч1
– стандарты частоты и времени;

Ч2
– частотомеры резонансные;

Ч3
– частотомеры электронно-счетные;

Ч4
– частотомеры гетеродинные, емкостные,
мостовые;

Ч5
– синхронизаторы
частоты, преобразователи частоты;

Ч6
– синтезаторы частот; делители и
умножители частоты;

Ч7
– компараторы частотные, фазовые,
временные.

Методы
измерения частоты:

• Метод
  линейной развертки. Сигнал
  измеряемой частоты подается на вход
  Y
  осциллографа. Измеряется интервал
  времени t_х,
  в который попадает целое число N
  периодов
  сигнала. Тогда частота f
  = 1/T=N/t_x
  .

• Метод
  синусоидальной развертки (фигур
  Лиссажу).
  К отклоняющим
  пластинам Y
  подводят напряжение измеряемой частоты
  f_y,
  а к
  пластинам
  Х
  – напряжение
  от образцового генератора с частотой
  f₀
  = f_x
  (рисунок 2.27, а). При этом частоту f₀
  изменяют
  до тех пор, пока на экране осциллографа
  не получится наиболее простая и
  неподвижная фигура Лиссажу. Определив
  затем по ней отношение частот n
  = f_y/f_x
  = f_y/f₀,
  находим f_y
  = n∙f_x.
  Практически величину n
  удобно
  находить как отношение числа точек
  пересечения фигуры Лиссажу горизонтальной
  линией к числу точек пересечения фигуры
  вертикальной линией (рисунок 2.27, б).

Рисунок
2.27

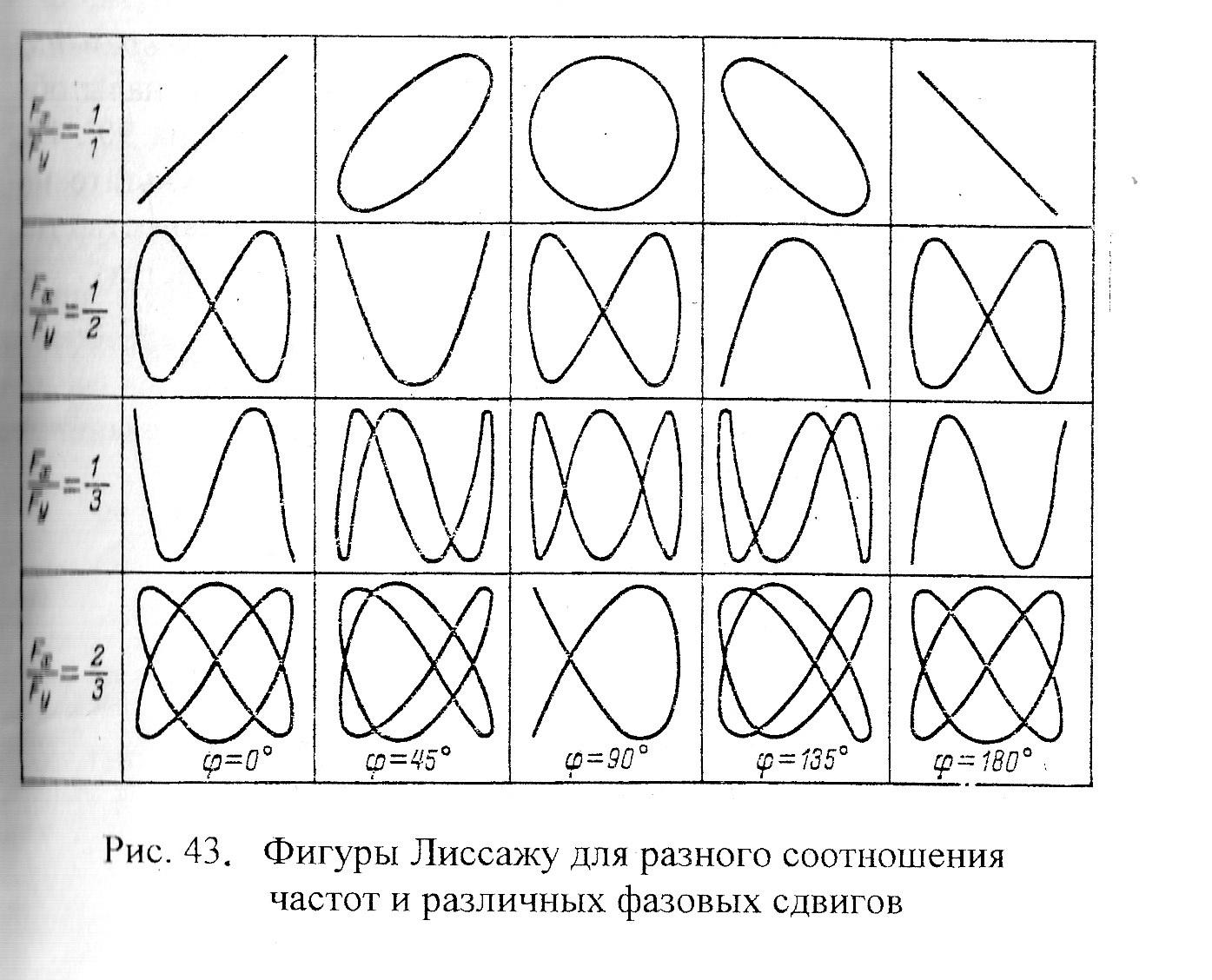
Рисунок
2.28. Фигуры Лиссажу для разного соотношения
частот и различных фазовых сдвигов

Данный
метод целесообразно использовать, если
n
не превышает 10.
При большем отношении частот фигура
получается неразборчивой. В этом случае
для измерения частоты необходимо
использовать метод круговой или
эллиптической развертки.

Пример:

Если
фигура Лиссажу на рисунке 2.19, б получилась
при частоте f₀=
1000 Гц, то n
= f_y/
f₀
= 6 / 2 = 3,
откуда f
_y
= n∙
f₀
= 3∙1000 = 3000
Гц.

На
рисунке 2.28 приведены фигуры Лиссажу
при различных частотах и фазовых углах
сдвига синусоидальных напряжений.
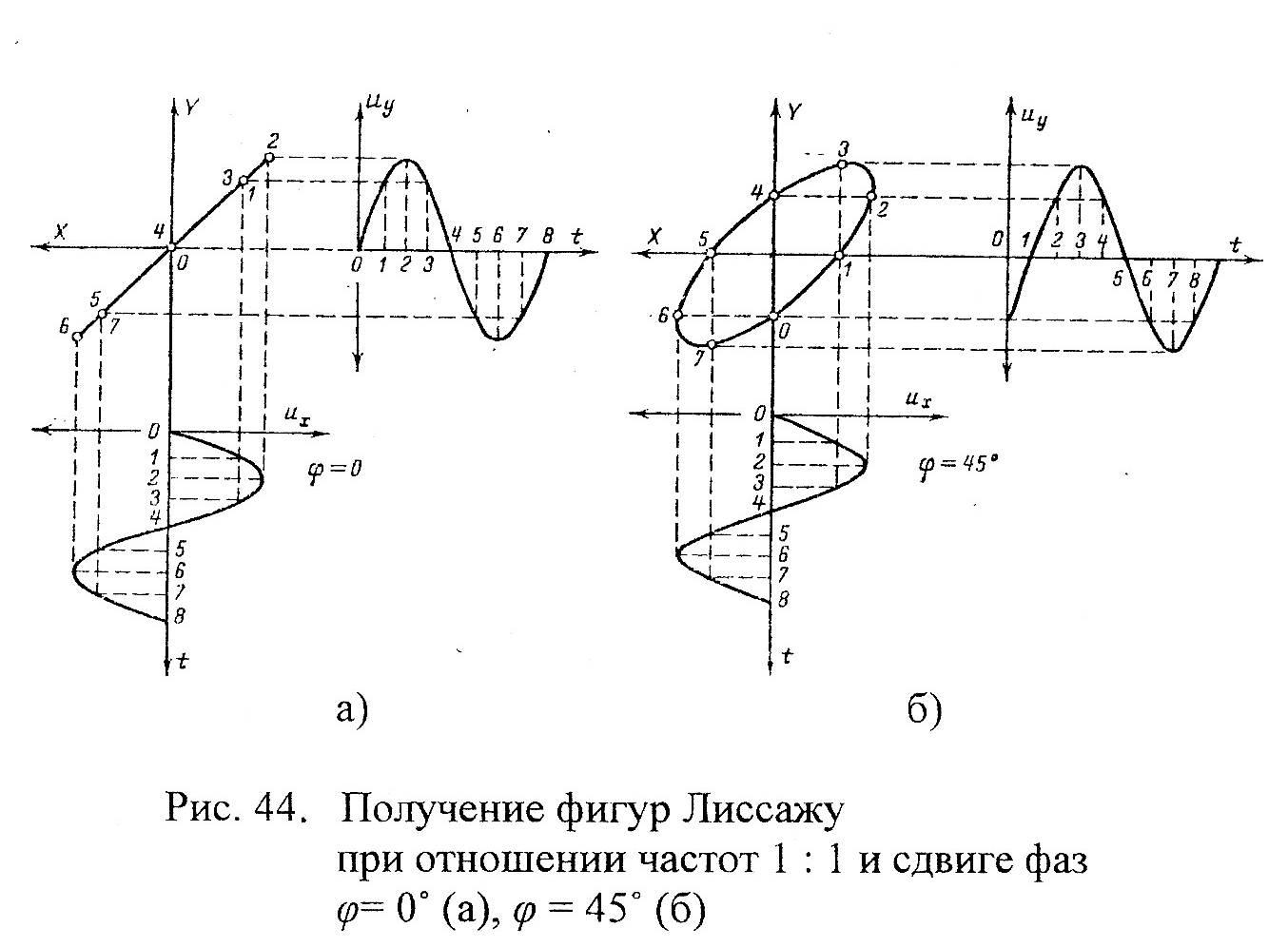
Кривые, приведенные на рисунке 2.29,
наглядно поясняют образование фигур
Лиссажу на экране осциллографа.

Рисунок
2.29. Получение фигур Лиссажу при отношении
частот 1:1 и сдвиге фаз φ = 0^о
(а), φ = 45^о
(б)

• Метод
  круговой развертки (яркостных меток
  времени).
  На входы X
  и Y
  осциллографа подаются синусоидальные
  сигналы образцовой частоты f₀,
  сдвинутые по фазе на 90º друг от друга,
  а на вход Z
  – сигнал
  измеряемой частоты f_х.
  В результате
  на экране осциллографа получается
  прерывистая окружность (рисунок 2.30),
  по количеству разрывов n
  которой находится отношение частот:
  f_х=
  n
  ∙f₀.
  

Рисунок
2.30

Измерение
интервалов времени дискретным методом
счета.
Измеряемый интервал времени ∆t_х
заполняется импульсами с известным
образцовым периодом их следования Тобр
<< t_х.
При этом число этих импульсов m,
пропорциональное ∆t_х
, подсчитывается. Импульсы, заполняющие
интервал ∆t_х
, называют счетными,
а период их следования – Тсч.
Таким образом:

∆tx
= m
∙ Тcч
.

Для
аппаратурного осуществления дискретного
метода счета необходимы генератор
счетных импульсов
и счетчик,
между которыми включается временной
селектор,
представляющий собой логический элемент
на два входа. Счетные импульсы, поступающие
непрерывно на один из входов, проходят
на счетчик только тогда, когда на второй
вход селектора поступает стробирующий
импульс,
длительность которого равна измеряемому
интервалу времени ∆t_х
. При этом число импульсов, фиксируемое
счетчиком и наблюдаемое с помощью
цифрового отображающего устройства –
дисплея, однозначно соответствует
измеряемому интервалу времени ∆t_х
.

Электронно-счетные
цифровые частотомеры.
Они используют метод дискретного счета
импульсов, т.е. осуществляют подсчет
числа периодов (импульсов) измеряемой
частоты за образцовый промежуток времени
(рисунок 2.31). Напряжение измеряемой
частоты подается на формирующее
устройство,
на выходе которого получаются однополярные
импульсы такой же частоты. Далее эти
импульсы поступают на счетчик
только тогда, когда открыт временной
селектор.
Устройство
управления
селектором формирует прямоугольный
импульс, который отпирает и запирает
селектор. Длительность этого импульса
стробирована кварцевым
генератором.

Делитель
частоты
позволяет получать интервалы времени,
кратные десяти (0,001; 0,01; 0,1; 1; 10). Измеряемая
частота представляет собой число
импульсов на выходе селектора в единицу
времени:

Fx
= n
/ ∆t
,

где
n
– показание счетчика, ∆t
– время счета.

Чем
больше время счета при неизменной
частоте, тем больше показание счетчика
и точнее измерения.

Особенности:
высокая точность; можно измерять период,
частоту и отношение частот; при измерении
низких частот прибор не обеспечивает
высокой точности измерения, поэтому в
диапазоне НЧ измеряют не частоту, а
период.

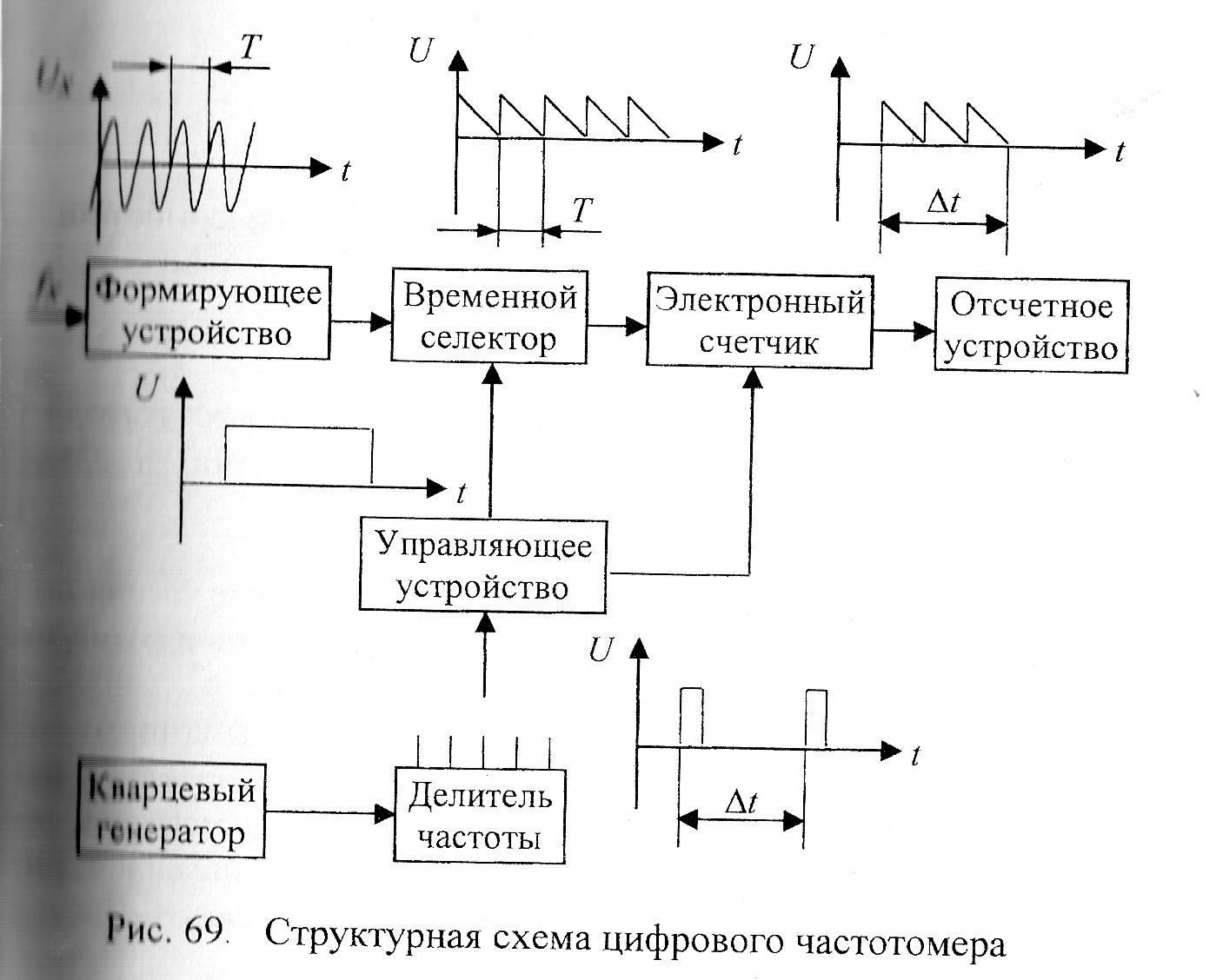
Рисунок
2.31. Структурная схема цифрового
частотомера

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #