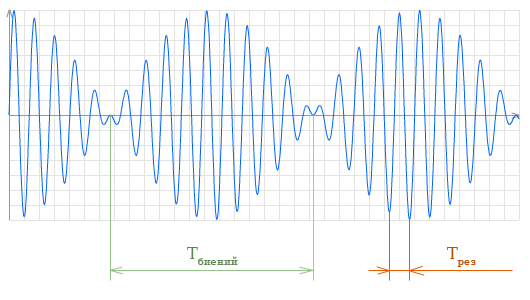
Частота биений, формула
Период биений
Период биений Тб — это промежуток между соседними моментами времени, в которые амплитуда обращается в нуль, а фаза изменяется на π.
Частота биений, Период биений, Результирующая частота
Поскольку при аргументе, равном π/2, 3π/2 …, косинус обращается в нуль, имеем:
[ frac{ω_{1}-ω_{2}}{2} T_{б} = π ]
Отсюда при
[ ω = 2πf ]
следует
[ frac{2πf_{1}-2πf_{2}}{2} = π f_{б} ]
Решая это уравнение относительно частоты биений, получаем
[ f_{б} = f_{1} – f_{2} ]
Частота биений
Частота биений есть отношение числа минимумов амплитуды ко времени. Частота биений определяется как разность частот составляющих колебаний.
Из (4) при
[ Т_{б} = frac{ 1 }{ f_{б}} ]
получаем
[ Т_{б} = frac{ T_1 T_2 }{ T_2 – T_1 } ]
Частота результирующих колебаний получается из формулы результирующего отклонения биений [2]
[ f_{рез} = frac{ f_1 + f_2 }{ 2 } = average{f} ]
Отсюда находим период результирующих колебаний Трез = 1/fрез
[ Т_{рез} = 2 frac{ T_1 T_2 }{ T_1 + T_2 } ]
Вычислить, найти частоту биенй по формуле (4)
Частота биений |
стр. 564 |
|---|
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Sound waves are referred to as the beat. The difference in frequency between two waves is called the beat frequency. Interference, both helpful and detrimental, is to blame. In sound, the beat frequency is defined as the rate at which the loudness of the sound fluctuates, whereas the ordinary frequency of the waves is defined as the pitch of the sound.
Beat Frequency
Beats are created when two waves of almost identical frequencies travelling in the same direction collide at a spot. Whenever two sound waves with different frequencies reach your ear, the opposing productive and harmful disruption enables the sound to alternately be loud and faint. This is known as beating.
Beat frequency is the total value of the frequency difference between the two waves.
Formula
fb = |f2 − f1|
where,
f1 and f2 denote the frequency of the two given waves.
Sample Problems
Question 1. Find the beat frequency given the wave frequencies are 550Hz and 380Hz.
Solution:
Given: f1 = 550 Hz and f2 = 380 Hz
Since, fb = |f2 − f1|
= |550 − 390|
= 210 Hz
Question 2. Find the beat frequency if the wave frequencies are 600 and 420 Hz.
Solution:
Given: f1 = 600 Hz and f2 = 420 Hz
Since, fb = |f2 − f1|
= |600 − 420|
= 180 Hz
Question 3. Find the beat frequency if the wave frequencies are 200 and 920 Hz.
Solution:
Given: f1 = 920 Hz and f2 = 200 Hz
Since, fb = |f2 − f1|
= |920 − 200|
= 720 Hz
Question 4. Find the beat frequency if the wave frequencies are 100 and 210 Hz.
Solution:
Given: f1 = 100 Hz and f2 = 210 Hz
Since, fb = |f2 − f1|
= |100 − 210|
= 110 Hz
Question 5. Find the beat frequency if the wave frequencies are 400 and 760 Hz.
Solution:
Given: f1 = 400 Hz and f2 = 760 Hz
Since, fb = |f2 − f1|
= |400 − 760|
= 360 Hz
Last Updated :
14 Mar, 2022
Like Article
Save Article
А = | А1 – А2 | – амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
Биения
Если два складываемых гармонических колебаний одинакового направления мало отличаются по частоте, то возникают биения.
Биениями называют периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами.
Пусть
х1 = A1 cos ωt
х2 = A2 cos (ω + Δω) t , тогда х = А′ cos ωt
Амплитуду А′ найдем по теореме косинусов: если А1=А2 ϕ01 = ϕ02 = 0 тогда
cos (x+y) = cos x·cos y – sin x·sin y 1 + cos2x = 2cos2x
|
A = |
A2 |
+ A2 |
+ 2A |
A cos |
ϕt = 2Acos( ωt 2) . |
(10.4) |
|
биен |
1 |
2 |
1 2 |
|||
|
x = (2Acos( ωt |
2))cos ωt |
(10.5) |
уравнение биений
Т. к. Δω / 2 << ω , то (10.5) почти не изменяется за то время, когда cos ω t совершит полное колебание частоты изменения амплитуды биения в два раза больше частоты изменения косинуса ( т. к. берется по модулю ).
|
ωбиен = |
ω , |
(10.6) |
|||
|
тогда частота биений равна разности частот складываемых колебаний. |
|||||
|
Tбиен = |
2π |
= |
2π |
. |
(10.7) |
|
ωT |
|||||
|
ω0 |
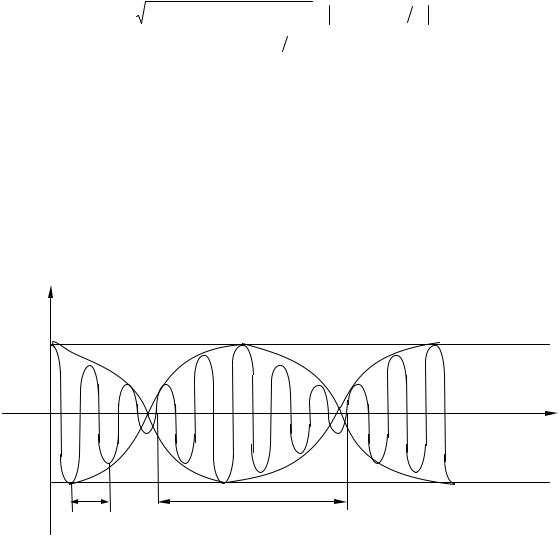
График результирующего колебания дают жирные линии, а огибающие их – график изменения с течением времени амплитуды.
х, Абиен
+ 2А
t
– 2А
ТТбиен
Рис. 10.2. Биения
Метод биений используется для настройки музыкальных инструментов, анализа слуха.
26
Формула частоты в физике
Формула частоты
Определение
Частота – это физический параметр, которые используют для характеристики периодических процессов.
Частота равна количеству повторений или свершения событий в единицу времени.
Чаще всего в физике частоту обозначают буквой $nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$
[nu =frac{1}{T}left(1right).]
Частота, в этом случае – это число полных колебаний ($N$), совершающихся за единицу времени:
[nu =frac{N}{Delta t}left(2right),]
где $Delta t$ – время за которое происходят $N$ колебаний.
Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:
[left[nu right]=с^{-1}=Гц.]
Герц – это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${nu }_1 и {nu }_2$) равна:
[{nu =nu }_1- {nu }_2left(3right).]
Еще одно величиной характеризующей колебательный процесс является циклическая частота (${omega }_0$), связанная с частотой как:
[{omega }_0=2pi nu left(4right).]
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Частота колебаний тела, имеющего массу$ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:
[nu =frac{1}{2pi sqrt{{m}/{k}}}left(5right).]
Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
[nu =frac{1}{2pi sqrt{{l}/{g}}}left(6right),]
где $g$ – ускорение свободного падения; $ l$ – длина нити (длина подвеса) маятника.
Физический маятник совершает колебания с частотой:
[nu =frac{1}{2pi sqrt{{J}/{mgd}}}left(7right),]
где $J$ – момент инерции тела, совершающего колебания относительно оси; $d$ – расстояние от центра масс маятника до оси колебаний.
Формулы (4) – (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.
Формулы для вычисления частоты дискретных событий, частота вращения
дискретных колебаний ($n$) – называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(8right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) – называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ – время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(9right).]
Примеры задач с решением
Пример 1
Задание. Колебательная система совершила за время равное одной минуте ($Delta t=1 мин$) 600 колебаний. Какова частота этих колебаний?
Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае – это число полных колебаний, совершающихся за единицу времени.
[nu =frac{N}{Delta t}left(1.1right).]
Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $Delta t=1 мин=60 с$. Вычислим частоту:
[nu =frac{600}{60}=10 left(Гцright).]
Ответ. $nu =10Гц$
Пример 2
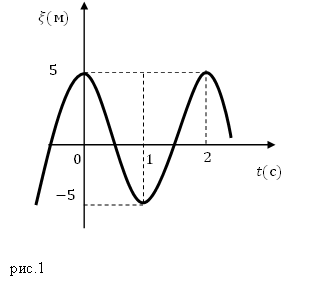
Задание. На рис.1 изображен график колебаний некоторого параметра $xi (t)$, Какова амплитуда и частота колебаний этой величины?
Решение. Из рис.1 видно, что амплитуда величины $xi left(tright)={xi }_{max}=5 (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:
[T=2 left(cright).]
Частота – величина обратная периоду колебаний, значит:
[nu =frac{1}{T}=0,5 left(Гцright).]
Ответ. 1) ${xi }_{max}=5 (м)$. 2) $nu =0,5$ Гц
Читать дальше: формулы математического маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Биения между двумя звуковыми частотами 300 Гц и 305 Гц
Анимация биений двух синусоидальных сигналов напряжения равной амплитуды близких частот. Колебания и их сумма изображены в виде вращающихся векторов (комплексных амплитуд)
Бие́ния — явление, возникающее при наложении двух периодических колебаний, например, гармонических, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Частота изменения амплитуды суммарного сигнала (частота биения) равна разности частот исходных сигналов (точнее, модулю этой разности).
Описание[править | править код]
Биения возникают от того, что один из двух сигналов линейно во времени отстаёт от другого по фазе, и, в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается максимален, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того, как нарастает отставание.
Математически это может быть рассмотрено на примере сложения двух колебаний с одинаковыми амплитудами.
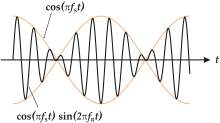
Можно считать, что колебания с частотами ω1 и ω2 заменены колебанием 


Это низкочастотное колебание является огибающей высокочастотного колебания. Поскольку модуль огибающей меняется от нуля до максимума дважды за период, частота биений равна удвоенной частоте огибающей 
Применение[править | править код]
Эффект биений используют для сравнения частот двух источников сигналов с целью подстройки одного источника (регулируемого) под частоту другого (эталонного). В процессе подстройки частоту регулируемого источника изменяют таким образом, чтобы период биений увеличивался, до тех пор, пока биения не исчезнут, это будет означать, что частоты совпадают.
Настройка музыкального инструмента по камертону, другому инструменту или электронному тюнеру. В первом и втором случаях музыкант (настройщик) улавливает колебания громкости суммарного звука (от инструмента и камертона или эталонного инструмента) непосредственно ухом. В третьем случае сравнение частот происходит с помощью электроники.
Если частота инструмента незначительно отличается от частоты камертона, то слышно, что звук пульсирует — это и есть биения. Струну для настройки в унисон с камертоном нужно подтягивать или ослаблять так, чтобы частота биений уменьшалась. При совпадении высоты звука с эталонным биения полностью исчезают. Биения звука также можно услышать при игре на музыкальных инструментах, например пианино или гитаре, когда различной высоты звуки создают интервалы и многозвучия (аккорды).
В современных аккордеонах и баянах (где нажатие на кнопку или клавишу открывает воздушный клапан и извлекается звук соответствующей ноты одной высоты с помощью трёх металлических язычков, колеблющихся в потоке воздуха) два других язычка, при изготовлении инструмента, специально немного расстраивают по частоте относительно язычка, настроенного в унисон к ноте, чтобы получить характерное звучание инструмента, называемое разливом, образующееся в результате эффекта биений[1].
Измерение частоты гетеродинным методом — поскольку при этом используются высокие частоты, суммарный сигнал подаётся на диодный детектор, для выделения огибающей. Выделенные на диоде низкочастотные колебания подаются на индикаторное устройство — стрелочный прибор, лампочку или головные телефоны. При таком способе можно измерять частоты даже в несколько раз выше максимальной частоты гетеродина, так как благодаря нелинейному элементу — диоду, образуются гармонические составляющие, с частотами, кратными частоте гетеродина.
Эффект биений используется в электронике для вычитания частот сигналов. Например, в супергетеродинных радиоприёмниках биения между частотами гетеродина и принимаемого сигнала преобразуются в промежуточную частоту, сигнал которой далее усиливается.
Примечания[править | править код]
- ↑ Газарян С. В мире музыкальных инструментов: Книга для учащихся старших классов. — 2-е изд. — М.: Просвещение, 1989. — 192 с: ил., с.43. Дата обращения: 11 марта 2021. Архивировано 3 марта 2022 года.
См. также[править | править код]
- Интерференция волн
- Гетеродин
- Частотомер
- Смеситель (электроника)
- Муаровый узор
- Фигуры Лиссажу
Литература[править | править код]
- [bse.sci-lib.com/article116414.html Биения] // Большая советская энциклопедия
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|