Как найти частоту дискредитации

Частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчётов непрерывного по времени сигнала при его дискретизации (в частности, аналого-цифровым преобразователем). Измеряется в герцах.

Термин применяется и при обратном, цифро-аналоговом преобразовании, особенно если частота дискретизации прямого и обратного преобразования выбрана разной (Данный приём, называемый также «Масштабированием времени», встречается, например, при анализе сверхнизкочастотных звуков, издаваемых морскими животными).

Чем выше частота дискретизации, тем более широкий спектр сигнала может быть представлен в дискретном сигнале.
Как следует из теоремы Котельникова, для того, чтобы однозначно восстановить исходный сигнал, частота дискретизации должна более чем в два раза превышать наибольшую частоту в спектре сигнала.

Некоторые из используемых частот дискретизации звука^[1]:

• 8 000 Гц — телефон, достаточно для речи, кодек Nellymoser;
• 11 025 Гц — четверть Audio CD, достаточно для передачи речи;
• 16 000 Гц;
• 22 050 Гц — половина Audio CD, достаточно для передачи качества радио;
• 32 000 Гц;
• 44 100 Гц — используется в Audio CD. Выбрано Sony из соображений совместимости со стандартами PAL (запись 3 значений на линию картинки кадра × 588 линий на кадр × 25 кадров в секунду) и NTSC (запись 3 значений на линию картинки кадра × 490 линий на кадр × 30 кадров в секунду), и достаточности (по теореме Котельникова) для качественного покрытия всего диапазона частот, различаемых человеком на слух (20 Гц — 20 КГц);
• 48 000 Гц — DVD, DAT;
• 96 000 Гц — DVD-Audio (MLP 5.1);
• 192 000 Гц — DVD-Audio (MLP 2.0);
• 2 822 400 Гц — SACD, процесс однобитной дельта-сигма модуляции, известный как DSD — Direct Stream Digital, совместно разработан компаниями Sony и Philips;
• 5 644 800 Гц — DSD с удвоенной частотой дискретизации, однобитный Direct Stream Digital с частотой дискретизации вдвое больше, чем у SACD. Используется в некоторых профессиональных устройствах записи DSD.

См. также[править | править код]

• Частота Найквиста
• Цифровой сигнал
• Дискретизация

Примечания[править | править код]

Как определить частоту дискретизации

Одной из основных характеристик цифровой аудиозаписи является частота дискретизации звука. Данный параметр указывает на то, сколько моментальных значений аналогового сигнала в секунду снималось при его оцифровке. Частоту дискретизации конкретной записи можно определить при помощи различных программных средств.

Вам понадобится

• – Winamp;
• – Sound Forge;
• – Virtual Dub.

Инструкция

Определите частоту дискретизации звука в медиа-файле при помощи проигрывателя Winamp. Он доступен для бесплатной загрузки на сайте winamp.com. Откройте окно редактора списка воспроизведения, если оно не отображено. Для этого нажмите сочетание клавиш Ctrl+E или в главном меню выберите пункты View и Playlist Editor. Добавьте файл в список воспроизведения, кликнув по кнопке Add и выбрав пункт Add file(s) появившегося контекстного меню. Правой кнопкой мыши кликните по записи в списке воспроизведения. Выберите пункт “View file info…” контекстного меню. Отобразится диалог, в котором среди прочих значений будет выведена частота дискретизации.

Воспользуйтесь аудио-редактором Sound Forge для определения частоты дискретизации. В главном меню выберите пункты File и “Open…”. Также можно нажать клавиши Ctrl+Alt+F2. В диалоге «Открыть» выделите нужный файл. В графе Audio блока со статистической информацией, расположенного снизу, появится нужное значение.

Если файл уже открыт в Sound Forge, нажмите клавиши Alt+Enter или Alt+2. Либо выберите пункты View и File Properties главного меню. Отобразится окно со списком атрибутов и соответствующих им значений. Найдите в нем графу Audio sample rate. Из поля Value получите значение частоты дискретизации.

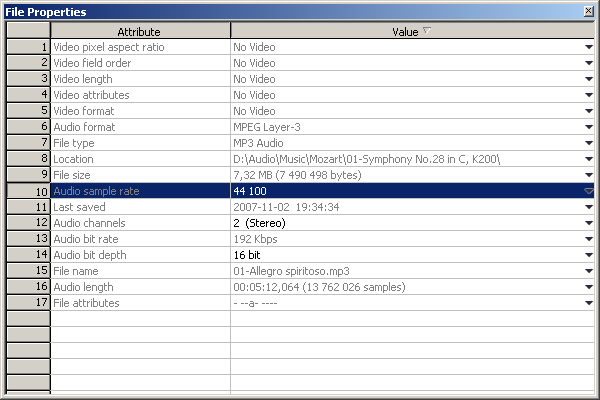
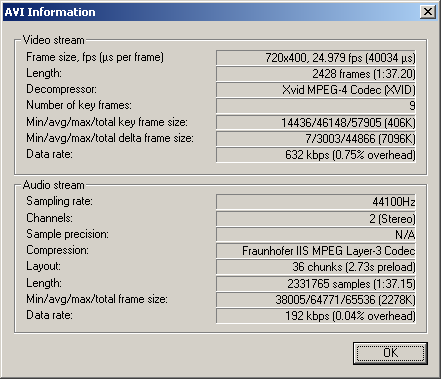
Узнайте частоту дискретизации звука, содержащегося в файле видео. Используйте редактор Virtual Dub. Он бесплатно распространяется на сайте virtualdub.org. Откройте видео в программе, выбрав пункты File и “Open…” главного меню. Отобразите диалог свойств файла. Для этого в меню выберите пункты File и “File Information…”. В группе элементов управления Audio stream найдите значение Sampling rate.

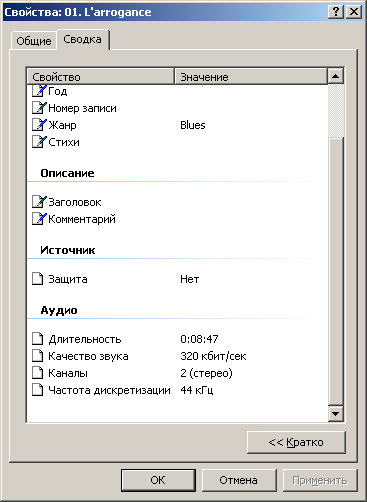
Узнайте частоту дискретизации при помощи диалога свойств графической оболочки Windows. В окне папки, проводника или какого-либо файлового менеджера кликните правой кнопкой по файлу. В контекстном меню выберите пункт «Свойства». переключитесь на вкладку «Сводка» отобразившегося диалога. В разделе «Аудио» найдите нужное значение.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

1.
Теорема Котельникова не соблюдается,
т.е. F_Д
< 2 х Fсигн.в.
= 5 кГц

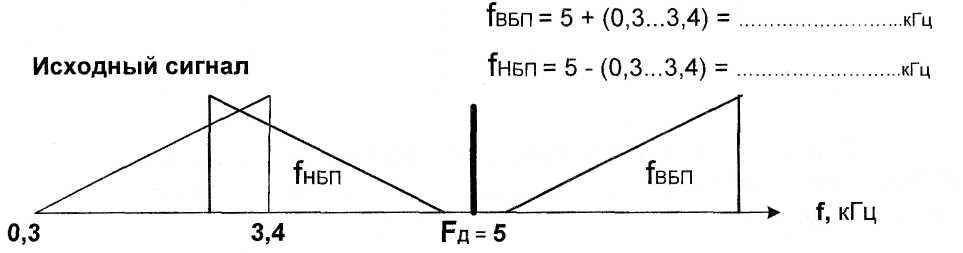
Вывод:
восстановить
исходный сигнал ,
т.к. он частично .

совпадает
с

Рис.12

2.
Теорема Котельникова соблюдается, т.е.
F_Д
= 2 х F_сигн.в.

=
6,8 кГц

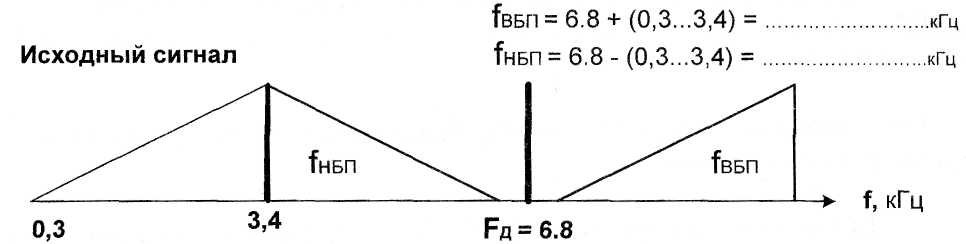
Вывод:
восстановить
исходный сигнал ,
но сложно, т.к. его

совпадает
с нижней
боковой полосы частот и для их

отделения
нужен сложный ФНЧ
– 3,4.

Рис.13

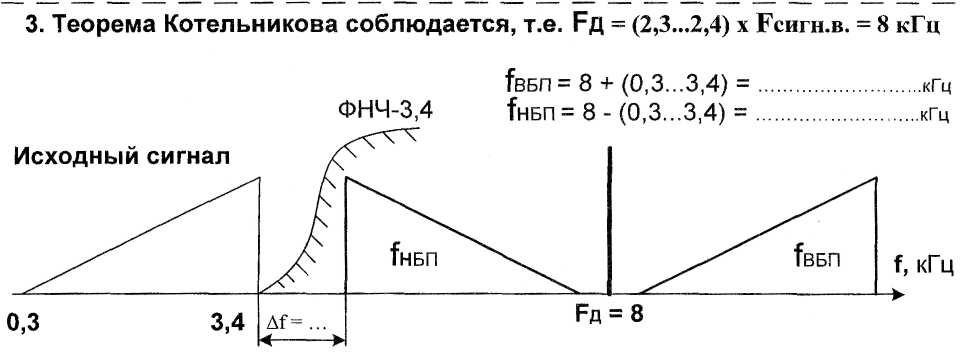
Рис.14

Вывод:
восстановить
исходный сигнал ….,
т.к. между ним и нижней боковой

полосой
частот имеется достаточный частотный
промежуток Δf
=………кГц

и
для отделения исходного сигнала от
нижней боковой полосы
частот

нужен………………………………………………………….ФНЧ–3,4.

ТЕОРЕМА
КОТЕЛЬНИКОВА

1-я
формулировка. Любой
непрерывный сигнал, ограниченный по
спектру

верхней
частотой Fb,
полностью
определяется
последовательностью своих
дискретных отсчетов, взятых через
промежуток времени Тд,
если

2-я
формулировка. Любой
непрерывный сигнал, ограниченный по
спектру верхней
частотой F_В,
может
быть представлен в виде его дискретных
отсчетов взятых через промежуток
времени Тд, а на приеме восстановлен
из этих отсчетов, если частота
дискретизации будет больше или равна
удвоенной верхней
частоте сигнала F_В
≥
2

F_В.

Так как спектр
частот телефонного сигнала составляет

Fтлф.сигн.
= 0,3…3,4 кГц. Fb
=
3,4 кГц.

Fд
тлф
≥ 2 хЗ,4
≥ 6,8
кГц.

На
рис. 12,13,14 изображены спектральные
диаграммы АИМ-сигнала на приеме для
трех вариантов выбора частоты
дискретизации:

1. Fд
<
2 х 3,4 кГц. Fд
=
1,5 х 3,4 = 5 кГц. (рис.
12)

1. Fд
   =
   2 х 3,4 = 6,8
   кГц. (рис.13)

2. Fд
   >
   2 х 3,4 кГц. Fд
   =
   (2,3…2,4)
   х 3,4
   = 8 кГц.
   (рис.14).

После
рассмотрения каждого варианта делается
вывод о возможности восстановления
исходного сигнала на приеме.

Чем
больше частота дискретизации Fд,
тем
точнее на приеме будет восста­новлен
исходный сигнал.

Но
увеличение частоты дискретизации
ведет
к увеличению тактовой частоты
системы, которая рассчитывается по
формуле:

Fт
= Fд
x
m
x
Nки

При
анализе этой формулы видно, что
………….
Fд
ведет
к

тактовой
частоты, а тактовой
частоты ведет к

затухания цепи.
Для сохранения тактовой частоты
неизменной можно:

1. Уменьшить
длины участков регенерации,
т.е. устанавливать

линейные
регенераторы, а это ведет к стоимости
линейного тракта.

2. Можно, число
телефонных каналов, но это приведет к

доходов.

Поэтому
Fд
тлф
=
8 кГц.

Рис.15

Рис.16

Амплитудная
характеристика квантования линейного
кодера

Рис.17

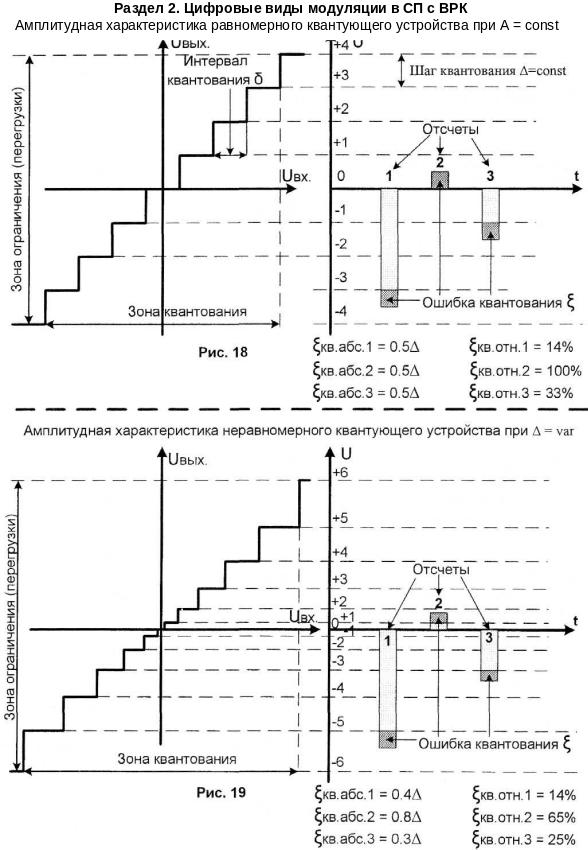
Рис. 18

Рис.19 2220000

ПРИНЦИП
ИМПУЛЬСНО
–
КОДОВОЙ МОДУЛЯЦИИ ИКМ

в ЦСП с ВРК ИКМ-ВД

Схема
построения 30-канальной ЦСП с ИКМ-ВД
приведена на рис.19.

ТРАКТ ПЕРЕДАЧИ

ФНЧ-3,4
– ограничивает спектр телефонного
сигнала верхней частотой 3,4 кГц
согласно условию теоремы

М
– амплитудно-импульсный модулятор –
для……………………………

непрерывного
телефонного сигнала.

КОДЕР
– для амплитуды
отсчета АИМ-сигнала в 8-разрядную комбинацию.

Пер.СУВ
–
передатчик сигналов управления и
взаимодействия между АТС
для СУВ
из импульсов разной длительности или
из другого­
вида (многочастотного и т.д.), поступающих
от АТС по проводу «с» или другим проводам,
в ……….вид
(символы «1»
или «0»).

ФСС
– формирователь синхросигналов – для
формирования цикловой и сверх­цикловой

(ЦС
и СЦС).

УСТРОЙСТВО
ОБЪЕДИНЕНИЯ УО
– для объединения 8-разрядных ко­довых
комбинаций телефонных
каналов, сигналов управления и
взаимодействия между АТС (СУВ),
синхросигналов.

ПКпер
– преобразователь кода передачи –
для кода
ВН

со
скважностью два (Q=2)
группового ИКМ-сигнала в код
с чередующейся ­
полярностью импульсов ЧПИ.

ЗГ
–
задающий
генератор с кварцевым резонатором –
для получения

основной
частоты, равной
частоте
системы.

ГОпер
– генераторное оборудование тракта
передачи – для формирования
импульсных последовательностей, работой
разных узлов тракта

Передачи.

При прохождении
по линии цифровой линейный сигнал ЦЛТ
затухает,
иска­жается,
подвергается воздействию помех,
изменяется взаимное расположение
символов(1
или 0),
поэтому его (регенерируют)
с помощью регенераторов
линейных РЛ и
регенераторов
станционных PC
в тракте приема противоположной…………………станции.

ТРАКТ
ПРИЕМА

ВТЧ
– выделитель тактовой частоты – для
выделения тактовой частоты из
цифрового сигнала
ЦЛС.

ГОпр
– генераторное оборудование тракта
приема – для формирования
импульсных ,
управляющих работой разных узлов тракта
приема.

ПКпр.
–
преобразователь кода приема –
для…………………………..

линейного
кода ЧПИ в код ВН с Q=2.

УСТРОЙСТВО
РАЗДЕЛЕНИЯ УР
– для разделения 8-разрядных кодовых
комбинаций
…..
телефонных каналов, СУВ-ов, синхросигналов.

Пр.
СУВ – приемник СУВ –
для
СУВ
из
цифрового
вида в импульсы разной длительности
или другой вид (многочастотный и т.д.),
посту­пающие
на АТС по проводу «с» или другим проводам
для управления приборами АТС
при установлении соединения между
абонентами.

ПРИЕМНИКИ
СИНХРОСИГНАЛОВ ПЦС и ПСЦС –
для установки, поддер­жания,
восстановления циклового и сверхциклового
между
пере­

дающей
и приемной станциями.

ДЕКОДЕР
–
для 8-разрядных
кодовых комбина­ций
в амплитуду отсчета -сигнала.

ВС
– временной селектор
для пропускания своего
канала.

ФНЧ-3,4
–
для непрерывного
телефонного сигнала из его

отсчетов.
Полезным исходным сигналом является
огибающая амплитуд отсчетов АИМ-сигнала.

Тактовая
частота fт
–
это частота следования символов
группового ИКМ-сигнала в линии,
fт
рассчитывается по формуле

fт
= Fд
x
m
x
Nkи,
кГц
(1)

где
Fд
= 8 кГц
–
частота дискретизации телефонного
сигнала;

m
= 8
– разрядность кодовой комбинации;

Nkи
–
число канальных интервалов в цикле
системы; складывается из числа те­лефонных
каналов Nтк,
одного
канального
интервала для передачи циклового
синхро­сигнала
ЦС и
одного
канального
интервала в
центре цикла для
передачи сигналов управлении
и взаимодействия между АТС «СУВ».

fт
= 8 х
8 х
(… + 1 + 1)
= … кГц.

Длительность
тактового интервала Тт
рассчитывается
по формуле

1

Тт
=
,
мкс
(2)

fт

1

Тт
= =
0,…
мкс.

…

Длительность
импульса τи
рассчитывается по формуле

τи
= Тт х
0,5,
мкс
(3)

τи
= 0,…
х 0,5
= 0,…
мкс.

Длительность
канального интервала Тки
рассчитывается
по формуле

Тки
= Тт х
m,
мкс
(4)

Тки
=
0,… х
8
= … мкс

Длительность
цикла Тц
рассчитывается по формуле

Тц
= Тки х
Nки,
mkc
(5)

Тц
=
… х …
= 125 мкс.

Длительность
сверхцикла Тсц
рассчитывается
по формуле

Тсц
= Тц х
S,
мкс
(6)

где
S
– число циклов в сверхцикле, рассчитывается
по формуле

Ntk

S
= ———-
+1, (7)

2 или 3

2
или 3
– число телефонных каналов Ntk,
которые
обеспечиваются СУВ-ами за один цикл

——

S
= ———
+1
= ……

2
или 3

Тсц
= 125 х
…. = …….
мкс.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решение задач на кодирование звуковой информации

Введение

Данное электронное пособие содержит группу
задач по теме «Кодирование звуковой информации». Сборник задач разбит на типы
задач исходя из указанной темы. Каждый тип задач рассматривается с учетом дифференцированного
подхода, т. е. рассматриваются задачи минимального уровня (оценка «3»), общего
уровня (оценка «4»), продвинутого уровня (оценка «5»). Приведенные задачи взяты
из различных учебников (список прилагается). Подробно рассмотрены решения всех задач,
даны методические рекомендации для каждого типа задач, приведен краткий
теоретический материал. Для удобства пользования пособие содержит ссылки на
закладки.

Типы задач:

1. Размер цифрового аудиафайла (моно и
стерео).

2. Определение качества
звука.

3. Двоичное кодирование звука.

При решении задач учащиеся опираются на следующие
понятия:

Временная дискретизация – процесс, при котором, во время
кодирования непрерывного звукового сигнала, звуковая волна разбивается на
отдельные маленькие временные участки, причем для каждого такого участка
устанавливается определенная величина амплитуды. Чем больше амплитуда сигнала,
тем громче звук.

Глубина звука  (глубина кодирования) – количество бит на кодировку
звука.

Уровни громкости  (уровни сигнала) – звук может иметь различные уровни
громкости. Количество различных уровней громкости рассчитываем по формуле N=
2^I  где I – глубина звука.

Частота
дискретизации – количество измерений уровня входного сигнала в
единицу времени (за 1 сек). Чем больше частота дискретизации, тем точнее
процедура двоичного кодирования. Частота измеряется в герцах (Гц). 1 измерение
за 1 секунду -1 ГЦ.

1000
измерений за 1 секунду 1 кГц. Обозначим частоту дискретизации буквой D. Для кодировки выбирают одну из трех
частот: 44,1 КГц, 22,05 КГц, 11,025 КГц.

Считается, что диапазон
частот, которые слышит человек, составляет от 20 Гц до 20 кГц.

Качество двоичного кодирования – величина, которая определяется
глубиной кодирования и частотой дискретизации.

Аудиоадаптер (звуковая плата) – устройство, преобразующее
электрические колебания  звуковой частоты в числовой двоичный код при вводе
звука и обратно (из числового кода в электрические колебания) при воспроизведении
звука.

Характеристики аудиоадаптера: частота дискретизации и
разрядность регистра.).

Разрядность регистра –число бит в регистре
аудиоадаптера. Чем больше разрядность, тем меньше погрешность каждого
отдельного преобразования величины электрического тока в число и обратно. Если
разрядность равна I, то при измерении входного сигнала может быть получено 2^I =N различных значений.

Размер цифрового моноаудиофайла  ( A)
измеряется по формуле:

A=D*T*I/8, где D –частота дискретизации (Гц), T – время звучания или записи звука, I разрядность регистра
(разрешение). По этой формуле размер измеряется в байтах.

Размер цифрового стереоаудиофайла  ( A)
измеряется по формуле:

A=2*D*T*I/8, сигнал записан для двух колонок, так
как раздельно кодируются левый и правый каналы звучания.

Учащимся полезно выдать таблицу 1, показывающую, сколько Мб будет
занимать закодированная одна минута звуковой информации при разной частоте
дискретизации:

1. Размер
цифрового файла

Уровень «3»

1. Определить размер (в
байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при
частоте дискретизации 22,05 кГц и разрешении 8 бит. Файл сжатию не подвержен.  ([1],
стр. 156, пример 1)

Решение:

Формула
для расчета размера (в байтах) цифрового аудио-файла: A=D*T*I/8.

Для перевода в байты полученную величину
надо разделить на 8 бит.

22,05 кГц =22,05
* 1000 Гц  =22050 Гц

A=D*T*I/8 = 22050
х 10 х 8 / 8 = 220500 байт.

Ответ: размер
файла  220500 байт.

2. Определить объем памяти
для хранения цифрового аудиофайла, время звучания которого составляет две
минуты при частоте дискретизации 44,1 кГц и разрешении 16 бит.  ([1], стр. 157,
№88)

Решение:

A=D*T*I/8. – объем памяти для хранения
цифрового аудиофайла.

44100 (Гц) х 120 (с) х 16 (бит) /8 (бит) =
10584000 байт= 10335,9375 Кбайт= 10,094 Мбайт.

Ответ: ≈ 10 Мб

Уровень «4»

3. В
распоряжении пользователя имеется память объемом 2,6 Мб. Необходимо записать
цифровой аудиофайл с длительностью звучания 1 минута. Какой должна быть частота
дискретизации и разрядность?  ([1], стр. 157, №89)

Решение:

Формула
для расчета частоты дискретизации и разрядности: D* I =А/Т

(объем
памяти в байтах) : (время звучания в секундах):

2, 6
Мбайт= 2726297,6 байт

D* I =А/Т= 2726297,6 байт: 60 = 45438,3 байт

D=45438,3 байт : I

 Разрядность
адаптера может быть 8 или 16 бит. (1 байт или 2 байта). Поэтому частота
дискретизации может быть либо  45438,3 Гц = 45,4 кГц ≈ 44,1
кГц –стандартная характерная частота дискретизации, либо 22719,15 Гц = 22,7
кГц ≈ 22,05 кГц – стандартная характерная частота дискретизации

Ответ:

4.  Объем свободной памяти на
диске — 5,25 Мб, разрядность звуковой платы — 16. Какова длительность звучания
цифрового аудиофайла, записанного с частотой дискретизации 22,05 кГц?  ([1],
стр. 157, №90)

Решение:

Формула для расчета
длительности звучания: T=A/D/I

(объем памяти в байтах)
: (частота дискретизации в Гц) : (разрядность звуковой платы в байтах):

5,25 Мбайт = 5505024 байт

5505024 байт: 22050 Гц
: 2 байта = 124,8 сек
Ответ: 124,8 секунды

5. Одна минута записи
цифрового аудиофайла занимает на диске 1,3 Мб, разрядность звуковой платы — 8.
С какой частотой дискретизации записан звук?  ([1], стр. 157, №91)

Решение:

Формула для расчета
частоты дискретизации : D =А/Т/I

(объем памяти в байтах) : (время записи в
секундах) : (разрядность звуковой платы в байтах)

1,3 Мбайт = 1363148,8 байт

1363148,8 байт  : 60 : 1 = 22719,1 Гц

Ответ: 22,05 кГц

6. Две минуты записи
цифрового аудиофайла занимают на диске 5,1 Мб. Частота дискретизации — 22050
Гц. Какова разрядность аудиоадаптера?  ([1], стр. 157, №94)

Решение:

Формула для расчета разрядности: (объем
памяти в байтах) : (время звучания в секундах): (частота дискретизации):

5, 1 Мбайт= 5347737,6 байт

5347737,6 байт: 120 сек : 22050 Гц= 2,02
байт =16 бит

Ответ: 16 бит

7. Объем свободной памяти на диске — 0,01 Гб,
разрядность звуковой платы — 16. Какова длительность звучания цифрового
аудиофайла, записанного с частотой дискретизации 44100 Гц?  ([1], стр. 157,
№95)

Решение:

Формула для расчета
длительности звучания T=A/D/I

(объем памяти в байтах) : (частота
дискретизации в Гц) : (разрядность звуковой платы в байтах)

0,01 Гб = 10737418,24 байт

10737418,24 байт : 44100 : 2 = 121,74 сек
=2,03 мин
Ответ: 20,3 минуты

8. Оцените информационный объем
моноаудиофайла длительностью звучания 1 мин. если “глубина”
кодирования и частота дискретизации звукового сигнала равны соответственно:
а) 16 бит и 8 кГц;
б) 16 бит и 24 кГц.

 ([2],
стр. 76, №2.82)

Решение:

а).
1) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 8 000 = 128000 бит = 16000 байт = 15,625 Кбайт/с
2) Информационный объем звукового файла длительностью 1 минута равен:
15,625 Кбайт/с х 60 с = 937,5 Кбайт

б).
1) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 24 000 = 384000 бит = 48000 байт = 46,875 Кбайт/с
2) Информационный объем звукового файла длительностью 1 минута равен:
46,875 Кбайт/с х 60 с =2812,5 Кбайт = 2,8 Мбайт

Ответ: а) 937,5 Кбайт; б) 2,8 Мбайт

Уровень «5»

Используется таблица 1

9. Какой объем памяти
требуется для хранения цифрового аудиофайла с записью звука высокого качества
при условии, что время звучания составляет 3 минуты?  ([1], стр. 157, №92)

Решение:

Высокое качество звучания достигается при
частоте дискретизации 44,1КГц и разрядности аудиоадаптера, равной 16.
Формула для расчета объема памяти: (время записи в секундах) x (разрядность
звуковой платы в байтах) x (частота дискретизации):
180 с х 2 х 44100 Гц = 15876000 байт = 15,1 Мб
Ответ: 15,1 Мб

10. Цифровой аудиофайл
содержит запись звука низкого качества (звук мрачный и приглушенный). Какова
длительность звучания файла, если его объем составляет 650 Кб?  ([1], стр. 157,
№93)

Решение:

Для мрачного и
приглушенного звука характерны следующие параметры: частота дискретизации — 11,
025 КГц, разрядности аудиоадаптера — 8 бит (см. таблицу 1). Тогда T=A/D/I.
Переведем объем в байты: 650 Кб = 665600 байт

Т=665600 байт/11025 Гц/1
байт ≈60.4 с

Ответ:
длительность звучания равна 60,5 с

11.  Оцените информационный
объем высокачественного стереоаудиофайла длительностью звучания 1 минута, если
“глубина” кодирования 16 бит, а частота дискретизации 48 кГц.   ([2],
стр. 74, пример 2.54)

Решение:

Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 48 000 х 2 = 1 536 000 бит = 187,5 Кбайт (умножили на 2, так как
стерео).

Информационный объем звукового файла длительностью 1 минута
равен:
187,5 Кбайт/с х 60 с ≈ 11 Мбайт

Ответ: 11 Мб

Ответ: а) 940 Кбайт; б) 2,8 Мбайт.

12.
 Рассчитайте
время звучания моноаудиофайла, если при 16-битном кодировании и частоте
дискретизации 32 кГц его объем равен:
а) 700 Кбайт;
б) 6300 Кбайт

 ([2], стр. 76, №2.84)

Решение:

а).
1) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 32 000 = 512000 бит = 64000 байт = 62,5 Кбайт/с
2) Время звучания моноаудиофайла объемом 700 Кбайт равно:
700 Кбайт : 62,5 Кбайт/с = 11,2 с

б).
1) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 32 000 = 512000 бит = 64000 байт = 62,5 Кбайт/с
2) Время звучания моноаудиофайла объемом 700 Кбайт равно:
6300 Кбайт : 62,5 Кбайт/с = 100,8 с = 1,68 мин

Ответ: а) 10 сек; б) 1,5
мин.

13. Вычислить, сколько байт информации занимает на
компакт-диске одна секунда стереозаписи (частота 44032 Гц, 16 бит на значение).
Сколько занимает одна минута? Какова максимальная емкость диска (считая
максимальную длительность равной 80 минутам)?  ([4], стр. 34, упражнение №34)  

Решение:

Формула для расчета объема памяти A=D*T*I:
(время записи в секундах) * (разрядность звуковой платы в байтах) * (частота
дискретизации). 16 бит -2 байта.
1) 1с х 2 х 44032 Гц = 88064 байт (1 секунда стереозаписи на компакт-диске)
2) 60с х 2 х 44032 Гц = 5283840 байт (1 минута стереозаписи на компакт-диске)
3) 4800с х 2 х 44032 Гц = 422707200 байт=412800 Кбайт=403,125 Мбайт (80 минут)

Ответ: 88064 байт (1 секунда), 5283840 байт (1 минута), 403,125 Мбайт (80 минут)

2. Определение качества звука.

Для определения качества звука надо найти частоту
дискретизации и воспользоваться таблицей №1

256 (2⁸)
уровней интенсивности сигнала -качество звучания радиотрансляции,
использованием 65536 (2¹⁶)  уровней интенсивности сигнала – качество
звучания аудио-CD. Самая качественная частота соответствует музыке, записанной
на компакт-диске. Величина аналогового сигнала измеряется в этом случае
44 100 раз в секунду.

Уровень «5»

13. Определите
качество звука (качество радиотрансляции, среднее качество, качество аудио-CD)
если известно, что объем моноаудиофайла длительностью звучания в
10 сек. равен:
а) 940 Кбайт;
б) 157 Кбайт.

 ([2], стр. 76,
№2.83)

Решение:

а).
1) 940 Кбайт= 962560 байт = 7700480 бит
2) 7700480 бит : 10 сек = 770048 бит/с
3) 770048 бит/с : 16 бит = 48128 Гц –частота дискретизации – близка к самой
высокой 44,1 КГц
Ответ: качество аудио-CD

б).
1) 157 Кбайт= 160768 байт = 1286144 бит
2) 1286144 бит : 10 сек = 128614,4 бит/с
3) 128614,4 бит/с : 16 бит = 8038,4 Гц
Ответ: качество радиотрансляции

Ответ: а) качество CD; б) качество
радиотрансляции.

14.  Определите длительность
звукового файла, который уместится на гибкой дискете 3,5”.
Учтите, что для хранения данных на такой дискете выделяется 2847 секторов
объемом 512 байт.
а) при низком качестве звука: моно, 8 бит, 8 кГц;
б) при высоком качестве звука: стерео, 16 бит, 48 кГц.

 ([2],
стр. 77, №2.85)

Решение:

а).
1) Информационный объем дискеты равен:
2847 секторов х 512 байт = 1457664 байт = 1423,5 Кбайт
2) Информационный объем звукового файла длительностью в
1 секунду равен:
8 бит х 8 000 = 64 000 бит = 8000 байт = 7,8 Кбайт/с
3) Время звучания моноаудиофайла объемом 1423,5 Кбайт равно:
1423,5 Кбайт : 7,8 Кбайт/с = 182,5 с ≈ 3 мин

б).
1) Информационный объем дискеты  равен:
2847 секторов х 512 байт = 1457664 байт = 1423,5 Кбайт
2) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 48 000 х 2= 1 536 000 бит = 192 000 байт = 187,5 Кбайт/с
3) Время звучания стереоаудиофайла объемом 1423,5 Кбайт равно:
1423,5 Кбайт : 187,5 Кбайт/с = 7,6 с

Ответ: а) 3 минуты; б) 7,6
секунды.

3. Двоичное кодирование звука.

При решении задач пользуется следующим теоретическим
материалом:

Для того, чтобы кодировать звук,
аналоговый сигнал, изображенный на рисунке,

плоскость разбивается
на вертикальные и горизонтальные линии. Вертикальное разбиение –это
дискретизация  аналогового сигнала (частота измерения сигнала), горизонтальное
разбиение  – квантование по уровню. Т.е. чем мельче сетка – тем
качественнее приближен аналоговый звук с помощью цифр. Восьмибитное квантование
применяется для оцифровки обычной речи (телефонного разговора) и радиопередач
на коротких волнах. Шестнадцатибитное – для оцифровки музыки и УКВ
(ультро-коротко-волновые) радиопередач.

Уровень «3»

15.  Аналоговый звуковой
сигнал был дискретизирован сначала с использованием 256 уровней интенсивности
сигнала (качество звучания радиотрансляции), а затем с использованием 65536
уровней интенсивности сигнала (качество звучания аудио-CD). Во сколько раз
различаются информационные объемы оцифрованного звука?   ([2], стр. 77, №2.86)

Решение:

Длина
кода аналогового сигнала с использованием 256 уровней интенсивности сигнала
равна 8 битам, с использованием  65536 уровней
интенсивности сигнала равна 16 битам. Так как длина кода одного сигнала 
увеличилась вдвое, то информационные объемы оцифрованного звука  различаются в
2 раза.

Ответ: в
2 раза.

Уровень
«4»

16. Согласно
теореме Найквиста—Котельникова, для того чтобы аналоговый сигнал можно было
точно восстановить по его дискретному представлению (по его отсчетам), частота
дискретизации должна быть как минимум вдвое больше максимальной звуковой
частоты этого сигнала.

·        
Какова должна быть
частота дискретизации звука, воспринимаемого человеком?

·        
Что должно быть больше:
частота дискретизации речи или частота дискретизации звучания симфонического
оркестра?

 Цель: познакомить учащихся с
характеристиками аппаратных и программных средств работы со звуком. Виды
деятельности: привлечение знаний из курса физики (или работа со справочниками).  ([3], стр. ??, задача 2)

Решение:

Считается, что
диапазон частот, которые слышит человек, составляет от 20 Гц до 20 кГц. Таким
образом, по теореме Найквиста—Котельникова, для того чтобы аналоговый сигнал
можно было точно восстановить по его дискретному представлению (по его
отсчетам), частота дискретизации должна быть как минимум вдвое больше
максимальной звуковой частоты этого сигнала. Максимальная звуковая
частота которую слышит человек -20 КГц, значит, аппаратура и программные
средства должны обеспечивать частоту дискретизации не менее 40 кГц, а точнее
44,1 КГц. Компьютерная обработка звучания симфонического оркестра предполагает
более высокую частоту дискретизации, чем обработка речи, поскольку диапазон
частот в случае симфонического оркестра  значительно больше.

Ответ: не меньше 40 кГц, частота
дискретизации симфонического оркестра больше.

Уровень»5»

17. На
рисунке изображено зафиксированное самописцем звучание 1 секунды речи.
Закодируйте его в двоичном цифровом коде с частотой 10 Гц и длиной кода 3 бита.
 ([3], стр. ??, задача 1)

Решение:

Кодирование с частотой 10 Гц означает, что
мы должны измерить высоту звука 10 раз за секунду. Выберем равноотстоящие
моменты времени:

Длина кода в
3 бита означает 2³ = 8 уровней квантования. То есть в качестве
числового кода высоты звука в каждый выбранный момент времени мы можем задать
одну из следующих комбинаций: 000, 001, 010, 011, 100, 101, 110, 111. Их всего
8, следовательно, высоту звука можно измерять на 8 «уровнях»:

«Округлять» значения высоты звука будем до
ближайшего нижнего уровня:

Используя
данный способ кодирования, мы получим следующий результат (пробелы поставлены
для удобства восприятия): 100 100 000 011 111 010 011 100 010 110.

Примечание.
Целесообразно обратить внимание
учащихся на то, насколько неточно код передает изменение амплитуды. То есть
частота дискретизации 10 Гц и уровень квантования 2³ (3 бита)
слишком малы. Обычно для звука (голоса) выбирают частоту дискретизации 8 кГц,
т. е. 8000 раз в секунду, и уровень квантования 2⁸ (код длиной 8
бит).

Ответ: 100
100 000 011 111 010 011 100 010 110.

18. Объясните, почему уровень
квантования относится, наряду с частотой дискретизации, к основным
характеристикам представления звука в компьютере. Цели: закрепить
понимание учащимися понятий «точность представления данных», «погрешность
измерения», «погрешность представления»; повторить с учащимися двоичное
кодирование и длину кода. Вид деятельности: работа с определениями понятий.  ([3], стр. ??, задача 3)

Решение:

В геометрии, физике, технике есть понятие
«точность измерения», тесно связанное с понятием «погрешность измерения». Но
есть еще и понятие «точность представления». Например, про рост человека
можно сказать, что он: а) около. 2 м, б) чуть больше 1,7
м, в) равен 1 м 72 см, г) равен 1 м 71
см 8 мм. То есть для обозначения измеренного роста можно использовать 1, 2, 3
или 4 цифры.
Так же и для двоичного кодирования. Если для записи высоты звука в конкретный
момент времени использовать только 2 бита, то, даже если измерения были точны,
передать можно только 4 уровня: низкий (00), ниже среднего (01), выше среднего
(10), высокий (11). Если использовать 1 байт, то можно передать 256 уровней.
Чем выше уровень квантования, или, что то же самое, чем больше битов
отводится для записи измеренного значения, тем точнее передается это значение.

Примечание. Следует отметить, что измерительный инструмент
тоже должен поддерживать выбранный уровень квантования (длину, измеренную
линейкой с дециметровыми делениями, нет смысла представлять с точностью до
миллиметра).

Ответ: чем
выше уровень квантования тем точнее передается звук.

Литература:

[1] Информатика. Задачник-практикум в 2 т. /Под ред. И.Г. Семакина, Е.К.
Хеннера: Том 1. – Лаборатория Базовых Знаний, 1999
г. – 304 с.: ил.

 [2] Практикум по информатике и информационным технологиям. Учебное пособие
для общеобразовательных учреждений / Н.Д. Угринович, Л.Л. Босова, Н.И.
Михайлова. – М.: Бином. Лаборатория Знаний, 2002. 400 с.: ил.

 [3] Информатика в школе: Приложение к журналу «Информатика и образование».
№4 — 2003. — М.: Образование и Информатика, 2003. — 96 с.: ил.

[4] Кушниренко А.Г., Леонов А.Г., Эпиктетов М.Г. и др. Информационная
культура: одирование информации. Информационные модели. 9-10
класс: Учебник для общеобразовательных учебных заведений. — 2-е изд. — М.:
Дрофа, 1996. — 208 с.: ил.

[5] Гейн А.Г.,
Сенокосов А.И. Справочник по информатике для школьников. — Екатеринбург:
«У-Фактория», 2003. — 346. с54-56.  

Unit Converter

Enter the sampling period (seconds) into the Sampling Frequency Calculator. The calculator will evaluate the Sampling Frequency. 

• All Frequency Calculators
• Sampling Rate Calculator
• Sampling Error Calculator
• Frequency Factor Calculator

Sampling Frequency Formula

The following two example problems outline the steps and information needed to calculate the Sampling Frequency.

Variables:

• fs is the Sampling Frequency (hz)
• Ts is the sampling period (seconds) 

To calculate the sampling frequency, divide 1 by the sampling period.

How to Calculate Sampling Frequency?

The following steps outline how to calculate the Sampling Frequency.

---

1. First, determine the sampling period (seconds). 
2. Next, gather the formula from above = fs = 1/Ts.
3. Finally, calculate the Sampling Frequency.
4. After inserting the variables and calculating the result, check your answer with the calculator above.

---

Example Problem : 

Use the following variables as an example problem to test your knowledge.

sampling period (seconds) = 30

fs = 1/Ts = ?