Звук представляет собой волну с меняющейся интенсивностью и частотой (громкостью и его тональностью соответственно). Чем больше амплитуда, тем громче звук. Чем больше частота, тем больше тон.
Хранение и передача аналогового звукового сигнала осуществляется за счёт представления его в виде электрического сигнала с помощью модуляции.
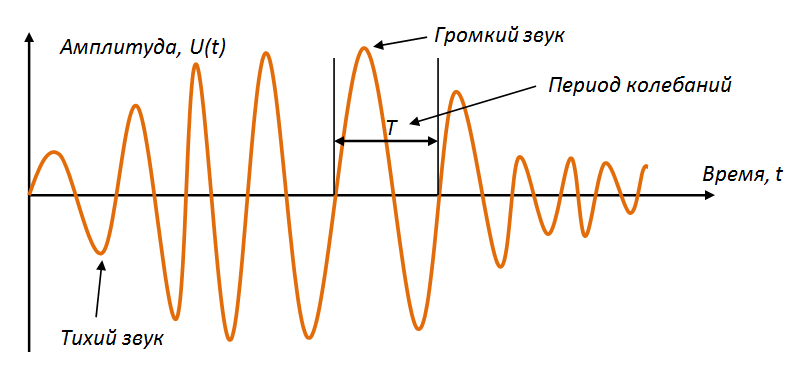
Модуляция – процесс изменения одного или нескольких параметров (амплитуды, частоты или фазы) высокочастотного колебания по закону низкочастотного сигнала (несущей частоты).
Существуют разные виды модуляции:
Амплитудная (АМ, amplitude modulation ) – изменение высокочастотных колебаний с частотой, равной частоте звукового сигнала. Например, несущей частотой может быть питание сети – 50 Гц. Или радиоволна СВ (MW) диапазона от 300 кГц до 3 МГц.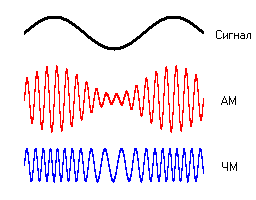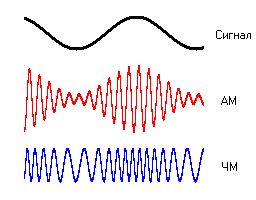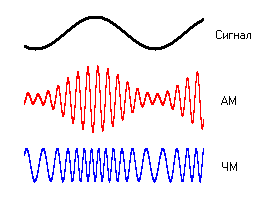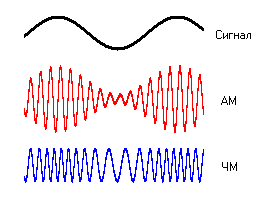
Частотная (FM, frequency modulation) – модуляция при которой информационный сигнал управляет несущей частотой. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.
Цифровой сигнал
Для того чтобы аналоговый (непрерывный) сигнал представить последовательностью чисел определённой разрядности, его необходимо превратить в дискретный (прерывистый) сигнал, а затем подвергнуть квантованию.
За кодирование звука отвечает звуковая карта, чем выше разрядность звуковой карты, тем больше уровней квантования она выдаёт и тем точнее становится звук при прослушивании.
На современном ПК карта всегда интегрирована в материнской плате, и имеет разрядность не ниже 24 бит.
Оцифровка звука – дискретизация и квантование аналогового сигнала.
1-й этап: Дискретизация сигнала по времени
Допустим, Вы, с помощью микрофона записали свой голос длительностью 5 сек. Этот фрагмент можно разбить на равные малые временный отрезки, которые в сумме дают нам 5 сек. Получаем частоту дискретизации (f, Гц), которая является обратной величиной времени: t сек. При частоте дискретизации 8 кГц=8 000 Гц, из формулы получаем отрезок, равный 0,000125 сек. или 125 миллисекунд.
2-й этап: Квантование сигнала по уровню
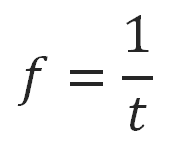2-й этап: Квантование сигнала по уровнюЧем больше уровней будет доступно для кодирования временных отрезков, тем ближе к аналогу будет закодированный файл, но при этом объём файла увеличится.
Например, возьмём 8 уровней, чтобы их закодировать в двоичный код нам достаточно 3 бита, что мы получаем из формулы Хартли:
2³=8 – комбинаций двоичного ряда чисел от 000 до 111.
Параметр (i) – называется глубина кодирования. 8 бит – 256 уровней, 16 бит – 65 536 уровней, 24 бита – более 16 млн. уровней.
3 этап: Определяем скорость потока звука
Частота дискретизации – 22 кГц, глубина кодирования – 16 бит. Произведение этих двух величин дает нам скорость потока 352 кбит/сек.
Именно такой канал передачи данных потребуется для воспроизведения звукового файла в режиме он-лайн.
Расчёт количество звуковой информации
Для определения информационного объёма звуковой информации, нам необходимы следующие параметры:
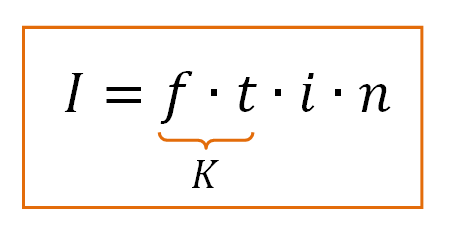
- f – частота дискретизации (Гц);
- t – время звучания звукового файла (сек.);
- i – глубина кодирования (бит);
- n – количество звуковых каналов (n = 1, моно; n = 2, стерео).
Задача 1:
Одна минута записи цифрового аудиофайла занимает 1,3 МБ, разрядность звуковой платы — 8 бит. С какой частотой дискретизации записан звук?
Решение:
Воспользуемся формулой: I=f∙t∙i∙n , из формулы видно что для нахождения частоты дискретизации формула примет вид: f=I/t∙i∙n.
1,3 МБ = 13,31,2 КБ = 1 363 148,8 Байт. Принимая во внимание что 8 бит = 1 Байту, делим 1 363 148,8 на 60, канал у нас записан 1, поэтому n=1.
Ответ: 22719,1 Гц или 22 050 Гц, см. основные настройки параметров звукового файла в программе Audacity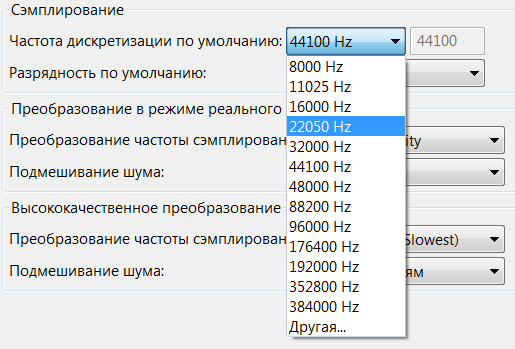 
Задача 2:
Две минуты записи цифрового аудиофайла занимают на диске 5,1 МБ. Частота дискретизации — 22 050 Гц. Какова разрядность аудиоадаптера?
Решение: 5,1 МБ = 5 347 737,6 Байт, делим по формуле: i = I / f∙ t ∙ n.
5 347 737,6 / 22 050 ∙ 120 = 2,02 Байт.
Ответ: 16 бит.
Кодирование видео
Информация хранится на различных носителях в виде файлов. Файл занимает память и может быть измерен в единицах измерения информации: бит, Байт, КБ и т.д.
Стремительное развитие интернета резко увеличило обмен информацией между людьми, для оптимизации хранения данных люди стали использовать специальные алгоритмы сжатия.
В основе цифрового видео лежит графический и звуковой файлы. Если рассчитать объём видеофайла без сжатия, нам необходимо учитывать тот факт, что человек начинает воспринимать смену кадров (картинок), как непрерывное плавное движение, если за 1 сек. будет мелькать 24 кадра.
Основы ТВ
Для приёма телевизионного сигнала используется антенна и приёмник. Приёмник – это электронная схема, которая преобразует сигнал в изображение на экране. В этом процессе участвует генератор кадровой развёртки и строчной.
Кадровая развёртка формируется на частоте, близкой к частоте переменного тока в бытовых электросетях – 50 Гц.
Кадровая развёртка, в сочетании со строчной служит для преобразования плоского двумерного изображения в одномерную последовательность, то есть, видеосигнал, а в телевизоре или мониторе компьютера для преобразования видеосигнала обратно в изображение на экране.
Для создания такой последовательности, используются специальные стандарты разложения:
576i, 625/50 — стандарт разложения, принятый для аналогового и цифрового телевидения в Европе, России, Австралии, странах Африки и Азии. 576 – это количество активных строк для аналогового телевидения и число пикселей по вертикали, для цифрового. Буква «i», англ. Interlace означает чересстрочную развёртку, передающую 25 целых кадров в 50 полях за 1 секунду.
480i, 525/60 — стандарт разложения, принятый в США, число активных строк составляет 480.
Существует также прогрессивная (p) кадровая развёртка, где все строки каждого кадра отображаются последовательно. Прогрессивная развертка стала широко распространена с появлением персональных компьютеров. Для комфортного чтения мелкого текста с экрана монитора, чересстрочная развертка стала малопригодна, так как мерцание строк вызывало быстрое утомление глаз.
Помимо развёртки существует ещё и соотношение сторон: аналоговое ТВ – 4:3, цифровое ТВ – 16:9, широкоформатное.
Форматы со сжатием
Давайте для начала посчитает объём видеофайла без сжатия, длительность 1 час 30 мин., 576i, 16:9. Звук записан с частотой дискретизации – 44 100 Гц, глубина кодирования 24 бит.
Решение:
Видео: I = 576 ∙ 1024 ∙ 25 ∙ 5400 ∙ 24 = 1 911 029 760 000 бит = 222,5 ГБ
Звук: I = 44 100 ∙ 5400 ∙ 24 = 5 715 360 000 бит = 681,3 МБ = 0,665 ГБ
Ответ: 223,2 ГБ.
Графический формат JPEG
Алгоритм JPEG (от англ. Joint Photographic Experts Group) в большей степени пригоден для реалистичных изображений с плавными переходами яркости и цвета, таковыми являются фотографии.
В основу алгоритма заложен переход от цветового пространства RGB к цветовому пространству YCbCr. Y – компонент яркости, Cb и Cr – синий и красный цветоразностные компоненты. Суть сжатия состоит в том что для каждого блока пикселей 2х2 записывается не 12 значений, а 6, за счёт использования усреднённого компонента цвета.
Видео и аудио форматы MPEG
Алгоритм MPEG (англ. Moving Picture Experts Group) – стандарты сжатия и передачи цифровой видео и аудио информации. Базовым объектом кодирования в стандарте MPEG является кадр телевизионного изображения. Поскольку в большинстве фрагментов фон изображения остается достаточно стабильным, а действие происходит только на переднем плане, сжатие начинается с создания исходного кадра.
При сжатии аудио используются хорошо разработанные психоакустические модели, чтобы выбросить звуки, которые не слышны человеческому уху.
Современные цифровые стандарты
Современные дисплеи и мониторы уже давно вышли за рамки старых добрых стандартов.
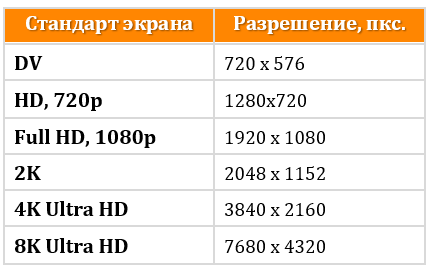
Стандарты современных дисплеев:
Часто производители аудио аппаратуры, особенно наушников, в процессе пиара своей продукции активно продвигают “кристальную чистоту” звука и широчайший частотный диапазон, который не только за 20 кГц переваливает, но и в некоторых случаях доходит даже до 100 кГц. Конечно это имеет свои плюсы, даже не смотря на то, что выше 20к Гц мы не слышим, а то и еще меньше. Но есть определенные проблемы, которые связанны с понятием частота дискретизации и вытекающие из теоремы Котельникова. Они в одночасье поставили жирный крест на применении слова “качественно” для большинства аудио-форматов и аудио устройств в моих глазах.
Любой процесс в природе является непрерывным. Например звуковой сигнал принятый микрофоном и преобразованный в электрический (аналоговый) сигнал — непрерывен.
Термин “Аналоговый сигнал” подчеркивает, что такой сигнал “аналогичен”, т.е. полностью подобен порождающему его процессу, или в данном случае звуку.
И непрерывный он не потому что будет длиться вечно, а потому, что его значение можно измерять в любые моменты времени. А между этими моментами сигнал будет продолжать непрерывно меняться.
Для лучшего понимания того, как устроен цифровой звук, советую посмотреть мой видос:
Содержание статьи
- Что такое частота дискретизации?
- Какая частота дискретизации считается достаточной?
- Вроде все нормально, так чего же тут не так?
- — А что же будет, если взять другие частоты???
- Частота дискретизации и Hi-Res звук
- В заключение
Что такое частота дискретизации?
Как только встает вопрос о переводе аналогового сигнала в цифровой, сразу возникает понятие дискретизации, т.е. разбиение непрерывного сигнала на кусочки по времени. Делается это непосредственно в процессе преобразования.
Через равные промежутки времени, называемые шагом дискретизации Δ, Аналогово-Цифровой-Преобразователь (АЦП) измеряет значение сигнала, поступающего на его вход и преобразует это значение в цифровой вид. То, как часто осуществляется измерение величины аналогово сигнала и называется частотой дискретизации.
Какая частота дискретизации считается достаточной?
Товарищ Котельников, еще в 1933 в работе «О пропускной способности эфира и проволоки в электросвязи» создал фундаментальную, для цифровой техники теорию, которая обычно формулируется следующим образом:
Любой непрерывный сигнал u(t) с конечным спектром (имеющим максимальное значение частоты F) можно представить в виде дискретных отсчетов u(kΔt), частота дискретизации которых должна быть выбрана не менее чем в два раза выше максимального значения спектра сигнала: f ≥ 2F, передать его по линии связи, а затем восстановить исходный аналоговый сигнал.
Говоря проще, для того чтобы можно было правильно воспроизвести (восстановить) аналоговый сигнал из цифрового вида, достаточно, чтобы частота дискретизации была вдвое выше максимальной частоты в сигнале.
Верхний порог слышимости человека принято ограничивать частотой в 20кГц. Из теоремы Котельникова следует, что для правильного воспроизведения сигнала частотой 20 кГц достаточно частоты дискретизации в 40кГц. Если заглянуть в свойства подавляющего большинства аудио файлов, то можно увидеть строчку:
Почему именно 44.1 кГц? Википедия отвечает так: “Эта цифра выбрана компанией Sony из соображений совместимости со стандартом телевещания PAL, за счёт записи 3 значений на линию картинки кадра x588 линий на кадр x25 кадров в секунду, и достаточности (по теореме Котельникова) для качественного покрытия всего диапазона частот, различаемых человеком на слух (20 Гц — 20 кГц).”
При частоте дискретизации в 44.1 кГц шаг дискретизации Δ составляет всего 0.00002267=22.67*10-6 секунды или 22.67 микросекунды. Это время между двумя точками сигнала.
Вроде все нормально, так чего же тут не так?
Начнем с частот, кратных частоте дискретизации. На частоте 441 Герц при нашей частоте дискретизации (44.1 кГц), на один период приходится 100 точек. Чтож, тут нет никаких претензий, синусоида идеальная. Если же повысить частоту на порядок, т.е. в 10 раз, то эти же 100 точек будут формировать уже не 1, а 10 периодов. И даже в этом случае Будет формироваться сигнал очень похожий на синусоиду.
А вот на частоте 22050, т.е. наивысшей частоте, удовлетворяющей теореме Котельникова (при частоте дискретизации 44.1кГц) на 100 точек приходится 50 периодов колебаний.
Эти сигналы генерировались в программе Audacity. И по началу создалось впечатление, что точек там достаточно, просто масштаб не позволяет разглядеть и поэтому так все угловато…
Читайте также:
Простой способ генерации сигналов разной формы в аудио редакторе Audacity
Чтож… приблизим и рассмотрим каждый период по отдельности:
Частота в 4410 Гц вполне себе достойная синусоида, чего никак не скажешь о частоте 22050Гц, с ее двумя точками на период. По факту это уже и не синусоида, а сигнал треугольной формы.
Конечно в любом реальном ЦАПе на выходе применяется НЧ-фильт, который срезает высокочастотную составляющую и скругляет этот треугольник. Однако чем выше класс вашего аудио устройства, тем заметнее будет угловатость звука
Ради эксперимента можете попробовать сгенерировать в Audcity сигналы одной и той же частоты но разных форм. У треугольной и прямоугольной форм из-за их “угловатости” и резких фронтов возникают дополнительные гармоники, а вот синусоидальный сигнал звучит гораздо более мягко и естественно.
Но даже и это не самое страшное. До этого момента рассматривались сигналы с частотами кратными частоте дискретизации.
— А что же будет, если взять другие частоты???
Знакомьтесь, цифровая синусоида равной амплитуды и частотой 15 кГц. Красивый узорчик, не правда ли? Как видите амплитуда меняется с частотой. Это уже интермодуляционные искажения. Наш истинный сигнал в 15 кГц промодулирован частотой кратной 44.1 кГц.
Вы можете возразить, мол узорчик то красивый, но может звучит он как ему и положено. Для того чтобы убедиться в этом своими ушами — сгенерируйте сигнал частота которого меняется от 20 герц до 20 кГц. И вы отчетливо услышите, что с какого-то момента частота перестанет равномерно расти, а начнет плавать туда-сюда.
Оно и понятно, вот так выглядят синусоиды на разных частотах выше 10’000Гц
В защиту теоремы Котельникова стоит отметить, что да, его теорема верна, иначе бы мы не смогли различать в музыке высокие звуки, и что тарелка что маракас звучали бы одинаково неправдоподобно, но она абсолютно не гарантирует высокого качества записи.
В жизни Вы врядли станете наслаждаться звучанием синусоиды, но это был очень наглядный пример проблем качества цифровых аудио записей.
Частота дискретизации и Hi-Res звук
Конечно сегодняшние технологии уже побороли данную проблему. Вероятно вам встречалось сокращение Hi-Res (High Resolution — высокое разрешение), которым обычно обзывают качество звука в 24 бита и частотой дискретизации в 192 кГц.
А это уже 10 точек на частоте 22’050 кГц, такую синусоиду уже явно можно считать идеальной. И вот там «кристально чистые верха» ваших наушников себя точно оправдают.
Возникает только 3 проблемы:
- Стоимость подобных устройств. Например портативный плеер с такой частотой дискретизации обычно стоит около 200$.
- Где брать записи в таком качестве.
- Размеры аудиофайлов очень велики. 1 альбом вашей любимой группы в Hi-Res легко может занимать более 1,5Гб дискового пространства.
В заключение
Конечно от плохого звучания высоких частот еще никто не умирал и, возможно я излишне драматизирую, говоря, что частота дискретизации в 44.1 кГц так уж плоха, однако, как видите особым качеством на высоких частотах она не блещет.
На мой взгляд в домашних условиях гораздо интереснее слушать винил. Но с виниловой вертушкой в метро не поездишь… Так что меломанские запросы придется удовлетворять цифровым плеером.
Всем качественного звука!
(P.S. — комментируем, не стесняемся 🙂
16
|
0.475 0.47 |
|||||||||||||||||
|
0.44 |
|||||||||||||||||
|
0.4 |
|||||||||||||||||
|
0.36 |
|||||||||||||||||
|
0.32 |
|||||||||||||||||
|
ε (N) |
0.28 |
||||||||||||||||
|
0.24 |
|||||||||||||||||
|
0.2 |
|||||||||||||||||
|
0.16 |
|||||||||||||||||
|
0.12 |
|||||||||||||||||
|
0.0830.083 1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
33 |
|
1 |
N |
33 |
||||||||||
|
а) |
||||||||||||
|
1.151 |
1.5 |
|||||||||||
|
1.3 |
||||||||||||
|
1.1 |
||||||||||||
|
0.9 |
||||||||||||
|
0.7 |
||||||||||||
|
x(l, N) 0.5 |
||||||||||||
|
0.3 |
||||||||||||
|
0.1 |
||||||||||||
|
0.1 |
||||||||||||
|
0.3 |
||||||||||||
|
− 0.132 |
0.5 |
0 |
25 |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
225 |
250 |
|
0 |
б) |
l |
235 |
|||||||||
|
Рис. 1.9. Графики зависимости погрешности дискретизации (а) |
ивосстановленного сигнала (б) для прямоугольного импульса
Осуществляется дискретизация с помощью специальных устройств,
называемых устройствами или схемами выборки – хранения (УВХ, СВХ).
Простейшая их схема (рис. 1.10, а) содержит ключ и запоминающий конденсатор (аналоговая память). Замкнутому состоянию ключа соответствует время выборки УВХ (tв), разомкнутому – время хранения (tхр). На графике выходного сигнала идеального УВХ x!(t) (рис. 1.10, б) время
выборки стремится к нулю, а время хранения равно периоду дискретизации. Математически такое УВХ эквивалентно фильтру-интерполятору нулевого порядка. Практически время хранения должно быть не менее
17
времени преобразования tпр АЦП: tхр ≥ tпр, при этом время выборки может быть увеличено до tв= Тд − tхр (рис.1.10, в).
|
x(t) |
x(nTд) |
x(t) |
|
|
x(nTд) |
x(t) |
||
|
fд |
x(t) |
||
|
Tд |
|||
|
t |
|||
|
а) |
||||||||
|
0 1 |
tпр |
nTд |
||||||
|
б) |
||||||||
x(t)
x(nTд)
x(t)
nTд
|
0 |
Tд |
2Tд |
3Tд |
n |
||||||||||
|
в) |
||||||||||||||
|
tхр=tпр |
tв |
|||||||||||||
Рис. 1.10. Простейшая схема УВХ (а) и ее идеализированные сигналы (б, в)
Реальные УВХ характеризуются также погрешностью, вызываемой разрядом конденсатора С (погрешностью хранения), которая не должна выходить за пределы единицы младшего разряда АЦП, и апертурным временем tа, отражающим неопределенность моментов времени nTд перехода схемы из режима выборки в режим хранения.
Апертурная погрешность ∆ ха, вносимая УВХ, определяется его апертурным временем tа и скоростью изменения сигнала в моменты времени nTд: ∆ ха = х’(t)tа. Она имеет случайную составляющую, обусловленную флуктуациями апертурного времени, и систематическую. Влияние случайной составляющей эквивалентно наложению на сигнал некоторого шума (шума апертуры), а систематической – влиянию некоторого эквивалентного фильтра, искажающего спектр дискретного сигнала. Спектр реального дискретного сигнала (рис. 1.11) равен периодическому по частоте
18
незатухающему спектру Хд(jω ) его математической модели хд(t) (или x(n)), умноженному на частотную характеристику эквивалентного фильтра На(jω ), зависящую от значения апертурного времени tа. В первом приближении ее отождествляют со спектром прямоугольного импульса длительностью tа:
На(jω ) = e-jω tа/2[sin(ω tа/2)/(ω tа/2)]. Первый нуль этой характеристики имеет частоту ω 1=2π /tа. Если время tа достаточно мало, то искажение спектра
|
дискретного |
сигнала |
в |
основной |
полосе |
частот ± ω д/2 |
|
практически несущественно. |
|Ha(jω |
)| |
|||
|
|X(jω |
)| |
|
–ω д -ω д/2 0 |
ω д/2 ω д |
2ω д |
|
Основная полоса |
Рис. 1.11. Апертурное искажение спектра дискретного сигнала
При использовании быстродействующего АЦП без УВХ, что возможно, если изменения сигнала за время преобразования АЦП не превосходят по значению единицы младшего разряда, время преобразования одновременно определяет и апертурное время АЦП.
Таким образом, общая погрешность, возникающая при дискретизации сигнала, складывается из методической погрешности, вызываемой наложением спектров, и инструментальной, вносимой УВХ и АЦП.
Влияние ВЧ-составляющих в спектре дискретизируемого сигнала эффективно уменьшается с помощью специальных УВХ усредняющего
(интегрирующего) типа [4, 5, 6].
Инструментальные погрешности и характеристики современных интегральных УВХ и АЦП рассмотрены в [7, 8, 9].
19
1.7. УСЛОВИЯ ВЫБОРА ЧАСТОТЫ ДИСКРЕТИЗАЦИИ
Частота дискретизации определяет скорость обработки сигнала и требуемое быстродействие АЦП и процессора ЦОС. Поэтому в каждом случае стремятся к ее минимально возможному значению, учитывающему особенности дискретизируемого сигнала и цели его обработки. Сложность выбора частоты дискретизации в соответствии с общим условием fд ≥ 2fm связана с неопределенностью или условностью верхней границы спектра реальных аналоговых сигналов fm .
Возможны случаи дискретизации с ограничением или без ограничения частотного спектра сигнала с помощью аналогового ФНЧ.
Без предварительного ограничения могут быть дискретизированы так называемые чистые или сильные сигналы с естественно убывающим по частоте спектром. При выборе частоты дискретизации таких сигналов исходят либо из максимальной частоты спектра fm (fд = 2fm), при которой искажения наложения интегрально не превышают допустимое значение во всей полосе частот ± fд/2 дискретного сигнала, либо из частоты спектра
сигнала fm/ (fд = 2α fm/ ), определяющей его полезную или информативную полосу (0− fm/ ), переносимую в основную полосу частот дискретного сигнала
|
с |
допустимой погрешностью наложения, оцениваемой в полосе частот |
|
(0− |
fm/ ) дискретного сигнала. Коэффициент α характеризует избыток |
дискретизации, обусловленный неограниченностью спектра преобразуемого сигнала.
Если же уровень не учитываемых в случае сильного сигнала шумов и помех с полосой, перекрывающей спектр полезного выделяемого сигнала, достаточно велик, то дискретизация без предварительного ограничения спектра с частотой, выбранной для чистого сигнала, приведет к
увеличению спектральной плотности мощности шума и помех в основной полосе частот дискретного сигнала ± fд/2 (включая и полосу
(0− fm/ ) из-за многократной трансформации в эту полосу их высокочастотных
составляющих, превышающих частоту Найквиста fд/2. Кратность трансформации или наложения при этом равна отношению максимальной частоты спектра шума и помех к половине принятой частоты дискретизации сигнала.
В данном случае, как и в случае дискретизации чистого сигнала с
|
выделяемой |
полезной |
полосой |
спектра |
(0− fm/ ), |
целесообразно |
||
|
предварительное |
ограничение |
спектра |
аналогового |
сигнала |
противомаскировочным ФНЧ с частотой среза fс= fm/ . При дискретизации
чистого сигнала это приводит к снижению необходимого коэффициента α , т. е. избытка дискретизации, а при дискретизации сигнала с наложенным на него шумом и помехами обеспечивает уменьшение их спектральной
кор.min
20
плотности мощности и снижение искажений в полезной полосе частот (0− fm/ ) или (0− fс) дискретного сигнала. Степень уменьшения при этом такая
же, как и увеличения при дискретизации без ограничения спектра.
Частота дискретизации при ограничении спектра аналогового сигнала определяется соотношением fд = 2α fm/ , где частота fm/ отождествляется
здесь с частотой среза аналогового ФНЧ fс. Коэффициент α зависит от наклона АЧХ фильтра и затухания ее в полосе задерживания, которые связаны, в свою очередь, с погрешностью дискретизации сигнала в полосе
(0− fm/ ). В [36] приведены значения наклонов АЧХ аналогового ФНЧ,
необходимые для ослабления эффекта наложения на 70 дБ для некоторых отношений частоты дискретизации к частоте среза фильтра, соответствующих удвоенным значениям коэффициента α . Для fд/fс = 3,75; 2,65 и 2,5 наклон равен соответственно –48; − 96 и − 120 дБ/октаву. При fд/fс = 2 он должен быть бесконечен.
Эти данные говорят о достаточно высоких требованиях к аналоговому ФНЧ и сложности его реализации. Поэтому в современных высококачественных цифровых системах, например, звуковых или музыкальных, сигнал после предварительного ограничения по полосе простым аналоговым фильтром дискретизируется с высокой частотой дискретизации и обрабатывается цифровым фильтром с крутыми срезами АЧХ, которым и осуществляется основное ограничение его частотного спектра. Для снижения скорости последующей обработки частота дискретизации выходного сигнала цифрового фильтра понижается путем прореживания сигнала по времени и приводится в соответствие с ограниченной полосой его спектра [38, 44].
Следует отметить, что понижение частоты дискретизации цифрового сигнала и уменьшение периода повторения его спектра создает дополнительные искажения наложения, зависящие от затухания АЧХ в полосе задерживания фильтра. Увеличивая затухание фильтра, можно сделать уровень этих искажений сколь угодно малым [11, 40].
Для видов обработки, предусматривающих восстановление сигнала с
целью, например, его аналоговой записи, контроля или акустического воспроизведения, при выборе частоты дискретизации в односкоростной системе нужно учитывать также проблему обеспечения требуемой точности восстановления сигнала. Она зависит от соотношения частоты его
дискретизации к частоте fm/ , ограничивающей полезную полосу частот
восстанавливаемого сигнала. Этим соотношением определяются требования к сглаживающему аналоговому ФНЧ на выходе ЦАП, которые аналогичны требованиям к противомаскировочному аналоговому фильтру на входе АЦП.
При дискретизации случайных сигналов выбор частоты дискретизации возможен также по минимальному времени корреляции случайного сигнала с ограниченным по частоте спектром: fд ≥ 2α /τ .
|
21 |
||||||||
|
Наибольшие особенности выбора частоты дискретизации связаны с |
||||||||
|
цифровой обработкой широко используемых в радиотехнике и других |
||||||||
|
областях узкополосных (модулированных) сигналов. Такие сигналы |
||||||||
|
характеризуются малым отношением информационной полосы спектра 2Fm к |
||||||||
|
центральной частоте fo. Цель их обработки состоит в выделении медленно |
||||||||
|
изменяющейся огибающей сигнала и извлечении заключенной в ней |
||||||||
|
информации, т. е. в демодуляции сигнала. Поэтому дискретизация таких |
||||||||
|
сигналов возможна с частотой fд << 2(fo+Fm) – намного меньшей удвоенной |
||||||||
|
максимальной частоты их спектра. Ее называют также субдискретизацией |
||||||||
|
сигнала [1, 4]. Она осуществляется за счет преобразования спектра сигнала |
||||||||
|
на высших гармониках частоты дискретизации kfд и обусловленного им |
||||||||
|
переноса информационных спектральных полос шириной 2Fm в |
||||||||
|
низкочастотную основную полосу ± fд/2 дискретного сигнала. Частота |
||||||||
|
дискретизации при этом выбирается так, чтобы периодизация и размножение |
||||||||
|
спектра узкополосного сигнала, порождаемые дискретизацией, не привели к |
||||||||
|
взаимному перекрытию и наложению его выделяемых информационных |
||||||||
|
полос. |
||||||||
|
Минимальная частота дискретизации узкополосных сигналов может |
||||||||
|
иметь значение fдmin = 4Fm при обработке вещественных сигналов и fдmin = 2Fm |
||||||||
|
− при квадратурной обработке комплексных сигналов. |
Например, |
условие |
||||||
|
fдmin = 4Fm выполняется, если нижняя и верхняя граничные частоты спектра |
||||||||
|
сигнала fн, fв находятся в соотношении |
||||||||
|
fн = 2iFm, fo = fн+Fm, |
fв = fн+2Fm, |
где i = 0, 1, 2, … |
– целые числа (рис. 1.12). |
|||||
|
X а ( jω |
) |
|||||||
|
2 Fm |
||||||||
|
− f0 |
ω |
) |
fВ f0 fH |
f |
||||
|
X Д ( j |
||||||||
|
− 2 f Д |
− |
f Д − |
f Д |
f Д |
f Д |
2 f Д |
f |
|
|
2 |
0 |
|||||||
|
2 |
||||||||
|
Рис.1.12. Преобразование спектра узкополосного сигнала |
||||||||
|
в случае fд = 4Fm, fo = (2i+1)Fm |
22
При нечетном i имеет место так называемая инверсия спектра огибающей. Для исключения ее нужно сместить спектр цифрового сигнала по частоте на fд/2, что реализуется достаточно простой операцией y(n) =
( − 1)n x( n ) [11, 40 ].
Восстановление узкополосного сигнала по его дискретным выборкам возможно с помощью интерполяционного ряда Котельникова, обобщенного на узкополосные сигналы [1]. В данном случае он определяется выражением
[6]:
|
∞ |
sin [2π Fm( t − nTд )] |
|||
|
x(t) = ∑ x (nTд) |
cos 2π fo ( t − |
nTд ) . |
||
|
2π Fm( t − |
nTд ) |
|||
|
n = −∞ |
Так как реально ограничение спектра узкополосного сигнала осуществляется полосовым фильтром, имеющим конечную переходную полосу ∆ fз, дискретизация с минимальной частотой fд min сопровождается искажениями наложения. Как и для рассмотренных выше сигналов со спектром, примыкающим к нулевой частоте, уменьшить искажения можно
|
повысив частоту дискретизации до значения fд = 4α Fm = 4 F/ |
, где F/ = Fm + |
|||||||||||||||
|
m |
m |
|||||||||||||||
|
∆ fз, α = 1+∆ |
fз/Fm. При этом нижняя и верхняя условные граничные частоты |
|||||||||||||||
|
спектра |
f / |
= |
f |
0 |
− F |
− Äf , |
f / |
= |
f |
0 |
+ |
F |
+ |
Äf |
должны также отвечать |
|
|
Н |
m |
З |
В |
m |
З |
|||||||||||
|
приведенным выше условиям: |
f / |
= |
2iF / |
; |
f / |
= 2(i + 1)F / . |
||||||||||
|
Н |
m |
В |
m |
|||||||||||||
|
Введение |
варьируемых |
защитных |
полос ∆ fз, |
разделяющих |
информационные полосы 2Fm в спектре дискретного сигнала, позволяет при заданном уровне искажений наложения найти минимально необходимое (оптимальное) значение частоты дискретизации для произвольных граничных частот fн, fв полосового сигнала [6 ].
Субдискретизация снижает необходимое быстродействие АЦП, но предъявляет высокие требования к апертурному времени УВХ, так как апертурная погрешность в данном случае обратно пропорциональна мгновенной скорости быстроизменяющегося высокочастотного сигнала. При дискретизации узкополосных сигналов применяют также УВХ интегрирующего типа.
Таким образом, используя субдискретизацию, можно выполнить цифровую обработку непосредственно на несущей или промежуточной частоте сигнала. Более подробно вопросы цифровой обработки узкополосных сигналов являются предметом изучения специальных дисциплин, например «Устройства приема и обработки сигналов». Достаточно полно они освещены также в [4, 6, 37].
К субдискретизации относится также когерентное стробоскопическое преобразование периодических высокочастотных или быстроизменяющихся сигналов, обеспечивающее трансформацию их спектра в область низких частот, где эффективно используются методы и
Соседние файлы в предмете Электроника
- #
13.09.201320.9 Mб12Бараночников М.Л. Микромагнитоэлектроника. Т.2. – М., ДМК Пр.pdf
- #
- #
- #
13.09.20137.25 Mб20Вишневский В.М. и др. – Широкополосные беспроводные сети пер.djv
- #
13.09.201317.1 Mб26Герасимов В.Г. (ред). – Электрические измерения и основы эле.pdf
- #
- #
- #
13.09.20134.01 Mб25Долуханов М.П. – Распространение радиоволн (1972).djvu
- #
- #
- #
Основы цифровой обработки сигналов: Теорема Котельникова, АЦП и ЦАП, Шум как случайный процесс
Рассмотрены 3 темы по основам цифровой обработки сигналов: Теорема Котельникова, АЦП и ЦАП, Шум как случайный процесс.
В данном посте освещены 3 темы по основам цифровой обработки сигналов:
- Теорема Котельникова,
- АЦП и ЦАП,
- Шум как случайный процесс.
Теорема Котельникова
В этой публикации мы поговорим об основном ограничении при дискретизации аналогового сигнала, описываемого теоремой Котельникова. Это ограничение тесно связано с понятием частоты периодического дискретного сигнала. Мы помним то, что чистота – это величина обратная периоду, и она может измеряться либо в секундах либо в отсчётах в зависимости от того, говорим о непрерывном сигнале или о дискретном сигнале. Частота может измеряться в радианах в единицу времени или циклах в единицу времени.
Важно отметить то, что цикл для непрерывного сигнала может быть равен 2・π радиан, а цикл для дискретного сигнала может быть равен 2・π・m радиан, где m – это целое число. Это приводит нас к понятию неоднозначности определения частоты дискретного сигнала. Не будем углубляться в формулы, давайте посмотрим на конкретном примере.
Мы говорим о том, что для непрерывных сигналов 2 синусоиды с разными частотами не равны друг другу, но случай двух дискретных синусоид, если частота одной отличается от другой на m・2・π мы не сможем их различить. Я поясню это на простом примере. Представьте себе обыкновенные часы. Мы явно видим минутную стрелку и часовую стрелку, потому что это непрерывно изменяющиеся величины. Но, если мы будем фотографировать эти часы в моменты времени, когда минутная стрелка накладывается на часовую стрелку, мы не увидим часовой стрелки. Фактически происходит наложение одного дискретного сигнала на другой дискретный сигнал. Тоже самое происходит при дискретизации 2 аналоговых сигналов.
Рассмотрим пример 2 синусоид. Одна синусоид изменяется медленно, другая синусоида изменяется быстро. Мы берём дискретные отсчеты этих синусоид в моменты времени 1, 2, 3, 4 и так далее, и мы можем наблюдать то, что форма 2 дискретных сигналов абсолютно одинакова.
Произошел эффект алиасинга или наложение двух сигналов при дискретизации. Слово “алиасинг” происходит от английского слова alias или псевдоним. В данном случае фактически один сигнал маскируется другим сигналом. Запомним то, что алиасинг – это эффект неразличимости сигналов при их дискретизации, и, конечно же, нам его надо избегать.
Как вы уже поняли из представленных графиков, выбранной частоты дискретизации хватает для того, чтобы описать в дискретном виде медленно изменяющуюся синусоиду, но явно не хватает, чтобы описать быстро изменяющуюся. Мы приходим к определению основного ограничения при дискретизации сигналов.
Теорема Котельникова гласит о том, что непрерывный сигнал с ограниченным спектром можно точно восстановить по его дискретным отсчётам, если они были взяты с частотой дискретизации, превышающего максимальную частоту сигнала минимум в два раза. В виде формулы это можно описать так:
В том случае, если это условие не выполняется, мы берём дискретные отсчеты слишком редко, мы не знаем, как меняется сигнал в промежутках между дискретами и конечно же теряем информацию. В том случае, если условие выполняется, между отдельными дискретными отсчётами сигнал меняется относительно медленно, и поэтому восстановление исходной формы аналогового сигнала возможно.
Давайте посмотрим на эффект алиасинга или наложения при невыполнении условий теоремы Котельникова в MATLAB. Создадим три синусоиды с частотами 250, 500 и 750 Гц. Частота дискретизации 2000 Гц.
В данном случае условия теоремы Котельникова выполняется для всех трёх синусоид. Давайте попробуем послушать, как они звучат. Мы услышали три нарастающих тона, и на графике также наблюдаем тремя цветами три различных сигнала.
Ну что будет, если мы поменяем частоту дискретизации на значение 1000 Гц. Для первого сигнала 250 Гц оно выполняется, для второго сигнала оно выполняется вплотную, и для третьего сигнала оно не выполняется. Давайте теперь послушаем и посмотрим на эти сигналы.
Мы услышали третий сигнал как будто его частота также 250 Гц, и на графике мы наблюдаем только два сигнала. В данном случае наш третий сигнал 750 Гц из-за несоблюдения условий теоремы Котельникова наложился на первый сигнал.
Для того, чтобы теорема Котельникова соблюдалась всегда, достаточно постоянно брать очень большое значение частоты дискретизации. Насколько это удачное решение? На самом деле не очень, потому что мы работаем с системами передачи данных, системами хранения данных, и, если мы медленно изменяющийся сигнал будем оцифровывать с огромной частотой дискретизации, то объемы данных, которые мы должны пропускать, обрабатывать и хранить будут сильно превышать требуемые, что конечно же будет требовать больших вычислительных ресурсов и памяти для хранения. Впрочем, принцип работы некоторых устройств как раз основан на выборе завышенных значений частоты дискретизации. Одно из них это сигма-дельта АЦП, аналого-цифровой преобразователь. О аналого-цифровых, цифро-аналоговых преобразователях наша следующая публикация.
Наверх
АЦП (аналого-цифровые преобразователи) и ЦАП (цифро-аналоговые преобразователи)
В этой публикации мы кратко поговорим об аналого-цифровых и цифро-аналоговых преобразователях.
Аналого-цифровой преобразователь или АЦП – это устройство, преобразующее входной аналоговый сигнал в дискретный цифровой код. Как вы уже поняли, АЦП осуществляет операции дискретизации и квантования. Напомним, при дискретизации отсчёты непрерывного сигнала берутся только в определённые моменты или дискреты времени, а при квантовании – значение сигнала в эти моменты времени округляется до одного из фиксированных уровней.
Квантованные уровни затем представляются в двоичном виде. Таким образом мы получаем цифровой сигнал из аналогового.
Но как же устроен АЦП. Боюсь, что у нас не хватит времени подробно говорить об устройстве аналого-цифровых преобразователей с точки зрения схемотехники, но ключевые узлы и базовые принципы постараемся очертить. В большинстве АЦП есть устройство выборки и хранения, которые фиксируют и сохраняют значение напряжения на своём ходе в моменты замыкания ключа. Моменты замыкания ключа определяется задающим генератором. Именно его частота и определяет частоту дискретизации выходного сигнала. Сигнал на выходе устройства выборки и хранения затем округляется до одного из уровней квантования.
Как же АЦП понимает с каким уровнем квантования проассоциировать значение сигнала. Рассмотрим простейший одноразрядный АЦП компаратор. Он принимает на свой ход два значения напряжения. В том случае, если напряжение на первом входе больше, чем на втором, он выдаёт логическую единицу, в противном случае – ноль. Допустим, мы зафиксировали значение на втором входе, это наш пороговый уровень, и, когда изменяющийся во времени сигнал на вервом входе больше этого уровня, устройство показывает единицу, когда меньше – ноль. Теперь представим, что компараторов несколько. Когда входной сигнал превышает определенный уровень, срабатывает соответствующий компарато. Выходы всех компараторов затем преобразуются схемой приоритетного кодера в двоичное представление, АЦП в которых в каждом из уровней квантования соответствует компаратор, называется АЦП прямого преобразования или флеш АЦП. Это один из типов преобразователей, но схем и типов АЦП так много, что для их описания потребуется отдельная публикация.
Давайте лучше поговорим об основных характеристиках АЦП.
- АЦП отличается по частоте дискретизации. Она, как я уже упоминал, определяется задающим генератором. В зависимости от назначения частота дискретизации может измеряться в кГц, МГц и даже ГГц.
- Далее идет разрядность, те количество бит в коде, который мы представляем отсчеты сигнала. От количества бит зависит количество уровней квантования, оно определяется как 2 в степени кол-во бит. Если у нас 3 бита, то это 8 возможных уровней квантования, если у нас 8 бит – это 256 уровней.
- Диапазон входного сигнала – это минимальное и максимальное значение напряжения на входе АЦП, при которых устройство работает корректно. Слишком маленькие сигналы АЦП может не различить и принять за нулевой уровень, слишком большие могут вызвать искажения, которые приведут к потере информации. Обычно АЦП оперируют единицами Вольт.
- Отношение сигнал/шум SNR (об этом параметре мы подробнее поговорим в дальнейших публикациях).
- Передаточная характеристика – это по определению зависимость числового эквивалента выходного кода от величины входного аналогового сигнала. Она имеет вид ступенчатой функции. Посмотрим на рисунок.
Окрестность значения входного напряжения 0,5 Вольт будет приравнена к четвертому уровню квантования. То есть значение к примеру 0,52 или 0,47 также будут представлены кодом 100.
Если мы рассматриваем АЦП с равномерным квантованием, то длина всех ступеней будет одинаковой, в некоторых АЦП специально используется неравномерное квантование, но их мы пока не рассматриваем.
Неравномерность ступенек в АЦП с равномерным квантованием – это одна из характеристик неидеальности. Мы называем её нелинейностью. Нелинейность АЦП – это отличие реальной передаточной характеристике от линейной.
Давайте вспомним, чем линейные системы отличаются от нелинейных. Линейная система передаёт входной сигнал на выход без изменения его формы, возможно усиление или аттенюация. Нелинейная система искажает формы выходного сигнала. В том случае, когда характеристика отличается от прямой линии, формы пиков сигнала изменяется, это называется нелинейным искажением, крайне нежелательные явления. Я говорил в предыдущих публикациях, что при искажениях мы безвозвратно теряем информацию.
Для АЦП желательно, чтобы в рабочем диапазоне входных сигналов, формы передаточной характеристики аппроксимировалась прямой, но на практике небольшие отклонения всё же присутствуют. Поэтому для всех АЦП производители указывают параметры интегральной и дифференциальной нелинейности.
Шум квантования. В АЦП происходит округление реального значения аналогового сигнала. Точность представления, то, насколько близко уровень квантования к реальным значениям зависит от разрядности АЦП (количество бит). Сигнал ошибки или разницы мы называем шумом кантования. Хотя шумом его можно считать только в рамках математической модели, так как он зависит от сигнала.
О математической модели шума мы поговорим подробнее в следующей публикации. Если мы квантуем непрерывный сигнал, то и шум квантования будет непрерывным. Если мы говорим о квантовании дискретного сигнала, то и сигнал ошибки также будет дискретным. Понятно, что для того, чтобы уменьшить шум квантования, надо повышать разрядность АЦП, но из-за этого увеличивается стоимость, энергопотребление, могут снизиться другие характеристики. Существует техника уменьшения влияния шума квантования без увеличения разрядности и с ними вы можете ознакомиться самостоятельно при желании.
Джиттер – это фазовый шум, вызванный нестабильностью задающего генератора. Когда мы рассматриваем идеальный процесс дискретизации непрерывного сигнала, шаг временной сетки или период дискретизации неизменен, но в реальности импульс задающего генератора могут идти не через равные промежутки времени. Это приводит к тому, что мы передаём устройство выборки и хранения не совсем то значение, которое должны были передать в случае идеально ровной временной сетки. Эти отклонения от так называемых реальных значений также можно представить в виде дискретного шума.
Нестабильность генераторов обычно измеряется в пико- и фемто-секундах, поэтому на медленный АЦП она особо не влияет. Шум квантования вносит гораздо больший вклад. Но если сам сигнал изменяется очень быстро, если мы говорим о частотах дискретизации 100 МГц и 1 ГГц, то в этом случае уже джиттер может стать главной проблемой.
В завершении давайте кратко поговорим о цифро-аналоговых преобразователях. Цифро-аналоговые преобразователи, как вы догадались, – это устройство преобразующее входной цифровой сигнал в аналоговый. Подробно устройства ЦАП мы не будем рассматривать, но основной принцип очертим.
На вход устройства поступает дискретные отсчеты в виде цифрового кода, который затем преобразуется в напряжение. Напряжение это соответствует набору уровней, как и случае с АЦП, многие ЦАП используют равномерные уровни при преобразовании. Уровень напряжение остается неизменным до момента прихода следующего отсчёта на вход. Таким образом формируется ступенчатый непрерывный сигнал, который в дальнейшем может быть сглажен фильтром нижних частот. Один из простейших видов ФАП – широтно-импульсный модулятор. Он часто используется для управления скоростью электромоторов. С особенностями широтно-импульсной модуляции также рекомендуется самостоятельно ознакомиться. На этом с темой ЦАП и ЦАП мы заканчиваем. Следующая публикация у нас будет посвящена случайным процессам.
Наверх
Шум как случайный процесс
В этой публикации мы поговорим о шуме и его описании в виде случайного процесса. Для начала давайте напомним себе, что же такое шум.
Шумом мы зачастую называем нежелательные явления, мешающие нам получать информацию из полезного сигнала. Шум присутствует повсюду, он случаен по своей природе, источником его может быть как физика самого процесса, который мы пытаемся зафиксировать, так и неидеальности приёмной аппаратуры или оцифровщиков. Мы различаем понятия шума и полезного сигнала в том числе и с точки зрения их математического описания. Давайте для начала посмотрим, как мы можем описать полезный сигнал.
Здесь в качестве математической модели мы используем детерминированный сигнал, заданный аналитической функцией. Значения сигнала можно определить в любой момент, подставив все необходимые аргументы в описывающую его аналитическую функцию. На примере представленной синусоиды: если мы зафиксируем параметры амплитуды, частоты и фазы, и будем передавать в формулу меняющееся значение времени – мы будем получать точное значение сигнала в эти моменты времени.
Детерминированный сигнал, описываемый аналитической функцией, как модель, очень удобен. Но сигналы реального мира подвержены воздействию множества физических факторов, их значения могут колебаться от наблюдения к наблюдению. Да и сами средства наблюдения также могут вносить погрешность измерений. Проще говоря, реальный сигнал будет отличаться от его аналитического описания на случайную величину ошибки.
Рассмотрим очередной бытовой пример: нагрев воды в чайнике на газовой горелке. Температура воды с течением времени монотонно нарастает, но мы наблюдаем некоторые флуктуации или отклонения. Это может быть обусловлено неравномерной подачей газа в горелке, ветром, термодинамикой, неидеальностью средства измерения, наконец.
Так или иначе, полученные отсчёты мы можем приблизить прямой линией. Прямая линия – это детерминированный сигнал, описываемый функцией. Мы можем узнать его значения между соседними отсчётами, то есть интерполировать данные эксперимента, или даже подсчитать величину сигнала за пределами периода наблюдения, то есть использовать его для прогнозирования значений температуры. Но реальные значения немного отличаются от линейной зависимости в большую или меньшую сторону. Записанный сигнал мы можем рассматривать как математическую модель типа «дет сигнал + случ. Процесс»!
Если с детерминированным описанием сигнала всё более-менее понятно, то с моделью случайного процесса нам только предстоит познакомиться.
Понятие случайного процесса связано с определением случайной функции.
Случайная функция – это функция, вид которой в результате проведения эксперимента мы не можем предугадать.
Случайный процесс – есть случайная функция времени.
Конкретный вид, результат протекания случайного процесса, называется реализацией.
Справа показан ансамбль реализаций одного случайного процесса. В отличие от сигналов, описываемых аналитической функцией, реализации случайного процесса практически всегда отличаются друг от друга. Но общие характеристики у них есть. Как же нам описать случайный процесс без необходимости хранения бесконечного числа его реализаций? Для описания мы используем теорию вероятностей и математическую статистику.
Поговорим о распределении случайной величины.
Простой пример дискретной случайной величины – число, выпадающее при броске игральных костей. Может выпасть значение от 1 до 6. Величина может принимать одно из шести дискретных значений, но совершенно случайно. Нетрудно подсчитать вероятность выпадения какого-либо числа – она равна одной шестой, или 16.67% для каждого из дискретных значений.
Теперь давайте рассмотрим пример непрерывной случайной величины. Рост человека. Он не изменяется дискретно, а может принимать любое значение в разумных пределах. Представим себе, что мы измеряем рост каждого посетителя, кто заходит в магазин. Измерив достаточное кол-во людей, мы можем построить вот такой график: по оси икс отложен рост в сантиметрах, по оси игрик – количество людей с таким ростом. На графике мы видим дискретные полоски, но эти полоски обозначают кол-во людей, чей рост попадает в определённые пределы, например, в пределы от 182 до 183 см. Взглянув на этот график, мы понимаем, что чаще всего в магазин заходили люди среднего роста, а посетителей ростом выше двух метров видели редко.
То, что было представлено на графике очень близко к понятию плотности распределения слуйчайной величины. Значение плотности распределения показывает вероятность того, что случайная величина примет определённое значение, а частичная площадь под графиком – вероятность того, что значение попадёт в выбранный предел. Как вы понимаете, площадь под графиком на всем диапазоне значений равна единице, или ста процентам.
В случае с игральными костями мы рассматривали равномерное распределение, то есть одинаковую вероятность того, что слуйчайная величина примет то или иное значение.
В случае с ростом человека мы наблюдали нормальное распределение, так же именуемое распределением Гаусса. Нормальное распределение широко распространено в природе и используется как удобная модель случайного процесса. Популярность эта вытекает из центральной предельной теоремы. Она гласит, что сумма большого количества слабо зависимых случайных величин имеет распределение, близкое к нормальному.
На отклонение величины от среднего влияет множество факторов, подобно тому, как множество факторов влияет на рост человека, поэтому сумму их влияния можно описать СП с Гауссовским или нормальным распределением. Убедимся в этом в MATLAB.
Создадим пять векторов со случайными значениями. Функция rand позволяет нам генерировать вектора и матрицы со случайными значениями отсчётов, лежащих в пределах от нуля до единицы с равномерным распределением. В нашем случае мы создаём пять векторов по 10 тысяч точек. Построим их на графиках и убедимся, что во временной области они выглядят как реализации случайного процесса.
Далее построим гистрограммы всех векторов. Гистрограммы – это по сути графики распределения.
И мы наблюдаем, что у всех векторов распределение близко к равномерному. Мы этого и ожидали при использовании функции ранд.
А затем мы начинаем последовательно складывать вектора между собой и находить среднее арифметическое командой миан. Отразим на гистограмме распределение одного вектора, суммы двух, трёх, четырёх и пяти слагаемых.
Мы наблюдаем, что чем больше случайных величин мы берём в расчёт, тем ближе распределение суммы к нормальному, что подтверждает центральную предельную теорему.
Плотность распределения – это лишь одна из характеристик, которыми мы описываем случайные процессы. О других хар-ках, а также о видах шумов, и соотношении сигнал/шум мы расскажем в следующей публикации.
Попробуем нестандартно в сравнении с книгами по радиоэлектронике и цифровым системам связи, простыми житейскими примерами объяснить суть теоремы Котельникова. Если читатель еще не знаком с теоремой отсчётов, то рекомендуется сначала изучить ее формулировку в деловом официальном стиле. Смотрите, например, прошлую статью.
Аналоговые и дискретные процессы в природе
Абсолютное большинство процессов в природе протекают непрерывно, (изменение температуры воздуха на улице, давления, влажности, изменение скорости ветра, колебание электрического тока в проводнике, сияние Солнца). Почему все эти процессы непрерывны? Нам кажется, что время течет непрерывно, а значит в каждый момент времени должно существовать какое-то значение температуры воздуха или значение силы тока в проводнике, или значение интенсивности света Солнца. Непрерывные процессы, функции или сигналы называют аналоговыми (от слова аналог – нечто сходное, подобное чему-то, т.е. функция как модель является аналогом какому-то физическому процессу). Можно наблюдать множество непрерывных процессов в природе, например, непрерывный поток воды в источнике. Струя воды при падении вниз сужается как раз в силу поддержания непрерывности потока.
Аналоговый сигнал даже на конечном временном промежутке подразумевает набор бесконечного числа значений. Однако регистрирующие устройства, как правило фиксируют конечное число значений, поэтому мы получаем дискретные сигналы (дискретный от лат. discretus означает раздельный, состоящий из отдельных частей).
Представление непрерывного и дискретного сигналов.
Дискретные процессы также многочисленны в природе, как и аналоговые состояния. Дискретные процессы не могут находиться в каком-то промежуточном состоянии между определенными значениями. Придумаем несколько примеров из жизни:
- Из квантовой физики 1-й постулат Бора: электрон в атоме может двигаться только по определенным (можно сказать по дискретным) орбитам, находясь на которых, он не излучает и не поглощает энергию. Электроны в атоме, находясь на определенных стационарных (т.е. дискретных) орбитах, имеет вполне определённые дискретные значения энергии Е1, Е2, Е3 и т.д.
- Если вы играете на пианино, то звучащая музыка во времени представляет собой перескоки с одной дискретной ноты на другую, то есть ноты – это отдельно выбранные дискретные звуки.
- Когда мы поднимаемся по лестнице, ступня в пространстве оси высот находится только на определенной дискретной координате (ступеньке)
Поскольку человек не может оперировать с бесконечными числами и величинами, обычно все округляем до ближайших целых чисел – в результате получаем цифровые сигналы. Например, мы наносим цифровую шкалу на столбик термометра и фиксируем округленное значение температуры. Непрерывное время мы разбиваем на секунды минуты, часы – наносим цифры на циферблат часов. Все символьные и знаковые системы, созданные человечеством для обмена информацией, использует конечное число возможных элементов.
Поскольку все вычислительные информационные устройства могут работать лишь с дискретными символьными системами и с цифровыми сигналами, постоянно возникает необходимость в переходе от существующих в природе непрерывных процессов, к дискретным и цифровым. С развитием цифровой связи и цифровых устройств (микроконтроллеров, компьютеров) постоянно и повсеместно на каждом шагу выполняется аналого-цифровое преобразование сигналов, неотъемлемой частью которого является дискретизация сигналов. Но здесь важно следующее: перейти от непрерывного сигнала к дискретному дело нехитрое – здесь удачно подходит выражение “ломать не строить”. По аналогии можно сказать “ломать аналоговый сигнал – не восстанавливать его”, здесь все просто реализовать, но главное при этом выполнить дискретизацию правильно. Одно дело просто произвести выборку отдельных значений сигнала, но есть еще другое дело – потом надо будет по этим значениям снова восстановить исходный непрерывный сигнал. Как правильно дискретизировать сигналы говорится в теореме о дискретизации сигналов, или ее можно называть в честь автора – теоремой Котельникова.
Если не знать теорему Котельникова
Итак, мы выяснили, что как и множество процессов в природе, электрические сигналы, используемые во всей электронике и системах связи бывают аналоговые и дискретные. В цифровых системах необходимо переходить от аналоговых сигналов к дискретным, при этом переход должен быть корректным.
Наглядный пример номер раз. Давайте посмотрим на примере двух музыкальных фрагментов, что будет, если осуществлять дискретизацию сигнала некорректно.
Вот что будет при неправильной оцифровке музыки
Исходная музыкальная запись
После неправильной дискретизации
Вот что будет при неправильной оцифровке речи
Исходная запись
После неправильной дискретизации
Наглядный пример № 2. На рисунке ниже представлены 7 сигналов, каждый из которых соответствует своей музыкальной ноте – До, Ре, Ми, Фа, Соль, Ля, Си. Все они оцифрованы с частотой дискретизации 1700 Гц.
Давайте послушаем, что из этого получилось.
Надеюсь, с музыкальным слухом все в порядке и вы услышали, что с последними двумя прозвучавшими нотами что-то не так. Если не знать теорему Котельникова, то будет непонятно, почему звук при дискретизации исказился. Поэтому давайте разбираться в этой теореме.
Наглядное, но нестандартное объяснение теоремы о дискретизации
Представим себе, что мы работники Animal Planet и хотим изучить траекторию движения в джунглях какой-нибудь редкой змейки из красной книги. Назовем, например, изучаемую змею Зигзагусс.
С целью исследования мест обитания змеи и ее повадок цепляем к ее хвосту GPS-датчик, который будет регистрировать ее местоположение в отдельные моменты времени.
Вопрос: как надо запрограммировать датчик, чтобы мы получили точную траекторию движения змейки, т.е. получили самый подробный график траектории движения юркой змейки со всеми ее виляниями и изгибами? Через сколько миллисекунд или секунд датчику необходимо будет записывать и посылать нам очередную координату положения в пространстве?
Допустим, наша змея Зигзагусс ползет гармонично – ее хвост совершает гармонические колебания и ее движения можно описать синусоидальными функциями.
Фото настоящего следа от змеи на песке.
Траектория движения представляет собой колебания с различными частотами. Так вот, по правилам теоремы о дискретизации, чтобы восстановить всю траекторию движения змейки, необходимо найти составляющую колебаний самой высокой частоты.
Если по дискретным точкам мы сможем восстановить составляющую колебаний самой высокой частоты, то мы сможем восстановить всю траекторию змейки. Определим периоды всех колебаний (см. рисунок ниже).
Как видно из рисунка, наименьшим периодом колебаний является период . Следовательно, необходимо подобрать частоту выборки дискретных точек именно для колебания с периодом , тогда и все остальные колебания мы сможем потом восстановить. Другими словами, в соответствии с теоремой о дискретизации (см. формулировку здесь) можно полностью восстановить данную синусоидальную функцию, если брать дискретные точки через интервал времени вдвое меньший длительности периода . Это означает, что необходимо брать точки с таким интервалом, чтобы на период колебания самой высокой частоты приходилось не менее 2-х точек.
В этом случае можно будет с высокой точностью восстановить всю непрерывную траекторию движения исследуемой змеи.
Предположим теперь, что Зигзагусс опьянилась запахом одурманивающего цветка и стала ползти негармонично, несуразно.
В этом случае для определения периода дискретизации нам необходимо самим отыскать гармонию в данной кривой функции, а она есть внутри любого сигнала всегда, что пытался в свое время доказать всем людям французский математик Жан-Батист Фурье. Также как любое тело можно разложить на множество атомов, также и полученную сложную функцию (от траектории змеи), можно разложить на множество гармонических функций. Физические тела разные, потому что они отличаются друг от друга структурой молекул. Например, мы говорим H2O – это вода, что означает: молекула воды состоит из двух атомов водорода H и одного атома кислорода O. Точно также можно сказать, что разные сигналы отличаются разным составом. Например, такой вот сигнал
состоит из двух гармонических функций (синус и косинус) с частотой 1000 Гц и одного синуса с частотой 2000 Гц (2000 Гц означает, что гармоника совершает 2 тысячи колебаний в секунду). В соответствии с условием теоремы Котельникова, о котором мы уже ранее говорили, для такого сигнала временной интервал между дискретными точками необходимо брать таким, чтобы он был меньше половины периода самой высокой частоты. В нашем случае имеется гармоника с максимальной частотой 2 тысячи колебаний в секунду (2000 Гц), значит период сигнала равен 1/2000 = 0.005 секунд и значит период между дискретными точками должен быть менее, чем 0.005/2 = 0.0025 секунды.
Чтобы определить требуемый период между дискретными точками для траектории нашей змейки, необходимо определить из каких гармонических функций она состоит, а точнее нас интересует значение частоты наивысшей гармонической функции (т.е. фиолетовой на рисунке).
Делим период фиолетовой гармоники пополам, и получаем граничное значение для периода дискретизации функции траектории одурманенной змеи. Все, задача решена, можно произвести дискретизацию данного сложного сигнала.
Знаем и соблюдаем условия теоремы Котельникова
Теперь, когда мы знаем теорему Котельникова, давайте еще раз рассмотрим задачу правильного перехода от аналоговых 7 сигналов- музыкальных нот к дискретным. Итак, у нас есть семь гармонических колебаний, с частотами
Для правильной дискретизации, чтобы не было искажений, необходимо взять частоту дискретизации не менее в два раза больше максимальной частоты сигнала. Ранее мы брали частоту 1700 Гц, но как можно посчитать, такая частота подходит для сигналов нот До – Соль (для ноты Соль требуется частота дискретизации 784*2=1568 Гц), а вот для сигналов нот Ля и Си значение 1700 Гц уже не годится.
Еще раз рассмотрим дискретизацию наших сигналов
Как видно из рисунка из-за несоблюдения условий теоремы Котельникова для сигналов Ля и Си с частотами 880 Гц и 988 Гц, через получившиеся дискретные отсчёты можно провести другие гармонические сигналы (красные функции), частоты которых меньше 1700 Гц / 2 = 850 Гц. Произошел эффект, который называют наложение спектров (в англоязычной литературе – aliasing). В рамках данной статьи “для чайников” мы не будем подробно рассматривать этот эффект, поскольку здесь уже требуются знания спектрального анализа сигналов. Этот эффект интересен тем, что объясняет условия теоремы Котельникова с позиций представления сигналов в частотной области (см. рисунок ниже). Если разобраться в этом, то теорема Котельникова и принципы восстановления сигналов станут более понятными. Описание этого эффекта можно найти почти в каждой книге по цифровой обработке сигналов.
Но сейчас новичкам в этой области главное запомнить результат несоблюдения теоремы отсчётов – восстановление сигналов по имеющимся дискретным отсчётам будет неоднозначно. Чтобы такого не происходило, необходимо чтить теорему Котельникова.
Максимальная частота среди наших 7 сигналов 988 Гц (нота Си), следовательно частота дискретизации должна быть больше, чем 2*988=1976 Гц. Важно здесь неуместно отметить, что в 1976 году был создан первый персональный компьютер – начался кустарный выпуск Apple I.
Значит надо выбрать частоту дискретизации больше значения 1976.
Вот как будут звучать семь наших сигналов при частоте дискретизации 2000 Гц.
Задачка для разминки мозгов
Нельзя сказать, что эта задачка очень простая для начинающих и ее решит любой. Новички в этой области не унывайте, если не получится (здесь нужны знания теории сигналов), ну а тот, кто решит, может собой гордиться.
С двух датчиков регистрируются сигналы
Какой должна быть минимальная частота дискретизации в АЦП по условию теоремы о дискретизации, если К – операция сложения и если К – операция умножения?
