Как найти частоту дискретизации кгц

Звук представляет собой волну с меняющейся интенсивностью и частотой (громкостью и его тональностью соответственно). Чем больше амплитуда, тем громче звук. Чем больше частота, тем больше тон.

Хранение и передача аналогового звукового сигнала осуществляется за счёт представления его в виде электрического сигнала с помощью модуляции.

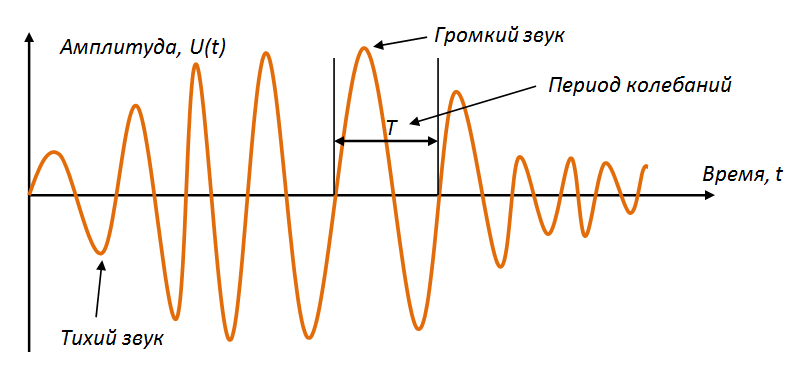
Модуляция – процесс изменения одного или нескольких параметров (амплитуды, частоты или фазы) высокочастотного колебания по закону низкочастотного сигнала (несущей частоты).

Существуют разные виды модуляции:

Амплитудная (АМ, amplitude modulation ) – изменение высокочастотных колебаний с частотой, равной частоте звукового сигнала. Например, несущей частотой может быть питание сети – 50 Гц. Или радиоволна СВ (MW) диапазона от 300 кГц до 3 МГц.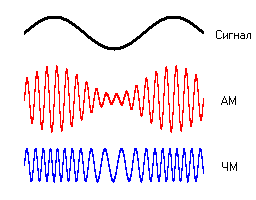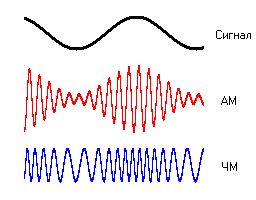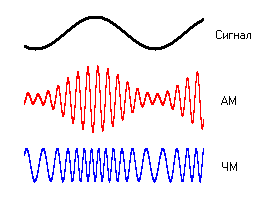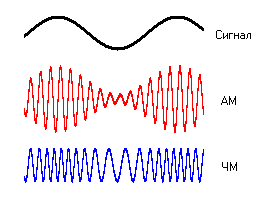

Частотная (FM, frequency modulation)  – модуляция при которой информационный сигнал управляет несущей частотой. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.

---

Цифровой сигнал

Для того чтобы аналоговый (непрерывный) сигнал представить последовательностью чисел определённой разрядности, его необходимо превратить в дискретный (прерывистый) сигнал, а затем подвергнуть квантованию.

За кодирование звука отвечает звуковая карта, чем выше разрядность звуковой карты, тем больше уровней квантования она выдаёт и тем точнее становится звук при прослушивании.

На современном ПК карта всегда интегрирована в материнской плате, и имеет разрядность не ниже 24 бит.

Оцифровка звука – дискретизация и квантование аналогового сигнала.

1-й этап: Дискретизация сигнала по времени

Допустим, Вы, с помощью микрофона записали свой голос длительностью 5 сек. Этот фрагмент можно разбить на равные малые временный отрезки, которые в сумме дают нам 5 сек. Получаем частоту дискретизации (f, Гц), которая является обратной величиной времени: t сек. При частоте дискретизации 8 кГц=8 000 Гц, из формулы получаем отрезок, равный 0,000125  сек. или 125 миллисекунд.

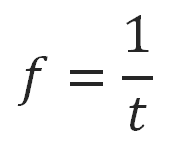 2-й этап: Квантование сигнала по уровню

Чем больше уровней будет доступно для кодирования временных отрезков, тем ближе к аналогу будет закодированный файл, но при этом объём файла увеличится.

Например, возьмём 8 уровней, чтобы их закодировать в двоичный код нам достаточно 3 бита, что мы получаем из формулы Хартли:

2³=8 – комбинаций двоичного ряда чисел от 000 до 111.

Параметр (i) – называется глубина кодирования. 8 бит – 256 уровней, 16 бит – 65 536 уровней, 24 бита – более 16 млн. уровней.

3 этап: Определяем скорость потока звука

Частота дискретизации – 22 кГц, глубина кодирования – 16 бит. Произведение этих двух величин дает нам скорость потока 352 кбит/сек.

Именно такой канал передачи данных потребуется для воспроизведения звукового файла в режиме он-лайн.

Расчёт количество звуковой информации

Для определения информационного объёма звуковой информации, нам необходимы следующие параметры:

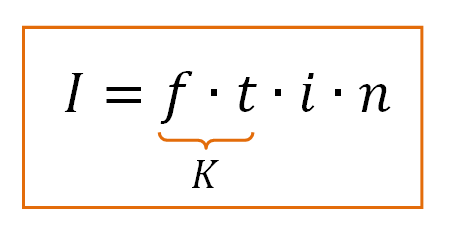
• f – частота дискретизации (Гц);
• t – время звучания звукового файла (сек.);
• i – глубина кодирования (бит);
• n – количество звуковых каналов (n = 1, моно; n = 2, стерео).

Задача 1:

Одна минута записи цифрового аудиофайла занимает 1,3 МБ, разрядность звуковой платы — 8 бит. С какой частотой дискретизации записан звук?

Решение:

Воспользуемся формулой: I=f∙t∙i∙n , из формулы видно что для нахождения частоты дискретизации формула примет вид: f=I/t∙i∙n.

1,3 МБ = 13,31,2 КБ = 1 363 148,8 Байт. Принимая во внимание что 8 бит = 1 Байту, делим 1 363 148,8 на 60, канал у нас записан 1, поэтому n=1.

Ответ: 22719,1 Гц  или 22 050 Гц, см. основные настройки параметров звукового файла в программе Audacity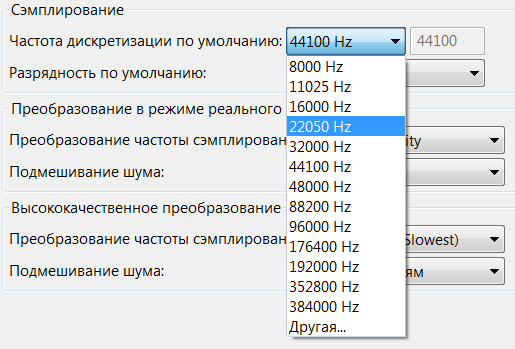 

Задача 2:

Две минуты записи цифрового аудиофайла занимают на диске 5,1 МБ. Частота дискретизации — 22 050 Гц. Какова разрядность аудиоадаптера?

Решение: 5,1 МБ = 5 347 737,6 Байт, делим по формуле: i  = I / f∙ t ∙ n.

5 347 737,6 / 22 050 ∙ 120 = 2,02 Байт.

Ответ: 16 бит.

---

Кодирование видео

Информация хранится на различных носителях в виде файлов. Файл занимает память и может быть измерен в единицах измерения информации: бит, Байт, КБ и т.д.

Стремительное развитие интернета резко увеличило обмен информацией между людьми, для  оптимизации хранения данных люди стали использовать специальные алгоритмы сжатия.

В основе цифрового видео лежит графический и звуковой файлы. Если рассчитать объём видеофайла без сжатия, нам необходимо учитывать тот факт, что человек начинает воспринимать смену кадров (картинок), как непрерывное плавное движение, если за 1 сек. будет мелькать 24 кадра.

Основы ТВ

Для приёма телевизионного сигнала используется антенна и приёмник. Приёмник – это электронная схема, которая преобразует сигнал в изображение на экране. В этом процессе участвует генератор кадровой развёртки и строчной.

Кадровая развёртка формируется на частоте, близкой к частоте переменного тока в бытовых электросетях – 50 Гц.

Кадровая развёртка, в сочетании со строчной служит для преобразования плоского двумерного изображения в одномерную последовательность, то есть, видеосигнал, а в телевизоре или мониторе компьютера для преобразования видеосигнала обратно в изображение на экране.

Для создания такой последовательности, используются специальные стандарты разложения:

576i, 625/50 — стандарт разложения, принятый для аналогового и цифрового телевидения в Европе, России, Австралии, странах Африки и Азии. 576 – это количество активных строк для аналогового телевидения и число пикселей по вертикали, для цифрового. Буква «i», англ. Interlace означает чересстрочную развёртку, передающую 25 целых кадров в 50 полях за 1 секунду.

480i, 525/60 — стандарт разложения, принятый в США, число активных строк составляет 480.

Существует также прогрессивная (p) кадровая развёртка, где все строки каждого кадра отображаются последовательно. Прогрессивная развертка стала широко распространена с появлением персональных компьютеров. Для комфортного чтения мелкого текста с экрана монитора, чересстрочная развертка стала малопригодна, так как мерцание строк вызывало быстрое утомление глаз.

Помимо развёртки существует ещё и соотношение сторон: аналоговое ТВ – 4:3, цифровое ТВ – 16:9, широкоформатное.

Форматы со сжатием

Давайте для начала посчитает объём видеофайла без сжатия, длительность 1 час 30 мин., 576i, 16:9. Звук записан с частотой дискретизации – 44 100 Гц, глубина кодирования 24 бит.

Решение:

Видео: I = 576 ∙ 1024 ∙ 25 ∙ 5400 ∙ 24 = 1 911 029 760 000 бит = 222,5 ГБ

Звук: I = 44 100 ∙ 5400 ∙ 24 = 5 715 360 000 бит = 681,3 МБ = 0,665 ГБ

Ответ: 223,2 ГБ.

Графический формат JPEG

Алгоритм JPEG (от англ. Joint Photographic Experts Group) в большей степени пригоден для реалистичных изображений с плавными переходами яркости и цвета, таковыми являются фотографии.

В основу алгоритма заложен переход от цветового пространства RGB к цветовому пространству YCbCr. Y – компонент яркости, Cb и Cr – синий и красный цветоразностные компоненты. Суть сжатия состоит в том что для каждого блока пикселей 2х2 записывается не 12 значений, а 6, за счёт использования усреднённого компонента цвета.

Видео  и аудио форматы MPEG

Алгоритм MPEG (англ. Moving Picture Experts Group) – стандарты сжатия и передачи цифровой видео и аудио информации. Базовым объектом кодирования в стандарте MPEG является кадр телевизионного изображения. Поскольку в большинстве фрагментов фон изображения остается достаточно стабильным, а действие происходит только на переднем плане, сжатие начинается с создания исходного кадра.

При сжатии аудио используются хорошо разработанные психоакустические модели, чтобы выбросить звуки, которые не слышны человеческому уху.

Современные цифровые стандарты

Современные дисплеи и мониторы уже давно вышли за рамки старых добрых стандартов.

Стандарты современных дисплеев:

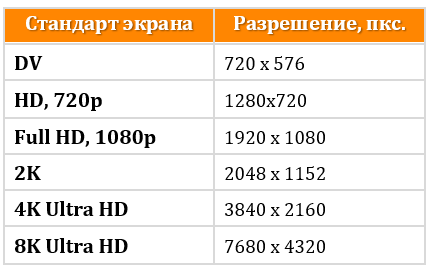
Среди
значений U₁(ω),
приведённых в таблице 2, определяем
максимум модуля спектральной плотности

U_1max=
25 мВс

Найдем
частоту, после которой значения U₁(ω)
не превышает уровень 0,1^.U₁max
= 2,5 мВс. Согласно данным, такой частотой
можно считать

fв
= 1,0 кГц. Эта частота принимается за
верхнюю границу спектра входного
сигнала, и частота дискретизации берется
равной f_д=2fв=2,0
кГц.

Однако
более точных расчетов при дискретизации
следует увеличить частоту дискретизации
до 5 кГц. Соответственно, период
дискретизации Т = 0,2мс.

Составим аналитическое выражение для:

5000nT,

U₁(n)=
-2500nT+10,

0,

Импульсная
характеристика дискретной цепи
определяется как:

Подставив
период дискретизации, получим:

Дискретные значения
сигнала на выходе цепи вычисляются с
помощью формулы дискретной свертки.

Например:

U2(0) =
U1(0)*h(0) = 10*0,0666 = 0,666;

U2(1) =
U1(0)*h(1) + U1(0)*h(1) = 10*0,0583 + 10*0,0666 = 1,249;

U2(2) =
U1(0)*h(2) + U1(1)*h(1) + U1(2)*h(0) = 10*0,051 + 10*0,0583 +
+ 10*0,0666 = 1,579;

Для
полученных результатов составим
таблицу.

Таблица
6.1 – Дискретные отсчеты

t,мс	0	0,2	0,4	0,6	0,8	1,0	1,2	1,4	1,6	1,8	2,0
N	0	1	2	3	4	5	6	7	8	9	10
U1,В	10	10	10	10	10	10	10	10	10	10	7,5
h(n)	0,0666	0,0583	0,051	0,045	0,039	0,034	0,03	0,026	0,023	0,02	0,018
U2,В	0,666	1,249	1,579	2,209	2,599	2,939	3,239	3,499	3,729	3,929	3,94

t,мс	2,2	2,4	2,6	2,8	3,0	3,2	3,4	3,6	3,8	4,0
N	11	12	13	14	15	16	17	18	19	20
U1,В	4,5	4	3,5	3	2,5	2	1,5	1	0,5	0
h(n)	0,015	0,014	0,012	0,01	0,009	0,008	0,007	0,006	0,005	0,0047
U2,В	3,75	3,55	3,34	3,12	2,9	2,67	2,44	2,2	1,96	1,72

Рис
6.1 Дискретизированный сигнал на входе
и выходе цепи.

7. Спектр дискретизированного сигнала.

Вычислим
значения спектральных характеристик
дискретизированного сигнала

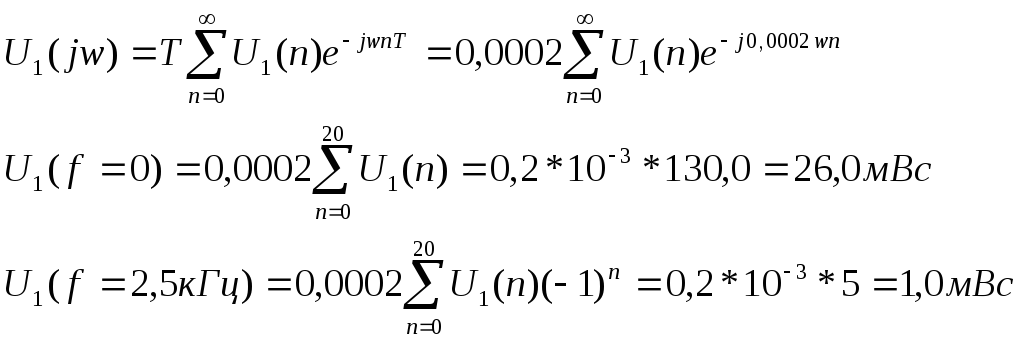
Таблица
7.1 – Значение спектра дискретизированного
сигнала

f,кГц	U1(f),мВс
0	26,0
0,625	3,512
1,25	1,75
1,875	0,91
2,5	1,0
3,125	0,91
3,75	1,75
4,375	3,512
5	26,0

Рис 7.1
Амплитудно-частотная характеристика
сигнала на выходе дискретной цепи.

Частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчётов непрерывного по времени сигнала при его дискретизации (в частности, аналого-цифровым преобразователем). Измеряется в герцах.

Термин применяется и при обратном, цифро-аналоговом преобразовании, особенно если частота дискретизации прямого и обратного преобразования выбрана разной (Данный приём, называемый также «Масштабированием времени», встречается, например, при анализе сверхнизкочастотных звуков, издаваемых морскими животными).

Чем выше частота дискретизации, тем более широкий спектр сигнала может быть представлен в дискретном сигнале.
Как следует из теоремы Котельникова, для того, чтобы однозначно восстановить исходный сигнал, частота дискретизации должна более чем в два раза превышать наибольшую частоту в спектре сигнала.

Некоторые из используемых частот дискретизации звука^[1]:

• 8 000 Гц — телефон, достаточно для речи, кодек Nellymoser;
• 11 025 Гц — четверть Audio CD, достаточно для передачи речи;
• 16 000 Гц;
• 22 050 Гц — половина Audio CD, достаточно для передачи качества радио;
• 32 000 Гц;
• 44 100 Гц — используется в Audio CD. Выбрано Sony из соображений совместимости со стандартами PAL (запись 3 значений на линию картинки кадра × 588 линий на кадр × 25 кадров в секунду) и NTSC (запись 3 значений на линию картинки кадра × 490 линий на кадр × 30 кадров в секунду), и достаточности (по теореме Котельникова) для качественного покрытия всего диапазона частот, различаемых человеком на слух (20 Гц — 20 КГц);
• 48 000 Гц — DVD, DAT;
• 96 000 Гц — DVD-Audio (MLP 5.1);
• 192 000 Гц — DVD-Audio (MLP 2.0);
• 2 822 400 Гц — SACD, процесс однобитной дельта-сигма модуляции, известный как DSD — Direct Stream Digital, совместно разработан компаниями Sony и Philips;
• 5 644 800 Гц — DSD с удвоенной частотой дискретизации, однобитный Direct Stream Digital с частотой дискретизации вдвое больше, чем у SACD. Используется в некоторых профессиональных устройствах записи DSD.

См. также[править | править код]

• Частота Найквиста
• Цифровой сигнал
• Дискретизация

Примечания[править | править код]

Unit Converter

Enter the sampling period (seconds) into the Sampling Frequency Calculator. The calculator will evaluate the Sampling Frequency. 

• All Frequency Calculators
• Sampling Rate Calculator
• Sampling Error Calculator
• Frequency Factor Calculator

Sampling Frequency Formula

The following two example problems outline the steps and information needed to calculate the Sampling Frequency.

Variables:

• fs is the Sampling Frequency (hz)
• Ts is the sampling period (seconds) 

To calculate the sampling frequency, divide 1 by the sampling period.

How to Calculate Sampling Frequency?

The following steps outline how to calculate the Sampling Frequency.

---

1. First, determine the sampling period (seconds). 
2. Next, gather the formula from above = fs = 1/Ts.
3. Finally, calculate the Sampling Frequency.
4. After inserting the variables and calculating the result, check your answer with the calculator above.

---

Example Problem : 

Use the following variables as an example problem to test your knowledge.

sampling period (seconds) = 30

fs = 1/Ts = ?

Часто производители аудио аппаратуры, особенно наушников, в процессе пиара своей продукции активно продвигают “кристальную чистоту” звука и широчайший частотный диапазон, который не только за 20 кГц переваливает, но и в некоторых случаях доходит даже до 100 кГц. Конечно это имеет свои плюсы, даже не смотря на то, что выше 20к Гц мы не слышим, а то и еще меньше. Но есть определенные проблемы, которые связанны с понятием частота дискретизации и вытекающие из теоремы Котельникова. Они в одночасье поставили жирный крест на применении слова “качественно” для большинства аудио-форматов и аудио устройств в моих глазах.

Любой процесс в природе является непрерывным. Например звуковой сигнал принятый микрофоном и преобразованный в электрический (аналоговый) сигнал — непрерывен.

Термин “Аналоговый сигнал” подчеркивает, что такой сигнал “аналогичен”, т.е. полностью подобен порождающему его процессу, или в данном случае звуку.

И непрерывный он не потому что будет длиться вечно, а потому, что его значение можно измерять в любые моменты времени. А между этими моментами сигнал будет продолжать непрерывно меняться.

Для лучшего понимания того, как устроен цифровой звук, советую посмотреть мой видос:

Что такое частота дискретизации?

Как только встает вопрос о переводе аналогового сигнала в цифровой, сразу возникает понятие дискретизации, т.е. разбиение непрерывного сигнала на кусочки по времени. Делается это непосредственно в процессе преобразования.

Через равные промежутки времени, называемые шагом дискретизации Δ, Аналогово-Цифровой-Преобразователь (АЦП) измеряет значение сигнала, поступающего на его вход и преобразует это значение в цифровой вид. То, как часто осуществляется измерение величины аналогово сигнала и называется частотой дискретизации.

Какая частота дискретизации считается достаточной?

Товарищ Котельников, еще в 1933 в работе «О пропускной способности эфира и проволоки в электросвязи» создал фундаментальную, для цифровой техники теорию, которая обычно формулируется следующим образом:

Любой непрерывный сигнал u(t) с конечным спектром (имеющим максимальное значение частоты F) можно представить в виде дискретных отсчетов u(kΔt), частота дискретизации которых должна быть выбрана не менее чем в два раза выше максимального значения спектра сигнала: f ≥ 2F, передать его по линии связи, а затем восстановить исходный аналоговый сигнал.

Говоря проще, для того чтобы можно было правильно воспроизвести (восстановить) аналоговый сигнал из цифрового вида, достаточно, чтобы частота дискретизации была вдвое выше максимальной частоты в сигнале.

Верхний порог слышимости человека принято ограничивать частотой в 20кГц. Из теоремы Котельникова следует, что для правильного воспроизведения сигнала частотой 20 кГц достаточно частоты дискретизации в 40кГц. Если заглянуть в свойства подавляющего большинства аудио файлов, то можно увидеть строчку:

Почему именно 44.1 кГц? Википедия отвечает так: “Эта цифра выбрана компанией Sony из соображений совместимости со стандартом телевещания PAL, за счёт записи 3 значений на линию картинки кадра x588 линий на кадр x25 кадров в секунду, и достаточности (по теореме Котельникова) для качественного покрытия всего диапазона частот, различаемых человеком на слух (20 Гц — 20 кГц).”

При частоте дискретизации в 44.1 кГц шаг дискретизации Δ составляет всего 0.00002267=22.67*10^-6 секунды или 22.67 микросекунды. Это время между двумя точками сигнала.

Вроде все нормально, так чего же тут не так?

Начнем с частот, кратных частоте дискретизации. На частоте 441 Герц при нашей частоте дискретизации (44.1 кГц), на один период приходится 100 точек. Чтож, тут нет никаких претензий, синусоида идеальная. Если же повысить частоту на порядок, т.е. в 10 раз, то эти же 100 точек будут формировать уже не 1, а 10 периодов. И даже в этом случае Будет формироваться сигнал очень похожий на синусоиду.

А вот на частоте 22050, т.е. наивысшей частоте, удовлетворяющей теореме Котельникова (при частоте дискретизации 44.1кГц) на 100 точек приходится 50 периодов колебаний.

Эти сигналы генерировались в программе Audacity. И по началу создалось впечатление, что точек там достаточно, просто масштаб не позволяет разглядеть и поэтому так все угловато…

Читайте также:

Простой способ генерации сигналов разной формы в аудио редакторе Audacity

Чтож… приблизим и рассмотрим каждый период по отдельности:

Частота в 4410 Гц вполне себе достойная синусоида, чего никак не скажешь о частоте 22050Гц, с ее двумя точками на период. По факту это уже и не синусоида, а сигнал треугольной формы.

Конечно в любом реальном ЦАПе на выходе применяется НЧ-фильт, который срезает высокочастотную составляющую и скругляет этот треугольник. Однако чем выше класс вашего аудио устройства, тем заметнее будет угловатость звука

Ради эксперимента можете попробовать сгенерировать в Audcity сигналы одной и той же частоты но разных форм. У треугольной и прямоугольной форм из-за их “угловатости” и резких фронтов возникают дополнительные гармоники, а вот синусоидальный сигнал звучит гораздо более мягко и естественно.

Но даже и это не самое страшное. До этого момента рассматривались сигналы с частотами кратными частоте дискретизации.

— А что же будет, если взять другие частоты???

Знакомьтесь, цифровая синусоида равной амплитуды и частотой 15 кГц. Красивый узорчик, не правда ли? Как видите амплитуда меняется с частотой. Это уже интермодуляционные искажения. Наш истинный сигнал в 15 кГц промодулирован частотой кратной 44.1 кГц.

Вы можете возразить, мол узорчик то красивый, но может звучит он как ему и положено. Для того чтобы убедиться в этом своими ушами — сгенерируйте сигнал частота которого меняется от 20 герц до 20 кГц. И вы отчетливо услышите, что с какого-то момента частота перестанет равномерно расти, а начнет плавать туда-сюда.

Оно и понятно, вот так выглядят синусоиды на разных частотах выше 10’000Гц

В защиту теоремы Котельникова стоит отметить, что да, его теорема верна, иначе бы мы не смогли различать в музыке высокие звуки, и что тарелка что маракас звучали бы одинаково неправдоподобно, но она абсолютно не гарантирует высокого качества записи.

В жизни Вы врядли станете наслаждаться звучанием синусоиды, но это был очень наглядный пример проблем качества цифровых аудио записей.

Частота дискретизации и Hi-Res звук

Конечно сегодняшние технологии уже побороли данную проблему. Вероятно вам встречалось сокращение Hi-Res (High Resolution — высокое разрешение), которым обычно обзывают качество звука в 24 бита и частотой дискретизации в 192 кГц.

А это уже 10 точек на частоте 22’050 кГц, такую синусоиду уже явно можно считать идеальной. И вот там «кристально чистые верха» ваших наушников себя точно оправдают.

Возникает только 3 проблемы:

• Стоимость подобных устройств. Например портативный плеер с такой частотой дискретизации обычно стоит около 200$.
• Где брать записи в таком качестве.
• Размеры аудиофайлов очень велики. 1 альбом вашей любимой группы в Hi-Res легко может занимать более 1,5Гб дискового пространства.

В заключение

Конечно от плохого звучания высоких частот еще никто не умирал и, возможно я излишне драматизирую, говоря, что частота дискретизации в 44.1 кГц так уж плоха, однако, как видите особым качеством на высоких частотах она не блещет. 

На мой взгляд в домашних условиях гораздо интереснее слушать винил. Но с виниловой вертушкой в метро не поездишь… Так что меломанские запросы придется удовлетворять цифровым плеером.

Всем качественного звука!

(P.S. — комментируем, не стесняемся 🙂