Как найти частоту дискретизации по графику

Среди
значений U₁(ω),
приведённых в таблице 2, определяем
максимум модуля спектральной плотности

U_1max=
25 мВс

Найдем
частоту, после которой значения U₁(ω)
не превышает уровень 0,1^.U₁max
= 2,5 мВс. Согласно данным, такой частотой
можно считать

fв
= 1,0 кГц. Эта частота принимается за
верхнюю границу спектра входного
сигнала, и частота дискретизации берется
равной f_д=2fв=2,0
кГц.

Однако
более точных расчетов при дискретизации
следует увеличить частоту дискретизации
до 5 кГц. Соответственно, период
дискретизации Т = 0,2мс.

Составим аналитическое выражение для:

5000nT,

U₁(n)=
-2500nT+10,

0,

Импульсная
характеристика дискретной цепи
определяется как:

Подставив
период дискретизации, получим:

Дискретные значения
сигнала на выходе цепи вычисляются с
помощью формулы дискретной свертки.

Например:

U2(0) =
U1(0)*h(0) = 10*0,0666 = 0,666;

U2(1) =
U1(0)*h(1) + U1(0)*h(1) = 10*0,0583 + 10*0,0666 = 1,249;

U2(2) =
U1(0)*h(2) + U1(1)*h(1) + U1(2)*h(0) = 10*0,051 + 10*0,0583 +
+ 10*0,0666 = 1,579;

Для
полученных результатов составим
таблицу.

Таблица
6.1 – Дискретные отсчеты

t,мс	0	0,2	0,4	0,6	0,8	1,0	1,2	1,4	1,6	1,8	2,0
N	0	1	2	3	4	5	6	7	8	9	10
U1,В	10	10	10	10	10	10	10	10	10	10	7,5
h(n)	0,0666	0,0583	0,051	0,045	0,039	0,034	0,03	0,026	0,023	0,02	0,018
U2,В	0,666	1,249	1,579	2,209	2,599	2,939	3,239	3,499	3,729	3,929	3,94

t,мс	2,2	2,4	2,6	2,8	3,0	3,2	3,4	3,6	3,8	4,0
N	11	12	13	14	15	16	17	18	19	20
U1,В	4,5	4	3,5	3	2,5	2	1,5	1	0,5	0
h(n)	0,015	0,014	0,012	0,01	0,009	0,008	0,007	0,006	0,005	0,0047
U2,В	3,75	3,55	3,34	3,12	2,9	2,67	2,44	2,2	1,96	1,72

Рис
6.1 Дискретизированный сигнал на входе
и выходе цепи.

7. Спектр дискретизированного сигнала.

Вычислим
значения спектральных характеристик
дискретизированного сигнала

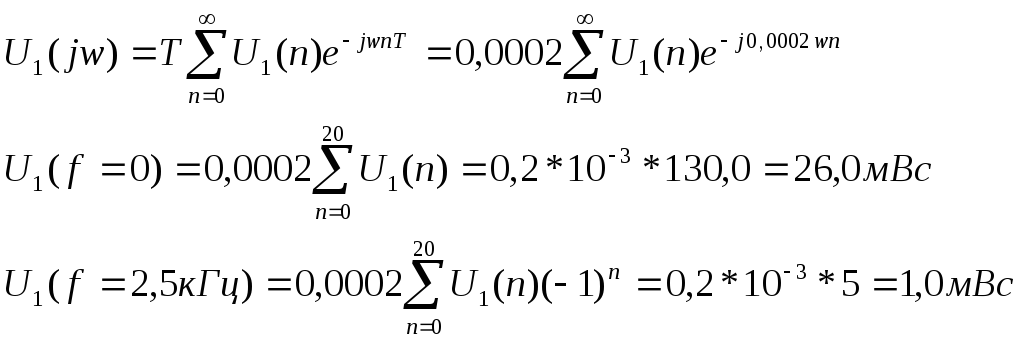
Таблица
7.1 – Значение спектра дискретизированного
сигнала

f,кГц	U1(f),мВс
0	26,0
0,625	3,512
1,25	1,75
1,875	0,91
2,5	1,0
3,125	0,91
3,75	1,75
4,375	3,512
5	26,0

Рис 7.1
Амплитудно-частотная характеристика
сигнала на выходе дискретной цепи.

Сигнал это изменение физической величины во времени или пространстве. К примеру, это может быть изменение одномерного сигнала в зависимости от времени. Если мы рассматриваем цифровое изображение это может быть изменение яркости пикселей в зависимости от его положения в пространстве.

Но с точки зрения математики сигнал это функция одной или нескольких независимых переменных. В нашем случае независимыми переменными являются время и положение в пространстве, а зависимыми переменными могут быть значения нашего сигнала x от t или яркости пикселей на цифровом изображении.

Непрерывные и дискретные сигналы:

Непрерывный аналоговый сигнал определен на всем промежутке времени, то есть мы в любой момент времени t можем узнать значение сигнала x. Если мы возьмем эти значения с периодом дискретизации T, то мы получаем дискретный сигнал, значение которого определены только в конкретные моменты времени.

Дискретный сигнал теперь записываем как x[n], и n это номера отчетов дискретной последовательности. Если взглянуть на процесс дискретизации с точки зрения математики, то выходная дискретная последовательность с x[n] формируется, когда мы подставляем в нашу функцию x(t) значение времени t равный nT, где n — это номер дискретного отчета, а T — это период дискретизации.

Периодические сигналы

Периодический сигнал это сигнал, форма которого повторяется во времени. Повторяться во времени может, как форма непрерывных сигналов, так и форма дискретных сигналов. Периодом сигнала называем интервал повторения.

К примеру, у дискретного сигнала y[n] форма повторяется каждые 4, 8, 12 и так далее отчетов, для непрерывного сигнала z[t] форма повторяется каждые 2, 4, 6 и так далее секунд.

Фундаментальным или основным периодом сигналом называется наименьший интервал повторения, то есть для нашего дискретного сигнала y[n] это 4 отчета, а для нашего непрерывно сигнала это две секунды.

Фундаментальная частота

От понятие фундаментального периода мы можем перейти к понятию фундаментальной частоты. Фундаментальная или основная частота также именуемая первая гармоника, это количество основных периода сигнала, приходящихся на единицу времени. Частота измеряется в Герцах, то есть в количестве периодов приходящейся на одну секунду, и фактически является обратной величиной основного периода.

Если мы рассмотрим наш непрерывный сигнал z[t] его основной период равен двум секундам, а это значит, что на одну секунду приходится ровно половина его периода.

Основная частота дискретного сигнала

Но если с непрерывным сигналом все более менее понятно, то есть можем взглянуть на него на временной оси, оценить величины основного периода и подсчитать значение основной частоты, то с дискретным сигналом все не так просто.

Нам доступны значение отчетов, мы знаем их номера в последовательности, но мы не знаем, как они соотносятся с его фундаментальной частотой, и как они соотносятся с частотой дискретизации. Давайте в этом попробуем разобраться на примере.

Возьмем дискретный сигнал, который мы используем для описания в предыдущих статьях. Он имеет период в 4 отчета, где два первых отчета в периоде имеют большую амплитуду, а два последних отчета имеют малую амплитуду.

Нашей задачи в данном примере будет при помощи такого сигнала услышать ноту ля первой октавы, то есть частоту 440 Гц. Для того чтобы это сделать нам обязательно надо понять, как основная частота соотносится с частотой дискретизации сигнала.

Для этого давайте перенесем наш сигнал на временную ось. Основной период данного сигнала высчитывается также, как для непрерывного сигнала, то есть это обратная величина его фундаментальной частоты, в нашем случае единицы делить на 440. Но мы также видим то, что период дискретизации нашего сигнала, обозначим здесь его как ∆t в 4 раза меньше, чем основной период, так как на основной период приходится ровно 4 отсчета.

Выразим частоту дискретизации через период дискретизации, частоту дискретизации можно записать, как единицу делить на ∆t, что получить равно 4 делить на T₀, то есть в нашем случае частота дискретизации должна быть в 4 раза больше, чем наша фундаментальная частота ноты ля первой октавы.

Изменение частоты дискретизации

Если мы рассмотрим наши манипуляции над дискретным сигналом, как манипуляции на аналоговом сигнале, а после этого дискретизацию аналогового сигнала, то вот к чему мы приходим. Когда мы увеличиваем частоту дискретизации, то мы фактически берем дискретные отчеты более быстрого аналогового сигнала, или кладем отчеты того же дискретного сигнала на другую временную сетку.

К примеру, наш дискретный сигнал с периодом дискретизации ∆t можно представить как оцифрованные значения аналогового сигнала с периодом Т₀,

Если теперь те же самые отчеты сигнала, мы положим на более плотную временную сетку с меньшим периодом ∆t, это фактически то же самое как если мы оцифровали более быстрый аналоговый сигнал с меньшим периодом Т₀.

В качестве эталонного, аналогового сигнала мы представили синусоиду, а почему мы так часто используем синусоиду, когда говорим о цифровой обработки сигналов об этом в следующей статье.

Звук.

Звук – это звуковая волна, у которой непрерывно меняется амплитуда и частота. При этом амплитуда определяет громкость звука, а частота — его тон. Чем больше амплитуда звуковых колебаний, тем он громче. А частота писка комара больше частоты сигнала автомобиля. Частоту измеряют в Герцах. 1Гц — это одно колебание в секунду.

Кодирование звука.

Компьютер является мощнейшим устройством для обработки различных типов информации, в том числе и звуковой. Но аналоговый звук непригоден для обработки на компьютере, его необходимо преобразовать в цифровой. Для этого используются специальные устройства — аналого-цифровые преобразователи или АЦП. В компьютере роль АЦП выполняет звуковая карта. Каким же образом АЦП преобразует сигнал из аналогового в цифровой вид? Давайте разберемся.

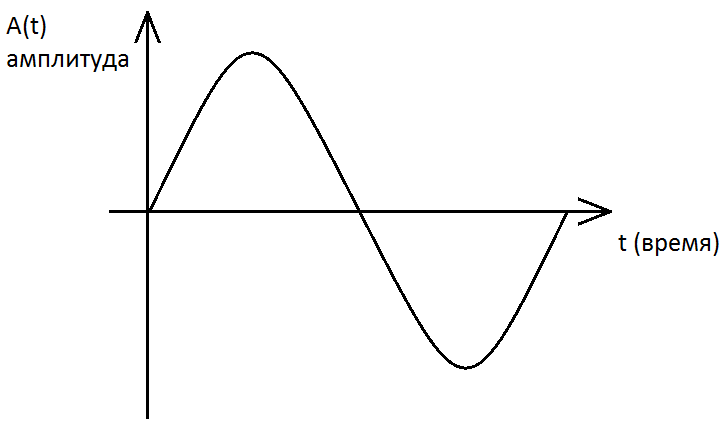
Пусть у нас есть источник звука с частотой 440Гц, пусть это будет гитара. Сначала звук нужно превратить в электрический сигнал. Для этого используем микрофон. На выходе микрофона мы получим электрический сигнал с частотой 440Гц. Графически он выглядит таким образом:

Следующая задача — преобразовать этот сигнал в цифровой вид, то есть в последовательность цифр. Для этого используется временная дискретизация — аналоговый звуковой сигнал разбивается на отдельные маленькие временные участки и для каждого такого участка устанавливается определенная величина интенсивности звука, которая зависит от амплитуды. Другими словами через какие-то промежутки времени мы измеряем уровень аналогового сигнала. Количество таких измерений за одну секунду называется частотой дискретизации. Частота дискретизации измеряется в Герцах. Соответственно, если мы будет измерять наш сигнал 100 раз в секунду, то частота дискретизации будет равна 100Гц.

Вот примеры некоторых используемых частот дискретизации звука:

• 8 000 Гц — телефон, достаточно для речи;
• 11 025 Гц;
• 16 000 Гц;
• 22 050 Гц — радио;
• 32 000 Гц;
• 44 100 Гц — используется в Audio CD;
• 48 000 Гц — DVD, DAT;
• 96 000 Гц — DVD-Audio (MLP 5.1);
• 192 000 Гц — DVD-Audio (MLP 2.0);
• 2 822 400 Гц — SACD, процесс однобитной дельта-сигма модуляции, известный как DSD — Direct Stream Digital, совместно разработан компаниями Sony и Philips;
• 5,644,800 Гц — DSD с удвоенной частотой дискретизации, однобитный Direct Stream Digital с частотой дискретизации вдвое больше, чем у SACD. Используется в некоторых профессиональных устройствах записи DSD.

Современные звуковые карты способны оцифровывать звук с частотой дискретизации 96Кгц и даже 192 кГц.

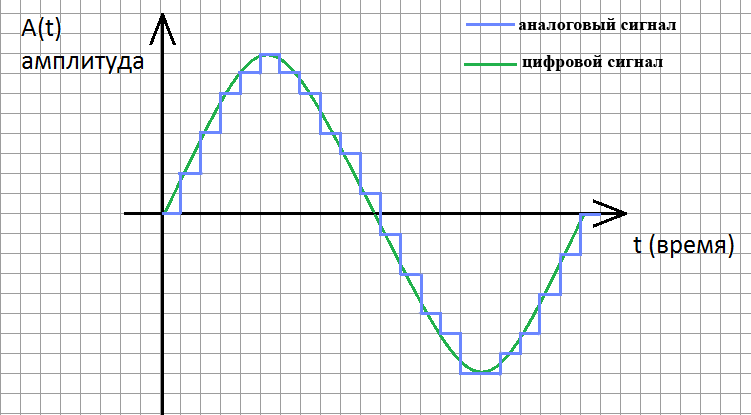
В итоге наш аналоговый сигнал превратится в цифровой, а график станет уже не гладким, а ступенчатым, дискретным:

Глубина кодирования звука — это количество возможных уровней сигнала. Другими словами глубина кодирования это точность измерения сигнала. Глубина кодирования измеряется в битах. Например, если количество возможных уровней сигнала равно 255, то глубина кодирования такого звука 8 бит. 16-битный звук уже позволяет работать с 65536 уровнями сигнала. Современные звуковые карты обеспечивают глубину кодирования в 16 и даже 24 бита, а это возможность кодирования 65536  и 16 777 216 различных уровней громкости соответственно.

Зная глубину кодирования, можно легко узнать количество уровней сигнала цифрового звука.  Для этого используем формулу:

N=2ⁱ,

где N — количество уровней сигнала, а i — глубина кодирования.

Например, мы знаем, что глубина кодирования звука 16 бит. Значит количество уровней цифрового сигнала равно 2¹⁶=65536.

Чтобы определить глубину кодирования если известно количество возможных уровней применяют эту же формулу. Например, если известно, что сигнал имеет 256 уровней сигнала, то глубина кодирования составит 8 бит, так как 2⁸=256.

Как понятно из данного вышеприведенного рисунка, чем чаще мы будем измерять уровень сигнала, т.е. чем выше частота дискретизации и чем точнее мы будем его измерять, тем более график цифрового сигнала будет похож на аналоговый график, соответственно, тем выше качество цифрового звука мы получим. И тем больший объем будет иметь файл.

Кроме того, мы рассматривали монофонический (одноканальный) звук, если же звук стереофонический, то размер файла увеличивается в 2 раза, так как он содержит 2 канала.

Рассмотрим пример задачи.

Какой объем будет иметь звуковой монофонический файл содержащий звук, если длительность звука 1 минута, глубина кодирования 8 бит, а частота дискретизации 22050Гц?

Зная частоту дискретизации и длительность звука легко установить количество измерений уровня сигнала за все время. Если частота дискретизации 22050Гц — значит за 1 секунду происходит 22050 измерений, а за минуту таких измерений будет 22050*60=1 323 000.

На одно измерение требуется 8 бит памяти, следовательно на 1 323 000 измерений потребуется 1 323 000*8 = 10 584 000 бит памяти. Разделив полученное число на 8 получим объем файла в байтах — 10584000/8=1 323 000 байт. Далее, разделив полученное число на 1024 получим объем файла в килобайтах — 1 291,9921875 Кбайт. А разделив полученное число еще раз на 1024 и округлив до сотых получим размер файла в мегабайтах — 1 291,9921875/1024=1,26Мбайт.

Ответ: 1,26Мбайт.

Автор:

Преобразование Фурье для дискретного сигнала. Определим связь между спектром X(jw) аналогового сигнала x(t) и спектром X_Т(jw) дискретного сигнала x_Т(t), определенного моделью (19.2). Учитывая, что x_Т(t) = x(t)f(t) согласно теоремы свертки (9.30) получим спектральную плотность дискретного сигнала

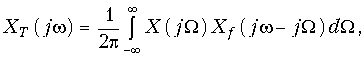(19.4)

где X_f(jw) – спектральная плотность дискретизирующей последовательности (19.1).

Для нахождения X_f(jw) разложим f(t) в комплексный ряд Фурье (5.6):

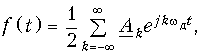(19.5)

где w_д = 2p/Т – частота дискретизации,

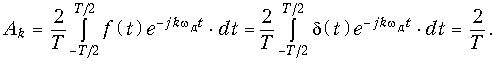
Отсюда согласно (9.42) получаем

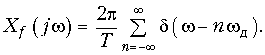(19.6)

Подставив (19.6) в формулу (19.4) после изменения порядка интегрирования и суммирования и с учетом фильтрующего свойства d-функции окончательно получим

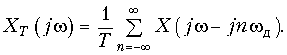(19.7)

Из (19.7) следует важный вывод: спектр дискретного сигнала x_T(t) (рис. 19.6 б) представляет собой сумму бесконечно большого числа «копий» спектра аналогового сигнала (рис. 19.6, а), расположенных на оси частот через одинаковые интервалы.

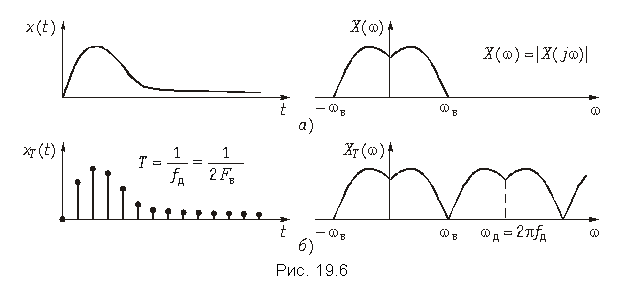
Следует отметь, что согласно (19.7) и рис. 19.6, б энергия спектра дискретного сигнала оказывается бесконечно велика, что является следствием идеализации реального сигнала моделью (19.2). Если же использовать вместо дискретизирующей последовательности (19.1) последовательность импульсов конечной энергии (например, прямоугольных импульсов), то получим спектр X_Т(jw), энергия которого убывает с ростом w («копии» X(jw) с ростом w уменьшаются). В то же время следует еще раз подчеркнуть, что представление дискретного сигнала в форме (19.2) существенно упрощает анализ дискретных сигналов и цепей и широко используется в расчетах.

Спектр дискретного сигнала X_Т(jw) можно найти и непосредственно из прямого преобразования Фурье (9.6) для дискретного сигнала (действует в момент t Õ 0).

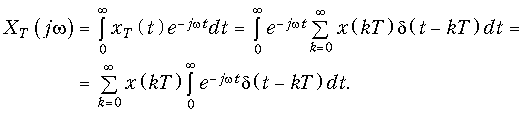
Отсюда с учетом фильтрующего свойства d-функции получим прямое преобразование Фурье для дискретных сигналов.

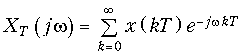(19.8)

и обратное преобразование Фурье:

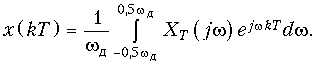(19.8)

На практике в формулах (19.8), (19.9) часто вместо зависимости X_Т(jw) рассматривают зависимости X_Т(jf), которые легко можно получить путем замены w = 2pf.

Пример. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета x_Т(t) = [a; 0; 0; 0; …].

Воспользуемся формулой (19.8), в которую подставим значения x_t(t) заданного сигнала

.

Пример. Рассчитаем спектр экспоненциальной дискретной функции x_Т(t) = 0,5^k, k 0.

График дискретной функции x_Т(t) приведен на рис. 19.7, а ее отсчеты можно записать в виде последовательности x{k} = {1; 0,5; 0,25; 0,125; 0,0625; …}.

Спектр дискретной экспоненты рассчитаем по формуле (19.8)

где для суммирования ряда использована формула

.

Используя формулу Эйлера , получим выражение для расчета спектра амплитуд X(f).

.

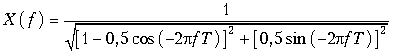Для построения графика будем задавать значения f от 0 до 1/Т с шагом 0,1/T и рассчитывать X(f).

График спектра амплитуд X(f) экспоненциальной дискретной функции x_T(t) = 0,5^k приведен на рисунке 19.8.

Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом f_д = 1/Т.

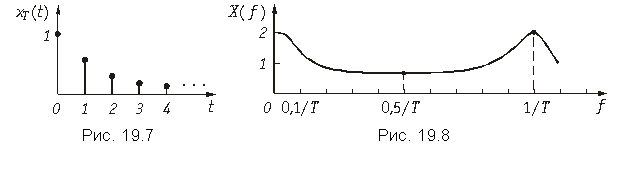
Следует отметить, что если не выполняется условие теоремы Котельникова: f_д 2f_в, то спектры в (19.7) частично перекрываются. На рис. 19.9, рис. 19.10 показан характер изменения спектра дискретного сигнала X_T(f) при изменении частоты дискретизации сигнала x_T(t), ограниченного во времени интервалом T_с (рис. 19.9) и неограниченного во времени (рис. 19.10).

Как следует из представленных графиков увеличение периода дискретизации T > 1/2F_в; F_д < 2F_в приводит к наложению смежных спектров в (19.7), что приводит к наложению спектра Х_T(f). Эти искажения называются ошибками наложения. Чтобы их устранить необходимо частоту дискретизации увеличить до F_д 2F_в.

Пример. Рассчитаем интервал дискретизации и минимально допустимую частоту дискретизации сигнала, спектральная плотность которого равна нулю при значениях частоты выше 100 кГц.

Из условия задачи следует, что граничная частота спектра F^в равна 100 кГц. Тогда в соответствии с теоремой Котельникова имеем интервал дискретизации

.

Минимально допустимая частота дискретизации f_д = 2F^в = 2×100 = 200 кГц.

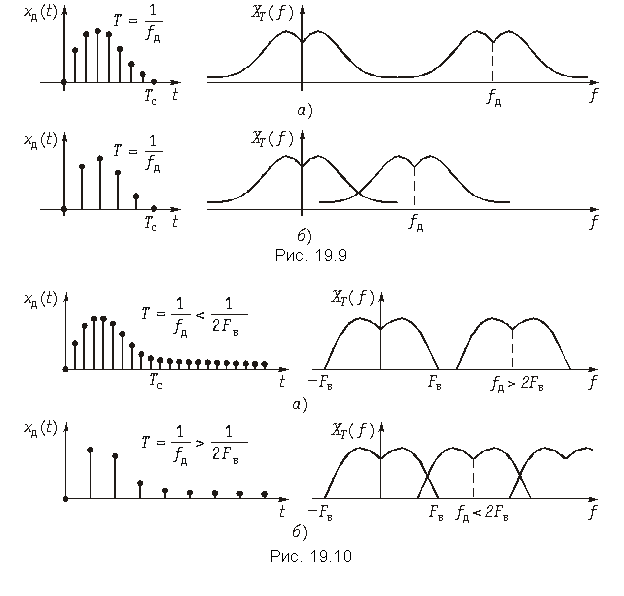
Пример. Определим дискретные отсчеты сигнала длительностью t_и = 3 мс, приведенного на рис. 19.11, а, если в качестве граничной частоты спектра F^в принять значение 3/t_и, выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным.

Хотя сигнал конечной длительности имеет бесконечный спектр частот, однако почти всегда можно определить граничную частоту спектра таким образом, чтобы отсекание частот превышающих F^в, привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.

Граничная частота спектра F^в = 3/t_и = 3/(3×10³) = 1 кГц.

Интервал дискретизации T = 1/(2F^в) = 1/(2×1×10³) = 0,5 мс.

Берем отсчеты сигнала, приведенного на рис. 19.11, а, через интервал времени T = 0,5 мс и получаем последовательность x{k} = {0; 2; 3,2; 4; 1; 0,3; 0}, изображенную графически на рис. 19.11, б.

Отметим, что аналоговый сигнал x(t) можно полностью восстановить по его дискретным отсчетам x(kT) с помощью ФНЧ, частота среза которого w_с = 0,5w_д = w_в. Этот вывод хорошо иллюстрирует рис. 19.10, а из которого видно, что спектр сигнала на выходе ФНЧ совпадает со спектром аналогового сигнала x(t).

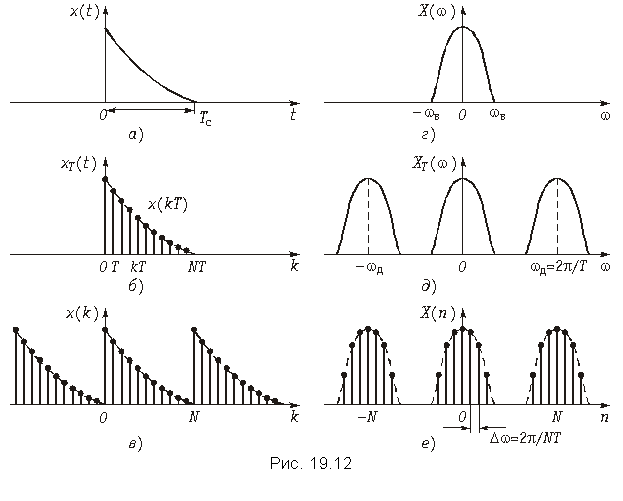
Дискретное преобразования Фурье. Как следует из формулы (19.7) X_T(jw) имеет периодическую структуру с w_д = 2p/T. Причем, как и спектр аналогового сигнала X(jw) спектр дискретного сигнала X_T(jw) является сплошным (см. рис. 19.6, б). Вместе с тем при цифровой обработке сигналов используется не только дискретизация во времени, но и дискретизация в частотной области.

Для сигнала x(t) ограниченного во времени интервалом T_с (рис. 19.12, а) справедлива обратная теорема Котельникова, которая может быть получена из (19.3) путем заменыt ->w; w_в->T_с/2; Т-> Dw:

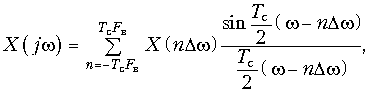(19.10)

где Dw = 2p/T_с; T_с – длительность сигнала;X(nDw) – отсчеты спектра сигнала в частотной области.

Переходя к дискретному сигналу x_T(t) (рис. 19.12, б) отметим, что общее количество отсчетов сигнала будет равно

где T = 2p/w_д = p/w_в.

Дискретный спектр (рис. 19.12, е) может быть получен путем периодического повторения последовательности {x(kT)} с периодом T_с = NT (рис. 19.12, в). При этом частотный интервал между дискретными отсчетами спектра (рис. 19.12, е) составляет

(19.11)

С учетом вышеизложенного дискретное преобразование Фурье (ДПФ) можно получить, если в преобразовании (19.8) сделать замену w = nDw. Тогда получим

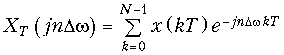
или с учетом (19.11)

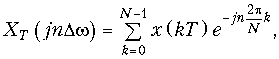(19.12)

где n = 0; ±1; ±2; ± … N/2.

Для упрощения записи аргумент nDw и kT обычно заменяют индексом n и k соответственно и опускают индекс T, при этом (19.12) примет вид

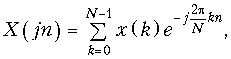(19.13)

которое определяет прямое ДПФ.

С помощью (19.13) можно определить отсчеты спектра X(jn) по временным отсчетам сигнала x(k).

Обратное ДПФ можно получить из (19.13) воспользовавшись дуальностью прямого и обратного преобразований Фурье:

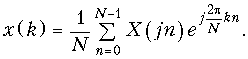(19.14)

При k < 0 обратное преобразование Фурье определит x(k), расположенную слева от 0 (рис. 19.12, в).

Для ДПФ по аналогии с непрерывными преобразованиями Фурье справедливы основные теоремы и свойства.

В частности, свойство линейности

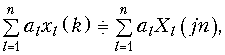(19.15)

сдвиг дискретного сигнала:

(19.16)

т. е. сдвиг последовательности отсчетов сигнала на m интервалов приводит лишь к изменению фазового спектра дискретного сигнала.

Теорема свертки:

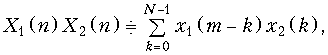(19.17)

где N = N₁ + N₂; N₁, N₂ – число отсчетов х₁ и х₂ соответственно.

Аналогично можно записать и другие теоремы для ДПФ. Заметим, что ДПФ можно использовать для определения не только спектра дискретных сигналов, но и спектра аналоговых сигналов, для чего его необходимо дискретизировать согласно теоремы Котельникова (19.3).

Пример. Рассчитаем ДПФ дискретного периодического сигнала, заданного тремя отсчетами x{k} = {0; 1; 2}.

Для расчета воспользуемся формулой ДПФ (19.13).

Поскольку

, ,

то ,

.

Графики заданного дискретного периодического сигнала x(k) и рассчитанного дискретного периодического спектра амплитуд X(n) приведены на рис. 19.13.

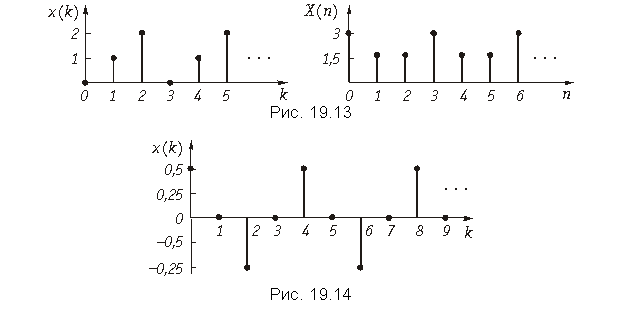
Пример. Рассчитаем значения дискретного сигнала x(k), ДПФ которого имеет вид X[n] = {0; 1; 0; 1}.
Значения дискретного сигнала x(k) будем рассчитывать по формуле (19.14)

;

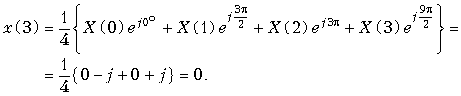
График последовательности x{k} = {0,5; 0; –0,5; 0} приведен на рис. 19.14. Сигнал x(k) дискретный и периодический.

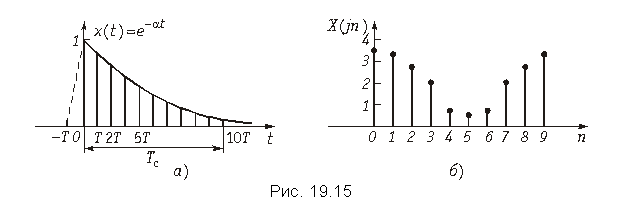
Пример. Определить с помощью ДПФ спектр аналогового сигнала, изображенного на рис. 19.15, а.

Ограничим длительность сигнала T_c, где (рис. 9.15, а). Например, при T_c = 3/a, . Выберем число отсчетов N = 10, определим частоту дискретизации

Согласно (19.13) находим отсчеты спектра сигнала

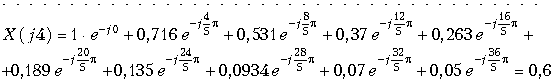
и т.д.

В таблице приведены результаты расчета спектра,

а на рис. 19.15, б спектр сигнала X(jn). Следует отметить, что с увеличением T (уменьшение числа отсчетов N) погрешность аппроксимации x(t) увеличивается (см. рис. 19.5, а).

Как следует из вышеприведенных примеров и формул (19.13), (19.14), для вычисления ДПФ содержащих N отсчетов необходимо осуществить в общем случае N² операций с комплексными числами. Если длина обрабатываемых массивов достаточно велика, то вычисление ДПФ даже на современных быстродействующих ЭВМ занимает достаточно много времени. Для сокращения вычислений используют обычно алгоритм быстрого преобразования Фурье (БПФ). Существует много разновидностей БПФ. Здесь мы рассмотрим один алгоритм, основанный на прореживании по времени.

Быстрое преобразование Фурье. Положим, что число отсчетов N = 2^q, где q – целое число. Разобьем дискретную последовательность отсчетов {x(k)} не две части:

четную {x(k)}_чт = {x(2k)}

и нечетную {x(k)}_нч = {x(2k + 1)}, где k = 0, 1, 2, … N/2 – 1.

Представим спектр (19.13) в виде

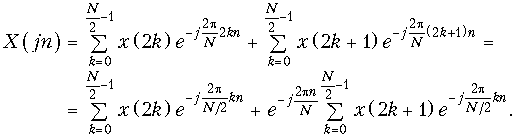(19.18)

Из (19.18) следует, что

(19.19)

где n = 0, 1, 2, …, ((N/2) – 1).

Из (19.19) следует, что первая половина X(jn) (n = 0, 1, 2, …, (N/2) – 1) выражается через ДПФ двух частных последовательностей: X_чт(jn) и X_нч(jn). Вторую половину (n N/2) X(jn) можно найти, если учесть периодичность его четной и нечетной части с периодом N/2:

и соотношение (при n N/2):

при этом получим

(19.20)

Формула (19.19) и (19.20) лежит в основе БПФ. Как следует из этих формул для вычисления X_чт(jn) и X_нч(jn) требуется (N/2)² операций и для выполнения операции умножения на exp{×} – N операций:

(19.21)

Для ДПФ (19.13) требуется операций, что существенно выше, чем N_БПФ. Например, при N = 10³, получаем N_ДПФ = 10⁶, а N_БПФ ~ 250×10³, т. е. для БПФ требуется в четыре раза меньше операций, чем при ДПФ.

В общем случае число операций, необходимое в БПФ равно

(19.22)

и выигрыш по сравнению с ДПФ равно

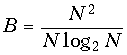(19.23)

и может достигать сотен и тысяч раз при достаточно больших входных массивах N.

В заключении отметим, что сам процесс вычисления по формулам (19.18), (19.19) производят по итерационному принципу: последовательность отсчетов с четными и нечетными номерами снова разбивают на две части и т. д. Процесс разбиения продолжается до тех пор, пока не получится последовательность, состоящая из одного элемента (исходного ДПФ). Более подробно с алгоритмами БПФ можно ознакомиться в специальной литературе (см. например, Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. М. «Радио и связь. 1990).