Как найти частоту электромагнитной волны в вакууме

Была ли эта статья полезной?

Длина, скорость и частота электромагнитной волны.

Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение,
видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.

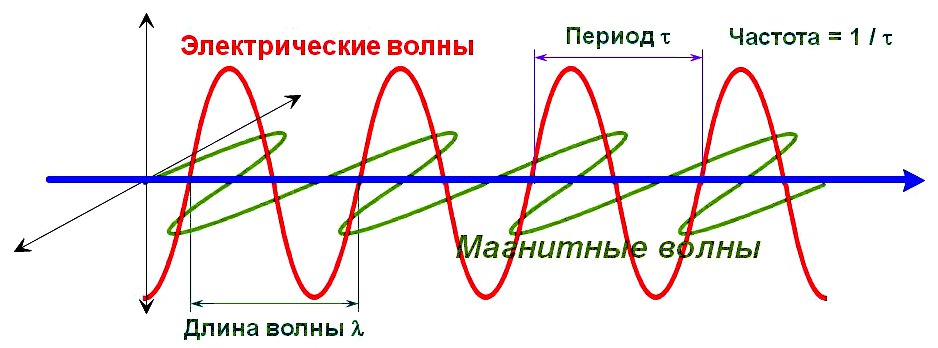
Электромагнитные колебания – это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении
напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны
(Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое
излучение, рентгеновские либо гамма-лучи.

Рис.1

Длина волны, обозначаемая буквой λ и измеряемая в метрах –
это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.

Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс
повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.

Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).

Скорость распространения электромагнитных волн в вакууме (v) равна скорости
света и составляет величину:
v = С = 299792458 м/сек.
В среде эта скорость уменьшается: v = С / n, где
n > 1 – это показатель преломления среды.
Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому
с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве.

Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).

И окончательно для воздушной среды:

λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).

Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн,
которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.

Диапазон	Полоса частот	Длина волны
Сверхдлинные радиоволны	3…30 кГц	100000…10000 м
Длинные радиоволны	30…300 кГц	10000…1000 м
Средние радиоволны	300…3000 кГц	1000…100 м
Короткие радиоволны	3…30 МГц	100…10 м
Метровый радиодиапазон	30…300 МГц	10…1 м
Дециметровый радиодиапазон	300…3000 МГц	1…0,1 м
Сантиметровый СВЧ диапазон	3…30 ГГц	10…1 см
Микроволновый СВЧ диапазон	30…300 ГГц	1…0,1 см
Инфракрасное излучение	0,3…405 ТГц	1000…0,74 мкм
Красный цвет	405…480 ТГц	740…625 нм
Оранжевый цвет	480…510 ТГц	625…590 нм
Жёлтый цвет	510…530 ТГц	590…565 нм
Зелёный цвет	530…600 ТГц	565…500 нм
Голубой цвет	600…620 ТГц	500…485 нм
Синий цвет	620…680 ТГц	485…440 нм
Фиолетовый цвет	680…790 ТГц	440…380 нм
Ультрафиолетовое излучение	480…30000 ТГц	400…10 нм
Рентгеновское излучение	30000…3000000 ТГц	10…0,1 нм
Гамма излучение	3000000…30000000 ТГц	0,1…0,01 нм

А теперь можно переходить к калькуляторам.

КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ

Частота электромагнитных колебаний f
Показатель преломления среды (по умолч. 1)
Длина волны

КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ

Длина электромагнитной волны в вакууме λ
Частота

В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь
существует некоторая путаница. Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме,
т. е. численно равной Kp = 1/n, где n – это, как мы помним, показатель преломления среды.
Другие, наоборот – как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.
Поэтому надо иметь в виду – если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а
если Kp < 1, то n = 1/Kp.

2.6. Электромагнитные волны

Любой колебательный контур излучает энергию. Изменяющееся электрическое поле возбуждает в окружающем пространстве переменное магнитное поле, и наоборот. Математические уравнения, описывающие связь магнитного и электрического полей, были выведены Максвеллом и носят его имя. Запишем уравнения Максвелла в дифференциальной форме для случая, когда отсутствуют электрические заряды () и токи (j = 0):

Величины и — электрическая и магнитная постоянные, соответственно, которые связаны со скоростью света в вакууме соотношением

Постоянные и характеризуют электрические и магнитные свойства среды, которую мы будем считать однородной и изотропной.

В отсутствие зарядов и токов невозможно существование статических электрического и магнитного полей. Однако переменное электрическое поле возбуждает магнитное поле, и наоборот, переменное магнитное поле создает электрическое поле. Поэтому имеются решения уравнений Максвелла в вакууме, в отсутствие зарядов и токов, где электрические и магнитные поля оказываются неразрывно связанными друг с другом. В теории Максвелла впервые были объединены два фундаментальных взаимодействия, ранее считавшихся независимыми. Поэтому мы говорим теперь об электромагнитном поле.

Колебательный процесс в контуре сопровождается изменением окружающего его поля. Изменения, происходящие в окружающем пространстве, распространяются от точки к точке с определенной скоростью, то есть колебательный контур излучает в окружающее его пространство энергию электромагнитного поля.

Электромагнитная волна — это распространяющееся в пространстве электромагнитное поле, в котором напряженность электрического и индукция магнитного полей изменяются по периодическому закону.

При строго гармоническом изменении во времени векторов и электромагнитная волна называется монохроматической.

Получим из уравнений Максвелла волновые уравнения для векторов и .

Волновое уравнение для электромагнитных волн

Как уже отмечалось в предыдущей части курса, ротор (rot) и дивергенция (div) — это некоторые операции дифференцирования, производимые по определенным правилам над векторами. Ниже мы познакомимся с ними поближе.

Возьмем ротор от обеих частей уравнения

При этом воспользуемся доказываемой в курсе математики формулой:

где — введенный выше лапласиан. Первое слагаемое в правой части равно нулю в силу другого уравнения Максвелла:

Получаем в итоге:

Выразим rotB через электрическое поле с помощью уравнения Максвелла:

и используем это выражение в правой части (2.93). В результате приходим к уравнению:

и вводя показатель преломления среды

запишем уравнение для вектора напряженности электрического поля в виде:

Сравнивая с (2.69), убеждаемся, что мы получили волновое уравнение, где v — фазовая скорость света в среде:

Взяв ротор от обеих частей уравнения Максвелла

и действуя аналогичным образом, придем к волновому уравнению для магнитного поля:

Полученные волновые уравнения для и означают, что электромагнитное поле может существовать в виде электромагнитных волн, фазовая скорость которых равна

В отсутствие среды (при ) скорость электромагнитных волн совпадает со скоростью света в вакууме.

Основные свойства электромагнитных волн

Рассмотрим плоскую монохроматическую электромагнитную волну, распространяющуюся вдоль оси х:

Возможность существования таких решений следует из полученных волновых уравнений. Однако напряженности электрического и магнитного полей не являются независимыми друг от друга. Связь между ними можно установить, подставляя решения (2.99) в уравнения Максвелла. Дифференциальную операцию rot, применяемую к некоторому векторному полю А можно символически записать как детерминант:

Подставляя сюда выражения (2.99), зависящие только от координаты x, находим:

Дифференцирование плоских волн по времени дает:

Тогда из уравнений Максвелла следует:

Отсюда следует, во-первых, что электрическое и магнитное поля колеблются в фазе:

Далее, ни у , ни у нет компонент параллельных оси х:

Иными словами и в изотропной среде,

электромагнитные волны поперечны: колебания векторов электрического и магнитного полей происходят в плоскости, ортогональной направлению распространения волны.

Тогда можно выбрать координатные оси так, чтобы вектор был направлен вдоль оси у (рис. 2.27):

Рис. 2.27. Колебания электрического и магнитного полей в плоской электромагнитной волне

В этом случае уравнения (2.103) приобретают вид:

Отсюда следует, что вектор направлен вдоль оси z:

Иначе говоря, векторы электрического и магнитного поля ортогональны друг другу и оба — направлению распространения волны. С учетом этого факта уравнения (2.104) еще более упрощаются:

Отсюда вытекает обычная связь волнового вектора, частоты и скорости:

а также связь амплитуд колебаний полей:

Отметим, что связь (2.107) имеет место не только для максимальных значений (амплитуд) модулей векторов напряженности электрического и магнитного поля волны, но и для текущих — в любой момент времени.

Итак, из уравнений Максвелла следует, что электромагнитные волны распространяются в вакууме со скоростью света. В свое время этот вывод произвел огромное впечатление. Стало ясно, что не только электричество и магнетизм являются разными проявлениями одного и того же взаимодействия. Все световые явления, оптика, также стали предметом теории электромагнетизма. Различия в восприятии человеком электромагнитных волн связаны с их частотой или длиной волны.

Шкала электромагнитных волн представляет собой непрерывную последовательность частот (и длин волн) электромагнитного излучения. Теория электромагнитных волн Максвелла позволяет установить, что в природе существуют электромагнитные волны различных длин, образованные различными вибраторами (источниками). В зависимости от способов получения электромагнитных волн их разделяют на несколько диапазонов частот (или длин волн).

На рис. 2.28 представлена шкала электромагнитных волн.

Рис. 2.28. Шкала электромагнитных волн

Видно, что диапазоны волн различных типов перекрывают друг друга. Следовательно, волны таких длин можно получить различными способами. Принципиальных различий между ними нет, поскольку все они являются электромагнитными волнами, порожденными колеблющимися заряженными частицами.

Уравнения Максвелла приводят также к выводу о поперечности электромагнитных волн в вакууме (и в изотропной среде): векторы напряженности электрического и магнитного полей ортогональны друг другу и направлению распространения волны.

http://www.femto.com.ua/articles/part_1/0560.html – Волновое уравнение. Материал из Физической Энциклопедии.

http://elementy.ru/trefil/24 – Уравнения Максвелла. Материал из «Элементов».

http://telecomclub.org/?q=node/1750 – Уравнения Максвелла и их физический смысл.

http://principact.ru/content/view/188/115/ – Кратко об уравнениях максвелла для электромагнитного поля.

Эффект Доплера для электромагнитных волн

Пусть в некоторой инерциальной системе отсчета К распространяется плоская электромагнитная волна. Фаза волны имеет вид:

Наблюдатель в другой инерциальной системе отсчета К’, движущейся относительно первой со скоростью V вдоль оси x, также наблюдает эту волну, но пользуется другими координатами и временем: t’, r’. Связь между системами отсчета дается преобразованиями Лоренца:

Подставим эти выражения в выражение для фазы , чтобы получить фазу волны в движущейся системе отсчета:

Это выражение можно записать как

где и — циклическая частота и волновой вектор относительно движущейся системы отсчета. Сравнивая с (2.110), находим преобразования Лоренца для частоты и волнового вектора:

Для электромагнитной волны в вакууме

Пусть направление распространения волны составляет в первой системе отсчета угол с осью х:

Тогда выражение для частоты волны в движущейся системе отсчета принимает вид:

Это и есть формула Доплера для электромагнитных волн.

Если , то наблюдатель удаляется от источника излучения и воспринимаемая им частота волны уменьшается:

Если , то наблюдатель приближается к источнику и частота излучения для него увеличивается:

При скоростях V 2 (солнечная постоянная). Найдем среднюю амплитуду колебаний E₀ вектора электрической напряженности в солнечном излучении. Вычислим амплитуды колебаний напряженности магнитного поля H₀ и вектора магнитной индукции B₀ в волне.

Ответ находим сразу из уравнений (3.127), где полагаем :

Электромагнитные волны поглощаются и отражаются телами, следовательно, они должны оказывать на тела давление. Рассмотрим плоскую электромагнитную волну, падающую нормально на плоскую проводящую поверхность. В этом случае электрическое поле волны возбуждает в теле ток, пропорциональный Е. Магнитное поле волны по закону Ампера будет действовать на ток с силой, направление которой совпадает с направлением распространения волны. В 1899 г. в исключительно тонких экспериментах П.И. Лебедев доказал существование светового давления. Можно показать, что волна, несущая энергию W, обладает и импульсом:

Пусть электромагнитная волна падает в вакууме по нормали на площадь А и полностью поглощается ею. Предположим, что за время площадка получила от волны энергию . Тогда переданный площадке импульс равен

На площадку действует со стороны волны сила

Давление Р, оказываемое волной, равно

Если средняя плотность энергии в волне равна , то на площадь А за время попадет энергия из объема и

Отсюда находим давление электромагнитной волны (света):

Если площадка идеально отражает всю падающую на нее энергию, то давление будет в два раза большим, что объясняется очень просто: одинаковый вклад в давление в этом случае дают как падающая, так и отраженная волны, в случае полностью поглощающей поверхности отраженной волны просто нет.

Пример 3. Найдем давление Р солнечного света на Землю. Используем значение солнечной постоянной из предыдущего примера. Искомое давление равно:

Пример 4. Найдем давление Р лазерного пучка на поглощающую мишень. Выходная мощность лазера N = 4.6 Вт, диаметр пучка d = 2.6 мм.

Волновое число: физический смысл, размерность, формулы, примеры расчета

Вы хотите знать, в чем разница между волновым числом и угловым волновым числом и как их рассчитать? Тогда эта статья как раз для вас. Мы подробно объясним эту тему и покажем на примере, как можно рассчитать эти величины.

Если вы рассматриваете электромагнитную волну с определенной длиной волны, то волновое число является обратным этой длине волны — оно ведет себя противоположным образом. Например, если длина волны увеличивается, волновое число уменьшается. Если, с другой стороны, длина волны уменьшается, то волновое число увеличивается.

Волновое число в спектроскопии

Волновое число k определяется в спектроскопии как обратная величина длины волны λ, то есть ξ = 1 / λ (называется еще пространственной частотой). Однако его также можно выразить через частоту f и скорость света в вакууме c, тогда ξ = f / c или также через число n длин волн, укладывающихся в определенную длину l, то есть ξ = n / l .

В целом, для волнового числа применимо следующее соотношение: ξ = 1 / λ = f / c = n / l .

Важно: Волновое число ξ не следует путать с частотой f. Частота имеет единицу измерения Гц = 1 / с = с -1 и определяется через обратную величину периода T: f = 1 / T . Она показывает, как часто электромагнитная волна колеблется в секунду.

Единица измерения волнового числа

Обычно волновое число выражается в в следующих единицах измерения (в СИ): 1 / м = м -1 , что соответствует числу колебаний на метр. Однако единица может быть также преобразована, например, в единицы 1 / см = см -1 или 1 / мм = мм -1 .

Между этими единицами измерения существует следующая взаимосвязь: 1 м -1 = 0,01 см -1 = 0,001 мм -1 , соответственно 1 мм -1 = 100 см -1 = 1000 м -1 .

Разница между волновым числом и угловым волновым числом

Угловое волновое число часто ошибочно называют просто волновым числом. Однако, угловое волновое число k является величиной волнового вектора k и связано с волновым числом ξ следующим образом: k = | k | = 2*π*ξ = ω / c = 2*π / λ . В этой формуле где ω представляет собой так называемую угловую частоту. Волновой вектор — это вектор, перпендикулярный волновому фронту волны. Эта формула показывает, что волновое число ξ также может быть вычислено из углового волнового числа k: ξ = k / 2*π .

Важно: Угловую частоту и частоту также нельзя путать друг с другом. Угловая частота ω связана с частотой f следующим образом: ω = 2*π*f .

Физический смысл волнового числа.

Волновое число численно равно числу периодов волны, укладывающихся в отрезок 2π метров. Это пространственный аналог круговой частоты ω (рад·с -1 ). Характеристика периодического процесса в пространстве.

Пример расчета волнового числа

Если мы наблюдаем электромагнитную волну с длиной волны λ = 500 нм и хотим вычислить по ней волновое число ξ, то поступаем следующим образом. Чтобы получить размерность м -1 сначала переведите длину волны в метры. То есть 500 нм = 500 * 10 -9 м = 5*10 -7 м.

Используя представленную выше формулу, вы можете определить соответствующее волновое число: ξ = 1 / λ = 1 / 5*10 -7 = 2*10 6 м -1 .

На одном метре волна колеблется 2 миллиона раз. Если преобразовать единицу измерения, то можно сказать, что волна колеблется 2000 раз на одном миллиметре: 2 * 10 6 м -1 = 0,001 * 2 * 10 6 мм -1 = 2000 мм -1 .

Пример расчета углового волнового числа

Если использовать ту же длину волны λ = 500 нм =5 *10 -7 м, как в предыдущем примере, и подставьте это значение в формулу для расчета углового волнового числа, то это приведет к следующим результатам: k = 2 * π / λ = 2 * π / 5 *10 -7 м = 1,2566 * 10 7 м -1 .

Легко видеть, что угловое волновое число k отличается от волнового числа ξ из предыдущего примера:

ξ = 2*10 6 м -1 ↔ k = 1,2566 * 10 7 м -1

Преобразование длины волны в волновой число

В следующей таблице показаны два направления преобразования из длины волны в волновое число и наоборот. Кроме того, в последней колонке перечислены некоторые области применения спектроскопии:

волновой вектор

ВОЛНОВОЙ ВЕКТОР – вектор k, определяющий направление распространения и пространственный период плоской монохроматич. волны

где – постоянные амплитуда и фаза волны, – круговая частота, r – радиус-вектор. Модуль В. в. наз. волновым числом k=, где – пространственный период или длина волны. В направлении В. в. происходит наибыстрейшее изменение фазы волны , поэтому оно и принимается за направление распространения. Скорость перемещения фазы в этом направлении, или фазовая скорость , определяется через волновое число . При классич. описании волновых процессов с В. в. связана плотность импульса , где – плотность энергии. В квантовом пределе соответственно импульс . Направление переноса энергии волной, вообще говоря, может и не совпадать с направлением В. в., как это имеет место, напр., в анизотропных средах или даже в изотропных средах с аномальной дисперсией, где возможен перенос энергии в направлении, противоположном В. в.

Понятие о В. в. может быть обобщено на случай квазигармонич. волн вида , если ввести локальный В. в. и мгновенную частоту . Однако, однозначная интерпретация этих величин допустима только при выполнении неравенств:

где k; – декартовы составляющие В. в. (i, j=1, 2, 3). Эти условия устанавливают применимость лучевого описания волновых процессов (приближения геометрической оптики и геометрической акустики, квазиклассич. приближения).

Для эл–магн. гармонической волны (в вакууме) В. в. k и величина (с – скорость света) объединяются в единый волновой четырёхвектор, компоненты к-рого подчиняются при переходе от одной инерциальной системы отсчёта к другой (движущейся с относит. скоростью u) Лоренца преобразованием:

Первое из этих соотношений определяет Доплера аффект, второе – эффект аберрации углов прихода волн (или формируемых ими лучей).

M. А. Миллер, Г. В. Пермитин.

[spoiler title=”источники:”]

http://www.asutpp.ru/volnovoe-chislo.html

http://www.femto.com.ua/articles/part_1/0562.html

[/spoiler]