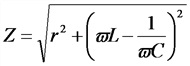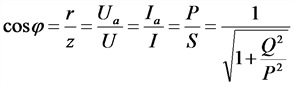Переменный ток имеет ряд важных характеристик, влияющих на его физические свойства. Одним из таких параметров является частота переменного тока. Если говорить с точки зрения физики, то частота – это некая величина, обратная периоду колебания тока. Если проще – то это количество полных циклов изменения ЭДС, произошедших за одну секунду.
Известно, что переменный ток заставляет электроны двигаться в проводнике сначала в одну сторону, потом — в обратную. Полный путь «туда-обратно» они совершают за некий промежуток времени, называемый периодом переменного тока. частота же является количеством таких колебаний за 1 секунду.
Васильев Дмитрий Петрович
Профессор электротехники СПбГПУ
Задать вопрос
В качестве единицы измерения частоты во всем мире принят 1 Гц (в честь немецкого ученого Г.Герца), который соответствует 1 периоду колебания за 1 секунду.
В республиках бывшего СССР стандартной считается частота тока в 50 Гц.
Это значит, что синусоида тока движется в течение 1 секунды 50 раз в одном направлении, и 50 — в обратном, 100 раз проходя чрез нулевое значение. Получается, что обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.
Для измерения частоты переменного тока применяют приборы, называемые частотомерами. Частотомеры используют несколько основных способов измерения, а именно:
Метод дискретного счета;
Метод перезаряда конденсатора;
Резонансный метод измерения частот.
Метод сравнения частот; в качестве:
Метод дискретного счета основывается на подсчете импульсов необходимой частоты за конкретный промежуток времени. Его наиболее часто используют цифровые частотомеры, и именно благодаря этому простому методу можно получить довольно точные данные.
Более подробно о частоте переменного тока Вы можете узнать из видео:
Метод перезаряда конденсатора тоже не несет в себе сложных вычислений. В этом случае среднее значение силы тока перезаряда пропорционально соотносится с частотой, и измеряется при помощи магнитоэлектрического амперметра. Шкала прибора, в таком случае, градуируется в Герцах.
Погрешность подобных частотомеров находится в пределах 2%, и поэтому такие измерения вполне пригодны для бытового использования.
Резонансный способ измерения базируется на электрическом резонансе, возникающем в контуре с подстраиваемыми элементами. Частота, которую необходимо измерить, определяется по специальной шкале самого механизма подстройки.
Абрамян Евгений Павлович
Доцент кафедры электротехники СПбГПУ
Задать вопрос
Такой метод дает очень низкую погрешность, однако применяется только для частот больше 50 кГц.
Метод сравнения частот применяется в осциллографах, и основан на смешении эталонной частоты с измеряемой. При этом возникают биения определенной частоты. Когда же частота этих биений достигает нуля, то измеряемая частота становится равной эталонной. Далее, по полученной на экране фигуре с применением формул можно рассчитать искомую частоту электрического тока.
Ещё одно интересное видео о частоте переменного тока:
Как определить частоту переменного тока
Содержание
- 1 Что такое частота
- 2 Как определяется
- 2.1 Измерение частоты
- 2.2 Расчёт частоты тока
- 3 Заключение
- 4 Видео по теме
В силу различных преимуществ большинство энергетических систем — от общегосударственных до бытовых, функционируют на переменном токе. Однако мало кто считается с тем, что кроме параметров напряжения и тока системы, важную роль играет также частота тока. Например, в функционале популярных мультитестеров измерение частоты переменного тока отсутствует. Между тем значения этой величины, которые выходят за требуемые пределы, грозят тяжёлыми последствиями. Мгновенно происходит разбалансированность системы энергоснабжения с неминуемыми катастрофическими последствиями для целых регионов.
Графическое отображение переменного тока
Что такое частота
Производство электроэнергии в подавляющем большинстве ситуаций называют контролируемым. Эту работу проделывают генераторы, преобразующие механическую энергию ротора турбины в электрическую. Как показано на схеме, на поверхности ротора имеется обмотка из медной проволоки, поэтому он представляет собой непрерывно вращающийся электромагнит.
Схематическое изображение генератора
Во время вращения ротора, созданное вокруг него магнитное поле, наводит электрический ток. Его направление периодически изменяется на противоположное, поскольку месторасположение полюсов электромагнита чередуется после каждого оборота ротора. Соответственно, ток тоже меняет своё направление два раза за цикл вращения.
Следствием и мерой скорости этих изменений является частота, которая измеряется количеством изменений месторасположения полюсов в секунду. Единица частоты получила наименование герц и обозначается двумя буквами — Гц. Таким образом, можно сказать, что генератор, который снабжён парой магнитных полюсов, вращающихся с угловой скоростью 3000 мин-1, будет производить ток частотой 50 Гц.
Мощность переменного тока изменяется по синусоидальному закону с чередованием положительных и отрицательных полюсов. При переходе каждого цикла из положительной области в отрицательную происходит соответствующее перемещение электронов. В конечном счете, эти циклы создают электрический нагрев или рассеивание мощности. Независимо от направления движения тока (т. е., положительного или отрицательного), если силы тока (напряжения) достаточно для удовлетворения требований электрического устройства, оно будет работать.
Синусоида переменного тока
Таким образом, количество полных циклов за секунду, когда переменный ток переходит от положительного полюса к отрицательному, называется частотой, а сам временной отрезок называется периодом. С точки зрения электрического тока частотой принято считать количество повторений синусоиды, а другими словами — это полное колебание, состоящее из положительной и отрицательной составляющих. Следовательно, частота и период связаны между собой обратно пропорциональной зависимостью:
Определение частоты
Частота и период переменного тока варьируются в зависимости от страны, причём не обязательно привязываются к местному стандарту напряжения. Например, в США, Канаде и других странах со стандартным линейным напряжением 110…120 В эталоном частоты является 60 Гц. В большинстве стран, где значения переменного напряжения равняются 220…240 В (в том числе и в нашей стране), за стандартную частоту принято 50 Гц, однако Южная Корея, Филиппины и многие страны Карибского бассейна используют 220…240 В с частотой 60 Гц. А есть ещё и Япония, где напряжение в сети достигает 100 В, но стандартная частота переменного тока в разных районах составляет 50 и 60 Гц.
Большинство электронных устройств могут работать, потребляя переменный ток, если его частота 50 или 60 Гц. Но, для электроприборов, использующих довольно мощные приводы, рассчитанные на конкретную частоту (холодильники, морозильники, стиральные и сушильные машины), разница в 10 Гц уже значительна. В первую очередь это касается устройств, включающихся периодически. Их электромоторам приходится вращаться то быстрее, то медленнее, что отрицательно сказывается на их долговечности. В таких случаях необходимо использовать преобразователи частоты или трансформаторы напряжения.
Внешний вид преобразователя частоты
Как определяется
Существует два способа установить, чему равна частота и амплитуда переменного тока — применять специальные приборы либо воспользоваться результатами расчётов.
Измерение частоты
Для измерения частоты переменного тока используется принцип механического резонанса. Он является достаточно простым, хотя и не очень точным. Основывается на том факте, что для каждого физического объекта, обладающего упругими свойствами, существует определенное значение частоты, при которой он начинает вибрировать.
Примером подобного устройства является камертон. Если по нему ударить, он будет довольно продолжительное время вибрировать со звуком, зависящим от его длины. Чем длиннее камертон, тем ниже будет резонансная частота и наоборот.
Если представить себе ряд камертонов с постепенно увеличивающимися размерами, установленными на общем основании, то это основание станет вибрировать с частотой измеряемого напряжения или тока. Для этого устройство следует снабдить электромагнитом.
Измерения частоты тока выполняются с помощью набора «камертонов», в качестве которых используются полоски листового металла. Это устройство называется частотомером вибрирующего геркона.
Схема вибрационного частотомера
Используя частотомер, можно наглядно увидеть, как концы всех полосок встряхиваются в зависимости от того, как меняется величина переменного напряжения, приложенного к катушке. Тот из лепестков, который будет ближе всего к резонансной частоте переменного тока, станет вибрировать наиболее интенсивно.
Особой точностью вибрационные частотомеры не отличаются, зато характеризуются простотой своего изготовления. Их применяют в небольших электроремонтных мастерских, а также в быту с целью калибровки частоты вращения двигателя.
Хотя подобный прибор будет иметь малую точность, этого нельзя сказать о самом принципе измерения. Заменив механический резонатор на электрический, можно получить частотомер на основе катушки индуктивности и параллельно включённого конденсатора. Вместе они образуют колебательный контур.
Один или оба компонента этого контура могут быть регулируемыми. В цепь включается измерительный блок, который показывает максимальную амплитуду напряжения на конденсаторе и катушке. Ручки регулировки предварительно откалибровываются, чтобы иметь возможность выставлять резонансную частоту для любого варианта настройки. Частота считывается после настройки устройства на максимальное показание шкалы измерителя.
Схема электрического частотомера
Фактически частотомер реализует схему настраиваемого фильтра, после чего отсчёт показаний происходит как в мостовой схеме (она вначале балансируется для условного нулевого состояния, после чего выполняется отсчёт). До тех пор, пока катушка и/или конденсатор смогут перехватывать достаточное поле магнитного или электрического рассеивания от тестируемой цепи, устройство будет сохранять свою работоспособность.
Метод не требует прямого подключения к цепи, поэтому часто применяется в бытовых условиях. Наиболее точные результаты дают электронные частотомеры.
Внешний вид электронного частотомера
Расчёт частоты тока
Для расчёта требуется знать период или временной отрезок, в течение которого значение переменного тока повторяется и образует одну полную волну. Между периодом и частотой переменного тока имеется зависимость, которую отражает следующая формула:
Определение частоты электротока
Если известно значение циклической частоты ɷ и амплитуда А, то по схожей зависимости можно вычислить силу тока I:
Определение силы электротока
Определение угловой частоты выполняется с помощью такого уравнения:
Формула угловой скорости
Заключение
Учитывая тенденцию к постепенному уменьшению производства электроэнергии с использованием традиционных видов топлива, всё чаще возникают вопросы оптимального управления частотными параметрами систем энергетики. Идеальным выходом их положения считают такой, при котором данные функции будут реализованы вследствие применения более стабильных и доступных форм генерации. К ним стоит отнести атомную энергетику, использование энергии солнца и ветра.
Видео по теме
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период – время одного колебания; Аплитуда – его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10-3сек.
1 мкс=0,001 мс = 0,000001сек =10-6сек.
1000 мкс = 1 мс.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 103 Гц = 1 кГц;
1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2
.
Рисунок 2. Радиан.
Тогда,
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.
Итак,
?= 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Переменный электрический ток
Переменный ток (AC – Alternating Current) – электрический ток, меняющий свою величину и направление с течением времени.
Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC – Direct Current – постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.
Величина тока будет равна квадратному корню из суммы квадратов двух величин – значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.
Термины AC и DC применимы как для тока, так и для напряжения.
Параметры переменного тока и напряжения
Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:
Период T – время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота f – величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz). Частота f = 1/T
Циклическая частота ω – угловая частота, равная количеству периодов за 2π секунд.
ω = 2πf = 2π/T
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза ψ – величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение – величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.
i = i(t); u = u(t)
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
i = Iampsin(ωt); u = Uampsin(ωt)
С учётом начальной фазы:
i = Iampsin(ωt + ψ); u = Uampsin(ωt + ψ)
Здесь Iamp и Uamp – амплитудные значения тока и напряжения.
Амплитудное значение – максимальное по модулю мгновенное значение за период.
Iamp = max|i(t)|; Uamp = max|u(t)|
Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) – максимальное отклонение от нулевого значения.
Среднее значение (avg) – определяется как среднеарифметическое всех мгновенных значений за период T.
Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение – среднеарифметическое модулей всех мгновенных значений за период.
Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.
Среднеквадратичное значение (rms) – определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.
Для синусоидального тока и напряжения амплитудой Iamp (Uamp)
среднеквадратичное значение определится из расчёта:
Среднеквадратичное – это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов.
Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода,
что и равный по величине его среднеквадратичному значению постоянный ток.
Коэффициент амплитуды и коэффициент формы
Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой
амплитудное, среднеквадратичное и средневыпрямленное значения.
Коэффициент амплитуды – отношение амплитудного значения к среднеквадратичному.
Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды KA = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды KA = 1
Коэффициент формы – отношение среднеквадратичного значения к средневыпрямленному.
Для переменного синусоидального тока или напряжения коэффициент формы KФ 
≈ 1.111
Для тока и напряжения треугольной или пилообразной формы KФ 
≈ 1.155
Для переменного тока и напряжения прямоугольной формы KФ = 1
Замечания и предложения принимаются и приветствуются!
В таблице представлены основные расчетные формулы по электротехнике для расчета тока, напряжения, сопротивления, мощности и других парметров электрических схем.
|
Измеряемые величины |
Формулы |
Обозначение и единицы измерения |
|
Сопротивление проводника омическое (при постоянном токе) |
|
s — сечение, мм2 |
|
Активное сопротивление при переменном токе |
|
r — активное сопротивление, Ом; k — коэффициент, учитывающий поверхностный эффект, а в магнитных проводниках — также явление намагничивания |
|
Зависимость омического сопротивления проводника от температуры |
|
|
|
Индуктивное (реактивное) сопротивление |
|
сопротивление, Ом; f— частота, Гц; L — коэффициент самоиндукции (индуктивность), Гц; С — емкость, Ф; Z — полное сопротивление, Ом |
|
Емкостное (реактивное) сопротивление |
|
|
|
Полное реактивное сопротивление |
|
|
|
Полное сопротивление переменному току |
|
|
|
Емкость пластинчатого конденсатора |
|
С — емкость, Ф; S — площадь между двумя электродами, см n — число пластин; b — толщина слоя диэлектрика, см |
|
Общая емкость цепи: а) при последовательном соединении емкостей б) при параллельном соединении емкостей |
|
|
|
Закон Ома; цепь переменного тока с реактивным сопротивлением |
|
I — ток в цепи, А; U — напряжение цепи, В; |
|
1-й закон Кирхгофа (для узла) |
|
точке, А; i = 1, 2… n; Е — ЭДС, действующая в контуре, В; r — сопротивление отдельных участков, Ом |
|
2-й закон Кирхгофа (для замкнутого контура) |
|
|
|
Распределение тока в двух параллельных ветвях цепи переменного тока |
|
|
|
Закон электромагнитного индукции для синусоидального тока |
|
f — частота, Гц; w — число витков обмотки; В — индукция магнитного поля в стали, Тс; S — сечение магнитопровода, см2 |
|
Электродинамический эффект тока для двух параллельных проводников |
|
F — сила, действующая на 1 (см) длины проводника, кГ; а — расстояние между проводниками, си; |
|
Подъемная сила электромагнита |
|
Р — подъемная сила, кГ; В3 — индукция в воздушном зазоре; В3 = 1000 Гс (электромагниты для подъема стружки и мелких деталей); В3 = 8000 — 10 000 Гс (электромагниты для подъема крупных деталей) S — сечение стального сердечника, см2 |
|
Тепловой эффект тока |
|
тепла, кал; t— время протекания тока, сек; r — сопротивление, Ом; А — количество вещества, от- ложившегося на электроде, мг; α — электрохимический эквивалент вещества |
|
Химический эффект тока |
|
|
|
Зависимости в цепи переменного тока при частоте 50 Гц: а) период изменения тока б) угловая скорость |
|
Т — период изменения тока, сек; f – частота тока, Гц; |
|
Зависимости токов и напряжений в цепи переменного тока: а) ток в цепи б) напряжение в цепи |
|
I — полный ток в цепи, А; тока, А; U— напряжение в цепи, В; напряжения, В; |
|
Соотношения токов и напряжений в трехфазной системе: а) соединение в звезду б) соединение в треугольник |
|
|
|
Коэффициент мощности |
|
Р — активная мощность, Вт; Q — реактивная мощность, нар; S —полная мощность, B*А; r — активное сопротивление, z – полное сопротивление, Ом |
|
Мощность в цепи постоянного тока |
|
|
|
Мощность в цепи переменного тока: а) цепь однофазно тока б) цепь трехфазного тока |
|
|
|
Энергия в цепи постоянного тока |
|
t —время ч |
|
Энергия в цепи переменного тока: а) цепь однофазного тока б) цепь трехфазного тока |
|
— омическое сопротивление, Ом;
— удельное сопротивление, Ом
— длина, м;
, 
— сопротивление проводника в омах соответственно при температуре 
и 
°C
— индуктивное
— угловая скорость; при частоте/= 50 Гц; = 314;
— емкостное сопротивление, Ом;
или 
— диэлектрическая постоянная изоляции;
, 
, 
— отдельные емкости, Ф
или 
— токи в отдельных ответвлениях, сходящихся в одной
— ток первой ветви, А; 
— ток второй ветви А;
— сопротивление первой ветви, Ом;
— сопротивление второй ветви, Ом
— наведенная ЭДС, В;
, 
— амплитудные значения токов в параллельных проводниках, А;
или 
— количество выделяемого
[радиан] или 360°
— угловая скорость
— активная составляющая
— реактивная составляющая тока, А;
— угол сдвига (град) во времени между током и напряжением в цепи;
— активная составляющая
— реактивная составляющая напряжения, В
— ток линейный, А;
— ток фазный, А;
— напряжение линейное, В;
— напряжение фазное, В
— активная энергия, Вт*ч;
— реактивная энергия, вар*ч;
