Колебательный контур LC
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
– Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
– Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.
Основные свойства индуктивности
– Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией  .
.
– Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Природа электромагнитных колебаний в контуре
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит .
.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.

Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t1,
которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 =  .
.
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит .
.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL.
Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС,
которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление.
Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4),
накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U
(в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников,
фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний  .
.
Частота свободных колебаний контура ƒ = 1 / T
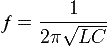
Частота свободных колебаний является частотой резонанса контура,
на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт частоты:
Частота резонанса колебательного контура LC.
ƒ = 1/(2π√(LC))
Расчёт ёмкости:
Ёмкость для колебательного контура LC
C = 1/(4𲃲L)
Расчёт индуктивности:
Индуктивность для колебательного контура LC
L = 1/(4𲃲C)
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.
Замечания и предложения принимаются и приветствуются!
Лучший ответ
Алексей Гуров
Просветленный
(33841)
9 лет назад
Формула индуктивного и емкостного сопротивления в явном виде содержит частоту.
Например, индуктивное:
XL = W * L = 2 * Pi * F * L, где
F и есть частота в Герцах.
Остальные ответы
Сергей Гаврилов
Искусственный Интеллект
(184997)
9 лет назад
Записать формулу для полного сопротивления. Подставить в нее то, что известно. Из полученного уравнения найти то, что неизвестно.
yuriy visotsky
Мудрец
(17374)
9 лет назад
В радиолюбительских справочниках есть эмперические таблицы и формулы. Приставил линейку к двум величинам, а на третьей шкале получил ответ. Такие таблицы часто давал журнал “Радио” до 1990 года. Ну а если Элементарно: – то чем меньше ёмкость и индуктивность, тем больше частота контура.
Как найти частоту
Частота характеризует собой циклические процессы колебаний или движение по окружности. Она равна количеству повторений процесса за единицу времени. Для ее измерения узнайте количество колебаний, которые произошли за некоторый промежуток времени. Иногда она измеряется более сложными способами. Если известен период повторений, ее можно просто рассчитать.
Вам понадобится
- – секундомер;
- – тестер;
- – калькулятор.
Инструкция
Наблюдая за колебаниями или другими повторяющимися движениями, отсчитайте некоторое их количество. Секундомером измерьте время, за которое произошли эти движения. Полным колебанием является возврат тела в исходную точку, как и полным оборотом. Для определения частоты ? поделите количество колебаний N на время t, за которое они произошли, измеренное в секундах. Например, если маятник за 20 секунд делал 30 колебаний, то частота равна ?=30/20=1,5 1/с (Герц). Если известен период колебаний (время одного колебания) найдите частоту ? поделив единицу на период Т (?=1/Т). Например, если период колебаний составляет 0,2 с, то частота этого колебания будет равна ?=1/0,2=5 Гц.
Для того чтобы определить частоту переменного тока возьмите тестер. Настройте его на измерение частоты специальным переключателем. Подключите прибор к цепи или источнику переменного тока, соблюдая осторожность. На экране тестера появится частота тока в сети. Например, в стандартной бытовой сети частота равна 50 Гц.
Чтобы измерить частоту колебательного контура, найдите индуктивность его катушки и емкость конденсатора, которые и составляют колебательный контур. Если они заранее неизвестны, подключите к ним тестер, настроенный, соответственно, на измерение индуктивности в Генри и электроемкости в Фарадах. Найдите частоту, используя формулу Томсона. Для этого число 2 умножьте на ??3,14 и корень квадратный из произведения индуктивности L и электроемкости C. Поделите число 1 на получившийся результат ?=1/(2•?•vL•C). Пример. Колебательный контур состоит и катушки индуктивностью 2 мГн и конденсатора электроемкостью 80 мкФ. Определите его частоту. Подставьте значения в формулу ?=1/(2•3,14•v2•10^(-3)•80•10^(-6))=1/(6.28•4•10^(-4))=0,04•10^4=400 Гц.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Главная > Теория > Резонансная частота: формула
Для генерации высокочастотных волн часто применяются схемы на основе колебательного контура. Подобрав параметры элементов цепи, можно производить частоты свыше 500 МГц. Схемы используются в ВЧ-генераторах, высокочастотном нагреве, телевизионных и радиоприемниках.

Колебательный контур
Колебательный контур – это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты. Оба компонента схемы способны хранить энергию.
Когда существует разность потенциалов на конденсаторных пластинах, он сохраняет энергию электрического поля. Аналогично энергия сохраняется в магнитном поле индуктивной катушки.
Работа колебательного контура
Когда первоначально конденсатор подключается к источнику постоянного тока, на нем возникает разность потенциалов. Одна пластина имеет избыток электронов и заряжена отрицательно, другая – недостаток электронов и заряжена положительно.
Что будет, если в цепь включить индуктивную катушку:
- При замыкании контакта, соединяющего электроцепь, конденсатор начинает разряжаться через катушку индуктивности. Накопленная им энергия электрического поля снижается;
- Ток, протекающий через катушку L, индуцирует ЭДС, противостоящую потоку электронов. Из-за этого скорость нарастания тока медленная. В катушке создается магнитное поле, которое начинает накапливать свою энергию. После полного разряда конденсатора поток электронов через катушку уменьшается до нуля. Электростатическая энергия, накопленная в конденсаторе, преобразуется в энергию магнитного поля катушки;
- Когда конденсатор разряжен, магнитное поле начинает постепенно разрушаться, но, согласно закону Ленца, индукционный ток катушки способствует заряду конденсатора с противоположной полярностью. Энергия, связанная с магнитным полем, снова превращается в электростатическую;
Важно! В идеальном случае, когда нет потерь на L и С, конденсатор зарядился бы до первоначального значения с противоположным знаком.
- После того, как уменьшающееся магнитное поле перезарядило конденсатор, он снова начинает разряжаться с потоком тока обратной направленности, а МП опять нарастает.
Последовательность зарядки и разрядки продолжается, то есть процесс преобразования электростатической энергии в магнитную и наоборот периодически повторяется, подобно маятнику, у которого потенциальная энергия циклически превращается в кинетическую и обратно.
Непрерывный процесс зарядки и разрядки приводит к меняющему направление движению электронов или к колебательному току.
Обмен энергией между L и С будет продолжаться бесконечно, если отсутствуют потери. Часть энергии теряется, рассеиваясь в виде тепла на проводах катушки, соединительных проводниках, из-за тока утечки конденсатора, электромагнитного излучения. Поэтому колебания будут затухающими.

Как работает контур колебаний
Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.
Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.
Вам это будет интересно Средства защиты от статического электричества

Важно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников.
Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.

При воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.
Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.

Важно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот.
Резонанс
Если схема с конденсатором, катушкой и резистором возбуждается напряжением, постоянно меняющимся во времени с определенной частотой, то также изменяются реактивные сопротивления: индуктивное и емкостное. Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.
Частота вращения: формула
Индуктивное сопротивление прямо пропорционально частоте:
X(L) = 2π x f x L,
а емкостное сопротивление обратно пропорционально этому показателю:
X(C) = 1/(2π x f x C).
Важно! На более низких частотах индуктивное сопротивление незначительное, а емкостное будет высоким и сможет создавать практически разомкнутый контур. На высоких частотах картина обратная.
При конкретной комбинации конденсатора и катушки схема становится резонансной, или настроенной, имеющей частоту колебаний, при которой индуктивное сопротивление идентично емкостному. И они компенсируют друг друга.
Следовательно, в цепи остается исключительно активное сопротивление, противостоящее протекающему току. Созданные условия получили наименование резонанса колебательного контура. Фазовый сдвиг между током и напряжением отсутствует.

Для расчета резонансной частоты колебательного контура учитывается следующее условие:
X(L) = X(C).
Следовательно, 2π x f x L = 1/(2πx f x C).
Отсюда получается формула резонансной частоты:
f = 1/(2π x √(L x C)).
Расчет резонансной частоты, индуктивности и емкости можно сделать на онлайн калькуляторе, подставив конкретные значения.
Скорость, с которой рассеивается энергия от LC-схемы, должна быть такой же, как энергия, подаваемая на схему. Устойчивые, или незатухающие, колебания производятся электронными схемами генераторов.
LC-цепи используются либо для генерации сигналов на определенной частоте, либо для выделения частотного сигнала из более сложного. Они являются ключевыми компонентами многих электронных устройств, в частности радиооборудования, используемого в генераторах, фильтрах, тюнерах и частотных микшерах.
Формула индуктивности
Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:
- Количество и расположение витков обмотки;
- Наличие или отсутствие сердечника;
- Материал сердечника.
Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.
Вам это будет интересно Особенности активно-емкостной нагрузки

Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках.
Виды и особенности
Схемы колебательных контуров бывают двух видов: последовательными и параллельными. Они отличаются типом соединения элементов емкости и индуктивности. В первом случае они соединены последовательно, а во втором — параллельно. Для работы необходима постоянная электрическая энергия, в противном случае происходит ее затухание, поскольку часть уходит на генерацию электромагнитного поля и нагрев провода обмотки катушки индуктивности. Контур также может быть открытым и закрытым. Открытый выпускается без специальной защитной крышки.
При решении задач по физике можно встретить интересное понятие — идеальный колебательный контур. Если в задании встречается такой термин, то это говорит о том, что энергия остается в системе, а не уходит на описанные выше процессы.
Устройство постоянно генерирует электромагнитные колебания, то есть является подобием вечного двигателя, однако такого не может быть вообще. На практике при расчете параметров учитываются затухания — постепенные уменьшения амплитуды электромагнитной волны.
Последовательное соединение
Последовательный контур — простейшая резонансно-колебательная система. Он состоит из двух элементов, подсоединенных последовательно. Через них при подключении переменного напряжения будет протекать ток переменной составляющей. Его величина определяется по закону Ома: i = U / Zlc. В этой формуле Zlc является суммой реактивных сопротивлений катушки индуктивности (Xl) и конденсатора (Xc).

Величины определяются по формулам Xl = wL и Xc = 1 / (wC). Параметр w — угловая частота, которую можно найти по такому соотношению через частоту переменного тока и число Pi: w = 2 * Pi * f. Из соотношений можно сделать вывод, что реактивное сопротивление на индуктивности растет с увеличением f, а для емкости — уменьшается. В первом случае тип зависимости называется прямо пропорциональным, а во втором — обратно пропорциональным.
При определенном значении частоты сопротивления двух элементов равны по модулю друг другу. Следовательно, это явление называется резонансом колебательной системы. Частоту w при таком условии называют собственной резонансной частотой контура. Рассчитать ее довольно просто, поскольку следует приравнять две формулы для получения уравнения: wL = 1 / (wC). Далее нужно выразить значение f: f = [(1 / (L * C))^(½)] / 2Pi. Последнее соотношение называется формулой Томсона.

Когда контур подключается к цепи генератора (источника) переменного напряжения с активным сопротивлением R, полный импеданс цепи (Z) определяется с помощью соотношения Z = [R2 + Zlc2]^(½). Если происходит резонанс, то Z = R, а реактивная составляющая исчезает.
У контура существуют еще две важные характеристики: добротность (Q) и характеристическое сопротивление (р). Последней называется величина сопротивления реактивного типа при резонансе. Вычисляется она по формуле р = (L * C)^(½) и показывает количество энергии катушки и конденсатора, которое было запасено. Для емкости значение определяется по соотношению Wс = (C * U2) / 2, а для индуктивности — Wl = (L * I2) / 2.
Отношение величины энергии, которая была запасена конденсатором и катушкой, к показателю потерь называется добротностью колебательного контура (Q). Параметр определяет амплитуду и ширину АЧХ резонанса и показывает превышение энергии запаса над потерями за одно колебание. При этом учитывается реактивная нагрузка R. Характеристика определяется по формуле Q = (1 / R) * [(L / C)^(½)].
В некоторых случаях описывать добротность можно другим тождеством: Q = p / R. Современные устройства выполняются на дискретных катушках, а их Q колеблется от нескольких единиц до сотен. Системы, построенные на принципе пьезоэлектронных устройств (кварцевые резонаторы), имеют высокий показатель Q. Его значение может достигать 1 тыс. и больше. Затухание контура (d) — характеристика, которая является обратной добротности. Она определяется по такому соотношению: d = 1 / Q.
Параллельный контур
Контур параллельного типа состоит также из конденсатора и катушки. Отличие заключается в том, что эти два элемента соединены параллельно между собой. Этот тип устройства применяется чаще, чем последовательный контур. Чтобы найти общее сопротивление индуктивного характера, нельзя просто сложить значения Xl и Xc. Складываются только проводимости двух элементов.
Из курса физики известно, что проводимость — величина, обратная сопротивлению, то есть Xc = 1 / Gc и Xl = 1 / Gl. Следовательно, формулы для параллельного соединения имеют такой вид:

- Gl = 1 / wL.
- Gc = wC.
- Q = R * [(С / L)^(½)].
Для примера необходимо рассмотреть электрическую цепь, состоящую из генератора переменного тока и параллельного контура. В какой-то момент времени их частоты будут совпадать. Кроме того, проводимости двух элементов равны по модулю между собой. В результате этого происходит явление резонанса токов.
В цепи будет только активное сопротивление Rэкв, которое называют в радиотехнике эквивалентным. Оно вычисляется по формуле Rэкв = Q * p. Если частота не соответствует резонансной, то в устройстве происходят другие процессы: на низких наблюдается уменьшение индуктивного сопротивления, а на высоких — емкостного.
Во время работы контура за период колебаний два раза происходит обмен энергией между катушкой и конденсатором. В радиоэлементе протекает ток, по силе превосходящий внешний в Q раз.
Электрическая цепь, состоящая из соединеных в контур конденсатора емкостью С и катушки индуктивностью L,
обладающая сопротивлением R(сопротивление активных потерь в катушке), называется электрическим колебательным контуром.
В контуре возникает колебательный процесс ввиду перехода энергии электрического поля в энергию магнитного и наоборот.
Реактивные сопротивления индуктивности и емкости зависят от частоты переменного тока.
При увеличении частоты реактивное сопротивление индуктивности растет, а емкости падает.
При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет.
При некоторой частоте ƒ0, емкостное сопротивление конденсатора и индуктивное сопротивление катушки
становятся численно равными: Xc = XL.
При этом токи индуктивной и емкостной ветвей также равны, что приводит к возрастанию амплитуды вынужденных колебаний.
Режим, возникающий в цепи, состоящей из генератора и параллельно включенных катушки и конденсатора, при равенстве
емкостного и индуктивного сопротивлений, называют режимом резонанса токов.
Явление резонанса токов используется в полосовых фильтрах для выделения определенной частоты.
Такая схема необходима для работы телевизора, радиоприемника, ёмкостного генератора и т.п.
Расчет частоты резонанса параллельного LC-контура описывается формулами:
XL
— индуктивное реактивное сопротивление, Ом;
XС
— ёмкостное реактивное сопротивление, Ом;
ƒ0
— резонансная частота, Гц;
Расчет частоты резонанса LC-контура
Введите значения индуктивности и ёмкости конденсатора, чтобы узнать резонансную частоту контура,
или введите резонансную частоту генератора, чтобы рассчитать необходимые значения индуктивности и емкости.
XL =
XC =
ƒ0 =
φ = °
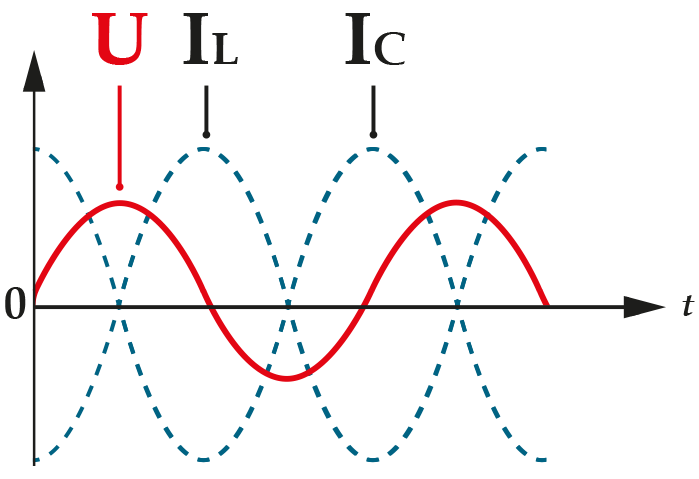
XL
>
XC
Цепь имеет емкостной характер,ее емкостное реактивное сопротивление меньше индуктивного.
Угол фазового сдвига между напряжением генератора и током в контуре приближается к 90°
Чем больше частота генератора отличается от собственной (резонансной) частоты контура, тем больше различаются токи IL и Іс,
тем больше реактивный ток в общей части цепи и меньше реактивное сопротивление контура.
Внимание! Производители объединяют элементы в серии или ряды: E6, E12, E24…
Для подбора компонентов будет использована серия E12.
Подбор конденсатора на сайте
Подбор катушки индуктивности на сайте
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
