Как найти частоту если известна лямбда

Была ли эта статья полезной?

Как вычислить частоту

Частота – физическая величина, отражающая число колебаний в механическом, электромагнитном или ином процессе. Помимо обычной линейной частоты, рассматривают циклическую (угловую) частоту при вращении тел. Нахождение данных величин в различных задачах осуществляется с использованием известных формул, соотношений параметров тел и показателей их движения.

Инструкция

В начале решения любой задачи приведите все известные величины к единицам, принятым в системе СИ. Линейная частота измеряется в герцах (Гц), циклическая – в радианах за одну секунду.

При решении задачи на распространение волн с известной длиной и скоростью колебаний вычислите их частоту по формуле: F=v/λ, где λ – длина волны (м), v – скорость распространения колебаний в среде (м/с). Если в задаче задан лишь период T (с) совершаемых телом колебаний, частота находится из соотношения: F=1/T (Гц).

Чтобы узнать линейную частоту колебаний F через заданную циклическую в момент вращения тела, используйте следующее выражение: F=ω/(2*π), где ω – циклическая частота (рад/с), π – константа, примерно равная 3,14. Отсюда можно вывести и обратную формулу нахождения циклической частоты по заданному значению линейной: ω=2*π*F.

Допустим задана колебательная система, состоящая из подвешенного груза известной массы M (м) и пружины с определенной жесткостью k (Н/м). Вычислите частоту колебаний груза F, проведя следующие действия. Найдите период колебаний по формуле T=2*π √(M/k), подставьте известные значения и высчитайте период в секундах. По выше приведенной формуле определите частоту колебаний подвешенного тела: F=1/T (Гц).

При решении задач из раздела электродинамики рассматривается электромагнитный колебательный контур. Пусть он состоит из пары параллельно соединенных конденсаторов емкостью С (Ф) и катушки индуктивности L (Гн). Вычислить частоту собственных колебаний можно по формуле: ω = 1/√(L*C) (рад/c).

Если значение силы тока I (А) задано следующим уравнением i = 0,28*sin70*π*t (t – выражено в секундах) и при этом требуется вычислить циклическую ω и линейную частоту F колебаний, выполните следующие действия. В общем виде уравнение синусоидального тока выглядит так: i = Im*sin(ωt+φ0). Следовательно в данном случае известно, что амплитуда колебаний Im = 0,28 А, начальная фаза φ0 равна нулю, угловая (циклическая) частота ω = 70*π рад/c, так как она является в заданном уравнении коэффициентом при t. Отсюда вычислите линейную частоту F = ω/(2*π) = 70*π/(2*π) = 35 Гц.

Видео по теме

Источники:

• линейная частота

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Обновлено: 22.05.2023

Скорость волны зависит от строения вещества и взаимодействия между её молекулами (атомами). Поэтому в различных средах скорость одной и той же волны будет отличаться.

Длина волны — расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.

Используется модель, в которой частицы среды заменяют шариками. Для удобства их можно пронумеровать (рис. (1)).

Частицы среды связаны между собой межмолекулярными силами взаимодействия, поэтому волна передаётся от одной частицы к другой.

Отклоним первый шарик от положения равновесия. Силы притяжения передадут движение второму, третьему шарику. Каждый элемент вещества (молекула, атом) повторит движение первой частицы с запаздыванием, которые называют сдвигом фазы. Это запаздывание зависит от расстояния, на котором находится рассматриваемый шарик по отношению к первому шарику.

Предположим, что первый шарик достиг максимального смещения от положения равновесия (рис. (2)). В этот момент четвёртый шарик только начнет движение, следовательно, он отстаёт от первого на (1/4) колебания.

В момент времени, когда смещение четвертого шарика будет наибольшим (рис. (3)), седьмой шарик будет отставать от него на (1/4) колебания. А если рассмотреть отставание седьмого шарика от первого, то оно составляет (1/2) колебания.

Первый и тринадцатый шарик совершают одно колебание, то есть двигаются в одной фазе (рис. (5)). Это значит, что между ними все шарики с первого по двенадцатый проходят полный колебательный процесс или составляют одну волну.

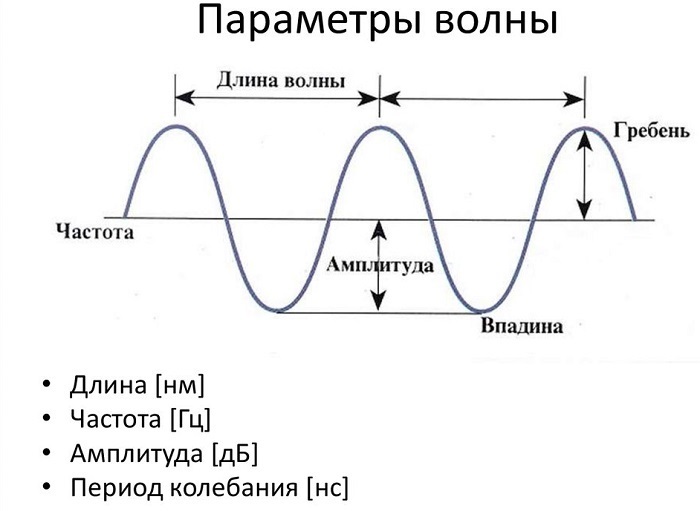
Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.

Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.

На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн

Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10 8 м/с поделить на длину в метрах.

Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

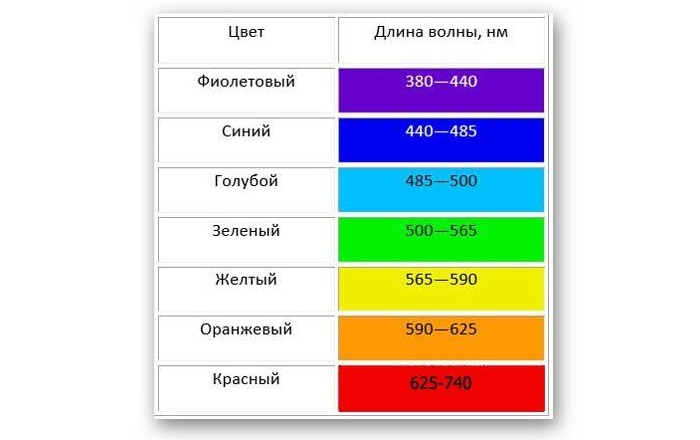
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

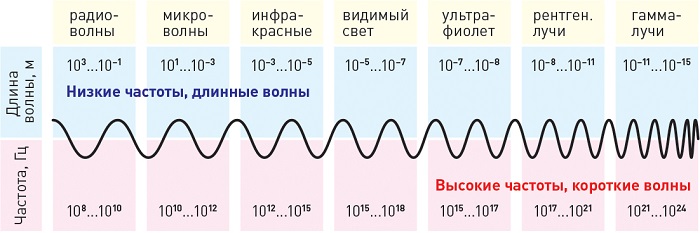
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн

Задача №1

Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2

Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3

Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

Буквой λ (лямбда) обозначается длина волны того или иного излучения. Эту величину можно измерить, можно рассчитать теоретически, а если излучение является видимым, то даже определить на глаз.

Чтобы рассчитать длину волны излучения, зная частоту и скорость распространения этого излучения, поделите вторую величину на первую. Если же вместо частоты известен период, умножьте его на скорость распространения излучения. Наконец, если известна циклическая частота излучения, умножьте скорость на 2π, а затем результат поделите на циклическую частоту.
Чтобы результат получился в системе СИ, предварительно переведите в нее же все величины из условия задачи. Затем переведите результат обратно в удобные для вас единицы.

Если излучение является световым, длину его волны в вакууме определите на глаз: красный – от 635 до 690 нм, оранжевый – 590, желтый – от 570 до 580, зеленый – от 510 до 520, синий – от 440 до 480, фиолетовый – от 380 до 400.

Имея специальный прибор – спектрометр, определить длину волны света можно точнее, чем на глаз. Если он является полихроматическим, определить его спектральный состав можно только с помощью этого прибора Для этого направьте световой поток во входное окно прибора. Он пройдет через щель, перпендикулярную призме, а затем и через саму призму, а затем попадет либо на шкалу, либо на линейку датчиков. Во втором случае, обработку результата измерения осуществит электронный блок прибора.

Для нахождения длины волны излучения дециметрового или сантиметрового диапазона подключите антенну к волномеру, после чего начните плавно менять ее размер. Когда он станет равен половине длины волны, показания волномера окажутся максимальными.

Направьте тонкий луч света строго перпендикулярно дифракционной решетке. На экране появится ряд пятен. Измерьте угол между воображаемой линией, продолжающей ход луча после решетки, линией, соединяющей точку входа луча в решетку с первым из пятен. Найдите синус этого угла, а затем умножьте на расстояние между двумя соседними линиями решетки. Получится длина волны, которая будет выражена в тех же единицах, что и расстояние между линиями.

Морские волны — далеко не все примеры волн. И длина волны — это не серферская характеристика, а вполне себе физическая величина. Сегодня разберемся, что такое волна и как ее охарактеризовать.

О чем эта статья:

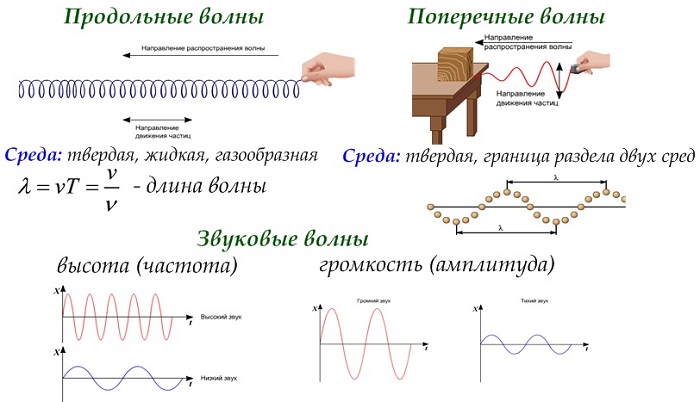
Волна: продольная и поперечная

Начнем с того, что волна — это распространение колебания в пространстве.

Волны бывают механическими и электромагнитными.

Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.

• Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.

Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.

Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.

Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.

Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.

Электромагнитные волны — это те волны, которые мы потрогать не можем.

Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 10 8 м/с. И источники у них разные.

Волны также принято делить на продольные и поперечные:

Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.

• Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.

Поперечные — волны, у которых колебание происходит поперек направления распространения волны.

• Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
• Видимый свет и дрожание гитарной струны — тоже поперечные волны.

На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.

Длина волны: определение и расчет

Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.

Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.

Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.

Формула периода колебания волны

T = t/N

N — количество колебаний [—]

Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.

Связь со скоростью

Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).

Формула скорости

𝑣 = S/t

Переходя к волнам, можно провести следующие аналогии:

А для скорости даже аналогия не нужна — скорость и в Африке скорость.

Формула скорости волны

𝑣 = λ/T

λ — длина волны [м]

Задачка

Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?

Решение:

Возьмем формулу скорости:

Резонанс

Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.

На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.

Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.

Формула частоты

ν = N/t

N — количество колебаний [—]

В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂

Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.

В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.

Любая волна распространяется с некоторой скоростью. Под скоростью волны понимают ско­рость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.

Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.

Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.

Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

,

где v — скорость волны, Т — период колебаний в волне, λ (греческая буква лямбда) — длина волны.

Формула выражает связь длины волны с ее скоростью и периодом. Учитывая, что пери­од колебаний в волне обратно пропорционален частоте v, т. е. Т = 1/v, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:

,

Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.

Длина волны — это пространственный период волны. На графике волны (рис. выше) длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Это как бы мгновенные фотогра­фии волн в колеблющейся упругой среде в моменты времени t и t + Δt. Ось х совпадает с направле­нием распространения волны, на оси ординат отложены смещения s колеблющихся частиц среды.

Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания час­тиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.

Читайте также:

  

• Газель некст номер двигателя где находится номер

  

• Как разобрать двигатель ваз 2115 инжектор

  

• Как заводить машину на механике для начинающих с нуля ваз 2107

  

• Geely vision 2008 где находится эбу

  

• Как разобрать дворники шкода октавия

Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной. 

Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.

На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн

Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества. 

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

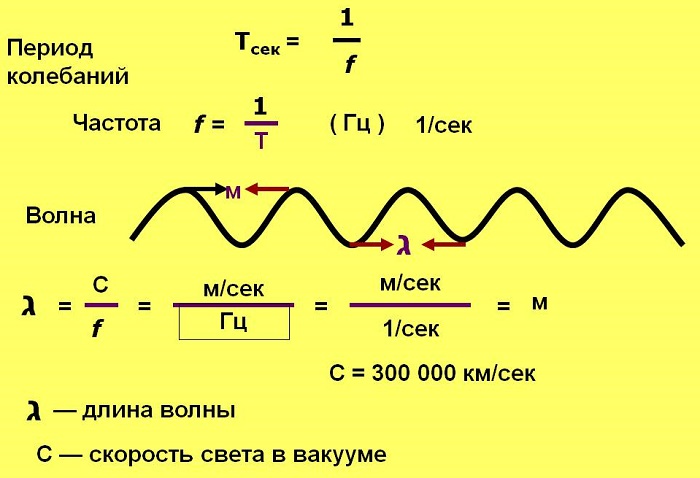
Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.

Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10⁸ м/с поделить на длину в метрах.

Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

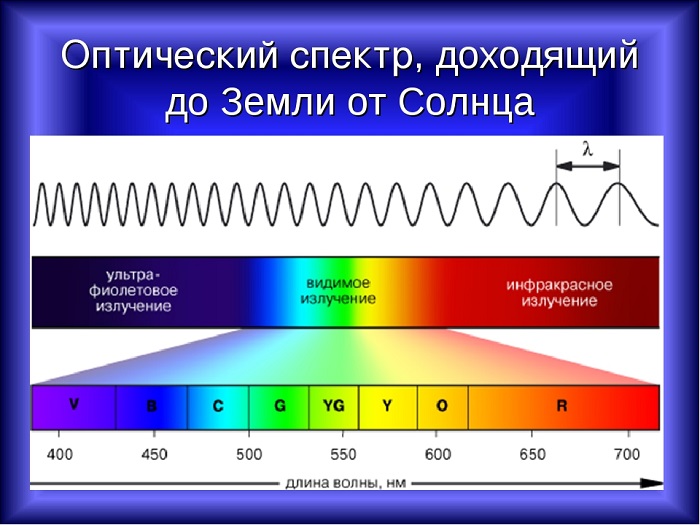
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания. 

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн

Задача №1

Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2

Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3

Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.