Рассмотрим цепочку из Nодинаковых атомов с массойMи межатомным расстояниемa,
атомы могут перемещаться вдоль прямой
линии. Каждый атом в такой системе
обладает одной степенью свободы. Эта
модель хорошо описывается примитивной
ячейкой Браве, в которой положение
атомов определяется вектором трансляции![]() ,
,
гдеn-целое число,
указывающее положение равновесия атомов
в цепочке.
Будем считать, что в момент времени t=0
смещен атом с номеромn=0
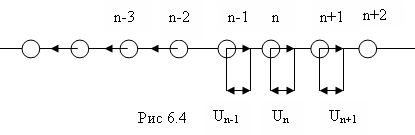
от положения равновесия на расстояние![]() (рис.6.4). Атомы связаны друг с другом,
(рис.6.4). Атомы связаны друг с другом,
поэтому возбуждение распространится
по цепочке в виде волны сжатия, и все
остальные атомы сместятся от положения
равновесия.
Пусть иn(x,
t) – смещение в
какой-то момент времениtn-ого атома относительно
его положения равновесия в точке с
координатойxn=na.
Если смещения атомов из положений
равновесия малы по сравнению с расстояниема, то силы межатомного взаимодействия
можно считать квазиупругими,
пропорциональными смещению. Атомы в
цепочке как бы связаны между собой
упругими пружинками, каждая из которых
характеризуется упругой постояннойС,
а смещениеunописывает колебания атома вблизи
положения равновесия.
Найдем уравнение движения n-ого
атома. Будем считать, что силы
короткодействующие, и рассматриваемый
атом взаимодействует только с (n+1)
и (n-1) атомами.
Взаимодействиеn-ого
атома с другими (n-2,n+2 и т.д.) пренебрежительно
мало. Наn-ный атом
действуют квазиупругие силы, результирующая
которых равна:
![]() ,
,
где β-силовая постоянная, которая
связана с упругой постоянной![]() .
.
 Уравнение движенияn-ого
Уравнение движенияn-ого
атома:
![]() ,
,
(6.2)
где M-масса атома.
Найдем нормальные моды колебаний,
т.е. такие типы движения, при которых
все атомы колеблются во времени с одной
и той же частотой ω по законуexp(-ωt).
Будем искать решение уравнения (6.2) в
виде
![]() ,
,
здесь и0определяет смещение
атома с номеромn=0 в
моментt=0,![]() -волновое
-волновое
число;
ω– циклическая частота данной моды.
 Из этого решения ясно, что вид нормальной
Из этого решения ясно, что вид нормальной
моды полностью определяется заданием
смещения единственного атома с номеромn=0. После подстановки
этого решения в (6.2) имеем:
![]()
– каждому значению волнового числа k
соответствует определенное значениеω2, причемω2является
четной функцией аргументаk.
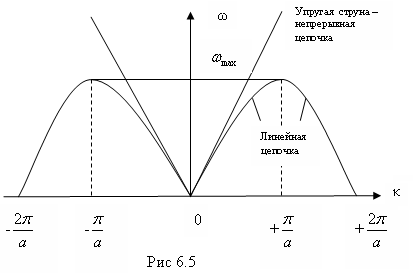
Дисперсионное соотношение для волн,
распространяющихся в линейной цепочке
из одинаковых атомов (рис.6.5) имеет вид:
![]() .
.
Частота колебаний n-ого
атома не зависит отn,
т.е. все атомы цепочки колеблются с
одинаковой частотойω, которая
принимает максимальное значение при![]() ,
,
т.е. при![]() ,
,
при этом![]() .
.
Таким образом, отличие дискретной
цепочки от непрерывной состоит в том,
что частота ωи волновое числоkне пропорциональны. Это связано с
дисперсией волн. Короткие волны вследствие
инерции, обусловленной массами частиц,
распространяются медленнее, чем длинные
волны. Наличие дисперсии волн проявляется
в отклонении кривой![]() от линейной зависимости, справедливой
от линейной зависимости, справедливой
для упругой струны (прямая на рис.6.5).
Цепочка из одинаковых атомов ведет себя
в отношении распространения акустических
волн как упругая струна только при![]() .
.
Скорость распространения акустической
волны вдоль дискретной цепочки в отличие
от скорости распространения волны вдоль
упругой струны зависит от длины волны:
![]() .
.
Фазовая скорость упругой волны в среде
с дискретной структурой равна
![]() ,
,
г рупповая
рупповая
скорость![]() ,
,
где υзв– скорость звука в данной
среде.
При малых значениях волнового числа
k(рис.6.6) фазовая и
групповая скорости совпадают и равны
скорости звука:
![]() .
.
Из рис.6.6 видно, что групповая скорость,
с которой переносится энергия колебаний
атомов в цепочке, для самых коротких
длин волн, т.е. для
![]() ,
,
обращается в ноль. Это означает, что
такие моды колебаний характеризуют в
цепочке стоячие волны вида
![]() ,
,
которые являются результатом сложения
двух бегущих волн с равными амплитудами,
частотами и длинами, но распространяющихся
в противоположных направлениях.
Состояние атомов дискретной цепочки
описывается уравнением движения
линейного гармонического осциллятора.
Полная энергия такого осциллятора
складывается из его кинетической и
потенциальной энергий:
![]() ,
,
где![]() – нормальная координата,М – масса
– нормальная координата,М – масса
осциллятора.
В квантовой механике гармонический
осциллятор описывается оператором
Гамильтона
![]() ,
,
где![]() –
–
оператор импульса,![]() – оператор координаты.
– оператор координаты.
Уравнение Шредингера для стационарных
состояний имеет вид:
![]() ,
,
Решением уравнения Шредингера являются
возможные (собственные) значения энергии:
![]() ,
,
n=0,1…-главное квантовое
число. Энергия осциллятора имеет лишь
дискретные значения.
Член
![]() представляет нулевую энергию. Он
представляет нулевую энергию. Он
показывает, что даже приТ=0 К атомы
не находятся в положениях равновесия,
а совершают колебания.
Таким образом, полная тепловая энергия
колебаний атомов в цепочке складывается
из энергии нормальных колебаний, ведущих
себя подобно линейным гармоническим
осцилляторам с собственной частотой
ωκ .
Соседние файлы в папке физика твёрдого тела
- #
- #
08.03.2015276.48 Кб71т6.doc
- #
- #
- #
- #
- #
Открыв страницу любой энциклопедии, справочника или книги с заголовком: «колебания атомов или молекул…», вы там найдете сложные математические выкладки, сложные графики и много всякого материала про колебания атомов и про вечное движение, и про фононы. Но! Вы не найдете ответ на главный вопрос: откуда эти колебания возникают? Кто или что эти колебания генерирует? Откуда это вечное движение?
Прежде чем ответить на поставленные вопросы о причине колебаний атомов в кристаллической решетке, немного о самом процессе колебаний.
Колебания атомов, ионов или молекул, входящих в кристалл, около положений равновесия узлов кристаллической решётки, дальше в тексте – колебания атомов. В физике данные колебания связывают с температурой вещества кристалла и взаимовлиянием соседних атомов друг на друга – тепловые, упругие и пр.
При повышении температуры происходит повышение частоты и амплитуды этих колебаний. В случае если амплитуда достигает некоторого критического значения, то кристаллическая решетка может разрушиться, иначе произойдет плавление вещества, и оно перейдет в жидкое состояние. При понижении температуры, до нуля, амплитуда падает тоже практически до нуля, но колебания присутствуют (нулевая энергия колебаний).
Оказывается, законами квантовой механики полное прекращение колебаний запрещено! А мы же понимаем, что природа законопослушна, вот поэтому нулевые колебания кристаллической решётки не прекращаются!
В кристалле одновременно могут присутствовать все возможные нормальные колебания, причем каждое протекает таким образом, что как будто без присутствия остальных. Там могут возникать и звуковые и оптические волны, и волны суперпозиции нормальных колебаний кристалла.
В какой-то момент могут возникать гармонические колебания, но это как исключение, в основном это ангармонизм. Слово плохо выговариваемое, но атомам это безразлично, у них свой язык. И этот язык до сих пор не расшифрован. Может быть атомы плохо слышат, поэтому чтобы сделать какое-то сообщение своему соседу, пытаются приблизиться к нему и прокричать на ухо. А может хотят получше разглядеть друг друга, но для нас все атомы на одно лицо. Так или иначе они не прекращают свои телодвижения ни днем, ни ночью.
Колебания кристаллической решетки один из основных видов внутренних движений твёрдого тела.
Упругие волны рассматриваются как распространение неких квазичастиц – фононов.
В данной работе я не касаюсь теории теплоемкости кристаллических тел (квантование колебательной энергии), разработанной Эйнштейном и, впоследствии, усовершенствованной Дебаем. Данная теория описана во всех учебниках по физике твердого тела.
Моя задача показать физику колебательных процессов в кристаллах и переноса ее в виде импульсов от атома к атому.
Для того чтобы это сделать необходимо вкратце описать сущность переноса энергии в современной физике. Для этого придется разобраться с фононом.
Фонон
Чтобы как-то объяснить вечный танец атомов нужна энергия, которую кто-то должен переносить, тогда ученые исхитрились и придумали некую виртуальную квазичастицу и назвали – фонон. Наделили ее энергией и импульсом, квантом упругих колебаний, считая, что для переноса энергии эта частица вполне может подойти. После чего внутреннюю энергию кристалла можно рассматривать как суммарную энергию движущихся фононов (квазичастиц).
Фонон (phone – от греч. звук), квант колебаний кристаллической решетки. Термин введен И. Таммом по аналогии с фотоном, квантом электромагнитного поля.
В Большом толковом словаре современного русского языка Д.Н. Ушакова, читаем: quasi (лат.) – яко бы, как будто. Первая часть сложных слов, имеющих значение мнимый, ненастоящий. А в некоторых изданиях трактуется как ложный.
Я, в свою очередь лишь констатирую, что такой частицы как фонон с ее квазиимпульсом не существует. Это действительно мнимое понятие.
Приведу цитату [27]: «Фонон во многих отношениях ведет себя так, как если бы он был частицей с энергией и импульсом. Однако в отличие от обычных частиц (электронов, протонов, фотонов и т.п.) фонон не может возникнуть в вакууме – для своего возникновения и существования фонон нуждается в некоторой среде. Подобного рода частицы называются квазичастицами. Таким образом, фонон является квазичастицей.
Импульс фонона обладает своеобразными свойствами. При взаимодействии фононов друг с другом их импульс может дискретными порциями передаваться кристаллической решетке, и, следовательно, не сохраняется. В связи с этим (p) в случае фононов называют не импульсом, а квазиимпульсом». (Конец цитаты).
p = ћk = ћω/v
k – волновое число, соответствующее колебанию частоты ?
v– скорость упругих волн в кристалле.
Сравните с импульсом фотона pf = hν/c.
Должен прокомментировать вышеприведенную цитату, т.к. в литературе сплошь и рядом такие высказывания повторяются.
Первое. В природе энергию и импульс переносят электромагнитные волны (фотоны), в том числе инфракрасного диапазона – крафоны (красные фотоны), которые присутствуют в любом теле (решетке) при комнатной и другой температуре. Крафоны перераспределяют тепловую энергию не только внутри какого-то тела, но между всеми телами, в том числе переносят ее в вакууме. Крафоны охлаждают всякое вещество или тело, выравнивая их температуру с окружающим пространством.
Второе. Импульс фонона якобы наделен своеобразными свойствами и может передаваться квантами кристаллической решетке. Должен сказать, что любой импульс электромагнитной волны, также как энергия передается квантами. Теплота квантуется, это доказано экспериментально американскими учеными [44]. Другое дело, что в любом кристалле есть замедление скорости переноса из-за сопротивления (плотности) электромагнитного эфира.
Третье. Что касается «столкновения фононов в кристалле», в интернете есть даже рисунки, показывающие упругие столкновения фононов между собой, которые при желании можно найти.
Как могут столкнуться электромагнитные волны между собой? Это большой вопрос. Что касается упругого столкновения с атомами ядер, то здесь вероятность прямого попадания также не велика, если учесть, что межатомные промежутки превосходят в сто тысяч раз размеры ядер. Попасть в такую мишень практически невозможно.
Импульсы в кристалле не передаются с помощью грубого или прямого столкновения, до этого дело не доходит. Все взаимодействия между атомами и крафонами происходят на полевом уровне.
Еще одна фраза из указанного источника [27, т. 5, с. 192]: «Формально оба представления весьма схожи – и фотоны, и фононы подчиняются одной и той же статистике».
По данному высказыванию хочу еще раз сказать, что фононы это крафоны, т.е. те же фотоны, но с меньшей энергией, поэтому никаких квазичастиц не существует. В природе есть только электромагнитные волны (ЭМВ), при комнатной температуре – это крафоны, которые и переносят импульсы движения. Крафонам не требуется особая среда кристаллического или другого содержания, они распространяются в любой среде, материи или в вакууме.
Крафон
Ответы на вопросы, поставленные в начале статьи: атомы в кристаллах раскачивают не мнимые частицы фононы, навечно замкнутые в кристалле, а настоящие – крафоны, с настоящими импульсами.
Крафон своим импульсом воздействует на решетку атома дважды: в момент прилета и в момент отлета (см. статью: «Сила гравитации»). В случае поглощения крафона, атом смещается импульсом навстречу. Отсюда та средняя частота колебаний атомов относительно своего среднего положения колебания около 1013 Гц. Данная частота соответствует инфракрасной области электромагнитного излучения (краснофотонное излучение). Проследим ситуацию на рисунке.
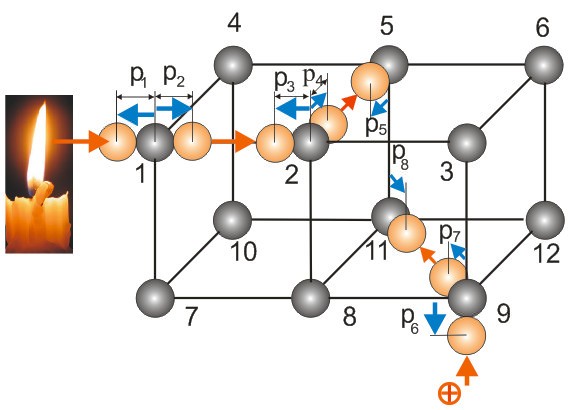
Вы решили провести романтический вечер при свечах. Поставили свечу на стол и зажгли фитиль. Перед этим, при приготовлении ужина, на стол просыпалось несколько крупинок соли. Пока не приступили к ужину, на голодный желудок информация воспринимается лучше и видится глубже, заглянем в кристаллическую решетку одной из крупинок соли.
Там мы увидим похожую картину, представленную на рисунке. Атомы (шарики стального цвета) в кубической решетке соли распределены симметрично по углам данной решетки. Для нас сейчас безразлично, какие это атомы Na или Cl. Оранжевые шарики – это фантомы стальных шариков, в момент, когда атомы отклоняются от своего стационарного состояния. Красные стрелки – это векторы движения крафонов. Синие векторы – это импульсы, вызывающие смещения атомов относительно своего центра.
Свеча довольно хороший источник излучения, с температурой около 1600о С в пламени, посмотрите, как плавится вокруг ее парафин. Фотоны от пламени, как от Солнца разлетаются по всем направлениям и один из них, в момент наблюдения, попал в кристалл соли. При взаимодействии полей атома №1 с фотоном свечи, данный атом получает импульс p1 навстречу фотону. Атом смещается влево, занимая условное положение оранжевого фантома. Поскольку фотон свечи обладает достаточной энергией, то он выдергивает из атома один или несколько электронов на более удаленные от ядра орбиты. После проделанной работы его энергия снижается, уменьшается частота, а в момент выхода из влияния поля атома, он снова его дергает, в направлении своего движения импульсом p2. На пути дальнейшего движения фотона свечи встает атом №2. Данный атом идентичен первому, поэтому сценарий повторяется. Единственное отличие состоит в том, что в силу потери части энергии фотона, второй атом на него имеет гораздо большее влияние и поглощает его, но в противоборстве получает импульс p3. После этого перегретый атом №2 генерирует свой красный фотон (крафон), который устремляется к атому под №5, при этом второй атом получает импульс «придачи» p4, направленный в том же направлении. Атом №5 поглощает крафон, присланный собратом и также получает встречный импульс p5, который придает ему колебания.
Кроме свечи и собратьев атомы соли колеблют еще в большей степени крафоны земли. На рис. показан один из них, который дергает импульсом p6 атом №9 по вектору вниз. После поглощения данный атом испускает свой крафон, который дергает атом импульсом p7 в сторону атома №11, который также получает встречный импульс p8, заставляя его сместиться на некоторое расстояние.
Учитывая, что крафонов вокруг любого тела огромное количество, то атомы постоянно взаимодействуют с ними и получают колебания, находясь в кристаллической решетке.
Вот так работает генератор, который заставляет атомы вечно колебаться относительно своего центра.
Таким же образом осуществляется и гравитационное взаимодействие между всеми материальными частицами и телами.
Поэтому, именно крафоны являются переносчиками механического импульса между атомами в кристаллической решетке.
Гравитационные импульсы источника и приемника передаются ядрам атомов, после чего они приобретают энергию движения относительно своего центра обитания.
Не нужно изобретать и плодить виртуальные частицы типа фонон, когда есть реальные электромагнитные волны (крафоны-термоны), которые являются переносчиками реальной энергии и импульса.
Краткие выводы.
- В природе не существует мнимых, даже квазичастиц, в природе существуют реальные переносчики импульса и энергии – это крафоны.
- Взаимодействие крафонов с атомами создает вечное колебание атомов в кристаллической решетке.
- С помощью излучения в виде крафонов, нагретое физическое тело избавляется от излишней энергии.
Назад Вперед
Теория Бора это попытка объяснить модель атома пользуясь идеями Планка , о дискретности электромагнитного излучения.
В соответствии с ними Н. Бор предположил, что процессы, происходящие при этом внутри атома, также подчиняются квантовым закономерностям.

Что такое теория Бора
Модель атома, предложенная Резерфордом, не могла удовлетворительно объяснить механизм излучения атомом электромагнитных волн, так как по мере излучения энергия электрона, а вместе с ней и скорость его движения вокруг ядра должны убывать и в конце концов электрон должен упасть на ядро.
В 1913 г. Н. Бор предложил новую теорию излучения света атомами, в основу которой были положены идеи М. Планка. Теория Н. Бора основывается на двух постулатах.
- Внутренняя энергия атома дискретна, т. е. может принимать только определенные дозволенные значения или уровни, кратные некоторым характерным для данного атома количествам или квантам энергии. Состояния, соответствующие этим уровням энергии, являются стационарными (равновесными): находясь в таком состоянии, атом не излучает электромагнитных волн несмотря на происходящее в нем движение электронов.
- Испускание (или поглощение) атомом электромагнитного излучения происходит при переходе из одного стационарного состояния в другое. При этом испускается (или поглощается) фотон монохроматического излучения с энергией Eф, равной разности энергетических уровней Е2 и Е1 соответствующих этим состояниям:
Еф = Е 2 — Е1.
Частота излучения v соответствует энергии фотона:
v = Eф/h = (E2 —E1)/h
где h — постоянная Планка.
Для согласования выдвинутых им положений с Резерфордовской моделью атома Н. Бор предложил считать, что стационарным состояниям или дозволенным энергетическим уровням атома соответствует движение электронов по орбитам определенного радиуса. Эти орбиты должны удовлетворять условию, чтобы момент количества движения lэ электрона был кратен постоянной Планка, деленной на 2π, т. е. где п — есть целое число, называемое квантовым числом атома, которое соответствует порядковому номеру орбиты. Число п может принимать значения: п — 1,2,3 …
Из этого условия можно определить радиусы дозволенных орбит электрона. В общем виде:
r = (h2/(4π2me2))(n2/Z)
где т — масса, е — заряд электрона, п — квантовое число или порядковый номер орбиты, Z — порядковый номер элемента.
Таким образом, радиусы дозволенных орбит прямо пропорциональны квадрату квантового числа и обратно пропорциональны порядковому номеру элемента. Например, для атома водорода (Z = 1) радиус наименьшей (п =1) орбиты r = 0,53•10-8 см. Эта величина и характеризует порядок размеров атома.
Энергия электрона в атоме состоит из кинетической энергии движения по орбите (скорость порядка 108 см/сек) и потенциальной энергии в поле ядра. Обе величины зависят от радиуса орбиты. Следовательно, определенным радиусам орбит соответствуют определенные энергетические уровни.
Изменение энергии электрона

Как изменяется энергия электрона и энергетический уровень атома при изменении радиуса орбиты.
- При увеличении радиуса орбиты скорость движения электрона уменьшается, соответственно уменьшается и его кинетическая энергия.
- Для того чтобы удалить электрон от ядра, надо совершить работу против сил притяжения, следовательно, потенциальная энергия электрона с увеличением радиуса орбиты увеличивается.
При этом потенциальная энергия возрастает на большую величину, чем уменьшается кинетическая, поэтому общая энергия электрона по мере увеличения радиуса орбиты увеличивается. Соответственно возрастают и энергетические уровни атома (рис. 2):
E1 < Е2 < Е3 < …
Разность энергии между двумя соседними стационарными уровнями по мере увеличения радиуса орбит, наоборот, уменьшается:
∆E‘ > ∆E» > ∆E»’ > где ∆E‘ = E2 — E1; ∆E »= E3 — E2, …
Стационарный уровень с наименьшей энергией называется основным, он характерен для атома в обычном состоянии (т. е. атома, не подвергающегося никаким внешним воздействиям). Остальные стационарные уровни называются возбужденными.
Возбуждение атома
Возбуждение атома требует сообщения ему дополнительной энергии и, следовательно, происходит в результате какого-либо внешнего воздействия на атом.
Это может быть соударение частиц в процессе теплового движения или при электрическом разряде в газах, поглощение фотона электромагнитного излучения и т. п. Возбужденное состояние может возникнуть также при рекомбинации ионов в газе, под действием частиц радиоактивного излучения и т. д.
Возбужденное состояние атома неустойчиво (метастабильно). Как правило, примерно через 10-8 сек электрон возвращается на основную орбиту, при чем излучает фотон, уносящий дополнительную энергию, полученную электроном при возбуждении атома (рис. , а).
При этом атом возвращается в основное состояние. Электрон может возвращаться на основную орбиту не сразу, а ступеньками через промежуточные уровни, В этом случае будет излучаться несколько фотонов с частотой, соответствующей разности энергетических уровней ступеней перехода (рис. , б).
При люминесценции возбуждение атомов происходит в результате поглощения энергии фотонов падающего на вещество излучения.
Если энергия фотона достаточно велика (ультрафиолетовое и еще более коротковолновое рентгеновское излучение), то при этом происходит возбуждение атома с последующим излучением (рис. , в).
Для того чтобы перевести внешний электрон на одну из возбужденных орбит, требуется в зависимости от природы атома энергия порядка нескольких электрон-вольт.
При возвращении электрона на основную орбиту будут излучаться фотоны с такой же энергией, что соответствует частоте видимого или близкого к нему ультрафиолетового излучения.
При переходах электрона с одной возбужденной орбиты на другую излучаются фотоны с еще меньшей энергией, относящиеся к инфракрасному излучению.
Таким образом, оптическое излучение связано преимущественно с переходом внешних электронов.
Спектр излучения атомов водорода

Пример спектра излучения атомов водорода в теории атома водорода по бору В зависимости от энергии, сообщенной атому при возбуждении, электрон может перейти на различные возбужденные орбиты.
При возвращении его на основную орбиту будут излучаться фотоны различной энергии, т. е. с различной частотой или длиной волны.
Каждой длине волны излучения соответствует линия в спектре, поэтому в спектре излучения атома водорода должно быть значительное число линий, расположение которых отражает энергетические уровни атома.
В спектре же газа, когда свет излучается громадным количеством атомов, будут присутствовать все возможные линии.
Еще до создания теории Н. Бора было установлено, что в спектре водорода имеются группы (серии) линий, расположение которых подчинено определенным закономерностям.
Например, четыре линии в видимой части спектра вместе с линиями в близкой ультрафиолетовой части составляют серию Бальмера. Частоты всех линий этой серии можно выразить общей формулой:
v = R ((1/22) — (1/n2))
где R — постоянная, равная 3,29•1015 сек-1, а п — переменное число, которое может принимать значение 3, 4, 5 и т. д.
Имеются и другие серии, например серия Лаймана в ультрафиолетовой части спектра, серии Пашена, Брекета и другие — в инфракрасной, частоты которых также могут быть выражены соответствующими формулами.
Расчеты частоты колебаний атомов водорода
Н. Бор произвел расчеты, в которых связал частоту колебаний, соответствующую длинам волн линий этих серий, с возможными в атоме водорода переходами между энергетическими уровнями.
На рис. 3 приведена диаграмма, в которой сопоставлены график распределения энергетических уровней (в), схема возможных переходов электрона (а), а также расположение линий в спектре (б).
При переходе электрона с любой возбужденной орбиты на основную разность энергетических уровней наибольшая, фотоны имеют наиболее короткую длину волны и излучение лежит в ультрафиолетовой области (серия Лаймана).
При аналогичном переходе электрона на первую возбужденную орбиту разность энергетических уровней меньше, спектральные линии относятся к видимой части спектра (серия Бальмера).
При переходе электрона на вторую возбужденную орбиту энергия фотонов еще меньше и излучение лежит в инфракрасной области (серия Пашена и др.).
Таким образом, теория Бора получила полное подтверждение в установленных экспериментально спектральных закономерностях.
Статья на тему Теория Бора
