Как найти частоту колебаний источника волны

В случае если известны длина волны и скорость распространения колебаний, частоту вычислите следующим образом:
F=v/λ, где F – частота (Гц) , v – скорость распространения колебаний в среде (м/с) , λ – длина волны (м) .

Если известна частота, период найти можно и в том случае, если скорость распространения колебаний неизвестна. Формула для вычисления периода по частоте выглядит следующим образом:
T=1/F, где T – период колебаний (с) , F – частота (Гц) .
Из сказанного выше следует, что найти частоту, зная период, можно также без информации о скорости распространения колебаний. Способ ее нахождения такой же:
F=1/T, где F – частота (Гц) , T – период колебаний (с) .

Для того чтобы узнать циклическую частоту колебаний, вначале вычислите их обычную частоту любым из указанных выше способов. Затем умножьте ее на 2π:
ω=2πF, где ω – циклическая частота (радиан в секунду) , F – обычная частота (Гц)

Отсюда следует, что для вычисления обычной частоты при наличии информации о циклической следует воспользоваться обратной формулой:
F=ω/(2π), где F – обычная частота (Гц) , ω – циклическая частота (радиан в секунду) .

При решении задач на нахождение периода и частоты колебаний, а также длины волны используйте следующие физические и математические константы:

– скорость света в вакууме: c=299792458 м/с (некоторые исследователи, в частности, креационисты, считают, что в прошлом данная физическая константа могла иметь другую величину) ;
– скорость звука в воздухе при атмосферном давлении и нуле градусов по Цельсию: Fзв=331 м/с;
– число «пи» (до пятидесятого знака) : π=3,14159265358979323846264338327950288419716939937510 (безразмерная величина).

Была ли эта статья полезной?

Механические колебания и волны

Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.

Отличительными признаками колебательного движения являются:

• повторяемость движения;
• возвратность движения.

Для существования механических колебаний необходимо:

• наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
• наличие малого трения в системе.

Механические волны – это процесс распространения колебаний в упругой среде.

Виды волн

• Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.

Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.

• Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.

Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.

Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.

Гармонические колебания

Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:

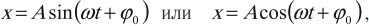
где ​( x )​ – координата тела – смещение тела от положения равновесия в данный момент времени; ​( A )​ – амплитуда колебаний; ​( omega t+varphi_0 )​ – фаза колебаний; ​( omega )​ – циклическая частота; ​( varphi_0 )​ – начальная фаза.

Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.

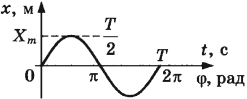
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.

Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:

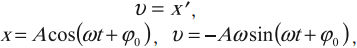
где ​( v )​ – мгновенное значение скорости, т. е. скорость в данный момент времени.

Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:

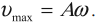
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:

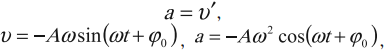
где ​( a )​ – мгновенное значение ускорения, т. е. ускорение в данный момент времени.

Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:

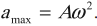
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:

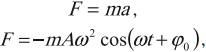
где ​( F )​ – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.

Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:

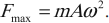
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:

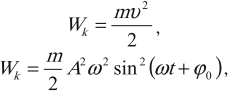
где ​( W_k )​ – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.

Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:

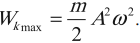
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:

• потенциальная энергия равна нулю;
• кинетическая энергия максимальна.

При максимальном отклонении от положения равновесия:

• кинетическая энергия равна нулю;
• потенциальная энергия максимальна.

Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:

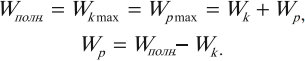
Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.

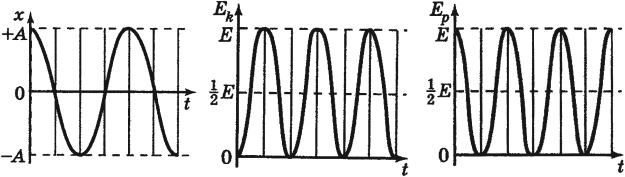
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.

Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).

Амплитуда и фаза колебаний

Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ​( A, (X_{max}) )​, единицы измерения – м.

Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ​( varphi )​, единицы измерения – рад (радиан).

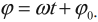
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
​( varphi_0 )​ – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.

Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.

Период колебаний

Период колебаний – это время одного полного колебания.
Обозначение – ​( T )​, единицы измерения – с.

Период гармонических колебаний – постоянная величина.

Частота колебаний

Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ​( nu )​, единицы времени – с^-1 или Гц (Герц).

1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:

Период и частота колебаний – взаимно обратные величины:

Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ​( omega )​, единицы измерения – рад/с.

Свободные колебания (математический и пружинный маятники)

Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.

Условия возникновения свободных колебаний:

• при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
• силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.

При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.

Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.

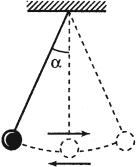
Период колебаний математического маятника:

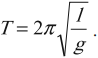
Частота колебаний математического маятника:

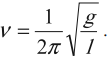
Циклическая частота колебаний математического маятника:

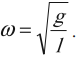
Максимальное значение скорости колебаний математического маятника:

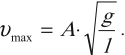
Максимальное значение ускорения колебаний математического маятника:

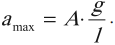
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:

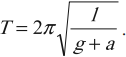
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:

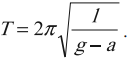
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:

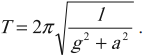
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ​( h )​, определяется по формуле:

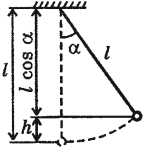
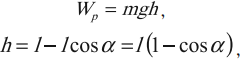
где ​( l )​ – длина нити, ​( alpha )​ – угол отклонения от вертикали.

Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.

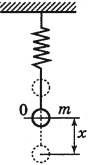
Период колебаний пружинного маятника:

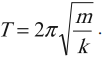
Частота колебаний пружинного маятника:

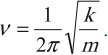
Циклическая частота колебаний пружинного маятника:

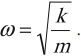
Максимальное значение скорости колебаний пружинного маятника:

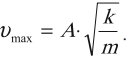
Максимальное значение ускорения колебаний пружинного маятника:

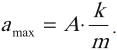
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:

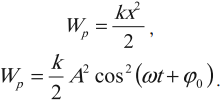
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:

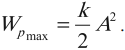
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.

Вынужденные колебания

Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.

Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.

Резонанс

Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.

Условие резонанса:

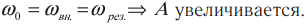
​( v_0 )​ – собственная частота колебаний маятника.

На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.

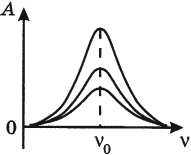
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.

Длина волны

Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ​( lambda )​, единицы измерения – м.

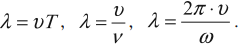
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.

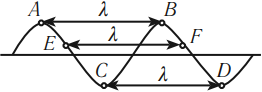
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.

Звук

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

• наличие источника звука;
• наличие упругой среды между источником и приемником звука;
• наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
• мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

• инфразвук (​( nu )​ < 16 Гц);
• звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
• ультразвук (( nu ) > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

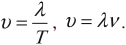
Скорость звука зависит

• от упругих свойств среды:

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

• от температуры среды:

в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

• Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
• Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
• Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.

Основные формулы по теме «Механические колебания и волны»