Как найти частоту колебаний нитяного маятника

В первой части нашей работы мы должны будем с вами с
помощью экспериментальной установки исследовать зависимость периода свободных
колебаний нитяного маятника от его длины.

Для выполнения этой работы нам предлагается использовать
оборудование из комплекта № 5 в составе: штатив с муфтой и креплением для нити,
груз с крючком, нить, электронный секундомер и метровую линейку или мерную
ленту.

Прежде чем приступить к работе давайте с вами вспомним, что маятником
называется твёрдое тело, совершающее под действием приложенных сил
колебания около неподвижной точки или вокруг оси.

Существует несколько видов маятников. Но наиболее часто
встречающиеся, это пружинный маятник, представляющий собой груз,
прикреплённый к пружине, и способный совершать колебания вдоль горизонтальной
или вертикальной оси.

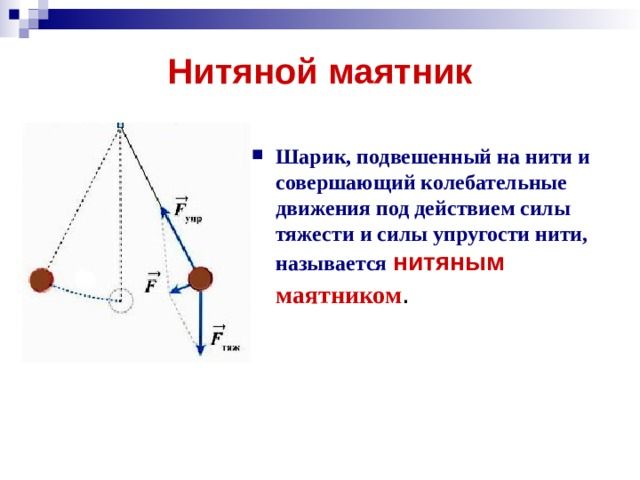
И нитяной маятник — шарик, подвешенный на нити,
способный совершать колебательное движение.

Теперь давайте вспомним, что любое колебательное движение
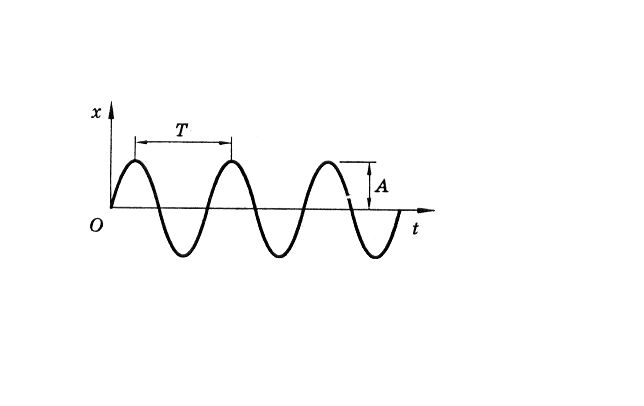
характеризуется амплитудой, частотой и периодом колебаний.

Амплитуда колебаний — это наибольшее смещение
колеблющегося тела от положения равновесия.

Частота
колебаний — это
число колебаний, совершаемых телом за единицу времени. Обозначается она
греческой буквой ν. А единицей её измерения в системе СИ является герц
[Гц]:

И, наконец, период
колебаний — это наименьший промежуток времени, через который полностью
повторяется состояние колебательной системы. Обозначается период большой буквой
Т. Единица измерения — секунда [с]:

Ещё в
середине XVII века нидерландский учёный Христиан Гюйгенс показал, что «период малых
колебаний математического маятника зависит от длины подвеса и ничего более»:

И в первой
части нашей работы мы с вами должны будем проверить, как зависит период
колебаний маятника от его длины.

Итак, для
начала давайте соберём экспериментальную установку. Для этого закрепим
перекладину в муфте у верхнего края стержня штатива. Штатив разместим на столе
так, чтобы конец перекладины выступал за край поверхности стола. Далее подвесим
к перекладине с помощью нити груз из набора. И сразу же установим длину нити в
1 м. Электронный секундомер переведём в ручной режим работы.

Далее мы
сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с
горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого
много меньше длины нити — это положение равновесия маятника. Далее изображаем
маятник в положении максимального отклонения (не более 15° от положения
равновесия.

Теперь
запишем формулы, которыми будем пользоваться при выполнении данной работы. Как
мы уже вспоминали, период колебаний равен отношению промежутка времени,
в течение которого тело совершило N полных колебаний, к числу этих
колебаний:

Так как нам необходимо будет провести несколько измерений, то
давайте с вами составим таблицу. В первой колонке мы укажем номера опытов. Во
второй колонке мы запишем значения длины маятника, которые нам даны в условии
задания. Число колебаний маятника мы запишем в третью колонку (во всех опытах
оно будет одинаковым и равно 30). Четвёртую колонку мы отведём для записи
времени совершения заданного числа колебаний. А в последнюю колонку будем
записывать значения периода колебаний маятника.

Теперь приступим непосредственно к работе. Итак, отклоняем
нить маятника на угол не более 10—15° (можно помочь себе транспортиром). Затем
отпускаем груз и даём маятнику совершить два — три полных колебания, чтобы
процесс колебаний стал установившимся. В момент прохождения маятником крайнего
положения запускаем секундомер. Теперь нам остаётся только дождаться, пока
маятник не совершит 30 полных колебаний. По окончании последнего колебаний
останавливаем секундомер.

Значение промежутка времени, за которое маятник совершил
заданное число колебаний, записываем в таблицу с учётом погрешности измерения:

Теперь уменьшим длину нити маятника в два раза и повторим
эксперимент. По окончании тридцатого колебания останавливаем секундомер и
записываем значение промежутка времени в таблицу.

Наконец уменьшаем длину маятника до 25 см и, включив секундомер,
вновь отсчитываем 30 полных колебаний. Не забываем записать в таблицу значение
промежутка времени с учётом погрешности измерения:

Прямые измерения мы с вами завершили. Теперь определяем
период колебаний. Для этого подставляем в расчётную формулу значения
промежутков времени и числа полных колебаний для каждого из трёх случаев:

Теперь хорошо видно, что чем меньше длина нити маятника, тем
меньше его период колебаний. Поэтому в выводе напишем: при уменьшении
длины нити период свободных колебаний нитяного маятника уменьшается.

Во второй части работы мы с вами должны будем
проверить, зависит ли период колебаний нитяного маятника от массы груза.

Оборудование мы будем использовать практически то же самое:
штатив с муфтой и креплением для нити, набор грузов с крючками, нить,
электронный секундомер и метровую линейку или мерную ленту.

Итак, для
начала давайте соберём экспериментальную установку. Для этого закрепим
перекладину в муфте у верхнего края стержня штатива. Штатив разместим на столе
так, чтобы конец перекладины выступал за край поверхности стола. Далее подвесим
к перекладине с помощью нити один груз из набора. Длина маятника по условию
задания у нас должна быть равна 1 м. Электронный секундомер переведём в ручной
режим работы.

Далее мы
сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с
горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого
много меньше длины нити — это положение равновесия маятника. Далее изображаем
маятник в положении максимального отклонения (не более 15° от положения
равновесия.

Теперь
запишем формулы, которыми будем пользоваться при выполнении данной работы. Как
мы уже вспоминали, период колебаний равен отношению промежутка времени,
в течение которого тело совершило N полных колебаний, к числу этих
колебаний:

Так как нам необходимо будет провести несколько измерений, то
давайте с вами составим таблицу. В первой колонке мы укажем номера опытов. Во
второй колонке мы запишем значения массы маятника, которые нам даны в условии
задания. Число колебаний маятника мы запишем в третью колонку (во всех опытах
оно будет одинаковым и равно 30). Четвёртую колонку мы отведём для записи
времени совершения заданного числа колебаний. А в последнюю колонку будем
записывать значения периода колебаний маятника.

Теперь приступим непосредственно к работе. Итак, отклоняем
нить маятника на угол не более 10—15° (можно помочь себе транспортиром). Затем
отпускаем груз и даём маятнику совершить два — три полных колебания, чтобы
процесс колебаний стал установившимся. В момент прохождения маятником крайнего
положения запускаем секундомер. Теперь нам остаётся только дождаться, пока
маятник не совершит 30 полных колебаний. По окончании последнего колебаний
останавливаем секундомер. Значение промежутка времени, за которое маятник
совершил 30 колебаний, записываем в таблицу с учётом погрешности измерения:

Теперь подвесим к маятнику второй груз и повторим
эксперимент. По окончании тридцатого колебания останавливаем секундомер и
записываем значение промежутка времени в таблицу.

Наконец, увеличиваем массу маятника до 300 г и, включив секундомер,
вновь отсчитываем 30 полных колебаний. Не забываем записать в таблицу значение
промежутка времени с учётом погрешности измерения:

Прямые измерения мы с вами завершили. Теперь определяем
период колебаний. Для этого подставляем в расчётную формулу значения
промежутков времени и числа полных колебаний для каждого из трёх случаев:

Таким образом видим, что в пределах погрешности измерений
период колебаний маятника остаётся неизменным. Поэтому в выводе мы
напишем: период колебаний нитяного маятника не зависит от массы груза.

Что касается исследования зависимости частоты колебаний
маятника от его длины, то вся работа остаётся примерно такой же,
что и в нашей первой работе, где мы определяли период колебаний. Отличие будет
состоять только в расчётной формуле. Ведь частота определяет число колебаний,
совершаемых телом за единицу времени:

То же самое
касается и исследования зависимости
частоты колебаний нитяного маятника от массы груза. Ведь в любом
случае, частота — это величина, обратная периоду колебаний.

План урока:

Колебательное движение

Период и частота колебаний

Свободные колебания

Амплитуда колебаний

Колебательные системы

Гармонические колебания

Величины, характеризующие колебательное движение

Затухающие колебания

Вынужденные колебания

Колебательное движение

В самом широком смысле, колебательное движение – это любое движение, повторяющееся с течением времени. Например, птица, машущая крыльями вверх-вниз, совершает ими колебательные движения. Ребенок, качающийся на качелях, тоже совершает колебательные движения. Игла швейной машины при шитье – тоже.

Но как же так, ведь в названных примерах тела движутся абсолютно по-разному? Крылья птицы и игла швейной машины движутся вертикально вверх-вниз (прямолинейно), ребенок на качелях движется горизонтально и по дуге (криволинейно). Это все неважно. Главный признак колебательного движения – его повторяемость через определенный промежуток времени, то есть через период колебаний.

Период и частота колебаний

Период колебаний (T) – это время, за которое тело совершает полный цикл движения, т.е. совершает одно колебание.

В случае с движением крыльев птицы, если считать, что один взмах начинается с верхней точки, полным колебанием будет считаться, когда крылья пройдут от верхней точки через середину до нижней и вернутся от нижней точки через середину до верхней (рисунок 1).

Рисунок 1 – Взмах крыльев птицы как пример полного колебания   

Период колебаний обозначается латинской буквой T. По определению период – это время, значит, единица измерения периода будет такой же, как и единица измерения времени. В СИ это секунда.

[T] = 1 с

Как же можно вычислить период колебаний?

Самый простой способ – это посчитать количество колебаний и секундомером измерить время, за которое эти колебания были совершены. Например, ребенок на качелях совершает N = 10 колебаний за t = 30 секунд. Нетрудно подсчитать, что время совершения одного полного колебания будет 30/10 = 3 с. Если обобщить, получится формула для нахождения периода колебаний:

где t – время, за которое совершено N колебаний.

Рассмотрим еще одну важную характеристику.

Частота колебаний (ν) – это количество колебаний, совершаемое телом за единицу времени.

Частота колебаний обозначается греческой буквой (читается как «ню»).

Если сравнить определение частоты колебаний с определением периода, можно заметить, что это обратные величины. То есть:

Гц – единица измерения, которую назвали в честь немецкого физика Генриха Герца. При решении задач одинаково часто употребляется и герц, и с^-1. Можно употреблять и то, и другое – в зависимости от того, что удобнее при решении конкретной задачи.

Следует так же отметить, что иногда физики пользуются циклической частотой колебаний:

Свободные колебания

Положение равновесия при колебательном движении

Сравним две ситуации:

1. Родитель толкает качели, на которых сидит ребенок, а потом просто наблюдает, как качели качаются сами по себе.

2. Родитель толкает качели с ребенком, а потом при каждом цикле движения подталкивает качели, поддерживая качания.

Физики говорят, что в первом случае система (качели и ребенок) совершает свободные колебания, то есть колебания под действием только внутренних сил. После выведения системы из равновесия (то есть толчка родителя) к ней больше не прикладывают внешних сил. Во втором случае говорят, что система совершает вынужденные колебания – то есть колебания, под действием периодического внешнего воздействия.

Поговорим о свободных колебаниях. Для простоты рассмотрим систему, состоящую из маленького тяжелого шарика на длинной крепкой нити. Такая система называется нитяным маятником (рисунок 2).

 Рис.2 – Нитяной маятник 

Без воздействия внешних сил шарик будет находиться в положении 1. Такое состояние называется положением равновесия. Далее к шарику прикладывают силу, направленную влево и он начинает совершать колебания. Траектория шарика будет: 1-2-1-3-1 (см. рисунок 1).

Как при этом будет меняться скорость тела? Для того, чтобы рассмотреть подробно, нужно помнить определения потенциальной и кинетической энергии*, а также в чем заключается закон сохранения энергии (систему считаем замкнутой – потерь энергии не происходит, а, значит, закон сохранения энергии выполняется – энергия колебательной системы остается постоянной):

• при движении из точки 1 в 2 шарик постепенно замедляется (уменьшается его кинетическая энергия, а потенциальная увеличивается);
• в точке 2 он на мгновенье останавливается (кинетическая энергия равна нулю, потенциальная максимальна);
• далее он начинает движение с ускорением, но уже в обратном направлении (кинетическая энергия увеличивается, потенциальная уменьшается) – при движении из 2 в 1 тело будет ускоряться;
• когда шарик дойдет до точки 1 его кинетическая энергия будет максимальна, а потенциальная минимальна.

При движении от точки 1 в 3 будет происходить то же самое, что и при движении из 1 в 2 – предлагаем описать процесс изменения величин (скорости и энергии) самостоятельно.

Если обобщить все сказанное, можно сделать вывод: при колебаниях в положении равновесия кинетическая энергия тела максимальна, а потенциальная минимальна (или равна нулю, в зависимости от выбранной точки отсчета). В крайних положениях потенциальная энергия максимальна, а кинетическая равна нулю. То есть положение равновесия маятника – это такое положение, в котором его потенциальная энергия минимальна (или равна нулю, в зависимости от точки отсчета). При удалении маятника от положения равновесия кинетическая энергия будет уменьшаться, а потенциальная увеличиваться.

*Потенциальная энергия тела зависит от его положения в пространстве; кроме того, это относительная величина – она зависит от того, какая точка отсчета выбрана.

Кинетическая энергия зависит от модуля скорости тела.

Амплитуда колебаний

Помимо частоты и периода важной характеристикой колебаний является амплитуда.

Амплитуда колебаний – это модуль максимального смещения тела от положения равновесия. Другими словами, это расстояние между положением равновесия и крайней точкой траектории маятника. Рассмотрим рисунок 3. На нем изображен уже знакомый вам нитяной маятник. В идеальном случае амплитуду колебаний маятника нужно считать как длину дуги от положения равновесия до крайней точки. Но если мы считаем, что колебания малые – то есть длина нити маятника (l) гораздо больше смещения (S), можно считать, что длина дуги совпадает с длиной отрезка между проекциями положения равновесия и крайней точки на ось ОХ.

Рис.3 – Амплитуда колебаний нитяного маятника

Обычно амплитуда обозначается большой латинской буквой A.

Колебательные системы

Для того, чтобы рассмотреть колебательные движения подробнее, рассмотрим несколько колебательных систем, на примере которых будет рассматривать все закономерности.

1. Маятник

В общем случае маятник – это система, способная совершать колебания под действием каких-либо сил, например, сил трения, упругости, тяжести.

2. Пружинный маятник

Пружинный маятник – это система, состоящая из упругой пружины, один конец которой закреплен, а на другой прикреплен груз.

Такой маятник может быть вертикальным (рисунок 4а), тогда колебания будут совершаться под действием сил тяжести и упругости; и горизонтальным (рисунок 4б), тогда на груз будут действовать сил упругости и трения.

Рис.4 – Пружинный маятник

Для пружинного маятника справедливы формулы:

где T –период колебаний пружинного маятника; π ~ 3.14;  m–масса груза;k–коэффициент жесткости пружины; – частота колебаний пружинного маятника.

*Ранее говорилось, что существует такая характеристика, как циклическая частота. Формула для ее нахождения будет выглядеть так:

3. Нитяной маятник

Этот вид маятника уже рассматривался ранее (см. рисунок 3), он состоит из длинной нити и тяжелого грузика, подвешенного на ней.

Для нитяного маятника справедливы формулы:

где T – период колебаний нитяного маятника; π ~ 3.14; l –длина нити; g – ускорение свободного падения (~9,8 м/с²), v – частота колебаний.

Интересно отметить, что период нитяного маятника и, следовательно, его частота не зависят от массы грузика, прикрепленного к нити.

*Следует отметить, что все приведенные формулы справедливы только для малых колебаний.

** Циклическая частота нитяного маятника:

Гармонические колебания

При решении задач часто используется не нитяной маятник, а его упрощенная модель – математический маятник. Это идеальная колебательная система, в которой нить считается очень длинной по сравнению с амплитудой колебаний и размерами грузика; сам груз достаточно тяжелым, чтобы пренебречь массой нити. Кроме того, считается, что не происходит потерь энергии.

Рассмотрим подробно, какие силы действуют на такую систему. В первую очередь, на грузик действует сила тяжести mg, направленная вниз (см. рисунок 5). Так же на него действует сила натяжения со стороны нити F, она направлена вдоль нити. Обозначим  угол, на который смещается тело от положения равновесия.

Рис.5 – Силы, действующие на математический маятник

Запишем 2-й закон Ньютона:

Рисунок 6 – Силы, действующие на математический маятник при смещении на угол φ

В случае малых углов sinφ можно считать равным φ. Из геометрического определения синуса:

Тогда в крайней точке 2-й закон Ньютона в проекции на ось OX перепишется следующим образом:

То есть ускорение, с которым движется маятник прямо пропорционально его смещению от положения равновесия. Минус в данном выражении означает, что ускорении направлено в противоположную сторону от смещения.

Интересно заметить, что ускорение грузика, подвешенного к ниточке (а значит и самого маятника), не зависит от его массы. Период колебаний математического маятника тоже не зависит от массы грузика:

В случаях, когда колебания происходят под действием силы, пропорциональной смещению тела от положения равновесия, говорят, что тело совершает гармонические колебания.*

График зависимости смещения от времени при гармоническом колебательном движении представляет собой синусоиду или косинусоиду (см. рисунок 7).

Для лучшего понимания, почему график выглядит именно так, можно посмотреть урок в курсе алгебры «Тригонометрические функции»:

 Рис. 7 – График зависимости смещения (x) от времени (t) при гармонических колебаниях   

На графическом представлении колебаний (рисунок 7) удобно находить период и амплитуду гармонических колебаний.

*Могло сложиться впечатление, что гармонические колебания может совершать только математический маятник. Это не так. Любое тело может совершать колебания, близкие к гармоническим (нужно учитывать не идеальность систем). Например, можно говорить о гармонических колебаниях пружины, если она достаточно жесткая, чтобы она деформировалась упруго, а колебания совершаются с небольшой амплитудой.

Величины, характеризующие колебательное движение

Ранее рассматривались такие характеристики колебаний, как период, частота и амплитуда. Помимо этих величин, колебания характеризуются фазой колебаний.

Фаза колебаний

На рисунке 7 изображен график зависимости смещения от времени при гармонических колебаниях. Такой график называется синусоидой (косинусоидой). В общем случае уравнение зависимости координаты Х от времени t будет выглядеть так:

Разность фаз

Понятие «разность фаз» применяется, когда мы хотим сравнить движение двух маятников. Пусть маятник 1 и маятник 2 двигаются по законам соответственно:

Найдем разность фаз колебаний этих двух маятников.

Если взять конкретный момент времени , фаза гармонических колебаний каждого из маятников в этот момент времени будет:

 – это начальные фазы колебания первого и второго маятников соответственно. Эти величины являются начальными условиями, и они не изменяются во время движения, следовательно, при одинаковой частоте колебаний маятников разность фаз остается постоянной.

Затухающие колебания

Во всех рассмотренных ранее случаях считалось, что на колеблющуюся систему не действуют силы извне. На самом деле, идеальных систем не существует, поэтому любой маятник во время движения будет преодолевать внешние силы сопротивления и терять энергию. Например, пружинный маятник (рисунок 8) будет преодолевать силу трению о поверхность.

Рисунок 8 – Пружинный маятник на шероховатой поверхности  

Колебания, энергия которых уменьшается с течением времени, называются затухающими.

Амплитуда затухающих колебаний уменьшается со временем. График таких колебаний изображен на рисунке 9.

Рисунок 9 – График зависимости координаты от времени при затухающих колебаниях  

Вынужденные колебания

Собственная частота колебаний. Частота вынуждающей силы. Установившиеся вынужденные колебания

В реальных (неидеальных) системах колебания всегда нужно поддерживать внешним воздействием.

Под действием периодической внешней изменяющейся силы возникают вынужденные колебания.

Почему же обязательно сила должны быть периодически изменяющейся? Ответ на этот вопрос легко найти, представив себе качели. Если на них действовать с постоянной по модулю и направлению силой, они никогда не начнут качаться. А толчками (то есть периодической изменяющейся силой) раскачать их не составит труда.

Внешняя сила, заставляющая систему совершать колебания, называется вынуждающей силой.

Так как эта сила периодическая, необходимо ввести частоту вынуждающей силы. А чтобы не запутаться, частоту свободных колебаний называют собственной частотой системы. Как показывают эксперименты, даже если изначально собственная частота системы и частота вынуждающей силы отличались, через некоторое время система начинает колебаться с частотой вынуждающей силы. В таких случаях говорят об установившихся вынужденных колебаниях.

Если частота вынуждающей силы равна собственной частоте системы, возникает резонанс – резкое увеличение амплитуды колебаний.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Формулы математического маятника в физике

Формулы математического маятника

Определение и формулы математического маятника

Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Уравнение движения математического маятника

Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:

[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]

где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.

Решением уравнения (1) является функция $varphi (t):$

[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]

где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.

Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

Циклическая частота и период колебаний математического маятника

Циклическая частота математического маятника зависит только от длины его подвеса:

[ {omega }_0=sqrt{frac{g}{l}}left(3right).]

Период колебаний математического маятника ($T$) в этом случае равен:

[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]

Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

Уравнение энергии для математического маятника

При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]

где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:

[varphi =frac{x}{l}left(6right).]

Максимальное значение потенциальной энергии математического маятника равно:

[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]

Максимальная величина кинетической энергии:

[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]

где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.

Примеры задач с решением

Читать дальше: формулы пружинного маятника.