Формула частоты в физике
Формула частоты
Определение
Частота – это физический параметр, которые используют для характеристики периодических процессов.
Частота равна количеству повторений или свершения событий в единицу времени.
Чаще всего в физике частоту обозначают буквой $nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$
[nu =frac{1}{T}left(1right).]
Частота, в этом случае – это число полных колебаний ($N$), совершающихся за единицу времени:
[nu =frac{N}{Delta t}left(2right),]
где $Delta t$ – время за которое происходят $N$ колебаний.
Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:
[left[nu right]=с^{-1}=Гц.]
Герц – это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${nu }_1 и {nu }_2$) равна:
[{nu =nu }_1- {nu }_2left(3right).]
Еще одно величиной характеризующей колебательный процесс является циклическая частота (${omega }_0$), связанная с частотой как:
[{omega }_0=2pi nu left(4right).]
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Частота колебаний тела, имеющего массу$ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:
[nu =frac{1}{2pi sqrt{{m}/{k}}}left(5right).]
Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
[nu =frac{1}{2pi sqrt{{l}/{g}}}left(6right),]
где $g$ – ускорение свободного падения; $ l$ – длина нити (длина подвеса) маятника.
Физический маятник совершает колебания с частотой:
[nu =frac{1}{2pi sqrt{{J}/{mgd}}}left(7right),]
где $J$ – момент инерции тела, совершающего колебания относительно оси; $d$ – расстояние от центра масс маятника до оси колебаний.
Формулы (4) – (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.
Формулы для вычисления частоты дискретных событий, частота вращения
дискретных колебаний ($n$) – называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(8right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) – называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ – время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(9right).]
Примеры задач с решением
Пример 1
Задание. Колебательная система совершила за время равное одной минуте ($Delta t=1 мин$) 600 колебаний. Какова частота этих колебаний?
Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае – это число полных колебаний, совершающихся за единицу времени.
[nu =frac{N}{Delta t}left(1.1right).]
Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $Delta t=1 мин=60 с$. Вычислим частоту:
[nu =frac{600}{60}=10 left(Гцright).]
Ответ. $nu =10Гц$
Пример 2
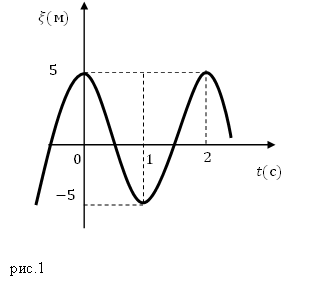
Задание. На рис.1 изображен график колебаний некоторого параметра $xi (t)$, Какова амплитуда и частота колебаний этой величины?
Решение. Из рис.1 видно, что амплитуда величины $xi left(tright)={xi }_{max}=5 (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:
[T=2 left(cright).]
Частота – величина обратная периоду колебаний, значит:
[nu =frac{1}{T}=0,5 left(Гцright).]
Ответ. 1) ${xi }_{max}=5 (м)$. 2) $nu =0,5$ Гц
Читать дальше: формулы математического маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
| Частота | |
|---|---|
 |
|
| Размерность | T−1 |
| Единицы измерения | |
| СИ | Гц |
Частота́ — физическая величина, характеристика периодического процесса, равная отношению количества повторяющихся событий (процессов) к промежутку времени, за который они произошли[1]. Стандартные обозначения в формулах — буква латинского алфавита «эф» f, F или буква греческого алфавита «ню» (ν).
Частота обратно пропорциональна периоду колебаний: ν = 1/T.
Единицей измерения частоты в Международной системе единиц (СИ) является герц (русское обозначение: Гц; международное: Hz), названной в честь немецкого физика Генриха Герца.
| Частота | 1 мГц (10−3 Гц) | 1 Гц (100 Гц) | 1 кГц (103 Гц) | 1 МГц (106 Гц) | 1 ГГц (109 Гц) | 1 ТГц (1012 Гц) |
|---|---|---|---|---|---|---|
| Период | 1 кс (103 с) | 1 с (100 с) | 1 мс (10−3 с) | 1 мкс (10−6 с) | 1 нс (10−9 с) | 1 пс (10−12 с) |
Частота, как и время, является одной из наиболее точно измеряемых физических величин: до относительной точности 10−17[2].
В природе известны периодические процессы с частотами от ~10−16 Гц (частота обращения Солнца вокруг центра Галактики) до ~1035 Гц (частота колебаний поля, характерная для наиболее высокоэнергичных космических лучей).
В квантовой механике частота колебаний волновой функции квантовомеханического состояния имеет физический смысл энергии этого состояния. Частоту ν и энергию E в формуле E = h2πν связывает постоянная Планка.
Глаз человека чувствителен к электромагнитным волнам с частотами от 4⋅1014 до 8⋅1014 Гц (видимый свет); частота колебаний определяет цвет наблюдаемого света. Слуховой анализатор человека воспринимает акустические волны с частотами от 20 Гц до 20 кГц. У различных животных частотные диапазоны чувствительности к оптическим и акустическим колебаниям различны.
Отношения частот звуковых колебаний выражаются с помощью музыкальных интервалов, таких как октава, квинта, терция и т. п. Интервал в одну октаву между частотами звуков означает, что эти частоты отличаются в 2 раза, интервал в чистую квинту означает отношение частот 3⁄2. Кроме того, для описания частотных интервалов используется декада — интервал между частотами, отличающимися в 10 раз. Так, диапазон звуковой чувствительности человека составляет 3 декады (20 Гц — 20 000 Гц). Для измерения отношения очень близких звуковых частот используются такие единицы, как цент (отношение частот, равное 21/1200) и миллиоктава (отношение частот 21/1000).
Мгновенная частота и частоты спектральных составляющих[править | править код]
Периодический сигнал характеризуется мгновенной частотой, являющейся (с точностью до коэффициента) скоростью изменения фазы, но тот же сигнал можно представить в виде суммы гармонических спектральных составляющих, имеющих свои (постоянные) частоты. Свойства мгновенной частоты и частоты́ спектральной составляющей различны[3].
Синусоидальные волны различных частот, нижние волны имеют более высокие частоты, чем верхние. Горизонтальная ось представляет время
Термины: циклическая частота, угловая частота[править | править код]
В научной и учебной литературе для частоты, измеряемой в герцах, можно встретить термин “циклическая частота”, и это оправдано, поскольку имеем дело с величиной, показывающей количество циклов в секунду. Также в теории электромагнетизма, в теоретической физике, электротехнике, электронике, радиотехнике используют скалярную физическую величину “угловая частота” (для неё принято обозначение ω). Синонимы угловой частоты: радиальная частота, круговая частота.
В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота в радианах в секунду выражается через циклическую частоту ν (равную числу циклов, колебаний, оборотов в секунду) как ω = 2πν[4]. При использовании для угловой частоты единицы измерений “градусы в секунду” связь с частотой ν такая: ω = 360°ν.
Введение угловой частоты позволяет упростить многие формулы в теоретической физике и электронике. Так, угловая частота резонанса в колебательном LC-контуре равна 

В механике при рассмотрении вращательного движения аналогом угловой частоты служит угловая скорость. Угловая частота вращательного движения равна модулю вектора угловой скорости.
Частота дискретных событий[править | править код]
Частота дискретных событий (частота импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий — секунда в минус первой степени (русское обозначение: с−1; международное: s−1). Частота 1 с−1 равна такой частоте дискретных событий, при которой за время 1 с происходит одно событие[5][6].
Частота вращения[править | править код]
Частота вращения — это физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с−1, s−1), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т. д.
Другие величины, связанные с частотой[править | править код]
Единицы измерения[править | править код]
В системе СИ единица измерения частоты: герц, Гц, Hz. Единица измерения герц первоначально введена в 1930 году Международной электротехнической комиссией[7], а в 1960 году принята для общего употребления 11-й Генеральной конференцией по мерам и весам, как единица СИ. До этого в качестве единицы частоты использовали цикл в секунду (1 цикл в секунду = 1 Гц) и производные (килоцикл в секунду, мегацикл в секунду, киломегацикл в секунду, равные соответственно килогерцу, мегагерцу и гигагерцу).
Метрологические аспекты[править | править код]
Для измерения частоты применяют частотомеры разных видов, в том числе: для измерения частоты импульсов — электронно-счётные и конденсаторные, для определения частот спектральных составляющих — резонансные и гетеродинные частотомеры, а также анализаторы спектра. Для воспроизведения частоты с заданной точностью используют различные меры — стандарты частоты (высокая точность), синтезаторы частот, генераторы сигналов и др. Сравнивают частоты компаратором частоты или с помощью осциллографа по фигурам Лиссажу.
Эталоны[править | править код]
Для поверки средств измерения частоты используются национальные эталоны частоты. В России к национальным эталонам частоты относятся:
- Государственный первичный эталон единиц времени, частоты и национальной шкалы времени ГЭТ 1-98 — находится во ВНИИФТРИ.
- Вторичный эталон единицы времени и частоты ВЭТ 1-10-82 — находится в СНИИМ (Новосибирск).
Вычисления[править | править код]
Вычисление частоты повторяющегося события осуществляют посредством учета количества появлений этого события в течение интервала времени наблюдения. Полученное количество относят к продолжительности интервала времени наблюдения. Пример: если на протяжении 15 секунд произошло 71 однородное событие, то частота составит
Если полученное количество отсчетов невелико, то более точным приемом является измерение временного интервала для заданного числа появлений рассматриваемого события, а не нахождение количества событий в пределах заданного промежутка времени[8]. Использование последнего метода вводит между нулевым и первым отсчетом случайную ошибку, составляющую в среднем половину отсчета; это может приводить к появлению средней ошибки в вычисляемой частоте Δν = 1/(2 Tm), или же относительной погрешности Δν/ν = 1/(2vTm), где Tm — временной интервал, а ν — измеряемая частота. Ошибка убывает по мере возрастания частоты, поэтому данная проблема является наиболее существенной для низких частот, где количество отсчётов N мало.
Методы измерения[править | править код]
Стробоскопический метод[править | править код]
Использование специального прибора — стробоскопа — является одним из исторически ранних методов измерения частоты вращения или вибрации различных объектов. В процессе измерения задействуется стробоскопический источник света (как правило, яркая лампа, периодически дающая короткие световые вспышки), частота работы которого подстраивается при помощи предварительно откалиброванной хронирующей цепи. Источник света направляется на вращающийся объект, а затем частота вспышек постепенно изменяется. Когда частота вспышек уравнивается с частотой вращения или вибрации объекта, последний успевает совершить полный колебательный цикл и вернуться в изначальное положение в промежутке между двумя вспышками, так что при освещении стробоскопической лампой этот объект будет казаться неподвижным. У данного метода, впрочем, есть недостаток: если частота вращения объекта (x) не равна частоте строба (y), но пропорциональна ей с целочисленным коэффициентом (2x, 3x и т. п.), то объект при освещении все равно будет выглядеть неподвижным.
Стробоскопический метод используется также для точной настройки частоты вращения (колебаний). В этом случае частота вспышек фиксирована, а изменяется частота периодического движения объекта до тех пор, пока он не начинает казаться неподвижным.
Метод биений[править | править код]
Близким к стробоскопическому методу является метод биений. Он основан на том, что при смешивании колебаний двух частот (опорной ν и измеряемой ν’1) в нелинейной цепи в спектре колебаний появляется также разностная частота Δν = |ν − ν’1|, называемая частотой биений (при линейном сложении колебаний эта частота является частотой огибающей суммарного колебания). Метод применим, когда более предпочтительным является измерение низкочастотных колебаний с частотой Δf. В радиотехнике этот метод также известен под названием гетеродинного метода измерения частоты. В частности, метод биений используется для точной настройки музыкальных инструментов. В этом случае звуковые колебания фиксированной частоты (например, от камертона), прослушиваемые одновременно со звуком настраиваемого инструмента, создают периодическое усиление и ослабление суммарного звучания. При точной настройке инструмента частота этих биений стремится к нулю.
Применение частотомера[править | править код]
Высокие частоты обычно измеряются при помощи частотомера. Это электронный прибор, который оценивает частоту определенного повторяющегося сигнала и отображает результат на цифровом дисплее или аналоговом индикаторе. Дискретные логические элементы цифрового частотомера позволяют учитывать количество периодов колебаний сигнала в пределах заданного промежутка времени, отсчитываемого по эталонным кварцевым часам. Периодические процессы, которые не являются по своей природе электрическими (такие, к примеру, как вращение оси, механические вибрации или звуковые волны), могут быть переведены в периодический электрический сигнал при помощи измерительного преобразователя и в таком виде поданы на вход частотомера. В настоящее время приборы этого типа способны охватывать диапазон вплоть до 100 ГГц; этот показатель представляет собой практический потолок для методов прямого подсчёта. Более высокие частоты измеряются уже непрямыми методами.
Непрямые методы измерения[править | править код]
Вне пределов диапазона, доступного частотомерам, частоты электромагнитных сигналов нередко оцениваются опосредованно, с помощью гетеродинов (то есть частотных преобразователей). Опорный сигнал заранее известной частоты объединяется в нелинейном смесителе (таком, к примеру, как диод) с сигналом, частоту которого необходимо установить; в результате формируется гетеродинный сигнал, или — альтернативно — биения, порождаемые частотными различиями двух исходных сигналов. Если последние достаточно близки друг к другу по своим частотным характеристикам, то гетеродинный сигнал оказывается достаточно мал, чтобы его можно было измерить тем же частотомером. Соответственно, в результате этого процесса оценивается лишь отличие неизвестной частоты от опорной, каковую следует определять уже иными методами. Для охвата ещё более высоких частот могут быть задействованы несколько стадий смешивания. В настоящее время ведутся исследования, нацеленные на расширение этого метода в направлении инфракрасных и видимо-световых частот (т. н. оптическое гетеродинное детектирование).
Примеры[править | править код]
Электромагнитное излучение[править | править код]
Полный спектр электромагнитного излучения с выделенной видимой частью
Видимый свет представляет собой электромагнитные волны, состоящие из осциллирующих электрических и магнитных полей, перемещающихся в пространстве. Частота волны определяет её цвет: 4×1014 Гц — красный цвет, 8×1014 Гц — фиолетовый цвет; между ними в диапазоне (4…8)×1014 Гц лежат все остальные цвета радуги. Электромагнитные волны, имеющие частоту менее 4×1014 Гц, невидимы для человеческого глаза, такие волны называются инфракрасным (ИК) излучением. Ниже по спектру лежит микроволновое излучение и радиоволны. Свет с частотой выше, чем 8×1014 Гц, также невидим для человеческого глаза; такие электромагнитные волны называются ультрафиолетовым (УФ) излучением. При увеличении частоты электромагнитная волна переходит в область спектра, где расположено рентгеновское излучение, а при ещё более высоких частотах — в область гамма-излучения.
Все эти волны, от самых низких частот радиоволн и до высоких частот гамма-лучей, принципиально одинаковы, и все они называются электромагнитным излучением. Все они распространяются в вакууме со скоростью света.
Другой характеристикой электромагнитных волн является длина волны. Длина волны обратно пропорциональна частоте, так что электромагнитные волны с более высокой частотой имеет более короткую длину волны, и наоборот. В вакууме длина волны
где с — скорость света в вакууме. В среде, в которой фазовая скорость распространения электромагнитной волны c′ отличается от скорости света в вакууме (c′ = c/n, где n — показатель преломления), связь между длиной волны и частотой будет следующей:
Ещё одна часто использующаяся характеристика волны — волновое число (пространственная частота), равное количеству волн, укладывающихся на единицу длины: k = 1/λ. Иногда эта величина используется с коэффициентом 2π, по аналогии с обычной и круговой частотой ks = 2π/λ. В случае электромагнитной волны в среде
Звук[править | править код]
Основная статья: Звук
Свойства звука (механических упругих колебаний среды) зависят от частоты. Человек может слышать колебания с частотой от 20 Гц до 20 кГц (с возрастом верхняя граница частоты слышимого звука снижается). Звук с частотой более низкой, чем 20 Гц (соответствует ноте ми субконтроктавы), называется инфразвуком[9]. Инфразвуковые колебания, хотя и не слышны, могут ощущаться осязательно. Звук с частотой выше 20 кГц называется ультразвуком, а с частотой выше 1 ГГц — гиперзвуком.
В музыке обычно используются звуки, высота (основная частота) которых лежит от субконтроктавы до 5-й октавы. Так, звуки стандартной 88-клавишной клавиатуры фортепиано укладываются в диапазон от ноты ля субконтроктавы (27,5 Гц) до ноты до 5-й октавы (4186,0 Гц). Однако музыкальный звук обычно состоит не только из чистого звука основной частоты, но и из примешанных к нему обертонов, или гармоник (звуков с частотами, кратными основной частоте); относительная амплитуда гармоник определяет тембр звука. Обертоны музыкальных звуков лежат во всём доступном для слуха диапазоне частот.
Частота переменного тока[править | править код]
Напряжение и частота: 220-240 В/60 Гц 220-240 В/50 Гц 100-127 В/60 Гц 100-127 В/50 Гц
В Европе (в том числе в России и всех странах бывшего СССР), большей части Азии, Океании (кроме Микронезии), Африке и в части Южной Америки промышленная частота переменного тока в силовой сети составляет 50 Гц. В Северной Америке (США, Канада, Мексика), Центральной и в некоторых странах северной части Южной Америки (Бразилия, Венесуэла, Колумбия, Перу), а также в некоторых странах Азии (в юго-западной части Японии, в Южной Корее, Саудовской Аравии, на Филиппинах и на Тайване) используется частота 60 Гц. См. Стандарты разъёмов, напряжений и частот электросети в разных странах. Почти все бытовые электроприборы одинаково хорошо работают в сетях с частотой 50 и 60 Гц при условии одинакового напряжения сети. В конце XIX — первой половине XX века, до стандартизации, в различных изолированных сетях использовались частоты от 162⁄3 до 1331⁄3 Гц[10]. Первая до сих пор используется на некоторых железнодорожных линиях мира напряжением 15 кВ, где была принята для использования электровозов без выпрямителей — тяговые двигатели постоянного тока питались напрямую от трансформатора.
В бортовых сетях самолётов, подводных лодок и т. д. используется частота 400 Гц. Более высокая частота силовой сети позволяет уменьшить массу и габариты трансформаторов и получить высокие частоты вращения асинхронных двигателей, хотя увеличивает потери при передаче на большие расстояния — из-за ёмкостных потерь, роста индуктивного сопротивления линии и потерь на излучение.
См. также[править | править код]
- Частоты
- Спектр
- Диапазон частот
- Частотомер
- Амплитудно-частотная характеристика
- Автоматическая подстройка частоты
Примечания[править | править код]
- ↑ Частота // Научно-технический энциклопедический словарь. Статья в Научно-техническом энциклопедическом словаре.
- ↑ Поставлен новый рекорд точности атомных часов (недоступная ссылка — история). Membrana (5 февраля 2010). Дата обращения: 4 марта 2011. Архивировано 9 февраля 2012 года.
- ↑ Финк Л. М. Сигналы, помехи, ошибки… Заметки о некоторых неожиданностях, парадоксах и заблуждениях в теории связи. — М.: Радио и связь, 1978, 1984.
- ↑ Угловая частота. Большой энциклопедический политехнический словарь. Дата обращения: 27 октября 2016.
- ↑ Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — С. 33. — 287 с.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 104. — 240 с. — ISBN 5-7050-0118-5.
- ↑ IEC History. Iec.ch. Дата обращения: 2 июня 2013. Архивировано 2 июня 2013 года.
- ↑ Bakshi K. A., Bakshi A. V., Bakshi U. A. Electronic Measurement Systems. — US: Technical Publications, 2008. — С. 4—14. — ISBN 978-81-8431-206-5.
- ↑ Иногда за границу между инфразвуком и слышимым звуком принимают частоту 16 Гц.
- ↑ Об измерении частоты переменных токов.: Доклад А. Кузнецова. // Электричество, №6, 1901. — С. 81-83.
Литература[править | править код]
- Финк Л. М. Сигналы, помехи, ошибки…. — М.: Радио и связь, 1984.
- Бурдун Г. Д., Базакуца В. А. Единицы физических величин. — Харьков: Вища школа, 1984.
- Яворский Б. М., Детлаф А. А. Справочник по физике. — М.: Наука, 1981.
Ссылки[править | править код]
- Радиотехнические цепи и Сигналы
- Очерк А. Б. Сергиенко «Аналоговая модуляция» (недоступная ссылка с 22-05-2013 [3645 дней] — история, копия)
- Сигналы и линейные системы
- ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАДИОТЕХНИКИ
Частота колебаний — величина, обратная периоду колебаний, т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени.
Разновидность частот колебаний :
Циклическая частота
Частота колебаний физического маятника
Частота пружинного маятника
Частота математического маятника
Частота электромагнитных колебаний
Частота колебаний крутильного маятника
В Формуле мы использовали :
— Частота колебаний
— Циклическая частота
— Период колебаний маятника
— Масса груза, или масса маятника
— Жесткость пружины
— Длина подвеса
— Ускорение свободного падения
— Момент инерции маятника относительно оси вращения
— Расстояние от оси вращения до центра масс
— Момент инерции тела
— Вращательный коэффициент жёсткости маятника
Частота колебаний, формула
Частота колебаний — это число циклов периодического процесса совершенных за одну секунду. Обозначается буквой f.
Единица измерения частоты:
[ 1 enspace [цикл enspace в enspace секунду] = 1 enspace [Герц] ]
Свое название данная единица измерения получила в честь немецкого физика Генриха Рудольфа Герца, который производил опыты с электрическими колебаниями.
Частота колебаний, формула
Чтобы определить частоту колебаний необходимо взять известный временной интервал и подсчитать количество циклов которые совершит система за это время.
Если
| ∆t | определенный временной интервал, | секунд |
|---|---|---|
| N | количество циклов, | шт. |
| T | период колебаний, | секунд |
то
[ f = frac{N}{∆t} = frac{1}{T} ]
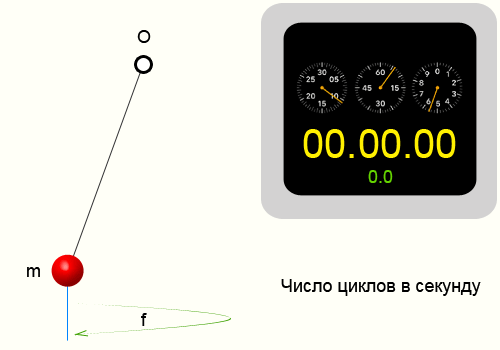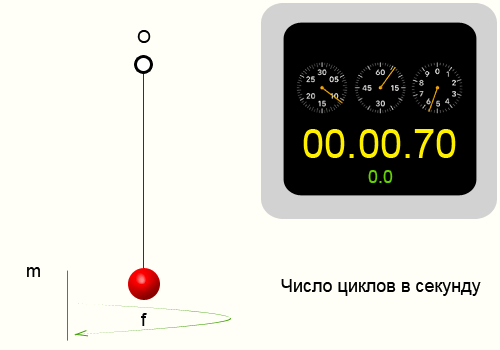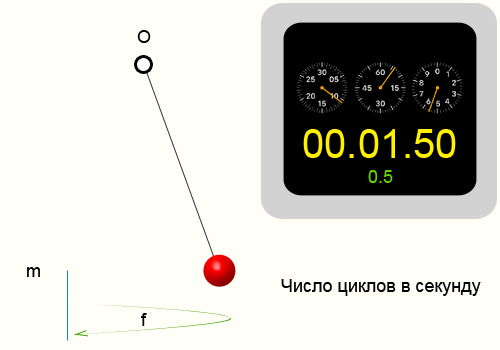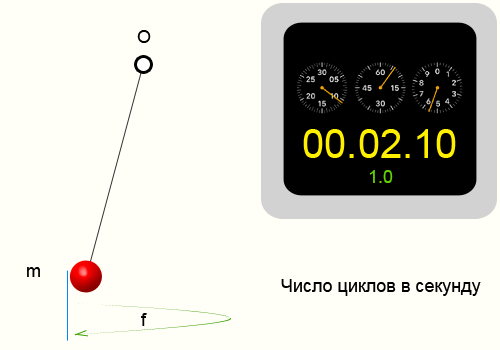
Пример определения частоты колебаний
Повторим опыт описанный в периоде колебаний. Тогда у нас получились следующие цифры: N = 10 циклов, ∆t = 14.35 секунд,
соответственно приблизительная частота колебаний нити 0.697 Герц.
Вычислить, найти частоту колебаний по формуле 1
Как найти частоту колебаний через период
Частота колебаний, формула |
стр. 534 |
|---|