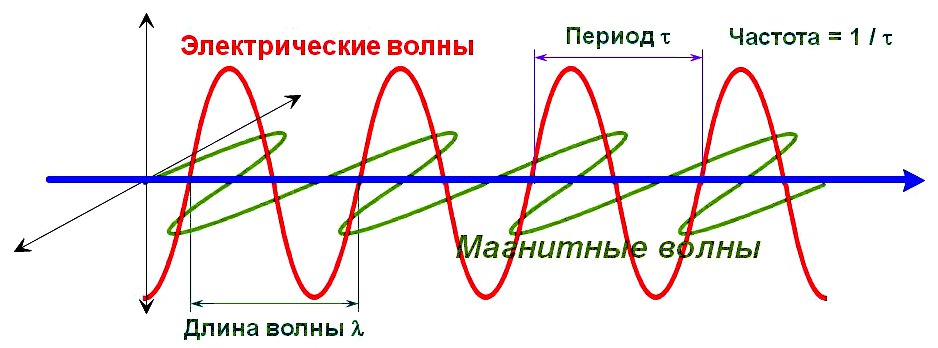
Длина, скорость и частота электромагнитной волны.
Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение,
видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.
Электромагнитные колебания – это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении
напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны
(Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое
излучение, рентгеновские либо гамма-лучи.
Рис.1
Длина волны, обозначаемая буквой λ и измеряемая в метрах –
это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.
Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс
повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.
Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).
Скорость распространения электромагнитных волн в вакууме (v) равна скорости
света и составляет величину:
v = С = 299792458 м/сек.
В среде эта скорость уменьшается: v = С / n, где
n > 1 – это показатель преломления среды.
Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому
с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве.
Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).
И окончательно для воздушной среды:
λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).
Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн,
которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.
| Диапазон | Полоса частот | Длина волны |
| Сверхдлинные радиоволны | 3…30 кГц | 100000…10000 м |
| Длинные радиоволны | 30…300 кГц | 10000…1000 м |
| Средние радиоволны | 300…3000 кГц | 1000…100 м |
| Короткие радиоволны | 3…30 МГц | 100…10 м |
| Метровый радиодиапазон | 30…300 МГц | 10…1 м |
| Дециметровый радиодиапазон | 300…3000 МГц | 1…0,1 м |
| Сантиметровый СВЧ диапазон | 3…30 ГГц | 10…1 см |
| Микроволновый СВЧ диапазон | 30…300 ГГц | 1…0,1 см |
| Инфракрасное излучение | 0,3…405 ТГц | 1000…0,74 мкм |
| Красный цвет | 405…480 ТГц | 740…625 нм |
| Оранжевый цвет | 480…510 ТГц | 625…590 нм |
| Жёлтый цвет | 510…530 ТГц | 590…565 нм |
| Зелёный цвет | 530…600 ТГц | 565…500 нм |
| Голубой цвет | 600…620 ТГц | 500…485 нм |
| Синий цвет | 620…680 ТГц | 485…440 нм |
| Фиолетовый цвет | 680…790 ТГц | 440…380 нм |
| Ультрафиолетовое излучение | 480…30000 ТГц | 400…10 нм |
| Рентгеновское излучение | 30000…3000000 ТГц | 10…0,1 нм |
| Гамма излучение | 3000000…30000000 ТГц | 0,1…0,01 нм |
А теперь можно переходить к калькуляторам.
КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ
|
Частота электромагнитных колебаний f |
||
Показатель преломления среды (по умолч. 1) |
||
Длина волны |
КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ
|
Длина электромагнитной волны в вакууме λ |
||
Частота |
В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь
существует некоторая путаница. Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме,
т. е. численно равной Kp = 1/n, где n – это, как мы помним, показатель преломления среды.
Другие, наоборот – как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.
Поэтому надо иметь в виду – если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а
если Kp < 1, то n = 1/Kp.
Download Article
Download Article
Frequency, also called wave frequency, is a measurement of the total number of vibrations or oscillations made within a certain amount of time. There are a few different ways to calculate frequency based on the information you have available to you. Keep reading to learn some of the most common and useful versions.
-
1
Learn the formula. The formula for frequency, when given wavelength and the velocity of the wave, is written as: f = V / λ[1]
- In this formula, f represents frequency, V represents the velocity of the wave, and λ represents the wavelength of the wave.
- Example: A certain sound wave traveling in the air has a wavelength of 322 nm when the velocity of sound is 320 m/s. What is the frequency of this sound wave?
-
2
Convert the wavelength into meters, if necessary. If the wavelength is given in nanometers, you need to convert this value into meters by dividing it by the number of nanometers in a single meter.[2]
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 322 nm
- 322 nm x (1 m / 10^9 nm) = 3.22 x 10^-7 m = 0.000000322 m
Advertisement
-
3
Divide the velocity by the wavelength. Divide the velocity of the wave, V, by the wavelength converted into meters, λ, in order to find the frequency, f.[3]
- Example: f = V / λ = 320 / 0.000000322 = 993788819.88 = 9.94 x 10^8
-
4
Write your answer. After completing the previous step, you will have completed your calculation for the frequency of the wave. Write your answer in Hertz, Hz, which is the unit for frequency.
- Example: The frequency of this wave is 9.94 x 10^8 Hz.
Advertisement
-
1
Learn the formula. The formula for the frequency of a wave in a vacuum is almost identical to that of a wave not in a vacuum. Since there are no outside influences on the velocity of the wave, though, you would use the mathematical constant for the speed of light, which electromagnetic waves would travel at under these conditions. As such, the formula is written as: f = C / λ[4]
- In this formula, f represents frequency, C represents the velocity or speed of light, and λ represents the wavelength of the wave.
- Example: A particular wave of electromagnetic radiation has a wavelength of 573 nm when passing through a vacuum. What is the frequency of this electromagnetic wave?
-
2
Convert the wavelength into meters, if necessary. When the problem gives you the wavelength in meters, no further action is needed. If, however, the wavelength is given in micrometers, you need to convert this value into meters by dividing it by the number of micrometers in a single meter.
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 573 nm
- 573 nm x (1 m / 10^9 nm) = 5.73 x 10^-7 m = 0.000000573
-
3
Divide the speed of light by the wavelength. The speed of light is a constant, so even if the problem does not provide you with a value, the value remains 3.00 x 10^8 m/s. Divide this value by the wavelength converted into meters.[5]
- Example: f = C / λ = 3.00 x 10^8 / 5.73 x 10^-7 = 5.24 x 10^14
-
4
Write your answer. With this, you should have calculated the value of the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 5.24 x 10^14 Hz.
Advertisement
-
1
Learn the formula. Frequency and the time taken to finish a single wave oscillation are inversely proportional. As such, the formula for calculating frequency when given the time taken to complete a wave cycle is written as: f = 1 / T
- In this formula, f represents frequency and T represents the time period or amount of time required to complete a single wave oscillation.
- Example A: The time for a certain wave to complete a single oscillation is 0.32 seconds. What is the frequency of this wave?
- Example B: In 0.57 seconds, a certain wave can complete 15 oscillations. What is the frequency of this wave?
-
2
Divide the number of oscillations by the time period. Usually, you will be told how long it takes to complete a single oscillation, in which case, you would just divide the number 1 by the time period, T. If given a time period for numerous oscillations, however, you will need to divide the number of oscillations by the overall time period required to complete them.[6]
- Example A: f = 1 / T = 1 / 0.32 = 3.125
- Example B: f = 1 / T = 15 / 0.57 = 26.316
-
3
Write your answer. This calculation should tell you the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example A: The frequency of this wave is 3.125 Hz.
- Example B: The frequency of this wave is 26.316 Hz.
Advertisement
-
1
Learn the formula. When told the angular frequency of a wave but not the standard frequency of that same wave, the formula to calculate the standard frequency is written as: f = ω / (2π)[7]
- In this formula, f represents the frequency of the wave and ω represents the angular frequency. As with any mathematical problem, π stands for pi, a mathematical constant.
- Example: A particular wave rotates with an angular frequency of 7.17 radians per second. What is the frequency of that wave?
-
2
Multiply pi by two. In order to find the denominator of the equation, you need to double the value of pi, 3.14.
- Example: 2 * π = 2 * 3.14 = 6.28
-
3
Divide the angular frequency by the double of pi. Divide the angular frequency of the wave, given in radians per second, by 6.28, the doubled value of pi.[8]
- Example: f = ω / (2π) = 7.17 / (2 * 3.14) = 7.17 / 6.28 = 1.14
-
4
Write your answer. This final bit of calculation should indicate what the frequency of the wave is. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 1.14 Hz.
Advertisement
Add New Question
-
Question
What is the frequency if 80 oscillations are completed in 1 second?
Frequency is the number of oscillations completed in a second. The answer would be 80 Hertz.
-
Question
Do atoms have a frequency and, if so, does it mean everything vibrates?
Atoms have energy. Energy is often characterized as vibration. Vibration possesses frequency. So, yes, everything could be thought of as vibrating at the atomic level.
-
Question
What’s the definition of frequency?
The rate at which a vibration occurs that constitutes a wave, either in a material (as in sound waves), or in an electromagnetic field (as in radio waves and light), usually measured per second. The rate at which something occurs or is repeated over a particular period of time or in a given sample.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To calculate the frequency of a wave, divide the velocity of the wave by the wavelength. Write your answer in Hertz, or Hz, which is the unit for frequency. If you need to calculate the frequency from the time it takes to complete a wave cycle, or T, the frequency will be the inverse of the time, or 1 divided by T. Display this answer in Hertz as well. Keep reading to learn how to calculate frequency from angular frequency!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,508,929 times.
Did this article help you?
Как найти период и частоту колебаний
У любой волны, распространяющейся в той или иной среде, имеются три взаимосвязанных между собой параметра: длина, период колебаний и их частота. Любой из них можно найти, зная любой другой, при этом в некоторых случаях необходима также информация о скорости распространения колебаний в среде.

Инструкция
Независимо от того, какой из параметров вы собираетесь вычислять, переведите все исходные величины в систему СИ. Тогда и результат получится в единицах той же системы. При необходимости пользуйтесь калькулятором, способным, помимо мантиссы, отображать и порядок числа, поскольку при решении задач по теме «Колебания и волны» приходится иметь дело как с очень малыми, так и с очень большими величинами.
В случае если известны длина волны и скорость распространения колебаний, частоту вычислите следующим образом:
F=v/λ, где F – частота (Гц), v – скорость распространения колебаний в среде (м/с), λ – длина волны (м).
Скорость света в вакууме обычно обозначают другой буквой – c (латинской). Помните, что скорость распространения света в любой другой среде, кроме вакуума, меньше скорости света в вакууме. Если та или иная частица пролетает через среду со скоростью, хотя и меньшей скорости света в вакууме, но большей скорости света в этой среде, возникает так называемое свечение Черенкова.
Если известна частота, период найти можно и в том случае, если скорость распространения колебаний неизвестна. Формула для вычисления периода по частоте выглядит следующим образом:
T=1/F, где T – период колебаний (с), F – частота (Гц).
Из сказанного выше следует, что найти частоту, зная период, можно также без информации о скорости распространения колебаний. Способ ее нахождения такой же:
F=1/T, где F – частота (Гц), T – период колебаний (с).
Для того чтобы узнать циклическую частоту колебаний, вначале вычислите их обычную частоту любым из указанных выше способов. Затем умножьте ее на 2π:
ω=2πF, где ω – циклическая частота (радиан в секунду), F – обычная частота (Гц).
Отсюда следует, что для вычисления обычной частоты при наличии информации о циклической следует воспользоваться обратной формулой:
F=ω/(2π), где F – обычная частота (Гц), ω – циклическая частота (радиан в секунду).
При решении задач на нахождение периода и частоты колебаний, а также длины волны используйте следующие физические и математические константы:
– скорость света в вакууме: c=299792458 м/с (некоторые исследователи, в частности, креационисты, считают, что в прошлом данная физическая константа могла иметь другую величину);
– скорость звука в воздухе при атмосферном давлении и нуле градусов по Цельсию: Fзв=331 м/с;
– число «пи» (до пятидесятого знака): π=3,14159265358979323846264338327950288419716939937510 (безразмерная величина).
Скорость света в веществе с показателем преломления, равным n (также безразмерная величина), вычислите, поделив скорость света на показатель преломления.
После окончания вычислений при необходимости переведите результат из системы СИ в удобные для вас единицы измерения.
Источники:
- как будет изменяться период колебаний
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание:
- 1 Калькулятор расчета метров длины волны по известной частоте.
- 2 Примечание к расчетам табличных формул.
- 3 Наиболее востребованные и популярные частоты.
- 4 Что такое волна и ее характеристики?
- 5 Формулы
- 6 Волны де Бройля
- 7 Примененение
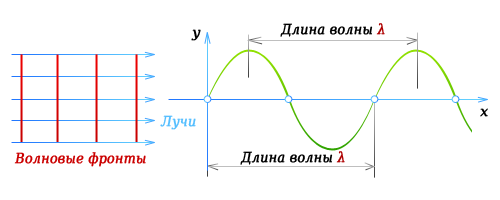
Расстояние между соседними волновыми фронтами называется длиной волны λ .
Длина волны есть расстояние между частицами, колеблющимися с одинаковой фазой. Длина волны не зависит от координат и времени.
| с | фазовая скорость, или скорость распространения волны, | метр/секунда |
|---|---|---|
| f | частота, с которой колеблется каждая частица в волне, | Герц |
| T=1/f | период, продолжительность полного колебания частицы, | Секунда |
| λ | длина волны, расстояние между частицами, колеблющимися с одинаковой фазой, | Метр |
Формула 1 справедлива для всех волн, в том числе и электромагнитных.
Калькулятор расчета метров длины волны по известной частоте.
Количество нолей : введите число и скопируйте / вставьте нули, например .
220 (Гц) и 000 = 220 КГц . 42 (Гц) и 000000 = 42 МГц .
2.4 (Гц) и 0 00000000 = 2.4 ГГц / или 2400 МГц . // первый знак разряда после запятой заменяет первый ноль (без точки!) . (можно ввести 24 и удалить последний ноль, кому как удобно) .
000 = КГц
000000 = МГц
000000000 = ГГц
то есть, 1 ГГц = 1000 МГц = 1000000 КГц = 1000000000 Гц .
Примечание к расчетам табличных формул.
Значение скорости света / волны
примерное = 300000 км/сек
точное = 299792458 м/с.
Калькулятор перевода частоты в длину волны.
Калькулятор может применяться для расчета антенн, телевизионных, радиолюбительских и радиотехнических расчетов.
Для удобства просмотра на экранах мобильных телефонов и планшетов таблица сделана вертикально.
В таблицу добавлены нестандартные значения λ для облегчения расчетов.
Наиболее востребованные и популярные частоты.
Наиболее востребованные и популярные частоты, используемые в радио / технической практике и расчетах длины волны :
— в диапазоне КГц : 1 кгц, 2 кгц, 3 кгц, 4 кгц, 5 кгц, 7 кгц, 8 кгц, 9 кгц, 10 кгц, 11 кгц, 16 кгц, 20 кгц, 22 кгц, 24 кгц, 30 кгц, 32 кгц, 40 кгц, 48 кгц, 50 кгц, 64 кгц, 100 кгц, 125 кгц .
— в диапазоне МГц : 1 мгц, 2 мгц, 3 мгц, 4 мгц, 5 мгц, 6 мгц, 7 мгц, 8 мгц, 10 мгц, 16 мгц, 20 мгц, 27 мгц, 50 мгц, 60 мгц, 100 мгц, 144 мгц, 145 мгц, 400 мгц, 433 мгц, 800 мгц, 900 мгц, 1333 мгц, 1600 мгц, 1800 мгц, 2400 мгц .
— в диапазоне ГГц : 1 ггц, 1.1 ггц, 1.3 ггц, 1.4 ггц, 1.6 ггц, 1.8 ггц, 2 ггц, 2.1 ггц, 2.2 ггц, 2.3 ггц, 2.4 ггц, 2.5 ггц, 2.8 ггц, 3 ггц, 3.4 ггц, 4 ггц, 4.5 ггц, 5 ггц, 6 ггц, 7 ггц, 8 ггц, 10 ггц, 15 ггц .
Калькулятор был разработан (без небольших исправлений) 11.10.2017 .
Что такое волна и ее характеристики?
Природа, в понятии суть Вселенной — не любит прямых углов . Нет, конечно — природа не избегает, однозначно, прямых углов и острых граней в строительстве мира . Но, ее живая, в постоянном движении, структура — истирает грани до округлости . Волны, базирующиеся на волновой структуре природы — полностью повторяют все ее многообразие . Волна — одно из самых известных и не изученных до конца (не классифицированных) явлений мироздания . Двигаясь, из точки рождения / возмущения — волна совершает равноудаленные колебательные движения, синхронизированные скоростью ее распространения . Волновые зависимости скорости, частоты и длины отражены описанием математической формулы .
Исходя из многообразия, длина волны λ также имеет множественные определения :
— как, кратчайшее расстояние между двумя точками колебания в одинаковой фазе .
— как, изменение фазы колебаний волны на 2π (где, 2π — не что иное, как — круг) .
— как, путь фронта волны, равный периоду колебательного процесса .
Длина волн является первой сравнительной характеристикой, от которых зависит длина вибраторов / габаритов антенны ; и конструкция напрямую предопределяет, какая будет частота волны приема / передачи . Однако — необязательно длина вибратора антенны должна быть равной длине волн : прекрасно работают антенны, где частота волны выбрана от &lambda / 2, &lambda / 4 и даже с дробными значениями длины .
Кроме прямых углов — природа не терпит пустоты . Эта особенность объясняет, почему колебания волны не расширяются до бесконечности : сама природа, породившая волну — стремится противодействовать ее колебаниям, стремясь к равновесию и балансу сил, тем активнее, чем выше частота, амплитуда и скорость колебаний волны . Перефразируя размышления Н. Теслы, можно сказать : кто познает природу волны — тот познает природу материи и мироздания .
Длина волны — важный физический параметр, необходимый для решения многих задач акустики и радиоэлектроники. Ее можно высчитать несколькими способами, в зависимости от того, какие параметры заданы. Удобнее всего это делать, зная частоту или период и скорость распространения.
Формулы
Основная формула, которая отвечает на вопрос о том, как найти длину волны через частоту, представлена ниже:
Здесь l — длина волны в метрах, v — скорость ее распространения в м/c, u — линейная частота в герцах.
Поскольку частота связана с периодом обратным соотношением, предыдущее выражение можно записать иначе:
Т — период колебаний в секундах.
Можно выразить этот параметр через циклическую частоту и фазовую скорость:
В этом выражении w — циклическая частота, выраженная в радианах за секунду.
Частота волны через длину, как можно заметить из предыдущего выражения, находится следующим образом:
Рассмотрим электромагнитную волну, которая распространяется в веществе с показателем преломления n. Тогда частота волны через длину выражается следующим отношением:
Если она распространяется в вакууме, то n = 1, и выражение приобретает следущий вид:
В последней формуле частота волны через длину выражается с помощью константы с — скорости света в вакууме, с = 300000 км/c.
Волны де Бройля
Для этих волн формулы будут иметь несколько иной вид. Они определяют плотность вероятности и используются в квантовой механике для нахождения параметров рассматриваемой частицы. Длина и частота определяются так:
h — постоянная Планка, p — импульс частицы, Е — энергия частицы.
Примененение
Приведенные формулы можно использовать для нахождения параметров как электромагнитных, так и волн другой природы, в вакууме, воздухе или другой среде. Чтобы определить, как выражается частота волны через длину или наоборот, нужно знать скорость ее распространения и свойства среды. Электромагнитная будет быстрее всего двигаться в вакууме или воздухе, из-за низкой электрической и магнитной проницаемости, поскольку ее скорость обратно пропорциональна корню из произведения этих параметров.
Со звуковой волной будет уже другая ситуация. Скорость звука в твердых телах и жидкостях больше, чем в воздухе. Наивысшая скорость будет в железе и литии (около 6000 м/c), стекле — 4800 (м/c), золоте, серебре, платине. Скорость звука в твердых и жидких средах определяется с помощью довольно сложных зависимостей, с учетом плотности среды и модуля Юнга.