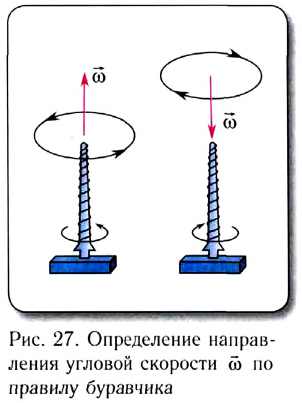
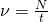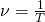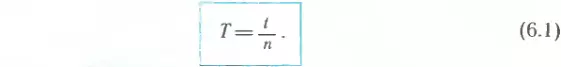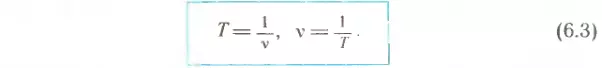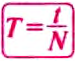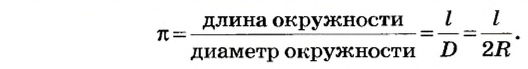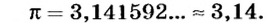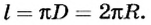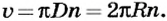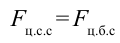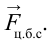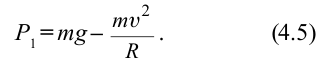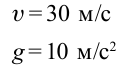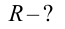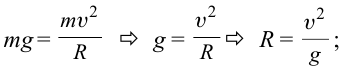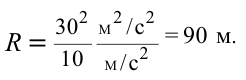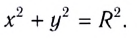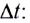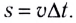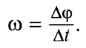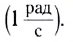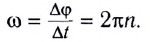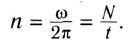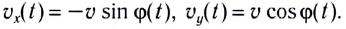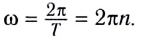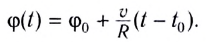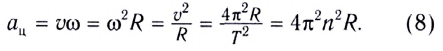Частота вращения (обращения) — это физическая величина, равная количеству оборотов, которые тело совершает за единицу времени (1 секунду).
Чтобы найти частоту вращения надо количество оборотов разделить на время совершения этих оборотов:
Частота вращения – величина, обратная периоду вращения:
Частота вращения показывает, сколько оборотов совершается за 1 с.
За единицу частоты вращения в СИ принимают частоту вращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: [1/с] или [с-1] (читается: секунда в минус первой степени). Единица частоты в СИ называется Герц [Гц].
Обозначения:
T — период обращения
ν — частота обращения
N — число оборотов
t — время, за которое тело совершило N оборотов по окружности
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения — это время, за которое совершается один оборот.
Если, например, за время t=4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой T и определяется по формуле
Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой ν (читается: ню) и определяется по формуле
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
Формулы (6.1) и (6.3) позволяют найти период обращения T, если известны число n и время оборотов t или частота обращения ν. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела v и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (lокр = 2πr, где π≈3,14— число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,
Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
Видео, не по теме но интересно
1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
Одним из распространенных в природе и технике видов движения является вращение. Этот вид перемещения тел в пространстве характеризуется набором физических величин. Важная характеристика любого вращения — это частота. Формулу частоту вращения можно найти, зная определенные величины и параметры.
Что такое вращение?
Под ним в физике понимают такое перемещение материальной точки вокруг некоторой оси, при котором ее расстояние до этой оси остается постоянным. Оно называется радиусом вращения.

Примерами этого движения в природе является вращение планет вокруг Солнца и вокруг собственной оси. В технике вращение представлено движением валов, шестеренок, колеса автомобиля или велосипеда, перемещением лопастей ветровых мельниц.
Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
n = θ/(2*pi);
L = θ*r.
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
ω = θ/t
Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
T = 2*pi/ω
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
f = 2*pi/T
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
f = ω
Это равенство означает следующее:
- формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
- так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
Линейная скорость вращения, частота и частота угловая
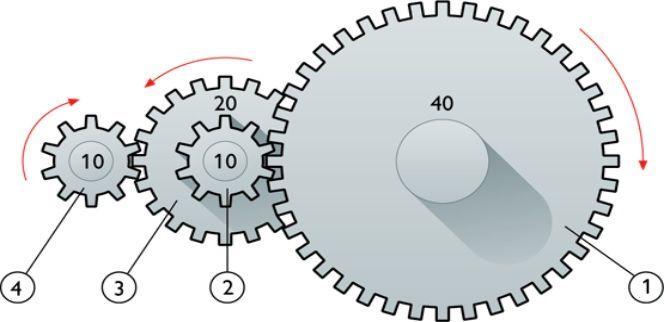
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.
Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:
μ = 1/T
Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:
f = 2*pi*μ
Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.
Линейная скорость v связана со скоростью угловой ω следующим равенством:
v = ω*r
Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:
f = v/r
Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.
Задача на определение циклической частоты вращения вала
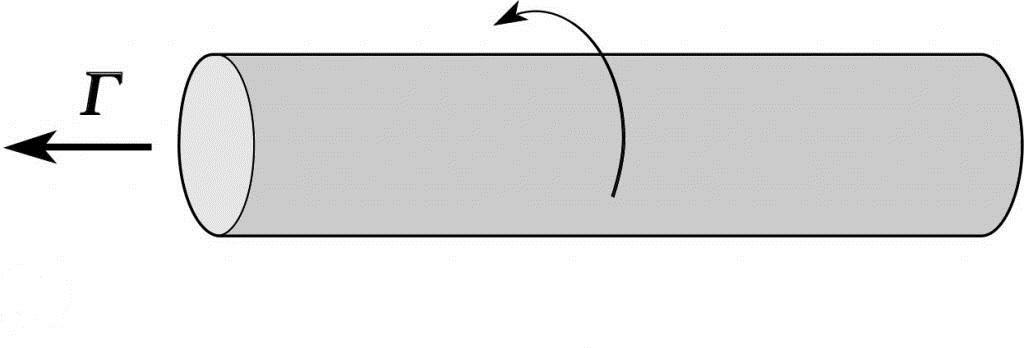
Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?
Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:
f = 2*pi*μ
Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
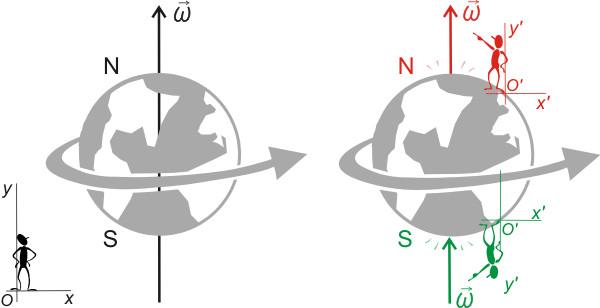
Вращение Земли
Связь со вторым законом Ньютона
Как вывести формулу центростремительного ускорения
Движение по циклоиде*
Содержание:
Вращательное движение тела:
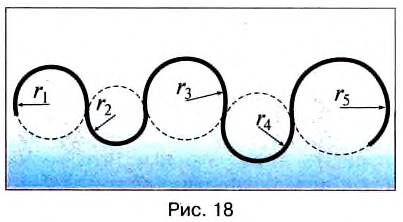
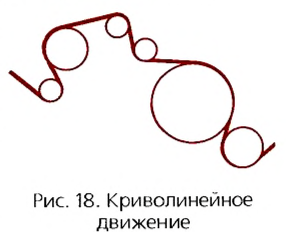
До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18).
Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности.
Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности.
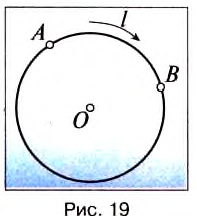
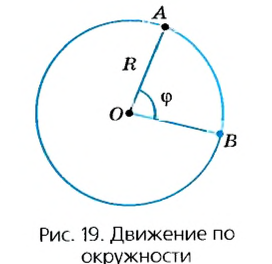
Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги
где 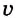
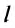
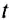
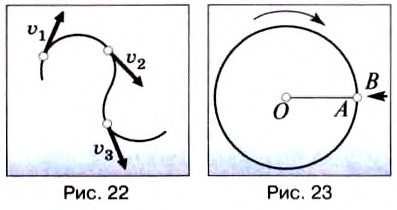
Направление скорости проще всего определить на опыте.
Опыт:
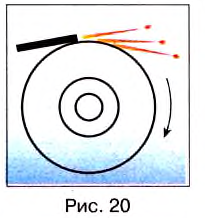
К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20).
Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом.
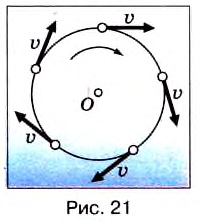
Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22).
Опыт:
Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени.
Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями.
Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения.
Период обращения – это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности.
Обозначается период обращения большой латинской буквой Т.
Если за время 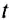
Единицей периода обращения в СИ является одна секунда (1 с).
Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с.
Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности
Обозначается частота обращения малой латинской буквой 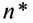
* В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой 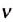
Если за время 
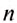

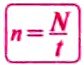


Из последней формулы видно, что частота обращения и период обращения связаны обратно пропорциональной зависимостью, а для определения единицы частоты обращения нужно единицу разделить на единицу периода обращения, т. е. на секунду.
Единицей частоты обращения в СИ является единица, разделённая на секунду 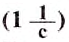
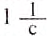
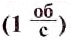
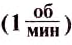
Движение точки по окружности
Движения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным.
Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться.
Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время 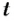

где 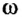

Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки – длина дуги окружности АВ – равна длине радиуса R.
Единицей угловой скорости является радиан в секунду (рад/с).
1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад.
При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с).
Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения.
Период вращения (Т) – это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения:
где t — время вращения, N — количество выполненных оборотов.
Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота):
где N — количество совершенных оборотов за время t .
Частота вращения измеряется в оборотах за секунду (об/с).
Частота вращения 
Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой 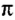
Таким образом, длина окружности
За один оборот материальная точка осуществляет угловое перемещение 2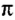
Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь 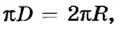
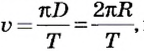
Вращение твердого тела
Твердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет.
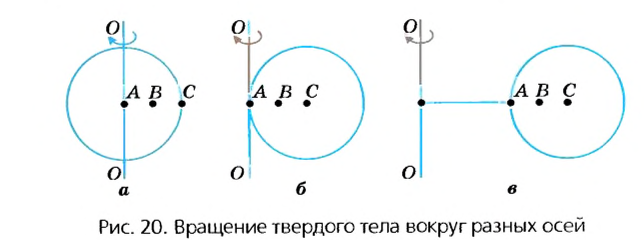
Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры.
В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких?
Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения.
Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния – чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение 
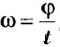
Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т – время одного полного вращения; вращательная частота (частота вращения) 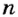
Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам.
Динамика вращательного движения
При просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен.
Проведем такой опыт. Нальем воду в ведро и раскрутим его в вертикальной плоскости. При определенной скорости вращения вода не выливается из ведра.
Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении.
Откуда появляется эта сила? От чего зависит ее величина?
Для этого вспомним о возникновении центростремительной силы в теле при равномерном вращательном движении:
По третьему закону Ньютона:
и при вращении появляется также центробежная сила.
Вот эта центробежная сила опрокинет резко разворачивающуюся машину, удержит воду в ведре при вращении и т.д.
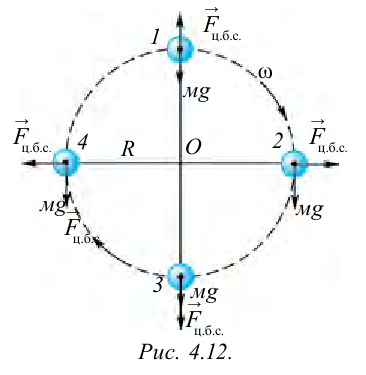
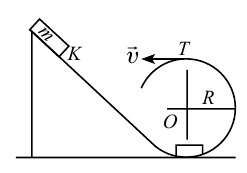
На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом 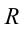
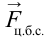
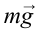
В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет:
Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения.
Кроме того, на поворотах дороги под воздействием центробежной силы наблюдается отклонение тела от вертикального положения. Чтобы это не приводило к авариям, велосипедисты или мотоциклисты должны двигаться с небольшим уклоном в сторону от центра вращения (рис. 4.13а).
Для уравновешивания этой силы специально для автомобилей на поворотах строят участки дороги с уклоном с одной стороны (рис. 4.13б). Для трамваев и поездов рельсы на поворотах дороги с внешней стороны круга делаются чуть выше.
- Заказать решение задач по физике
Пример
При движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки 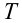
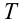
Дано:
Найти:
Решение:
Чтобы тело не упало из точки 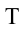
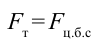
Ответ: 90 м.
Кинематика вращательного движения
При криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке.
Движение тела (МТ) по окружности является частным случаем криволинейного движения по траектории, лежащей в одной плоскости.
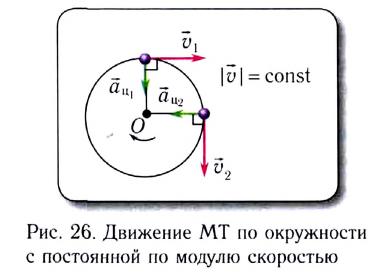
Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление.
Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них.
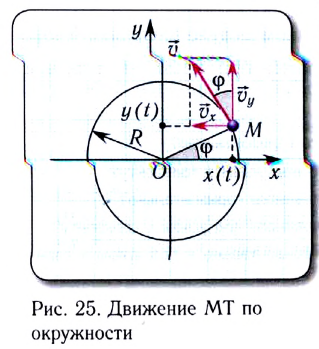
Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота 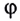
радиус-вектора точки М. Он отсчитывается от оси Ох против хода часовой стрелки и связан с декартовыми координатами соотношениями:
По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению
Скорость 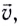
Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения
Модуль угловой скорости 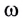
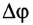
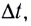
Угловая скорость 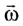
Единица угловой скорости в СИ — радиан в секунду
При движении по окружности с постоянной по модулю скоростью v угловая скорость 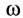
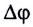
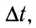
Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:
Единица частоты вращения в СИ — секунда в минус первой степени 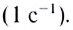
Следовательно,
В СИ период измеряется в секундах (1с).
При совершении полного оборота 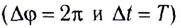
Модуль постоянной линейной скорости тела (МТ), движущегося по окружности, вычисляется по формуле
Проекции скорости 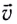
Модуль угловой скорости определяется соотношением
Следовательно, соотношение между модулями линейной и угловой скорости имеет вид
Поскольку 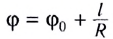
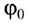
При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным 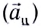
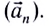
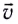
Нормальное ускорение 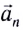
Как и при прямолинейном равноускоренном движении, ускорение 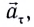
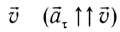
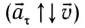
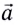
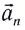
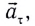
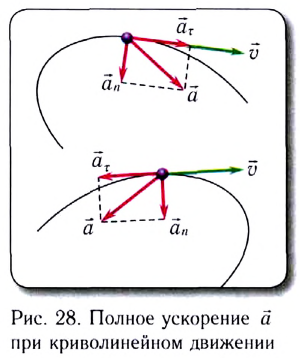
Полное ускорение 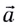
Модуль полного ускорения находится по теореме Пифагора:
где 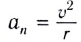
окружности радиусом r, заменяющей траекторию в окрестности рассматриваемой точки. Этот радиус r называют радиусом кривизны траектории.
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Поступательное движение
- Равномерное и неравномерное движение
- Равномерное движение
- Неравномерное движение