Различают вероятностные (математические) и статистические показатели надежности. Математические показатели надежности выводятся из теоретических функций распределения вероятностей отказов. Статистические показатели надежности определяются опытным путем при испытаниях объектов на базе статистических данных эксплуатации оборудования.
Надежность является функцией многих факторов, большинство из которых случайны. Отсюда ясно, что для оценки надежности объекта необходимо большое количество критериев.
Критерий надежности – это признак, по которому оценивается надежность объекта.
Критерии и характеристики надежности носят вероятностный характер, поскольку факторы, влияющие на объект, носят случайный характер и требуют статистической оценки.
Количественными характеристиками надежности могут быть:
• вероятность безотказной работы;
• среднее время безотказной работы;
• интенсивность отказов;
• частота отказов;
• различные коэффициенты надежности.
1. Вероятность безотказной работы
Служит одним из основных показателей при расчетах на надежность.
Вероятность безотказной работы объекта называется вероятность того, что он будет сохранять свои параметры в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации.
В дальнейшем полагаем, что эксплуатация объекта происходит непрерывно, продолжительность эксплуатации объекта выражена в единицах времени t и эксплуатация начата в момент времени t=0.
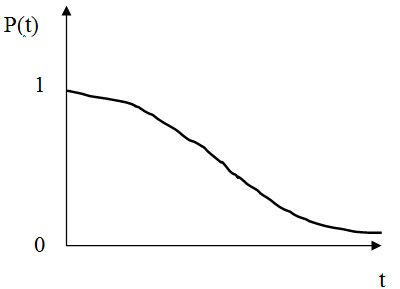
Обозначим P(t) вероятность безотказной работы объекта на отрезке времени [0,t]. Вероятность, рассматриваемую как функцию верхней границы отрезка времени, называют также функцией надежности.
Вероятностная оценка: P(t) = 1 – Q(t), где Q(t) — вероятность отказа.
Типичная кривая вероятности безотказной работы
Из графика очевидно, что:
1. P(t) – невозрастающая функция времени;
2. 0 ≤ P(t) ≤ 1;
3. P(0)=1; P(∞)=0.
На практике иногда более удобной характеристикой является вероятность неисправной работы объекта или вероятность отказа:
Q(t) = 1 – P(t).
Статистическая характеристика вероятности отказов: Q*(t) = n(t)/N
2. Частота отказов
Частотой отказов называется отношение числа отказавших объектов к их общему числу перед началом испытания при условии что отказавшие объекты не ремонтируются и не заменяются новыми, т.е
a*(t) = n(t)/(NΔt)
где a*(t) — частота отказов;
n(t) – число отказавших объектов в интервале времени от t – t/2 до t+ t/2;
Δt – интервал времени;
N – число объектов, участвующих в испытании.
Частота отказов есть плотность распределения времени работы изделия до его отказа. Вероятностное определение частоты отказов a(t) = -P(t) или a(t) = Q(t).
Таким образом, между частотой отказов, вероятностью безотказной работы и вероятностью отказов при любом законе распределения времени отказов существует однозначная зависимость: Q(t) = ∫ a(t)dt.
Отказ трактуют в теории надежности как случайное событие. В основе теории лежит статистическое истолкование вероятности. Элементы и образованные из них системы рассматривают как массовые объекты, принадлежащие одной генеральной совокупности и работающие в статистически однородных условиях. Когда говорят об объекте, то в сущности имеют в виду наугад взятый объект из генеральной совокупности, представительную выборку из этой совокупности, а часто и всю генеральную совокупность.
Для массовых объектов статистическую оценку вероятности безотказной работы P(t) можно получить, обработав результаты испытаний на надежность достаточно больших выборок. Способ вычисления оценки зависит от плана испытаний.
Пусть испытания выборки из N объектов проведены без замен и восстановлений до отказа последнего объекта. Обозначим продолжительности времени до отказа каждого из объектов t1, …, tN. Тогда статистическая оценка:
P*(t) = 1 — 1/N ∑η(t-tk)
где η — единичная функция Хевисайда.
Для вероятности безотказной работы на определенном отрезке [0, t] удобна оценка P*(t) = [N — n(t)]/N,
где n(t) – число объектов, отказавших к моменту времени t.
Частота отказов, определяемая при условии замены отказавших изделий исправными, иногда называется средней частотой отказов и обозначается ω(t).
3. Интенсивность отказов
Интенсивностью отказов λ(t) называется отношение числа отказавших объектов в единицу времени к среднему числу объектов, работающих в данный отрезок времени, при условии, что отказавшие объекты не восстанавливаются и не заменяются исправными: λ(t) = n(t)/[NсрΔt]
где Nср = [Ni + Ni+1]/2 — среднее число объектов, исправно работавших в интервале времени Δt;
Ni – число изделий, работавших в начале интервала Δt;
Ni+1 – число объектов, исправно работавших в конце интервала времени Δt.
Ресурсные испытания и наблюдения над большими выборками объектов показывают, что в большинстве случаев интенсивность отказов изменяется во времени немонотонно.
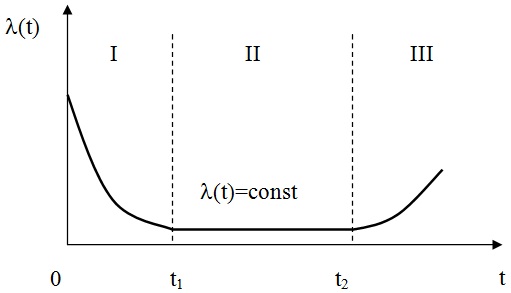
Типичная кривая изменения интенсивности отказов объекта
Из кривой зависимости отказов от времени видно, что весь период работы объекта можно условно поделить на 3 периода.
I — й период – приработка.
Приработочные отказы являются, как правило, результатом наличия у объекта дефектов и дефектных элементов, надежность которых значительно ниже требуемого уровня. При увеличении числа элементов в изделии даже при самом строгом контроле не удается полностью исключить возможность попадания в сборку элементов, имеющих те или иные скрытые дефекты. Кроме того, к отказам в этот период могут приводить и ошибки при сборке и монтаже, а также недостаточная освоенность объекта обслуживающим персоналом.
Физическая природа таких отказов носит случайный характер и отличается от внезапных отказов нормального периода эксплуатации тем, что здесь отказы могут иметь место не при повышенных, а и при незначительных нагрузках («выжигание дефектных элементов»).
Снижение величины интенсивности отказов объекта в целом, при постоянном значении этого параметра для каждого из элементов в отдельности, как раз и объясняется «выжиганием» слабых звеньев и их заменой наиболее надежными. Чем круче кривая на этом участке, тем лучше: меньше дефектных элементов останется в изделии за короткий срок.
Чтобы повысить надежность объекта, учитывая возможность приработочных отказов, нужно:
• проводить более строгую отбраковку элементов;
• проводить испытания объекта на режимах близких к эксплуатационным и использовать при сборке только элементы, прошедшие испытания;
• повысить качество сборки и монтажа.
Среднее время приработки определяют при испытаниях. Для особо важных случаев необходимо увеличить срок приработки в несколько раз по сравнению со средним.
II — й период – нормальная эксплуатация
Этот период характеризуется тем, что приработочные отказы уже закончились, а отказы, связанные с износом, еще не наступили. Этот период характеризуется исключительно внезапными отказами нормальных элементов, наработка на отказ которых очень велика.
Сохранение уровня интенсивности отказов на этом этапе характеризуется тем, что отказавший элемент заменяется таким же, с той же вероятностью отказа, а не лучшим, как это происходило на этапе приработки.
Отбраковка и предварительная обкатка элементов, идущих на замену отказавших, имеет для этого этапа еще большее значение.
Наибольшими возможностями в решении этой задачи обладает конструктор. Нередко изменение конструкции или облегчение режимов работы всего одного-двух элементов обеспечивает резкое повышение надежности всего объекта. Второй путь – повышение качества производства и даже чистоты производства и эксплуатации.
III – й период – износ
Период нормальной эксплуатации заканчивается, когда начинают возникать износовые отказы. Наступает третий период в жизни изделия – период износа.
Вероятность возникновения отказов из-за износов с приближением к сроку службы возрастает.
С вероятностной точки зрения отказ системы в данном промежутке времени Δt = t2 – t1 определяется как вероятность отказа:
∫a(t) = Q2(t) — Q1(t)
Интенсивность отказов есть условная вероятность того, что в промежуток времени Δt произойдет отказ при условии, что до этого он не произошел λ(t) = [Q2 — Q1]/[ΔtP(t)]
λ(t) = lim [Q2 — Q1]/[ΔtP(t)] = [dQ(t)]/[P(t)dt] = Q'(t)/P(t) = -P'(t)/P(t)
так как a(t) = -P'(t), то λ(t) = a(t)/P(t).
Эти выражения устанавливают зависимость между вероятностью безотказной работы, частотой и интенсивностью отказов. Если a(t) – невозрастающая функция, то справедливо соотношение:
ω(t) ≥ λ(t) ≥ a(t).
4. Среднее время безотказной работы
Средним временем безотказной работы называется математическое ожидание времени безотказной работы.
Вероятностное определение: среднее время безотказной работы равно площади под кривой вероятности безотказной работы.
T = ∫P(t)dt
Статистическое определение: T* = ∑θi/N0
где θI – время работы i-го объекта до отказа;
N0 – начальное число объектов.
Очевидно, что параметр Т* не может полностью и удовлетворительно характеризовать надежность систем длительного пользования, так как является характеристикой надежности только до первого отказа. Поэтому надежность систем длительного использования характеризуют средним временем между двумя соседними отказами или наработкой на отказ tср:
tср = ∑θi/n = 1/ω(t),
где n – число отказов за время t;
θi – время работы объекта между (i-1)-м и i-м отказами.
Наработка на отказ – среднее значение времени между соседними отказами при условии восстановления отказавшего элемента.
2.2.1. Вероятностное определение
Частота
отказов – это производная
по времени
от вероятности отказа
а(t)
= q’(t).
(2-23)
Зная
частоту отказов, можно определить
вероятность отказа
и
ВБР
t
q(t)
= ∫а(t)dt
(2-24)
0
В
теории вероятностей кроме понятия
функции распределения случайной
величины существует понятие плотности
распределения. Это производная по
времени от функции распределения этой
случайной величины.
В
случае нашей случайной величины –
наработки до отказа Т
–
–
частота отказов как раз и будет
представлять собой плотность
распределения наработки до отказа.
а(t)
= q’(t)
= f(t).
2-25)
Зависимости
вероятности и частоты отказов от
времени представлены на рисунке 2.4.
Рис
2.4.
Частота и вероятность отказов
2.2.2. Статистическая оценка
Если
частота отказов – это производная по
времени от вероятности отказа, то ее
статистическая оценка
∆q*(t)
a*(t)
= ——–,
(2-26)
∆t
где
n(t+∆t)
– n(t)
∆q*(t)
= q*(t+∆t)
– q*(t)
= —————. (2-27)
N(0)
Разделив
выражение (2-27) на ∆t,
получим выражение статистической оценки
частоты отказов
n(t+∆t)
– n(t)
∆n(t,t+∆t)
а*(t,t+∆t)
= ————— = ———–. (2-28)
∆t
N(0)
∆t
N(0)
Статистически
частота отказов представляет собой
отношение числа отказов в единицу
времени (числитель, деленный на ∆t)
к первоначальному числу изделий,
поставленных на испытания. Мера
приближения статистической оценки к
теоретическому значению (устойчивость
оценки) возрастает с увеличением N(0)
и уменьшением
интервала ∆t.
2.3. Интенсивность отказов
ГОСТ
27.002-95 дает
следующее определение интенсивности
отказов:
Интенсивность
отказов (t)–
условная плотность
вероятности возникновения отказа
объекта, определяемая при условии, что
до рассматриваемого момента времени
отказ не возник.
Ранее
мы рассмотрели условную вероятность
возникновения отказа объекта, определяемую
при условии, что до рассматриваемого
момента времени отказ не возник. Разделив
её на ∆t,
получим
q(t,t+∆t)
q(t+∆t)
– q(t)
∆q(t,t+∆t)
а(t)
——–
= ————— = ——— = —— .
∆t
∆t
р(t)
∆t
р(t)
р(t)
Условная
плотность
вероятности возникновения отказа
объекта определяется как отношение
частоты отказов к ВБР.
(t)
= а(t)/р(t)
= f(t)/р(t).
(2-29)
Статистическая
оценка интенсивности отказов должна
представлять собой отношение
статистической частоты отказов к
статистической ВБР
а*(t)
n(t+∆t)
– n(t)
∆n(t,t+∆t)
*(t)
= ——– = ————– = ———. (2-30)
р*(t)
∆t
N(t)
∆t
N(t)
Статистическая
оценка интенсивности отказов – отношение
числа отказов в единицу времени к числу
изделий, исправно
работающих в
момент времени t,
то есть, в
начале интервала.
Задача.
Интенсивность отказов полупроводниковых
вентилей равна
1.25 10-2
1/час. В
системе 100
вентилей. За 4
часа работы функция надежности изменяется
на 0,02.
Определить число отказов вентилей за
этот промежуток времени и общее число
отказавших вентилей в начале
рассматриваемого периода.
Прежде
всего, запишем данные и искомые величины
символами Теории надёжности. Общее
число объектов N(0)
= 100. Заданный
интервал времени ∆t
= 4 часа.
∆p(t,t+∆t)
= 0,02.
Число
отказов вентилей за эти 4 часа работы
∆n(t,t+∆t).
∆n(t,
t+∆t)
= N(0) ∆p(t,
t+∆t)
= 100 0,02 = 2.
Применяя
к интенсивности отказов выражение
(2-30), отметим, что в нём нам неизвестна
лишь величина
N(t) – число
исправных изделий к моменту начала
интервала. Умножив обе части выражения
(2-30) на эту величину и разделив на
заданную нам величину λ*(t,
t+∆t),
получим
∆n(t,t+∆t)
2 200
N(t)
=
—————– =
———— =
——— = 40.
∆t
λ*(t,t+∆t)
4 1.25 10-2
4
1.25
Преобразуя
выражение (2-14), определим вторую искомую
величину
n(t
) = N(0) – N(t) = 100 – 40 = 60.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как умирает техника? Элементы теории надёжности
Время на прочтение
5 мин
Количество просмотров 55K
Некоторые люди, которые интересуются нашими услугами, задают вопрос: «Серверы, которые вы предоставляете, новые или б/у?» Именно этот вопрос побудил нас немного углубиться в теорию надёжности и рассказать, чем не совсем новый сервер лучше совсем нового, а также какой смысл надписи «Срок службы» в документации к Вашему холодильнику, почему и из каких соображений нужно заранее думать о замене рабочего ноута и некоторые другие интересные вещи.
В случае с серверами переживать заставляет в первую очередь состояние жёстких дисков. Многие убеждены, что если им поставят в сервер новые диски, только что привезённые с завода, они прослужат долго и счастливо. Но не все знают, что на кривой жизненного цикла есть определённый участок, на котором новенькое устройство может умереть так же быстро, как и видавшее виды. К этому мы вернёмся немного позже, а пока…
Немного теории
Теория надёжности (также иногда называется теорией отказов) — научное направление, которое занимается изучением принципов, закономерностей и составлением статистических моделей отказов технических устройств. Она возникла как ответвление от статистики и теории вероятности ещё в XIX веке и первоначально использовалась морскими страховыми компаниями и компаниями по страхованию жизни для оценки, какие тарифы будут прибыльными в реалиях тех времён. В 30-40-х годах XX века были заложены принципы расчёта надёжности энергосистем. С тех пор наука об отказах техники развивается параллельно с самой техникой.
Все технические объекты согласно теории надёжности делятся на восстанавливаемые и невосстанавливаемые. При этом причисление к невосстанавливаемым не обязательно означает полную невозможность ремонта, но также включает случаи, когда такой ремонт экономически нецелесообразен. Например, если в Вашем ноутбуке 3-летней давности окончательно умер аккумулятор вместе с контроллером, и замена будет стоить как треть нового и более современного ноутбука, лучше причислить Ваш старый к невосстанавливаемым и списать в утиль. Это может показаться очевидным, но на практике далеко не все производят соответствующую оценку и делают правильные выводы. Особенно этим грешат владельцы отечественных автомобилей производства 70-80-х годов, которые порой умудряются за несколько лет эксплуатации вкладывать в них денег на стоимость б/у иномарки начала 90-х.
Техническое состояние делится на 5 типов: исправность/неисправность, работоспособность/неработоспособность и предельное состояние. Первые два состояния характеризуют соответствие устройства технической документации, вторые два — способность устройства выполнять свои функции. Некоторые люди путают эти понятия, хотя на практике неисправность не всегда значит неработоспособность. Пример из личной жизни: сдавал на ремонт планшет, по какой-то причине в нём заменили системную плату. Новая плата была из другой серии, и оперативной памяти вместо 512 Мб стало 384 Мб. Планшет, естественно, вполне успешно работает. Но технической документации уже не соответствует, потому принимать из ремонта его как исправный нельзя.
Предельное состояние — это состояние, когда дальнейшая эксплуатация или ремонт являются недопустимыми, невозможными или нецелесообразными. Тут же стоит ввести понятие ресурса — суммарной наработки (продолжительности/объёма работы) устройства до перехода в предельное состояние. В быту ресурс работы часто можно встретить на лампочках-экономках. При этом, естественно, указывается средний ресурс — математическое ожидание, основанное на тестировании продукции.
Схожее с ресурсом, но содержащее в себе больше гипотез понятие — срок службы. По сути оно является попыткой перевести фактический ресурс устройства в какой-то календарный срок, т.е. указывает время, за которое в среднем ресурс будет исчерпан. При расчёте используется информация о том, сколько времени средний общечеловек проводит перед телевизором или сколько раз в неделю стирает вещи.
Существует несколько параметров, количественно описывающих надёжность того или иного устройства. Определяются они, как правило, экспериментально на тестовой партии, иногда с применением экстраполяции, если дождаться отказа всей экспериментальной партии не представляется возможным (например, в случае долгоживущих высоконадёжных устройств).
Вероятность безотказной работы P(t) — вероятность, что за промежуток времени t не откажет ни одно устройство из выборки. Также называется законом распределения надёжности.
Вероятность отказа F(t) — характеристика, противоположная P(t) и показывающая вероятность хотя бы одного отказа до момента времени t. Графически обе функции выглядят примерно так:
Всегда справедливо выражение: P(t) + F(t) = 1.
Плотность распределения безотказной работы называется частотой отказов и вычисляется как производная по времени от вероятности отказа:
a(t) = d F(t) / dt,
а интенсивность появления отказов в единицу времени (или просто интенсивность отказов) λ(t) определяется как соотношение частоты отказов к вероятности безотказной работы:
λ(t) = a(t) / P(t)
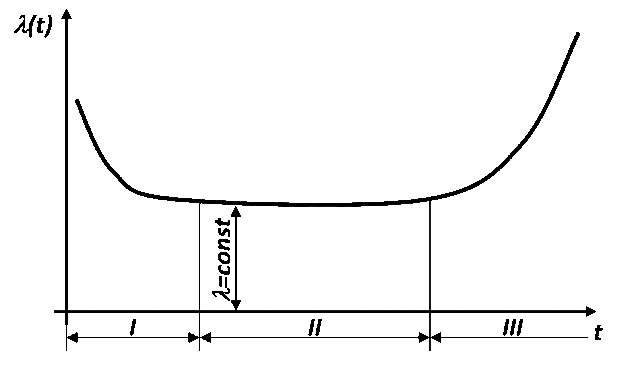
График интенсивности отказов выглядит следующим образом:
Кривая делится на 3 зоны: I — этап приработки, II — нормальная эксплуатация, III — старение (износ). На этапе приработки умирают в основном бракованные изделия. И в случае, если в партии устройств много брака, последствия массовой эксплуатации такой партии могут варьироваться от непредсказуемых до катастрофических. В комментариях к статье о том, как люди лишались своих данных, человек рассказывал об опыте использования жёстких дисков из одной бракованной партии в сервере, когда в течение часа один за одним умерли 24 диска.
И тут мы плавно подбираемся к тому, что новые диски, да и любая другая только что сошедшая с конвейера техника, вовсе не являются синонимом безотказности. А заодно к тому, что успешно проработавшая 2-3-5 месяцев техника, скорее всего, прослужит ещё долгие годы (или сколько там ей отведено).
Отдельно стоит рассмотреть этап старения. Считается, что для некоторых устройств и деталей износ практически не характерен. В частности, к ним относят полупроводниковые приборы. Считается, что при предусмотренных стандартами условиях эксплуатации ресурс таких устройств практически вечен. В компьютерной технике к таковым можно отнести процессоры и энергозависимую (оперативную) память. Практика показывает, что с большей вероятностью они отправятся в лучший из миров из-за сбоя по питанию (скачок напряжения или что-либо в этом духе). А вот все известные мне устройства хранения, к сожалению, подвержены старению. В HDD изнашивается механика и осыпаются блины, в SSD изнашиваются ячейки памяти (впрочем, изнашивает их только запись, что существенно облегчает ситуацию, если Вам нужно редко писать и долго хранить), магнитные носители размагничиваются, на оптических блекнет отражающий слой.
Кстати, занятный факт: жизненный цикл живых организмов чем-то похож на жизненный цикл технических устройств. Ниже приведён график зависимости вероятности смерти от возраста на основании реальных статистических данных по США за 2003 год.
Как бы печально и, возможно, даже жестоко это ни звучало, но у людей тоже есть этап приработки, в течение которого уходят в лучший из миров слабые детки.
А что на практике?
А на практике всем нам стоит помнить, что у всего есть свой ресурс и свой срок службы. И мы избавим себя от множества проблем, если будем следить за наработкой устройств как в промышленности, так и в быту. Даже больше это касается быта, т.к. в промышленных масштабах за этим зачастую следят специалисты.
Надеюсь, эта статья поможет кому-то решиться на покупку новой машины или ноутбука, отставив в сторону мысль «у меня ещё старый не рассыпался». Или заставит установить на серверы систему мониторинга «здоровья» жёстких дисков и, видя участившиеся ошибки, произвести замену раньше, чем наступит отказ или предельное состояние.
Частотой отказов называется отношение числа отказавших образцов аппаратуры в единицу времени к числу образцов, первоначально установленных на испытание при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными.
Так как число отказавших образцов в интервале времени может зависеть от расположения этого промежутка по оси времени, то частота отказов является функцией времени. Эта характеристика в дальнейшем обозначается α(t).
Согласно определению
, (1.10)
где n(t) – число отказавших образцов в интервале времени от до
; N0 – число образцов аппаратуры, первоначально установленных на испытание;
– интервал времени.
Выражение (1.10) является статистическим определением частоты отказов. Этой количественной характеристике надежности легко дать вероятностное определение. Вычислим в выражении (1.10) n (t), т.е. число образцов, отказавших в интервале. Очевидно,
n(t) = -[N(t + ) – N(t)], (1.11)
где N(t) – число образцов, исправно работающих к моменту времени t; N(t + ) – число образцов, исправно работающих к моменту времени t +
.
При достаточно большом числе образцов (N0) справедливы соотношения:
N(t) = N0P(t);
N(t+) = N0P(t+
). (1.12)
Подставляя выражение (1.11) в выражение (1.10) и учитывая выражение (1.12), получим:
,
а с учетом выражения (1.4) получим:
α(t) = Q/(t) (1.13)
Из выражения (1.13) видно, что частота отказов характеризует плотность распределения времени работы аппаратуры до ее отказа. Численно она равна взятой с обратным знаком производной от вероятности безотказной работы. Выражение (1.13) является вероятностным определением частоты отказов.
Таким образом, между частотой отказов, вероятностью безотказной работы и вероятностью отказов при любом законе распределения времени возникновения отказов существуют однозначные зависимости. Эти зависимости на основании (1.13) и (1.4) имеют вид:
; (1.14)
. (1.15)
Частота отказов, являясь плотностью распределения, наиболее полно характеризует такое случайное явление, как время возникновения отказов. Вероятность безотказной работы, математическое ожидание, дисперсия и т.п. являются лишь удобными характеристиками распределения и всегда могут быть получены, если известна частота отказов α(t). В этом ее основное достоинство как характеристики надёжности.
Характеристика α(t) имеет также существенные недостатки. Эти недостатки становятся ясными при детальном рассмотрении выражения (1.10). При определении a(t) из экспериментальных данных фиксируется число отказавших образцов n(t) за промежуток времени при условии, что все отказавшие ранее образцы не восполняются исправными. Это означает, что частоту отказов можно использовать для оценки надежности только такой аппаратуры, которая после возникновения отказа не ремонтируется и в дальнейшем не эксплуатируется (например, аппаратуры разового использования, простейших элементов, не поддающихся ремонту, и т.п.). В противном случае частота отказов характеризует надежность аппаратуры лишь до первого ее отказа.
Оценить с помощью частоты отказов надежность аппаратуры длительного пользования, которая может ремонтироваться, затруднительно. Для этой цели необходимо иметь семейство кривых α(t), полученных: до первого отказа, между первым и вторым, вторым и третьим отказами и т.д. Следует, однако, заметить, что при отсутствии старения аппаратуры указанные частоты отказов будут совпадать. Поэтому α(t) хорошо характеризует надежность аппаратуры также в том случае, когда отказы подчиняются экспоненциальному распределению.
Надежность аппаратуры длительного использования можно характеризовать частотой отказов, полученной при условии замены отказавшей аппаратуры исправной. При этом внешне формула (1.10) не изменяется, однако меняется ее внутреннее содержание.
Частота отказов, полученная при условии замены отказавшей аппаратуры исправной (новой или восстановленной), иногда называется средней частотой отказов и обозначается .
Средней частотой отказов называется отношение числа отказавших образцов в единицу времени к числу испытываемых образцов при условии, что все образцы, вышедшие из строя, заменяются исправными (новыми или восстановленными).
Таким образом,
, (1.16)
где n(t) – число отказавших образцов в интервале времени от до
, N0 – число испытываемых образцов (N0 остается в процессе испытания постоянным, так как все отказавшие образцы заменяются исправными),
– интервал времени.
Средняя частота отказов обладает следующими важными свойствами:
1) . Это свойство становится очевидным, если учесть, что
;
2) независимо от вида функции α(t) при средняя частота отказов стремится к некоторой постоянной величине;
3) главное достоинство средней частоты отказов как количественной характеристики надежности состоит в том, что она позволяет довольно полно оценить свойства аппаратуры, работающей в режиме смены элементов. К такой аппаратуре относятся сложные автоматические системы, предназначенные для длительного использования. Подобные системы после возникновения отказов ремонтируются и затем вновь эксплуатируются;
4) средняя частота отказов может быть также использована для оценки надежности сложных систем разового применения в процессе их хранения;
5) она также довольно просто позволяет определить число отказавших в аппаратуре элементов данного типа. Это свойство может быть использовано для вычисления необходимого количества элементов для нормальной эксплуатации аппаратуры в течение времени t. Поэтому
является наиболее удобной характеристикой для ремонтных предприятий;
1) знание позволяет также правильно спланировать частоту профилактических мероприятий, структуру ремонтных органов, необходимое количество и номенклатуру запасных элементов.
К недостаткам средней частоты отказов следует отнести сложность определения других характеристик надежности, и в частности основной из них вероятности безотказной работы, при известной .
Сложная система состоит из большого числа элементов. Поэтому представляет интерес найти зависимость средней частоты отказов. Введем понятие суммарной частоты отказов сложной системы.
Суммарной частотой отказов называется число отказов аппаратуры в единицу времени, приходящееся на один ее экземпляр.
В дальнейшем эта характеристика обозначается . Согласно определению, для одного образца
, (1.17)
где n (t) – число отказов аппаратуры за время от до
;
– интервал времени.
Если для определения используется несколько образцов, то суммарная частота отказов вычисляется по формуле:
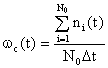
где ni(t) – число отказов i-го образца аппаратуры за время от до
; N0 – число испытываемых образцов аппаратуры;
— интервал времени,.
Отказы сложной системы состоят из отказов отдельных элементов, поэтому число отказов n(t) аппаратуры в выражении (1.18) будет равно сумме всех отказов элементов. Если Ni-число элементов i-го типа, а — средняя частота отказов элементов i-го типа, то за промежуток времени
произойдет
отказов элементов i-го типа, а всего отказов будет:
где r – число типов элементов.
Подставляя выражение для n (t) в формулу (1.18), получим:
(1.19)
т.е. суммарная частота отказов сложной системы в момент времени t равна сумме средних частот отказов элементов.
From Wikipedia, the free encyclopedia
Failure rate is the frequency with which an engineered system or component fails, expressed in failures per unit of time. It is usually denoted by the Greek letter λ (lambda) and is often used in reliability engineering.
The failure rate of a system usually depends on time, with the rate varying over the life cycle of the system. For example, an automobile’s failure rate in its fifth year of service may be many times greater than its failure rate during its first year of service. One does not expect to replace an exhaust pipe, overhaul the brakes, or have major transmission problems in a new vehicle.
In practice, the mean time between failures (MTBF, 1/λ) is often reported instead of the failure rate. This is valid and useful if the failure rate may be assumed constant – often used for complex units / systems, electronics – and is a general agreement in some reliability standards (Military and Aerospace). It does in this case only relate to the flat region of the bathtub curve, which is also called the “useful life period”. Because of this, it is incorrect to extrapolate MTBF to give an estimate of the service lifetime of a component, which will typically be much less than suggested by the MTBF due to the much higher failure rates in the “end-of-life wearout” part of the “bathtub curve”.
The reason for the preferred use for MTBF numbers is that the use of large positive numbers (such as 2000 hours) is more intuitive and easier to remember than very small numbers (such as 0.0005 per hour).
The MTBF is an important system parameter in systems where failure rate needs to be managed, in particular for safety systems. The MTBF appears frequently in the engineering design requirements, and governs frequency of required system maintenance and inspections. In special processes called renewal processes, where the time to recover from failure can be neglected and the likelihood of failure remains constant with respect to time, the failure rate is simply the multiplicative inverse of the MTBF (1/λ).
A similar ratio used in the transport industries, especially in railways and trucking is “mean distance between failures”, a variation which attempts to correlate actual loaded distances to similar reliability needs and practices.
Failure rates are important factors in the insurance, finance, commerce and regulatory industries and fundamental to the design of safe systems in a wide variety of applications.
Failure rate data[edit]
Failure rate data can be obtained in several ways. The most common means are:
- Estimation
- From field failure rate reports, statistical analysis techniques can be used to estimate failure rates. For accurate failure rates the analyst must have a good understanding of equipment operation, procedures for data collection, the key environmental variables impacting failure rates, how the equipment is used at the system level, and how the failure data will be used by system designers.
- Historical data about the device or system under consideration
- Many organizations maintain internal databases of failure information on the devices or systems that they produce, which can be used to calculate failure rates for those devices or systems. For new devices or systems, the historical data for similar devices or systems can serve as a useful estimate.
- Government and commercial failure rate data
- Handbooks of failure rate data for various components are available from government and commercial sources. MIL-HDBK-217F, Reliability Prediction of Electronic Equipment, is a military standard that provides failure rate data for many military electronic components. Several failure rate data sources are available commercially that focus on commercial components, including some non-electronic components.
- Prediction
- Time lag is one of the serious drawbacks of all failure rate estimations. Often by the time the failure rate data are available, the devices under study have become obsolete. Due to this drawback, failure-rate prediction methods have been developed. These methods may be used on newly-designed devices to predict the device’s failure rates and failure modes. Two approaches have become well known, Cycle Testing and FMEDA.
- Life Testing
- The most accurate source of data is to test samples of the actual devices or systems in order to generate failure data. This is often prohibitively expensive or impractical, so that the previous data sources are often used instead.
- Cycle Testing
- Mechanical movement is the predominant failure mechanism causing mechanical and electromechanical devices to wear out. For many devices, the wear-out failure point is measured by the number of cycles performed before the device fails, and can be discovered by cycle testing. In cycle testing, a device is cycled as rapidly as practical until it fails. When a collection of these devices are tested, the test will run until 10% of the units fail dangerously.
- FMEDA
- Failure modes, effects, and diagnostic analysis (FMEDA) is a systematic analysis technique to obtain subsystem / product level failure rates, failure modes and design strength. The FMEDA technique considers:
- All components of a design,
- The functionality of each component,
- The failure modes of each component,
- The effect of each component failure mode on the product functionality,
- The ability of any automatic diagnostics to detect the failure,
- The design strength (de-rating, safety factors) and
- The operational profile (environmental stress factors).
Given a component database calibrated with field failure data that is reasonably accurate[1]
, the method can predict product level failure rate and failure mode data for a given application. The predictions have been shown to be more accurate[2] than field warranty return analysis or even typical field failure analysis given that these methods depend on reports that typically do not have sufficient detail information in failure records.[3]
Failure rate in the discrete sense[edit]
The failure rate can be defined as the following:
- The total number of failures within an item population, divided by the total time expended by that population, during a particular measurement interval under stated conditions. (MacDiarmid, et al.)
Although the failure rate, 



-
, where
is the time to (first) failure distribution (i.e. the failure density function).
over a time interval 






Hazard rate and ROCOF (rate of occurrence of failures) are often incorrectly seen as the same and equal to the failure rate.[clarification needed] To clarify; the more promptly items are repaired, the sooner they will break again, so the higher the ROCOF. The hazard rate is however independent of the time to repair and of the logistic delay time.
Failure rate in the continuous sense[edit]
Calculating the failure rate for ever smaller intervals of time results in the hazard function (also called hazard rate), 

A continuous failure rate depends on the existence of a failure distribution, 
where 
The failure distribution function is the integral of the failure density function, f(t),
The hazard function can be defined now as
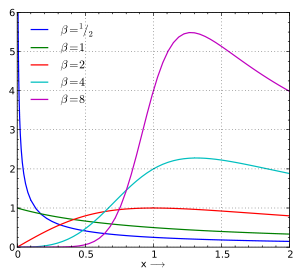
Exponential failure density functions. Each of these has a (different) constant hazard function (see text).
Many probability distributions can be used to model the failure distribution (see List of important probability distributions). A common model is the exponential failure distribution,
which is based on the exponential density function. The hazard rate function for this is:
Thus, for an exponential failure distribution, the hazard rate is a constant with respect to time (that is, the distribution is “memory-less”). For other distributions, such as a Weibull distribution or a log-normal distribution, the hazard function may not be constant with respect to time. For some such as the deterministic distribution it is monotonic increasing (analogous to “wearing out”), for others such as the Pareto distribution it is monotonic decreasing (analogous to “burning in”), while for many it is not monotonic.
Solving the differential equation
for 
Decreasing failure rate[edit]
A decreasing failure rate (DFR) describes a phenomenon where the probability of an event in a fixed time interval in the future decreases over time. A decreasing failure rate can describe a period of “infant mortality” where earlier failures are eliminated or corrected[4] and corresponds to the situation where λ(t) is a decreasing function.
Mixtures of DFR variables are DFR.[5] Mixtures of exponentially distributed random variables are hyperexponentially distributed.
Renewal processes[edit]
For a renewal process with DFR renewal function, inter-renewal times are concave.[5][6] Brown conjectured the converse, that DFR is also necessary for the inter-renewal times to be concave,[7] however it has been shown that this conjecture holds neither in the discrete case[6] nor in the continuous case.[8]
Applications[edit]
Increasing failure rate is an intuitive concept caused by components wearing out. Decreasing failure rate describes a system which improves with age.[9]
Decreasing failure rates have been found in the lifetimes of spacecraft, Baker and Baker commenting that “those spacecraft that last, last on and on.”[10][11] The reliability of aircraft air conditioning systems were individually found to have an exponential distribution, and thus in the pooled population a DFR.[9]
Coefficient of variation[edit]
When the failure rate is decreasing the coefficient of variation is ⩾ 1, and when the failure rate is increasing the coefficient of variation is ⩽ 1.[12] Note that this result only holds when the failure rate is defined for all t ⩾ 0[13] and that the converse result (coefficient of variation determining nature of failure rate) does not hold.
Units[edit]
Failure rates can be expressed using any measure of time, but hours is the most common unit in practice. Other units, such as miles, revolutions, etc., can also be used in place of “time” units.
Failure rates are often expressed in engineering notation as failures per million, or 10−6, especially for individual components, since their failure rates are often very low.
The Failures In Time (FIT) rate of a device is the number of failures that can be expected in one billion (109) device-hours of operation.[14]
(E.g. 1000 devices for 1 million hours, or 1 million devices for 1000 hours each, or some other combination.) This term is used particularly by the semiconductor industry.
The relationship of FIT to MTBF may be expressed as: MTBF = 1,000,000,000 x 1/FIT.
Additivity[edit]
Under certain engineering assumptions (e.g. besides the above assumptions for a constant failure rate, the assumption that the considered system has no relevant redundancies), the failure rate for a complex system is simply the sum of the individual failure rates of its components, as long as the units are consistent, e.g. failures per million hours. This permits testing of individual components or subsystems, whose failure rates are then added to obtain the total system failure rate.[15][16]
Adding “redundant” components to eliminate a single point of failure improves the mission failure rate, but makes the series failure rate (also called the logistics failure rate) worse—the extra components improve the mean time between critical failures (MTBCF), even though the mean time before something fails is worse.[17]
Example[edit]
Suppose it is desired to estimate the failure rate of a certain component. A test can be performed to estimate its failure rate. Ten identical components are each tested until they either fail or reach 1000 hours, at which time the test is terminated for that component. (The level of statistical confidence is not considered in this example.) The results are as follows:
Estimated failure rate is
or 799.8 failures for every million hours of operation.
See also[edit]
- Annualized failure rate
- Burn-in
- Failure
- Failure mode
- Failure modes, effects, and diagnostic analysis
- Force of mortality
- Frequency of exceedance
- Reliability engineering
- Reliability theory
- Reliability theory of aging and longevity
- Survival analysis
- Weibull distribution
References[edit]
- ^ Electrical & Mechanical Component Reliability Handbook. exida. 2006.
- ^ Goble, William M.; Iwan van Beurden (2014). Combining field failure data with new instrument design margins to predict failure rates for SIS Verification. Proceedings of the 2014 International Symposium – BEYOND REGULATORY COMPLIANCE, MAKING SAFETY SECOND NATURE, Hilton College Station-Conference Center, College Station, Texas.
- ^ W. M. Goble, “Field Failure Data – the Good, the Bad and the Ugly,” exida, Sellersville, PA [1]
- ^ Finkelstein, Maxim (2008). “Introduction”. Failure Rate Modelling for Reliability and Risk. Springer Series in Reliability Engineering. pp. 1–84. doi:10.1007/978-1-84800-986-8_1. ISBN 978-1-84800-985-1.
- ^ a b Brown, M. (1980). “Bounds, Inequalities, and Monotonicity Properties for Some Specialized Renewal Processes”. The Annals of Probability. 8 (2): 227–240. doi:10.1214/aop/1176994773. JSTOR 2243267.
- ^ a b Shanthikumar, J. G. (1988). “DFR Property of First-Passage Times and its Preservation Under Geometric Compounding”. The Annals of Probability. 16 (1): 397–406. doi:10.1214/aop/1176991910. JSTOR 2243910.
- ^ Brown, M. (1981). “Further Monotonicity Properties for Specialized Renewal Processes”. The Annals of Probability. 9 (5): 891–895. doi:10.1214/aop/1176994317. JSTOR 2243747.
- ^ Yu, Y. (2011). “Concave renewal functions do not imply DFR interrenewal times”. Journal of Applied Probability. 48 (2): 583–588. arXiv:1009.2463. doi:10.1239/jap/1308662647. S2CID 26570923.
- ^ a b Proschan, F. (1963). “Theoretical Explanation of Observed Decreasing Failure Rate”. Technometrics. 5 (3): 375–383. doi:10.1080/00401706.1963.10490105. JSTOR 1266340.
- ^ Baker, J. C.; Baker, G. A. S. . (1980). “Impact of the space environment on spacecraft lifetimes”. Journal of Spacecraft and Rockets. 17 (5): 479. Bibcode:1980JSpRo..17..479B. doi:10.2514/3.28040.
- ^ Saleh, Joseph Homer; Castet, Jean-François (2011). “On Time, Reliability, and Spacecraft”. Spacecraft Reliability and Multi-State Failures. p. 1. doi:10.1002/9781119994077.ch1. ISBN 9781119994077.
- ^ Wierman, A.; Bansal, N.; Harchol-Balter, M. (2004). “A note on comparing response times in the M/GI/1/FB and M/GI/1/PS queues” (PDF). Operations Research Letters. 32: 73–76. doi:10.1016/S0167-6377(03)00061-0.
- ^ Gautam, Natarajan (2012). Analysis of Queues: Methods and Applications. CRC Press. p. 703. ISBN 978-1439806586.
- ^
Xin Li; Michael C. Huang; Kai Shen; Lingkun Chu.
“A Realistic Evaluation of Memory Hardware Errors and Software System Susceptibility”.
2010.
p. 6. - ^
“Reliability Basics”.
2010. - ^ Vita Faraci.
“Calculating Failure Rates of Series/Parallel Networks” Archived 2016-03-03 at the Wayback Machine.
2006. - ^
“Mission Reliability and Logistics Reliability: A Design Paradox”.
Further reading[edit]
- Goble, William M. (2018), Safety Instrumented System Design: Techniques and Design Verification, Research Triangle Park, NC: International Society of Automation
- Blanchard, Benjamin S. (1992). Logistics Engineering and Management (Fourth ed.). Englewood Cliffs, New Jersey: Prentice-Hall. pp. 26–32. ISBN 0135241170.
- Ebeling, Charles E. (1997). An Introduction to Reliability and Maintainability Engineering. Boston: McGraw-Hill. pp. 23–32. ISBN 0070188521.
- Federal Standard 1037C
- Kapur, K. C.; Lamberson, L. R. (1977). Reliability in Engineering Design. New York: John Wiley & Sons. pp. 8–30. ISBN 0471511919.
- Knowles, D. I. (1995). “Should We Move Away From ‘Acceptable Failure Rate’?”. Communications in Reliability Maintainability and Supportability. International RMS Committee, USA. 2 (1): 23.
- MacDiarmid, Preston; Morris, Seymour; et al. (n.d.). Reliability Toolkit (Commercial Practices ed.). Rome, New York: Reliability Analysis Center and Rome Laboratory. pp. 35–39.
- Modarres, M.; Kaminskiy, M.; Krivtsov, V. (2010). Reliability Engineering and Risk Analysis: A Practical Guide (2nd ed.). CRC Press. ISBN 9780849392474.
- Mondro, Mitchell J. (June 2002). “Approximation of Mean Time Between Failure When a System has Periodic Maintenance” (PDF). IEEE Transactions on Reliability. 51 (2): 166–167. doi:10.1109/TR.2002.1011521.
- Rausand, M.; Hoyland, A. (2004). System Reliability Theory; Models, Statistical methods, and Applications. New York: John Wiley & Sons. ISBN 047147133X.
- Turner, T.; Hockley, C.; Burdaky, R. (1997). The Customer Needs A Maintenance-Free Operating Period. 1997 Avionics Conference and Exhibition, No. 97-0819, P. 2.2. Leatherhead, Surrey, UK: ERA Technology Ltd.
- U.S. Department of Defense, (1991) Military Handbook, “Reliability Prediction of Electronic Equipment, MIL-HDBK-217F, 2
External links[edit]
- Bathtub curve issues Archived 2014-11-29 at the Wayback Machine, ASQC
- Fault Tolerant Computing in Industrial Automation Archived 2014-03-26 at the Wayback Machine by Hubert Kirrmann, ABB Research Center, Switzerland