Решение №1
Подставим в формулу то, что нам известно:
(2 = 1500cdot cfrac{f-749}{f+749} )
Преобразуем это выражение. Сначала домножим на знаменатель (он не может равняться нулю, так как частота всегда положительна).
(2 = 1500cdot cfrac{f-749}{f+749} \ 2cdot (f+749) = 1500cdot (f-749) \ 2f + 2cdot 749 = 1500f – 1500cdot 749\ 2cdot 749 +1500cdot 749 = 1498f \ 749(2+1500) = 1498f\ f = cfrac{749cdot 1502}{1498} = 751\)
Ответ: 751 МГц.
Решение №2
Задача сводится к решению неравенства V меньше либо равно двум при известных значениях
(1500cdotfrac{f-749}{f+749}le2 )
(750cdotfrac{f-749}{f+749}le1)
(750f-750cdot749le f+749)
(fle 751)
Ответ: 751

ЕГЭ-Центр «Пять с плюсом» основан в 2008 году. С основания и по настоящий момент Центр возглавляет Елизавета Владимировна Глазова, мать пятерых детей, профессиональный педагог и преподаватель русского языка и литературы.
– Oбразование как Стиль Жизни
Присылайте свои колонки
и предложения
У вас есть интересная новость
или материал из сферы образования
или популярной науки?
Расскажите нам!
© 2014-2023 Newtonew. 12+
Просветительский медиа-проект об образовании,
посвящённый самым актуальным и полезным
концепциям, теориям и методикам, технологиям
и исследованиям, продуктам и сервисам. Мы
говорим о том, как развиваются и изменяются
образование и наука.
Копирование материалов возможно только
с разрешения редакции Newtonew.
Мы используем файлы cookie для улучшения пользовательского опыта. Подробнее вы можете посмотреть в нашем пользовательском соглашении.
Задания
Версия для печати и копирования в MS Word
Тип 8 № 28327 
i
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ульт-развуковые импульсы частотой 248 МГц. Скорость погружения батискафа вычисляется по формуле где
м/с — скорость звука в воде,
— частота испускаемых импульсов, f — частота отражённого от дна сигнала, регистрируемая приёмни-ком (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 12 м/с.
Решение.
Это задание ещё не решено, приводим решение прототипа.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле где
м/с — скорость звука в воде,
— частота испускаемых импульсов, f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
Задача сводится к решению уравнения м/с при известных значениях
м/с — скорости звука в воде и
МГц — частоты испускаемых импульсов:
МГц.
Ответ: 751.
Аналоги к заданию № 27981: 42439 501981 629171 … Все
Классификатор алгебры: Рациональные уравнения и неравенства
Прототип задания
·
Видеокурс
|
|
Макеты страниц
При отражении радиолокационный сигнал претерпевает ряд изменений, связанных со свойствами отражающих объектов. При этом естественно различать полезный сигнал, полученный в результате отражения от цели, обнаружение и измерение координат которой является задачей данного радиолокатора, и сигналы, обусловленные наличием всякого рода отражающих объектов, маскирующих цель (пассивные помехи). Такими объектами могут быть поверхность суши или моря, облака дипольных отражателей, гидрометеоры и т. д. Ряд общих свойств полезного сигнала и мешающих отражений могут быть при некоторых допущениях рассмотрены без конкретизации вида отражающего объекта, чем и оправдывается объединение этих вопросов при изложении.
Начнем с качественного рассмотрения свойств сигнала, отраженного от (цели. При этом постараемся установить связь между статистическими характеристиками отраженного сигнала, необходимыми для дальнейшего, и обычно используемыми в инженерной практике радиолокационными характеристиками цели.
Прежде всего следует отметить, что мощность отраженного сигнала зависит от дальности цели и ее
эффективной отражающей поверхности, частота и задержка сигнала — от скорости и дальности цели относительно радиолокатора. Кроме того, как известно, амплитуда и фаза отраженного от цели сигнала зависят от ее ракурса.
Зависимость мощности эхо-сигнала от ракурса цели представляется обычно в виде диаграммы вторичного излучения, которая для большинства радиолокационных целей при используемых рабочих частотах радиолокаторов является сильно изрезанной с большими перепадами между ее экстремумами. Для целей простой геометрической формы диаграмма вторичного излучения может быть рассчитана теоретически в результате более или менее строгого решения соответствующей электродинамической задачи. Однако для реальных целей провести такой расчет почти никогда не удается и приходится определять диаграмму вторичного излучения экспериментально.
Диаграммы вторичного излучения являются лишь статическими характеристиками отраженного сигнала. В реальных условиях за счет движения цели и изменения условий распространения радиоволн отраженный сигнал всегда флюктуирует по амплитуде и фазе. Флюктуации, связанные с изменениями условий распространения, не являются специфическими для радиолокации и на них мы останавливаться не будем; флюктуации же, связанные с движением цели, обусловлены изменением ракурса цели (рыскания) и вибрацией ее поверхности. При рысканиях диаграмма вторичного излучения поворачивается случайным образом относительно направления на радиолокатор, а за счет вибрации меняется вид этой диаграммы, которая в результате оказывается случайной функцией времени.
В силу всех указанных причин сигнал, отраженный от цели, представляет собой случайный процесс и может быть записан как

где  мощность сигнала;
мощность сигнала;  комплексный закон модуляции, введенный в предыдущем параграфе;
комплексный закон модуляции, введенный в предыдущем параграфе;  задержка и допплеровский сдвиг частоты отраженного сигнала;
задержка и допплеровский сдвиг частоты отраженного сигнала;  законы амплитудных и фазовых флюктуаций зхо-сигнала.
законы амплитудных и фазовых флюктуаций зхо-сигнала.
Формула (1.3.1) является приближенной и верна в предположении о достаточно малых размерах цели, когда «размыванием» закона модуляции при отражении от отдельных ее частей можно пренебречь.
Адэкватное описание случайного процесса  возможно лишь с (привлечением статистической теории. Наиболее полной характеристикой такого процесса, которая вместе с тем является необходимой при решении целого ряда задач анализа и синтеза радиолокационных систем, является совокупность многомерных распределений вероятности значений этого процесса. При стремлении числа измерений к бесконечности можно получить так называемый функционал плотности вероятности, представляющий собой плотность вероятности реализации процесса (см. § 1.4).
возможно лишь с (привлечением статистической теории. Наиболее полной характеристикой такого процесса, которая вместе с тем является необходимой при решении целого ряда задач анализа и синтеза радиолокационных систем, является совокупность многомерных распределений вероятности значений этого процесса. При стремлении числа измерений к бесконечности можно получить так называемый функционал плотности вероятности, представляющий собой плотность вероятности реализации процесса (см. § 1.4).
Найти распределения вероятностей непосредственно, исходя из реальных свойств цели и ее движения, очень трудно. Представляется неизбежным в связи с этим использовать более или менее упрощенную радиолокационную модель цели. В качестве такой модели очень удобным является представление цели в виде совокупности большого числа независимо и случайно (в соответствии с определенным законом распределения) расположенных отражающих элементов, перемещающихся друг относительно друга и относительно радиолокатора. В силу центральной предельной теоремы [20] сигнал от такой совокупности отражающих элементов представляет собой нормальный случайный процесс. Все многомерные распределения такого процесса являются гауссовыми и имеют вид

Здесь  совокупность значений процесса
совокупность значений процесса  в рассматриваемые моменты времени;
в рассматриваемые моменты времени;  определитель корреляционной матрицы, составленной из значений функции корреляции
определитель корреляционной матрицы, составленной из значений функции корреляции  сигнала
сигнала  матрица, обратная корреляционной; ее элементы определяются уравнениями:
матрица, обратная корреляционной; ее элементы определяются уравнениями:

где  дельта-символ Кронекера:
дельта-символ Кронекера:

Для отыскания элементов обратной матрицы удобно пользоваться равенством [18]

 алгебраическое дополнение элемента
алгебраическое дополнение элемента  корреляционной матрицы.
корреляционной матрицы.
В формуле (1.3.2) математическое ожидание отраженного сигнала  положено равным нулю. Это соблюдается в случае малого изменения средней плотности отражателей на интервале, равном длине волны, когда для фазы
положено равным нулю. Это соблюдается в случае малого изменения средней плотности отражателей на интервале, равном длине волны, когда для фазы  естественно принять равномерное в интервале
естественно принять равномерное в интервале  распределение вероятностей.
распределение вероятностей.
Использование описанной модели радиолокационной цели оправдывается тем, что в большом числе случаев цель имеет размеры, значительно превышающие длину волны, благодаря чему при расчете сигнала, отраженного от такой цели, можно использовать приближение геометрической оптики. С учетом этого сигнал от цели рассматривается как сумма сигналов от отдельных «блестящих точек» на поверхности цели. Число этих точек для целей обычно очень велико, а их взаимное расположение меняется весьма неопределенным образом в зависимости от ракурса цели, так что его вполне можно считать случайным. Результаты экспериментального определения одномерного закона распределения для сигнала, отраженного, например, от летящего самолета,
показали, что этот закон достаточно точно аппроксимируется нормальным. Ширина спектра флюктуаций эхо-сигнала имеет порядок десятков герц [19].
Предположение о нормальности отраженного радиолокационного сигнала еще в большей степени оправдано в случае мешающих отражений от земной поверхности, облаков металлизированных диполей и тому подобных объектов, ибо в этих случаях число случайно расположенных элементарных отражателей, образующих мешающий сигнал, очень велико.
Для того чтобы полностью охарактеризовать нормальный случайный процесс, каким мы будем считать отраженный сигнал, достаточно найти его функцию корреляции.
Проведем расчет функции корреляции для произвольной совокупности отражающих объектов, а затем конкретизируем полученный результат для полезного сигнала и пассивных помех (мешающих отражений). Расчет функции корреляции сигнала, отраженного от пассивной помехи, для ряда частных случаев проводится в работах  Ниже расчет функции корреляции отраженного сигнала будет проведен в более общем виде, с тем чтобы полученные результаты были пригодны для возможно большего числа случаев.
Ниже расчет функции корреляции отраженного сигнала будет проведен в более общем виде, с тем чтобы полученные результаты были пригодны для возможно большего числа случаев.
Рассмотрим сначала случаи одночастотной работы. Сигнал, отраженный от каждого элементарного отражающего объекта, представляет собой задержанный на время распространения зондирующий сигнал с измененной амплитудой — и фазой и может быть записан в виде

где  сферические координаты рассматриваемого отражающего объекта, отсчитываемые от антенны радиолокатора;
сферические координаты рассматриваемого отражающего объекта, отсчитываемые от антенны радиолокатора;  излученная мощность;
излученная мощность;  несущая частота;
несущая частота;  — длина волны;
— длина волны;
О и  выигрыши передающей и приемной антенн;
выигрыши передающей и приемной антенн;  эффективная отражающая поверхность объекта, усредненная по всем возможным ориентациям;
эффективная отражающая поверхность объекта, усредненная по всем возможным ориентациям;  произведение нормированных коэффициентов направленности передающей и приемной антенн.
произведение нормированных коэффициентов направленности передающей и приемной антенн.
Подставляя в выражение (1.3.4) значения этих функций в один и тот же (момент времени, мы пренебрегаем смещением приемной диаграммы за время распространения сигнала.
Коэффициент  учитывает отражающие свойства объекта на рассматриваемой частоте в данный момент,
учитывает отражающие свойства объекта на рассматриваемой частоте в данный момент,  представляет собой отношение эффективной отражающей (поверхности к ее среднему значению,
представляет собой отношение эффективной отражающей (поверхности к ее среднему значению,  характеризует фазовый сдвиг при отражении. Этот коэффициент учитывает также поляризационные свойства отражающего объекта и является фазным для антенных систем с разной поляризацией. Изменением
характеризует фазовый сдвиг при отражении. Этот коэффициент учитывает также поляризационные свойства отражающего объекта и является фазным для антенных систем с разной поляризацией. Изменением  за время распространения мы пренебрегли.
за время распространения мы пренебрегли.
Сигнал от совокупности отражателей  представляет собой сумму сигналов
представляет собой сумму сигналов  по всем
по всем  Верхний предел этой суммы (число отражателей)
Верхний предел этой суммы (число отражателей)  также может быть случайной функцией времени (например, при рассмотрении сигнала, отраженного от сильно пересеченной местности, или сигнала, отраженного от облака диполей, когда постановка помехи во время наблюдения продолжается). Однако обычно за время корреляции отраженного сигнала
также может быть случайной функцией времени (например, при рассмотрении сигнала, отраженного от сильно пересеченной местности, или сигнала, отраженного от облака диполей, когда постановка помехи во время наблюдения продолжается). Однако обычно за время корреляции отраженного сигнала  меняется мало и это изменение практически не влияет на результаты. Поэтому в дальнейшем мы его учитывать не будем.
меняется мало и это изменение практически не влияет на результаты. Поэтому в дальнейшем мы его учитывать не будем.
Имея в виду отмеченное выше равенство нулю среднего значения отраженного сигнала и считая положения отражателей независимыми, для функции корреляции  получаем
получаем

где

 координаты отражателя в момент
координаты отражателя в момент  в момент
в момент 
Усреднение в (1.3.5) должно производиться по случайным переменным 
Чтобы получить более простое выражение для  наложим следующие дополнительные условия, обычно выполняющиеся на практике:
наложим следующие дополнительные условия, обычно выполняющиеся на практике:
1. Пренебрежем изменением угловых координат за время корреляции отраженного сигнала, считая, что за это время отражатель смещается на малую долю ширины диаграммы направленности.
2. Выделим и рассмотрим отдельно две составляющие движения каждого отражателя: одну, связанную с движением всей совокупности отражателей в целом, и другую, связанную со случайными перемещениями отражателей. Будем считать, что регулярное движение происходит с неизменяющейся за время корреляции радиальной скоростью  При этом
При этом

где  случайное перемещение за время
случайное перемещение за время 
3. Случайные перемещения и изменения ориентации отражателя будем считать независящими от его начального положения. При этом относительное изменение  за время корреляции отраженного сигнала будем считать мальгм.
за время корреляции отраженного сигнала будем считать мальгм.
4. Разности регулярных радиальных перемещений отражателей, попадающих в луч антенны, будем считать малыми по сравнению с интервалом разрешения по дальности. Это позволит нам подставлять в аргумент  величину
величину  — где
— где  среднее для всех отражателей значение скорости
среднее для всех отражателей значение скорости 
5. Свойства всех отражателей будем считать одинаковыми.
При сделанных допущениях усреднение в (1.3.5) должно производиться по  и по Усреднение по
и по Усреднение по  сводится к умножению суммы на плотность вероятности
сводится к умножению суммы на плотность вероятности  и к интегрированию по всему пространству. При этом в силу одинаковости слагаемых под интеграл войдет величина
и к интегрированию по всему пространству. При этом в силу одинаковости слагаемых под интеграл войдет величина  представляющая собой среднюю плотность отражателей в точке
представляющая собой среднюю плотность отражателей в точке  в момент времени
в момент времени  В результате получаем 1
В результате получаем 1

Если в рассматриваемую совокупность входят отражатели разных видов, то все результаты останутся справедливыми, но (1.3.5) и (1.3.6) следует просуммировать по всем разновидностям отражателей.
В полученной формуле удобно объединить все члены, не зависящие от закона модуляции и определяемые характером флюктуаций, обусловленных движением отражателей относительно радиолокатора и вращением антенны. При этом (1.3.6) переписывается в виде

где

где  закон модуляции колебания с несущей частотой
закон модуляции колебания с несущей частотой  Обычно на практике при многочастотной работе используемые частоты разнесены достаточно далеко, так что соответствующие отраженные сигналы являются статистически независимыми. Такой выбор рабочих частот позволяет получить выигрыш в дальности обнаружения цели и улучшить качество селекции движущейся цели на фоне пассивных помех
Обычно на практике при многочастотной работе используемые частоты разнесены достаточно далеко, так что соответствующие отраженные сигналы являются статистически независимыми. Такой выбор рабочих частот позволяет получить выигрыш в дальности обнаружения цели и улучшить качество селекции движущейся цели на фоне пассивных помех  Формула (1.3.8) позволяет сформулировать условия независимости отраженных сигналов, имеющие большое практическое значение.
Формула (1.3.8) позволяет сформулировать условия независимости отраженных сигналов, имеющие большое практическое значение.
Как видно из (1.3.8), для обращения любого слагаемого с в нуль достаточно, чтобы длина волны разностной частоты  была мала по сравнению с интервалом заметного изменения
была мала по сравнению с интервалом заметного изменения  и разностная частота
и разностная частота  была мала по сравнению с суммой ширин спектров модуляции
была мала по сравнению с суммой ширин спектров модуляции  сигналов. При использовании непрерывного излучения без модуляции
сигналов. При использовании непрерывного излучения без модуляции  и степень коррелированности сигналов полностью определяется соотношением между и протяженностью совокупности отражающих объектов по дальности. То же самое получается в случае малой протяженности источника отражения по сравнению с интервалами разрешения по дальности, соответствующими рассматриваемым сигналам. При этом
и степень коррелированности сигналов полностью определяется соотношением между и протяженностью совокупности отражающих объектов по дальности. То же самое получается в случае малой протяженности источника отражения по сравнению с интервалами разрешения по дальности, соответствующими рассматриваемым сигналам. При этом  можно вынести в (1.3.8) за знак интеграла.
можно вынести в (1.3.8) за знак интеграла.
Условию независимости отраженных сигналов можно придать следующую наглядную формулировку: отраженные сигналы являются статистически независимыми в том случае, если длина волны, соответствующая разностной частоте, мала по сравнению с протяженностью рассматриваемого отражающего объекта по дальности при данном ракурсе его относительно радиолокатора) или с протяженностью интервалов разрешения, соответствующих законам модуляции рассматриваемых сигналов.
Конкретизируем полученные общие соотношения для случая сигналов, отраженных от цели, и мешающих отражений. Размеры цели в дальнейшем будем предполагать малыми как по сравнению с шириной диаграммы
направленности антенны, так и по сравнению с протяженностью интервалов разрешения по дальности и будем пренебрегать размытием модуляции отраженного сигнала за счет протяженности цели. Кроме того, в большинстве случаев будем пренебрегать искажением модуляции отраженного сигнала за счет допплеровского эффекта.
Функция корреляции отраженного от цели сигнала записывается в виде

где  коэффициент корреляции флюктуаций отраженного сигнала;
коэффициент корреляции флюктуаций отраженного сигнала;  мощность.
мощность.
Множитель  можно при решении ряда задач включать в закон модуляции отраженного сигнала и
можно при решении ряда задач включать в закон модуляции отраженного сигнала и 
Аналогичным образом преобразуется в этом случае функция корреляции при многочастотном излучении

 коэффициент корреляции флюктуаций (предполагается примерно одинаковым для всех используемых частот);
коэффициент корреляции флюктуаций (предполагается примерно одинаковым для всех используемых частот);  допплеровский сдвиг
допплеровский сдвиг  несущей частоты;
несущей частоты;  амплитуда
амплитуда  отраженного сигнала.
отраженного сигнала.
Коэффициент  определяет степень коррелированности
определяет степень коррелированности  сигналов
сигналов

где  плотность распределения отражающей поверхности.
плотность распределения отражающей поверхности.
Для мешающих отражений от малоразмерных объектов (в дальнейшем будем называть такие объекты дискретными помехами либо помехами типа «мешающая, ложная цель») функция корреляции отраженного сигнала также может быть записана в виде (1.3.9), (1.3.10).
Значительный интерес представляет случай медленного изменения функции  соответствующий протяженной пассивной помехе. Физически очевидно, что этот случай является наиболее сложным с точки зрения защиты радиолокатора от воздействия мешающих отражений. Поэтому анализ и синтез средств защиты от помех в расчете на этот случай соответствуют минимаксному подходу, обеспечивая наилучший эффект в наихудшем случае. Практическое использование результатов синтеза не требует при этом знания распределения элементарных отражателей в пространстве, что выгодно отличает данный случай от остальных.
соответствующий протяженной пассивной помехе. Физически очевидно, что этот случай является наиболее сложным с точки зрения защиты радиолокатора от воздействия мешающих отражений. Поэтому анализ и синтез средств защиты от помех в расчете на этот случай соответствуют минимаксному подходу, обеспечивая наилучший эффект в наихудшем случае. Практическое использование результатов синтеза не требует при этом знания распределения элементарных отражателей в пространстве, что выгодно отличает данный случай от остальных.
В случае протяженной помехи выражение для функции корреляции можно существенно упростить. Если зондирующий сигнал представляет собой сложно-модулированную одиночную посылку и  мало меняется на интервале, равном длительности посылки, то из (1.3.7) получаем
мало меняется на интервале, равном длительности посылки, то из (1.3.7) получаем

где  — допплеровская частота помехи;
— допплеровская частота помехи;

Множитель а в этой формуле учитывает искажения модуляции за счет движения цели. Обычно они достаточно слабы и их последствия мотут не учитываться. Учет этих искажений будет проведен  § 4.9.
§ 4.9.
Если  периодический сигнал, то для получения формулы, аналогичной (1.3.12), достаточно потребовать малого изменения
периодический сигнал, то для получения формулы, аналогичной (1.3.12), достаточно потребовать малого изменения  за длительность периода, а в случае стационарной шумовой модуляции зондирующего сигнала — за время, в несколько раз превышающее
за длительность периода, а в случае стационарной шумовой модуляции зондирующего сигнала — за время, в несколько раз превышающее
время корреляции модулирующего случайного процесса. При этом в соответствии с  и (1.2.2)
и (1.2.2)

Как идно из (1.3.12) и (1.3.13), в случае протяженной пассивной помехи нестационарность обусловлена лишь наличием множителя  Возвращаясь к формуле (1.3.5), легко усмотреть, что
Возвращаясь к формуле (1.3.5), легко усмотреть, что  зависит не только от разности
зависит не только от разности  но и от их абсолютных значений, что связано с изменением положения диаграммы направленности. В режиме обнаружения положение диаграммы направленности изменяется обычно достаточно медленно. При протяженной по углам помехе
но и от их абсолютных значений, что связано с изменением положения диаграммы направленности. В режиме обнаружения положение диаграммы направленности изменяется обычно достаточно медленно. При протяженной по углам помехе  можно рассматривать как медленную функцию
можно рассматривать как медленную функцию  которая достаточно быстро убывает с увеличением
которая достаточно быстро убывает с увеличением  В дальнейшем будем считать это предположение выполненным. При этом, как следует из
В дальнейшем будем считать это предположение выполненным. При этом, как следует из  и (1.3.13), сигнал, отраженный от протяженной пассивной помехи, можно рассматривать как квазистационарный случайный процесс. В гл. 4 будет показано, что для использования в задачах анализа и синтеза результатов, полученных для стационарной помехи, достаточно потребовать малости изменения
и (1.3.13), сигнал, отраженный от протяженной пассивной помехи, можно рассматривать как квазистационарный случайный процесс. В гл. 4 будет показано, что для использования в задачах анализа и синтеза результатов, полученных для стационарной помехи, достаточно потребовать малости изменения  на интервале разрешения по дальности.
на интервале разрешения по дальности.
В случае протяженной пассивной помехи и многочастотного излучения приведенные выше условия независимости отраженных сигналов, соответствующих различным несущим частотам, совпадают с условиями, при которых возможен раздельный прием этих сигналов (§ 1.2), и всегда выполняются. Поэтому функция корреляции отраженного сигнала в этом случае представляет собой сумму функций корреляции отдельных составляющих.
Ранее указывалось, что нормальность отраженного радиолокационного сигнала основана на представлении цели в виде совокупности большого числа случайно перемещающихся друг относительно друга «блестящих» точек. Параметры нормального случайного процессз, используемого для описания этого сигнала, зависят,
естественно, от ракурса цели, ибо с изменением ее ориентации относительно радиолокатора меняется количество и особенности тех «блестящих» точек, которые участвуют в формировании эхо-сигналов. В большинстве случаев цель (например, самолет) в течение длительного интервала времени практически не меняет своей ориентации, так что представление отраженного сигнала в виде нормального случайного процесса с фиксированными значениями параметров является исчерпывающим. В некоторых случаях цель в этом смысле не стабилизируется и участвует в сложных вращательных движениях (например, искусственные спутники Земли). При этом отраженный сигнал для каждой ориентации цели можно по-прежнему рассматривать как нормальный, но сама ориентация цели является случайной.
Обычно вращательные движения цели достаточно медленны, и в ряде случаев за интересующие нас интервалы времени параметры нормального случайного процесса (эхо-сигнала) практически не меняются, хотя и остаются неопределенными. В связи с этим при расчете характеристик радиолокационных систем, работающих по таким баллистическим целям, можно по-прежнему пользоваться идеализацией отраженного сигнала в виде нормального случайного процесса, усредняя затем вычисленные характеристики радиолокатора с учетом вероятности различных ориентации цели. При этом усреднении, если вид функции корреляции эхо-сигнала практически не зависит от ориентации цели, достаточно ограничиться такими ее характеристиками, как вероятности различных величин эффективной отражающей поверхности, которая определяет интенсивность отраженного сигнала.
Проведенное выше рассмотрение характеристик отраженного радиолокационного сигнала связано с теми его изменениями, которые обусловлены процессом отражения от цели. При некогерентном импульсном сигнале имеются еще дополнительные случайные изменения эхо-сигнала, связанные со «скачками» начальной фазы высокочастотного заполнения соседних импульсов зондирующего сигнала. В связи с этим распределение вероятностей для некогерентного эхо-сигнала, учитывающее его изменения от импульса к импульсу, не является
нормальным. Подробнее этот вопрос будет рассмотрен в главах, посвященных расчету характеристик некогерентных радиолокационные систем.
Оглавление
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. СИГНАЛЫ И ПОМЕХИ В РАДИОЛОКАЦИИ
- § 1.2. ЗОНДИРУЮЩИЙ РАДИОЛОКАЦИОННЫЙ СИГНАЛ
- 1.2.2. Функция автокорреляции зондирующего сигнала
- 1.2.3. Частотная модуляция
- 1.2.4. Фазокодовая манипуляция
- 1.2.5. Импульсная модуляция
- 1.2.6. Случайная модуляция
- 1.2.7. Многочастотный сигнал
- § 1.3. ОТРАЖЕННЫЙ РАДИОЛОКАЦИОННЫЙ СИГНАЛ
- § 1.4. ПРИНЯТЫЙ РАДИОЛОКАЦИОННЫЙ СИГНАЛ
- § 1.5. ПОМЕХИ В РАДИОЛОКАЦИИ
- § 1.6. ЗАКЛЮЧЕНИЕ
- ГЛАВА ВТОРАЯ. ВОЗДЕЙСТВИЕ СИГНАЛОВ И ПОМЕХ НА ЭЛЕМЕНТЫ РАДИОПРИЕМНОГО УСТРОЙСТВА
- § 2.2. ШУМЫ В ПРИЕМНИКЕ. КОЭФФИЦИЕНТ ШУМА И ЭФФЕКТИВНАЯ ШУМОВАЯ ТЕМПЕРАТУРА ПРИЕМНОГО УСТРОЙСТВА
- § 2.3. ПРОХОЖДЕНИЕ СИГНАЛА И ПОМЕХ ЧЕРЕЗ УСИЛИТЕЛЬ ПРОМЕЖУТОЧНОЙ ЧАСТОТЫ
- § 2.4. ДЕТЕКТИРОВАНИЕ ШУМА СОВМЕСТНО С ПОЛЕЗНЫМ СИГНАЛОМ
- 2.4.2. Характеристики шума на выходе квадратичного детектора
- 2.4.3. Воздействие шума совместно с сигналом на квадратичный детектор
- § 2.5. О ПРОХОЖДЕНИИ СИГНАЛА И ПОМЕХ ЧЕРЕЗ ВИДЕОУСИЛИТЕЛЬ И УСИЛИТЕЛЬ НИЗКИХ ЧАСТОТ
- § 2.6. ХАРАКТЕРИСТИКИ НАПРЯЖЕНИЙ НА ВЫХОДАХ ФАЗОВОГО И ИМПУЛЬСНОГО ДЕТЕКТОРОВ
- § 2.7. ВОЗДЕЙСТВИЕ СИГНАЛОВ И ПОМЕХ НА ПРИЕМНОЕ УСТРОЙСТВО С АВТОМАТИЧЕСКОЙ РЕГУЛИРОВКОЙ УСИЛЕНИЯ
- 2.7.2. Воздействие сигнала, флюктуирующего по амплитуде и модулированного по синусоидальному закону, на приемное устройство с АРУ
- 2.7.3. Характеристики флюктуаций сигнала на выходе приемного устройства с квадратичным детектором и системой АРУ
- 2.7.4. Воздействие флюктуирующего сигнала на двухпетлевую систему АРУ
- 2.7.5. Воздействие хаотической импульсной помехи
- 2.7.6. Воздействие прерывистой помехи
- § 2.8. ЗАКЛЮЧЕНИЕ
- ГЛАВА ТРЕТЬЯ. ОБЩИЕ ВОПРОСЫ ТЕОРИИ ОБНАРУЖЕНИЯ
- § 3.2. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
- § 3.3. ДВУАЛЬТЕРНАТИВНЫЕ РЕШЕНИЯ
- § 3.4. СРАВНЕНИЕ «ОБНАРУЖЕНИЯ НА ИНТЕРВАЛЕ» С «ОБНАРУЖЕНИЕМ ПО ТОЧКАМ»
- § 3.5. ДВУАЛЬТЕРНАТИВНЫЕ РЕШЕНИЯ С ИСПОЛЬЗОВАНИЕМ ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА
- § 3.6. МНОГОАЛЬТЕРНАТИВНЫЕ РЕШЕНИЯ. ОБНАРУЖЕНИЕ ЦЕЛИ С ОДНОВРЕМЕННОЙ ОЦЕНКОЙ ЕЕ ПАРАМЕТРОВ
- § 3.7. ДОСТАТОЧНЫЕ СТАТИСТИКИ. ПРИНЦИП ОБРАТНОЙ ВЕРОЯТНОСТИ
- § 3.8. ОПТИМИЗАЦИЯ ОБЗОРА ПРОСТРАНСТВА
- § 3.9. ОПТИМИЗАЦИЯ ПОИСКА ЦЕЛИ
- § 3.10. ЗАКЛЮЧЕНИЕ
- ГЛАВА ЧЕТВЕРТАЯ. ОБНАРУЖЕНИЕ КОГЕРЕНТНОГО СИГНАЛА
- § 4.2. ОТНОШЕНИЕ ПРАВДОПОДОБИЯ И ЕГО СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДЛЯ ГАУССОВЫХ СИГНАЛА И ПОМЕХИ
- § 4.3. ОПТИМАЛЬНОЕ ОБНАРУЖЕНИЕ СИГНАЛА В ШУМЕ
- 4.3.2. Случай быстрых флюктуаций
- 4.3.3. Случай медленных флюктуаций
- 4.3.4. Оптимальная обработка при произвольном …
- § 4.4. ХАРАКТЕРИСТИКИ ОБНАРУЖЕНИЯ СИГНАЛА НА ФОНЕ ШУМА
- 4.4.2. Случай медленных флкжтуаций. Зависимость порогового сигнала от ширины спектра флкжтуаций
- 4.4.3. Зависимость порогового отношения сигнал/шум от закона модуляции опорного сигнала и характеристики укорачивающего фильтра
- 4.4.4. Зависимость порогового отношения сигнал/шум от ширины полосы пропускания фильтра
- § 4.5. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ ОБНАРУЖЕНИЙ
- § 4.6. ОБНАРУЖЕНИЕ ЦЕЛИ ПРИ МНОГОЧАСТОТНОМ ИЗЛУЧЕНИИ
- § 4.7. НЕКОТОРЫЕ ВОПРОСЫ ОПТИМИЗАЦИИ ОБЗОРА И ПОИСКА
- § 4.8. ОБНАРУЖЕНИЕ ОДНОГО ВИДА СИГНАЛОВ С НЕГАУССОВЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ
- § 4.9. ОПТИМАЛЬНОЕ ОБНАРУЖЕНИЕ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ ПРИ НАЛИЧИИ ПАССИВНЫХ ПОМЕХ
- 4.9.2. Случай дискретной помехи
- 4.9.3. Случай протяженной помехи
- § 4.10. ХАРАКТЕРИСТИКИ ОБНАРУЖЕНИЯ ЦЕЛИ НА ФОНЕ ПАССИВНЫХ ПОМЕХ
- 4.10.2. Зависимость качества обнаружения от закона модуляции опорного сигнала
- 4.10.3. Выбор закона модуляции зондирующего сигнала с точки зрения помехоустойчивости по отношению к пассивным помехам
- 4.10.4. К вопросу о выборе разрешающей способности по дальности
- § 4.11. РАЗДЕЛЬНАЯ ОБРАБОТКА ПЕРИОДОВ ПРИНЯТОГО СИГНАЛА ПРИ НАЛИЧИИ ПАССИВНЫХ ПОМЕХ
- 4.11.2. Характеристики обнаружения при оптимальной междупериодной обработке
- 4.11.3. Эффективность системы череспериодиой компенсации (ЧПК) с внутренней когерентностью
- 4.11.4. Эффективность системы ЧПК с внешней когерентностью
- 4.11.5. Проблема слепых скоростей. Вобуляция периода повторения
- 4.11.6. Проблема слепых скоростей. Использование нескольких частотных каналов
- § 4.12. ВОЗДЕЙСТВИЕ АКТИВНЫХ ПОМЕХ НА СИСТЕМЫ ОБНАРУЖЕНИЯ КОГЕРЕНТНОГО СИГНАЛА
- 4.12.2. Помеха — стационарный случайный процесс
- 4.12.3. Ретрансляционная помеха
- § 4.13. ЗАКЛЮЧЕНИЕ
- ГЛАВА ПЯТАЯ. ОБНАРУЖЕНИЕ НЕКОГЕРЕНТНОГО ИМПУЛЬСНОГО СИГНАЛА
- § 5.2. ОТНОШЕНИЕ ПРАВДОПОДОБИЯ ДЛЯ НЕКОГЕРЕНТНОГО СИГНАЛА
- § 5.3. ХАРАКТЕРИСТИКИ СИСТЕМЫ С СУММИРОВАНИЕМ КВАДРАТОВ ОГИБАЮЩИХ
- § 5.4. ЭФФЕКТИВНОСТЬ ИСПОЛЬЗОВАНИЯ НЕСКОЛЬКИХ ЧАСТОТНЫХ КАНАЛОВ И НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ЦИКЛОВ ОБЗОРА
- § 5.5. ВИЗУАЛЬНОЕ ОБНАРУЖЕНИЕ
- § 5.6. ВОЗДЕЙСТВИЕ АКТИВНЫХ ПОМЕХ НА СИСТЕМУ С НАКОПЛЕНИЕМ КВАДРАТОВ ОГИБАЮЩИХ
- § 5.7. СИСТЕМА С ИНТЕГРИРОВАНИЕМ РАЗВЕРТКИ ПО ДАЛЬНОСТИ
- § 5.8. СИСТЕМА ОБНАРУЖЕНИЯ С ДВОИЧНЫМ НАКОПЛЕНИЕМ СИГНАЛА
- § 5.9. ЗАКЛЮЧЕНИЕ

Принцип действия НРЛС с использованием эффекта Доплера состоит в том, что при относительном движении НРЛС и объекта частота принимаемых отраженных сигналов не остается постоянной, а изменяется по определенному закону. Это свойство было открыто в 1842 г. австрийским физиком X. Доплером [10].
Явление эффекта Доплера можно объяснить без использования специальной теории относительности на основе простейших соотношений кинематики. На рис.9.1 изображен
зондирующий радиоимпульс длительностью τи , начало излучения которого происходит в момент t = 0.
Рис.9.1.
Он достигает цель, находящейся в момент излучения сигнала на расстоянии Do , в момент tз / 2 (пересечение графиков пройденного расстояния от времени для излученного радиоимпульса
|
D = ct |
и для |
цели |
D = Do + vpt , |
где |
vp – радиальная скорость |
||||||||||||||
|
движения облучаемой цели) и возвращается в момент времени |
tз . |
||||||||||||||||||
|
Срез (тыл) импульса возвращается в момент времени |
tз + τ‘и , |
где |
|||||||||||||||||
|
τ‘и τи |
(для этого случая, |
когда |
vp 0 ). |
Как видно из приведенного |
|||||||||||||||
|
рисунка, |
= 2с−1 (D + v t |
/ 2); |
|||||||||||||||||
|
t |
з |
з |
|||||||||||||||||
|
o |
p |
)+ v |
(t |
)/ 2]. |
|||||||||||||||
|
t |
з |
+ τ‘ |
− τ |
и |
= 2с−1 [(D + v |
τ |
и |
p |
з |
+ τ‘ − τ |
и |
||||||||
|
и |
o |
p |
и |
|
Отсюда |
τ‘и = τи (1+ vp / c)/(1− vp / c), |
то есть изменяется временной масштаб – импульс расширяется при vp 0 (удаление) и сужается при vp 0 (сближение).
Точно также преобразуется период следования импульсов и период вторичных колебаний:
|
T ‘ |
=T |
(1+ v |
p |
/ c)/(1− v |
p |
/ c) |
и T |
=T |
(1+ v |
p |
/ c)/(1− v |
p |
/ c), откуда |
|
п |
п |
o |
c |
можно найти частоту отраженного сигнала: fo =1/ To .
Так как практически vp с, то разложение в ряд Маклорена
дает
fo = fc (1− 2vp / c + 2vp2 / c −…),
где fc – частота излучаемого радиосигнала.
Пренебрегая членами второго порядка малости и выше, получим
Существует два равноправных и взаимосвязанных определения эффекта Доплера в радиолокации [10]:
1. Эффект Доплера заключается в изменении фазы отраженного сигнала в соответствии с изменением расстояния до цели.
2. Эффект Доплера состоит в изменении частоты отраженных колебаний в соответствии со скоростью движения цели. Величина изменения частоты зависит от скорости и направления относительного перемещения РЛС и объекта, а также от длины волны (частоты) радиолокационной станции.
В НРЛС с использованием эффекта Доплера (ДРЛС) передатчик излучает зондирующие сигналы в виде непрерывных
немодулированных колебаний частотой fс. Частота fо сигналов, отраженных от объекта и попадающих в приемную антенну РЛС, будет отличаться от частоты fс зондирующих сигналов на величину
|
так называемой доплеровской частоты FD , то есть: |
|
|
fo = fc ± FD . |
(56) |
Знак плюс соответствует сближению РЛС и объекта, а минус — удалению.
Ослабленные зондирующие сигналы и принимаемые отраженные сигналы, поступая на вход приемника, создают биения с

разностной частотой fc ± fo и после детектирования на выходе приемника получаются колебания доплеровской частоты, которая
|
равна |
F = |
f |
c |
± f |
o |
= |
2 |
vp |
, |
(57) |
|||
|
D |
λ |
||||||||||||
где vp — радиальная составляющая скорости перемещения объекта;
λ — длина волны зондирующих сигналов ДРЛС.
Если выразить длину волны в сантиметрах, а радиальную скорость объекта — в км/ч, то расчетная формула доплеровской частоты в герцах примет вид: [11]
|
F = 55,6 |
2 |
vp |
. |
|
D |
λ |
||
Зависимость доплеровской частоты объекта (цели), находящегося в охарактеризована диаграммой в представленной на рис.9.2 [11].
от направления движения точке О, может быть полярных координатах,
Рис.9.2.
В этой диаграмме радиус-вектор характеризует направление движения объекта, а длина вектора — значение доплеровской частоты с учетом знака. Увеличение доплеровской частоты отмечено на диаграмме знаком плюс, а уменьшение — знаком минус.
Эффект Доплера вызывает смещение частотного спектра отраженного сигнала, который можно иллюстрировать графиками
(рис.9.3).
Если допустить, что зондирующий и отраженный сигналы представляют собой синусоидальное колебание бесконечной длительности, то частотный спектр характеризуется одной спектральной линией.

Рис.9.3.
Приближение и удаление объекта относительно РЛС вызывает соответствующий сдвиг частоты отраженных сигналов от
fomin = fc − FD до fomax = fc + FD . Следовательно, спектральные линии будут перемещаться по оси частоты f, как показано на рис.9.3.
В связи с тем, что отраженный сигнал практически представляет собой синусоидальное колебание конечной длительности, а также из-за флюктуации эффективной поверхности отражения (ЭПО) объектов, сканирования луча антенны и ускорения объектов спектр отраженного сигнала будет несколько шире (отмечено штрихами).
Доплеровские РЛС с непрерывным излучением сигналов широко используются для измерения путевой скорости самолетов, скорости ветра, скорости автомобильного транспорта и пр.
Доплеровские РЛС могут использовать в судовождении для измерения скорости причаливания судов. Это объясняется тем, что появление крупнотоннажных судов, в частности танкеров водоизмещением 150—200 тыс. т и более, вызвало необходимость принятия мер, предотвращающих повреждения при швартовке таких судов к причалу.
Оснащение судов подруливающими устройствами, использование швартовных буксиров и тому подобные меры не решают проблемы полностью. При швартовке судоводитель должен иметь исчерпывающую информацию о положении судна относительно причала и его скорости. Применяемые до настоящего времени визуальные методы определения скорости судна и расстояния до причала по береговым предметам при швартовке крупнотоннажных судов становятся непригодными. Многие из существующих причалов не могут выдержать соприкосновения с ними судна водоизмещением 150—200 тыс.т, если его скорость превышает 3—5 м/мин. Следовательно, возникает необходимость в точном измерении скорости судна, достигающей 0,5…1 м/мин [11].

Структурная схема доплеровской РЛС показана на рис. 9.4. Она содержит: генератор непрерывных немодулированных
колебаний сверхвысокой частоты fс (ГСВЧ), развязывающее устройство РУ, направленную антенну А, смеситель См, усилитель доплеровской частоты УДЧ и индикатор. Зондирующие колебания
сверхвысокой частоты fс через развязывающее устройство попадают в антенну. После ослабления в развязывающем устройстве, подаются на вход смесителя приемника.
Отраженные сигналы с частотой fo = fc ± FD поступают на вход смесителя и смешиваются с частотой зондирующих сигналов fс.
Рис.9.4. Структурная схема доплеровской РЛС
Возникающие биения разностной частоты создают на выходе смесителя доплеровскую частоту FD, усиливаемую каскадами УДЧ.
Индикатором служит устройство, измеряющее доплеровскую частоту. Поскольку радиальная скорость объекта vp и доплеровская
|
частота связаны между собой линейной зависимостью v |
= F |
λ |
, |
||
|
p |
D |
2 |
то указанный индикатор — частотомер может быть отградуирован в единицах скорости (например, метрах в минуту). Практически при использовании доплеровской РЛС в качестве измерителя скорости движения объектов оказывается необходимым выяснить, в каком направлении движется объект относительно ДРЛС, то есть объект приближается или удаляется.
Эта задача выполняется несколькими способами. Например, с помощью отдельных фильтров, настроенных на частоты fo = fc − FD
Соседние файлы в предмете Радионавигационные приборы
- #
- #
- #
- #
Зона Френеля
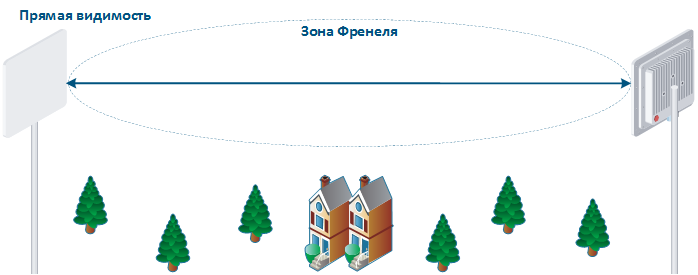
, зная который, можно определить наличие в зоне Френеля препятствий:
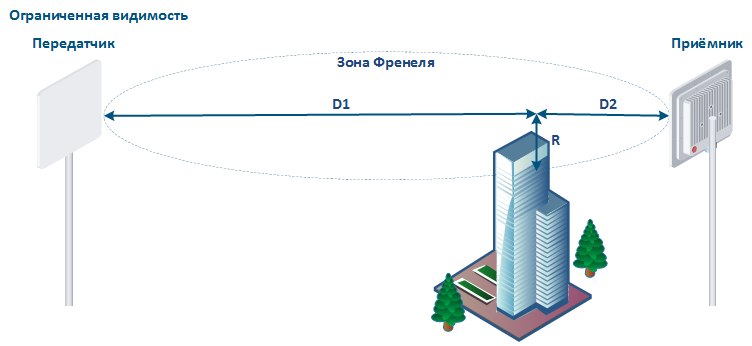
Величина радиуса зоны Френеля в произвольной точке рассчитывается по формуле:
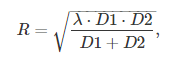
где
- D1 − расстояние от передатчика до точки измерения,
- D2 − расстояние от приёмника до точки измерения,
- R − радиус зоны Френеля,
- λ − длина волны.
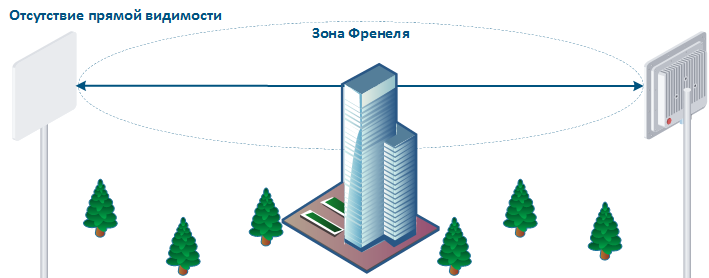
Эффекты при распространении электромагнитных волн
Затухание в свободном пространстве
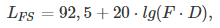
где
- D − расстояние между передатчиком и приёмником в км,
- F − частота в ГГц,
- LFS − величина затуханий в дБ.
Ключевым выводом из данной формулы является прямая зависимость между величиной затухания и частотой сигнала, т.е. чем выше частота электромагнитной волны, тем она быстрее затухает при распространении в свободном пространстве. Таким образом, при прочих равных, эксплуатация системы связи на низких частотах позволит достигнуть большей дальности, чем на высоких частотах, либо лучших энергетических показателей, при одинаковых дистанциях. Однако, как будет показано в уроке “Антенны”, использование низких частот потребует применения антенн больших габаритов.
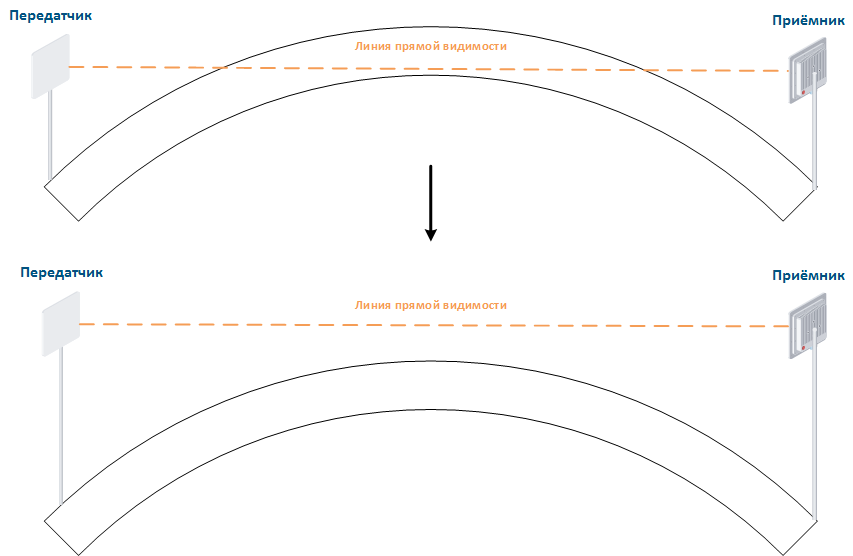
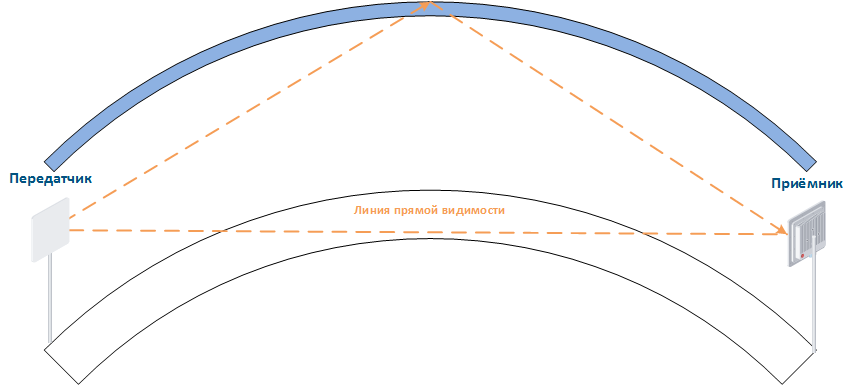
Дифракция
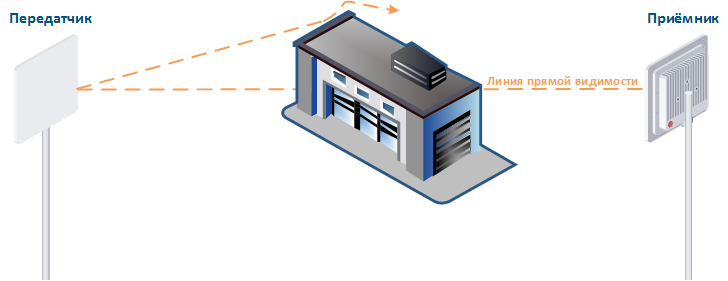
Зону Френеля между приёмником и передатчиком преграждает строение, однако радиосигнал от передатчика огибает угол здания и достигает приёмника. Следует иметь в виду, что часть энергии сигнала при дифракции будет рассеиваться в окружающую среду, что снижает дальность распространения сигнала относительно LOS.
Поглощение
Отражение
Рассеяние

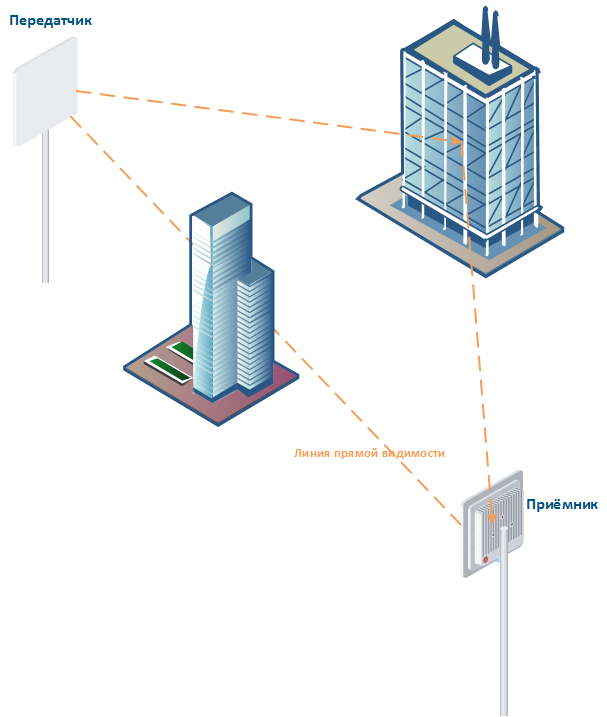
Многолучёвость
нала, пришедших по различным путям, как на рисунке 7. Данный эффект получил название многолучёвости.
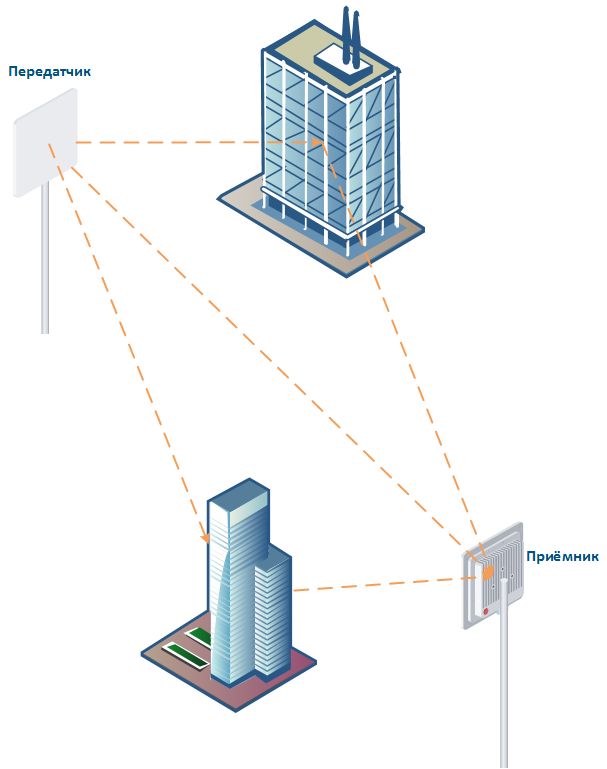
Важно понимать, что отражённый сигнал может отличаться от исходного своими параметрами: амплитуда, частота, фаза и поляризация. Кроме того, каждая из копий сигнала, полученная на приёмной стороне, прошла разный путь, затратив разное время, что отрицательно влияет на задержку сигнала. На рисунке 8 красным и зелёным цветом показаны копии сигнала на приёмной стороне, сдвинутые по фазе из-за разного времени распространения, а синим – результирующий сигнал. Так, в первом случае, рисунок 8(а), сдвиг фаз сигналов составляет 0-120 градусов и в этом случае результирующий сигнал по амплитуде превосходит каждую из принятых копий, во втором случае – 121-179 градусов, рисунок 8(б), амплитуда результирующего сигнала ниже принятых копий, а в третьем случае, рисунок 8(в), принятые копии находятся в противофазе и результирующий сигнал равен нулю.
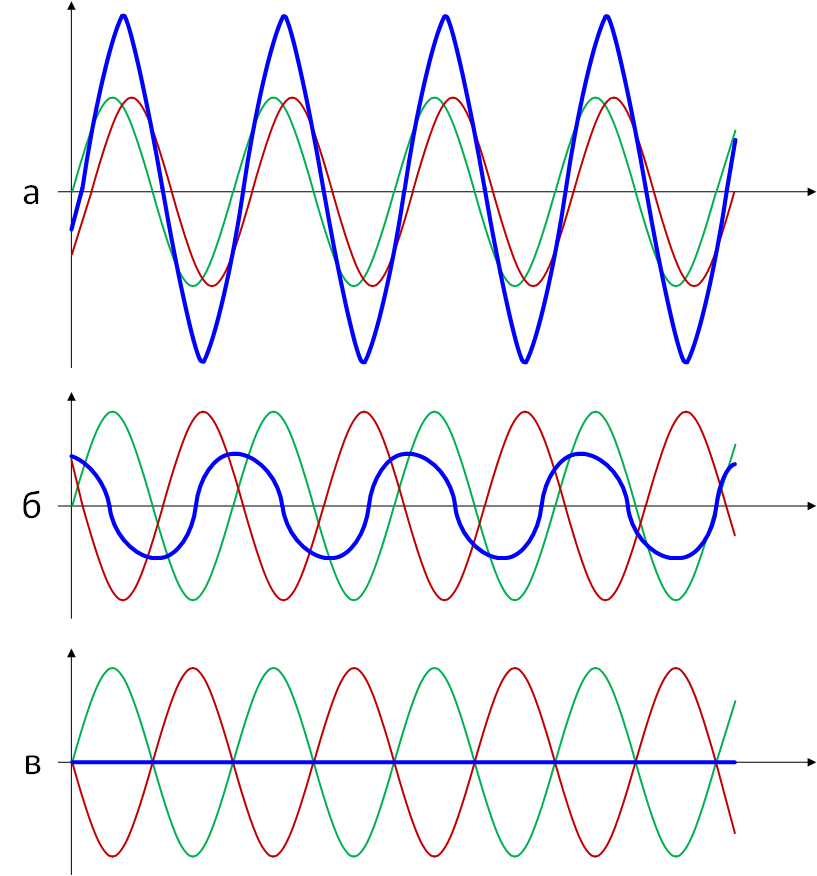
На рисунке 8 представлен результирующий сигнал при многолучевом распространении, когда на приёмной стороне присутствуют две копии сигнала. В условиях плотной застройки, чаще на приёмной стороне присутствует большее число копий сигнала, что приводит к искажениям результирующего сигнала, как показано на рисунке 9:
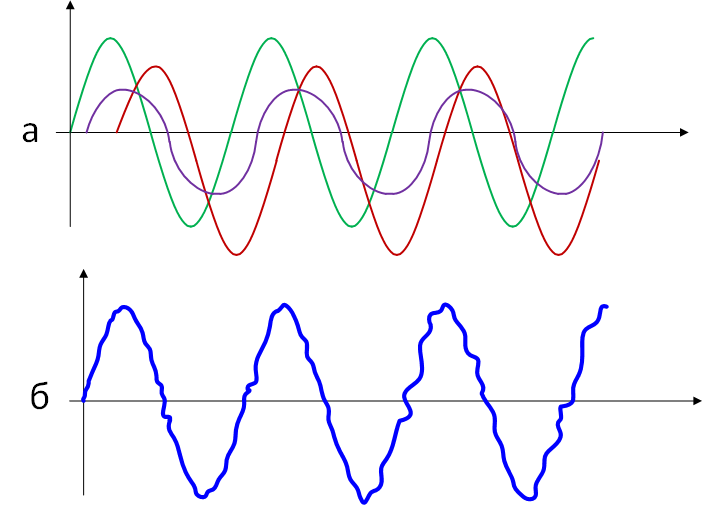
Рефракция