Как работает конденсатор и катушка в цепи переменного тока
Содержание
- 1 Особенности работы конденсатора
- 2 Формула ёмкости
- 3 Особенности электроцепи с емкостью и индуктивностью
- 4 Виды конденсаторов
- 5 Различные характеристики конденсаторов
- 6 Где используются конденсаторы
- 7 Видео по теме
Работа многих электрических схем строится на использовании конденсаторов. Основной особенностью этих радиоэлементов является то, что они хорошо проводят переменный ток, но не пропускают постоянный.
Особенности работы конденсатора
Радиодеталь представляет собой две пластины, к которым прикреплены металлические выводы. Пластины не соприкасаются между собой. Обычно между ними проложен слой изолятора. Постоянный электроток через конденсатор проходить не может, так как нет контакта между проводниками, но для переменного он не является препятствием.
Когда конденсатор включен в цепь переменного тока, частота напряжения меняется по закону синусоиды. Сначала электродвижущая сила растёт до своего максимума. После этого она уменьшается до нуля, а затем переходит в отрицательную область, где постепенно возрастает до амплитуды, взятой со знаком минус. Затем отрицательная ЭДС уменьшается по абсолютной величине до нуля и начинает возрастать в положительной области до наибольшего значения. Описанный цикл изменений повторяется снова и снова.
Когда конденсатор работает в цепи переменного тока, в нем циклически происходят следующие процессы:
- При возрастании амплитуды от нулевого значения до максимального происходит накопление заряда. Пластины накапливают равные по абсолютной величине, но противоположные по знаку заряды.
- При уменьшении до нуля накопление прекращается, заряд уменьшается, так как начинает стекать с пластин конденсатора.
- Когда напряжение меняется на противоположное, на пластины начинают поступать заряды, которые имеют знаки, противоположные тем, что были раньше.
- Как только ЭДС достигнет максимального отрицательного значения и станет уменьшаться по абсолютной величине, начнётся разрядка конденсатора.
Описанный здесь цикл повторится с началом возрастания ЭДС. Он будет осуществляться до тех пор, пока переменный ток не будет отключён.
Формула ёмкости
Одна из самых важных характеристик конденсатора — ёмкость. Её обозначают символом C. Несмотря на то, что контакта между пластинами нет, ток будет идти через конденсатор в цепи переменного тока то к пластинам, то от них. Это обусловлено циклически происходящими процессами зарядки и разрядки конденсатора.
Величина ёмкости характеризует способность конденсатора накапливать заряд при поступлении на обкладки определённой разности потенциалов. Ее можно найти по формуле:
Используя эту формулу наряду с законом изменения напряжения, можно узнать силу тока, возникающего в процессе зарядки или разрядки пластин конденсатора в цепи переменного тока. Но для этого необходимо сделать соответствующие преобразования.
Сначала находим напряжение, возникающее на конденсаторе в цепи переменного тока, воспользовавшись формулами для определения ёмкости и разности потенциалов. После преобразований получаем выражение:
Из него находим величину заряда:
Теперь можно получить выражение для электротока в цепи с конденсатором:
Надо сказать, что при выводе формулы для нахождения силы электрического тока были использованы следующие приемы:
- От выражения для заряда была взята производная по времени.
- Затем было выполнено эквивалентное тригонометрическое преобразование.
- Um соответствует максимальному значению амплитуды колебаний электронапряжения.
Полученное выражение позволяет узнать ток зарядки и разрядки конденсатора в любой момент. Изменения тока опережают напряжение на половину «пи». Величина тока будет максимальной при нулевом напряжении. И, наоборот, значение тока станет нулевым, когда напряжение достигнет максимума.
Для определения ёмкости может быть использована еще такая формула:
Как видно из формулы, ёмкость конденсатора увеличивается при увеличении площади пластин и уменьшении расстояния между ними.
Емкостное сопротивление — ещё одна важная характеристика конденсатора. Его можно найти по формуле:
Если взять формулу для определения амплитуды электротока:
И подставить в нее значение ХС, то получим:
После изучения данной формулы становится понятно, что емкостное и активное сопротивление из закона Ома играют одну и ту же роль. Поэтому емкостное можно считать сопротивлением конденсатора переменному электротоку.
Пример использования формул для решения простых задач по нахождению емкости конденсатора можно увидеть на изображении ниже:
Особенности электроцепи с емкостью и индуктивностью
Рассматривая ранее цепь переменного тока с включенным конденсатором, мы могли видеть, что частота колебаний электротока на конденсаторе опережает частоту колебаний электронапряжения на π/2. При включении катушки индуктивности наблюдается обратное явление, то есть, электроток отстает от электронапряжения на π/2. Его амплитуда определяется по формуле:
Знаменатель в данной формуле представляет собой выражение, используемое для определения индуктивного сопротивления:
В итоге получаем формулу для силы электротока:
Индуктивное сопротивление, как и емкостное, зависит от частоты электротока. Поэтому катушка, включенная в постоянную цепь, будет иметь нулевое индуктивное сопротивление.
Конденсатор и катушка индуктивности в цепи переменного тока образуют, так называемый, колебательный контур. Его колебания определяются по формуле:
При вынужденных колебаниях сила элетротока достигает максимума, если колебания электронапряжения и самого контура становятся равными:
Виды конденсаторов
На данный момент существует огромный выбор конденсаторов:
- Наиболее распространены радиодетали с двумя обкладками, но их может быть и больше.
- Плоский конденсатор состоит из двух пластин, между которыми расположен тонкий слой диэлектрика. Его толщина должна быть небольшой по сравнению с размерами пластин.
- В цилиндрическом конденсаторе обе пластины имеют цилиндрическую форму. Одна из них находится внутри другой. Между цилиндрами имеется равномерный тонкий промежуток, который заполнен диэлектриком.
- Существуют сферические конденсаторы, обкладки которых представляют собой сферы, одна из которых находится внутри другой.
Конденсаторы различаются в зависимости от вида диэлектрика. В частности, может использоваться не только твёрдый, но и жидкий или газообразный диэлектрик. Есть также вакуумные конденсаторы, в которых внутри между обкладками находится вакуум.
Существуют оксидно-полупроводниковые конденсаторы. Один из их электродов является анодом. Диэлектриком выступает покрывающий его оксид. Катодом является полупроводниковый слой, который наносится на слой оксида.
Для изолирующего слоя могут использоваться как органические, так и неорганические материалы. В первом случае применяются бумажные или плёночные материалы. Неорганический диэлектрик выполняется из керамики, стекла, слюды или неорганических синтетических плёнок. Есть и такие, внутри которых содержится электролитический раствор. Конденсаторы с подобным диэлектриком характеризуются относительно высокой ёмкостью.
Еще одна разновидность конденсаторов — подстроечные. Их использование предоставляет возможность изменять значение емкости в определенных пределах, чтобы деталь могла работать наиболее эффективно.
Наряду с конденсаторами общего назначения существуют и те, которые предназначены для специального применения. Примерами таких видов являются дозиметрические, высоковольтные, пусковые, импульсные, помехоподавляющие и некоторые другие радиоэлементы.
Различные характеристики конденсаторов
Основной характеристикой конденсатора является ёмкость. Но при выборе необходимо учитывать и другие.
Для каждого конденсатора существует номинальное напряжение. Если эксплуатация детали будет осуществляться исключительно при таком значении, производитель гарантирует качественную работу в течение всего срока службы.
При увеличении подаваемого на пластины напряжения заряд будет увеличиваться. Если разность потенциалов станет слишком большой, произойдёт пробой радиодетали. В результате между обкладками пройдёт искра, а сам конденсатор станет неисправной. Конденсатор в цепи переменного тока необходимо эксплуатировать в строго заданных параметрах. Иначе срок его эксплуатации существенно сокращается.
Ещё одна характеристика — удельная ёмкость. Она равна отношению ёмкости и массы используемого диэлектрика. С её повышением улучшаются характеристики, но возрастает вероятность пробоя.
В формуле для определения ёмкости используется понятие диэлектрической проницаемости диэлектрика, который находится между пластинами. Эта характеристика определяет то, насколько сильно данное вещество ослабляет влияние электрического поля между обкладками.
В диэлектриках электроны сильно привязаны к ядрам атомов, из-за чего они не перемещаются под действием электрического поля и не образуют электрический ток. Однако при воздействии электрического поля осуществляется поляризация атомов за счет смещения электронов внутри них. Следствием этого является ослабление электрического поля. Его величина зависит от того, какое вещество используется в качестве диэлектрика. Возмущение электрического поля, создаваемое диэлектриком, ослабляет то, которое было приложено к пластинам, и препятствует притоку заряда к пластинам.
Где используются конденсаторы
Радиодетали этого вида находят применение в разных сферах деятельности современного человека:
- Конденсатор и катушка индуктивности в цепи переменного тока образуют колебательный контур, его используют во многих устройствах.
- Конденсаторы меняют свои характеристики в зависимости от температуры или влажности окружающей среды, поэтому применяются в самых разных измерительных приборах.
- Еще одна сфера применения— блоки питания.
- Используются в цепях с преобразователями переменного тока в постоянный.
- Применяются в частотных фильтрах.
- Без конденсатора трудно представить усилитель.
- Конденсатор является важным элементом для процессоров и других микросхем.
Здесь приведены только некоторые варианты использования. На самом деле их гораздо больше.
Видео по теме
Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока. Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор.
Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.
Почему сразу переменного? Да просто потому, что конденсатор в цепи постоянного тока ничем не примечателен. Через него течет ток только в первый момент, пока конденсатор разряжен. Потом конденсатор заряжается и все, тока нет (да-да, слышу, уже начали кричать, что заряд конденсатора теоретически длится бесконечно долгое время, да еще у него может быть сопротивление утечки, но пока что мы этим пренебрегаем). Заряженный конденсатор для постоянного тока – это как разрыв цепи. Когда же у нас случай переменного тока – тут все намного интереснее. Оказывается, в этом случае через конденсатор может протекать ток и конденсатор в этом случае как бы эквивалентен резистору с некоторым вполне определенным сопротивлением (если пока забить забыть про всякие там сдвиги фазы, об этом ниже). Нам надо каким-нибудь образом получить связь между током и напряжением на конденсаторе.
Пока мы будем исходить из того, что в цепи переменного тока находится только конденсатор и все. Без каких-либо других компонентов типа резисторов или индуктивностей. Напомню, что в случае, когда у нас в цепи находится исключительно одни только резисторы, подобная задача решается очень просто: ток и напряжения оказываются связанными между собой через закон Ома. Мы про это уже не один раз говорили. Там все очень просто: делим напряжение на сопротивление и получаем ток. А как же быть в случае конденсатора? Ведь конденсатор-то это не резистор. Там совсем иная физика протекания процессов, поэтому вот так вот с наскока не получится просто связать между собой ток и напряжение. Тем не менее, сделать это надо, поэтому давайте попробуем порассуждать.
Сперва давайте вернемся назад. Далеко назад. Даже очень далеко. К самой-самой первой моей статье на этом сайте. Старожилы должно быть помнят, что это была статья про силу тока. Вот в этой самой статье было одно интересное выражение, которое связывало между собой силу тока и заряд, протекающий через сечение проводника. Вот это самое выражение
Кто-нибудь может возразить, что в той статье про силу тока запись была через Δq и Δt – некоторые весьма малые величины заряда и времени, за которое этот заряд проходит через сечение проводника. Однако здесь мы будем применять запись через dq и dt – через дифференциалы. Такое представление нам потребуется в дальнейшем. Если не лезть глубоко в дебри матана, то по сути dq и dt здесь особо ничем не отличаются от Δq и Δt. Безусловно, глубоко сведущие в высшей математике люди могут поспорить с этим утверждением, но да сейчас я не хочу концентрировать внимание на данных вещах.
Итак, выражение для силы тока мы вспомнили. Давайте теперь вспомним, как связаны между собой емкость конденсатора С, заряд q, который он в себе накопил, и напряжение U на конденсаторе, которое при этом образовалось. Ну, мы же помним, что если конденсатор накопил в себе какой-то заряд, то на его обкладках неизбежно возникнет напряжение. Про это все мы тоже говорили раньше, вот в этой вот статье. Нам будет нужна вот эта формула, которая как раз и связывает заряд с напряжением
Давайте-ка выразим из этой формулы заряд конденсатора:
А теперь есть очень большой соблазн подставить это выражение для заряда конденсатора в предыдущую формулу для силы тока. Приглядитесь-ка повнимательнее – у нас ведь тогда окажутся связанными между собой сила тока, емкость конденсатора и напряжение на конденсаторе! Сделаем эту подстановку без промедлений:
Емкость конденсатора у нас является величиной постоянной. Она определяется исключительно самим конденсатором, его внутренним устройством, типом диэлектрика и всем таким прочим. Про все это подробно мы говорили в одной из прошлых статей. Следовательно, емкость С конденсатора, поскольку это константа, можно смело вынести за знак дифференциала (такие вот правила работы с этими самыми дифференциалами). А вот с напряжением U нельзя так поступить! Напряжение на конденсаторе будет изменяться со временем. Почему это происходит? Ответ элементарный: по мере протекания тока на обкладках конденсатора, очевидно, заряд будет изменяться. А изменение заряда непременно приведет к изменению напряжения на конденсаторе. Поэтому напряжение можно рассматривать как некоторую функцию времени и его нельзя выносить из-под дифференциала. Итак, проведя оговоренные выше преобразования, получаем вот такую вот запись:
Господа, спешу вас поздравить – только что мы получили полезнейшее выражение, которое связывает между собой напряжение, приложенное к конденсатору, и ток, который течет через него. Таким образом, если мы знаем закон изменения напряжения, мы легко сможем найти закон изменения тока через конденсатор путем простого нахождения производной.
А как быть в обратном случае? Допустим, нам известен закон изменения тока через конденсатор и мы хотим найти закон изменения напряжения на нем. Читатели, сведущие в математике, наверняка уже догадались, что для решения этой задачи достаточно просто проинтегрировать написанное выше выражение. То есть, результат будет выглядеть как-то так:
По сути оба этих выражений про одно и тоже. Просто первое применяется в случае, когда нам известен закон изменения напряжения на конденсаторе и мы хотим найти закон изменения тока через него, а второе – когда нам известно, каким образом меняется ток через конденсатор и мы хотим найти закон изменения напряжения. Для лучшего запоминания всего этого дела, господа, я приготовил для вас поясняющую картинку. Она изображена на рисунке 1.
Рисунок 1 – Поясняющая картинка
На ней, по сути, в сжатой форме изображены выводы, которые хорошо бы запомнить.
Господа, обратите внимание – полученные выражения справедливы для любого закона изменения тока и напряжения. Здесь не обязательно должен быть синус, косинус, меандр или что-то другое. Если у вас есть какой-то совершенно произвольный, пусть даже совершенно дикий, не описанный ни в какой литературе, закон изменения напряжения U(t), поданного на конденсатор, вы, путем его дифференцирования можете определить закон изменения тока через конденсатор. И аналогично если вы знаете закон изменения тока через конденсатор I(t) то, найдя интеграл, сможете найти, каким же образом будет меняться напряжение.
Итак, мы выяснили как связать между собой ток и напряжение для абсолютно любых, даже самых безумных вариантов их изменения. Но не менее интересны и некоторые частные случаи. Например, случай успевшего уже нам всем полюбиться синусоидального тока. Давайте теперь разбираться с ним.
Пусть напряжение на конденсаторе емкостью C изменяется по закону синуса вот таким вот образом
Какая физическая величина стоит за каждой буковкой в этом выражении мы подробно разбирали чуть раньше. Как же в таком случае будет меняться ток? Используя уже полученные знания, давайте просто тупо подставим это выражение в нашу общую формулу и найдем производную
Или можно записать вот так
Господа, хочу вам напомнить, что синус ведь только тем и отличается от косинуса, что один сдвинут относительно другого по фазе на 90 градусов. Ну, или, если выражаться на языке математики, то . Не понятно, откуда взялось это выражение? Погуглите формулы приведения

Господа, отмечу сразу один момент. В своих статьях я не буду рассказывать про правила нахождения производных и взятия интегралов. Надеюсь, хотя бы общее понимание этих моментов у вас есть. Однако даже если вы не знаете, как это делать, я буду стараться излагать материал таким образом, чтобы суть вещей была понятна и без этих промежуточных выкладок. Итак, сейчас мы получили немаловажный вывод – если напряжение на конденсаторе изменяется по закону синуса, то ток через него будет изменяться по закону косинуса. То есть ток и напряжение на конденсаторе сдвинуты друг относительно друга по фазе на 90 градусов. Кроме того, мы можем относительно легко найти и амплитудное значение тока (это множители, которые стоят перед синусом). Ну то есть тот пик, тот максимум, которого ток достигает. Как видим, оно зависит от емкости C конденсатора, амплитуды приложенного к нему напряжения Um и частоты ω. То есть чем больше приложенное напряжение, чем больше емкость конденсатора и чем больше частота изменения напряжения, тем большей амплитуды достигает ток через конденсатор. Давайте построим график, изобразив на одном поле ток через конденсатор и напряжение на конденсаторе. Пока без конкретных цифр, просто покажем качественный характер. Этот график представлен на рисунке 2 (картинка кликабельна).
Рисунок 2 – Ток через конденсатор и напряжение на конденсаторе
На рисунке 2 синий график – это синусоидальный ток через конденсатор, а красный – синусоидальное напряжение на конденсаторе. По этому рисунку как раз очень хорошо видно, что ток опережает напряжение (пики синусоиды тока находятся левее соответствующих пиков синусоиды напряжения, то есть наступают раньше).
Давайте теперь проделаем работу наоборот. Пусть нам известен закон изменения тока I(t) через конденсатор емкостью C. И закон этот пусть тоже будет синусоидальным
Давайте определим, как в таком случае будет меняться напряжение на конденсаторе. Воспользуемся нашей общей формулой с интегральчиком:
По абсолютнейшей аналогии с уже написанными выкладками, напряжение можно представить вот таким вот образом
Здесь мы снова воспользовались интересными сведениями из тригонометрии, что . И снова формулы приведения придут вам на помощь, если не понятно, почему получилось именно так.
Какой же вывод мы можем сделать из данных расчетов? А вывод все тот же самый, какой уже был сделан: ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга на 90 градусов. Более того, они не просто так сдвинуты. Ток опережает напряжение. Почему это так? Какая за этим стоит физика процесса? Давайте разберемся.
Представим, что незаряженный конденсатор мы подсоединили к источнику напряжения. В первый момент никаких зарядов в конденсаторе вообще нет: он же разряжен. А раз нет зарядов, то нет и напряжения. Зато ток есть, он возникает сразу при подсоединении конденсатора к источнику. Замечаете, господа? Напряжения еще нет (оно не успело нарасти), а ток уже есть. И кроме того, в этот самый момент подключения ток в цепи максимален (разряженный конденсатор ведь по сути эквивалентен короткому замыканию цепи). Вот вам и отставание напряжения от тока. По мере протекания тока, на обкладках конденсатора начинает накапливаться заряд, то есть напряжение начинает расти а ток постепенно уменьшаться. И через некоторое время накопится столько заряда на обкладках, что напряжение на конденсаторе сравняется с напряжением источника и ток в цепи совсем прекратится.
Теперь давайте этот самый заряженный конденсатор отцепим от источника и закоротим накоротко. Что получим? А практически то же самое. В самый первый момент ток будет максимален, а напряжение на конденсаторе останется таким же, какое оно и было без изменений. То есть снова ток впереди, а напряжение изменяется вслед за ним. По мере протекания тока напряжение начнет постепенно уменьшаться и когда ток совсем прекратится, оно тоже станет равным нулю.
Для лучшего понимания физики протекающих процессов можно в который раз уже использовать водопроводную аналогию. Представим себе, что заряженный конденсатор – это некоторый бачок, полный воды. У этого бачка есть внизу краник, через который можно спустить воду. Давайте этот краник откроем. Как только мы его откроем, вода потечет сразу же. А давление в бачке будет падать постепенно, по мере того, как вода будет вытекать. То есть, грубо говоря, ручеек воды из краника опережает изменение давления, подобно тому, как ток в конденсаторе опережает изменение напряжения на нем.
Подобные рассуждения можно провести и для синусоидального сигнала, когда ток и напряжения меняются по закону синуса, да и вообще для любого. Суть, надеюсь, понятна.
Давайте проведем небольшой практический расчет переменного тока через конденсатор и построим графики.
Пусть у нас имеется источник синусоидального напряжения, действующее значение равно 220 В, а частота 50 Гц. Ну, то есть все ровно так же, как у нас в розетках. К этому напряжению подключают конденсатор емкостью 1 мкФ. Например, пленочный конденсатор К73-17, рассчитанный на максимальное напряжение 400 В (а на меньшее напряжение конденсаторы ни в коем случае нельзя подключать в сети 220 В), выпускается с емкостью 1 мкФ. Чтобы вы имели представление, с чем мы имеем дело, на рисунке 3 я разместил фотографию этого зверька (спасибо Diamond за фото 
Рисунок 3 – Ищем ток через этот конденсатор
Требуется определить, какая амплитуда тока будет протекать через этот конденсатор и построить графики тока и напряжения.
Сперва нам надо записать закон изменения напряжения в розетке. Если вы помните, амплитудное значение напряжения в этом случае равно около 311 В. Почему это так, откуда получилось, и как записать закон изменения напряжения в розетке, можно прочитать вот в этой статье. Мы же сразу приведем результат. Итак, напряжение в розетке будет изменяться по закону
Теперь мы можем воспользоваться полученной ранее формулой, которая свяжет напряжение в розетке с током через конденсатор. Выглядеть результат будет так
Мы просто подставили в общую формулу емкость конденсатора, заданную в условии, амплитудное значение напряжения и круговую частоту напряжения сети. В результате после перемножения всех множителей имеем вот такой вот закон изменения тока
Вот так вот, господа. Получается, что амплитудное значение тока через конденсатор чуть меньше 100 мА. Много это или мало? Вопрос нельзя назвать корректным. По меркам промышленной техники, где фигурируют сотни ампер тока, очень мало. Да и для бытовых приборов, где десятки ампер не редкость – тоже. Однако для человека даже такой ток представляет большую опасность! Отсюда следует вывод, что хвататься за такой конденсатор, подключенный к сети 220 В не следует 
Все это хорошо, но мы чуть не забыли про графики, которые должны построить. Надо срочно исправляться! Итак, они представлены на рисунке 4 и рисунке 5. На рисунке 4 вы можете наблюдать график напряжения в розетке, а на рисунке 5 – закон изменения тока через конденсатор, включенный в такую розетку.
Рисунок 4 – График напряжения в розетке
Рисунок 5 – График тока через конденсатор
Как мы можем видеть из этих рисунков, ток и напряжение сдвинуты на 90 градусов, как и должно быть. И, возможно, у читателя возникла мысль – если через конденсатор течет ток и на нем падает какое-то напряжение, вероятно, на нем должна выделяться и некоторая мощность. Однако спешу предупредить вас – для конденсатора дело обстоит совершенно не так. Если рассматривать идеальный конденсатор, то мощность на нем не будет вообще выделяться, даже при протекании тока и падении на нем напряжения. Почему? Как же так? Об этом – в будущих статьях. А на сегодня все. Спасибо что читали, удачи, и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Содержание
- – Как найти частоту емкостного реактивного сопротивления?
- – Как найти частоту RC-цепи?
- – Почему на высокой частоте конденсатор короче?
- – Как вы рассчитываете частоту и сопротивление?
- – Как найти резонансную частоту?
- – Что происходит с емкостным реактивным сопротивлением при увеличении рабочей частоты?
- – Что такое единица измерения XC?
- – Какая формула конденсатора?
- – Что такое частота 3 дБ?
Частота f в герцах равна 1, деленному на 2, умноженное на π, умноженное на сопротивление R в омах, умноженное на емкость C в фарадах.
Как найти частоту емкостного реактивного сопротивления?
Емкостное реактивное сопротивление, обозначаемое как x sub c (XC), равняется постоянному одному миллиону (или 106), деленному на произведение 2п (или 6,28) умножить частоту на емкость . где: XC = Емкостное реактивное сопротивление, измеренное в Ом. f = – частота переменного тока в герцах.
Как найти частоту RC-цепи?
Как рассчитать частоту RC-цепи?
- Сначала измерьте сопротивление. Измерьте сопротивление резистора.
- Затем измерьте емкость. Измерьте емкость конденсатора.
- Наконец, рассчитайте частоту. Используйте приведенное выше уравнение для расчета частоты.
Почему на высокой частоте конденсатор короче?
На высоких частотах емкостное сопротивление конденсатора становится очень маленьким, почти приближается к нулю и конденсатор ведет себя как провод. Итак, это действует как короткое замыкание.
Как вы рассчитываете частоту и сопротивление?
Рассчитайте сопротивление по новому значению импеданса, 144 Ом. Поскольку нагрузка нереактивна, сопротивление R в Ом = Х = 144 Ом на более высокой частоте. Вычислите новое значение мощности в ваттах на более высокой частоте, решив I = V / X, = 240 вольт / 144 Ом = 1,667 ампер.
Как найти резонансную частоту?
Использовать формула v = λf найти резонансную частоту одиночной непрерывной волны. Буква «v» обозначает скорость волны, а «λ» – расстояние до длины волны. Эта формула утверждает, что скорость волны равна расстоянию длины волны, умноженному на резонансную частоту.
Что происходит с емкостным реактивным сопротивлением при увеличении рабочей частоты?
Емкостное сопротивление конденсатора уменьшается по мере увеличения частоты на нем емкостное реактивное сопротивление обратно пропорционально частоте. … Кроме того, по мере увеличения частоты ток, протекающий через конденсатор, увеличивается в значении, потому что скорость изменения напряжения на его пластинах увеличивается.
Что такое единица измерения XC?
Единица емкостного реактивного сопротивления Xc является Ом. Емкостное реактивное сопротивление определяется как мера сопротивления конденсатора переменному току. Оно сложнее, чем сопротивление, поскольку значение зависит от частоты сигнала, проходящего через конденсатор.
Какая формула конденсатора?
Основное уравнение для конструкции конденсатора: C = εA / d, В этом уравнении C – емкость; ε – диэлектрическая проницаемость, термин, обозначающий, насколько хорошо диэлектрический материал сохраняет электрическое поле; А – площадь параллельной пластины; и d – расстояние между двумя проводящими пластинами.
Что такое частота 3 дБ?
Точка 3 дБ или частота 3 дБ точка, в которой сигнал был ослаблен на 3 дБ (в полосовом фильтре). Обычно это считается точкой для определения полосы пропускания фильтра. Полоса пропускания определяется как разница между верхней и нижней точками 3 дБ.
Интересные материалы:
Что значит бездельничать в отношениях?
Что значит Бивис?
Что значит Bluetooth?
Что значит бодаться?
Что значит бойня?
Что значит Боттон?
Что значит братан?
Что значит Браво?
Что значит Брэггест?
Что значит бродить по улицам?
Для школьников.
Кроме активного сопротивления, в цепях переменного тока возможно существование емкостного и индуктивного сопротивлений. Про индуктивное сопротивление будет говориться в следующей статье, а сейчас речь пойдёт об емкостном сопротивлении.
Рассмотрим опыты, позволяющие увидеть существование емкостного сопротивления.
Две маленькие одинаковые электрические лампочки подключались к источникам одинакового напряжения. Но одна (правая) подключалась к источнику постоянного тока (аккумуляторной батарее), а другая (левая) – к источнику переменного тока.
Лампочки светили одинаково, так как количество выделяющегося тепла не зависит от того, какой ток протекает по нитям лампочек (постоянный или переменный).
Подсоединение в цепи конденсаторов большой ёмкости (рис. б) показало, что лампочка, включенная в цепь переменного тока, светила также ярко, а лампочка, включенная в цепь постоянного тока, не светила совсем.
При постоянном источнике тока результат понятен – конденсатор разрывает электрическую цепь, его сопротивление постоянному току бесконечно велико.
Но что происходит, когда цепь, состоящая из лампочки и конденсатора подсоединена к источнику переменного тока, почему лампочка при этом светит или почему конденсатор не препятствует прохождению по цепи переменного тока?
Опыты показывают, что конденсатор пропускает переменный ток, но оказывает ему сопротивление. Это сопротивление назвали емкостным сопротивлением).
Существование емкостного сопротивления обнаружено, например, при проведении следующего опыта.
Конденсатор ёмкостью 10 мкФ, с последовательно соединённым с ним амперметром, включали в городскую осветительную сеть переменного тока с частотой 50 Гц и напряжением 220 В.
Амперметр показал ток 0,69 А. Подсчитали сопротивление конденсатора переменному току, разделив напряжение 220 В на показание амперметра.
Оно оказалось равным 319 Ом.
Расчёт и опыт показали, что емкостное сопротивление для синусоидального тока находится по формуле :
(Формула для емкостного сопротивления получена путём сравнения выражений закона Ома для участка цепи постоянного тока, содержащего активное сопротивление и закона Ома для участка цепи переменного тока, содержащего конденсатор).
Таким образом, емкостное сопротивление зависит от ёмкости конденсатора и частоты переменного тока.
Емкостное сопротивление конденсатора тем меньше, чем больше его ёмкость и чем больше частота переменного тока (чем меньше период).
Чем больше ёмкость, тем больший электрический заряд накапливается на его обкладках при зарядке.
Чем больше частота переменного тока, тем за более короткое время этот заряд будет проходить по проводам, тем больший ток будет пропускать конденсатор.
Посмотрим, что происходит в цепи переменного тока, содержащей только ёмкость.
Если цепь переменного тока содержит только емкостное сопротивление
то ток и напряжение в цепи колеблются с одинаковой частотой, но ток опережает напряжение по фазе на “пи” пополам (на 90 градусов), поэтому в уравнении тока сдвиг по фазе записываем со знаком “плюс”(см. уравнение ниже).
На рисунке синусоиды тока и напряжения смещены в соответствии с записанными уравнениями для мгновенных значений напряжения и тока
Поясним, почему ток в такой цепи (содержащей источник переменного тока и конденсатор) опережает напряжение, воспользовавшись следующим рисунком
По оси ординат откладываются мгновенные значения приложенного к цепи напряжения (напряжение на зажимах источника) и мгновенные значения возникающего в цепи тока в согласии с приведёнными выше формулами для мгновенных значений тока и напряжения, когда в цепи источника переменного тока находится только конденсатор.
Конденсатор заряжается от источника, между его обкладками возникает напряжение, которое в каждый момент времени равное напряжению на клеммах источника, так как ток распространяется по цепи с огромной скоростью (скоростью света).
Когда конденсатор заряжен до максимума (напряжение на нём и напряжение источника имеют максимальные значения), ток равен нулю, а вся энергия цепи есть электрическая энергия заряженного конденсатора (точка а на рисунке).
При уменьшении напряжения источника уменьшается напряжение между обкладками конденсатора, то есть конденсатор начинает разряжаться. В цепи появляется ток, направленный навстречу напряжению источника. На рисунке он изображён как отрицательный (точки лежат ниже оси времени).
К моменту времени Т/4 конденсатор полностью разряжен (напряжение между его обкладками равно нулю), а ток в цепи достигает максимального значения (точка в). В этот момент электрическая энергия становится равной нулю, вся энергия цепи сводится к энергии магнитного поля, создаваемого током.
Затем напряжение источника изменяет знак (заряд на обкладках изменился на обратный), ток начинает ослабевать, сохраняя прежнее направление.
Когда напряжение источника (и конденсатора) достигнет максимума, вся энергия цепи снова становится электрической, а ток равным нулю (точка с).
В дальнейшем напряжение источника (и конденсатора) начинает убывать, конденсатор разряжается, ток нарастает, имея теперь положительное направление (совпадающее с напряжением между обкладками конденсатора), ток достигает максимального значения (точка d) и т. д.
Рассуждая так (сравнивая синусоиды тока и напряжения), видим, что ток раньше, чем напряжение, достигает максимума и проходит через нуль, то есть ток опережает напряжение по фазе на 90 градусов (или на”пи” пополам), или по времени на четверть периода Т/4.
Можно сказать ещё так: при замыкании цепи сначала ток приносит заряд на обкладки конденсатора, а уж потом появляется напряжение на конденсаторе, то есть ток является первичным, а напряжение вторичным, то есть ток опережает напряжение на участке цепи содержащей электрическую ёмкость.
Свойством конденсатора брать из сети ток, опережающий напряжение, широко пользуются на практике для повышения коэффициента мощности сети.
Таким образом, если электрическая цепь переменного тока состоит только из конденсатора, то роль конденсатора сводится к периодическому накоплению им электрической энергии (при зарядке) и возвращению этой энергии обратно источнику тока (при разрядке).
На следующем рисунке показано, как в цепи, содержащей только емкостное сопротивление, меняется мощность в зависимости от времени (пунктирная синусоида).
Мгновенные значения мощности находятся через произведение мгновенных значений тока и напряжения.
Из рисунка видно, что мощность цепи переменного тока, содержащая только конденсатор, изменяется с двойной частотой.
Из рисунка также видно, что в первую и третью части периода, когда напряжение между обкладками конденсатора растёт, мощность цепи с конденсатором положительна (горизонтально заштрихованная площадь). В эти части периода конденсатор получает энергию от источника тока.
Во вторую и четвёртую части периода, когда напряжение между обкладками конденсатора уменьшается, мощность цепи с конденсатором имеет отрицательный знак (вертикально заштрихованная площадь). В эти части периода конденсатор возвращает энергию источнику тока.
Средняя мощность за период цепи с конденсатором равна нулю.
Таким образом, в конденсаторе в каждый момент времени либо запасается энергия от источника (при зарядке), либо возвращается обратно источнику тока (при разрядке конденсатора).
Для электрической цепи промышленного тока факт возвращения энергии источнику тока является отрицательным. Энергия, поступающая в цепь, должна использоваться ею наиболее полно, а не возвращаться источнику.
Рассмотренную мощность называют реактивной емкостной мощностью.
Реактивной её называют потому что она не совершает никакой работы в цепи и не превращается в другие виды энергии, например в тепло (конденсатор остаётся холодным).
Напряжение на конденсаторе:
Ток в цепи, содержащей только конденсатор, равен отношению напряжения на зажимах источника к емкостному сопротивлению цепи:
Пример.
Конденсатор ёмкостью 10 мкФ включен в цепь переменного тока напряжением 120 В и частотой 50 Гц. Какой ток будет проходить через конденсатор и какую мощность будет брать этот конденсатор из сети?
Используя приведённые ниже формулы, получим ответ на поставленные вопросы.
Ответ: 0,4 А; 51 Вт.
Итак, присутствие электрической ёмкости С в цепи переменного тока приводит к сдвигу фаз между током и напряжением (колебания тока опережают колебания напряжения).
Емкостная мощность не совершает механической работы, не нагревает проводники.
Процесс прохождения переменного тока через конденсатор – это многократное повторение зарядки и разрядки конденсатора. При зарядке конденсатора источник отдаёт ему некоторое количество энергии, которая запасается в конденсаторе в виде энергии электрического поля. При разрядке конденсатор возвращает эту энергию источнику (в сеть).
Ещё можно сказать, что замкнутость цепи переменного тока, содержащей конденсатор, объясняется существованием между обкладками конденсатора тока смещения, составной частью которого является ток поляризации в диэлектрике.
О токе смещения и токе поляризации говорится в статьях: “Какое одинаковое свойство имеют изменяющееся во времени электрическое поле. Направление тока поляризации” и “Вектор электрического смещения. Замкнутость цепи переменного тока с конденсатором током смещения”
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Предыдущая запись: Характеристики переменного тока. Переменный ток в цепях, содержащих только активное сопротивление.
Следующая запись :Катушка индуктивности в цепи переменного тока. Индуктивное сопротивление.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70.
Конденсатор в цепи переменного тока
Положим
теперь, что участок цепи содержит
конденсатор емкости C,
причем сопротивлением и индуктивностью
участка можно пренебречь, и посмотрим,
по какому закону будет изменяться
напряжение на концах участка в этом
случае. Обозначим напряжение между
точками а
и b
через u
и будем
считать заряд конденсатора q
и силу тока i
положительными, если они соответствуют
рис.4.
Тогда
,
и,
следовательно,
.
Если сила тока в
цепи изменяется по закону
,
(1)
то заряд конденсатора
равен
.
Постоянная
интегрирования q0
здесь обозначает произвольный постоянный
заряд конденсатора, не связанный с
колебаниями тока, и поэтому мы положим
.
Следовательно,
.
(2)
|
Рис.4. Конденсатор |
Рис.5. Зависимости |
Сравнивая
(1) и (2), мы видим, что при синусоидальных
колебаниях тока в цепи напряжение на
конденсаторе изменяется также по закону
косинуса. Однако колебания напряжения
на конденсаторе отстают по фазе от
колебаний тока на /2.
Изменения тока и напряжения во времени
изображены графически на рис.5. Полученный
результат имеет простой физический
смысл. Напряжение на конденсаторе в
какой-либо момент времени определяется
существующим зарядом конденсатора. Но
этот заряд был образован током, протекавшим
предварительно в более ранней стадии
колебаний. Поэтому и колебания напряжения
запаздывают относительно колебаний
тока.
Формула
(2) показывает, что амплитуда напряжения
на конденсаторе равна
.
Сравнивая
это выражение с законом Ома для участка
цепи с постоянным током (),
мы видим, что величина
играет
роль сопротивления участка цепи, она
получила название емкостного сопротивления.
Емкостное сопротивление зависит от
частоты и
при высоких частотах даже малые емкости
могут представлять совсем небольшое
сопротивление для переменного тока.
Важно отметить,
что емкостное сопротивление определяет
связь между амплитудными, а не мгновенными
значениями тока и напряжения.
Мгновенная
мощность переменного тока
меняется
со временем по синусоидальному закону
с удвоенной частотой. В течение времени
от 0 до T/4
мощность
положительна, а в следующую четверть
периода ток и напряжение имеют
противоположные знаки и мощность
становится отрицательной.
Поскольку
среднее значение за период колебаний
величины
равно нулю, то средняя мощность переменного
тока на конденсаторе.
Катушка индуктивности в цепи переменного тока
Рассмотрим,
наконец, третий частный случай, когда
участок цепи содержит только индуктивность.
Обозначим по-прежнему через U
напряжение между точками а
и б
и будем считать ток I
положительным, если он направлен от а
к б
(рис.6). При наличии переменного тока в
катушке индуктивности возникнет ЭДС
самоиндукции, и поэтому мы должны
применить закон Ома для участка цепи,
содержащего эту ЭДС:
.
В
нашем случае R
= 0, а ЭДС самоиндукции
.
Поэтому
.
(3)
Если сила тока в
цепи изменяется по закону
,
то
.
(4)
|
Рис.6. Катушка
переменного |
индуктивности |
Видно,
что колебания напряжения на индуктивности
опережают по фазе колебания тока на
/2.
Когда сила тока, возрастая, проходит
через нуль, напряжение уже достигает
максимума, после чего начинает уменьшаться;
когда сила тока становится максимальной,
напряжение проходит через нуль, и т.д.
(рис.7).
Из
(4) следует, что амплитуда напряжения
равна
,
и , следовательно,
величина
играет
ту же роль, что сопротивление участка
цепи. Поэтому
называют индуктивным сопротивлением.
Индуктивное сопротивление пропорционально
частоте переменного тока, и поэтому при
очень больших частотах даже малые
индуктивности могут представлять
значительное сопротивление для переменных
токов.
Мгновенная
мощность переменного тока
также,
как и в случае идеальной емкости, меняется
со временем по синусоидальному закону
с удвоенной частотой. Очевидно, что
средняя за период мощность равна нулю.
Таким
образом, при протекании переменного
тока через идеальные емкость и
индуктивность обнаруживается ряд общих
закономерностей:
-
Колебания
тока и напряжения происходят в различных
фазах – сдвиг по фазе между этими
колебаниями равен /2. -
Амплитуда
переменного напряжения на емкости
(индуктивности) пропорциональна
амплитуде протекающего через этот
элемент переменного тока
где
X
– реактивное (емкостное или индуктивное
сопротивление). Важно иметь в виду, что
это сопротивление связывает между собой
не мгновенные значения тока и напряжения,
а только их максимальные значения.
Реактивное сопротивление отличается
от омического (резистивного) сопротивления
еще и тем, что оно зависит от частоты
переменного тока.
-
На
реактивном сопротивлении не рассеивается
мощность (в среднем за период колебаний),
это означает, что, например, через
конденсатор может протекать переменный
ток очень большой амплитуды, но
тепловыделение на конденсаторе будет
отсутствовать. Это является следствием
фазового сдвига между колебаниями тока
и напряжения на реактивных элементах
цепи (индуктивности и емкости).
Резистивный
элемент, который описывается в
рассматриваемом частотном диапазоне
законом Ома для мгновенных
токов и напряжений
,
называют омическим
или активным сопротивлением. На активных
сопротивлениях происходит выделение
мощности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #




































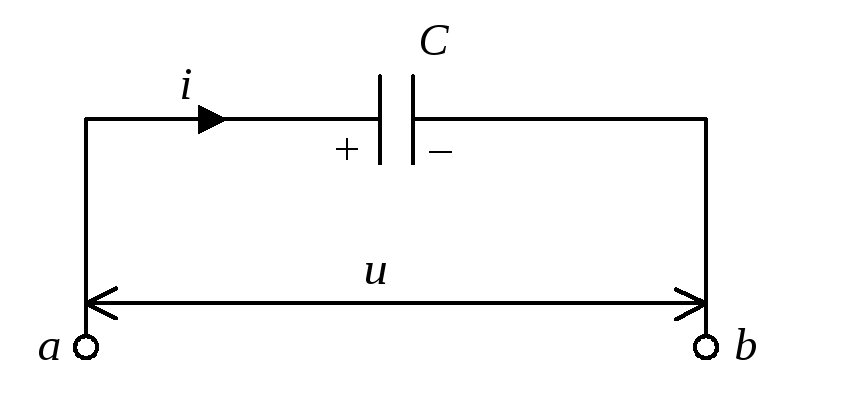
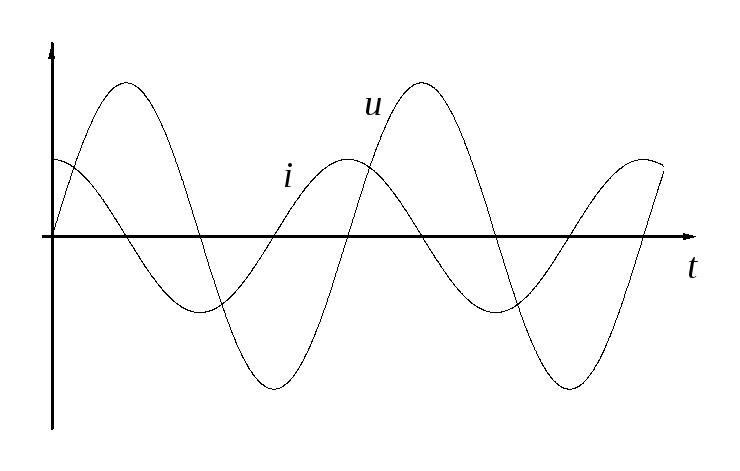
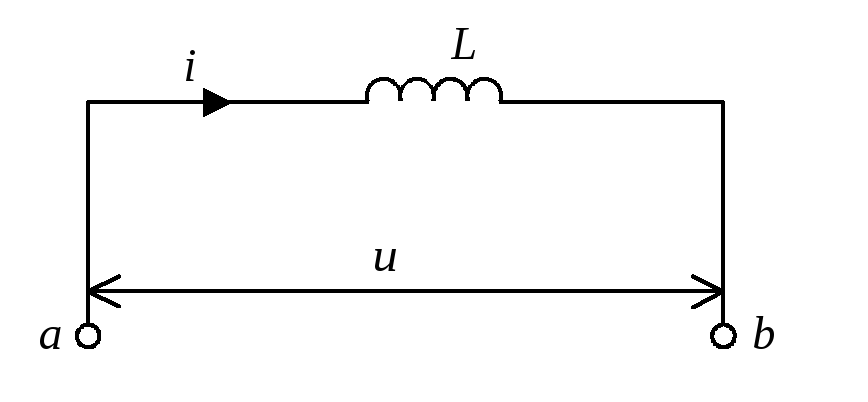
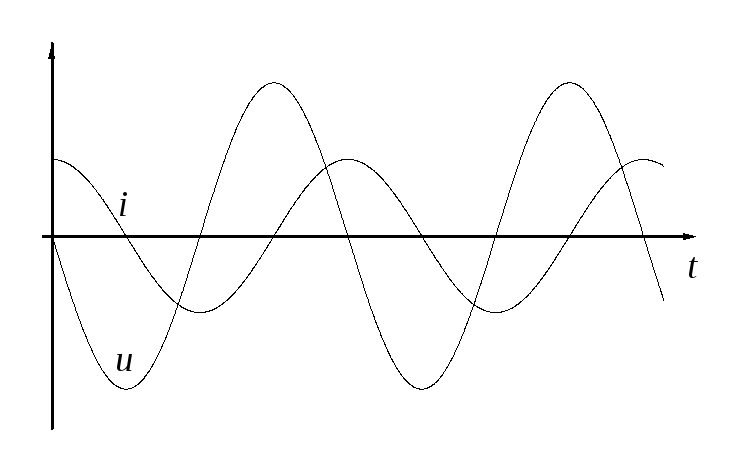 Рис.7.
Рис.7.